Effect of Upstream Side Flow of Wind Turbine on Aerodynamic Noise: Simulation Using Open-Loop Vibration in the Rod in Rod-Airfoil Configuration
Abstract
:1. Introduction
2. Material and Methods
2.1. Governing Equations
2.1.1. k-ω-SST model
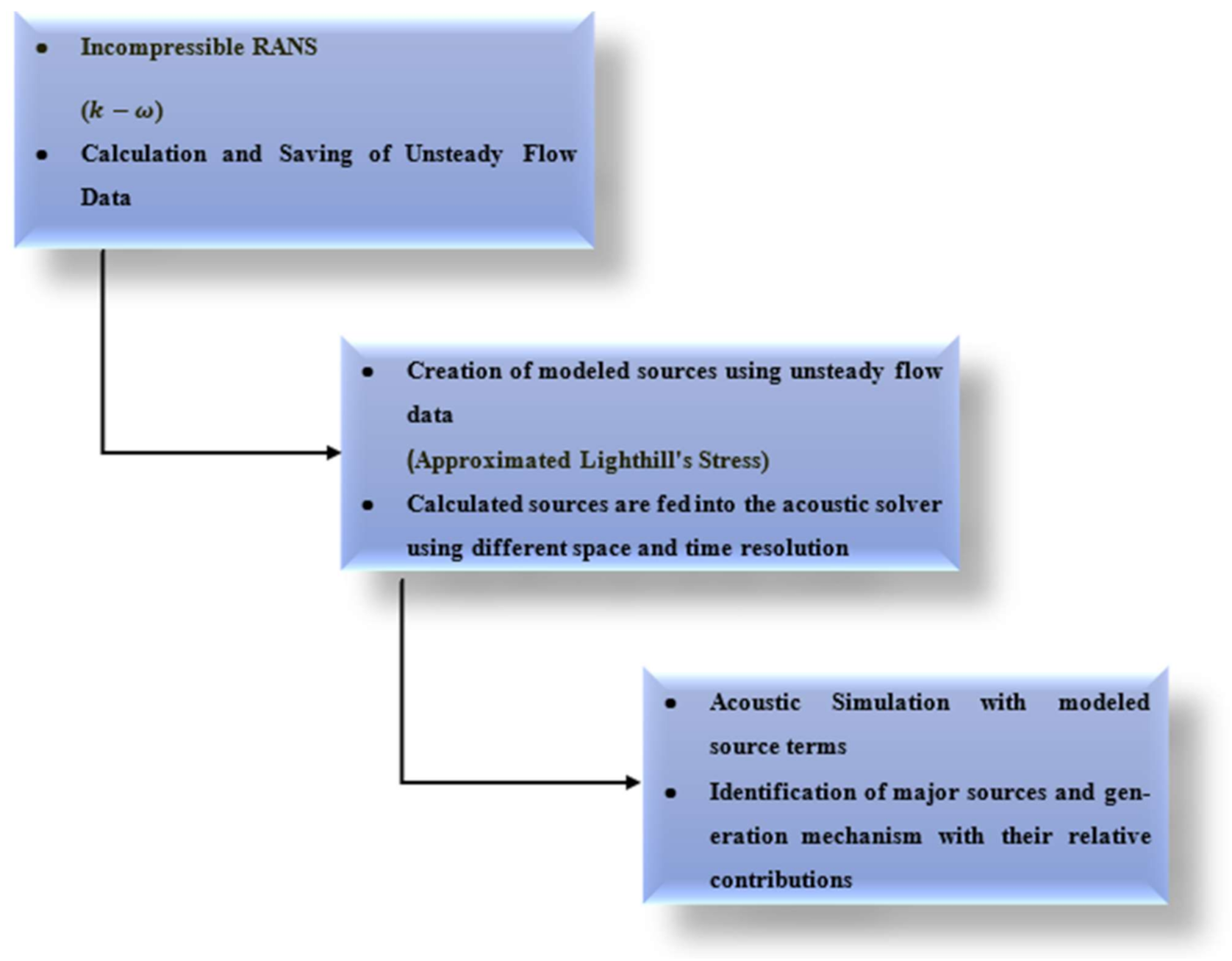
2.1.2. Acoustic Analogy
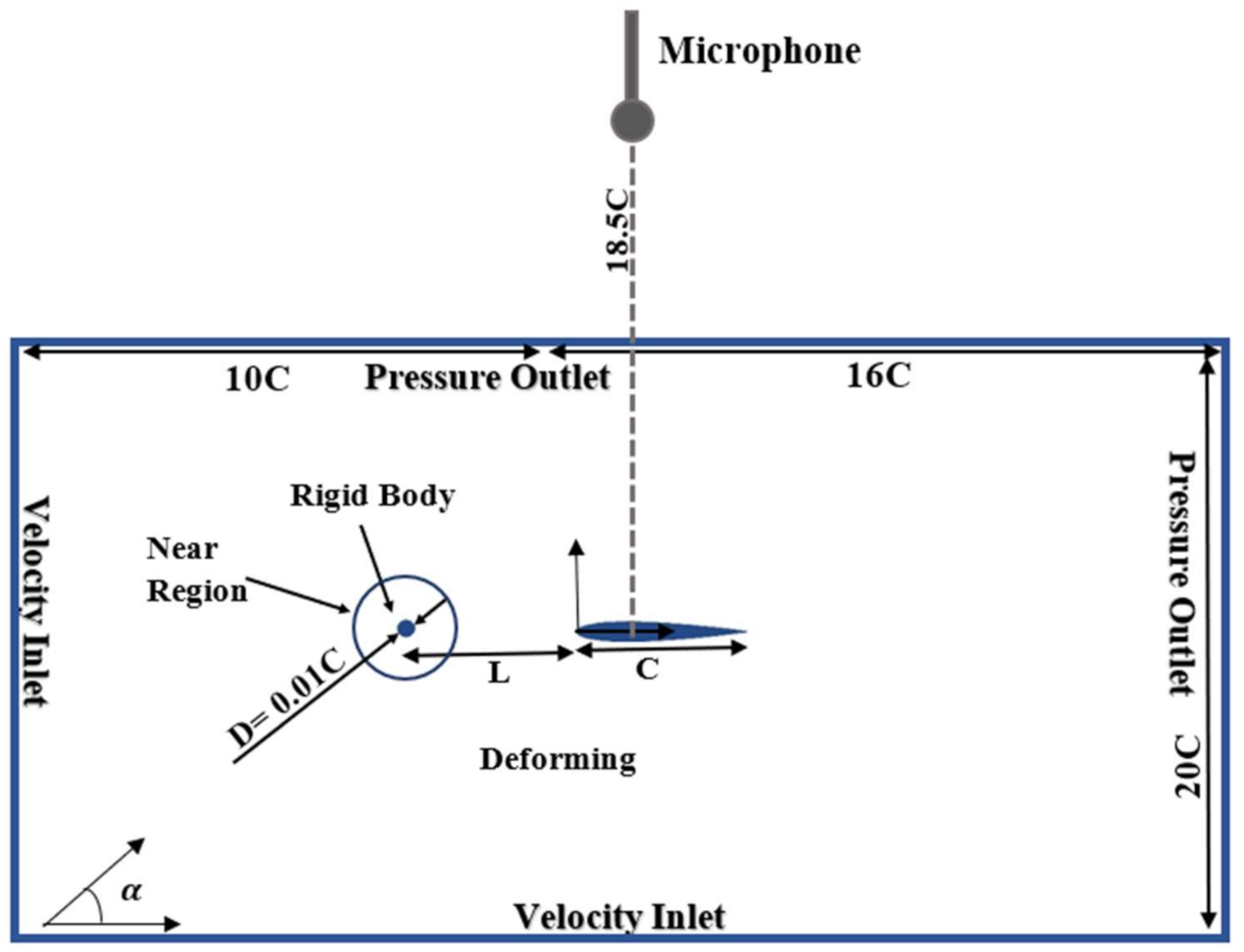
2.2. Geometric Model
2.3. Meshing Process
2.4. Solver Settings
3. Results and Discussion
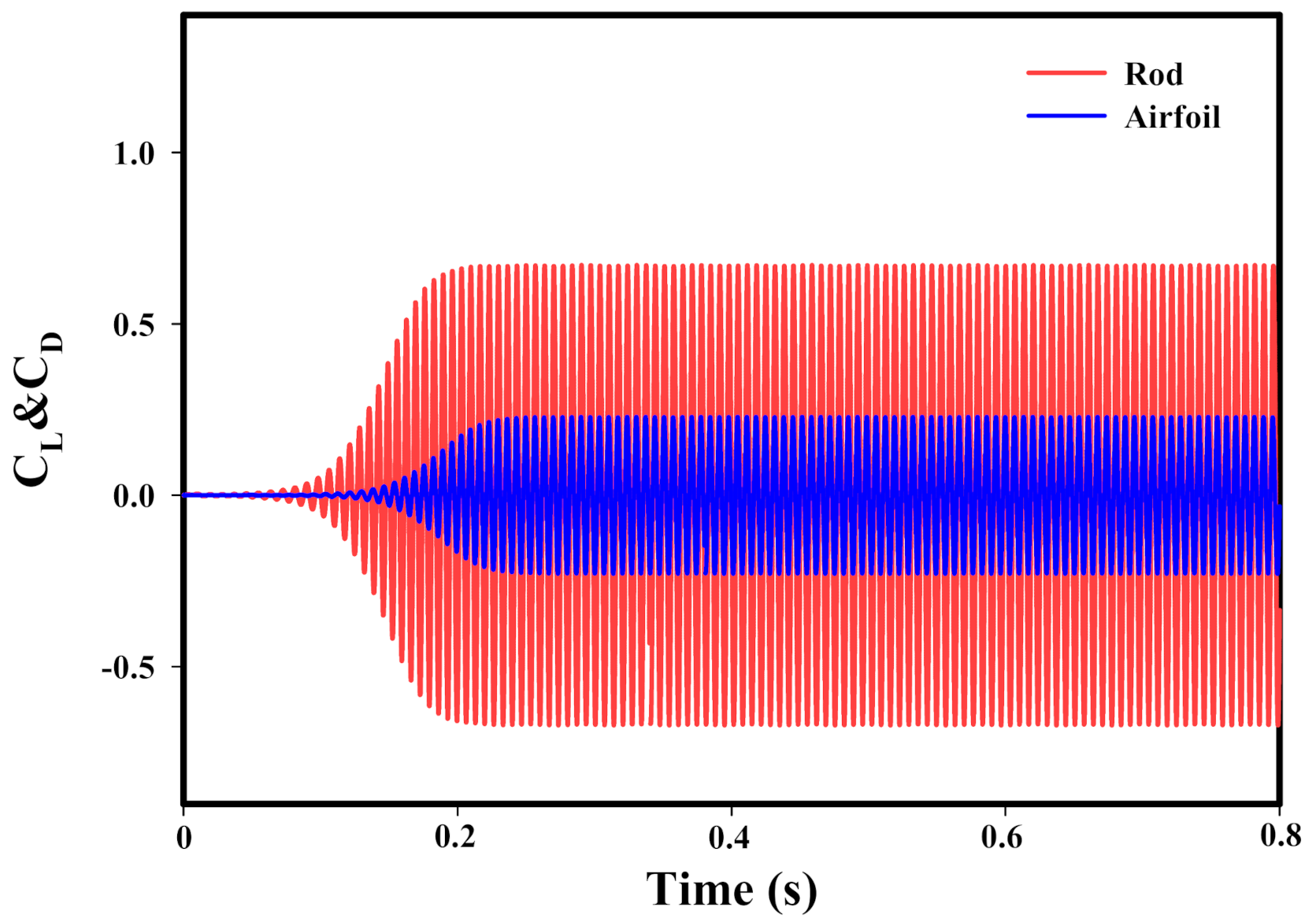
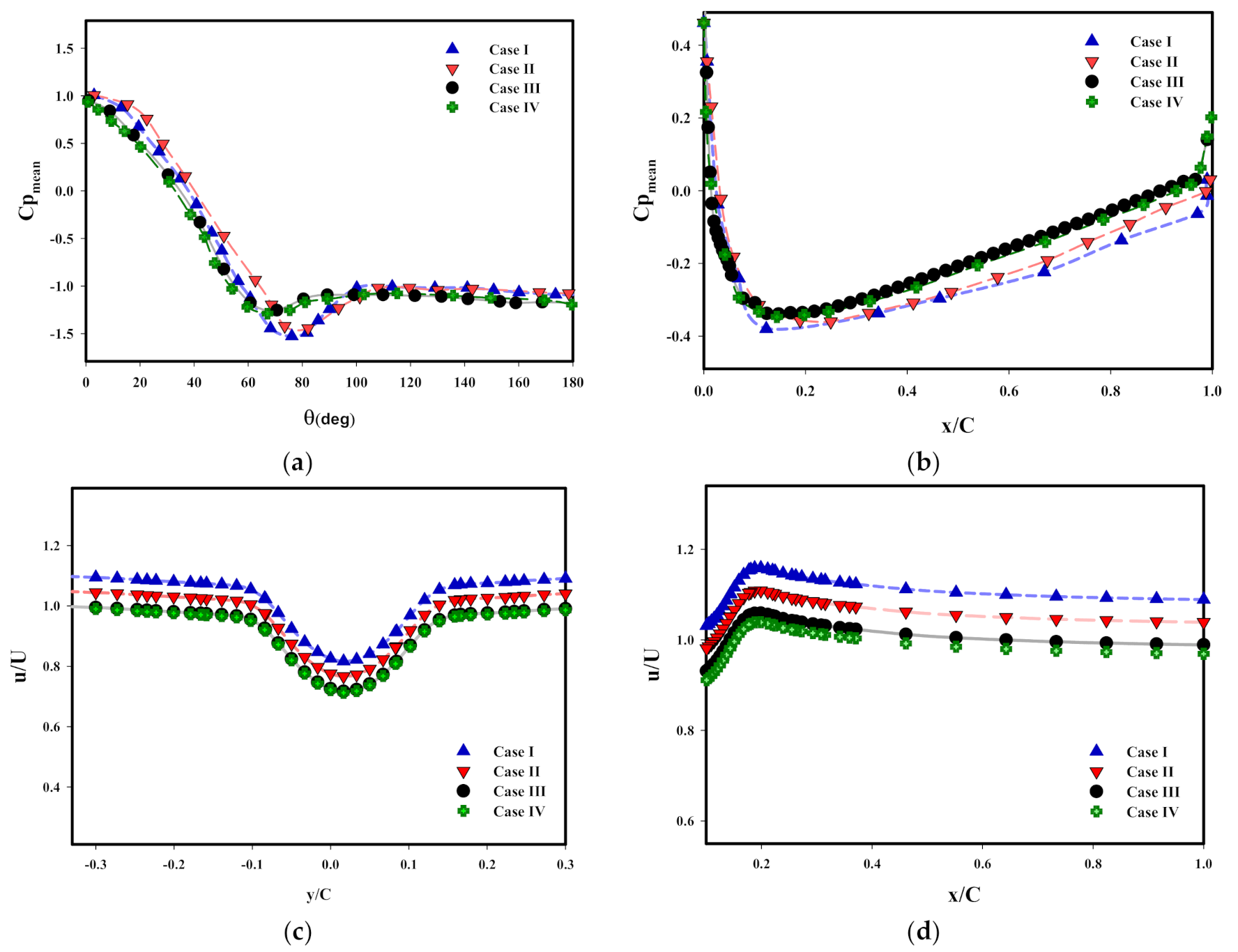
3.1. Examination of Independence from the Grid
3.2. Validation of Results
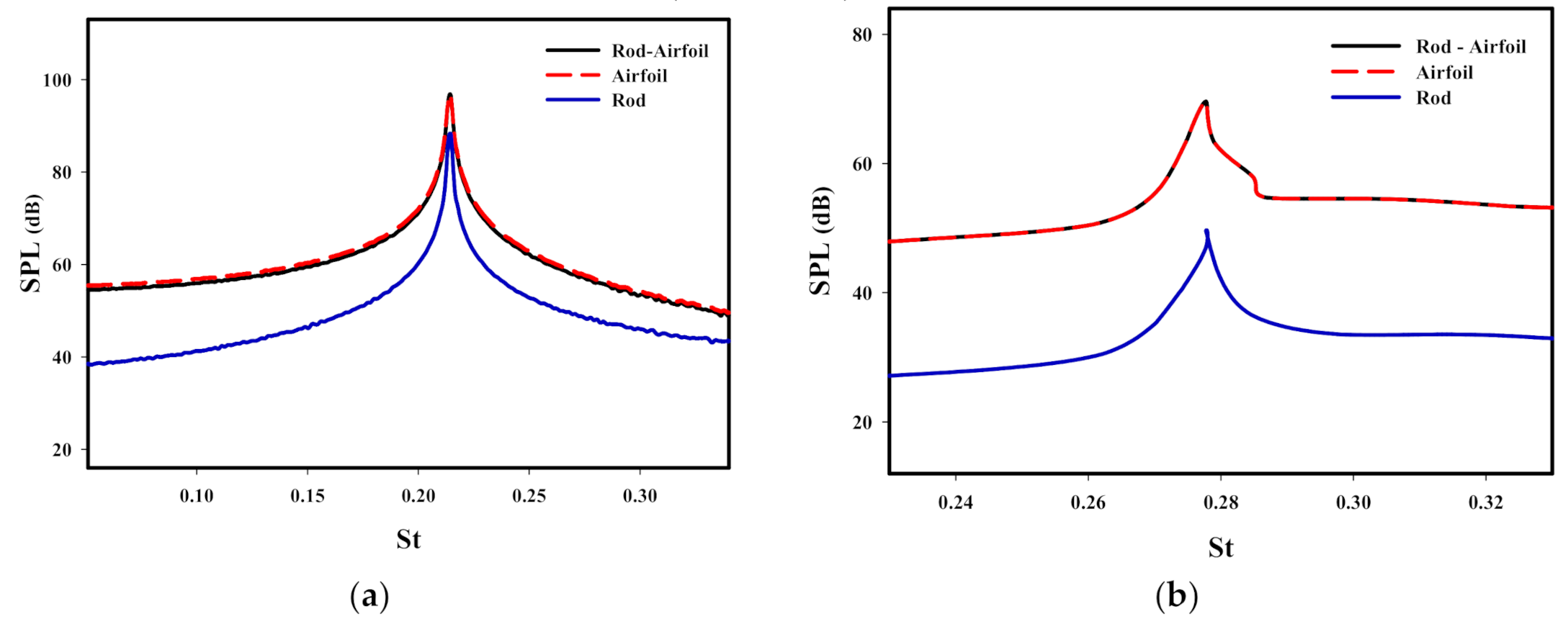
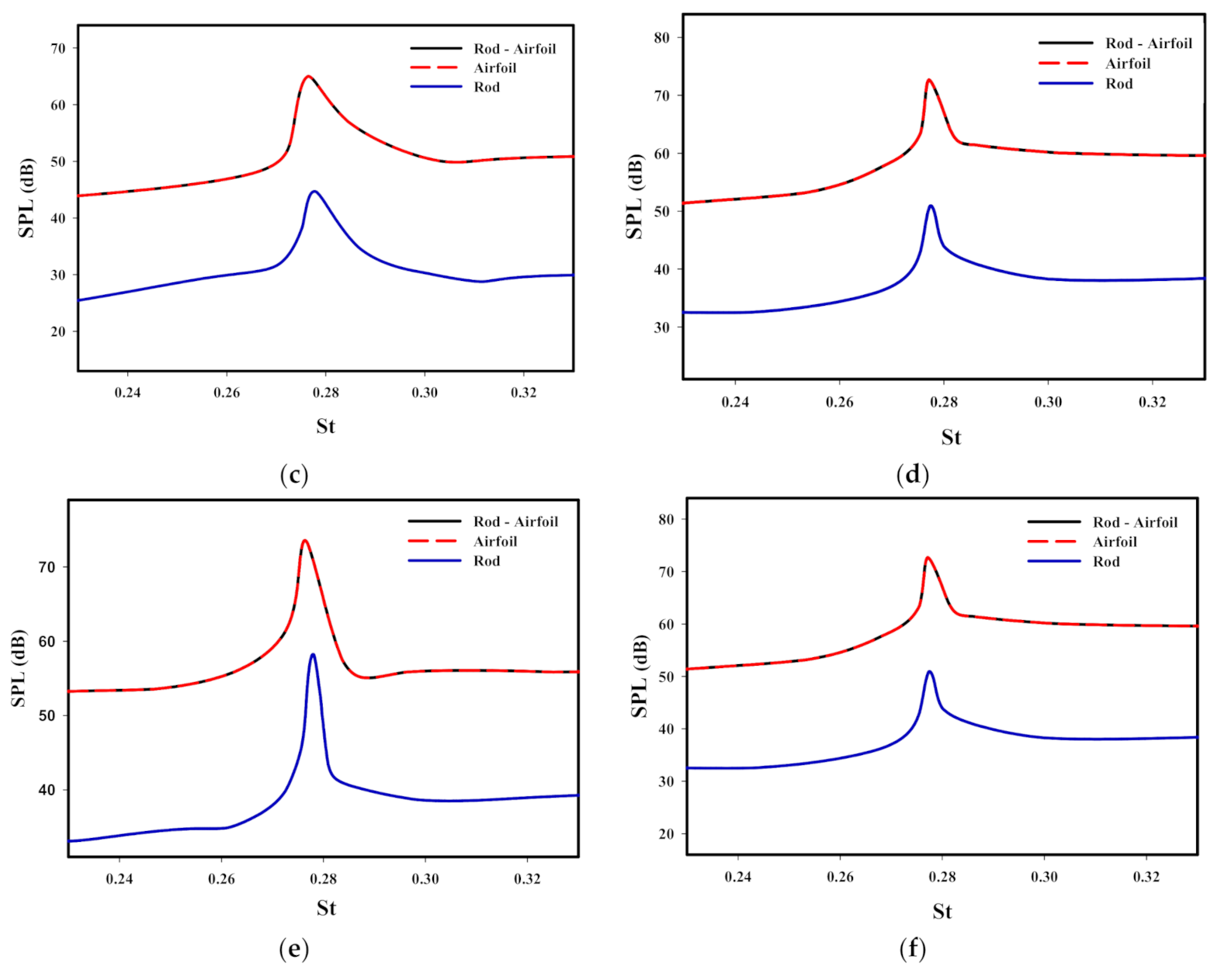
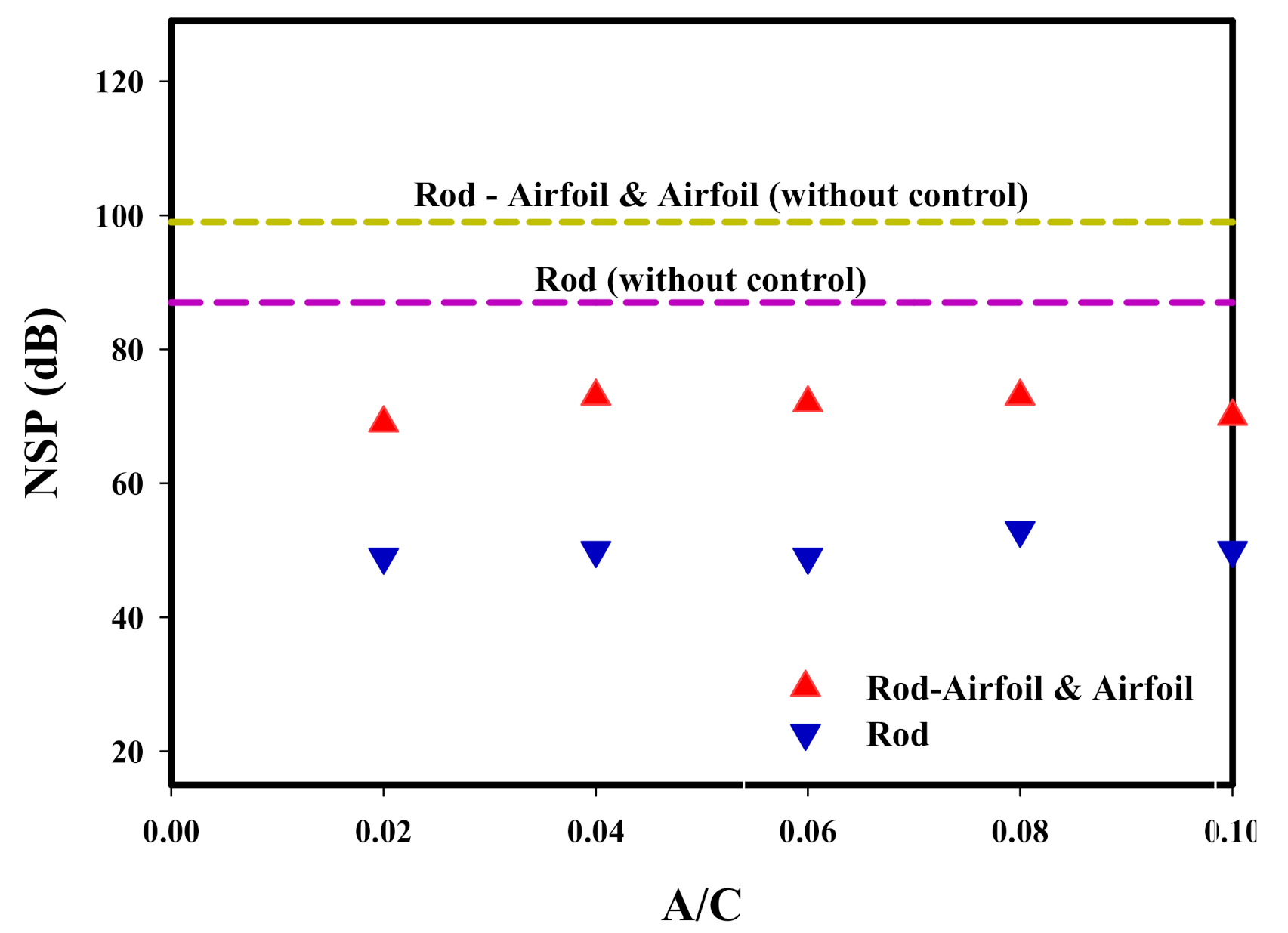
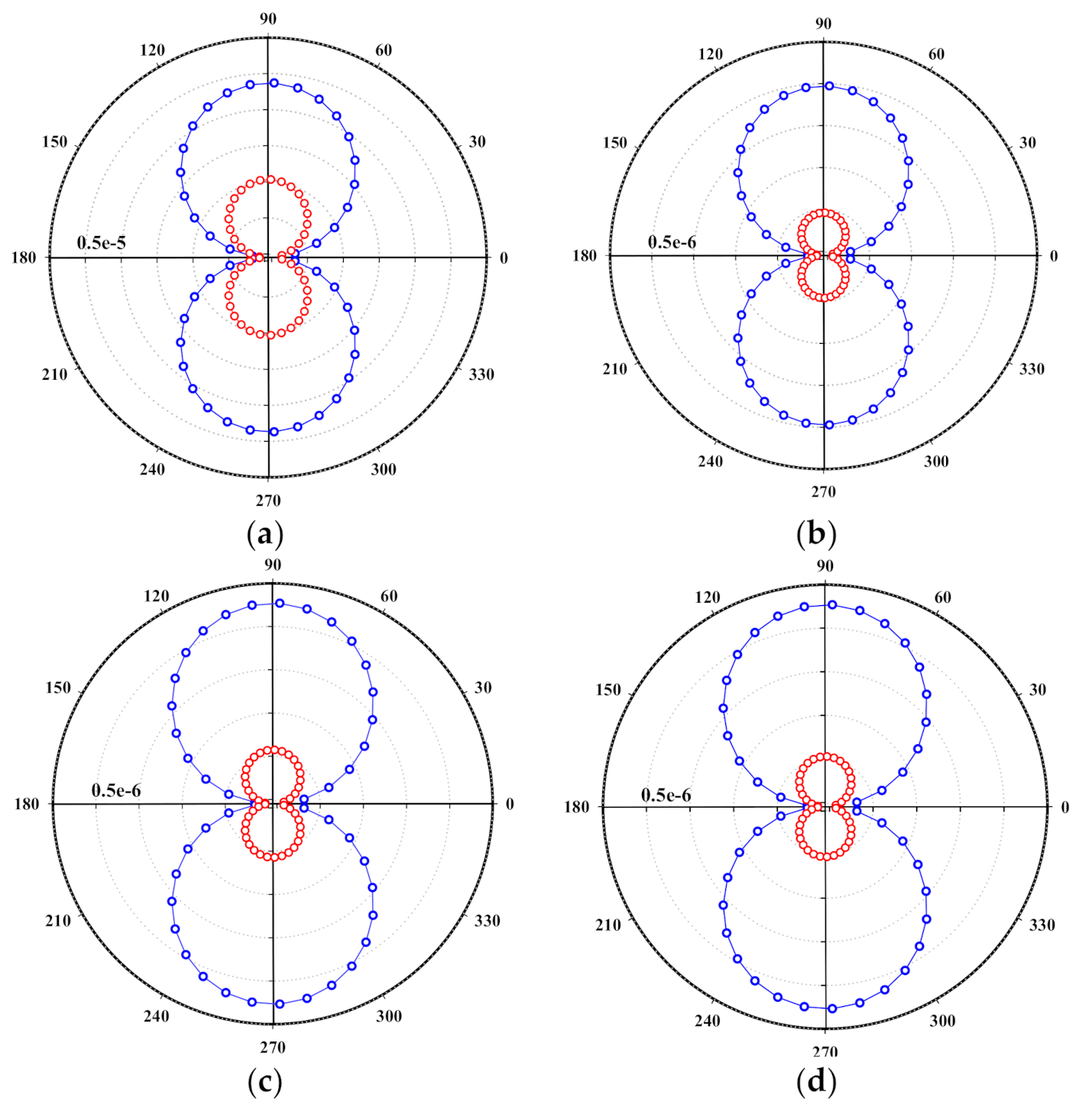
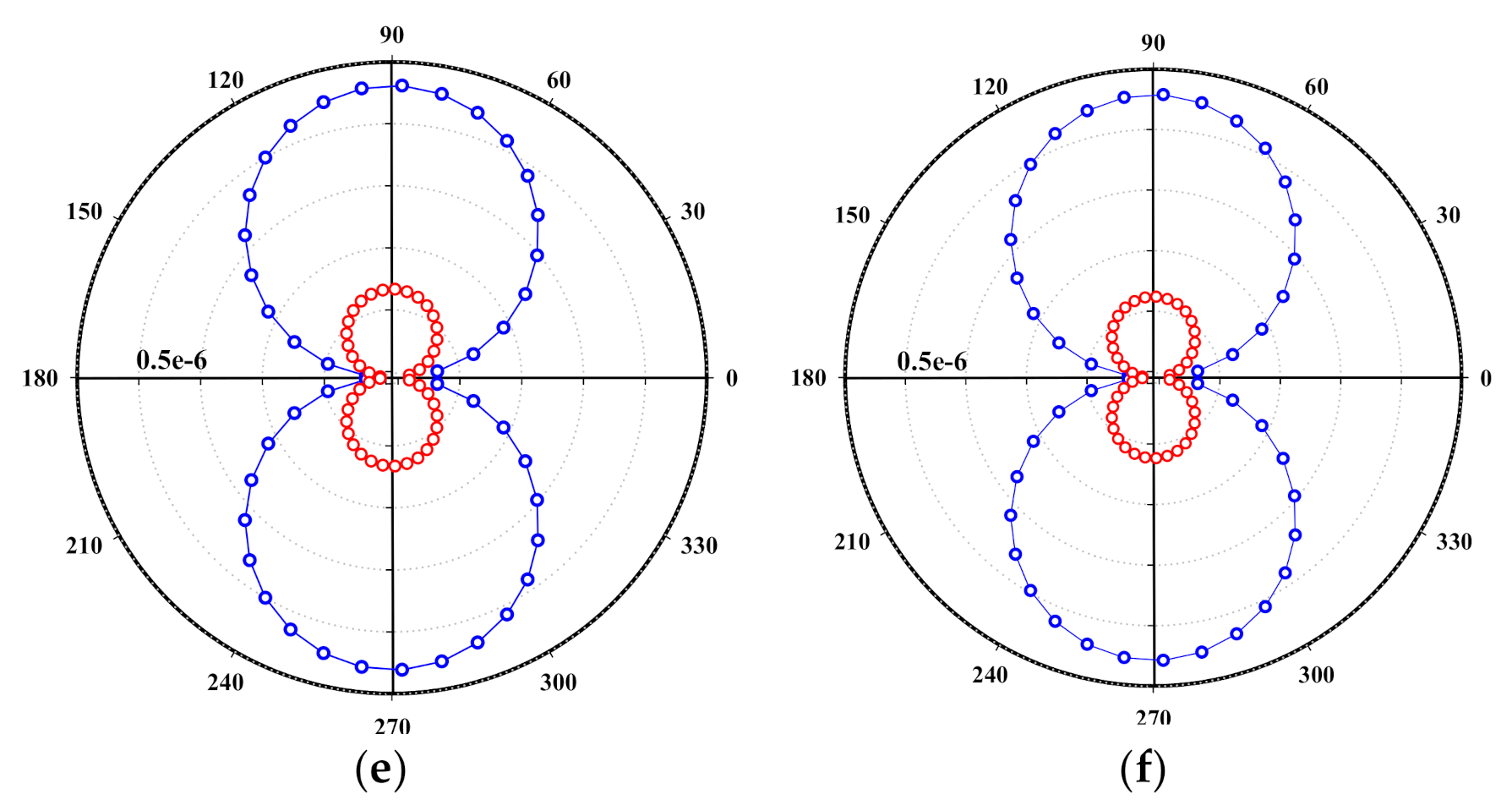
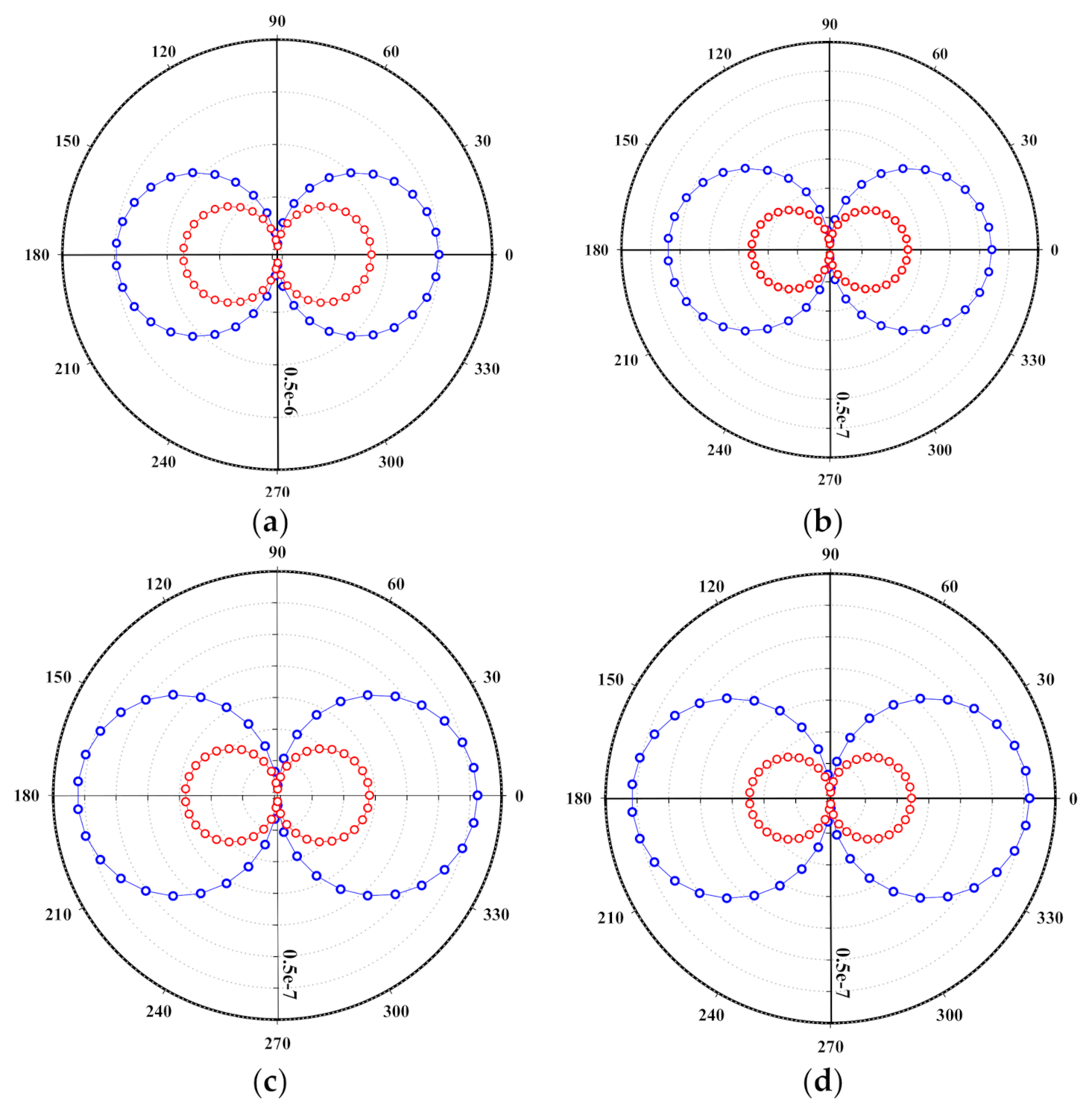
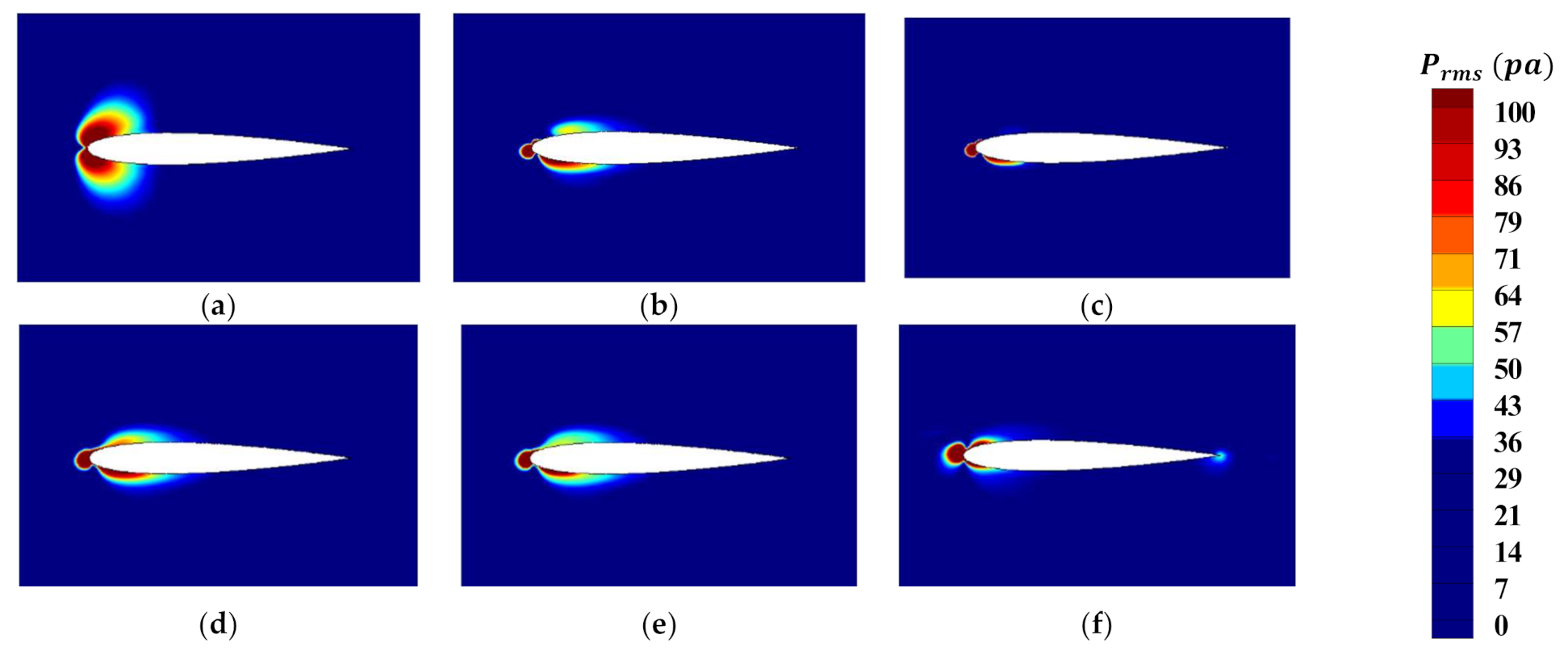
3.3. Applying Control and Study of Its Effect on Aerodynamic Noise
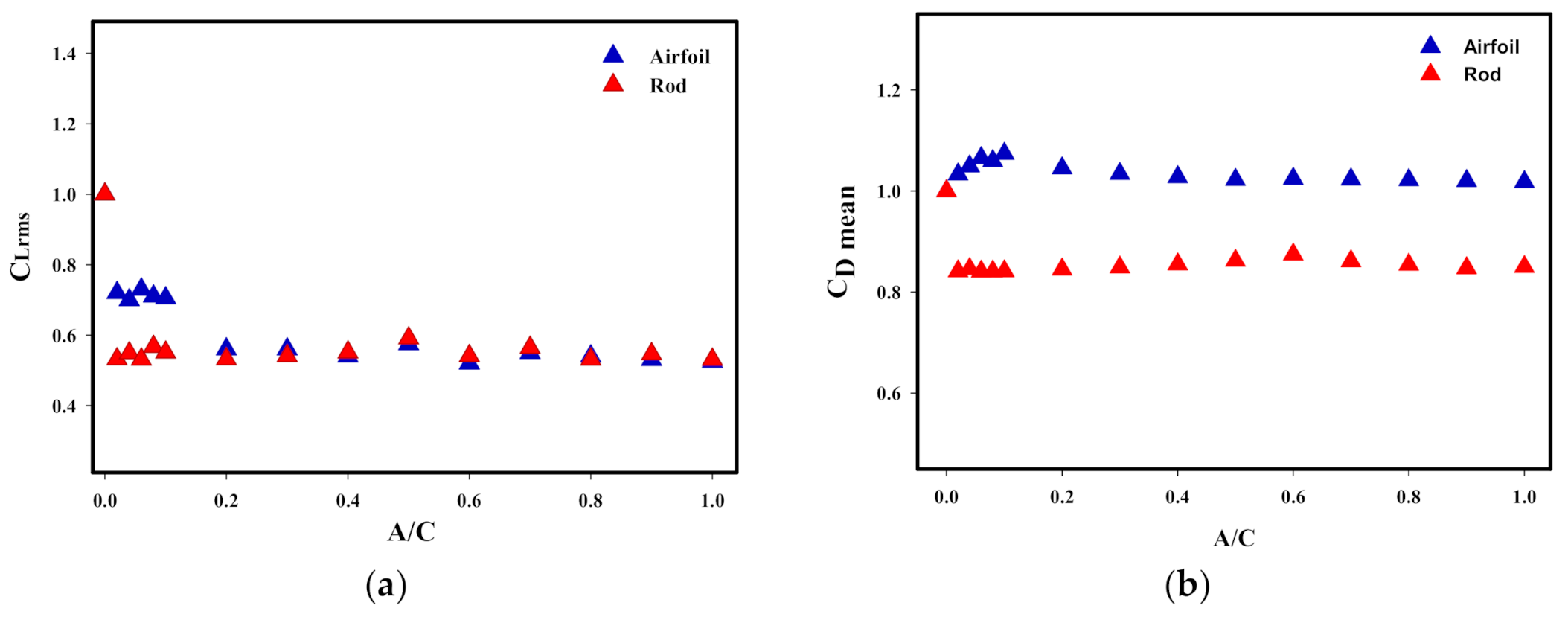
3.4. Effect of Flow Control on Aerodynamic Coefficients
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Oscillation range |
| C | Airfoil chord |
| Mean drag coefficient | |
| CFD | Computational Fluid Dynamics |
| Mean lift coefficient | |
| Root mean square of Lift coefficient | |
| Speed of sound | |
| D | Rod diameter |
| DES | Detached eddy simulation |
| DNS | Direct Numerical Simulation |
| FW-H | Ffowcs Williams-Hawkings |
| L | The distance between the rod and the airfoil |
| LES | Large Eddy Simulation |
| NSP | Noise spectrum peak |
| The compressive stress tensor | |
| Root mean square of pressure disturbances | |
| SPL | Sound pressure level |
| St | Strouhal number |
| URANS | Unsteady Reynolds Averaged Navier–Stokes |
| x, y, z | Coordinates from the leading edge |
| Kronecker delta | |
| The effective viscosity | |
| Density | |
| The viscous stress | |
| Turbulent frequency transfer |
References
- Soltani, M.; Kashkooli, F.M.; Dehghani-Sanij, A.; Kazemi, A.; Bordbar, N.; Farshchi, M.; Elmi, M.; Gharali, K.; Dusseault, M.B. A comprehensive study of geothermal heating and cooling systems. Sustain. Cities Soc. 2019, 44, 793–818. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.; Soltani, M.; Raahemifar, K. A new design of wind tower for passive ventilation in buildings to reduce energy consumption in windy regions. Renew. Sustain. Energy Rev. 2015, 42, 182–195. [Google Scholar] [CrossRef] [Green Version]
- Gharali, K.; Gharaei, E.; Soltani, M.; Raahemifar, K. Reduced frequency effects on combined oscillations, angle of attack and free stream oscillations, for a wind turbine blade element. Renew. Energy 2018, 115, 252–259. [Google Scholar] [CrossRef]
- Fredianelli, L.; Licitra, G.; Gallo, P.; Palazzuoli, D. The suitable parameters to assess noise impact of a wind farm in a complex terrain: A case-study in Tuscan hills. In Proceedings of the Euronoise Prague, Prague, Czech Republic, 10–14 June 2012. [Google Scholar]
- Barlas, E.; Zhu, W.J.; Shen, W.Z.; Dag, K.O.; Moriarty, P. Consistent modelling of wind turbine noise propagation from source to receiver. J. Acoust. Soc. Am. 2017, 142, 3297–3310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oerlemans, S.; Sijtsma, P.; López, B.M. Location and quantification of noise sources on a wind turbine. J. Sound Vib. 2007, 299, 869–883. [Google Scholar] [CrossRef]
- Botha, J.; Shahroki, A.; Rice, H. An implementation of an aeroacoustic prediction model for broadband noise from a vertical axis wind turbine using a CFD informed methodology. J. Sound Vib. 2017, 410, 389–415. [Google Scholar] [CrossRef] [Green Version]
- Maizi, M.; Mohamed, M.; Dizene, R.; Mihoubi, M. Noise reduction of a horizontal wind turbine using different blade shapes. Renew. Energy 2018, 117, 242–256. [Google Scholar] [CrossRef]
- Ghasemian, M.; Nejat, A. Aerodynamic noise prediction of a Horizontal Axis Wind Turbine using Improved Delayed Detached Eddy Simulation and acoustic analogy. Energy Convers. Manag. 2015, 99, 210–220. [Google Scholar] [CrossRef]
- Tadamasa, A.; Zangeneh, M. Numerical prediction of wind turbine noise. Renew. Energy 2011, 36, 1902–1912. [Google Scholar] [CrossRef]
- Cho, T.; Kim, C.; Lee, D. Acoustic measurement for 12% scaled model of NREL Phase VI wind turbine by using beamforming. Curr. Appl. Phys. 2010, 10, S320–S325. [Google Scholar] [CrossRef]
- Mo, J.-O.; Lee, Y.-H. Numerical simulation for prediction of aerodynamic noise characteristics on a HAWT of NREL phase VI. J. Mech. Sci. Technol. 2011, 25, 1341–1349. [Google Scholar] [CrossRef]
- Mohamed, M. Aero-acoustics noise evaluation of H-rotor Darrieus wind turbines. Energy 2014, 65, 596–604. [Google Scholar] [CrossRef]
- Mohamed, M. Reduction of the generated aero-acoustics noise of a vertical axis wind turbine using CFD (Computational Fluid Dynamics) techniques. Energy 2016, 96, 531–544. [Google Scholar] [CrossRef]
- Homicz, G.; George, A. Broadband and discrete frequency radiation from subsonic rotors. J. Sound Vib. 1974, 36, 151–177. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zhuang, M. Improvement of the aerodynamic performance of vertical axis wind turbines with leading-edge serrations and helical blades using CFD and Taguchi method. Energy Convers. Manag. 2018, 177, 107–121. [Google Scholar] [CrossRef]
- Munekata, M.; Kawahara, K.; Udo, T.; Yoshikawa, H.; Ohba, H. An experimental study on aerodynamic sound generated from wake interference of circular cylinder and airfoil vane in tandem. J. Therm. Sci. 2006, 15, 342–348. [Google Scholar] [CrossRef]
- Munekata, M.; Koshiishi, R.; Yoshikawa, H.; Ohba, H. An experimental study on aerodynamic sound generated from wake interaction of circular cylinder and airfoil with attack angle in tandem. J. Therm. Sci. 2008, 17, 212–217. [Google Scholar] [CrossRef]
- Jacob, M.C.; Boudet, J.; Casalino, D.; Michard, M. A rod-airfoil experiment as a benchmark for broadband noise modeling. Theor. Comput. Fluid Dyn. 2005, 19, 171–196. [Google Scholar] [CrossRef]
- Khokhlova, T.D.; Wang, Y.-N.; Simon, J.C.; Cunitz, B.W.; Starr, F.; Paun, M.; Crum, L.A.; Bailey, M.R.; Khokhlova, V.A. Ultrasound-guided tissue fractionation by high intensity focused ultrasound in an in vivo porcine liver model. Proc. Natl. Acad. Sci. USA 2014, 111, 8161–8166. [Google Scholar] [CrossRef] [Green Version]
- Magagnato, F.; Sorgüven, E.; Gabi, M. Far Field Noise Prediction by Large Eddy Simulation and Ffowcs Williams Hawkings Analogy. In Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head, SC, USA, 12–14 May 2003; p. 3206. [Google Scholar]
- Boudet, J.; Grosjean, N.; Jacob, M.C. Wake-Airfoil Interaction as Broadband Noise Source: A Large-Eddy Simulation Study. Int. J. Aeroacoust. 2005, 4, 93–115. [Google Scholar] [CrossRef]
- Greschner, B.; Thiele, F.; Jacob, M.C.; Casalino, D. Prediction of sound generated by a rod–airfoil configuration using EASM DES and the generalised Lighthill/FW-H analogy. Comput. Fluids 2008, 37, 402–413. [Google Scholar] [CrossRef]
- Agrawal, B.R.; Sharma, A. Aerodynamic Noise Prediction for a Rod-Airfoil Configuration using Large Eddy Simulations. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 3295. [Google Scholar]
- Giret, J.-C.; Sengissen, A.; Moreau, S.; Sanjosé, M.; Jouhaud, J.-C. Noise Source Analysis of a Rod–Airfoil Configuration Using Unstructured Large-Eddy Simulation. AIAA J. 2015, 53, 1062–1077. [Google Scholar] [CrossRef]
- Casalino, D.; Jacob, M.; Roger, M. Prediction of Rod-Airfoil Interaction Noise Using the Ffowcs-Williams-Hawkings Analogy. AIAA J. 2003, 41, 182–191. [Google Scholar] [CrossRef]
- Caraeni, M.; Dai, Y.; Caraeni, D. Acoustic Investigation of Rod Airfoil Configuration with DES and FWH. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007; p. 4106. [Google Scholar]
- Gerolymos, G.; Vallet, I. Influence of Temporal Integration and Spatial Discretization on Hybrid RSM-VLES Computations. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 4094. [Google Scholar]
- Jiang, Y.; Mao, M.-L.; Deng, X.-G.; Liu, H.-Y. Numerical investigation on body-wake flow interaction over rod-airfoil configuration. J. Fluid Mech. 2015, 779, 1. [Google Scholar] [CrossRef]
- Chen, W.; Qiao, W.; Tong, F.; Wang, L.; Wang, X. Numerical Investigation of Wavy Leading Edges on Rod–Airfoil Interaction Noise. AIAA J. 2018, 56, 2553–2567. [Google Scholar] [CrossRef]
- Siozos-Rousoulis, L.; Lacor, C.; Ghorbaniasl, G. A flow control technique for noise reduction of a rod-airfoil configuration. J. Fluids Struct. 2017, 69, 293–307. [Google Scholar] [CrossRef]
- Siozos-Rousoulis, L.; Ghorbaniasl, G.; Lacor, C. Noise control by a rotating rod in a rod-airfoil configuration. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2826. [Google Scholar]
- Abbasi, S.; Souri, M. Reducing Aerodynamic Noise in a Rod-Airfoil Using Suction and Blowing Control Method. Int. J. Appl. Mech. 2020, 12, 2050036. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Wang, X. Flow/noise control of a rod-airfoil configuration using “natural rod-base blowing”: Numerical experiments. Eur. J. Mech. Fluids 2020. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation k-w Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Kashkooli, F.M.; Soltani, M. Comprehensive study of the impacts of surrounding structures on the aero-dynamic performance and flow characteristics of an outdoor unit of split-type air conditioner. Build. Simul. 2017, 11, 325–337. [Google Scholar] [CrossRef]
- Soltani, M.; Dehghani-Sanij, A.; Sayadnia, A.; Kashkooli, F.M.; Gharali, K.; Mahbaz, S.; Dusseault, M.B. Investigation of Airflow Patterns in a New Design of Wind Tower with a Wetted Surface. Energies 2018, 11, 1100. [Google Scholar] [CrossRef] [Green Version]
- Zargar, B.; Kashkooli, F.M.; Soltani, M.; Wright, K.E.; Ijaz, M.K.; Sattar, S.A. Mathematical modeling and simulation of bacterial distribution in an aerobiology chamber using computational fluid dynamics. Am. J. Infect. Control 2016, 44, S127–S137. [Google Scholar] [CrossRef] [PubMed]
- Kashkooli, F.M.; Sefidgar, M.; Soltani, M.; Anbari, S.; Shahandashti, S.-A.; Zargar, B. Numerical Assessment of an Air Cleaner Device under Different Working Conditions in an Indoor Environment. Sustainability 2021, 13, 369. [Google Scholar] [CrossRef]
- Mohamed, M.; Ali, A.; Hafiz, A.A. CFD analysis for H-rotor Darrieus turbine as a low speed wind energy converter. Eng. Sci. Technol. Int. J. 2015, 18, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zarei, A.; Ashouri, A.; Hashemi, S.; Bushehri, S.F.; Izadpanah, E.; Amini, Y. Experimental and numerical study of hydrodynamic performance of remotely operated vehicle. Ocean Eng. 2020, 212, 107612. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Abbasi, S.; Souri, M. On the passive control of aeroacoustics noise behind a square cylinder. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–16. [Google Scholar] [CrossRef]
- Samion, S.R.L.; Ali, M.S.M.; Abu, A.; Doolan, C.J.; Porteous, R.Z.-Y. Aerodynamic sound from a square cylinder with a downstream wedge. Aerosp. Sci. Technol. 2016, 53, 85–94. [Google Scholar] [CrossRef]
- Abdilghanie, A.M.; Collins, L.R.; Caughey, D.A. Comparison of Turbulence Modeling Strategies for Indoor Flows. J. Fluids Eng. 2009, 131, 051402. [Google Scholar] [CrossRef]
- Arnold, B.; Lutz, T.; Kramer, E. Design of a boundary-layer suction system for turbulent trailing-edge noise reduction of wind turbines. Renew. Energy 2018, 123, 249–262. [Google Scholar] [CrossRef]
- Chong, W.-T.; Muzammil, W.K.; Wong, K.-H.; Wang, C.-T.; Gwani, M.; Chu, Y.-J.; Poh, S.-C. Cross axis wind turbine: Pushing the limit of wind turbine technology with complementary design. Appl. Energy 2017, 207, 78–95. [Google Scholar] [CrossRef]
- Rocha, P.C.; Rocha, H.B.; Carneiro, F.M.; da Silva, M.V.; Bueno, A.V. k–ω SST (shear stress transport) turbulence model calibration: A case study on a small scale horizontal axis wind turbine. Energy 2014, 65, 412–418. [Google Scholar] [CrossRef]
- Zhang, J.; Chu, W.; Zhang, H.; Wu, Y.; Dong, X. Numerical and experimental investigations of the unsteady aerodynamics and aero-acoustics characteristics of a backward curved blade centrifugal fan. Appl. Acoust. 2016, 110, 256–267. [Google Scholar] [CrossRef]
- Liu, H.; Azarpeyvand, M.; Wei, J.; Qu, Z. Tandem cylinder aerodynamic sound control using porous coating. J. Sound Vib. 2015, 334, 190–201. [Google Scholar] [CrossRef] [Green Version]
- Cheong, C.; Joseph, P.; Park, Y.; Lee, S. Computation of aeolian tone from a circular cylinder using source models. Appl. Acoust. 2008, 69, 110–126. [Google Scholar] [CrossRef]
- Rasuo, B. Scaling between Wind Tunnels—Results Accuracy in Two-Dimensional Testing. Trans. Jpn. Soc. Aeronaut. Space Sci. 2012, 55, 109–115. [Google Scholar] [CrossRef] [Green Version]
- Rasuo, B. The influence of Reynolds and Mach numbers on two-dimensional wind-tunnel testing: An experience. Aeronaut. J. 2011, 115, 249–254. [Google Scholar] [CrossRef]
- Jazarević, V.; Rašuo, B. Numerical prediction of aerodynamic noise generated from missile for low Mach number flows. Teh. Vjesn. Tech. Gaz. 2017, 24, 663–670. [Google Scholar] [CrossRef] [Green Version]
- Jazarević, V.; Rašuo, B. Numerical Calculation of Aerodynamic Noise Generated from an Aircraft in Low Mach Number Flight; Springer: Cham, Switzerland, 2017; pp. 113–127. [Google Scholar] [CrossRef]
- Sun, Y.; Fattah, R.J.; Zhang, X. Airfoil Leading Edge Noise Predictions Using a Viscous Mean Flow. In Proceedings of the 24th International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
- Chauhan, M.K.; Dutta, S.; More, B.S.; Gandhi, B.K. Experimental investigation of flow over a square cylinder with an attached splitter plate at intermediate reynolds number. J. Fluids Struct. 2018, 76, 319–335. [Google Scholar] [CrossRef]









| (I) | Transient term | Accumulation of k (rate of change of k) |
| (II) | Convective transport | Transport of k by convection |
| (III) | Diffusive transport | Turbulent diffusion transport of k |
| (IV) | Production term | Rate of production of k |
| (V) | Dissipation | Rate of dissipation of k |
| Case | ||
|---|---|---|
| - | Rod | Airfoil |
| Coarse mesh | 29.787 | 38.475 |
| Medium-sized mesh | 12.474 | 14.35 |
| Fine mesh | 3.212 | 3.894 |
| Rousoulis et al. [29] | ||
| Case | Elements | Number of Cells | Body | SPL | St |
|---|---|---|---|---|---|
| I (Coarse mesh) | Quadrangular | 4800 | Rod | 32 | |
| Airfoil | 40 | 0.361 | |||
| Triangular | 36,000 | ||||
| Rod-Airfoil | 40 | ||||
| II (Medium-sized mesh) | Quadrangular | 9300 | Rod | 64 | |
| Airfoil | 70 | 0.274 | |||
| Triangular | 69,000 | ||||
| Rod-Airfoil | 72 | ||||
| III (Fine mesh) | Quadrangular | 14,000 | Rod | 88 | |
| Airfoil | 99 | 0.2120 | |||
| Triangular | 95,000 | ||||
| Rod-Airfoil | 99 | ||||
| IV | Quadrangular | 20,000 | Rod | 89 | |
| Airfoil | 100 | 0.2118 | |||
| Triangular | 125,000 | ||||
| Rod-Airfoil | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souri, M.; Moradi Kashkooli, F.; Soltani, M.; Raahemifar, K. Effect of Upstream Side Flow of Wind Turbine on Aerodynamic Noise: Simulation Using Open-Loop Vibration in the Rod in Rod-Airfoil Configuration. Energies 2021, 14, 1170. https://doi.org/10.3390/en14041170
Souri M, Moradi Kashkooli F, Soltani M, Raahemifar K. Effect of Upstream Side Flow of Wind Turbine on Aerodynamic Noise: Simulation Using Open-Loop Vibration in the Rod in Rod-Airfoil Configuration. Energies. 2021; 14(4):1170. https://doi.org/10.3390/en14041170
Chicago/Turabian StyleSouri, Mohammad, Farshad Moradi Kashkooli, Madjid Soltani, and Kaamran Raahemifar. 2021. "Effect of Upstream Side Flow of Wind Turbine on Aerodynamic Noise: Simulation Using Open-Loop Vibration in the Rod in Rod-Airfoil Configuration" Energies 14, no. 4: 1170. https://doi.org/10.3390/en14041170
APA StyleSouri, M., Moradi Kashkooli, F., Soltani, M., & Raahemifar, K. (2021). Effect of Upstream Side Flow of Wind Turbine on Aerodynamic Noise: Simulation Using Open-Loop Vibration in the Rod in Rod-Airfoil Configuration. Energies, 14(4), 1170. https://doi.org/10.3390/en14041170








