A Novel Canopy Drag Coefficient Model for Analyzing Urban Wind Environments Based on the Large Eddy Simulation
Abstract
:1. Introduction
2. Numerical Model and Methodology
2.1. Introduction of the Drag Model
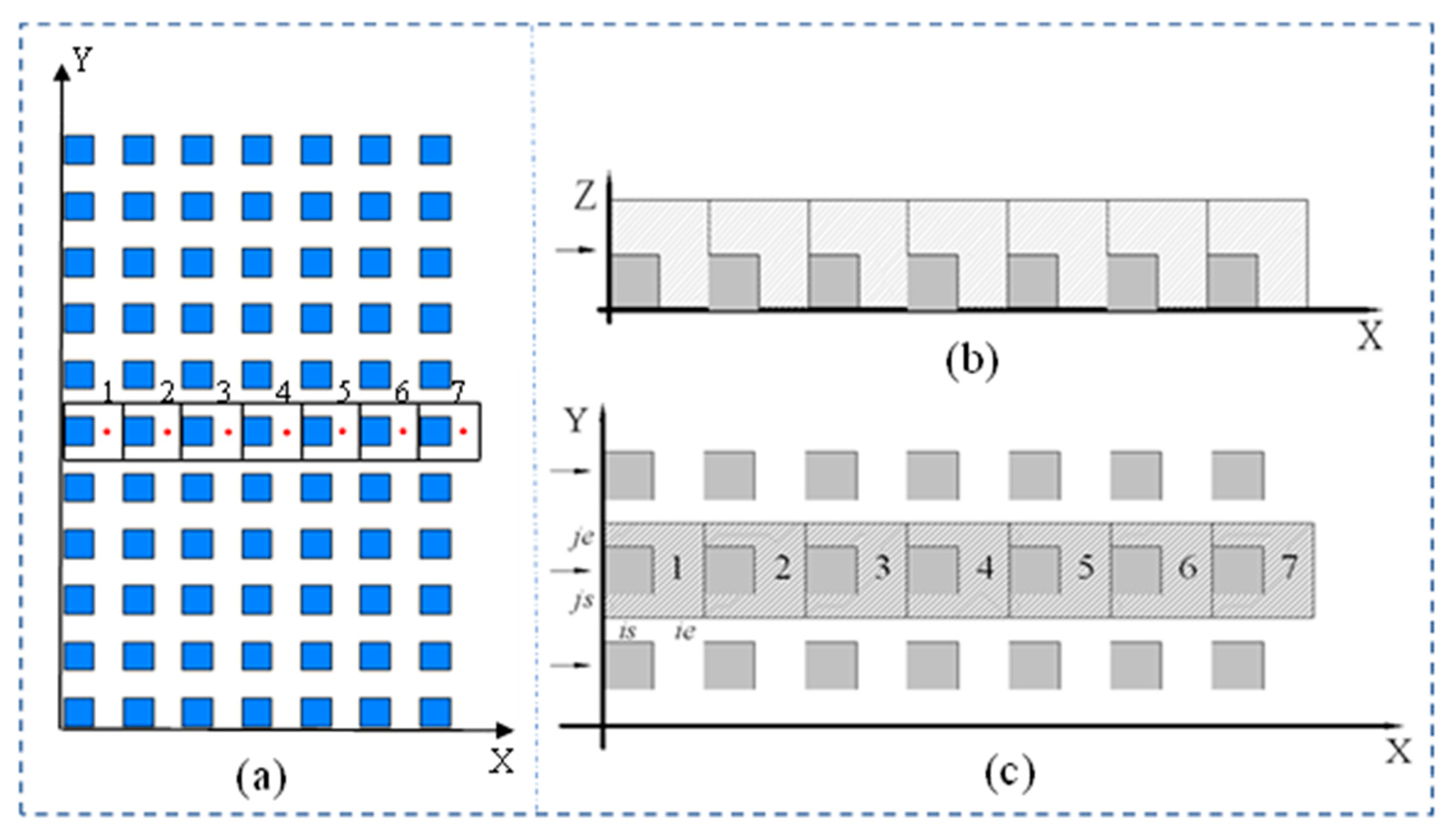
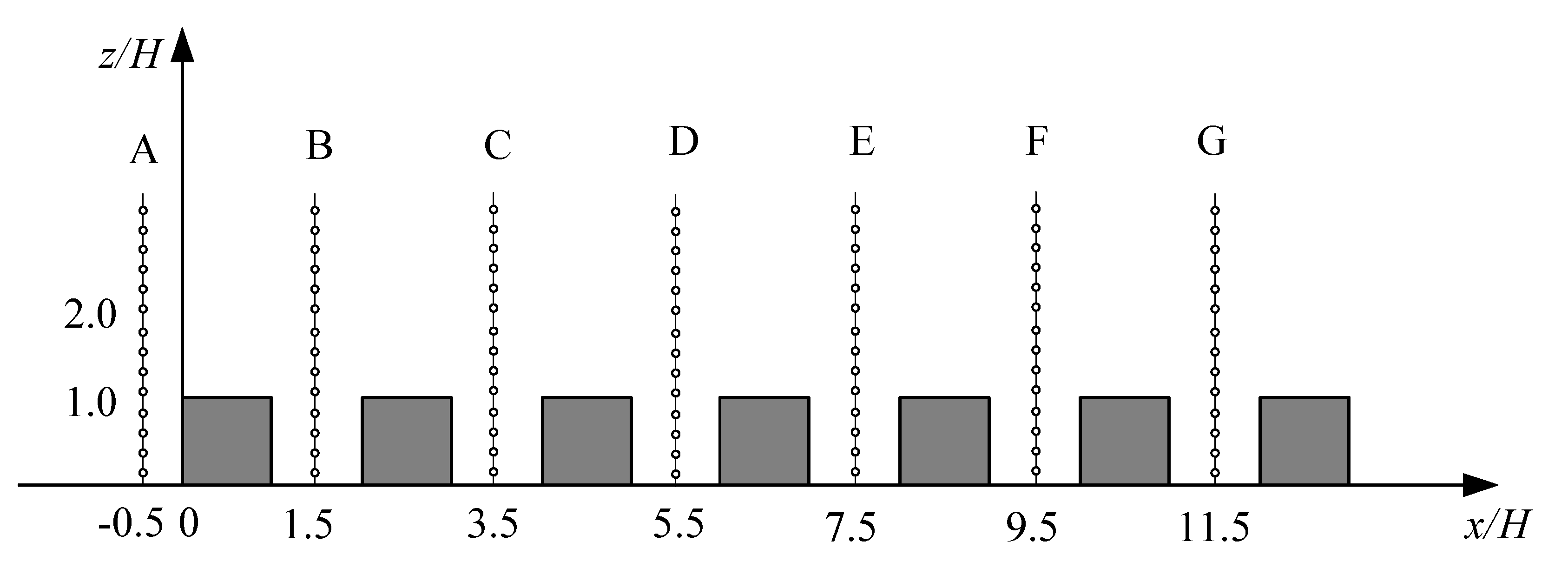
2.2. Set-Up of the Computational Model for Wind Tunnel Validation
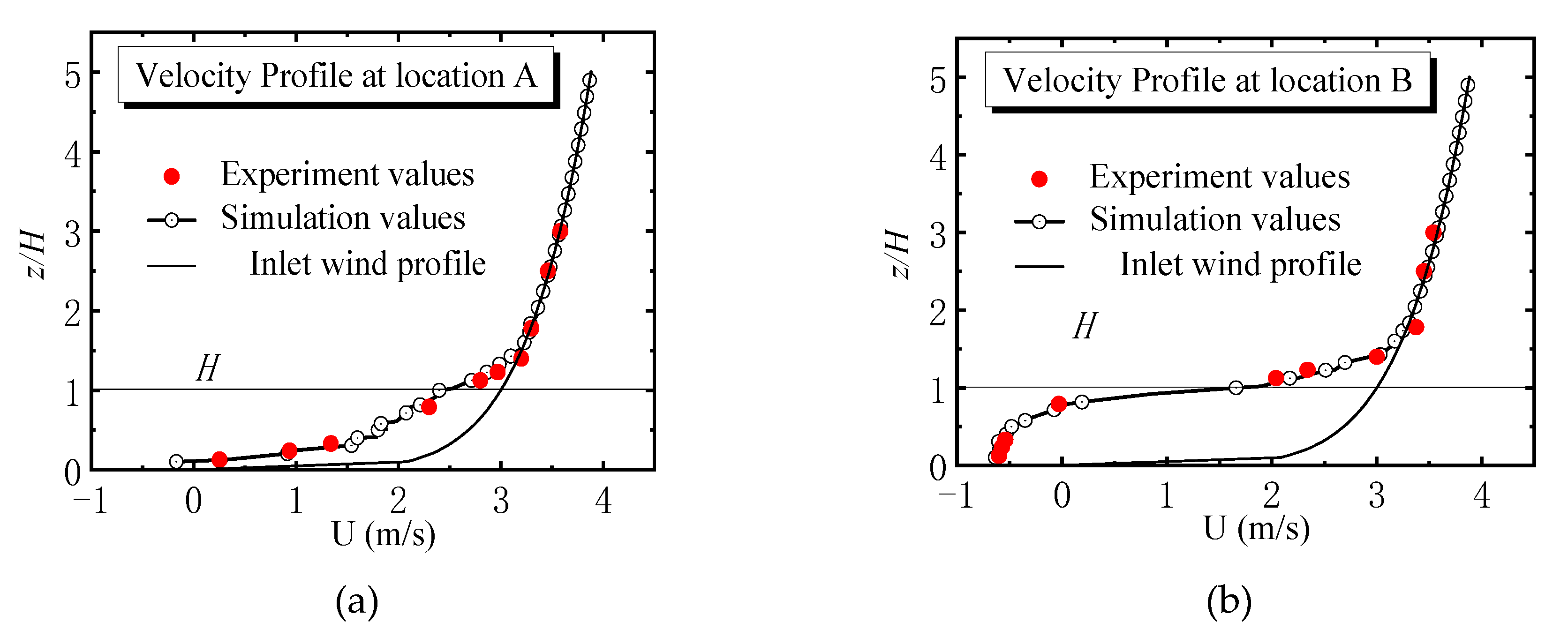
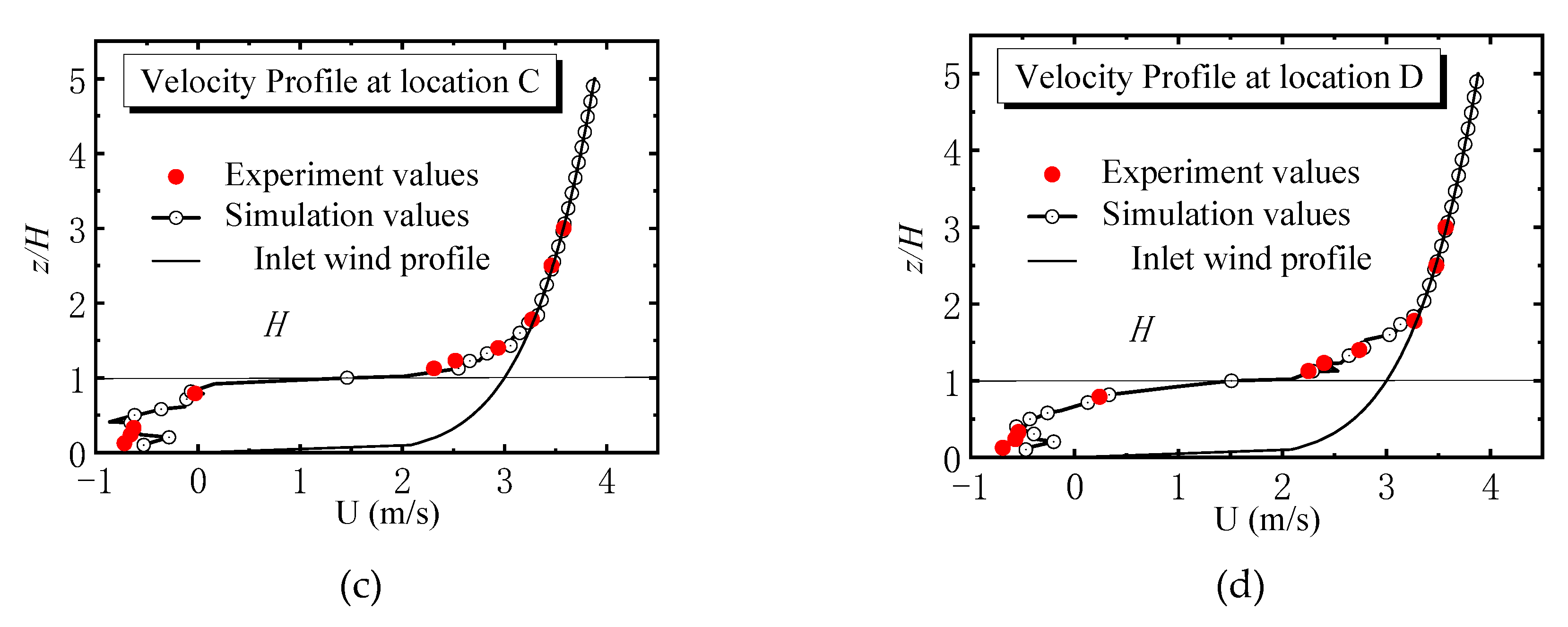
2.3. Results and Validation of the Simulated Wind Field
- (1)
- Mean wind velocity (U)
- (2)
- Turbulent kinetic energy (TKE)
- (3)
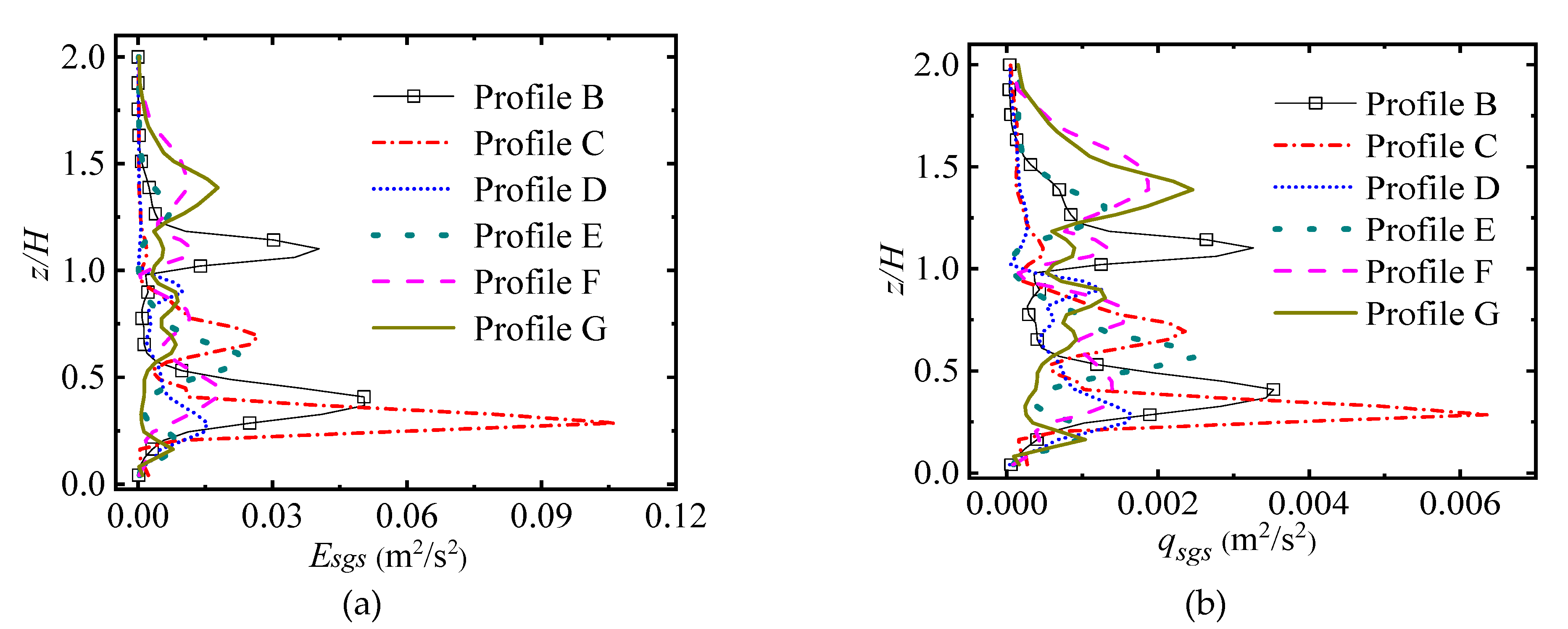
- SGS TKE and SGS dissipation
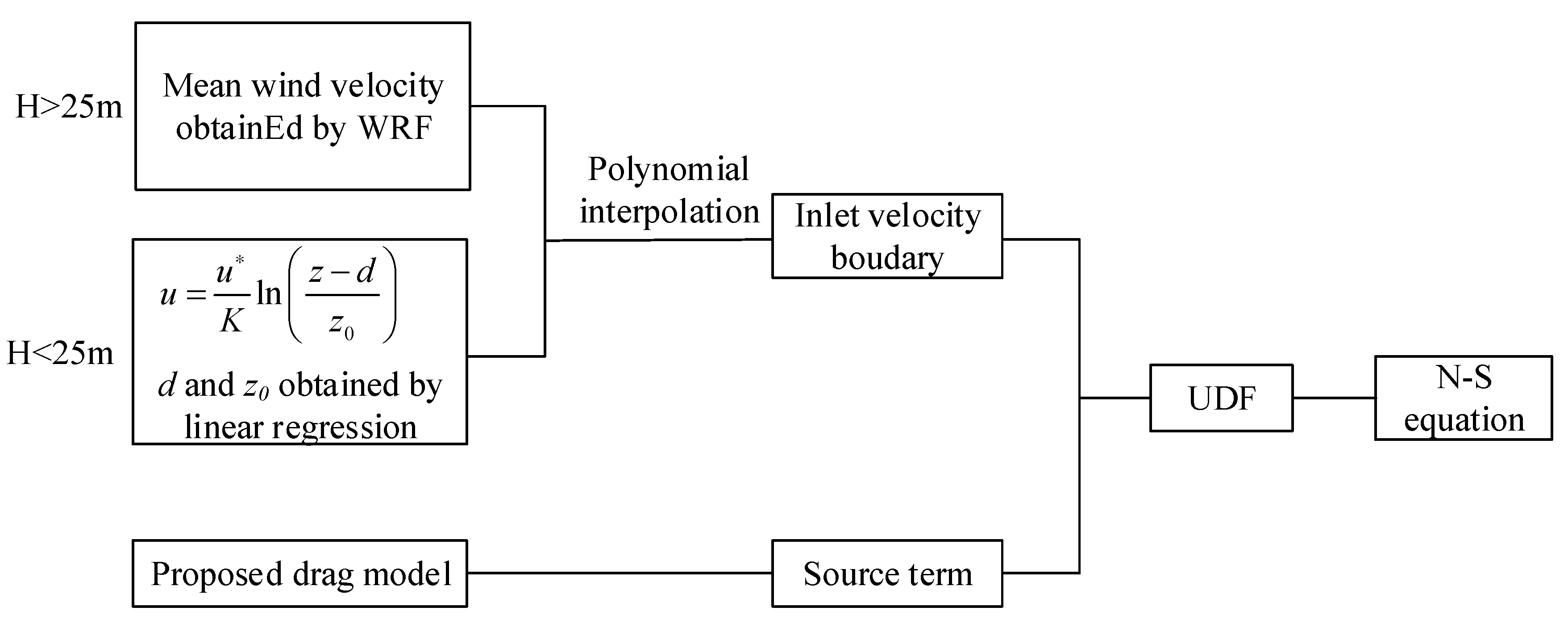
2.4. Proposed Modified Drag Model Procedure
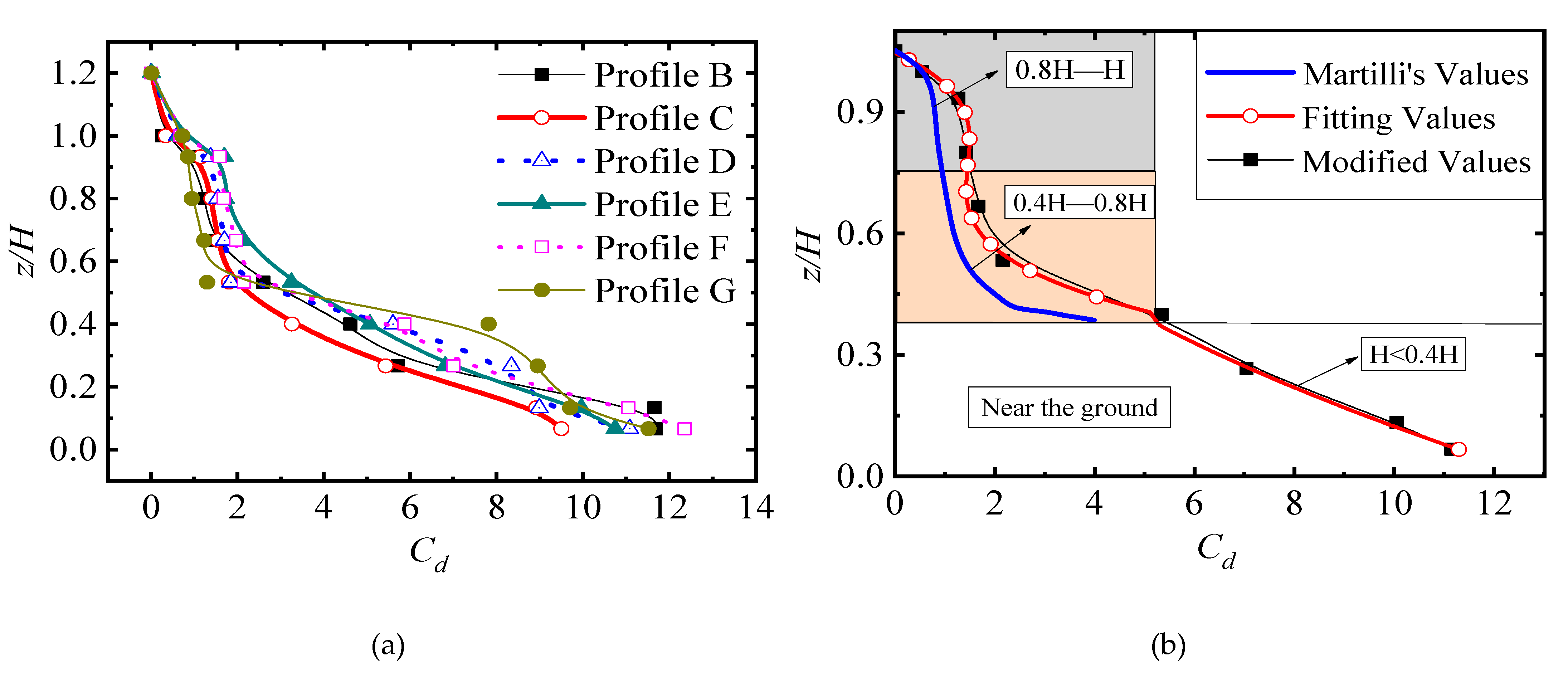
2.5. Validation of the Variation in the Drag Coefficient with Height
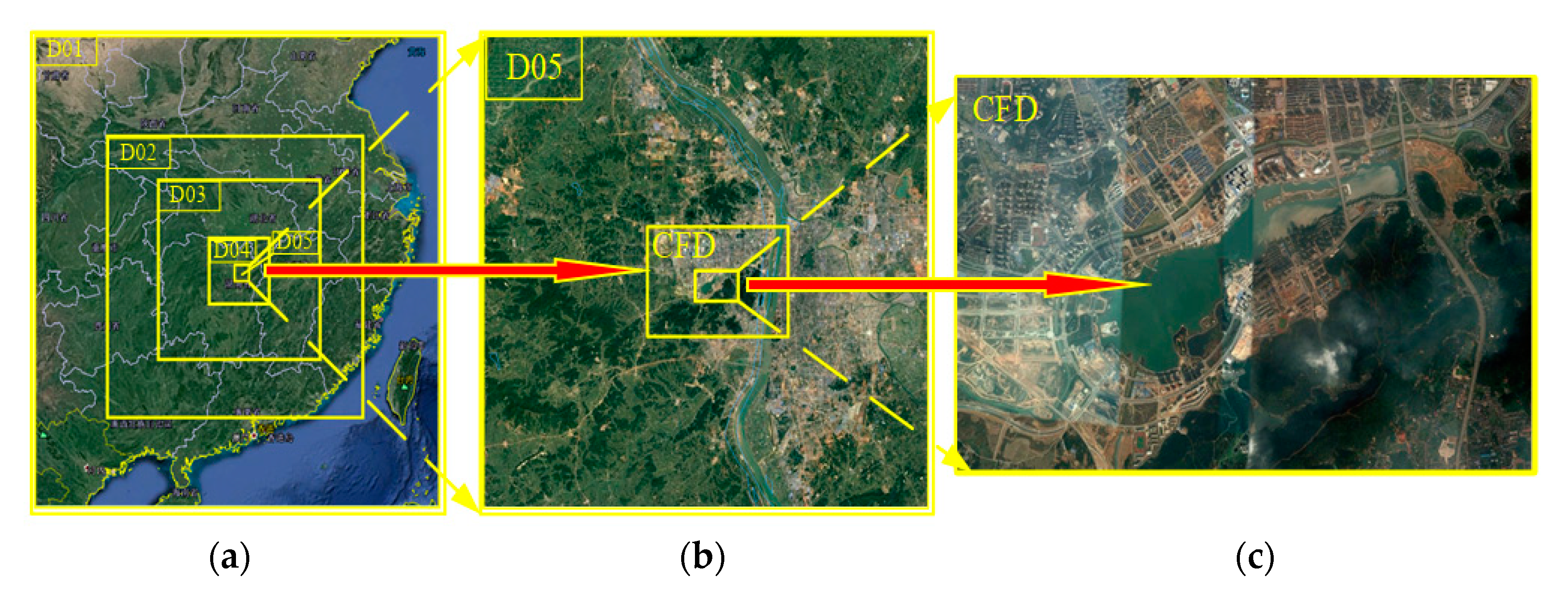
3. Case Study
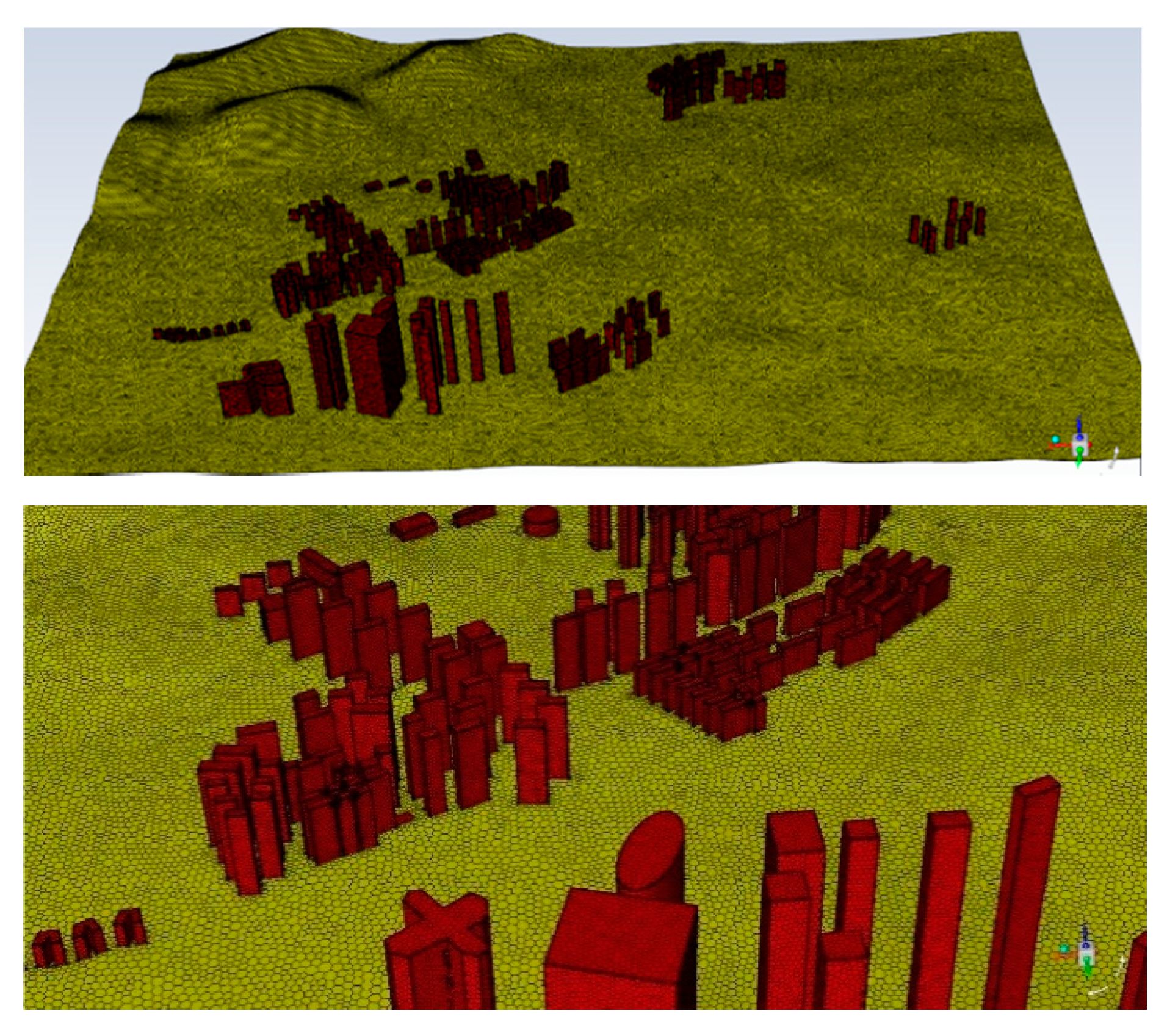
3.1. Calculation Models and Meshes
3.2. Mesoscale Coupling Wind Profile and Wind Velocity Profile Parameters
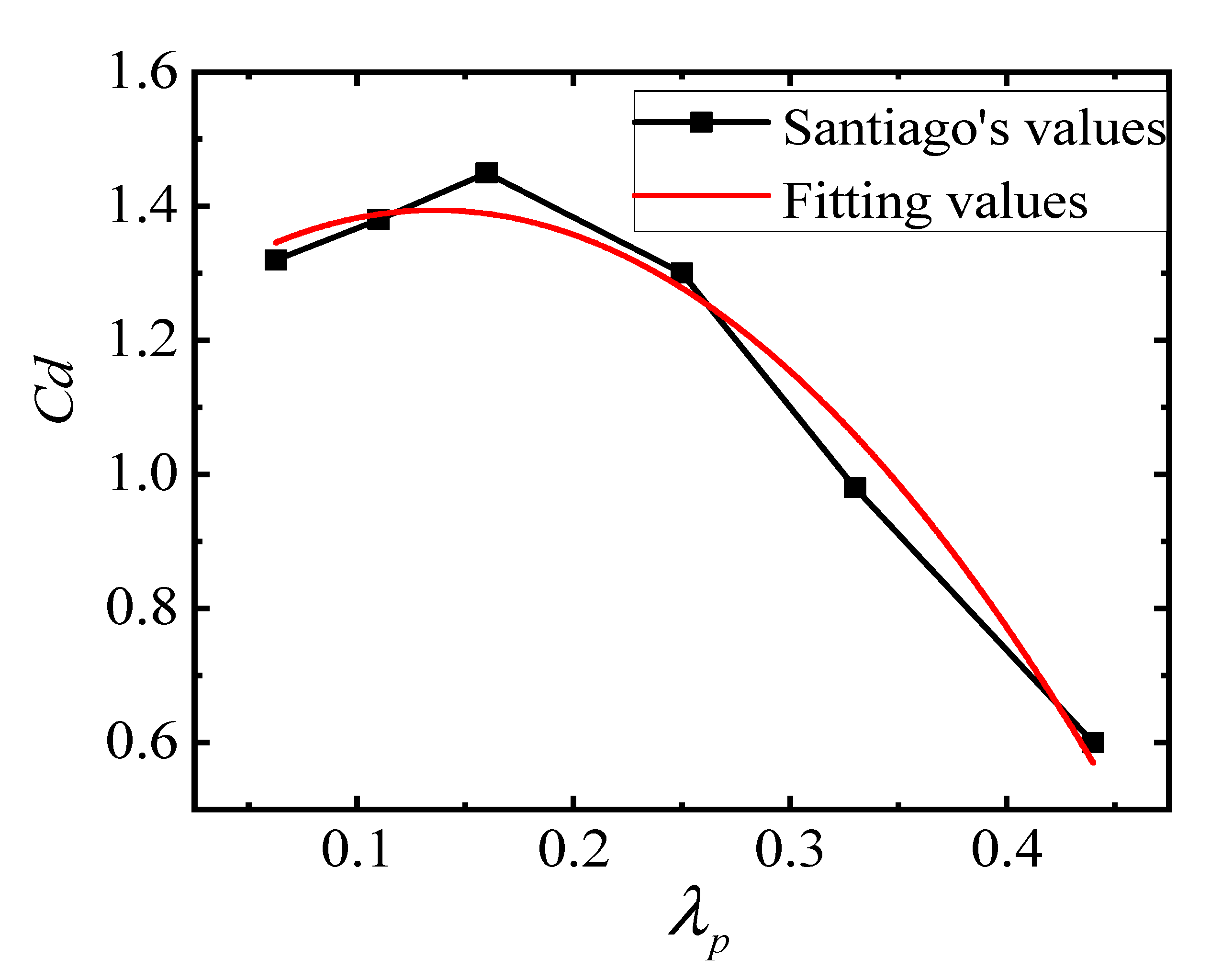
3.3. Drag Model Parameters
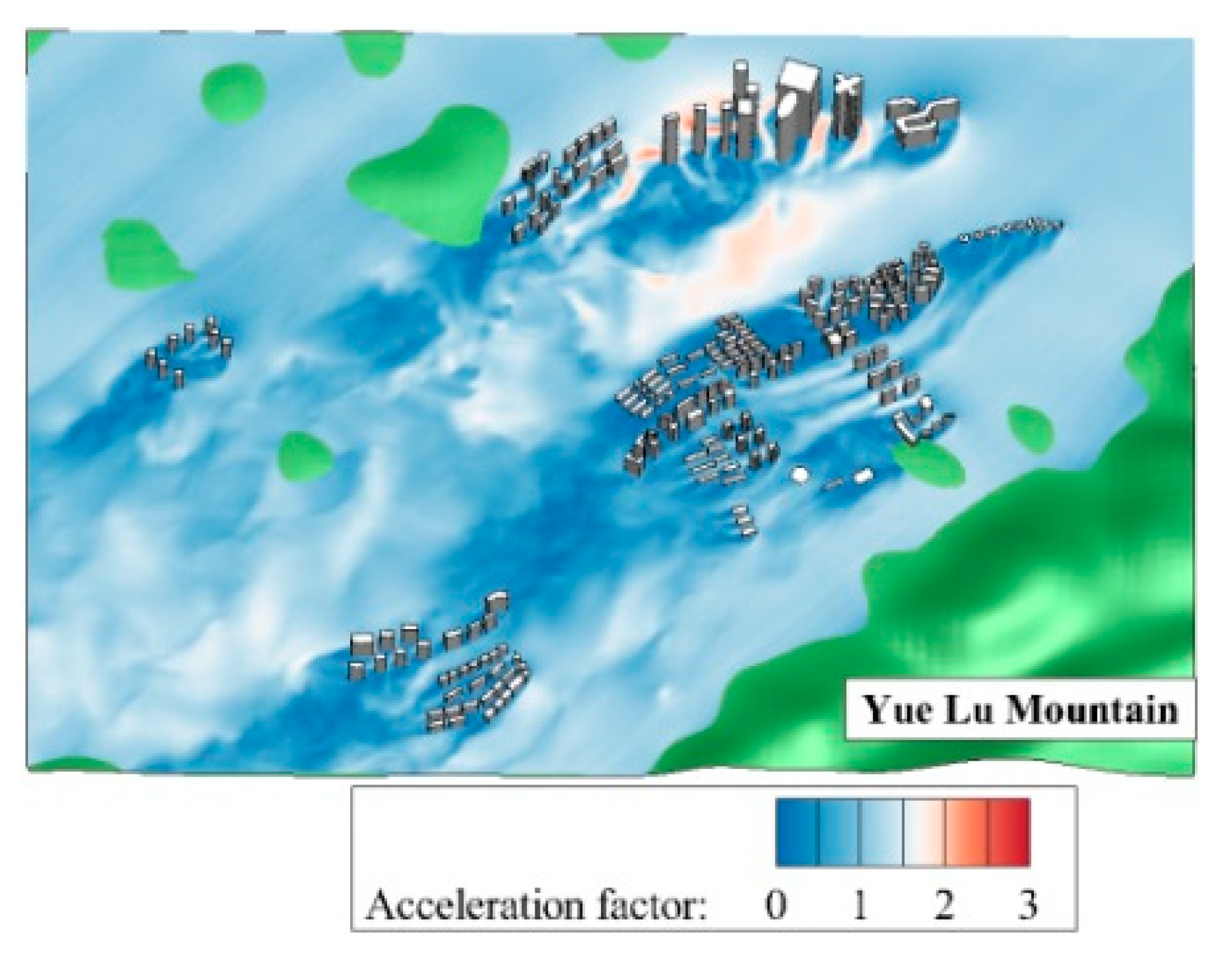
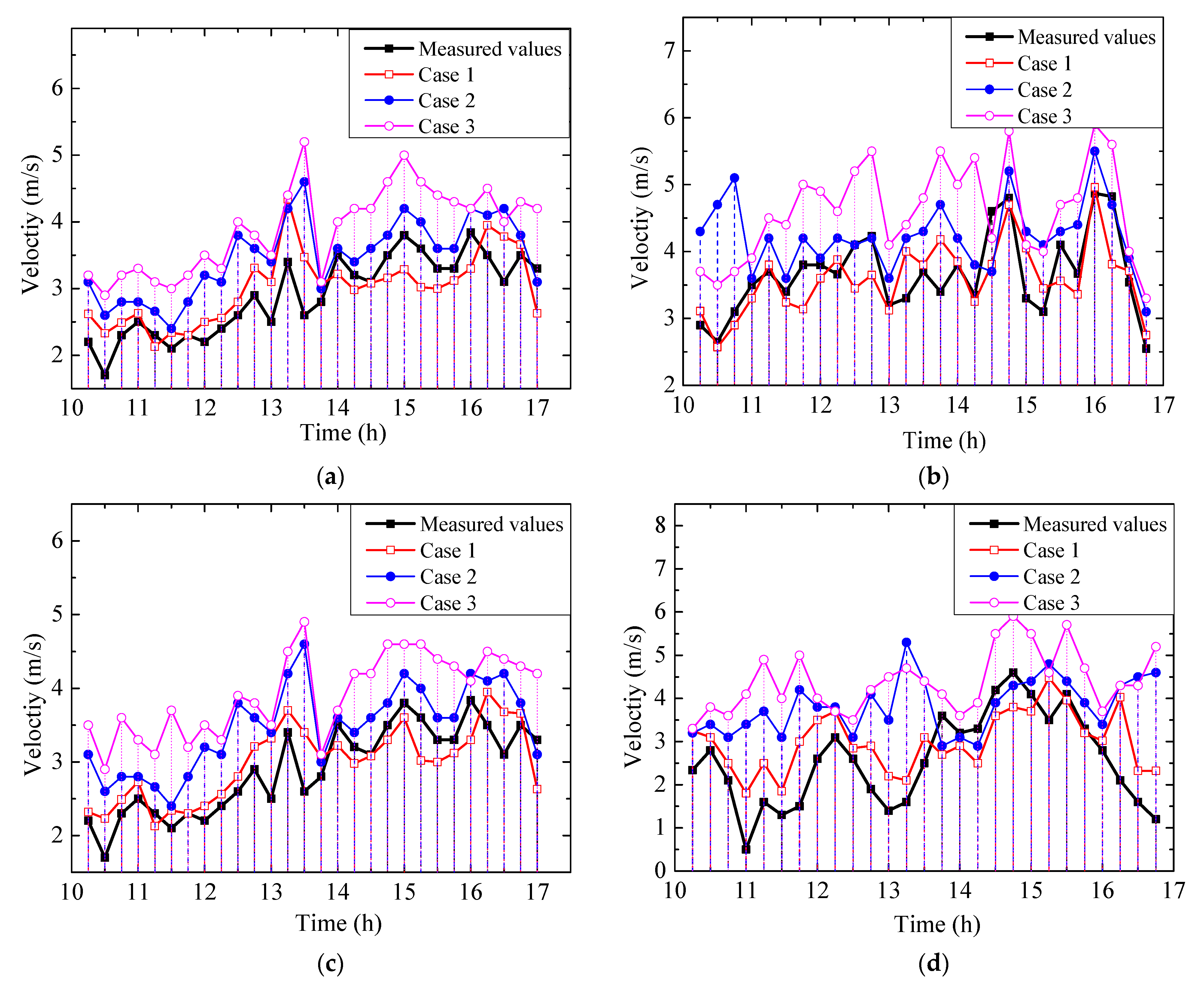
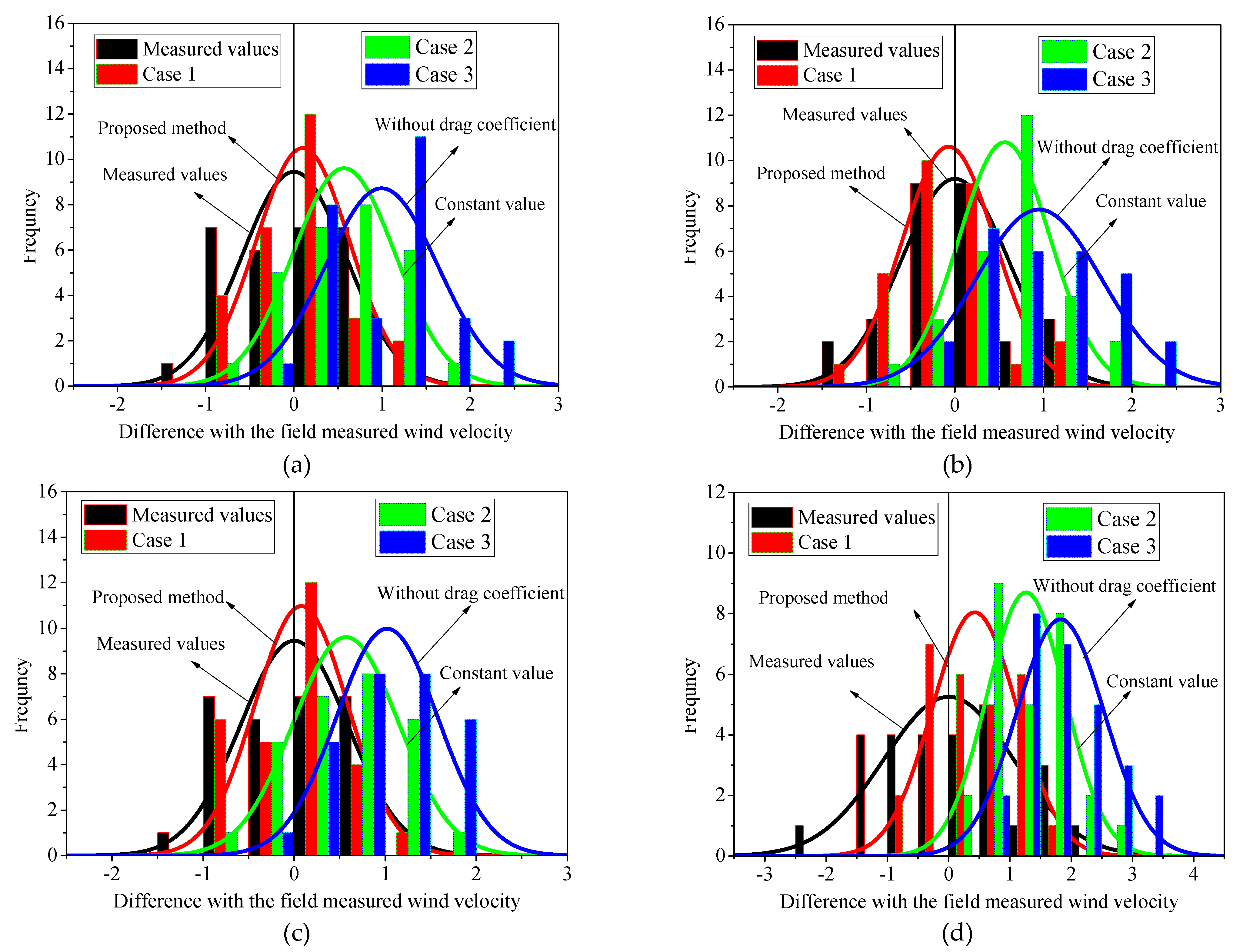
3.4. Results and Discussion
4. Conclusions
- (1)
- The mean velocity profiles near the ground demonstrate significant fluctuations. When the height is more than twice that of the buildings, the wind profile is consistent with the inlet profile. The maximum value of TKE usually appears near the height of 1.2H. High-precision numerical simulations should consider the effects of the SGS TKE and SGS dissipation on the numerical simulation.
- (2)
- Compared with the current studies, the drag coefficient at positions below 0.4 times of building height was obtained. The result shows that the drag coefficient is relatively large near the ground and decreases with the increase in height. The decay rate of drag coefficient below 0.4H is significantly higher than the height greater than 0.4H.
- (3)
- The numerical simulation considered three types of drag models (e.g., the proposed method, Belcher’s method, and no drag effect), comparing the mean values and standard deviations with the measured velocities. It found that the proposed model simulation results were in good agreement with the measured values. Belcher’s method’s accuracy was second-best, while that of the model with no drag effect was the worst.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| mean wind velocity at the height of z | |
| U0 | mean wind velocity at the height of h |
| h0 | reference height |
| power law exponent | |
| shear velocity of the flow | |
| z0 | roughness height |
| Δt | time step |
| AKE | average kinetic energy |
| SGS | sub-grid scale |
| TKE | turbulent kinetic energy |
| K | Von Kármán constant |
| d | size of grids near the ground |
| sub-grid scale dissipation | |
| sub-grid scale turbulent kinetic energy | |
| reference average wind | |
| the reference height | |
| H | height of the building model |
| drag force | |
| canopy drag length scale | |
| drag coefficient drag at the height of z | |
| average frontal area | |
| fractional volume | |
| P | pressure |
| W | outer surface area of the buildings |
| first surface area of cube (i, j) | |
| the scalar for the i direction | |
| the pressures at the corners of the cubes | |
| js, je | the corners of cubes in the Y direction |
| is, ie | the corners in the X direction |
| cube density | |
| number of grid points divided by the cubes | |
| building density | |
| frontal area density | |
| fitted parameters | |
| X | the ratio of average height to the maximum height |
| the maximum building height | |
| a, b, c | regression parameters |
| Macdonald roughness height | |
| standard deviation of the building height |
Appendix A
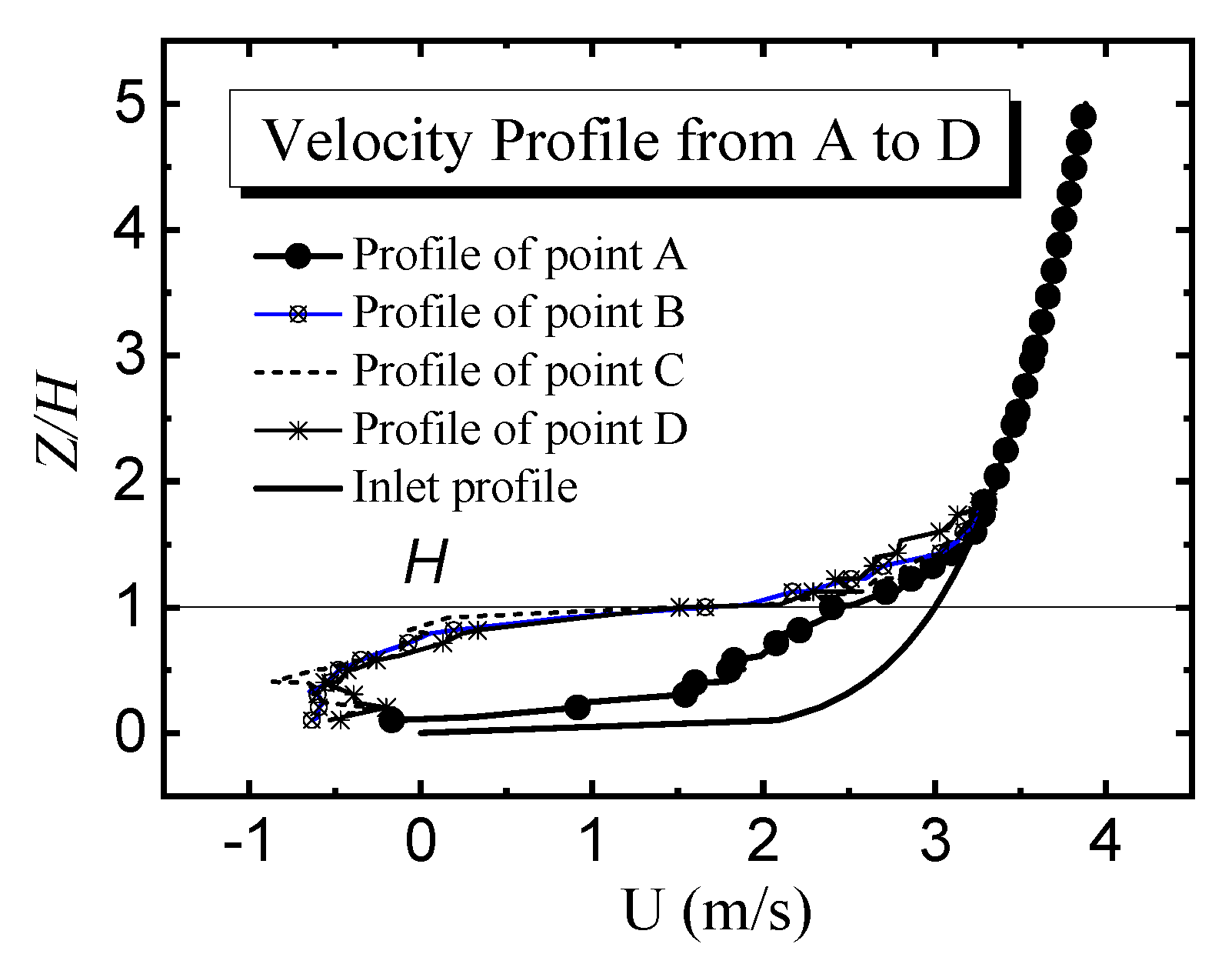
| Location | zref | α | Adj. R-Square |
|---|---|---|---|
| Inlet | 0.15 | 0.16 | 100% |
| Point A | 0.28 | 0.34 | 0.897 |
| Point B | 0.38 | 0.67 | 0.75 |
| Point C | 0.38 | 0.68 | 0.73 |
| Point D | 0.39 | 0.662 | 0.77 |
Appendix B
| Domain | Grid Numbers | Grid Span (km) | Size (km × km) | Time Step (s) | Layer Numbers |
|---|---|---|---|---|---|
| 1 | 50 | 40.5 | 2025 × 2025 | 243 | 50 |
| 2 | 91 | 13.5 | 1228.5 × 1228.5 | 81 | 50 |
| 3 | 161 | 4.5 | 724.5 × 724.5 | 27 | 50 |
| 4 | 181 | 1.5 | 271.5 × 271.5 | 9 | 50 |
| 5 | 101 | 0.5 | 50 × 50 | 3 | 50 |
References
- United Nations Publications. World Urbanization Prospects. 2014: Highlights; United Nations Publications: New York, NY, USA, 2014. [Google Scholar]
- Grimmond, C.S.B.; Salmond, J.A.; Oke, T.R.; Offerle, B.; Lemonsu, A. Flux and turbulence measurements at a densely built-up site in Marseille: Heat, mass (water and carbon dioxide), and momentum. J. Geophys. Res. Space Phys. 2004, 109, D24101. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Van Beeck, J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Du, Y.; Mak, C.M.; Kwok, K.; Tse, K.-T.; Lee, T.-C.; Ai, Z.; Liu, J.; Niu, J. New criteria for assessing low wind environment at pedestrian level in Hong Kong. Build. Environ. 2017, 123, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Kent, C.W.; Grimmond, S.; Barlow, J.; Gatey, D.; Kotthaus, S.; Lindberg, F.; Halios, C.H. Evaluation of urban local-scale aerodynamic parameters: Implications for the vertical profile of wind speed and for source areas. Bound. Layer Meteorol. 2017, 164, 183–213. [Google Scholar] [CrossRef]
- Barlow, J.F. Progress in observing and modelling the urban boundary layer. Urban Clim. 2014, 10, 216–240. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Iungo, G.V.; Leonardi, S.; Anderson, W. Parametric study of urban-like topographic statistical moments relevant to a priori modeling of bulk aerodynamic parameters. Bound. Layer Meteorol. 2016, 162, 231–253. [Google Scholar] [CrossRef]
- Sadique, J.; Yang, X.I.A.; Meneveau, C.; Mittal, R. Aerodynamic Properties of Rough Surfaces with High Aspect-Ratio Roughness Elements: Effect of Aspect Ratio and Arrangements. Bound. Layer Meteorol. 2017, 163, 203–224. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Du, Y.; Mak, C.M.; Li, Y. Application of a multi-variable optimization method to determine lift-up design for optimum wind comfort. Build. Environ. 2018, 131, 242–254. [Google Scholar] [CrossRef]
- Baik, J.J.; Park, S.B.; Kim, J.J. Urban flow and dispersion simulation using a CFD model coupled to a mesoscale model. J. Appl. Meteorol. Climatol. 2009, 48, 1667–1681. [Google Scholar] [CrossRef]
- Kong, L.; Lau, K.K.-L.; Yuan, C.; Chen, Y.; Xu, Y.; Ren, C.; Ng, E. Regulation of outdoor thermal comfort by trees in Hong Kong. Sustain. Cities Soc. 2017, 31, 12–25. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Blocken, B.; Janssen, W.; Van Hooff, T. CFD simulation for pedestrian wind comfort and wind safety in urban areas: General decision framework and case study for the Eindhoven University campus. Environ. Model. Softw. 2012, 30, 15–34. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near Wall Flow over Urban-like Roughness. Bound. Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Hagishima, A.; Tanimoto, J. Investigations of urban surface conditions for urban canopy model. Build. Environ. 2005, 40, 1638–1650. [Google Scholar] [CrossRef]
- Hagishima, A.; Tanimoto, J.; Nagayama, K.; Meno, S. Aerodynamic Parameters of Regular Arrays of Rectangular Blocks with Various Geometries. Bound. Layer Meteorol. 2009, 132, 315–337. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Castro, I.P.; Belcher, S.E. Mean Flow and Turbulence Statistics over Groups of Urban-like Cubical Obstacles. Bound. Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Belcher, S.E. Spatial Variability of Flow Statistics within Regular Building Arrays. Bound. Layer Meteorol. 2007, 125, 537–552. [Google Scholar] [CrossRef]
- Martilli, A.; Santiago, J.L. CFD simulation of airflow over a regular array of cubes. Part II: Analysis of spatial average properties. Bound. Layer Meteorol. 2006, 122, 635–654. [Google Scholar] [CrossRef]
- Zhang, N. Numerical Simulation Study of the Wind Environment for Urban Roads along River Based on Porous Medium Model. Ph.D. Thesis, Central South University, Changsha, China, 2005. [Google Scholar]
- Santiago, J.L.; Coceal, O.; Martilli, A.; Belcher, S.E. Variation of the Sectional Drag Coefficient of a Group of Buildings with Packing Density. Bound. Layer Meteorol. 2008, 128, 445–457. [Google Scholar] [CrossRef]
- Kanda, M.; Inagaki, A.; Miyamoto, T.; Gryschka, M.; Raasch, S. A New Aerodynamic Parametrization for Real Urban Surfaces. Bound. Layer Meteorol. 2013, 148, 357–377. [Google Scholar] [CrossRef]
- Lien, F.-S.; Yee, E. Numerical Modelling of the Turbulent Flow Developing Within and Over a 3-D Building Array, Part I: A High-Resolution Reynolds-Averaged Navier—Stokes Approach. Bound. Layer Meteorol. 2004, 112, 427–466. [Google Scholar] [CrossRef]
- Wooding, R.A.; Bradley, E.F.; Marshall, J.K. Drag due to regular arrays of roughness elements of varying geometry. Bound. Layer Meteorol. 1973, 5, 285–308. [Google Scholar] [CrossRef]
- Coceal, O.; Belcher, S.E. A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 2004, 130, 1349–1372. [Google Scholar] [CrossRef] [Green Version]
- Brown, M.J.; Lawson, R.E.; DeCroix, D.S.; Lee, R.L. Comparison of centerline velocity measurements obtained around 2D and 3D building arrays in a wind tunel. Int. Soc. Environ. Hydraul. Conf. 2001, 4162–4164. Available online: https://www.researchgate.net/publication/236512119_COMPARISON_OF_CENTERLINE_VELOCITY_MEASUREMENTS_OBTAINED_AROUND_2D_AND_3D_BUILDING_ARRAYS_IN_A_WIND_TUNNEL (accessed on 30 December 2020).
- Franke, J.; Jensen, C.; Hirsch, A.G.; Krüs, H.W.; Schatzmann, M.; Westbury, P.S.; Miles, S.D.; Wisse, J.A.; Wright, N.G. Recommendations on the use of CFD in wind engineering. In Proceedings of the International Conference on Urban Wind Engineering and Building Aerodynamics, COST Action C14, Impact of wind and Storm on City Life Built Environment, von Karman Institute, Rhode-Saint-Genèse, Belgium, 5–7 May 2004; Academic: Sint-Genesius-Rode, Belgium, 2004. [Google Scholar]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Shen, L.; Han, Y.; Cai, C.S.; Xu, G.; Hua, X. Exceedance Probability Assessment of Pedestrian Wind Environment Based on Multiscale Coupling Numerical Simulation. J. Aerosp. Eng. 2020, 33, 05020002. [Google Scholar] [CrossRef]
- Han, Y.; Shen, L.; Xu, G.J.; Cai, C.S.; Dong, G.C.; Zhang, J.R. Multiscale simulation of wind field on a long-span bridge site in mountainous area. J. Wind Eng. Ind. Aerodyn. 2018, 177, 260–274. [Google Scholar] [CrossRef]
- Fluent. Fluent User’s Guide: Version: ANSYS 18.0; Fluent: Lebanon, NH, USA, 2018. [Google Scholar]
- Macdonald, R.; Griffiths, R.; Hall, D. An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
- Belcher, S.E.; Jerram, N.; Hunt, J.C.R. Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 2003, 488, 369–398. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Type |
|---|---|
| Time discretization | Second-order implicit |
| Pressure discretization | Second-order upwind |
| Momentum discretization | Bounded central difference |
| Pressure–velocity coupling | Pressure-implicit with splitting operators (PISO) |
| Under relaxation factors | 0.3 for the pressure and 0.7 for the momentum |
| Locations | Measured (m/s) | Proposed Method, Case 1 (m/s) | Constant Drag Coefficient, Case 2 (m/s) | Without Drag Coefficient, Case 3 (m/s) |
|---|---|---|---|---|
| Station 1 | 2.91 | 3.01 | 3.47 | 3.90 |
| Station 2 | 3.66 | 3.59 | 4.23 | 4.61 |
| Station 3 | 2.91 | 2.98 | 3.47 | 3.93 |
| Station 4 | 2.57 | 3.00 | 3.83 | 4.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Han, Y.; Xu, G.; Cai, C.; Yang, Y.; Hua, X. A Novel Canopy Drag Coefficient Model for Analyzing Urban Wind Environments Based on the Large Eddy Simulation. Energies 2021, 14, 796. https://doi.org/10.3390/en14040796
Shen L, Han Y, Xu G, Cai C, Yang Y, Hua X. A Novel Canopy Drag Coefficient Model for Analyzing Urban Wind Environments Based on the Large Eddy Simulation. Energies. 2021; 14(4):796. https://doi.org/10.3390/en14040796
Chicago/Turabian StyleShen, Lian, Yan Han, Guoji Xu, Chunsheng Cai, Ying Yang, and Xugang Hua. 2021. "A Novel Canopy Drag Coefficient Model for Analyzing Urban Wind Environments Based on the Large Eddy Simulation" Energies 14, no. 4: 796. https://doi.org/10.3390/en14040796
APA StyleShen, L., Han, Y., Xu, G., Cai, C., Yang, Y., & Hua, X. (2021). A Novel Canopy Drag Coefficient Model for Analyzing Urban Wind Environments Based on the Large Eddy Simulation. Energies, 14(4), 796. https://doi.org/10.3390/en14040796





