Modelling of a Flow-Induced Oscillation, Two-Cylinder, Hydrokinetic Energy Converter Based on Experimental Data
Abstract
:1. Introduction
2. Physical Model and Mathematical Model
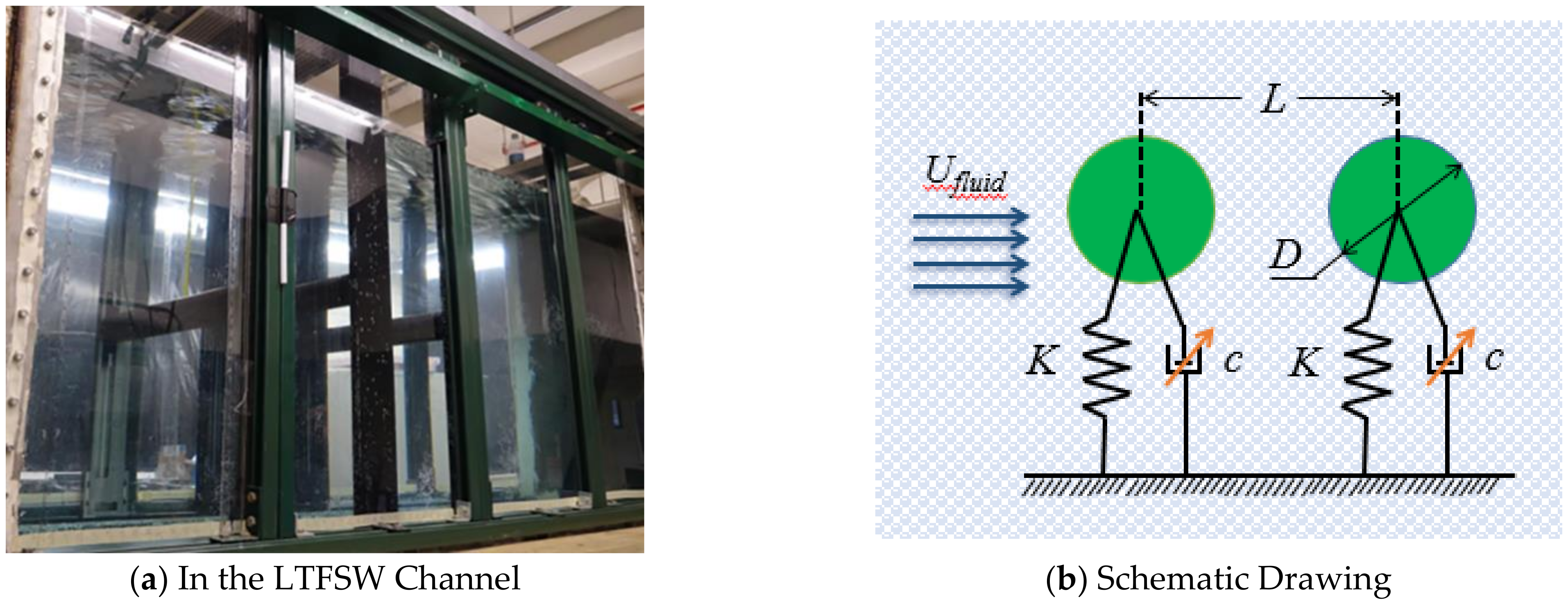
2.1. Experimental Facility: LTFSW Channel
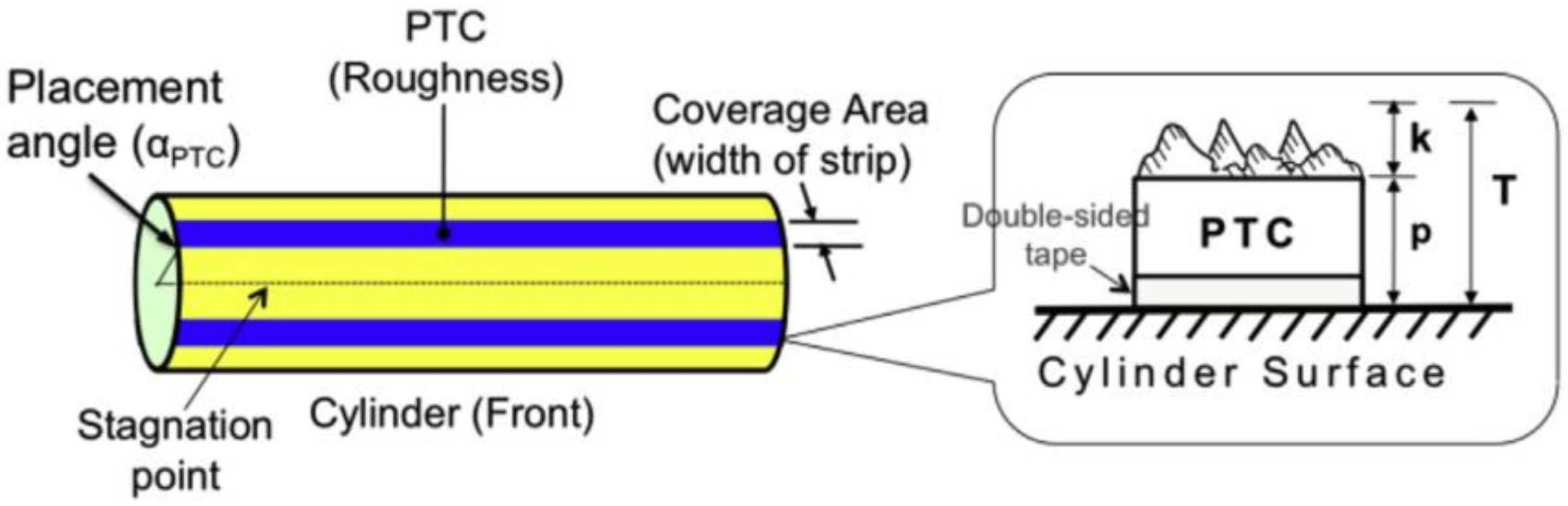
2.2. Cylinders with Distributed Roughness
2.3. Vck System
2.4. Mathematical Model of Harnessed Power and Harnessing Efficiency
3. Modeling of the Converter
3.1. Principle of BP Neural Network
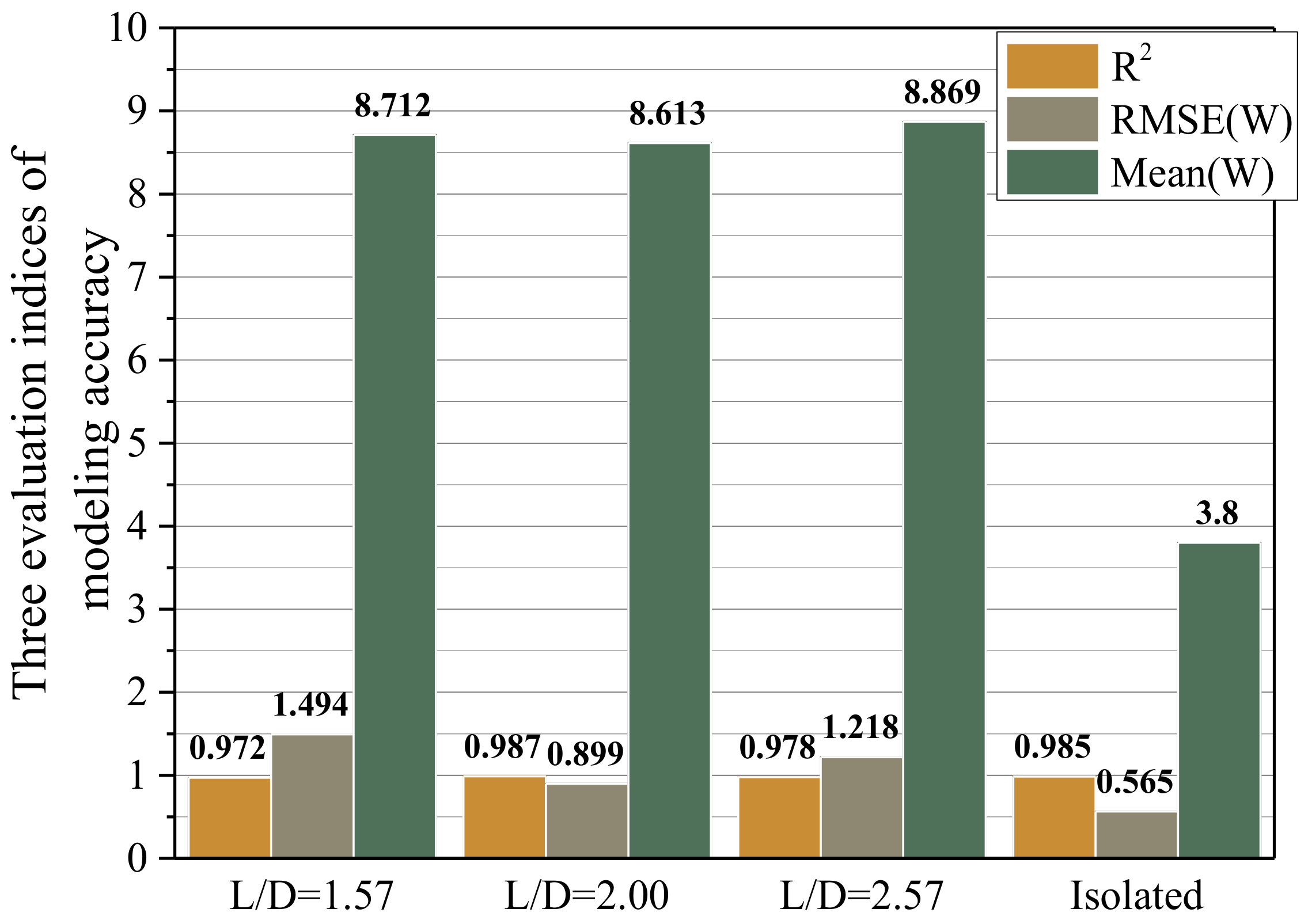
3.2. Construction and Validation of Surrogate Model
3.2.1. Range of Input Variables
3.2.2. Neural Network Structure
3.2.3. Sample Training
3.2.4. Sample Testing
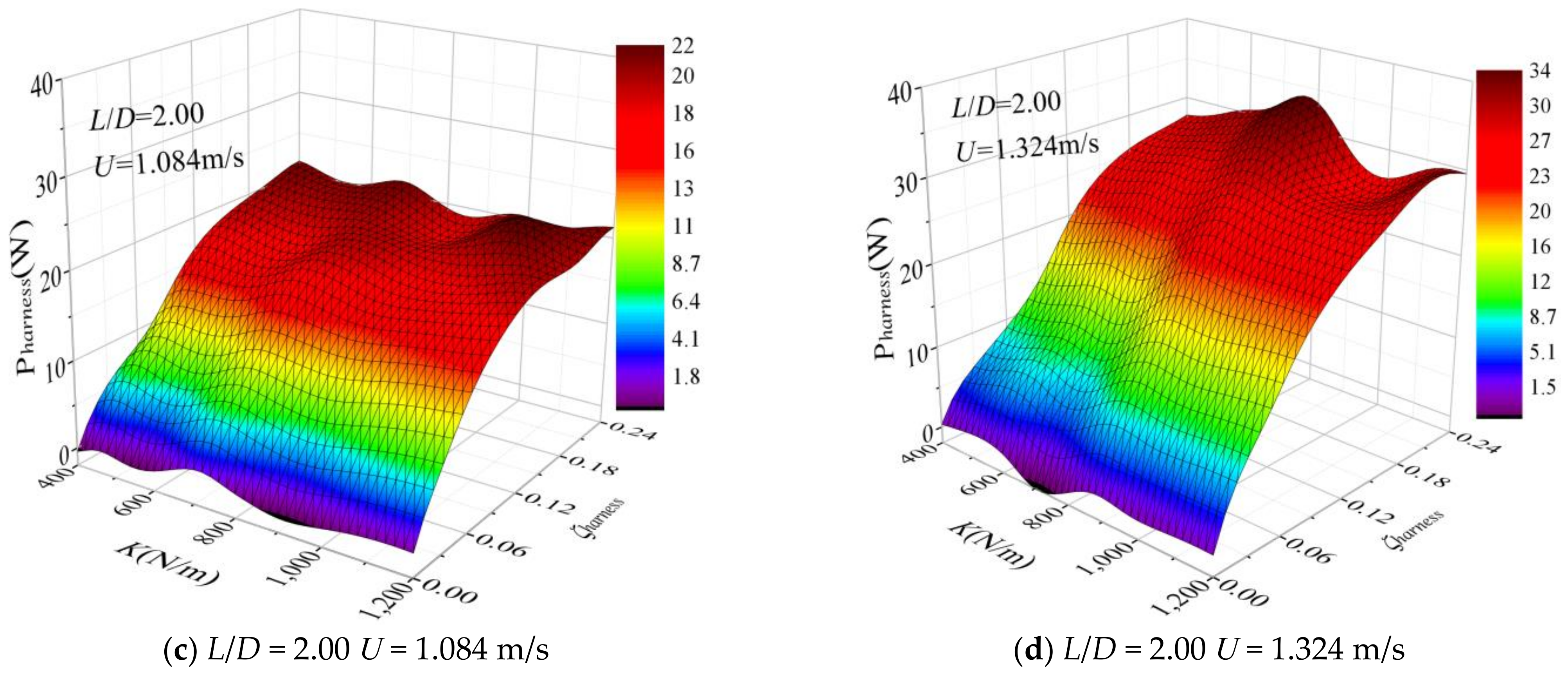
3.3. Modeling Prediction of the Harnessed Power
4. Prediction, and Discussion of Results
4.1. Effect of Harnessing Damping Ratio on Power and Efficiency
- (a)
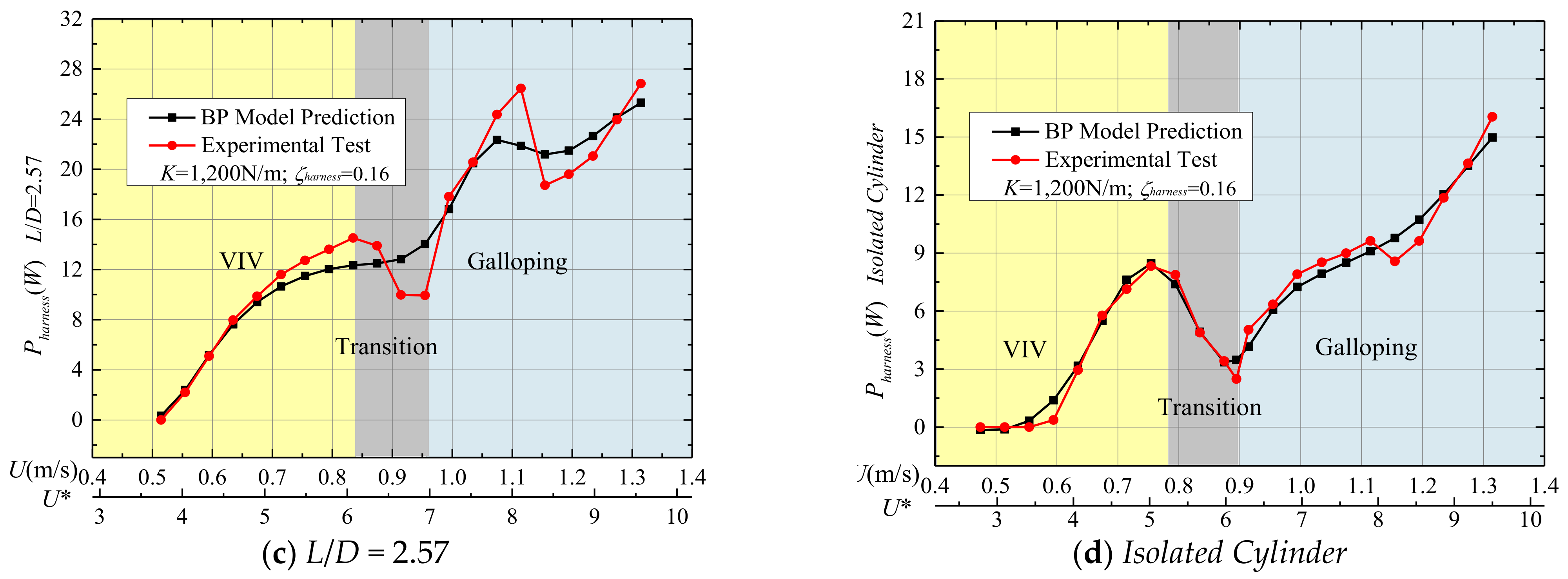
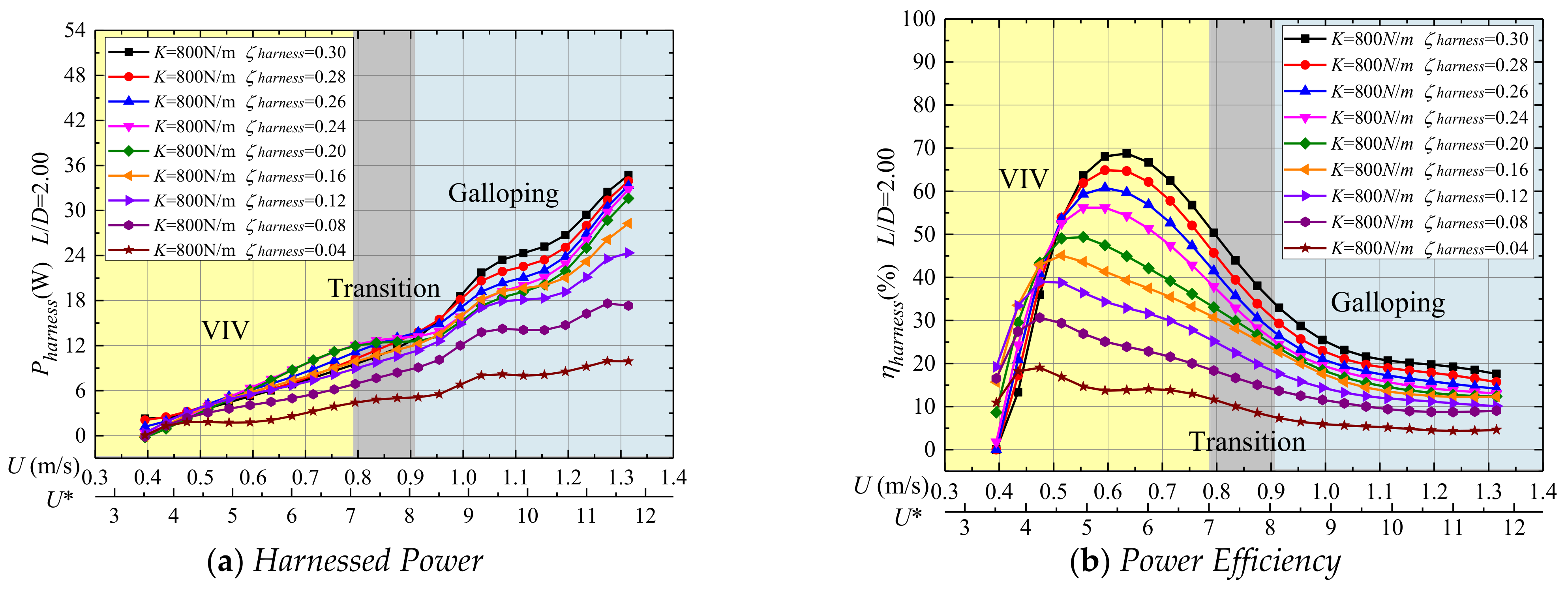
- The velocity range of the VIV region for all surrogate models is: 0.39 m/s < U < 0.67 m/s for L/D = 1.57, 0.39 m/s < U < 0.79 m/s for L/D = 2.00 and 2.57, and 0.39 < U < 0.75 m/s for isolated cylinder. As can be seen in Figure 9a, Figure 10a, Figure 11a and Figure 12a, for almost every ζharness within the range of 0.04–0.30, increasing the flow velocity in VIV is accompanied by an increase in Pharness. In addition, the coverage range of the VIV-galloping transition region is: 0.79 m/s < U < 0.91 m/s for L/D = 2.57, 0.75 m/s < U < 0.87 m/s for the isolated single cylinder. An interesting phenomenon is that the cases of spacing ratio L/D = 1.57 and 2.00 both have no obvious transition region owing to the positive synergy between two closely spaced oscillators. Nevertheless, the same phenomenon that occurs with a single-cylinder is that for L/D = 2.57, the dropping tendency of Pharness becomes obvious in the transition region. In galloping, for all spacing ratios, Pharness continually increases with the increase of velocity. The above results are highly consistent with the experimental results in [23], indicating that these surrogate models have high accuracy. It should be pointed out that the area covered in gray in Figure 9, Figure 10, Figure 11 and Figure 12 represents the transition region.
- (b)
- For L/D = 1.57, Figure 9a shows that, with the increase of damping within the range of 0.20–0.30, the variation of Pharness is negligible. Figure 9b illustrates that, in the VIV range, increasing the damping from 0.20 to 0.30 will translate the curve of ηharness to higher velocity and is followed by a significant decrease in ηharness. The above phenomenon is owing to the negative interaction between two tandem cylinders in the sense that the higher damping limits the oscillating amplitude of the downstream cylinder, which is then shielded by the upstream cylinder. As shown in Figure 9b, the optimal ηharness occurs at the upper branch of VIV, and as the damping ratio increases from 0.2 to 0.3, the optimal efficiency increases as well. For instance, the optimal efficiency changes from 40.82% (K = 1200 N/m, ζharness = 0.20, U = 0.59 m/s) to 50.51% (K = 1200 N/m, ζharness = 0.30, U = 0.71 m/s). Additionally, for U > 0.71 m/s, increasing ζharness results in an obvious increase in ηharness on account of the decrease of the amplitude of oscillation. According to Equation (3), the lower amplitude reduces the value of PFluid in the denominator of the efficiency.
- (c)
- For L/D = 2.00: Different from the variation trend of Pharness in Figure 9a, as shown in Figure 10a, increase of ζharness in the range of 0.20–0.30 has an obvious influence on the variation of Pharness. Specifically, in the VIV upper branch (0.59 m/s < U < 0.79 m/s), as ζharness increases, the corresponding Pharness decreases. However, using the transition region as a turning point, in galloping (U > 0.91 m/s), increasing ζharness increases the harnessed power with the maximum predicted value of Pharness is 34.73W (K = 800 N/m, ζharness = 0.30, U = 1.31 m/s). Figure 10b shows that, except for the initial VIV branch, in all selected FIO regions, as ζharness increases within the range 0.04 < ζharness < 0.30, the corresponding ηharness increases. As the harnessing damping ratio increases from 0.20 to 0.30, the increment rate of harnessing efficiency will reach up to 59.52% at U = 0.71 m/s, and the maximum harnessing efficiency is 68.78% at U = 0.63 m/s.
- (d)
- For L/D = 2.57: Being different from the predicted results for L/D = 1.57 and 2.00, for L/D = 2.57, in the VIV initial stage and the entire galloping region, the value of Pharness shows a drop downtrend as ζharness increases from 0.20 to 0.30, as shown in Figure 11a. Here, the optimal harnessed power changes from 31.37 W (K = 400 N/m, ζharness = 0.20) to 27.54 W (K = 400 N/m, ζharness = 0.30) at U = 1.31 m/s. In contrast, it is found that increasing the harnessing damping ratio from 0.20 to 0.30 is followed by an increase of power efficiency in the whole FIO region except at the end region of galloping. For instance, the efficiency changes from 52.09% (K = 400 N/m, ζharness = 0.20) to 64.92% (K = 400 N/m, ζharness = 0.30) at U = 0.43 m/s. Due to the low spring stiffness (K = 400 N/m), the initial velocity of power harvesting is lower than 0.39m/s. Besides that, the amplitude at low velocity has a relative low value, resulting in high efficiency. As mentioned above, for two tandem cylinders with spacing ratio L/D = 2.57 and K = 400 N/m, it can be observed that increasing the damping ratio from 0.20 to 0.30 will decrease the harnessed power; however, it enhances the power efficiency of the VIVACE Converter.
- (e)
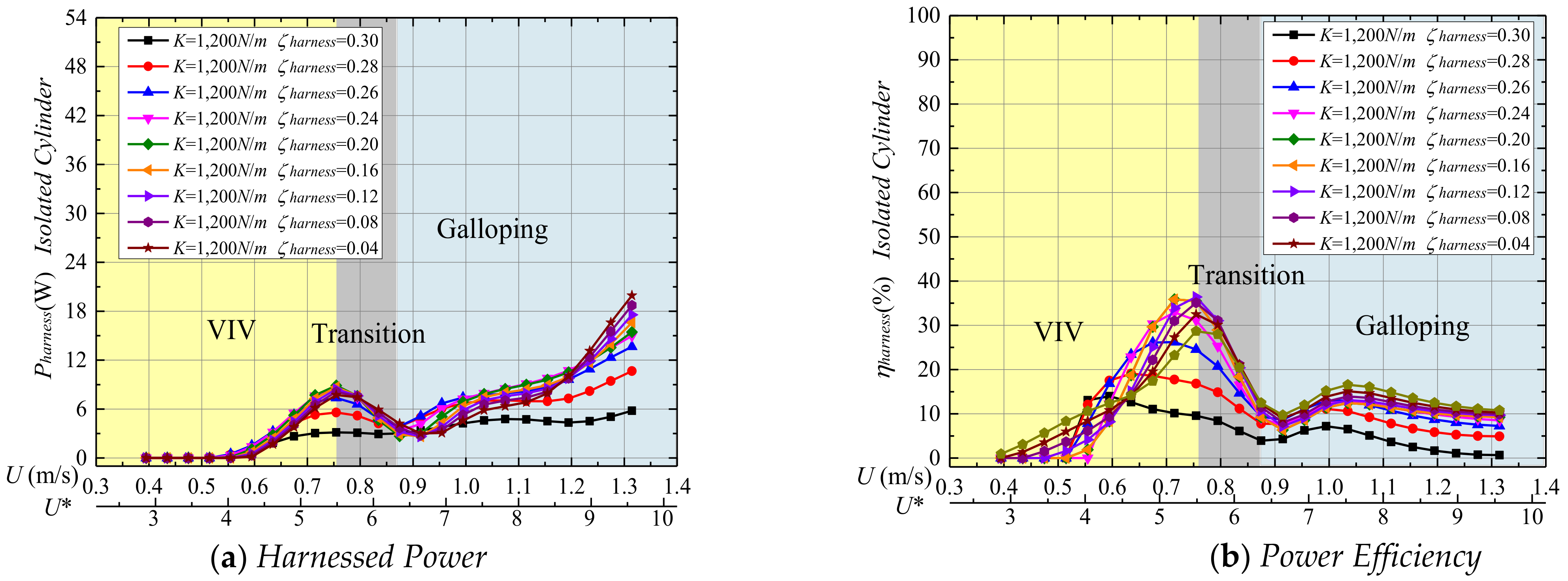
- For an isolated cylinder in general, with the increase of spacing ratio, the interaction between the upstream cylinder and downstream cylinder becomes weaker. Therefore, the changes of curves of harnessed power between the spacing ratio of L/D = 2.57 and the isolated single-cylinder cases are similar. However, in this section, the selected fixed stiffness for isolated cylinder and two cylinders with tandem spacing ratio L/D = 2.57 are different. Thus, a large difference in oscillating response exists between these two cases. As we can see in Figure 12a, except for the initial galloping region, the value of Pharness decreases with the increase of harnessing damping ratio (0.2 < ζharness < 0.30). Moreover, as ζharness increases, the reduction between two adjacent damping ratios increases. Because of the large decrease in Pharness, the corresponding ηharness decreases as well when the damping ratio increases.
- (f)
- Comparing the power efficiency between the four cases (spacing ratio of L/D = 1.57, 2.00, 2.57 and isolated single cylinder), it is observed that the efficiency of tandem cylinders is much larger than that of the isolated cylinder. For L/D = 2.00, the optimal efficiency for K = 800 N/m and ζharness = 0.04–0.30, reaches 1.91 times the hydrokinetic power efficiency of one isolated cylinder. As the spacing ratio increases from 1.57 to 2.00 to 2.57, the optimal efficiency increases from 50.51% to 68.78% to 64.92%, indicating that the smaller spacing of 1.57 induces a negative effect on the power efficiency due to the strong interaction between the two cylinders.
4.2. Effect of Spring Stiffness on Power and Efficiency
- (a)
- As shown in Figure 13a–d, in the VIV region, with the increase of flow velocity, the value of Pharness increases. An important finding is that, for the spacing ratio L/D = 1.57 and 2.00, the transition region is not apparent due to the close spacing between the cylinders. Contrary, the spacing ratio L/D = 2.57 and the isolated single-cylinder have a relatively obvious transition. Therefore, the correctness of surrogate models has verified again.
- (b)
- For L/D = 1.57: As shown in Figure 13a, the power for K = 400–1200 N/m in the VIV region (0.39 m/s ≤ U ≤ 0.67 m/s) and the galloping region have, respectively, approximate and lower values than that of the K = 1200–1600 N/m. More concretely, when U > 0.71 m/s, as K increases from 1200 N/m to 1600 N/m, the power increases; and the optimal power changes from 39 W (K = 1200 N/m, ζharness = 0.20, U = 1.31 m/s) to 44.74 W (K = 1600 N/m, ζharness = 0.20, U = 1.11 m/s). However, when U > 1.27 m/s, the power of high stiffness case have the approximate values. Considering the above analysis, selecting the stiffness in the range of 1200 N/m < K < 1,600N/m in galloping improves power harvesting. It is also observed that, for L/D = 1.57, increasing K increases power harvesting.
- (c)
- For L/D = 2.00: As shown in Figure 13b, considering the spring stiffness, all the curves of Pharness show a similar tendency. Moreover, in galloping, two local peaks of Pharness appear at the K = 800 N/m and 1000 N/m, respectively. This phenomenon of K = 800 N/m is in good agreement with the experimental data [23]. Almost in all cases, in the VIV upper branch and the galloping region, the harnessed power shows the downward trend with increase of K in the range 1200 N/m < K < 1600 N/m. Nevertheless, in galloping, the decrement of Pharness between adjacent stiffness values is small. In consequence, for a given harnessing damping ratio of 0.20, increasing K from 1200 N/m to 1600 N/m is adverse to the value of Pharness.
- (d)
- For L/D = 2.57: As shown in Figure 13c, at low flow velocity (0.39 m/s < U < 0.51 m/s), the VIVACE Converter cannot initiate FIO and, thus, cannot harvest any power at high spring stiffness (1200 N/m < K < 1600 N/m). FIO initiates with VIV a little before the natural frequency of the system in quiescent water; thus, higher stiffness values start FIO at higher flow velocity. This phenomenon is different from that of the low spacing ratio values of L/D = 1.57 and 2.00. From the VIV upper branch to the initial stage of galloping, as K increases within the range 1200 N/m < K < 1600 N/m, the harnessed power decreases. In the end galloping (1.11 m/s ≤ U ≤ 1.31 m/s), when U = 1.19 m/s, the value of Pharness rapidly increases from 21.40W (K = 1200 N/m, ζharness = 0.20) to 29.73 W (K = 1600 N/m, ζharness = 0.20) as stiffness increases. However, combined with the variable trend of harnessed power when K = 400–1200 N/m in Figure 13c, it can be concluded that expanding the K from 400–1200 N/m to 400–1600 N/m is not conducive to increase the power harvesting at low flow velocities. Increase can be observed in the end region of galloping (1.07 m/s < U < 1.23 m/s).
- (e)
- For an isolated cylinder, as shown in Figure 13d, an isolated single-cylinder with high spring stiffness cannot induce VIV at low flow velocity due to the high natural frequency of the oscillator in quiescent water, fn,water. This is due to the strong restoring force provided by the hard spring. For the same reason, as K increases from 600 N/m to 1600 N/m, the initial flow velocity of power harvesting increases as well. This increase is expected to follow the square root of K as in fn,water. Of course, the curve of Pharness of the isolated single cylinder will shift to higher velocity. Therefore, in the VIV region, expanding the selected range of K from 400–1200 N/m to 400–1600 N/m has no effect on the increase of Pharness. On the contrary, in the transition region and initial galloping, expanding the selected range of K is beneficial for enhancing the power harvesting. The range of synchronization in VIV shifts to the right proportionally to the square root of K while galloping initiation is independent of K. When U = 0.83–1.11 m/s, as K increases from 1200 N/m to 1600 N/m, Pharness increases. In the transition region, the optimal harnessed power can reach up to 10.82W (K = 1400 N/m, ζharness = 0.20, U = 0.79 m/s), which is 10.3 times the harnessed power for K = 400 N/m (Pharness = 1.05W, ζharness = 0.20, U = 0.79 m/s). Besides that, taking U = 1.03 m/s as the turning point, when U > 1.03 m/s, Pharness shows a drop tendency as K increases from 1200 to 1600 N/m.
4.3. Optimal Power and Efficiency Envelope for Two Cylinders in Tandem
- (a)
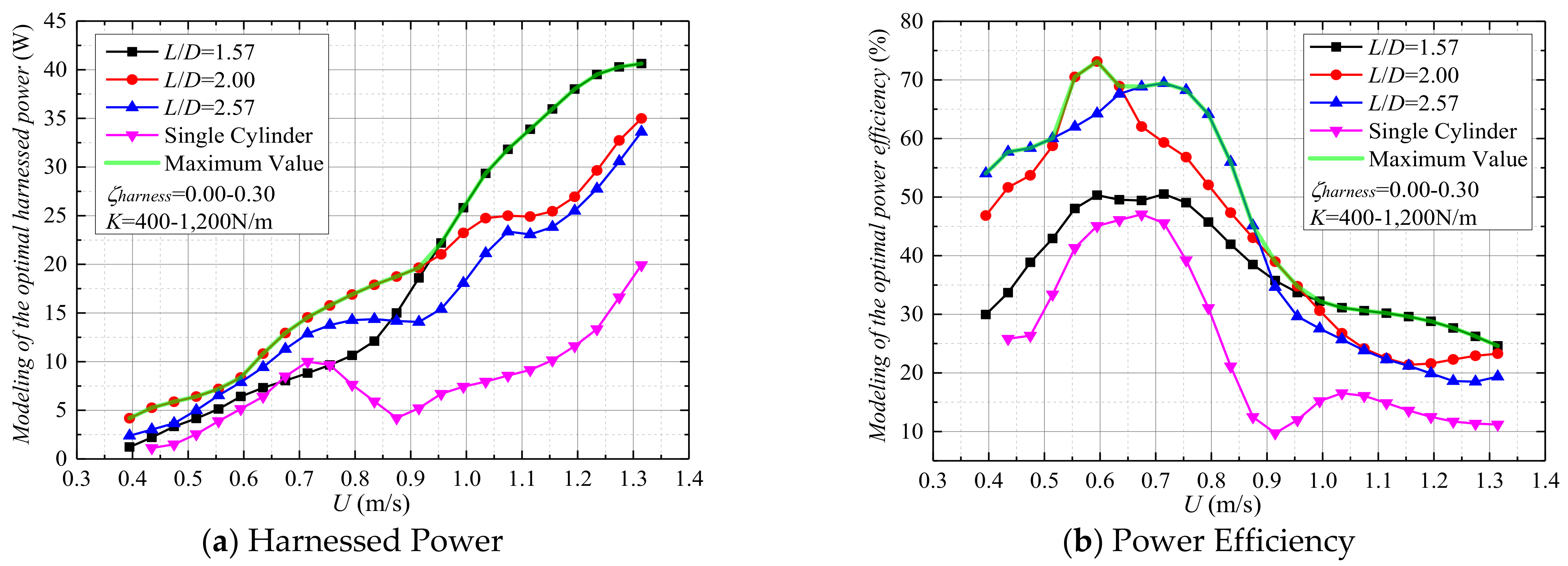
- In the VIV region (0.39 m/s < U < 0.79 m/s), a continuous growth of harnessed power can be observed for spacing L/D = 1.57, 2.00 and 2.57. Besides that, the power for L/D = 2.00 is higher than that of the other two spacing ratios, as shown in Figure 14a. In this region, the maximum power is: Pharness = 10.64 W (L/D = 1.57, K = 680 N/m, ζharness = 0.205), Pharness = 16.89 W (L/D = 2.00, K = 640 N/m, ζharness = 0.30), Pharness = 14.27 W (L/D = 2.57, K = 1200 N/m, ζharness = 0.255).
- (b)
- In the initial VIV branch (U < 0.47 m/s), as shown in Table A1, the combination of lower stiffness with lower harnessing damping ratio stimulates the onset of VIV for lower velocity U < 0.39 m/s, which is consistent with the conclusion in Ref. [23]. Additionally, for spacing L/D = 2.00 and 2.57, increasing the flow velocity is accompanied by an increase in power efficiency. The efficiency exhibits a local maximum after which it decreases as shown in Figure 14b. The maximum efficiency for L/D = 2.00 and 2.57 are, respectively, ηharness = 73.14% (L/D = 2.00, K = 680 N/m, ζharness = 0.30, U = 0.59 m/s) and ηharness = 69.44% (L/D = 2.57, K = 1200 N/m, ζharness = 0.30, U = 0.71 m/s), as shown in Table A2. That optimum is located near the end of the VIV upper branch. An interesting phenomenon can be observed that there are two local maxima for spacing L/D = 1.57. The higher one is ηharness = 50.51% (L/D = 1.57, K = 1200 N/m, ζharness = 0.30, U = 0.71 m/s). The local optima can be explained by studying carefully Equations (4)–(6). The swept area dominating the denominator in Equation (3) changes at a different rate than the cylinder velocity square dominating the numerator in Equation (4).
- (c)
- In the transition region from VIV to galloping (0.79 m/s < U < 0.91 m/s), power harvesting for spacing L/D = 1.57 and 2.00 almost have a direct proportional relation with flow velocity. For spacing L/D = 2.57, however, a downward trend is observed. With increasing flow velocity, the efficiency decreases. Before the onset of galloping, the power efficiency for L/D = 1.57 is lower than that of the other two spacing ratios.
- (d)
- In galloping (U > 0.91 m/s), increasing the flow velocity is beneficial for power harvesting; however, it is detrimental to the power efficiency due to the dramatic increase in amplitude and thus, swept area. When U > 0.95 m/s, the lowest spacing results in highest power or efficiency with higher spring stiffness. In this region, the maximum power is: Pharness = 40.62 W (L/D = 1.57, K = 1200 N/m, ζharness = 0.275, U = 1.31 m/s), Pharness = 34.99 W (L/D = 2.00, K = 780 N/m, ζharness = 0.30, U = 1.31 m/s), Pharness = 33.61 W (L/D = 2.57, K = 600 N/m, ζharness = 0.20, U = 1.31 m/s).
- (e)
- To better analyze the synergy effect of the two tandem cylinders, the optimal harnessed power and efficiency of the isolated single cylinder are also modeled, and are added in Figure 14a,b, respectively. The corresponding optimal parameters for an isolated cylinder are presented in Appendix A, Table A3. Specifically, the green line in Figure 14 represents the maximum optimal value at each velocity for three cases of the tandem cylinder. As shown in Figure 14a, it can be observed that at almost every selected flow velocity, the optimal harnessed power of two tandem cylinders has a higher value than that of the isolated cylinder. More concretely, the two cylinders in tandem can harness 2.01–4.67 times the power of the isolated cylinder at the selected range of flow velocity except for the upper branch of VIV. Further, the two tandem cylinders can achieve 1.46–4.01 times the efficiency of the isolated one.
5. Conclusions
- (1)
- The structure of BPNN is simpler than that of RBFNN when solving the problems with the same precision requirements, and the number of hidden layer neurons of RBF neural network is much higher than that of BPNN when there are more training samples, which makes the complexity and computation of RBFNN increase greatly. Therefore, this paper selected the BPNN to establish the surrogate model of the VIVACE Converter.
- (2)
- By training and testing experimental sample data, an efficient and accurate surrogate model of the VIVACE Converter was established. The harnessed power and corresponding efficiency of the Converter can be predicted accurately under different combinations of incoming flow velocity, spacing ratio, spring stiffness, and harnessing damping ratio.
- (3)
- Under a specified spring stiffness, expanding the selected range of harnessing damping ratio from 0–0.24 to 0–0.30 results in no appreciable power increase for the isolated single cylinder and two tandem cylinders for spacing (L/D = 1.57 and 2.57). On the contrary, the corresponding efficiency increases significantly due to the decreased oscillating amplitude, which directly results in decrease of PFluid. Specifically, for L/D = 2.57, the efficiency changes from 52.09% (K = 400 N/m, ζharness = 0.24) to 64.92% (K = 400 N/m, ζharness = 0.30) at U = 0.43 m/s.
- (4)
- Increasing the spring stiffness range from 400–1200 N/m to 400–1600 N/m improves the ability of power harvesting in galloping for the VIVACE Converter with two tandem cylinders (L/D = 1.57).
- (5)
- Due to synergy between two tandem cylinders, the VIVACE Converter with two tandem cylinders has a better performance of power harvesting compared to that of the isolated single cylinder. Analysis of the optimal harnessed power and efficiency shows that the two tandem cylinders can harness 2.01–4.67 times the power of the isolated cylinder. In addition, two tandem cylinders can achieve 1.46–4.01 times the efficiency of the isolated one.
- (a)
- During field-tests or in commercial use of a two-cylinder VIVACE Converter, flow speed changes. To maintain near-optimal performance, parameters should be adjusted. The derived model can provide real-time guidance to that effect.
- (b)
- The model can be tested against field-data and be modified or expanded accordingly.
- (c)
- This Converter has been studied experimentally and with field-tests for over a decade using many different parameters and various size oscillators. One of the most powerful ways of increasing its harnessed power or its harnessing efficiency is an adaptive change of parameters. For example, in [18] the spring stiffness was adjusted based on response amplitude. In [25], the damping was adjusted based on the speed of the oscillating cylinder.
- (d)
- One of the greatest advantages of the VIVACE Converter is that it is fish-friendly because it operates on alternating lift like fish rather than steady lift like wings. Nevertheless, until recently [6], there was no physics-based mathematical model of the alternating lift force in VIV or galloping, which is required for proper control. The model developed in this paper serves as a guide for a numerical control model.
- (e)
- Recently [13], a physics-based force model was developed following the revealing of an eigen-relation at the interface between fluid and structure in VIV and galloping. The eigen-relation matched experimental results with extreme accuracy changing completely the modeling of VIV and galloping. On the other hand, an eigen-relation is amplitude and energy independent while control requires a specific amplitude input for modeling. That can be provided by the model developed in this paper.
- (f)
- It should be pointed out that in future research, RBFNN method can be considered to establish the surrogate model of VIVACE Converter with double series cylinder and compared with BPNN, it must have a certain research value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Optimal Harvested Power (W) | Stiffness K [N/m] | Harnessing Damping Ratio ζharness | |||||||
|---|---|---|---|---|---|---|---|---|---|
| U [m/s] | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 |
| 0.39 | 1.23 | 4.18 | 2.38 | 700 | 400 | 500 | 0.01 | 0.3 | 0.105 |
| 0.43 | 2.21 | 5.26 | 3.02 | 680 | 400 | 540 | 0.13 | 0.3 | 0.12 |
| 0.47 | 3.34 | 5.88 | 3.67 | 680 | 420 | 580 | 0.13 | 0.3 | 0.16 |
| 0.51 | 4.15 | 6.41 | 5.01 | 680 | 440 | 720 | 0.135 | 0.3 | 0.2 |
| 0.55 | 5.13 | 7.19 | 6.53 | 720 | 660 | 740 | 0.24 | 0.225 | 0.21 |
| 0.59 | 6.42 | 8.37 | 7.88 | 720 | 600 | 760 | 0.24 | 0.3 | 0.225 |
| 0.63 | 7.32 | 10.81 | 9.42 | 700 | 580 | 960 | 0.23 | 0.3 | 0.23 |
| 0.67 | 8.05 | 12.94 | 11.29 | 680 | 580 | 980 | 0.22 | 0.3 | 0.24 |
| 0.71 | 8.82 | 14.54 | 12.88 | 660 | 600 | 1080 | 0.21 | 0.3 | 0.235 |
| 0.75 | 9.65 | 15.78 | 13.76 | 660 | 620 | 1120 | 0.205 | 0.3 | 0.24 |
| 0.79 | 10.64 | 16.89 | 14.27 | 680 | 640 | 1200 | 0.205 | 0.3 | 0.255 |
| 0.83 | 12.11 | 17.89 | 14.37 | 820 | 660 | 1200 | 0.165 | 0.3 | 0.255 |
| 0.87 | 15.00 | 18.74 | 14.18 | 840 | 680 | 1200 | 0.165 | 0.3 | 0.25 |
| 0.91 | 18.61 | 19.65 | 14.08 | 860 | 680 | 1200 | 0.165 | 0.3 | 0.21 |
| 0.95 | 22.19 | 21.03 | 15.41 | 880 | 700 | 1080 | 0.17 | 0.3 | 0.175 |
| 0.99 | 25.82 | 23.23 | 18.07 | 1200 | 700 | 1100 | 0.25 | 0.3 | 0.17 |
| 1.03 | 29.34 | 24.75 | 21.13 | 1200 | 700 | 1180 | 0.25 | 0.3 | 0.18 |
| 1.07 | 31.83 | 25.00 | 23.36 | 1200 | 700 | 1200 | 0.255 | 0.3 | 0.19 |
| 1.11 | 33.88 | 24.90 | 23.08 | 1200 | 720 | 1200 | 0.265 | 0.3 | 0.19 |
| 1.15 | 35.96 | 25.45 | 23.84 | 1200 | 760 | 640 | 0.28 | 0.3 | 0.2 |
| 1.19 | 38.01 | 26.94 | 25.50 | 1200 | 760 | 620 | 0.29 | 0.3 | 0.185 |
| 1.23 | 39.50 | 29.65 | 27.77 | 1200 | 780 | 600 | 0.295 | 0.3 | 0.185 |
| 1.27 | 40.28 | 32.73 | 30.58 | 1200 | 780 | 600 | 0.285 | 0.3 | 0.19 |
| 1.31 | 40.62 | 34.99 | 33.61 | 1200 | 780 | 600 | 0.275 | 0.3 | 0.2 |
| Optimal Converted Efficiency (%) | Stiffness K [N/m] | Harnessing Damping Ratio ζharness | |||||||
|---|---|---|---|---|---|---|---|---|---|
| U [m/s] | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 | L/D = 1.57 | L/D = 2.00 | L/D = 2.57 |
| 0.39 | 29.95 | 46.86 | 54.03 | 460 | 400 | 400 | 0.16 | 0.195 | 0.235 |
| 0.43 | 33.70 | 51.65 | 57.71 | 460 | 440 | 400 | 0.215 | 0.22 | 0.3 |
| 0.47 | 38.87 | 53.72 | 58.37 | 480 | 460 | 400 | 0.25 | 0.235 | 0.3 |
| 0.51 | 42.94 | 58.74 | 60.04 | 820 | 640 | 720 | 0.23 | 0.3 | 0.23 |
| 0.55 | 48.06 | 70.50 | 62.00 | 740 | 660 | 800 | 0.295 | 0.3 | 0.245 |
| 0.59 | 50.33 | 73.14 | 64.24 | 800 | 680 | 1000 | 0.3 | 0.3 | 0.3 |
| 0.63 | 49.54 | 68.92 | 67.61 | 980 | 680 | 1060 | 0.3 | 0.3 | 0.3 |
| 0.67 | 49.41 | 62.04 | 68.84 | 1120 | 680 | 1140 | 0.3 | 0.3 | 0.3 |
| 0.71 | 50.51 | 59.31 | 69.44 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.75 | 49.05 | 56.81 | 68.26 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.79 | 45.74 | 52.07 | 64.15 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.83 | 41.95 | 47.33 | 55.98 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.87 | 38.50 | 43.07 | 45.14 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.91 | 35.75 | 38.97 | 34.66 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.3 |
| 0.95 | 33.71 | 34.78 | 29.64 | 1200 | 1200 | 1180 | 0.3 | 0.3 | 0.21 |
| 0.99 | 32.24 | 30.61 | 27.56 | 1200 | 1200 | 1180 | 0.3 | 0.3 | 0.215 |
| 1.03 | 31.12 | 26.76 | 25.70 | 1200 | 1200 | 1200 | 0.3 | 0.3 | 0.22 |
| 1.07 | 30.62 | 24.14 | 23.84 | 1200 | 680 | 1200 | 0.255 | 0.23 | 0.225 |
| 1.11 | 30.19 | 22.51 | 22.29 | 1200 | 700 | 980 | 0.25 | 0.23 | 0.3 |
| 1.15 | 29.61 | 21.38 | 21.20 | 1200 | 760 | 1000 | 0.25 | 0.3 | 0.3 |
| 1.19 | 28.79 | 21.59 | 19.91 | 1200 | 780 | 1020 | 0.25 | 0.3 | 0.3 |
| 1.23 | 27.67 | 22.30 | 18.61 | 1200 | 800 | 1000 | 0.255 | 0.3 | 0.3 |
| 1.27 | 26.22 | 22.92 | 18.51 | 1200 | 800 | 660 | 0.265 | 0.3 | 0.3 |
| 1.31 | 24.61 | 23.29 | 19.37 | 1200 | 820 | 640 | 0.285 | 0.3 | 0.3 |
| Parameters for Optimal Pharness | Parameters for Optimal ηharness | |||||
|---|---|---|---|---|---|---|
| U [m/s] | Pharness [W] | K [N/m] | ζharness | ηharness [%] | K [N/m] | ζharness |
| 0.43 | 1.13 | 400 | 0.155 | 25.83 | 780 | 0.3 |
| 0.47 | 1.51 | 400 | 0.15 | 26.36 | 820 | 0.3 |
| 0.51 | 2.55 | 600 | 0.185 | 33.40 | 620 | 0.22 |
| 0.55 | 3.89 | 600 | 0.18 | 41.34 | 680 | 0.22 |
| 0.59 | 5.15 | 640 | 0.185 | 45.09 | 720 | 0.24 |
| 0.63 | 6.41 | 880 | 0.225 | 46.10 | 880 | 0.24 |
| 0.67 | 8.50 | 940 | 0.245 | 47.06 | 920 | 0.28 |
| 0.71 | 10.00 | 980 | 0.26 | 45.56 | 960 | 0.3 |
| 0.75 | 9.66 | 1020 | 0.275 | 39.22 | 1020 | 0.3 |
| 0.79 | 7.63 | 1200 | 0.22 | 31.07 | 1200 | 0.24 |
| 0.83 | 5.91 | 1200 | 0.3 | 21.10 | 1200 | 0.28 |
| 0.87 | 4.20 | 1200 | 0.3 | 12.47 | 1200 | 0.3 |
| 0.91 | 5.22 | 1200 | 0.105 | 9.72 | 1200 | 0.3 |
| 0.95 | 6.70 | 1200 | 0.115 | 11.97 | 1200 | 0.3 |
| 0.99 | 7.43 | 1200 | 0.125 | 15.20 | 1200 | 0.3 |
| 1.03 | 7.94 | 1200 | 0.165 | 16.55 | 1200 | 0.3 |
| 1.07 | 8.56 | 1200 | 0.175 | 16.08 | 1200 | 0.3 |
| 1.11 | 9.15 | 1200 | 0.17 | 14.85 | 1200 | 0.3 |
| 1.15 | 10.14 | 1080 | 0.175 | 13.57 | 1200 | 0.3 |
| 1.19 | 11.61 | 1080 | 0.18 | 12.50 | 1200 | 0.3 |
| 1.23 | 13.35 | 1140 | 0.3 | 11.70 | 1200 | 0.3 |
| 1.27 | 16.61 | 1180 | 0.3 | 11.35 | 1040 | 0.3 |
| 1.31 | 19.93 | 1200 | 0.3 | 11.19 | 1060 | 0.3 |
References
- Bull, S.R. Renewable Energy Today and Tomorrow. IEEE Proc. 2001, 89, 1216–1226. [Google Scholar] [CrossRef]
- Lund, H. Renewable energy strategies for sustainable development. Energy 2007, 32, 912–919. [Google Scholar] [CrossRef] [Green Version]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Hongda, M. Research on Power Control Method of Oscillating Float Type Ocean Wave Energy Power Generation. IOP Conf. Ser. Earth Environ. Sci. 2020, 546, 022027. [Google Scholar] [CrossRef]
- Wang, J.L.; Su, Z.; Li, H.; Ding, L.; Zhu, H.J.; Gaidai, O. Imposing a wake effect to improve clean marine energy harvesting by flow-induced vibrations. Ocean Eng. 2020, 208, 107455. [Google Scholar] [CrossRef]
- You, Y.G.; Li, W.; Liu, W.M.; Li, X.Y.; Wu, F. Development Status and Perspective of Marine Energy Conversion Systems. Autom. Electr. Power Syst. 2010, 34, 1–12. [Google Scholar]
- Bernitsas, M.M. Harvesting Energy by Flow Included Motions. In Springer Handbook of Ocean Engineering; Dhanak, M.R., Xiros, N.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Chapter 47; pp. 1163–1244. ISBN 978-3-319-16648-3. [Google Scholar]
- VanZwieten, J.H.; Smentek-Duerr, A.E.; Alsenas, G.M.; Hanson, H.P. Global Ocean Current Energy Assennment: An Initial Look. In Proceedings of the 1st Marine Energy Technology Symposium, Washington, DC, USA, 10–11 April 2013. [Google Scholar]
- Yang, L.F.; Haas, K.A.; Fritz, H.M. Theoretical Assessment of Ocean Current Energy Potential for the Gulf Stream System. Mar. Technol. Soc. J. 2013, 47, 101–112. [Google Scholar] [CrossRef]
- Martinez, R.; Ordonez-Sanchez, S.; Matthem, A.; Catherine, L.; Tim, O.D.; Gregory, G.; Benoit, G.; Cameron, J. Analysis of the effects of control strategies and wave climates on the loading and performance of a laboratory scale horizontal axis tidal turbine. Ocean Eng. 2020, 212, 107713. [Google Scholar] [CrossRef]
- Sleiti, A.K. Overview of Tidal Power Technology. Energy Sources Part B Econ. Plan. Policy 2015, 10, 8–13. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-Induced Vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef] [Green Version]
- Bernitsas, M.M.; Ofuegbe, J.; Chen, J.-U.; Sun, H. Eigen-Relation for Flow Induced Oscillations (VIV & Galloping) Revealed at the Fluid-Structure Interface. In Proceedings of the 38th OMAE 2019 Conference, Glasgow, Scotland, 9–14 June 2019. Paper #96823. [Google Scholar]
- Jauvtis, N.; Williamson, C.H.K. Vortex-induced vibration of a cylinder with two degrees of freedom. J. Fluids Struct. 2003, 17, 1035–1042. [Google Scholar] [CrossRef]
- Ji, C.N.; Li, F.F.; Chen, W.L.; Song, X.Y. Progress and Prospect of the Study on Vortex-Induced Vibration of Circular Cylinders. J. Ocean Technol. 2015, 34, 106–118. [Google Scholar]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (vortex induced vibration aquatic clean energy): A new concept in generation of clean and renewable energy from fluid flow. In Proceedings of the 25th International Conference on Offshore Mechanicals and Arctic Engineering-OMAE, Hamburg, Gemany, 4–9 June 2006. [Google Scholar]
- Prasanth, T.K.; Mittal, S. Flow-induced oscillation of two circular cylinders in tandem arrangement at low Re. J. Fluids Struct. 2009, 25, 1029–1048. [Google Scholar] [CrossRef]
- Ma, C.H.; Sun, H.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Nonlinear piecewise restoring force in hydrokinetic power conversion using flow induced motions of single cylinder. Ocean Eng. 2016, 128, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Bernitsas, M.M.; Kumar, A.R. Using the map of passive turbulence control to flow induced motions to suppress circular cylinder motion at 31,000 ≤ Re ≤ 120,000. J. Offshore Mech. Arctic Eng. Trans. ASME 2012, 134, V007T08A003. [Google Scholar]
- Park, H.R.; Kumar, R.A.; Bernitsas, M.M. Enhancement of flow induced motions of rigid circular cylinder on springs by localized surface roughness at 3 × 104 ≤ Re ≤ 1.2 × 105. Ocean Eng. 2013, 72, 403–415. [Google Scholar] [CrossRef]
- Raghavan, K.; Bernitsas, M.M. Enhancement of high damping VIV though roughness distribution for energy harnessing at 8 × 103 < Re < 1.5 × 105. In Proceedings of the 27th International Conference on Offshore Mechanicals and Arctic Engineering-OMAE, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Sun, H.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Effect of mass-ratio, damping, and stiffness on optimal kydrokinetic energy conversion of a single, rough cylinder in flow induced motions. Renew. Energy 2016, 99, 936–959. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Ma, C.H.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Hydrokinetic energy conversion by two rough tandem-cylinders in flow induced motions: Effect of spacing and stiffness. Renew. Energy 2017, 107, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Zhang, L.; Bernitsas, M.M. Numerical simulation and experimental validation for energy harvesting of single-cylinder VIVACE converter with passive turbulence control. Renew. Energy 2016, 85, 1246–1259. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Bernitsas, M.M.; Turkol, M. Adaptive harnessing damping in hydrokinetic energy conversion by two rough tandem-cylinders using flow-induced vibrations. Renew. Energy 2020, 149, 828–860. [Google Scholar] [CrossRef]
- Lee, J.H.; Bernitsas, M.M. High-damping, high-Reynolds VIV tests for energy harnessing using the VIVACE converter. Ocean Eng. 2011, 38, 1679–1712. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, L.; Kim, E.S.; Bernitsas, M.M. 2D-URANS vs. Experiments of Flow Induced Motions of Multiple Circular Cylinders with Passive Turbulence Control. J. Fluids Struct. 2015, 54, 612–628. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Zhang, L.; Wu, C.M.; Kim, E.S.; Bernitsas, M.M. Numerical study on the effect of tandem spacing on flow-induced motions of two cylinders with passive turbulence control. J. Offshore Mech. Arctic Eng. 2017, 139, 021801. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of Metamodeling Techniques in Support of Engineering Design Optimization. J. Mech. Des. 2016, 129, 370–380. [Google Scholar] [CrossRef]
- Sultan, I.A.; Ahmed, M.R.; Gareth, L.F. Evaluation of slug flow-induced flexural loading in pipelines using a surrogate model. J. Offshore Mech. Arctic Eng. 2013, 135, 031703. [Google Scholar] [CrossRef]
- Zhang, J.; Chowdhury, S.; Messac, A. An adaptive hybrid surrogate model. Struct. Multidiscip. 2012, 46, 223–238. [Google Scholar] [CrossRef]
- Matias, S.; Nestor, R.G.; Yang, H.; Shen, W.Z. Aerodynamic wind-turbine rotor design using surrogate modeling and three-dimensional viscous-inviscid interaction technique. Renew. Energy 2016, 93, 620–635. [Google Scholar]
- Wu, W.H.; Sun, H.; Lv, B.C.; Bernitsas, M.M. Modelling of a hydrokinetic energy converter for flow-induced vibration based on experimental data. Ocean Eng. 2018, 155, 392–410. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Radial basis functions, multi-variable functional interpolation and adaptive networks. Royal Radar Est. 1988. [Google Scholar]
- Yasav, A.K.; Sharma, V.; Malik, H.; Chandel, S.S. Daily array yield prediction of grid-interaction photovoltaic plant using relief attribute evaluator based Radial Basis Function Neural Network. Renew. Sustain. Energy Rev. 2018, 81, 2115–2127. [Google Scholar]
- Jin, W.; Li, Z.J.; Wei, L.S.; Zhen, H. The improvements of BP neural network learning algorithm. In Proceedings of the 5th International Conference on Signal Processing Proceedings 16th World Computer Congress, Beijing, China, 21–25 August 2000. [Google Scholar]
- Sadeghi, B.H.M. A BP-neural network predictor model for plastic injection molding process. J. Mater. Process. Technol. 2000, 103, 411–416. [Google Scholar] [CrossRef]
- Kim, E.S.; Bernitsas, M.M.; Kumar, R.A. Multicylinder Flow-Induced Motions: Enhancement by Passive Turbulence Control at 28,000 < Re < 120,000. J. Offshore Mech. Arctic Eng. 2013, 135, 021802. [Google Scholar]
- Sun, H.; Kim, E.S.; Bernitsas, P.M.; Bernitsas, M.M. Virtual spring–damping system for flow-induced vibration experiments. J. Offshore Mech. Arctic Eng. 2015, 137, 061801. [Google Scholar] [CrossRef]
- Shi, Y.W.; Wang, C.K.; Shen, J.F. Utilization and prospect of ocean energy resource in china. Acta Energ. Sol. Sin. 2011, 6, 913–923. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence-IJCAI, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]










| Surrogate Model | Variables | Values |
|---|---|---|
| L/D = 1.57 L/D = 2.00 L/D = 2.57 Isolated cylinder | Incoming flow velocity (U) | 0.39–1.31 m/s |
| Spring stiffness (K) | 400 N/m, 600 N/m, 800 N/m, 1000 N/m, 1200 N/m | |
| Harnessing damping ratio (ζharness) | 0.00, 0.04, 0.08, 0.12, 0.16, 0.20, 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Sun, L.; Bernitsas, M.M.; Jiang, M.; Sun, H. Modelling of a Flow-Induced Oscillation, Two-Cylinder, Hydrokinetic Energy Converter Based on Experimental Data. Energies 2021, 14, 827. https://doi.org/10.3390/en14040827
Lv Y, Sun L, Bernitsas MM, Jiang M, Sun H. Modelling of a Flow-Induced Oscillation, Two-Cylinder, Hydrokinetic Energy Converter Based on Experimental Data. Energies. 2021; 14(4):827. https://doi.org/10.3390/en14040827
Chicago/Turabian StyleLv, Yanfang, Liping Sun, Michael M. Bernitsas, Mengjie Jiang, and Hai Sun. 2021. "Modelling of a Flow-Induced Oscillation, Two-Cylinder, Hydrokinetic Energy Converter Based on Experimental Data" Energies 14, no. 4: 827. https://doi.org/10.3390/en14040827
APA StyleLv, Y., Sun, L., Bernitsas, M. M., Jiang, M., & Sun, H. (2021). Modelling of a Flow-Induced Oscillation, Two-Cylinder, Hydrokinetic Energy Converter Based on Experimental Data. Energies, 14(4), 827. https://doi.org/10.3390/en14040827





