An Experimental Study of Gas Flow Regime and Pressure Drop in a Random Packed Bed with Sinter Particles
Abstract
:1. Introduction
2. Experimental Description
3. Results and Discussion
3.1. Analysis of Gas Flow Regime
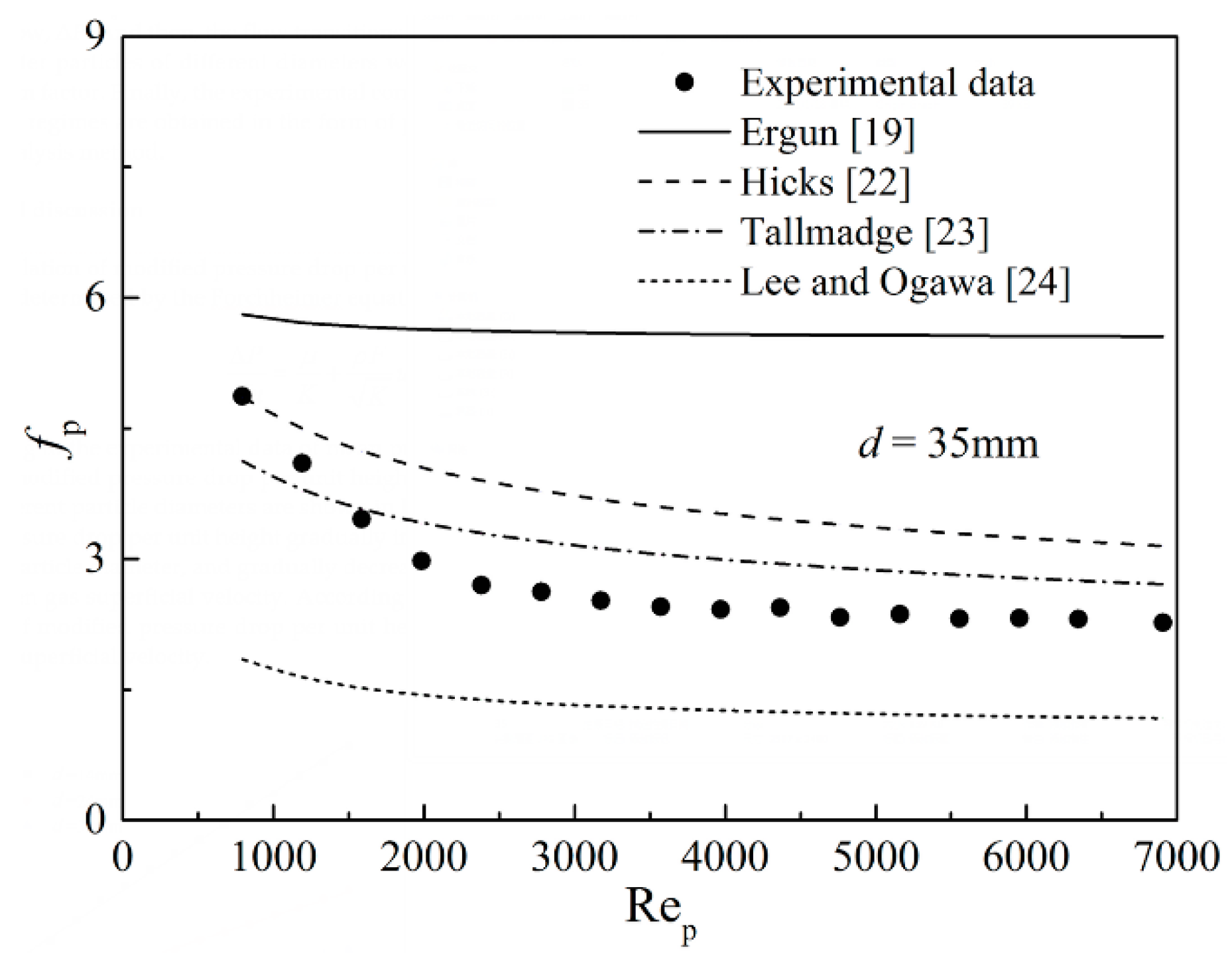
3.2. Determination of the Particle Friction Factor
4. Conclusions
- (1)
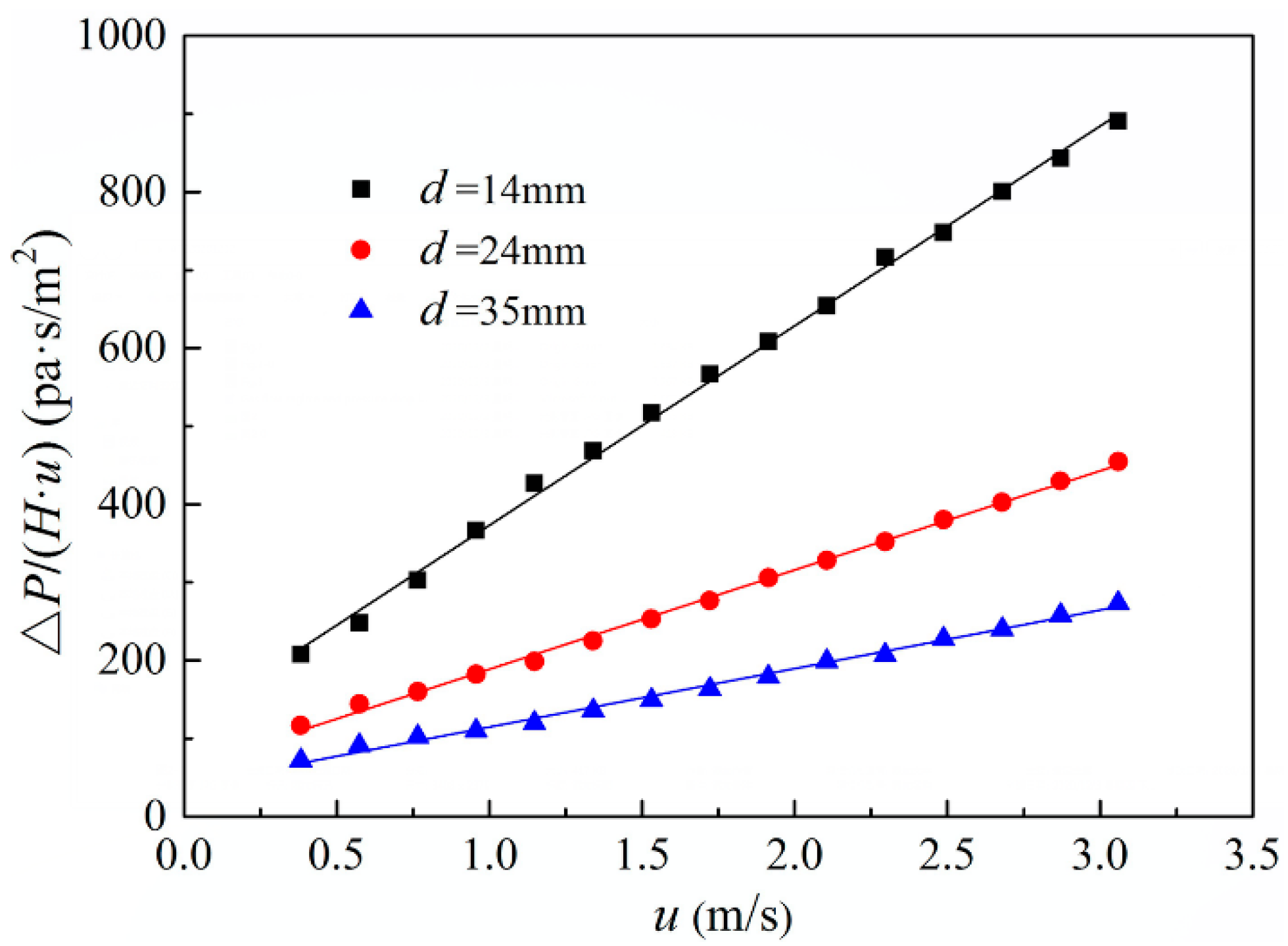
- For a certain particle diameter, the modified pressure drop per unit height, ΔP/Hu, increased linearly with the increase in gas superficial velocity, and the decrease in the particle friction factor, fp, demonstrated a power exponential relationship with the increasing particle Reynolds number, Rep.
- (2)
- Because of the differences in the modified coefficients α and β for various flow regimes, when the gas superficial velocity was larger than 1.15 m/s under atmospheric conditions, the gas flow regime in the sinter bed layer at that moment was the turbulent flow.
- (3)
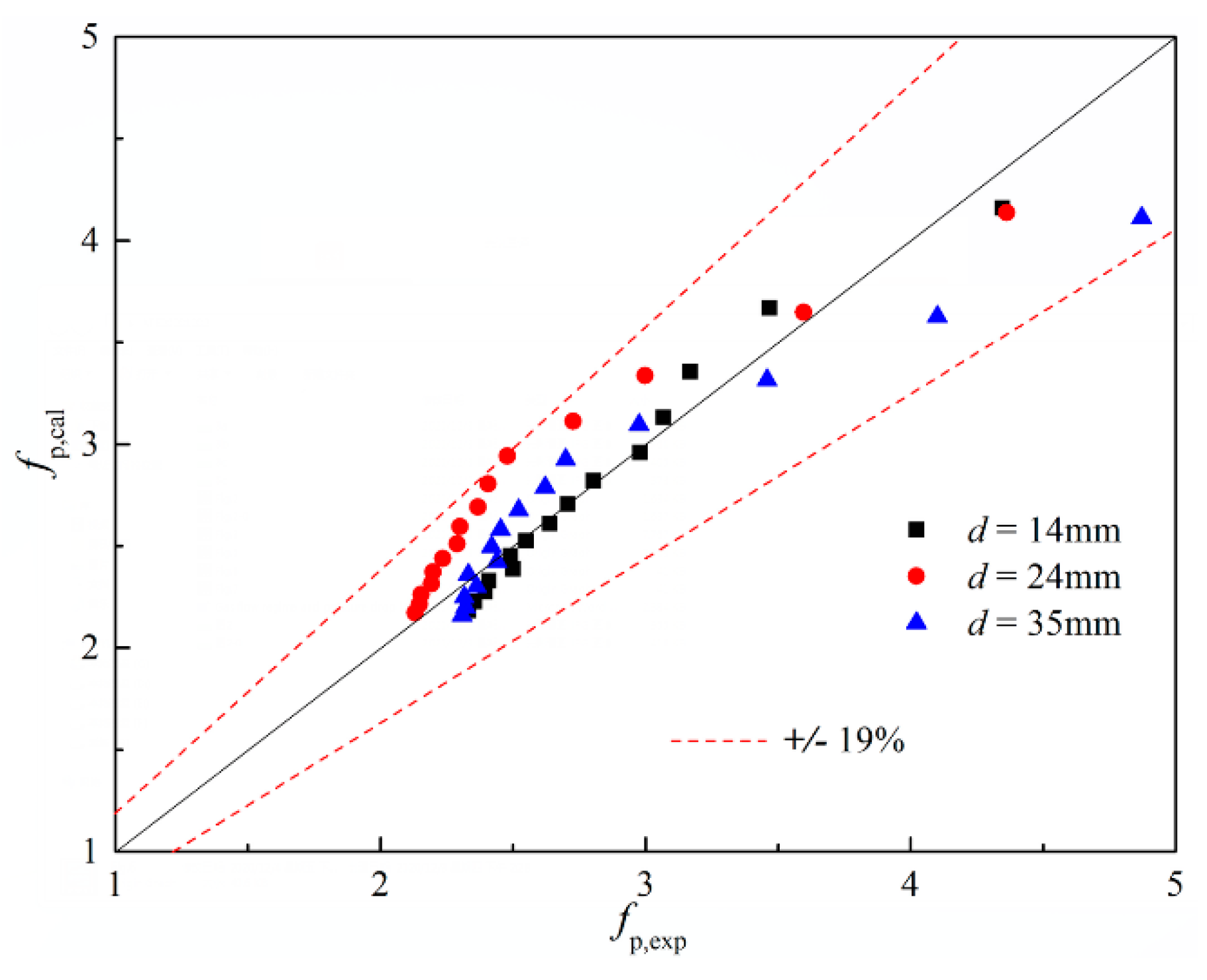
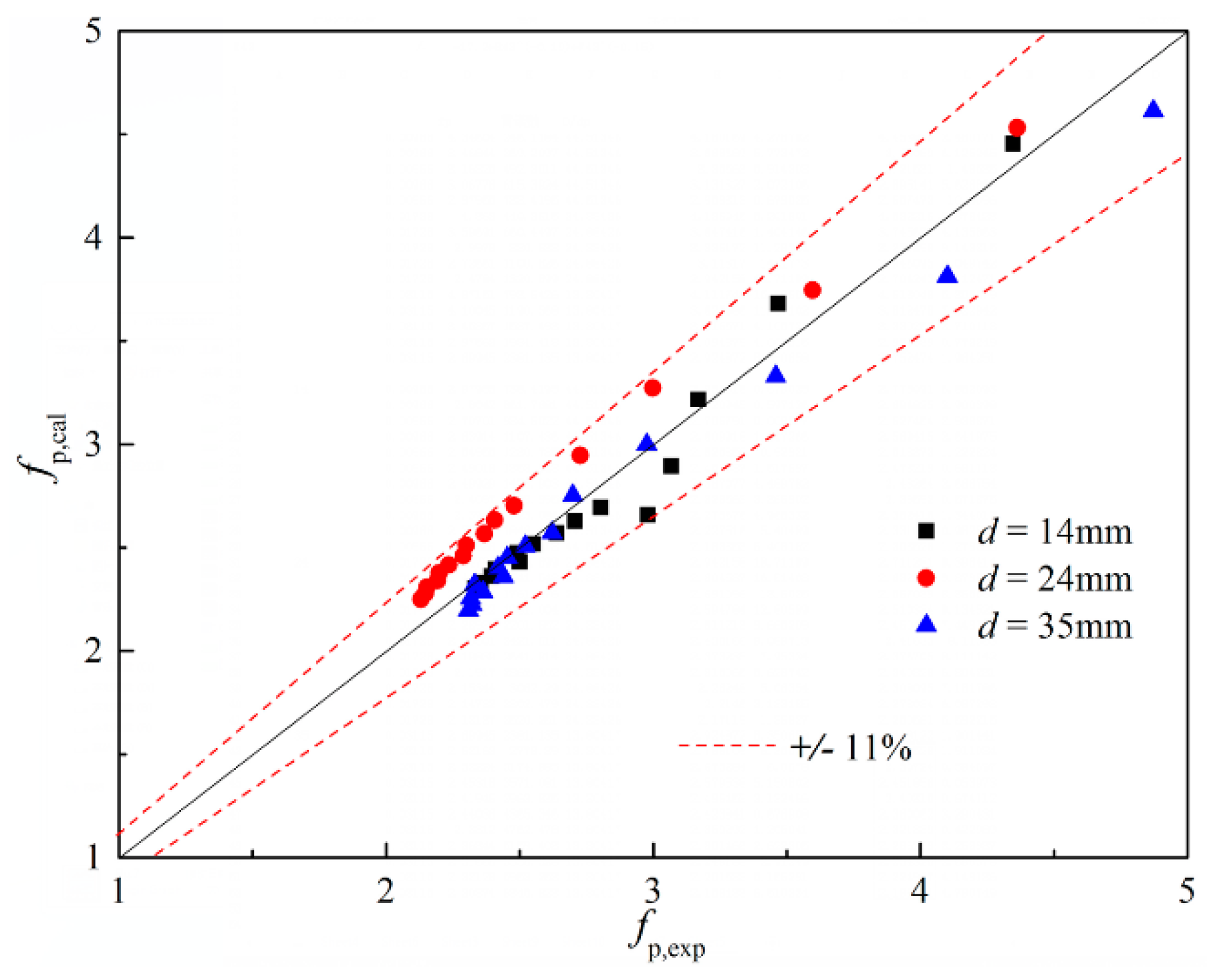
- On the basis of the dimensional analysis method, the specific equations of particle friction factor for the whole flow, the Forchheimer flow, and the turbulent flow in a sinter bed layer were determined. Compared with the experimental correlation of whole flow, the pressure drop correlations, obtained by the piecewise fitting method, provided a better prediction of the experimental data, and the average deviations of the obtained equations for the Forchheimer flow and the turbulent flow were 5.31% and 4.07%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| d | average particle diameter (m) |
| D | inner diameter of sinter bed layer (m) |
| dp | particle equivalent diameter (m) |
| F | Forchheimer coefficient (−) |
| fp | particle friction factor (−) |
| H | height of sinter bed layer (m) |
| K | permeability (m2) |
| P0 | atmospheric pressure (MPa) |
| Rep | particle Reynolds number (−) |
| T0 | ambient temperature (K) |
| u | gas superficial velocity (m/s) |
| Greek symbols | |
| ΔP | gas flow pressure drop through bed layer (Pa) |
| ΔP | gas flow pressure drop through bed layer (Pa) |
| μ | gas dynamic viscosity (Pa·s) |
| ε | bed voidage (−) |
| ρ | gas density (kg/m) |
| Φ | particle sphericity (−) |
| Subscripts | |
| c | critical point |
| cal | calculated value |
| exp | experimental value |
| p | particle |
References
- Barton, N.G. Simulations of air-blown thermal storage in a rock bed. Appl. Therm. Eng. 2013, 55, 43–50. [Google Scholar] [CrossRef]
- Bansal, P.; Jain, S.; Moon, C. Performance comparison of an adiabatic and an internally cooled structured packed-bed dehumidifier. Appl. Therm. Eng. 2011, 31, 14–19. [Google Scholar] [CrossRef]
- Bindra, H.; Bueno, P.; Morris, J.F.; Shinnar, R. Thermal analysis and exergy evaluation of packed bed thermal storage systems. Appl. Therm. Eng. 2013, 52, 255–263. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, Y.; Cai, J.J.; Zhou, J.W.; Ma, G.Y. On the air leakage problem in sintering cooling system. Iron Steel 2012, 47, 95–99. [Google Scholar]
- Cai, J.J.; Dong, H. Method and Device of Sinter Waste Heat Recovery and Utilization with Vertical Tank. Chinese Patent 200910187381.8, 5 January 2011. [Google Scholar]
- Dong, H.; Li, L.; Liu, W.J.; Wang, B.; Suo, Y.S.; Cai, J.J. Process of waste heat recovery and utilization for sinter in vertical tank. China Metall. 2012, 22, 6–11. [Google Scholar]
- Jolls, K.R.; Hanratty, T.J. Transition to turbulence for flow through a dumped bed of spheres. Chem. Eng. Sci. 1966, 21, 1185–1190. [Google Scholar] [CrossRef]
- Bu, S.S.; Yang, J.; Dong, Q.T.; Wang, Q.W. Experimental study of flow transitions in structured packed beds of spheres with electrochemical technique. Exp. Therm. Fluid. Sci. 2015, 60, 106–114. [Google Scholar] [CrossRef]
- Bu, S.S.; Yang, J.; Dong, Q.T.; Wang, Q.W. Experimental study of transition flow in packed beds of spheres with different particle sizes based on electrochemical microelectrodes measurement. Appl. Therm. Eng. 2014, 73, 1525–1532. [Google Scholar] [CrossRef]
- Yang, J.; Bu, S.S.; Dong, Q.T.; Wu, J.Q.; Wang, Q.W. Experimental study of flow transitions in random packed beds with low tube to particle diameter ratios. Exp. Therm. Fluid Sci. 2015, 66, 117–126. [Google Scholar] [CrossRef]
- Johns, M.L.; Sederman, A.J.; Bramley, A.S.; Gladden, L.F.; Alexander, P. Local transitions in flow phenomena through packed beds identified by MRI. AIChE J. 2000, 46, 2151–2161. [Google Scholar] [CrossRef]
- Horton, N.A.; Pokrajac, D. Onset of turbulence in a regular porous medium: An experimental study. Phys. Fluids 2009, 21, 104–113. [Google Scholar] [CrossRef] [Green Version]
- Saayman, J.; Nicol, W.; Ommen, J.R.V.; Mudde, R.F. Fast X-ray tomography for the quantification of the bubbling-, turbulentand fast fluidization-flow regimes and void structures. Chem. Eng. J. 2013, 234, 437–447. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Ommen, J.R.V.; Liu, D.; Mudde, R.F.; Chen, X.; Pan, S.; Liang, C. Fluidization dynamics of cohesive Geldart B particles. Part II: Pressure fluctuation analysis. Chem. Eng. J. 2019, 368, 627–638. [Google Scholar] [CrossRef] [Green Version]
- Fand, R.M.; Kim, B.Y.Y.; Lam, A.C.C.; Phan, R.T. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluids Eng. 1987, 109, 268–273. [Google Scholar] [CrossRef]
- Kececioglu, I.; Jiang, Y. Flow through porous media of packed spheres saturated with water. J. Fluids Eng. 1994, 116, 164–170. [Google Scholar] [CrossRef]
- Liu, S.; Masliyah, J.H. Single fluid flow in porous media. Chem. Eng. Commun. 1996, 148, 653–732. [Google Scholar] [CrossRef]
- Çarpinlioglu, M.Ö.; Özahi, E.; Gündogdu, M.Y. Determination of laminar and turbulent flow ranges through vertical packed beds in terms of particle friction factors. Adv. Powder Technol. 2009, 20, 515–520. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Rose, H.E. On the resistance coefficient–Reynolds number relationship for fluid flow through beds of granular materials. Proc. Inst. Mech. Eng. 1945, 153, 154–168. [Google Scholar] [CrossRef]
- Rose, H.E.; Rizk, A.M.A. Further researches in fluid flow through beds of granular material. Proc. Inst. Mech. Eng. 1949, 160, 493–511. [Google Scholar] [CrossRef]
- Hicks, R.E. Pressure drop in packed beds of spheres. Ind. Eng. Chem. Fundam. 1970, 9, 500–502. [Google Scholar] [CrossRef]
- Tallmadge, J.A. Packed bed pressure drop—An extension to higher Reynolds numbers. AIChE J. 1970, 16, 1092–1093. [Google Scholar] [CrossRef]
- Lee, J.S.; Ogawa, K. Pressure drop through packed beds. J. Chem. Eng. Jpn. 1974, 27, 691–693. [Google Scholar] [CrossRef] [Green Version]
- Montillet, A.; Akkari, E.; Comiti, J. About a correlating equation for predicting pressure drops through packed beds of spheres in a large range of Reynolds numbers. Chem. Eng. Process. 2007, 46, 329–333. [Google Scholar] [CrossRef]
- Özahi, E.; Gündogdu, M.Y.; Çarpınlıoglu, M.Ö. A modification on Ergun’s correlation for use in cylindrical packed beds with non-spherical particles. Adv. Powder Technol. 2008, 19, 369–381. [Google Scholar] [CrossRef]
- Antohe, B.V.; Lage, J.L.; Price, D.C.; Weber, R.M. Experimental determination of permeability and inertial coefficients of mechanically compressed aluminum porous matrices. J. Fluids Eng. 1997, 11, 404–412. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Cavallini, A.; Rossetto, L. Pressure drop during air flow in aluminum foam. Int. J. Heat Mass Trans. 2010, 53, 3121–3130. [Google Scholar] [CrossRef]
- Feng, J.S.; Dong, H.; Liu, J.Y.; Liang, K.; Gao, J.Y. Experimental study of gas flow characteristics in vertical tank for sinter waste heat recovery. Appl. Therm. Eng. 2015, 91, 73–79. [Google Scholar] [CrossRef]
- Feng, J.S.; Dong, H.; Dong, H.D. Modification of Ergun’s correlation in vertical tank for sinter waste heat recovery. Powder Technol. 2015, 280, 89–93. [Google Scholar] [CrossRef]



| d (mm) | Φ | dp (mm) | u (m/s) |
|---|---|---|---|
| 14 | 0.69 | 9.66 | 0.3827, 0.5741, 0.7655, 0.9569, 1.15, 1.34, 1.531, 1.722, 1.9138, 2.105, 2.2965, 2.4879, 2.6793, 2.8707, 3.06 |
| 24 | 0.72 | 17.28 | 0.3827, 0.5741, 0.7655, 0.9569, 1.15, 1.34, 1.531, 1.722, 1.9138, 2.105, 2.2965, 2.4879, 2.6793, 2.8707, 3.06 |
| 35 | 0.89 | 31.15 | 0.3827, 0.5741, 0.7655, 0.9569, 1.15, 1.34, 1.531, 1.722, 1.9138, 2.105, 2.2965, 2.4879, 2.6793, 2.8707, 3.06 |
| Coefficients | Forchheimer Flow | Turbulent Flow | ||||
|---|---|---|---|---|---|---|
| d = 14 mm | d = 24 mm | d = 35 mm | d = 14 mm | d = 24 mm | d = 35 mm | |
| α | 456.8 | 1305.2 | 2798.1 | 745.6 | 753.1 | 1658 |
| β | 2.35 | 1.5 | 1.55 | 1.96 | 1.92 | 2.03 |
| Flow Regions | Fitting Parameters | ||
|---|---|---|---|
| k | a1 | a2 | |
| Whole flow | 71.6 | −0.31 | −0.3 |
| Forchheimer flow | 395.2 | −0.47 | −0.5 |
| Turbulent flow | 17.2 | −0.19 | −0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Wang, H.; Feng, J.; Dong, H. An Experimental Study of Gas Flow Regime and Pressure Drop in a Random Packed Bed with Sinter Particles. Energies 2021, 14, 872. https://doi.org/10.3390/en14040872
Cheng Z, Wang H, Feng J, Dong H. An Experimental Study of Gas Flow Regime and Pressure Drop in a Random Packed Bed with Sinter Particles. Energies. 2021; 14(4):872. https://doi.org/10.3390/en14040872
Chicago/Turabian StyleCheng, Zude, Haitao Wang, Junsheng Feng, and Hui Dong. 2021. "An Experimental Study of Gas Flow Regime and Pressure Drop in a Random Packed Bed with Sinter Particles" Energies 14, no. 4: 872. https://doi.org/10.3390/en14040872






