Dimensioning Methodology of an Energy Storage System Based on Supercapacitors for Grid Code Compliance of a Wave Power Plant
Abstract
:1. Introduction
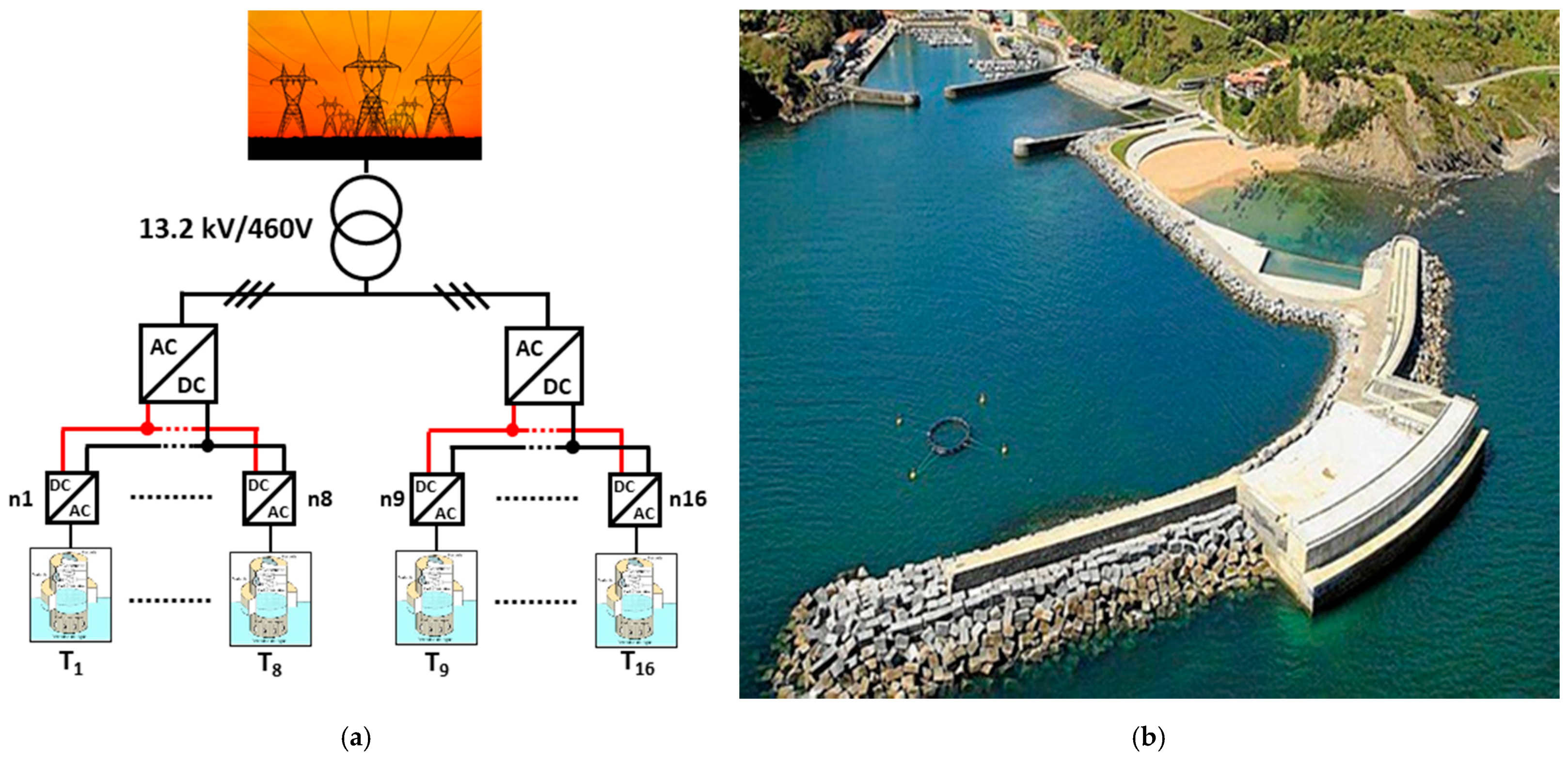
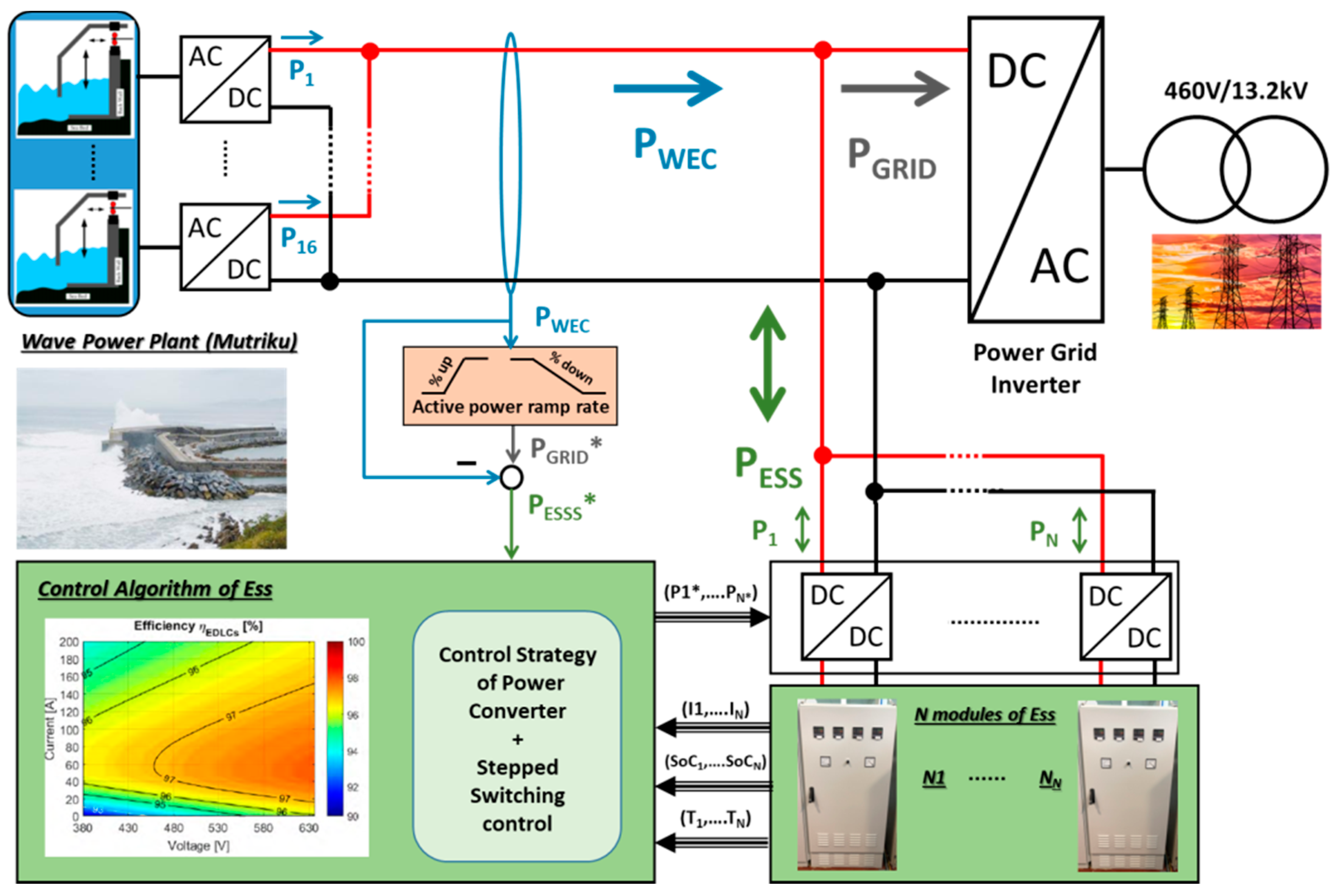
2. Wave Power Generation Plant
3. Description of an Energy Storage System Based on SCs
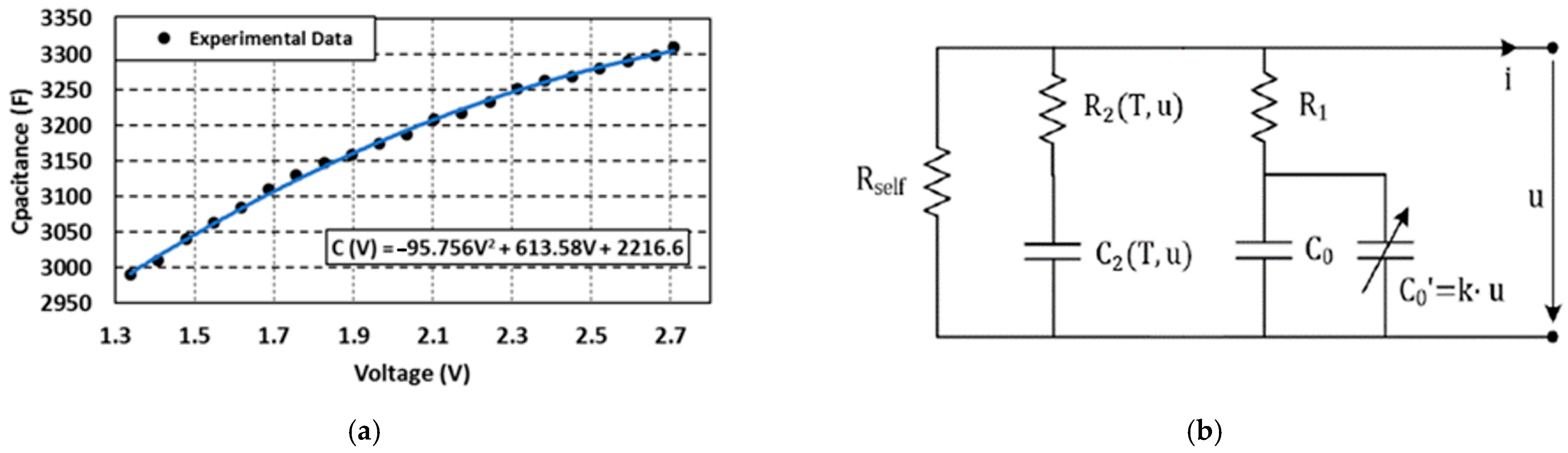
- V: Voltage measured in the terminals of the SC (V);
- C (V): Capacitance as a function of the voltage (F).
- UMAX: Maximum operating voltage measured on the SC (V);
- UMIN: Minimum operating voltage measured on the SC (V);
- C: Average value of SC capacitance (F).
3.1. Description of the Real SCESS Module on Which this Study Is Based
3.2. Operation Limits and Calculation of Power Losses and Performance of the SCESS
- USUPERCAP_max: 2.65 V;
- USUPERCAP_max: 0.6·UMAX;
- ISUPERCAP_max: 200 A.
3.2.1. Power Losses in the Equivalent Series Resistance (ESR)
- PESR(t): Instantaneous power losses;
- USC(t): SC voltage;
- iSC(t): Instantaneous current through the SCs.
- ISC(i): Harmonic component of the current;
- w: Angular frequency.
- UESR (i): Voltage across ESR
- ESR (iw): ESR value for each frequency
- IRMS: r.m.s value of the current;
- ESR (eq): Total ESR.
- USC: SC voltage;
- Irms: r.m.s value of the current through the SC.
3.2.2. Voltage Balancing System Power Losses
- : Voltage balancing system power losses;
- : Power dissipation resistance;
- : Current dissipation as a function of the measured voltage.
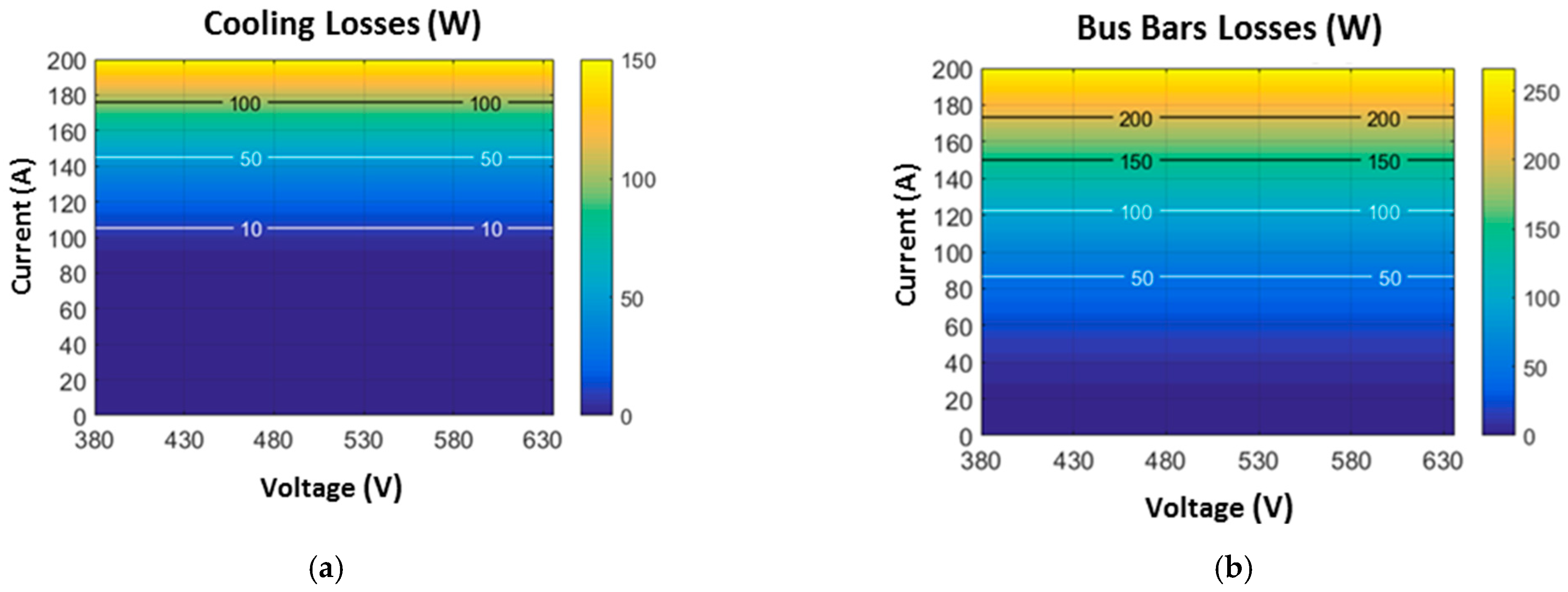
3.2.3. Cooling System and Electrical Connection Plates Power Losses
- : Resistance of connection bars;
- : Aluminum resistivity;
- : Connection plate length;
- : Connection plate section.
- : Current through the SCs;
- : Number of SCs connected in series.
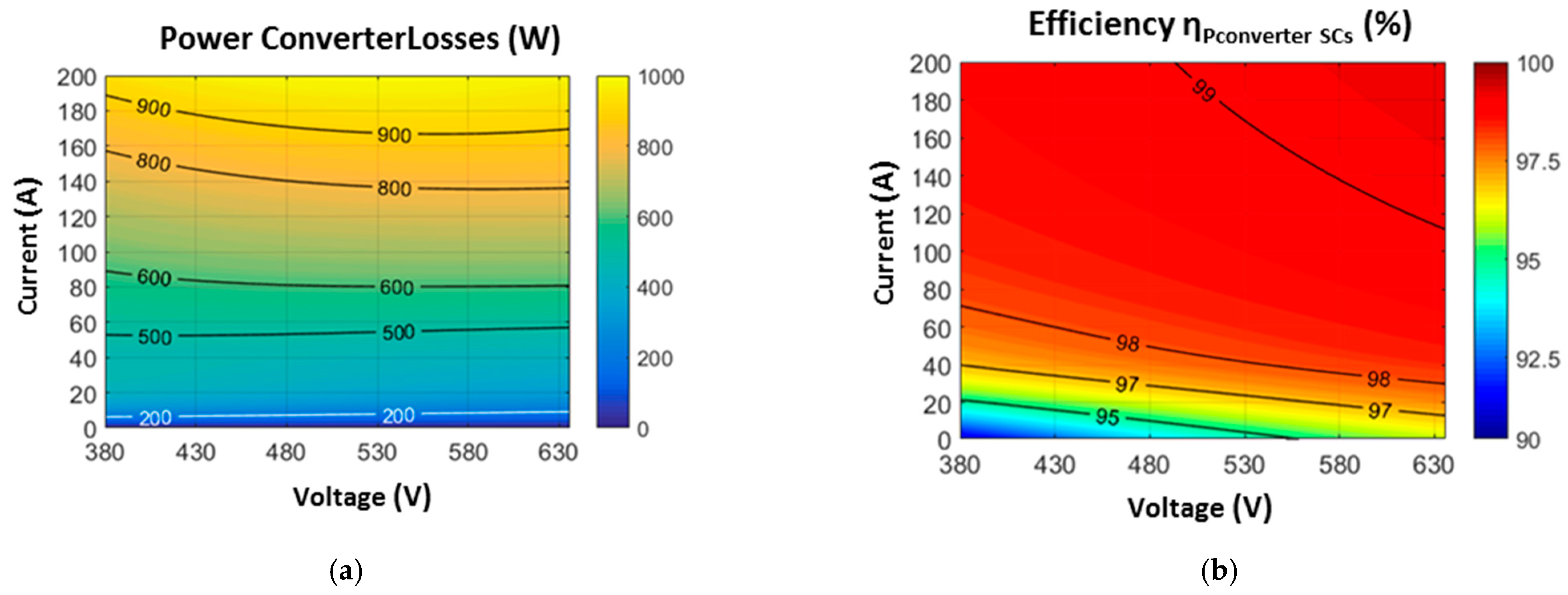
3.2.4. Power Converter and Total Losses
- : Voltage of the SCs system;
- : Current through the SCs;
- : Power converter losses.
4. Description and Results Obtained from the Simulation Model Developed
4.1. Scheme of the Model Elaborated in SIMULINK‒MATLAB and Its Input Parameters
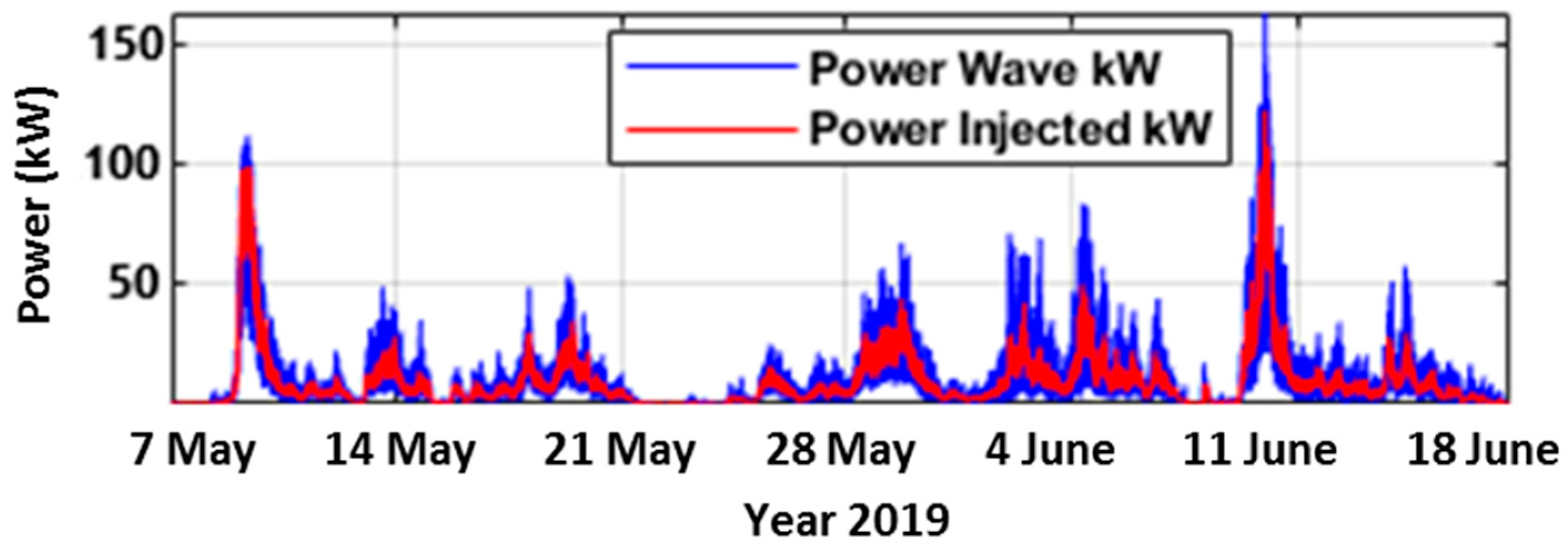
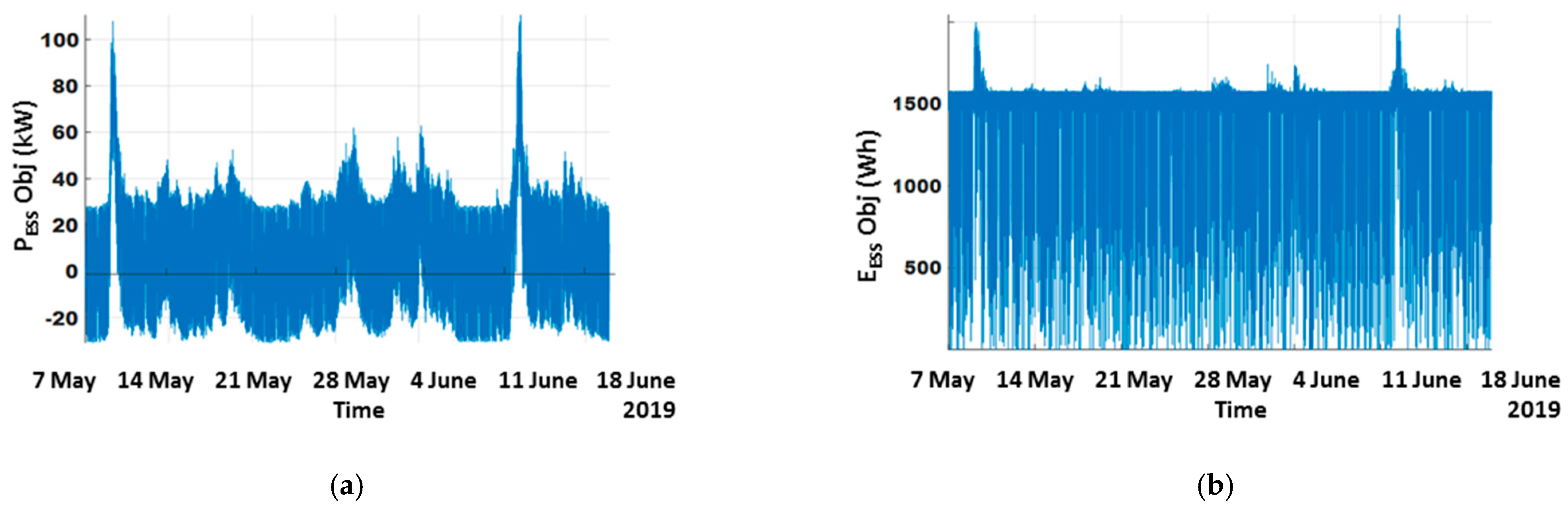
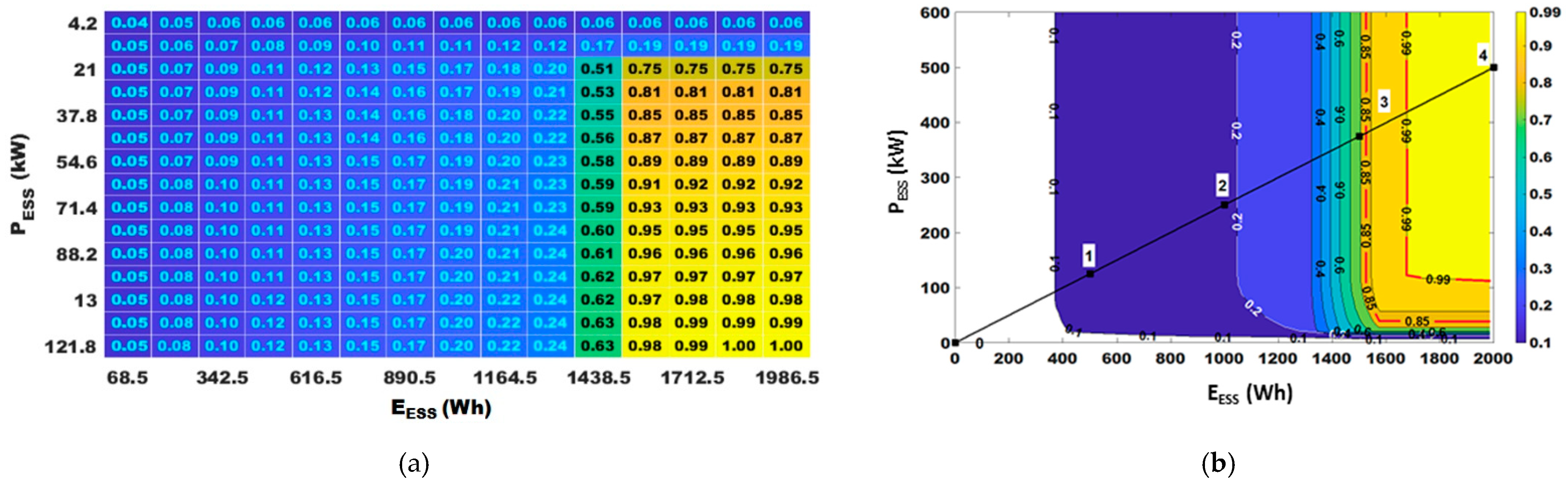
4.2. Results Obtained in the Simulation Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Robles, E.; Haro-Larrode, M.; Santos-Mugica, M.; Etxegarai, A.; Tedeschi, E. Comparative analysis of European grid codes relevant to offshore renewable energy installations. Renew. Sustain. Energy Rev. 2019, 102, 171–185. [Google Scholar] [CrossRef]
- Cruz, J. Ocean Wave Energy; Springer Berlin Heidelberg: Berlin, Germany, 2008. [Google Scholar]
- Villalba, I.; Blanco, M.; Pérez-Díaz, J.I.; Fernández, D.; Díaz, F.; Lafoz, M.; Perez-Diaz, J.I.; Fernandez, D.; Díaz, F. Wave farms grid code compliance in isolated small power systems. IET Renew. Power Gener. 2019, 13, 171–179. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean Wave Energy Converters: Status and Challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, M.; Karimpour, F.; Goudey, C.A.; Jacobson, P.T.; Alam, M.R. Ocean wave energy in the United States: Current status and future perspectives. Renew. Sustain. Energy Rev. 2017, 74, 1300–1313. [Google Scholar] [CrossRef]
- Khojasteh, D.; Mousavi, S.M.; Glamore, W.; Iglesias, G. Wave energy status in Asia. Ocean Eng. 2018, 169, 344–358. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Al-Shetwi, A.Q.; Hannan, M.A.; Jern, K.P.; Mansur, M.; Mahlia, T.M.I. Grid-connected renewable energy sources: Review of the recent integration requirements and control methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- Eltigani, D.; Masri, S. Challenges of integrating renewable energy sources to smart grids: A review. Renew. Sustain. Energy Rev. 2015, 52, 770–780. [Google Scholar]
- Blanco, M.; Navarro, G.; Lafoz, M.; Perez, J.I. Study of the impact of wave energy generation in the frequency of an island electric grid. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Blavette, A.; O’Sullivan, D.L.; Alcorn, R.; Lewis, T.W.; Egan, M.G. Impact of a medium-size wave farm on grids of different strength levels. IEEE Trans. Power Syst. 2014, 29, 917–923. [Google Scholar] [CrossRef]
- Macdowell, J.; Wang, Y.; Quint, R.; Chi, Y.; Ernst, B.; Saylors, S.; Jacobson, D.; Andresen, B.; Sorensen, P.E.; Portales, R.; et al. A journey through energy systems integration: Trending grid codes, standards, and IEC collaboration. IEEE Power Energy Mag. 2019, 17, 79–88. [Google Scholar] [CrossRef]
- Wu, Y.K.; Chang, S.M.; Mandal, P. Grid-connected wind power plants: A survey on the integration requirements in modern grid codes. In Proceedings of the Conference Record—Industrial and Commercial Power Systems Technical Conference, Calgary, AB, Canada, 5–8 May 2019; pp. 1–9. [Google Scholar] [CrossRef]
- Karbouj, H.; Rather, Z.H. A Comparative Study on the Impact of Grid Code Regulations on Stability of Wind Integrated Power Systems. In Proceedings of the 2019 IEEE 1st Global Power, Energy and Communication Conference, GPECOM 2019, Nevsehir, Turkey, 12–15 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 342–347. [Google Scholar]
- Karray, I.; Ben Kilani, K.; Elleuch, M. Wind Plant Control under Grid Code Requirements. In Proceedings of the 16th International Multi-Conference on Systems, Signals and Devices, SSD 2019, Istanbul, Turkey, 21–24 March 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 706–711. [Google Scholar]
- Attya, A.B. Provision of frequency support by wind power plants: Assessment of compliance with grid codes. In Proceedings of the 2019 IEEE Milan PowerTech, PowerTech 2019, Milan, Italy, 23–27 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; p. 8810978. [Google Scholar]
- Lin, D.; Li, X.; Ding, S. An Investigation on Cost-effectiveness of Photovoltaic Power Ramp Rate Control by Using the Levelized Cost of Electricity. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Wilson, D.G.; Abdelkhalik, O.; Korde, U.A.; Robinett, R.D. A comparison of control strategies for wave energy converters. Int. J. Mar. Energy 2017, 20, 45–63. [Google Scholar] [CrossRef]
- Hong, Y.; Waters, R.; Boström, C.; Eriksson, M.; Engström, J.; Leijon, M. Review on electrical control strategies for wave energy converting systems. Renew. Sustain. Energy Rev. 2014, 31, 329–342. [Google Scholar] [CrossRef]
- Li, L.; Yuan, Z.; Gao, Y.; Zhang, X. Wave Force Prediction Effect on the Energy Absorption of a Wave Energy Converter With Real-Time Control. IEEE Trans. Sustain. Energy 2019, 10, 615–624. [Google Scholar] [CrossRef] [Green Version]
- Göteman, M.; Engström, J.; Eriksson, M.; Isberg, J.; Leijon, M. Methods of reducing power fluctuations in wave energy parks. J. Renew. Sustain. Energy 2014, 6, 043103. [Google Scholar]
- Chabane, S.B.; Alamir, M.; Fiacchini, M.; Riah, R.; Kovaltchouk, T.; Bacha, S. Electricity Grid Connection of a Tidal Farm: An Active Power Control Framework Constrained to Grid Code Requirements. IEEE Trans. Sustain. Energy 2018, 9, 1948–1956. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Benbouzid, M.; Frédéric Charpentier, J.; Scuiller, F.; Tang, T. A review of energy storage technologies for marine current energy systems. Renew. Sustain. Energy Rev. 2013, 18, 390–400. [Google Scholar] [CrossRef] [Green Version]
- Chauhan, A.; Saini, R.P. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Anwar, M.B.; El Moursi, M.S.; Xiao, W. Novel Power Smoothing and Generation Scheduling Strategies for a Hybrid Wind and Marine Current Turbine System. IEEE Trans. Power Syst. 2017, 32, 1315–1326. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.P.; Ju, P. Application of the Battery Energy Storage in Wave Energy Conversion system. In Proceedings of the 1st International Conference on Sustainable Power Generation and Supply, SUPERGEN 09, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Rojas-Delgado, B.; Alonso, M.; Amaris, H.; de Santiago, J. Wave Power Output Smoothing through the Use of a High-Speed Kinetic Buffer. Energies 2019, 12, 2196. [Google Scholar] [CrossRef] [Green Version]
- Rajapakse, G.; Jayasinghe, S.; Fleming, A.; Negnevitsky, M. Grid Integration and Power Smoothing of an Oscillating Water Column Wave Energy Converter. Energies 2018, 11, 1871. [Google Scholar] [CrossRef] [Green Version]
- Rajapakse, G.; Jayasinghe, S.; Fleming, A. Power management of an oscillating water column wave energy converter with battery/supercapacitor hybrid energy storage. In Proceedings of the 2018 8th International Conference on Power and Energy Systems, ICPES 2018, Colombo, Sri Lanka, 21–22 December 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 246–251. [Google Scholar]
- Moreno-Torres, P.; Blanco, M.; Navarro, G.; Lafoz, M. Power smoothing system for wave energy converters by means of a supercapacitor-based energy storage system. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2015. [Google Scholar]
- Agarwal, A.; Iyer, V.M.; Anurag, A.; Bhattacharya, S. Adaptive control of a hybrid energy storage system for wave energy conversion application. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 4994–5001. [Google Scholar]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D. Modelling of a wave-to-wire system for a wave farm and its response analysis against power quality and grid codes. Renew. Energy 2020, 162, 2041–2055. [Google Scholar] [CrossRef]
- Tedeschi, E.; Santos-Mugica, M. Modeling and control of a wave energy farm including energy storage for power quality enhancement: The bimep case study. IEEE Trans. Power Syst. 2014, 29, 1489–1497. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, X.P. Adaptive energy filters smoothing renewable power fluctuations at different power levels. In IET Conference Publications; Institution of Engineering and Technology: London, UK, 2019; Volume 2019. [Google Scholar]
- Kovaltchouk, T.; Multon, B.; Ahmed, H.B.; Aubry, J.; Venet, P. Enhanced aging model for supercapacitors taking into account power cycling: Application to the sizing of an energy storage system in a direct wave energy converter. In Proceedings of the 2014 9th International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014; pp. 1–10. [Google Scholar] [CrossRef] [Green Version]
- Torres, J.; Moreno-Torres, P.; Navarro, G.; Blanco, M.; Lafoz, M. Fast Energy Storage Systems Comparison in Terms of Energy Efficiency for a Specific Application. IEEE Access 2018, 6, 40656–40672. [Google Scholar] [CrossRef]
- Energías Marinas—EVE. Available online: https://eve.eus/Actuaciones/Marina?lang=es-es (accessed on 4 February 2021).
- Electric Double Layer Capacitor—An Overview. Electric Double Layer Capacitor—An Overview|ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/engineering/electric-double-layer-capacitor (accessed on 5 January 2021).
- International Electrotechnical Commission Electrical Energy Storage—White Paper; International Electrotechnical Commission: Geneva, Switzerland, 2011; pp. 1–78.
- Grbović, P. Ultra-Capacitor Energy Storage Devices. In Ultra-Capacitors in Power Conversion Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 22–77. [Google Scholar]
- Rafik, F.; Gualous, H.; Gallay, R.; Crausaz, A.; Berthon, A. Frequency, thermal and voltage supercapacitor characterization and modeling. J. Power Sources 2007, 165, 928–934. [Google Scholar] [CrossRef]
- Chaoui, H.; Gualous, H. Online Lifetime Estimation of Supercapacitors. IEEE Trans. Power Electron. 2017, 32, 7199–7206. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.; Robbins, R. Power Electronics Converters, Applications and Design; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Navarro, G.; Nájera, J.; Torres, J.; Blanco, M.; Santos, M.; Lafoz, M. Development and Experimental Validation of a Supercapacitor Frequency Domain Model for Industrial Energy Applications Considering Dynamic Behaviour at High Frequencies. Energies 2020, 13, 1156. [Google Scholar] [CrossRef] [Green Version]
- Maxwell Technologies Maxwell Technologies Ultracapacitors, Supercapacitors, Microelectronics and High Voltage. Available online: https://www.maxwell.com/ (accessed on 10 February 2021).
- Zuo, X.; Li, G.Z. Isolated voltage balancing in super-capacitor energy storage system. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May–2 June 2014; IEEE Computer Society: Washington, DC, USA, 2014; pp. 5124–5128. [Google Scholar]
- Li, L.; Huang, Z.; Liu, W.; Li, H.; Li, H.; Yang, Y. A controllable voltage equalizer with state of charge prediction for supercapacitors in large current applications. In IFAC Proceedings Volumes (IFAC-PapersOnline); IFAC Secretariat: Laxenburg, 2014; Volume 19, pp. 3623–3628. [Google Scholar]
- MATLAB - El Lenguaje del Cálculo Técnico—MATLAB & Simulink. Available online: https://es.mathworks.com/products/matlab.html (accessed on 4 January 2021).
- Castano, S.; Gauchia, L.; Sanz-Feito, J. Effect of packaging on supercapacitors strings modeling: Proposal of functional unit defined around balancing circuit. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 1390–1398. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, X. A unified analytical modeling of the interleaved pulse width modulation (PWM) DC-DC converter and its applications. IEEE Trans. Power Electron. 2013, 28, 5147–5158. [Google Scholar] [CrossRef]
- Arango, E.; Ramos-Paja, C.; Calvente, J.; Giral, R.; Serna, S. Asymmetrical Interleaved DC/DC Switching Converters for Photovoltaic and Fuel Cell Applications—Part 1: Circuit Generation, Analysis and Design. Energies 2012, 5, 4590–4623. [Google Scholar] [CrossRef] [Green Version]
- BiMEP BiMEP Mutriku. Available online: https://www.bimep.com/area-mutriku/servicios/ (accessed on 10 February 2021).
- Blanco, M.; Navarro, G.; Lafoz, M.; Pérez, J.I. How harmful is the wave energy penetration in an electric grid? In Proceedings of the Twelfth European Wave and Tidal Energy Conference; Lewis, A., Ed.; University College Cork: Cork, Ireland, 2017; p. 942. [Google Scholar]
- Lafoz, M.; Blanco, M.; Beloqui, L.; Navarro, G.; Moreno-Torres, P. Dimensioning methodology for energy storage devices and wave energy converters supplying isolated loads. IET Renew. Power Gener. 2016, 10, 1468–1476. [Google Scholar] [CrossRef]
- Moreno-Torres, P.; Lafoz, M.; Navarro, G.; Blanco, M.; García-Tabarés, L. Sistema para el acondicionamiento de la potencia eléctrica generada en un sistema de generación undimotriz. 2016, pp. 1–32. Available online: https://www.patentes-y-marcas.com/fr/brevet/sistema-para-el-acondicionamientode-la-potencia-electrica-generada-en-un-sistema-de-generacion-undimotriz-p201530980 (accessed on 5 January 2021).
- Lafoz, M.; Blanco, M.; Ramirez, D. Grid connection for wave power farms. In Proceedings of the 2011 14th European Conference on Power Electronics and Applicationsm, Birmingham, UK, 30 August–1 September 2011; IEEE: New York, NY, USA, 2011; pp. 1–10. [Google Scholar]
- ENTSO-E European Network of Transmission System Operators for Electricity (ENTSO-E); European Union: Brussels, Belgium, 2016.
- EASE. EERA European Energy Storage Technology Development Roadmap - 2017; EERA: Brussels, Belgium, 2017. [Google Scholar]
- Gatta, F.M.; Geri, A.; Lauria, S.; Maccioni, M.; Palone, F. Battery energy storage efficiency calculation including auxiliary losses: Technology comparison and operating strategies. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Funaki, T. Evaluating energy storage efficiency by modeling the voltage and temperature dependency in EDLC electrical characteristics. IEEE Trans. Power Electron. 2010, 25, 1231–1239. [Google Scholar] [CrossRef]








| Parameter | Meaning | Value |
|---|---|---|
| % ramp-up | Maximum ramp-up (%/min) | 10 |
| UMAX | Maximum voltage per cell in the SC cabinets | 2.65 V |
| UMIN | Minimum voltage per cell in the SC cabinets | 1.59 V |
| SoC_INITIAL | Initial State of charge of the SC cabinets | 60% |
| Energy_USABLE | Usable energy respect to the total energy of each SC cabinet | 0.5 kWh |
| PESS_MAX | Maximum Power provided by one SCESS module | 125 kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, G.; Blanco, M.; Torres, J.; Nájera, J.; Santiago, Á.; Santos-Herran, M.; Ramírez, D.; Lafoz, M. Dimensioning Methodology of an Energy Storage System Based on Supercapacitors for Grid Code Compliance of a Wave Power Plant. Energies 2021, 14, 985. https://doi.org/10.3390/en14040985
Navarro G, Blanco M, Torres J, Nájera J, Santiago Á, Santos-Herran M, Ramírez D, Lafoz M. Dimensioning Methodology of an Energy Storage System Based on Supercapacitors for Grid Code Compliance of a Wave Power Plant. Energies. 2021; 14(4):985. https://doi.org/10.3390/en14040985
Chicago/Turabian StyleNavarro, Gustavo, Marcos Blanco, Jorge Torres, Jorge Nájera, Álvaro Santiago, Miguel Santos-Herran, Dionisio Ramírez, and Marcos Lafoz. 2021. "Dimensioning Methodology of an Energy Storage System Based on Supercapacitors for Grid Code Compliance of a Wave Power Plant" Energies 14, no. 4: 985. https://doi.org/10.3390/en14040985










