Effects of Voltage Interharmonics on Cage Induction Motors
Abstract
1. Introduction
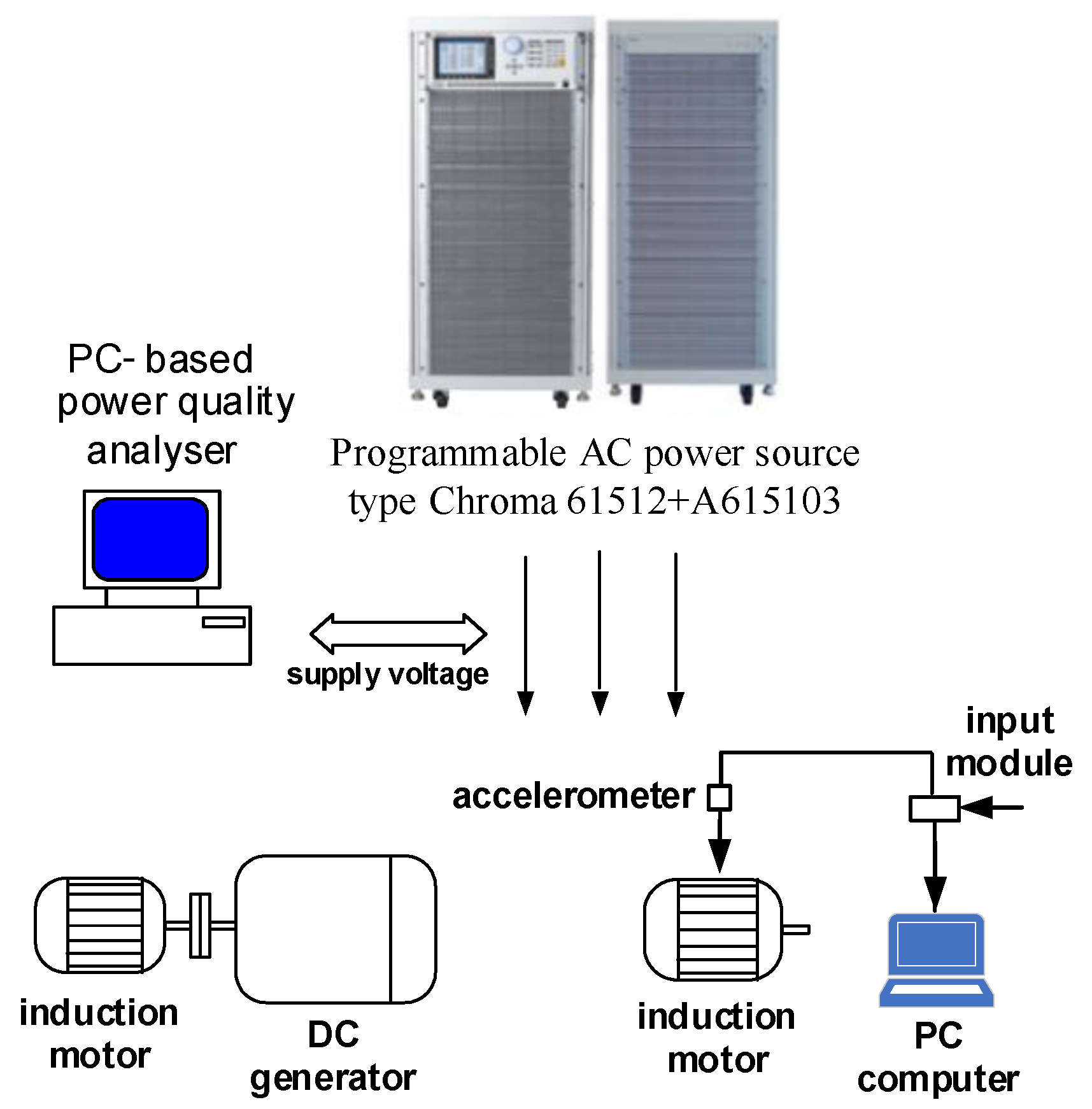
2. Methodology
3. Results
3.1. Preliminary Remarks
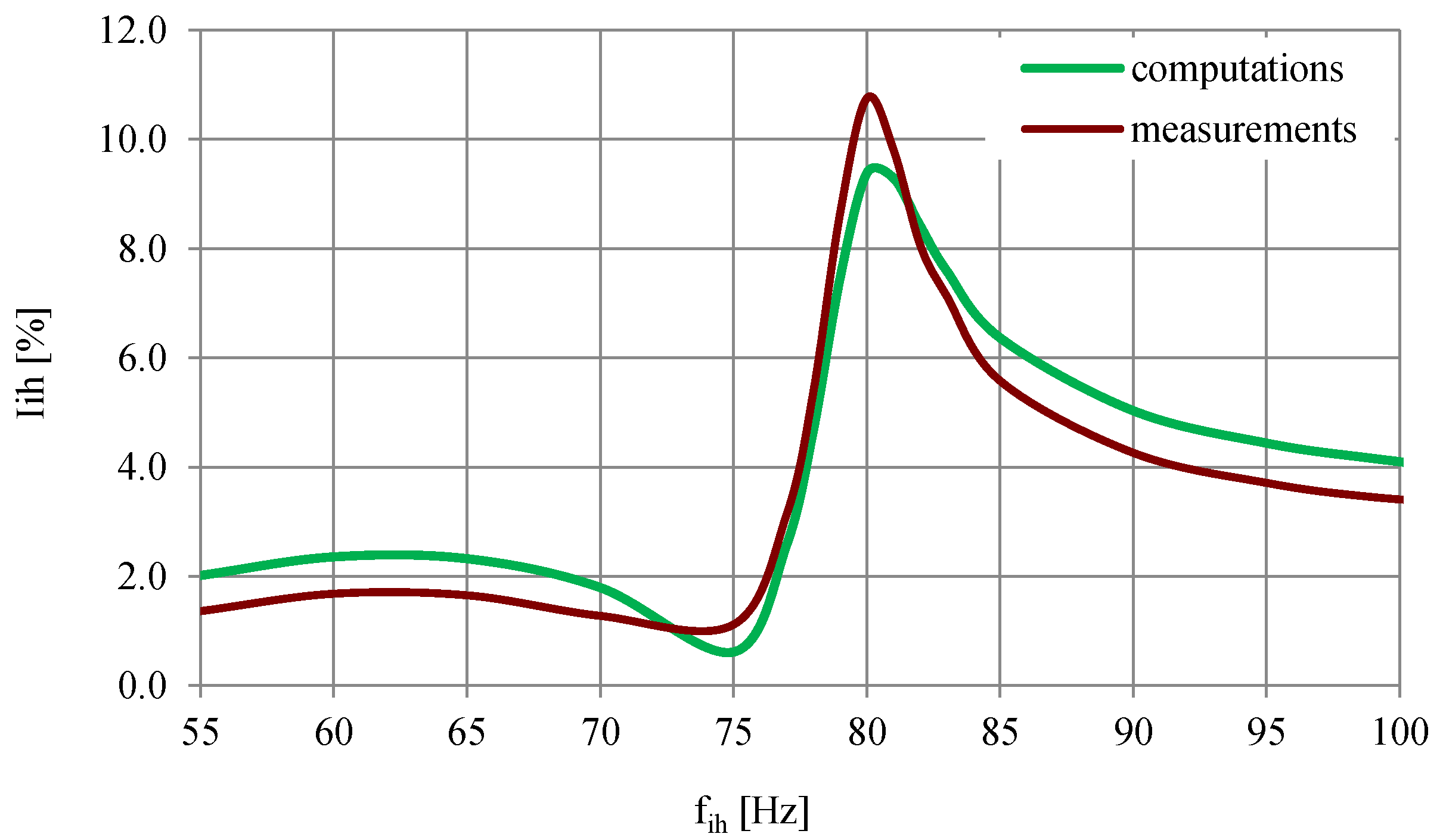
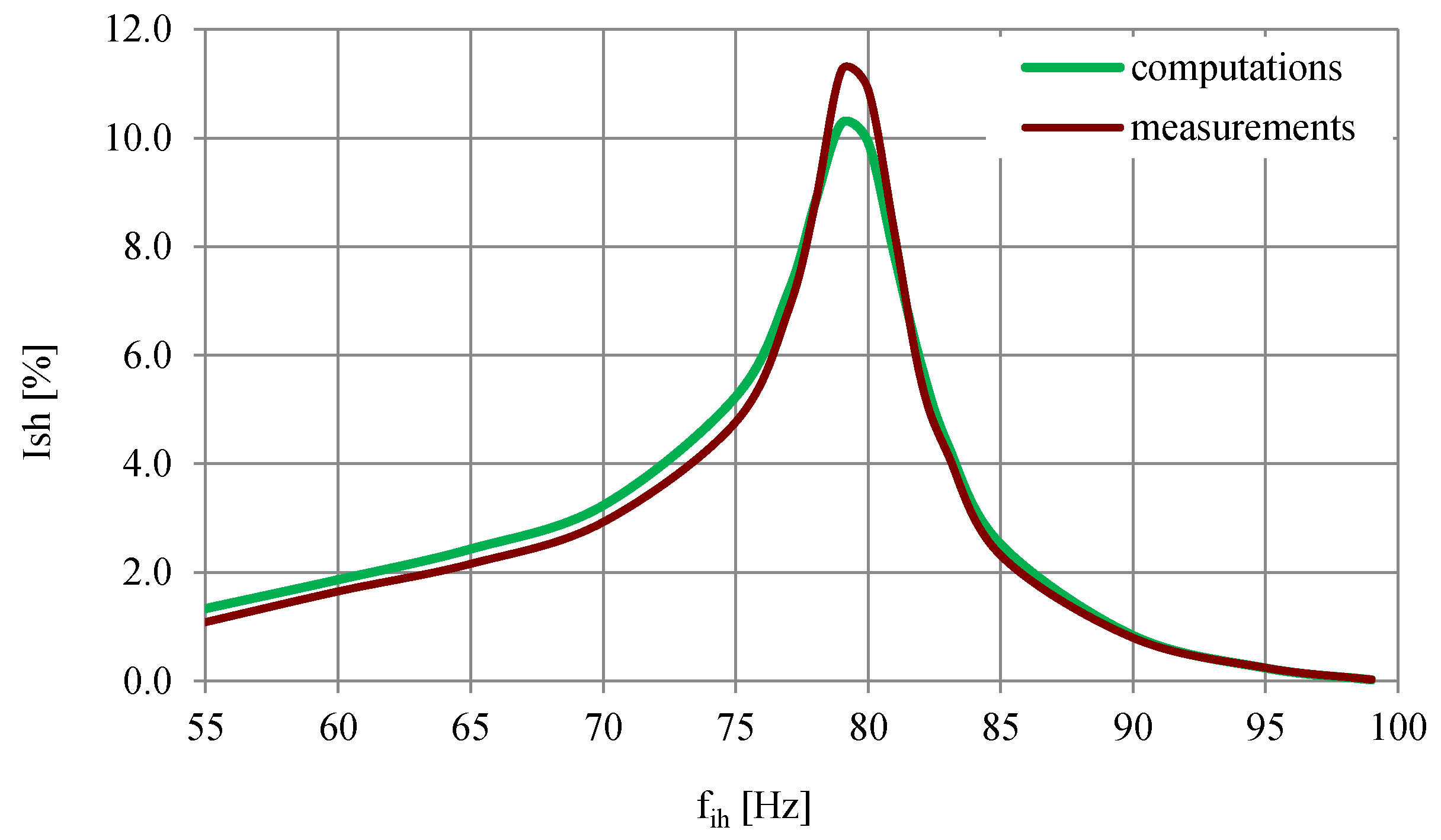
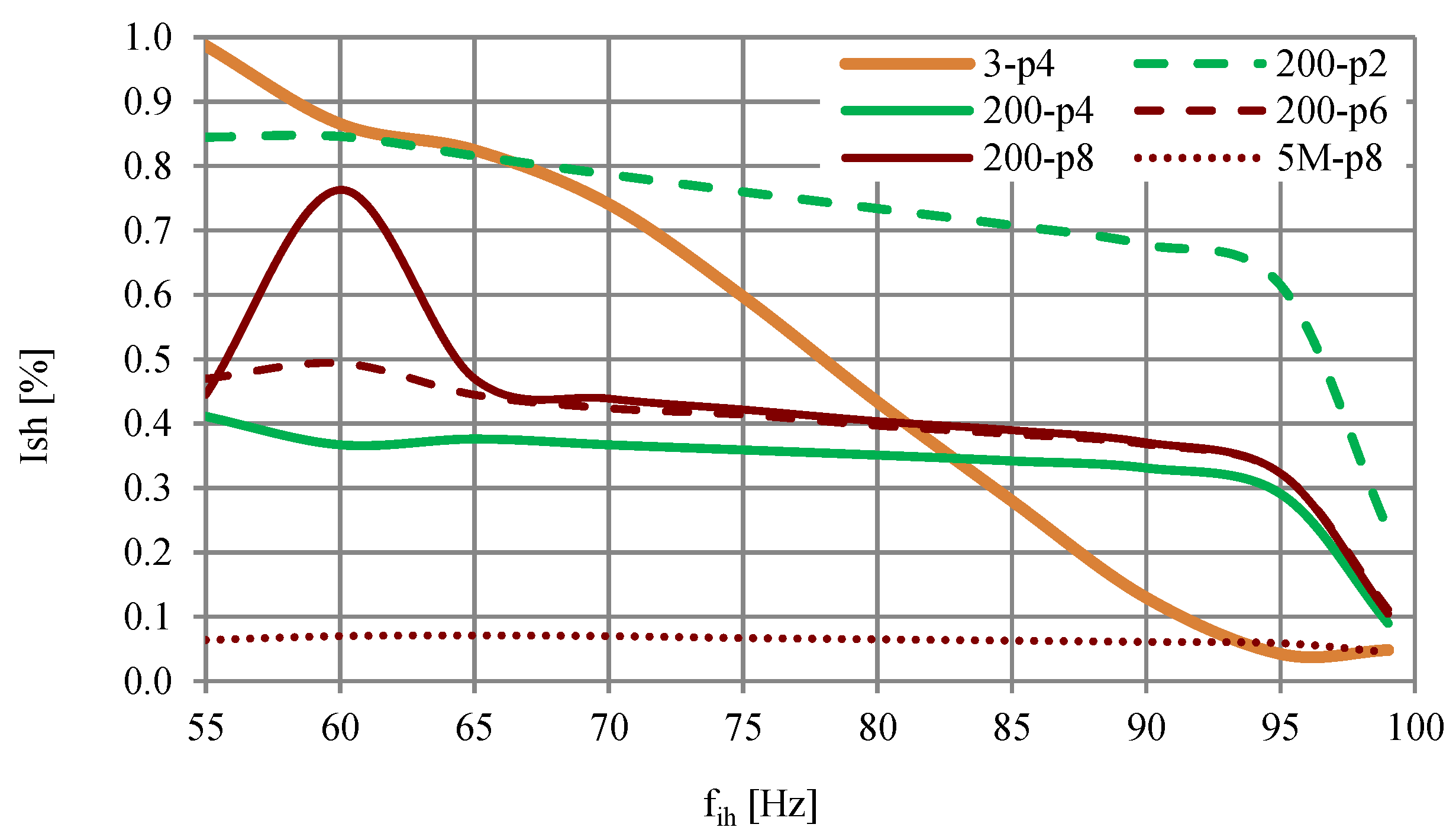
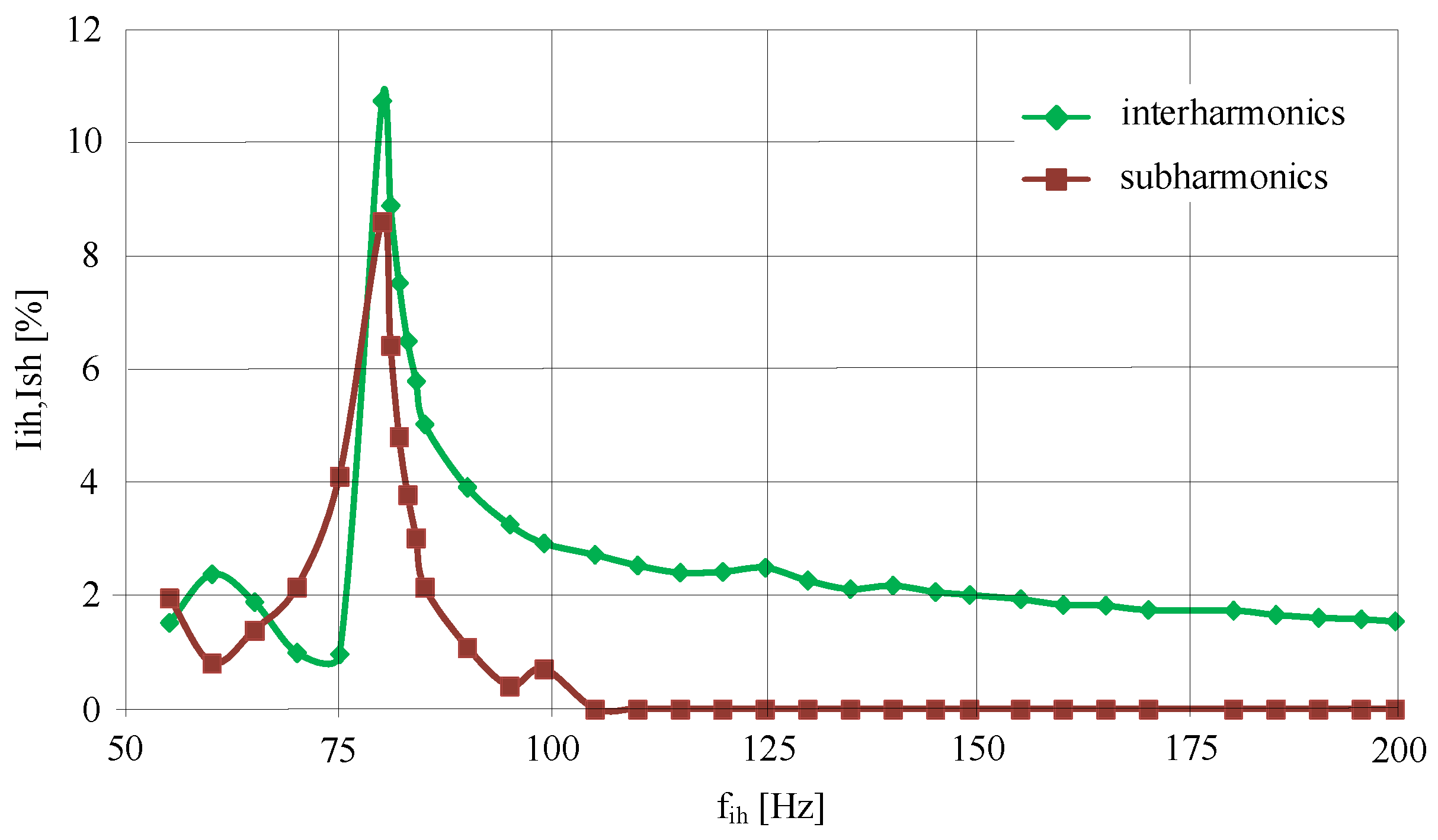
3.2. Effect of Interharmonics on Current
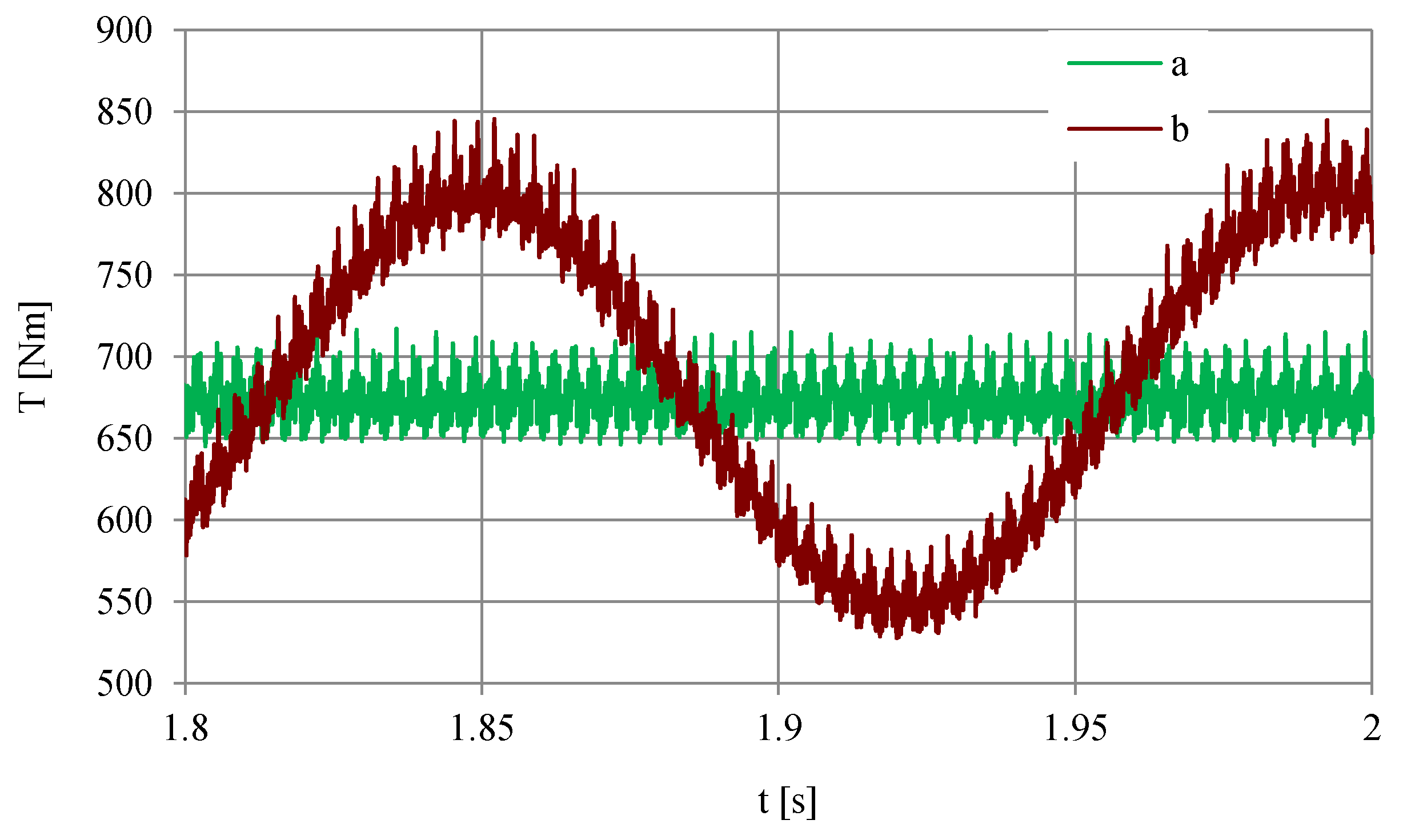
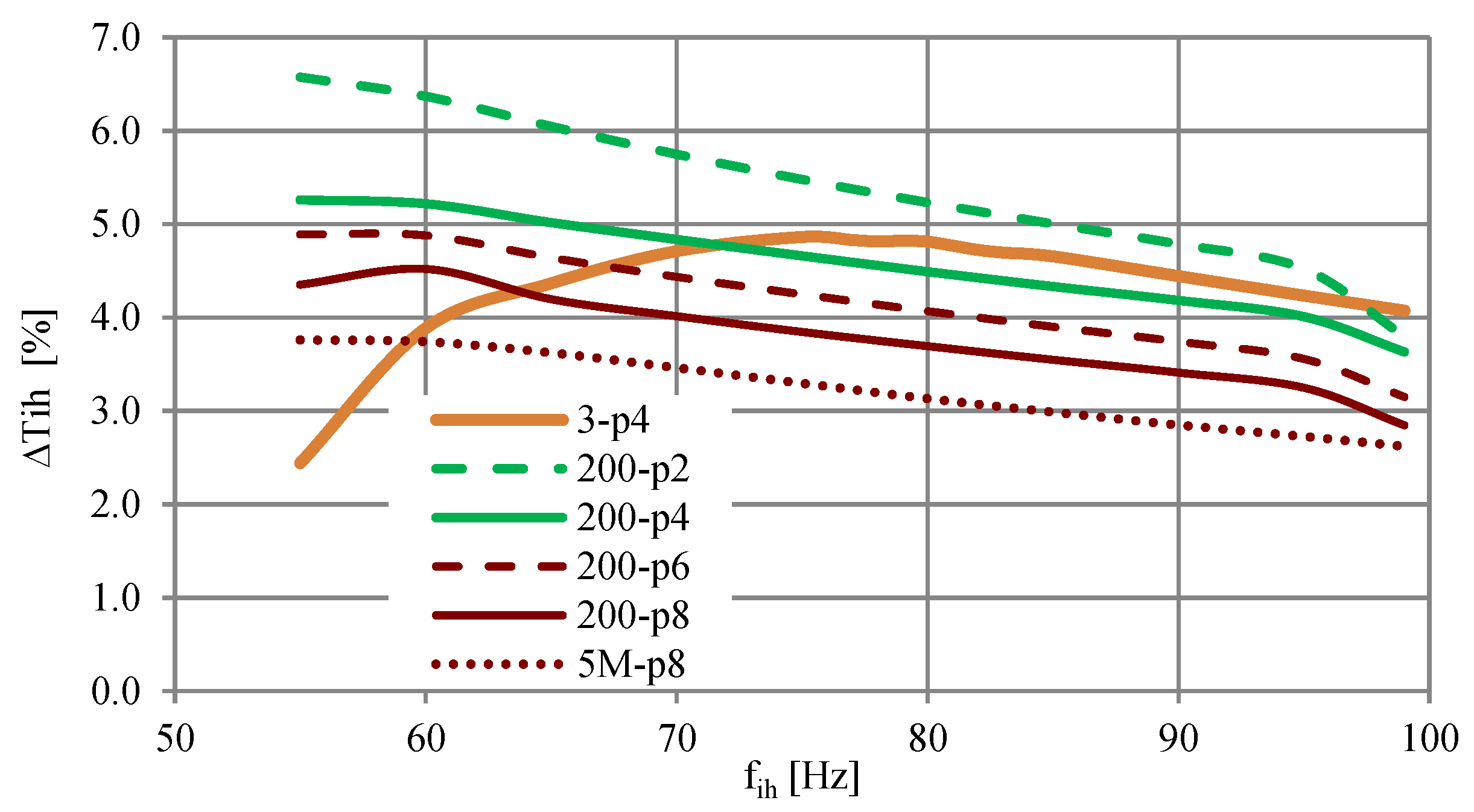
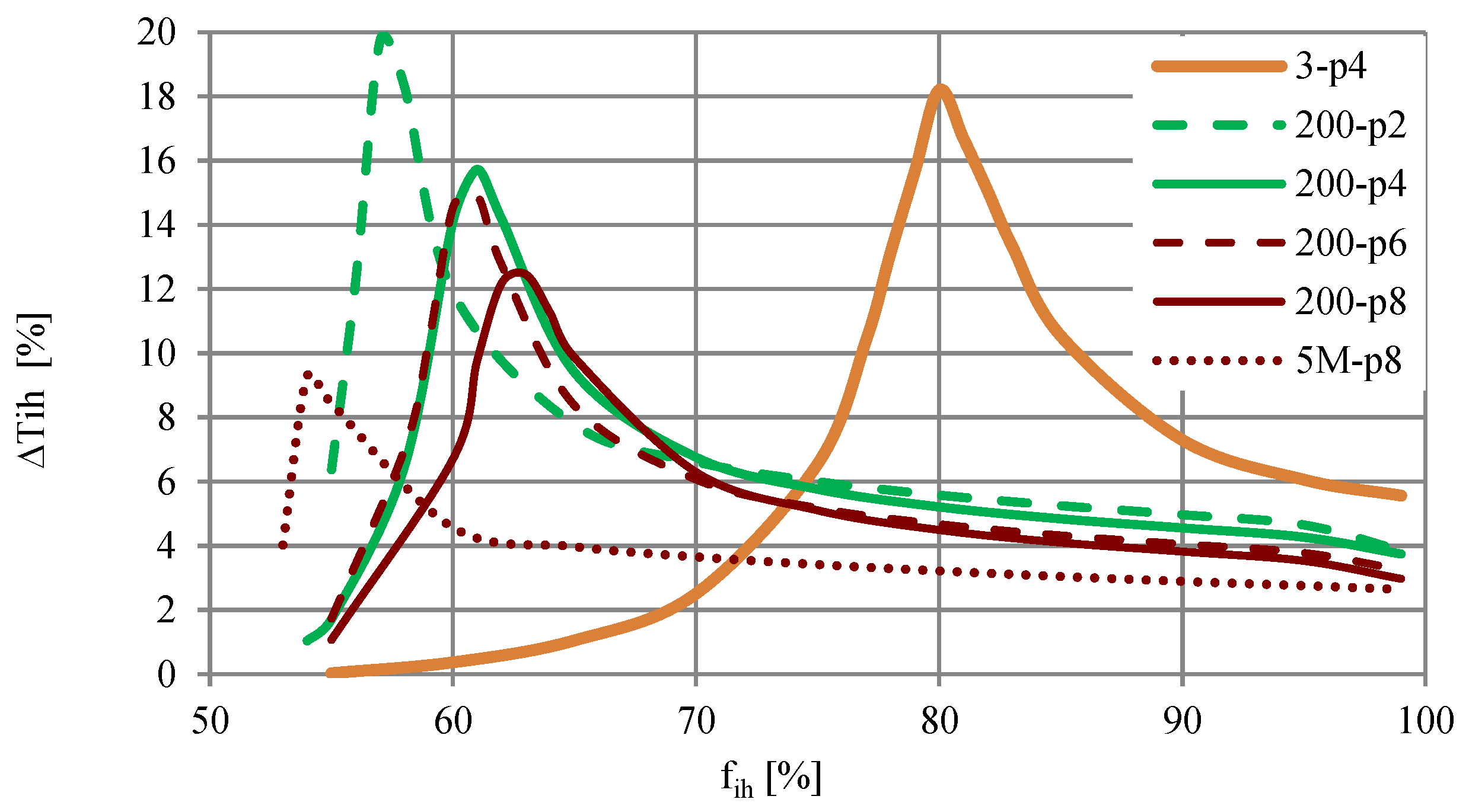
3.3. Effect of Interharmonics on Torque Pulsations
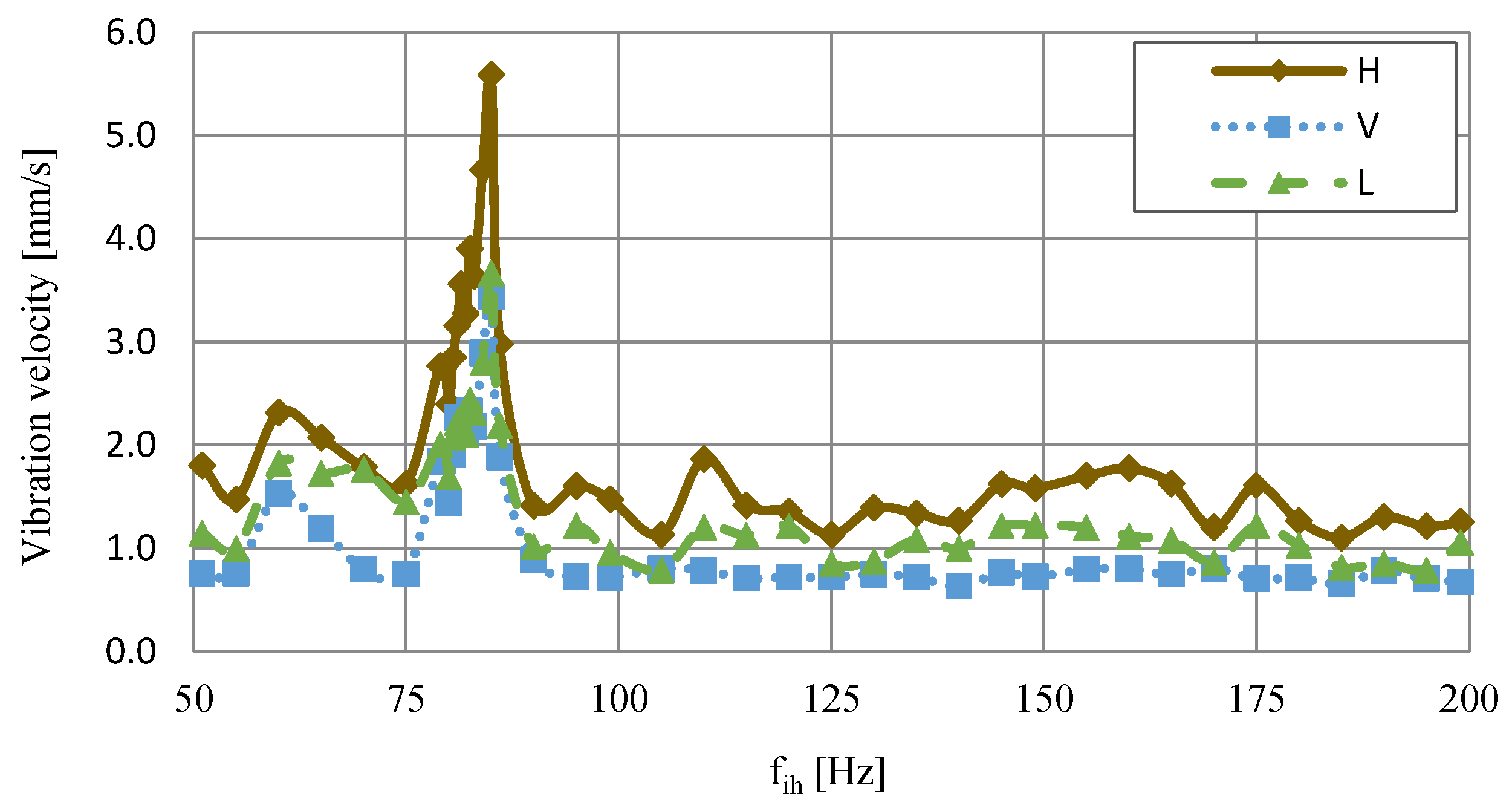
3.4. Effect of Interharmonics on Vibration
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bolen, M.H.J.; Gu, I.Y.H. Origin of Power Quality Variations. Processing of Stationary Signals. In Signal Processing of Power Quality Disturbances; Wiley: New York, NY, USA, 2006; pp. 41–276. [Google Scholar]
- Testa, A.; Akram, M.F.; Burch, R.; Carpinelli, G.; Chang, G.; Dinavahi, V.; Hatziadoniu, C.; Grady, W.M.; Gunther, E.; Halpin, M.; et al. Interharmonics: Theory and modeling. IEEE Trans. Power Deliv. 2007, 22, 2335–2348. [Google Scholar] [CrossRef]
- Nassif, A.B. Assessing the impact of harmonics and interharmonics of top and mudpump variable frequency drives in drilling rigs. IEEE Trans. Ind. Appl. 2019, 55, 5574–5583. [Google Scholar] [CrossRef]
- Soltani, H.; Davari, P.; Zare, F.; Blaabjerg, F. Effects of modulation techniques on the input current interharmonics of adjustable speed drives. IEEE Trans. Ind. Electron. 2018, 65, 167–178. [Google Scholar] [CrossRef]
- Arkkio, A.; Cederström, S.; Awan, H.A.A.; Saarakkala, S.E.; Holopainen, T.P. Additional losses of electrical machines under torsional vibration. IEEE Trans. Energy Convers. 2018, 33, 245–251. [Google Scholar] [CrossRef]
- Arkkio, A.; Mölsä, E.; Holopainen, T.P. Reducing the losses of electrical machines under torsional vibration. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1303–1309. [Google Scholar]
- Zhiyuan, M.; Xiong, M.W.; Le, L.; Zhong, X. Interharmonics analysis of a 7.5 kW air compressor motor. CIRED Open Access Proc. J. 2017, 2017, 738–741. [Google Scholar] [CrossRef]
- Uz-Logoglu, E.; Salor, O.; Ermis, M. Online characterization of interharmonics and harmonics of ac electric arc furnaces by multiple synchronous reference frame analysis. IEEE Trans. Ind. Appl. 2016, 52, 2673–2683. [Google Scholar] [CrossRef]
- Sürgevil, T.; Akpnar, E. Effects of electric arc furnace loads on synchronous generators and asynchronous motors. In Proceedings of the 2009 International Conference on Electrical and Electronics Engineering-ELECO, Bursa, Turkey, 5–8 November 2009; p. I-49. [Google Scholar]
- Seferi, Y.; Blair, S.M.; Mester, C.; Stewart, B.G. Power quality measurement and active harmonic power in 25 kV 50 Hz AC railway systems. Energies 2020, 13, 5698. [Google Scholar] [CrossRef]
- Pan, Y.; Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A phase-shifting MPPT method to mitigate interharmonics from cascaded H-bridge PV inverters. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 157–163. [Google Scholar]
- Ravindran, V.; Rönnberg, S.K.; Busatto, T.; Bollen, M.H. Inspection of interharmonic emissions from a grid-tied PV inverter in North Sweden. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Ravindran, V.; Busatto, T.; Rönnberg, S.K.; Meyer, J.; Bollen, M.H. Time-varying interharmonics in different types of grid-tied PV inverter systems. IEEE Trans. Power Deliv. 2019, 35, 483–496. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Sera, D.; Soltani, H.; Blaabjerg, F. Analysis and modeling of interharmonics from grid-connected photovoltaic systems. IEEE Trans. Power Electron. 2018, 33, 8353. [Google Scholar] [CrossRef]
- Yang, K.; Bollen, M.H. Interharmonic currents from a Type-IV wind energy conversion system. Electr. Power Syst. Res. 2017, 143, 357–364. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, Z.; Liu, F.; Li, Y.; Peng, Y.; Xu, Z. Study on power quality issues of wind farm. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 10490–10494. [Google Scholar]
- Voltage Characteristics of Electricity Supplied by Public Distribution Network; EN Standard 50160; CENELEC: Brussels, Belgium, 2010.
- Tennakoon, S.; Perera, S.; Robinson, D. Flicker attenuation—Part I: Response of three-phase induction motors to regular voltage fluctuations. IEEE Trans. Power Deliv. 2008, 23, 1207–1214. [Google Scholar] [CrossRef]
- Kushare, B.E.; Ghatol, A.A.; Aphale, M.S. Survey of interharmonics in Indian power system network. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007; pp. 1230–1235. [Google Scholar]
- Feola, L.; Langella, R.; Testa, A. On the effects of unbalances, harmonics and interharmonics on PLL systems. IEEE Trans. Instrum. Meas. 2013, 62, 2399–2409. [Google Scholar] [CrossRef]
- Hou, R.; Wu, J.; Song, H.; Qu, Y.; Xu, D. Applying directly modified RDFT method in active power filter for the power quality improvement of the weak power grid. Energies 2020, 13, 4884. [Google Scholar] [CrossRef]
- Guillen-Garcia, E.; Zorita-Lamadrid, A.L.; Duque-Perez, O.; Morales-Velazquez, L.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.J. Power consumption analysis of electrical installations at healthcare facility. Energies 2017, 10, 64. [Google Scholar] [CrossRef]
- Gnacinski, P.; Peplinski, M.; Murawski, L.; Szelezinski, A. Vibration of induction machine supplied with voltage containing subharmonics and interharmonics. IEEE Trans. Energy Convers. 2019, 34, 1928–1937. [Google Scholar] [CrossRef]
- Knockaert, J.; Debruyne, C.; Desmet, J. Interharmonics and LED flicker: An assessment by CFD. In Proceedings of the 25th International Conference on Electricity Distribution Madrid, Madrid, Spain, 3–6 June 2019. Paper No. 675. [Google Scholar]
- IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Standard 519-2014 (Revision of IEEE Standard 519-1992); IEEE: New York, NY, USA, 2014.
- Farah, M.J.; Abdollahi, R. An analytical investigation of induction motor behavior in the case of flicker occurrence using finite element method. Univ. Politeh. Buchar. Sci. Bull. Ser. C Electr. Eng. Comput. Sci. 2019, 81, 181–192. [Google Scholar]
- Ghaseminezhad, M.; Doroudi, A.; Hosseinian, S.H.; Jalilian, A. Analysis of voltage fluctuation impact on induction motors by an innovative equivalent circuit considering the speed changes. IET Gener. Transm. Distrib. 2017, 11, 512–519. [Google Scholar] [CrossRef]
- Ghaseminezhad, M.; Doroudi, A.; Hosseinian, S.H.; Jalilian, A. Analytical field study on induction motors under fluctuated voltages. Iran. J. Electr. Electron. Eng. 2021, 17, 1620. [Google Scholar]
- Ghaseminezhad, M.; Doroudi, A.; Hosseinian, S.H.; Jalilian, A. An investigation of induction motor saturation under voltage fluctuation conditions. J. Magn. 2017, 22, 306–314. [Google Scholar] [CrossRef]
- Ghaseminezhad, M.; Doroudi, A.; Hosseinian, S.H.; Jalilian, A. Investigation of increased ohmic and core losses in induction motors under voltage fluctuation conditions. Iran. J. Sci. Technol. Trans. Electr. Eng. 2018, 43, 1–10. [Google Scholar] [CrossRef]
- Gnacinski, P.; Peplinski, M.; Hallmann, D. Currents and Power Losses of Induction Machine Under Voltage Interharmonics. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019; p. P-1. [Google Scholar]
- Gnacinski, P.; Peplinski, M. Induction cage machine supplied with voltage containing subharmonics and interharmonics. IET Electr. Power Appl. 2014, 8, 287–295. [Google Scholar] [CrossRef]
- Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts—Part 1: General Guidelines; ISO Standard 10816-1; ISO: Genova, Switzerland, 1995.
- Gnacinski, P.; Klimczak, P. High-Power induction motors supplied with voltage containing subharmonics. Energies 2020, 13, 5894. [Google Scholar] [CrossRef]
- Gnacinski, P.; Peplinski, M.; Hallmann, D.; Jankowski, P. The effects of voltage subharmonics on cage induction machine. Int. J. Electr. Power Energy Syst. 2019, 111, 125–131. [Google Scholar] [CrossRef]
- Tsypkin, M. The origin of the electromagnetic vibration of induction motors operating in modern industry: Practical experience—Analysis and diagnostics. IEEE Trans. Ind. Appl. 2017, 53, 1669–1676. [Google Scholar] [CrossRef]
- Bruha, M. Importance of control engineering to minimize torsional vibration in variable speed drive systems. In Proceedings of the 2016 Petroleum and Chemical Industry Conference Europe (PCIC Europe), Berlin, Germany, 14–16 June 2016; pp. 1–8. [Google Scholar]
- Feese, T.; Ryan, M. Torsional vibration problem with motor/ID fan system due to PWM variable frequency drive. In Proceedings of the 37th Turbomachinery Symposium; Texas A&M University, Turbomachinery Laboratories: College Station, TX, USA, 2008. [Google Scholar]
- Rotating Electrical Machines. Part 1: Rating and Performance; IEC Standard 60034-1; IEC: Genova, Switzerland, 2004.
- Mechanical Vibration—Measurement and Evaluation of Machine Vibration—Part 1: General Guidelines; ISO Standard 20816-1; ISO: Genova, Switzerland, 2016.


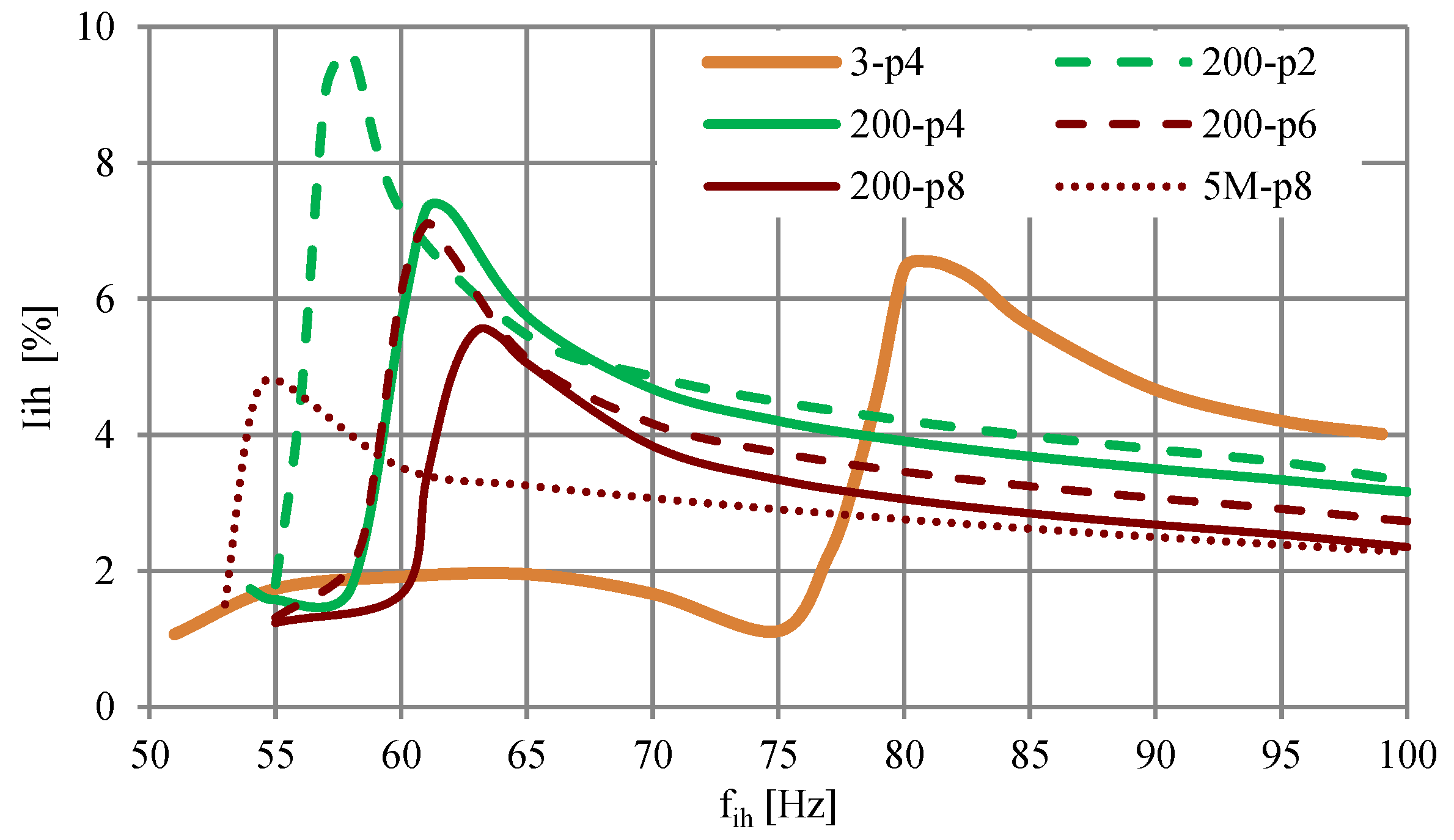
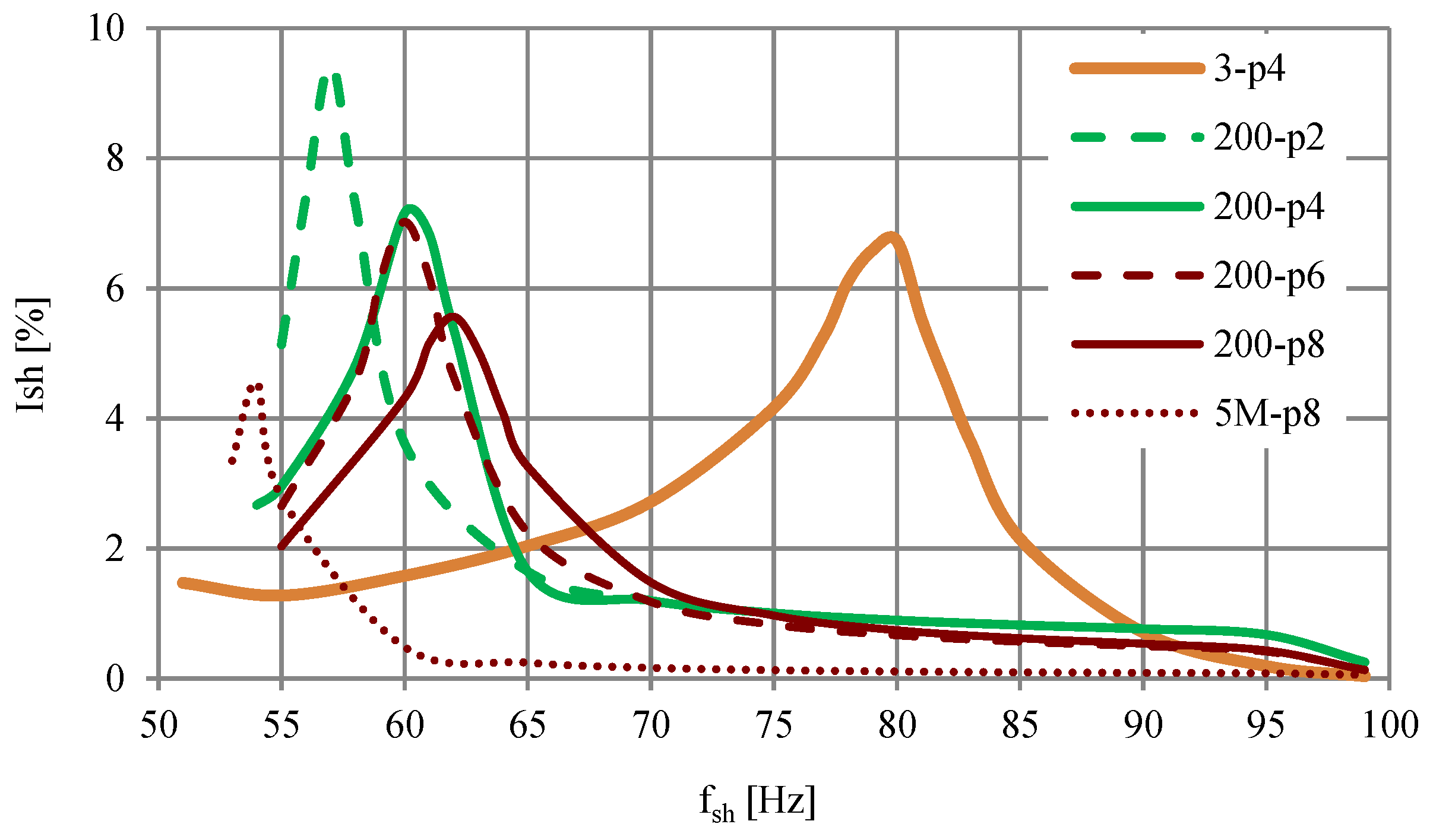
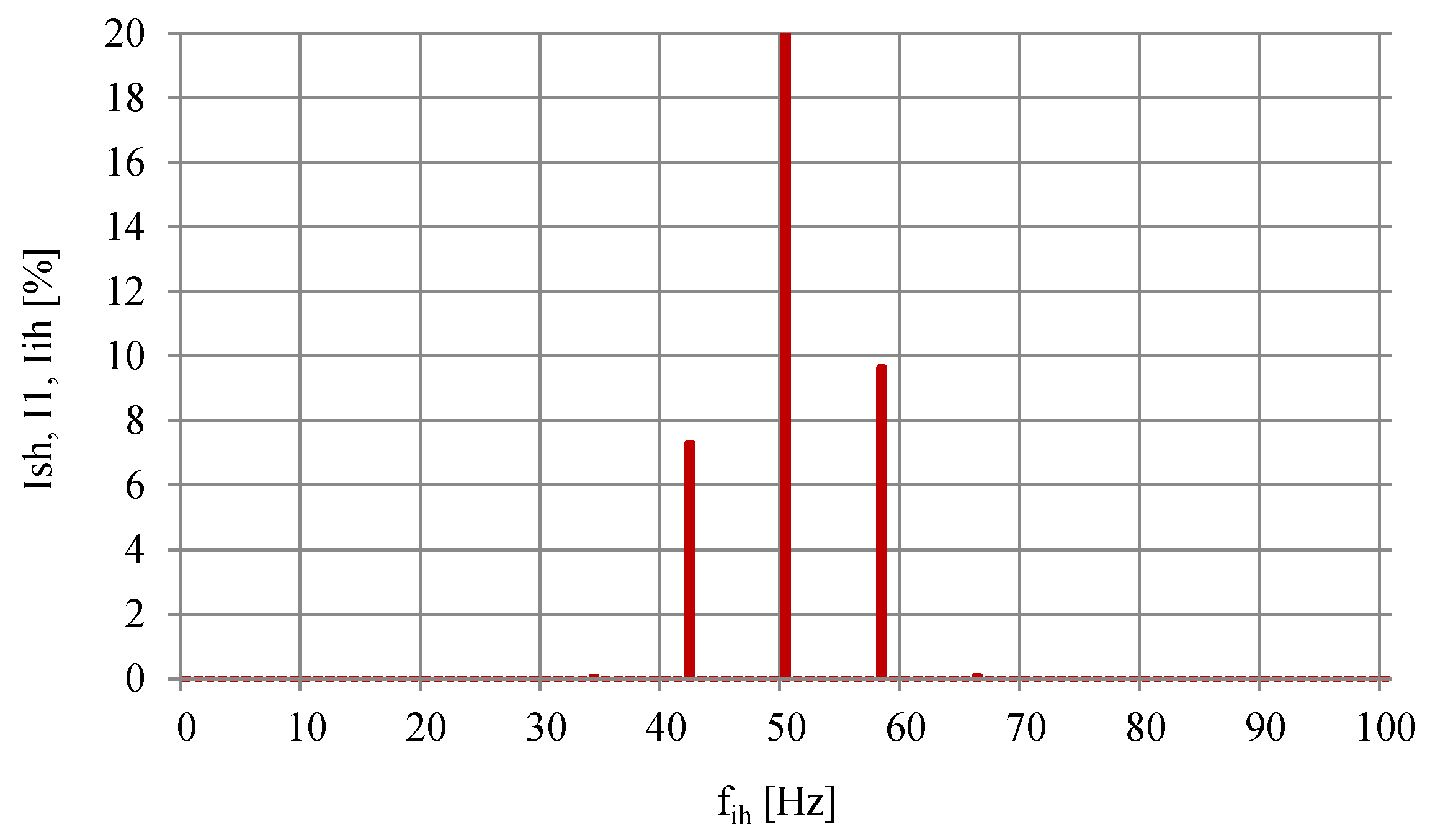
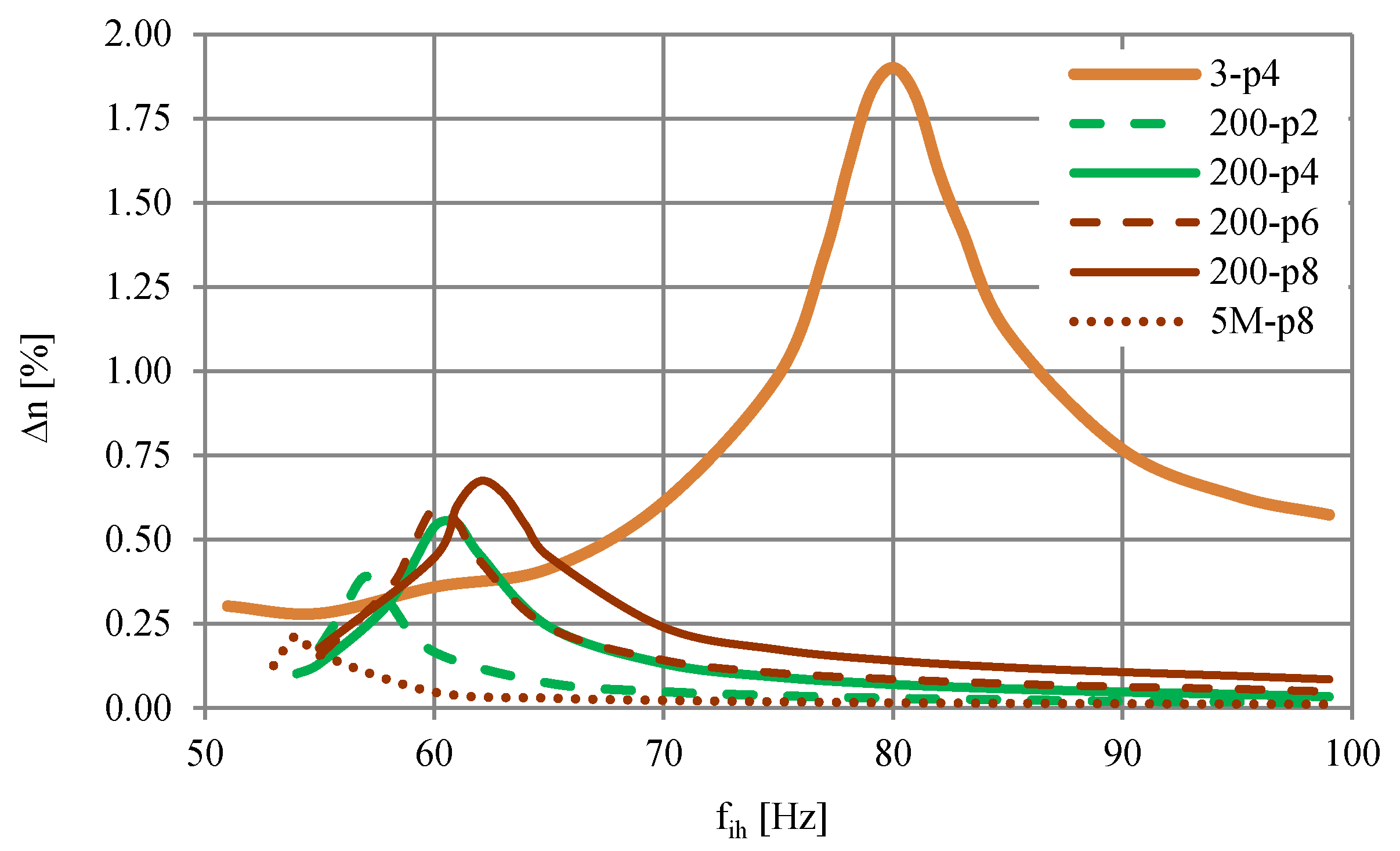
| Motor | Type | Rated Power (kW) | Number of Poles | Rated Speed (Rpm) | Rated Voltage (V) | Rated Current (A) |
|---|---|---|---|---|---|---|
| motor 3-p4 | TSg100L-4B | 3 | 4 | 1420 | 380 Δ | 6.9 |
| motor 4-p4 | 1LE1003-1BB22-2AA4 | 4 | 4 | 1460 | 400 Y | 7.9 |
| motor 200-p2 | SLgm 315 ML2B | 200 | 2 | 2982 | 400 Δ | 335 |
| motor 200-p4 | SEE 315 L4 | 200 | 4 | 1487 | 400 Δ | 346 |
| motor 200-p6 | 3SIE 355 ML6A | 200 | 6 | 989 | 400 Δ | 350 |
| motor 200-p8 | SEE 355 ML8B | 200 | 8 | 740 | 400 Δ | 384 |
| motor 5M-p8 | Sfw 900 HV8D | 5 600 | 8 | 745 | 10500 Y | 375 |
| Motor | Motor 200-p2 | Motor 200-p4 | Motor 200-p6 | Motor 200-p8 | Motor 5M-p8 |
|---|---|---|---|---|---|
| Natural frequency (Hz) | 30 | 32.5 | 31 | 30 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gnaciński, P.; Hallmann, D.; Klimczak, P.; Muc, A.; Pepliński, M. Effects of Voltage Interharmonics on Cage Induction Motors. Energies 2021, 14, 1218. https://doi.org/10.3390/en14051218
Gnaciński P, Hallmann D, Klimczak P, Muc A, Pepliński M. Effects of Voltage Interharmonics on Cage Induction Motors. Energies. 2021; 14(5):1218. https://doi.org/10.3390/en14051218
Chicago/Turabian StyleGnaciński, Piotr, Damian Hallmann, Piotr Klimczak, Adam Muc, and Marcin Pepliński. 2021. "Effects of Voltage Interharmonics on Cage Induction Motors" Energies 14, no. 5: 1218. https://doi.org/10.3390/en14051218
APA StyleGnaciński, P., Hallmann, D., Klimczak, P., Muc, A., & Pepliński, M. (2021). Effects of Voltage Interharmonics on Cage Induction Motors. Energies, 14(5), 1218. https://doi.org/10.3390/en14051218








