Abstract
This paper presents a new version of the incremental conductance algorithm for more accurate tracking of the maximum power point (MPP). The modified algorithm is called self-predictive incremental conductance (SPInC), and it recognizes the operational region. It is capable of detecting dynamic conditions, and it detects sudden changes in power resulting from changes in the intensity of radiation or temperature. By selecting the appropriate step size, it obtains maximum power from the panel at any moment. The improved algorithm reduces output power ripple and increases the efficiency of the system by detecting the operating area and selecting the appropriate step size for each region. The SPInC algorithm divides the system’s work areas into three operating zones. It calculates the size of the appropriate step changes for each region after identifying the regions, which allows for more accurate tracking of the MPP and increases the system efficiency at a speed equal to the speed of the conventional method. These additional operations did not result in a system slowdown in the tracking maximum power. According to the MATLAB/Simulink simulation results, the SPInC algorithm is more efficient than conventional InC, and the ripple output power is reduced. SPInC is also compared to the improved perturb and observe (P&O) algorithm. In general, SPInC can compete with the popular algorithms that have been recently proposed for MPPT in the other researches.
1. Introduction
In recent years, most developed countries have been using renewable energy sources to supply their energy. These sources include wind energy, geothermal energy, biomass, and, most importantly, solar energy. The amount of solar energy that the Earth receives in a single day is several times the annual energy consumption of everyone on Earth [1]. This has led to an increase in the installation of photovoltaic systems. The advantage of solar energy over other renewable energies is its stability and availability in most places [2]. Furthermore, photovoltaic arrays are suitable for most applications because they do not produce air pollutants and have low maintenance costs [3,4]. Currently, the most significant obstacle to the commercialization of photovoltaic systems is the high cost of the initial investment. In order to reduce the ratio of output power to the unit cost, photovoltaic arrays must generate the maximum power. One of the ways to maximize power from photovoltaic arrays is to use maximum power point tracking (MPPT) algorithms [5,6,7].
To maximize power from photovoltaic arrays, many MPPT techniques have been developed, the most popular being hill climbing (HC), perturb and observe (P&O), and incremental conductance (InC) algorithms. In addition to these three methods, the open-circuit voltage tracking algorithm and the short-circuit algorithm were also proposed. However, since the accuracy of these two methods in tracking the maximum power point is low, they were not given much attention [8,9]. The reason for the popularity of the HC algorithm is its simplicity and easy implementation. In this method, the power value is continuously compared to the previous value, and according to the result of the two power comparisons, the value of the step size changes is determined for each moment until the maximum power point is detected and then starts to oscillate around of this point [10,11]. As the name of the perturbation and observation (P&O) algorithm implies, the algorithm perturbs Vpv and observes the effect of this change on the output power of the photovoltaic system. This method is extensively used in MPPT because it is uncomplicated, and it requires only measurements of Vpv and Ipv. The disadvantage of P&O is that if the irradiance changes quickly, the tracking path will deviate significantly, and, subsequently, the losses will increase [12,13,14]. The InC technique operates according to the slope of the P–V curve. It has the advantage of traceability accuracy and low oscillation around the MPP for maximum power point tracking. However, this algorithm is more complicated than the P&O method due to the division operations in its structure [15,16,17]. The step size in all of these algorithms is constant, and its precise determination is important, because the small size of the step decreases the speed of the MPP tracking, and its large size increases the oscillations around the MPP. To solve this problem, the authors implemented many ideas by modifying common algorithms [18,19,20], for example, the developed P&O algorithm [21] and the modified InC method [22], the self-adaptive incremental conductance algorithm [23], the low-cost improved incremental conductance algorithm [17], etc. In all of these methods, by improving the performance of the system under steady-state conditions, the performance of the system under dynamic conditions is reduced. To solve this problem, optimization tools, such as the spider monkey algorithm and the fuzzy logic control algorithm [24,25], as well as other methods, have been developed [26,27,28,29,30,31,32,33,34,35]. However, these methods complicate system computations and, as a result, reduce tracking speed. For this reason, the development of tracking algorithms is of great importance.
In this paper, a new version of the self-predictive incremental conductance (SPInC) algorithm is presented. The SPInC algorithm recognizes the operational region and is also capable of detecting dynamic conditions. In addition, it detects sudden changes in power caused by changes in the intensity of radiation or temperature. By selecting the appropriate step size, it receives the maximum power from the panel at any moment. The improved algorithm reduces output power ripple and increases the efficiency of the system by detecting the operating area and selecting the appropriate step size for each region. The SPInC algorithm divides the system’s work areas into three operating zones. It calculates the size of the appropriate step changes for each region after identifying each region, which allows for more accurate tracking of the MPP and increases the system efficiency at a speed equal to the speed of the conventional method. These additional operations have not resulted in system slowdown in tracking maximum power. Furthermore, system implementation is simplified by removing the division operations from the conventional algorithm structure extracted from [17]. Thus, SPInC is a good tool to determine the maximum power point, with higher efficiency and lower oscillation around the MPP than other methods. The simulation results show the competence of the SPInC algorithm.
This paper consists of six sections: first, the PV system is introduced, which includes PV modeling and introducing the DC/DC converter structure; in the third section, the conventional InC and the free-division InC are discussed, and in the fourth section, the proposed SPInC is comprehensively explained; Section 5 shows the simulation results, in which the SPInC is compared with the conventional InC and proposed P&O; the sixth section is the conclusion.
2. PV system Configuration
2.1. PV Modeling
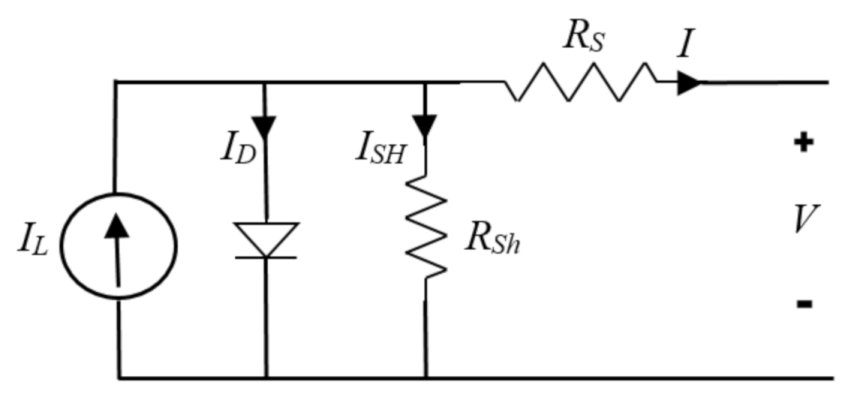
A photovoltaic cell is modeled in Figure 1. Equations (1) and (2) show the relationship between voltage and current for a photovoltaic cell. The PV module for this research is Green Energy Technology GET-100A-1.
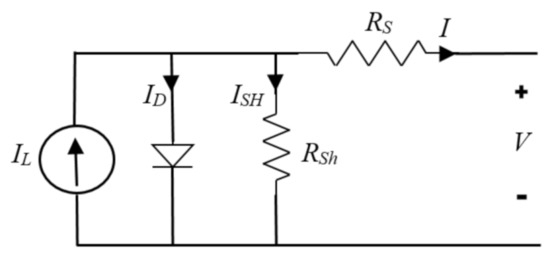
Figure 1.
Photovoltaic module characteristic.
According to Equations (1) and (2), we can determine the effects of radiation intensity and temperature [3]. Table 1 shows the specifications of the PV module at 25 ℃ and 1000 W/m2 and defines the variables used in the Equations (1) and (2).

Table 1.
PV module specifications at 25 °C and 1000 W/m2.
2.2. Boost Converter
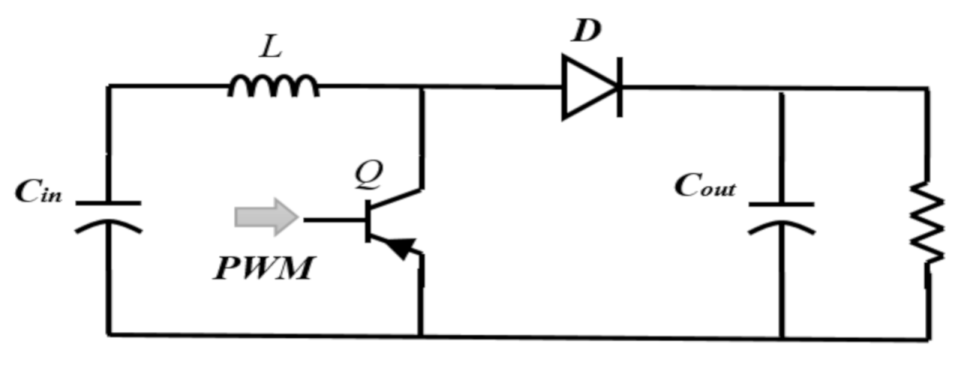
The structure of the boost converter is shown in Figure 2. The relationship between the input and output voltage in this converter is shown in Equation (3) [15]. To calculate the size of the converter’s inductor, it should be considered that the small size of the inductor generates large ripples in the voltage and current. The large inductor increases the converter losses, so the inductor should be large enough to have an acceptable voltage and current ripple rate [16]. The switching frequency for this research is 5 kHz.
where IL, Vin, and Vout are input current, input voltage, and output voltage of the boost converter, respectively and D is duty ratio. R, C, L are load resistance, output capacitor and input inductor L, respectively.
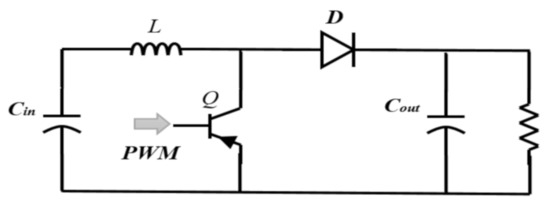
Figure 2.
Boost converter.
3. MPPT
The structures of the conventional InC and free division InC are discussed below.
3.1. Conventional InC Algorithm
The basis of the InC algorithm is formed by the P–V curve slope [7]:
Where P, V, I are the output power and voltage and current, respectively, and are the current and voltage changes, respectively.
Since
Then
3.2. Free-Division InC Algorithm
The incremental conductance algorithm was improved by removing divide operations from the algorithm structure [17]:
Finally,
4. Improved Self-Predictive InC
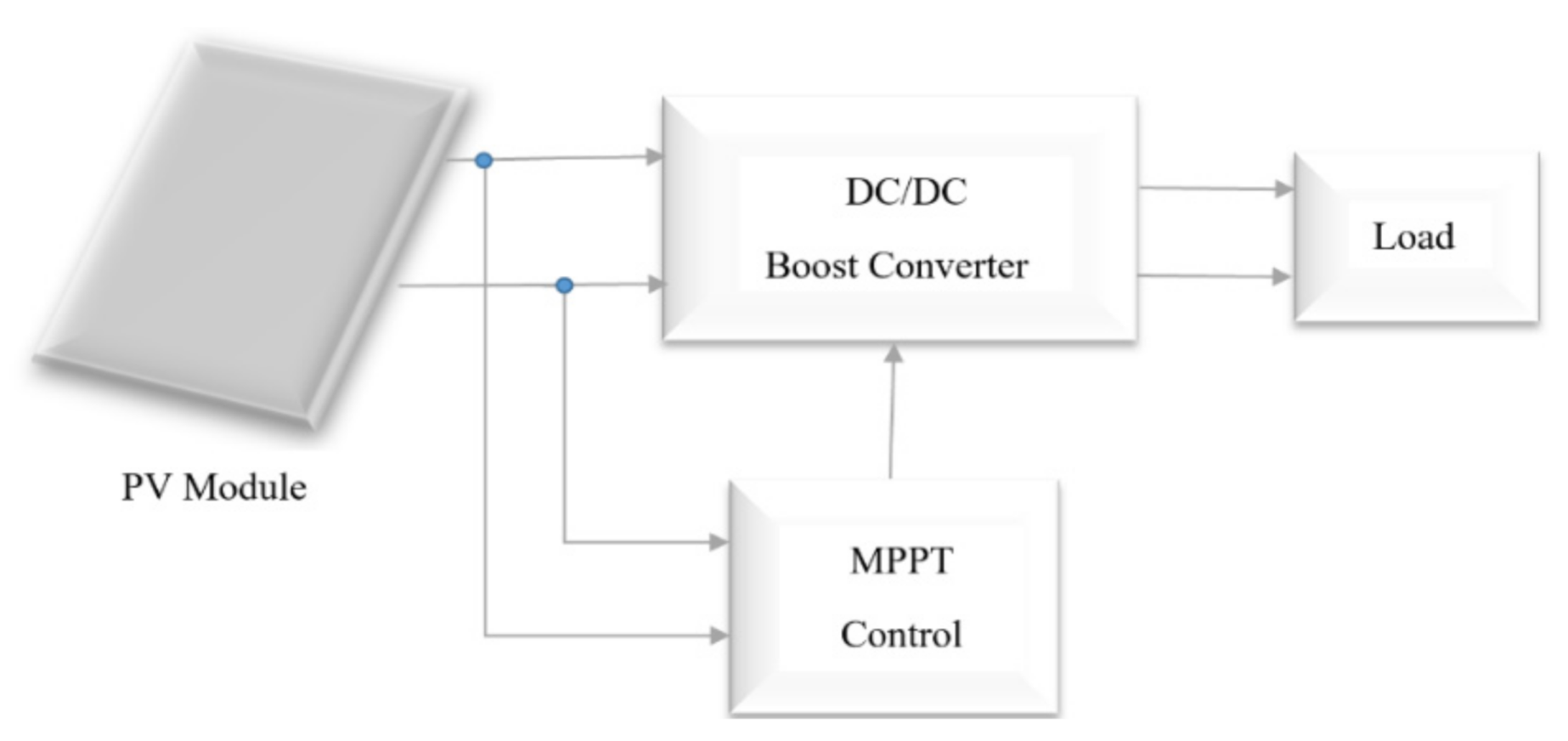
The system considered in this article is illustrated in Figure 3. A boost converter was used for the DC-to-DC converter. The improved MPPT method is a combination of the free-division incremental conductance algorithm and a self-predictive step-size correction algorithm. In general, in SPInC, the implementation of the algorithm is simplified by eliminating the division operation and, being able to determine the operating region, determining the appropriate step size for each region and detecting radiation changes. The improved algorithm first determines the operating region. In general, the algorithm divides the operating areas into three modes: the MPPT region, the normal region, and dynamic conditions. If the slope of the P–V curve is too low, the algorithm departs from the normal work area and enters the MPPR. In this area, the slope of the P–V curve is too low, and the algorithm reduces output power ripple by changing the step size after detecting the MPPR. However, if the power changes increase, the algorithm detects the dynamic state entry and then resizes so that the maximum new power point can be detected faster.
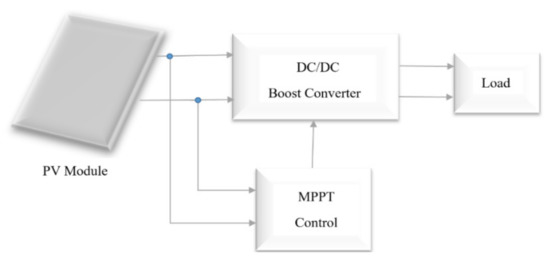
Figure 3.
Complete schematic of a photovoltaic system with a boost converter.
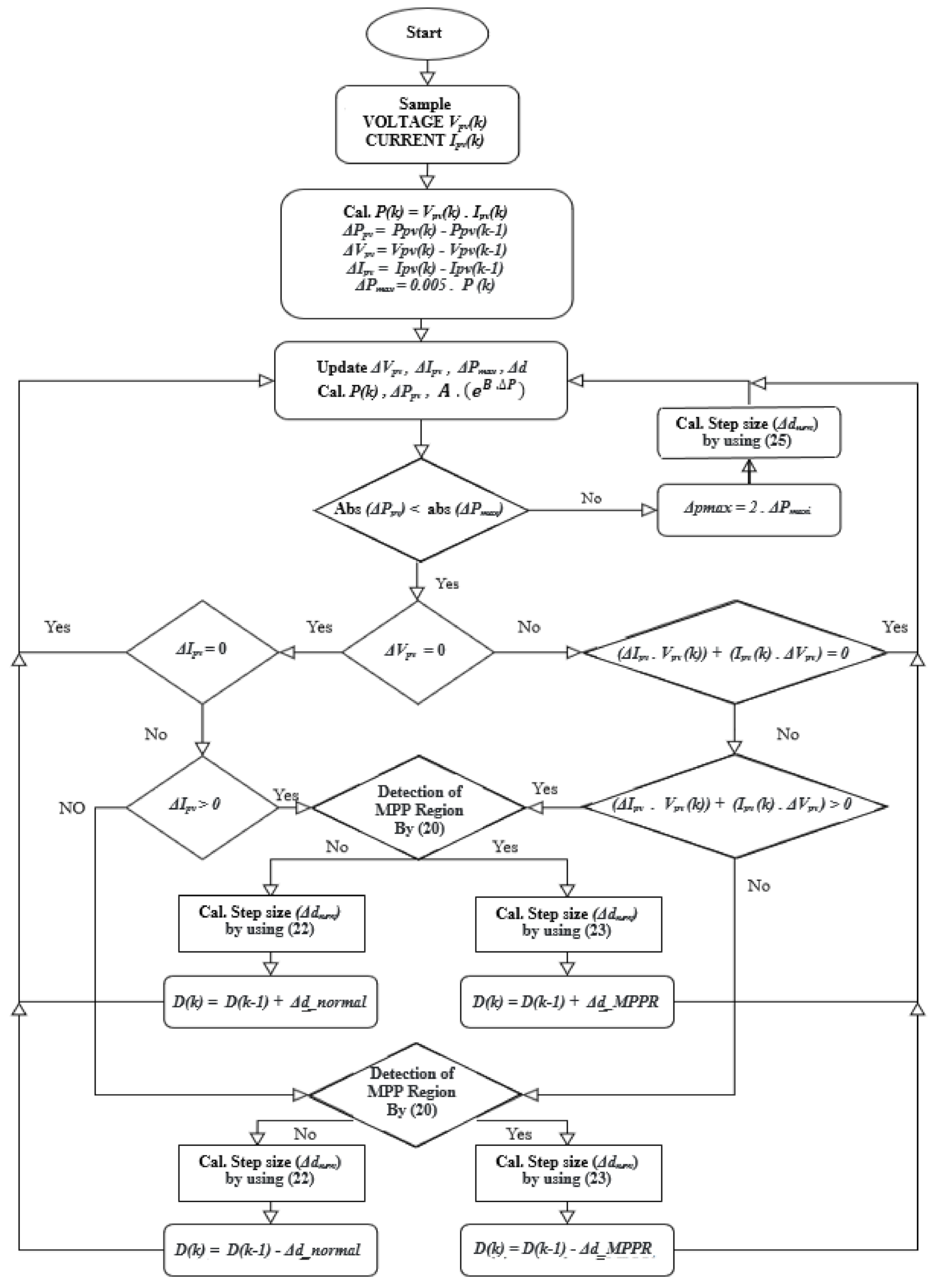
The flowchart of the SPInC algorithm is shown in Figure 4. In general, SPInC initially checks the condition to enter the dynamic condition. For this purpose, the initial value of ∆Pmax is considered equal to ∆Pmaxi. ∆Pmax is the maximum power change value. ∆Pmax should not be too large, as its large size prevents the algorithm from detecting some changes in radiation and temperature. Its small value makes the system overly sensitive and constantly detects dynamic conditions. considering these two conditions, ∆Pmax is equal to the appropriate coefficient of the power value. If ∆Pmax is not greater than ∆P, it means that the power changes are greater than normal; therefore, the algorithm detects the dynamic conditions, and by selecting a larger ∆d, the maximum power point tracking time is reduced. The ∆Pmax value is also considered twice the initial value to cover the changes. The algorithm uses the slope of the P–V curve to detect two other regions. If the slope of the P–V curve is greater than 0.005, it means that the power is very different from the maximum power point. Thus, the system is in the normal region, and SPInC uses the ∆dNormal for MPPT, which must be large enough to ensure that the tracking speed does not decrease. The algorithm continues tracking to reach the maximum power region. If the slope of the P–V curve is less than 0.005, the system has entered the MPPR. In this region, due to the proximity of the maximum point power, a smaller ∆d than the normal value is selected. In the MPPR, due to the small slope of the P–V curve, the power difference of any point in this region with the maximum power value is very small; thus, the algorithm must track the maximum power point with a smaller ∆d for more accurate tracking. Therefore, SPInC reduces ∆d by 75% immediately after reaching the MPPR, which reduces the size of the fluctuations by 75%. Then, the algorithm goes to the next iteration, and if the system is still in the MPPR due to the dependence of ∆d on the ∆P value and because ∆P in this area is small, the step size in this area will be smaller in each tracking iteration. The following section explains how to identify each of these conditions.
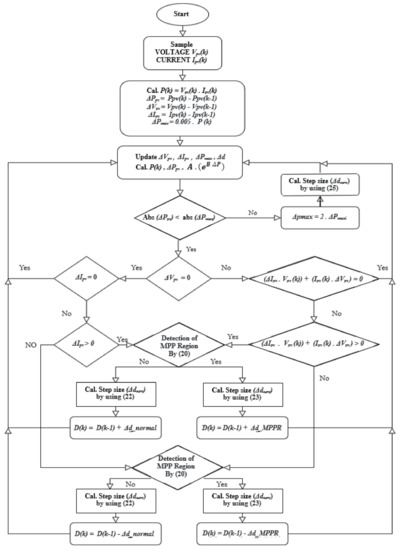
Figure 4.
Self-predictive incremental conductance (SPInC) flowchart.
4.1. Detection of MPP Region (MPPR)
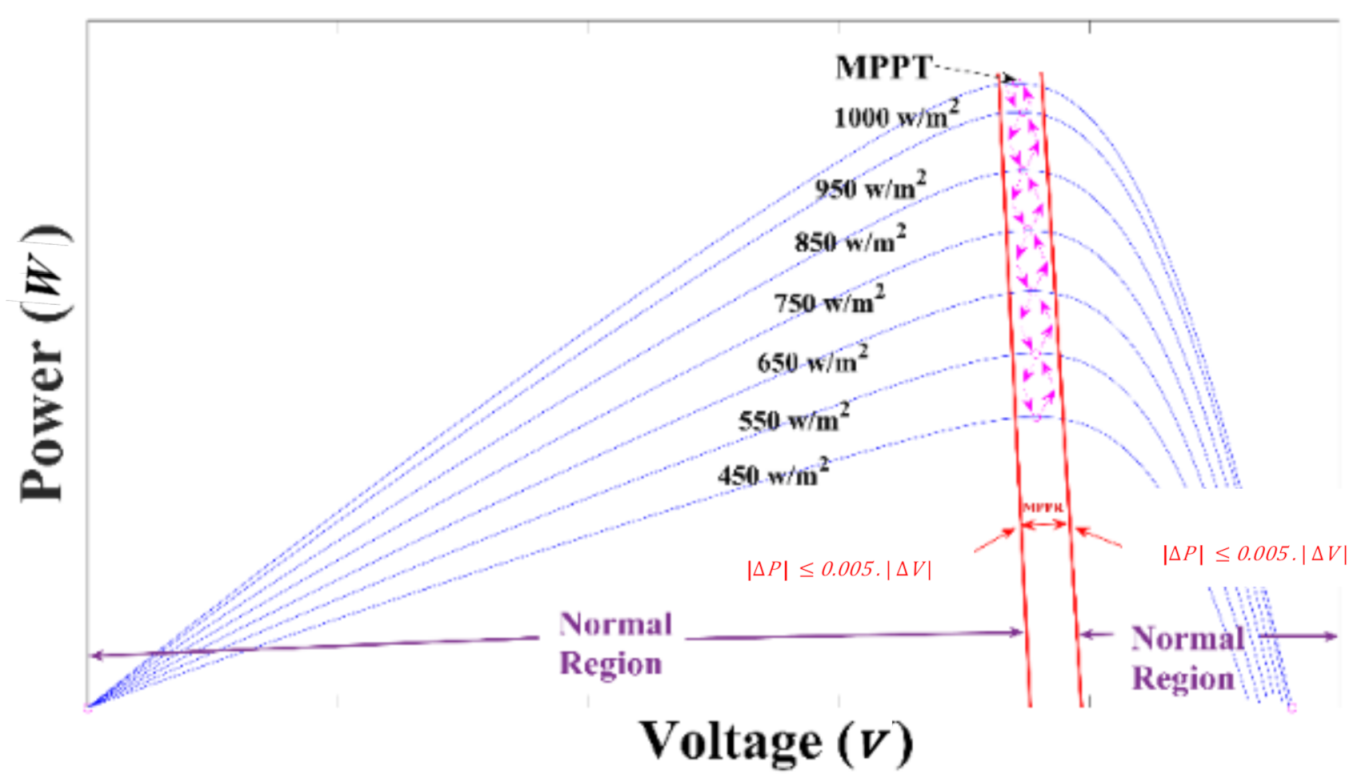
The MPPR is a small area in the P–V curve where the power size of each point in this region has very minute differences to the maximum power. If the slope of the P–V curve falls below 0.005, the algorithm enters the MPPR. Otherwise, the algorithm is in the normal region. Equation (20) is obtained by changing Equation (21). The division operation in Equation (20) is omitted. The slope of the P–V curve at the MPP is equal to zero; according to Equation (21), the slope of the P–V curve at the MPPR is very low, so this region is a good approximation of the MPP. Figure 5 shows the different operating areas for different radiation intensities. According to Figure 5, the boundary condition (20) continuously forces the system to oscillate near the MPP.
where P and V are the output power and voltage changes, respectively.
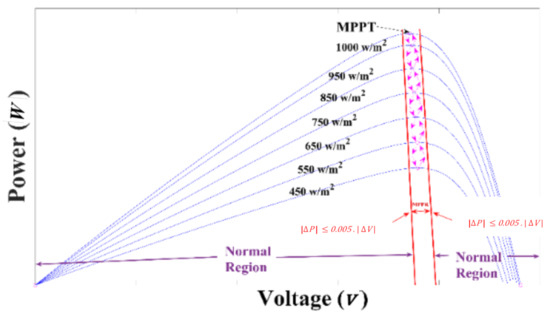
Figure 5.
Maximum power point region (MPPR) and normal regions under irradiance change at 25 °C.
4.2. Step Size Determination
The step size for the normal region is calculated from Equation (22). According to this equation, the step size has an exponential relation with the value of the power changes at any moment. However, at the MPPR, due to its proximity to the MPP, the step size must be smaller than the normal region to reduce the output power ripple and track the maximum power point more accurately. In this region, the algorithm determines the step size according to Equation (23):
where A and B are positive scalar and are obtained by the trial-and-error method, 0.02 is the most appropriate value for A, and 0.1 is the most appropriate value for B. and the step size of the normal region and the MPPR, respectively.
4.3. Detection of Dynamic Conditions
SPInC uses Pmax to detect power sudden changes. The initial value of Pmax is determined by the following equation:
where P is the output power of the panel. The Pmax value changes during the simulation. During the simulation to detect sudden changes in radiation, the algorithm continuously checks Pmax < P. If the condition Pmax < P is met, the algorithm enters the dynamic condition, and the radiation rate changes suddenly. Therefore, in order for the system to be able to detect the new MPPs faster, must be increased. The following changes in and Pmax size are made for faster detection of the new MPP:
∆dDynamic and ∆Pmaxi are the step size of dynamic condition and initial value of ∆Pmax, respectively. A and B are positive scalar.
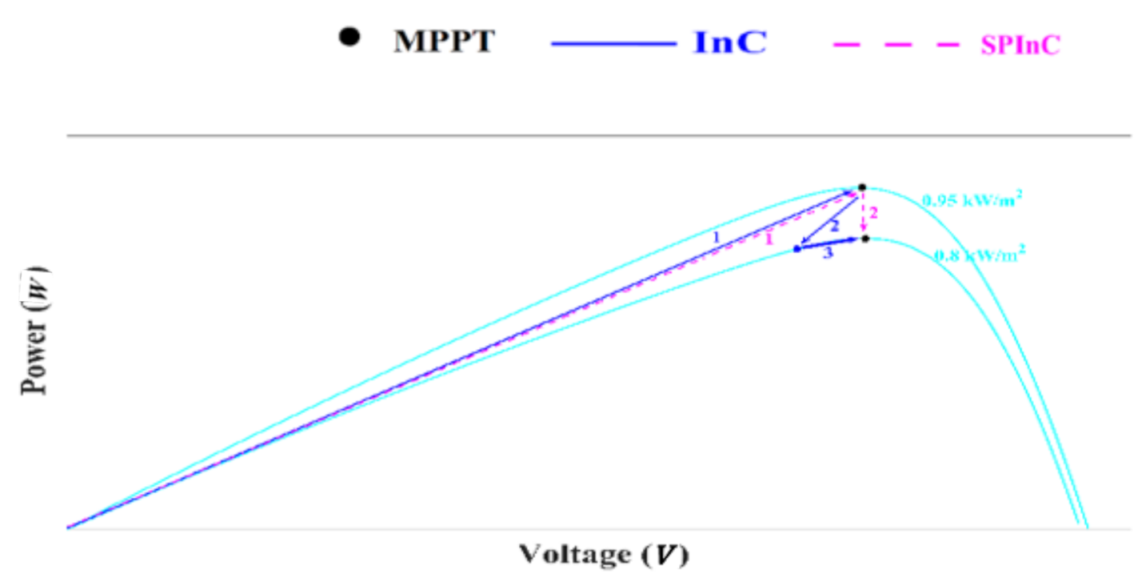
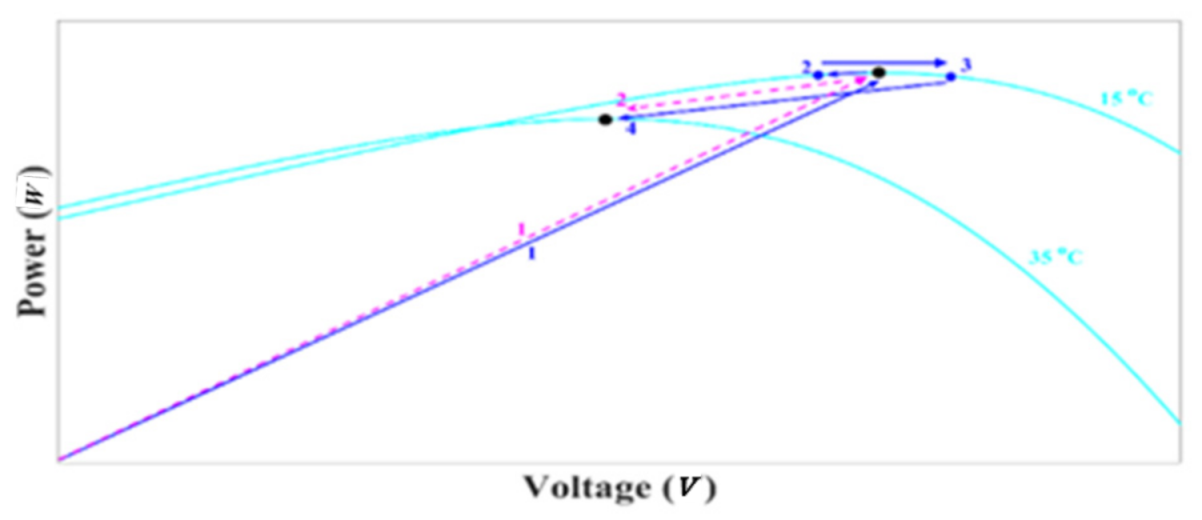
Figure 6 and Figure 7 show the performance of two algorithms for dynamic conditions. Figure 6 is at a constant temperature of 25 °C and shows the performance of the system under conditions of decreasing radiation intensity from 0.95 to 0.8 kW/m2. For both algorithms, the operating point starts from the start point and finally reaches the maximum power of each radiation, as shown in Figure 6. For the SPInC algorithm, it correctly traces the path and reaches the MPP due to the correct selection, but in the conventional InC algorithm, it follows path 2 and then reaches the MPP by following path 3. As shown in Figure 6, with decreasing radiation intensity, SPInC traces the correct path without error and reaches the new MPP, but the conventional method first loses the tracking path and follows path 2, and after finding the correct path, it reaches the new MPP. Figure 7 shows the performance of the two algorithms at constant radiation intensity of 1000 W/m2 and variable temperature. In Figure 7, the temperature is first assumed to be 15 °C and then increases to 35 °C. As the temperature increases, the conventional InC loses the right tracking path, but SPInC traces the MPP without error.
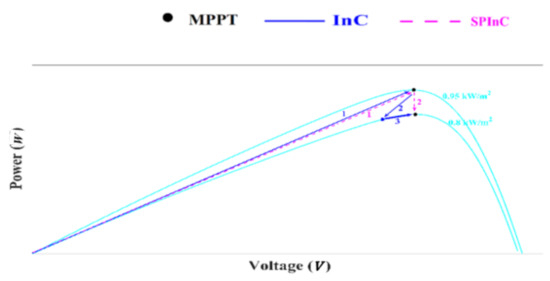
Figure 6.
P–V curve for a sudden decrease in irradiance.
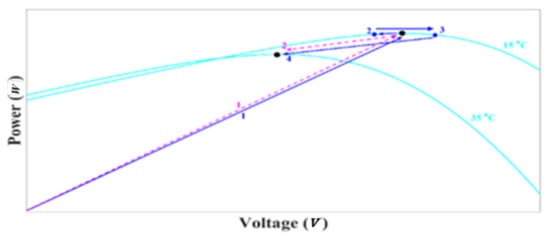
Figure 7.
P–V curve for a sudden increase in temperature.
5. Simulation Results
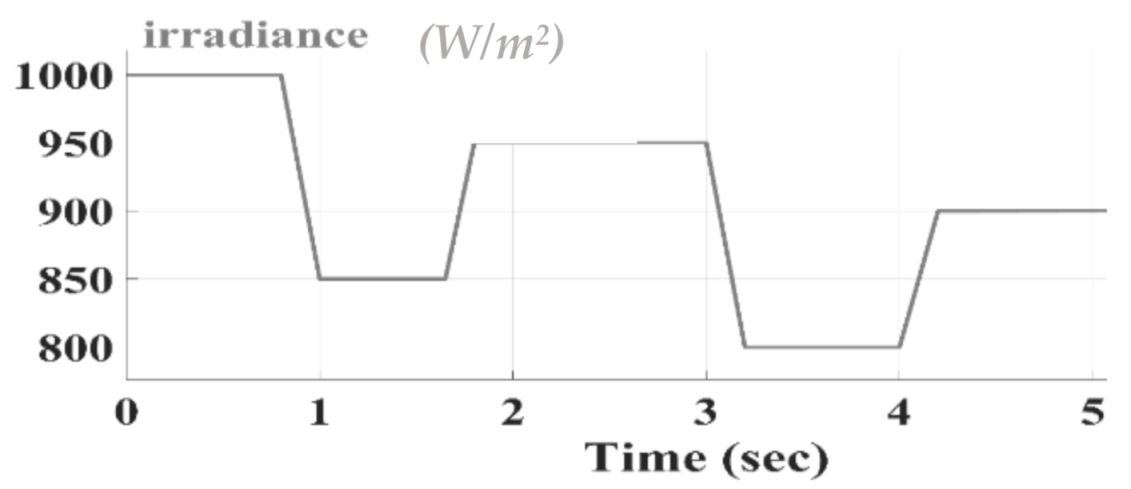
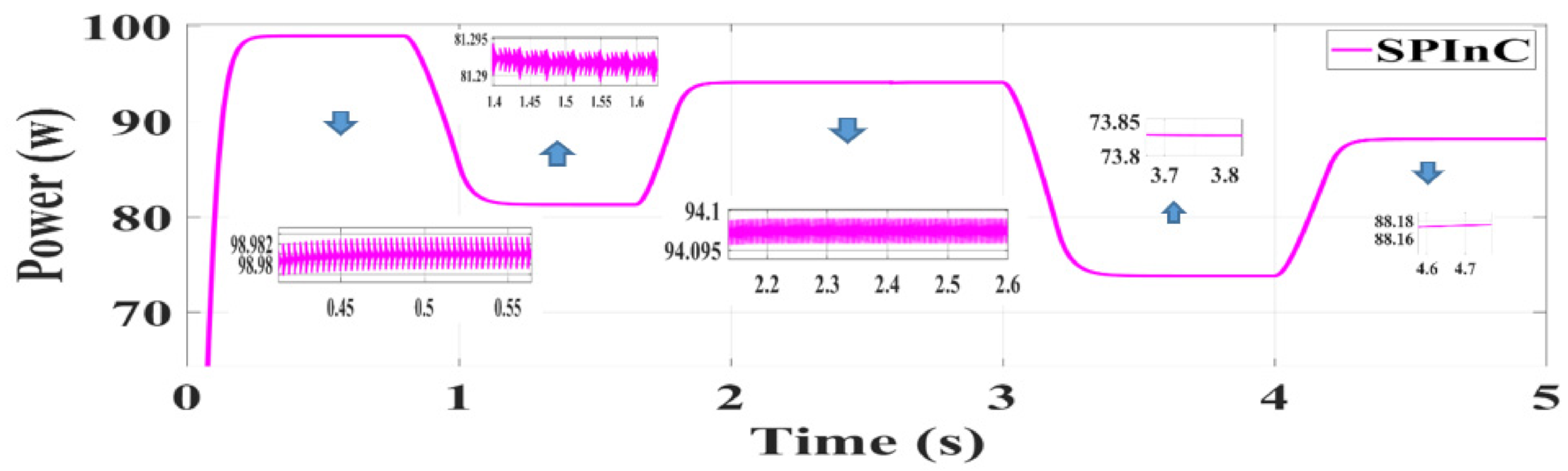
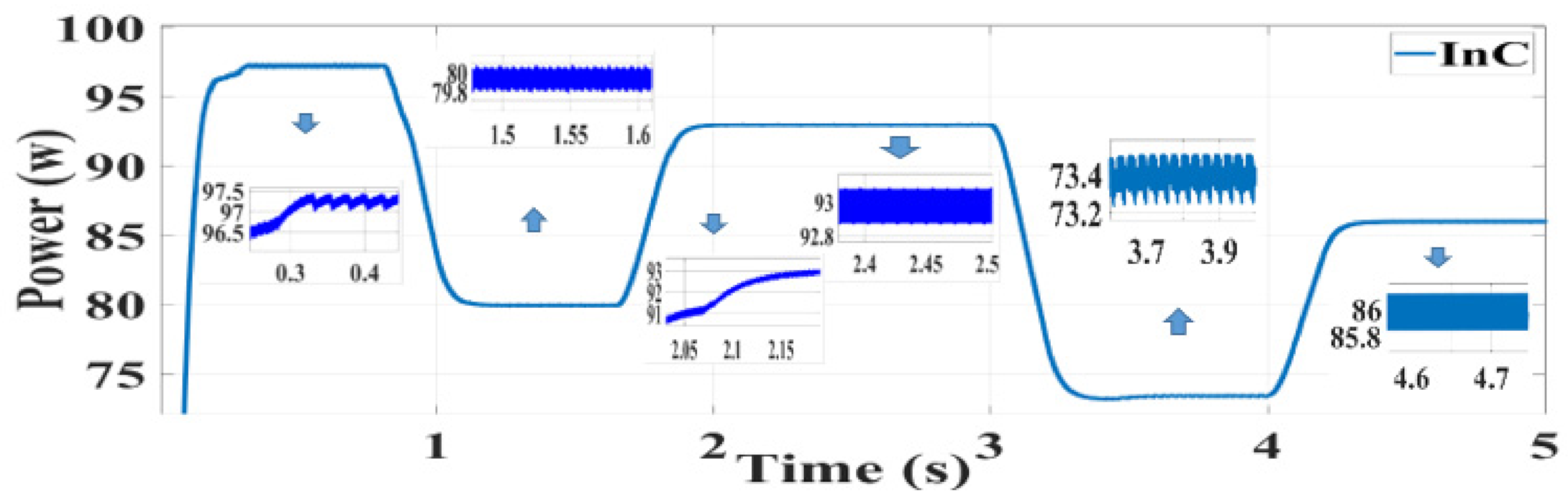
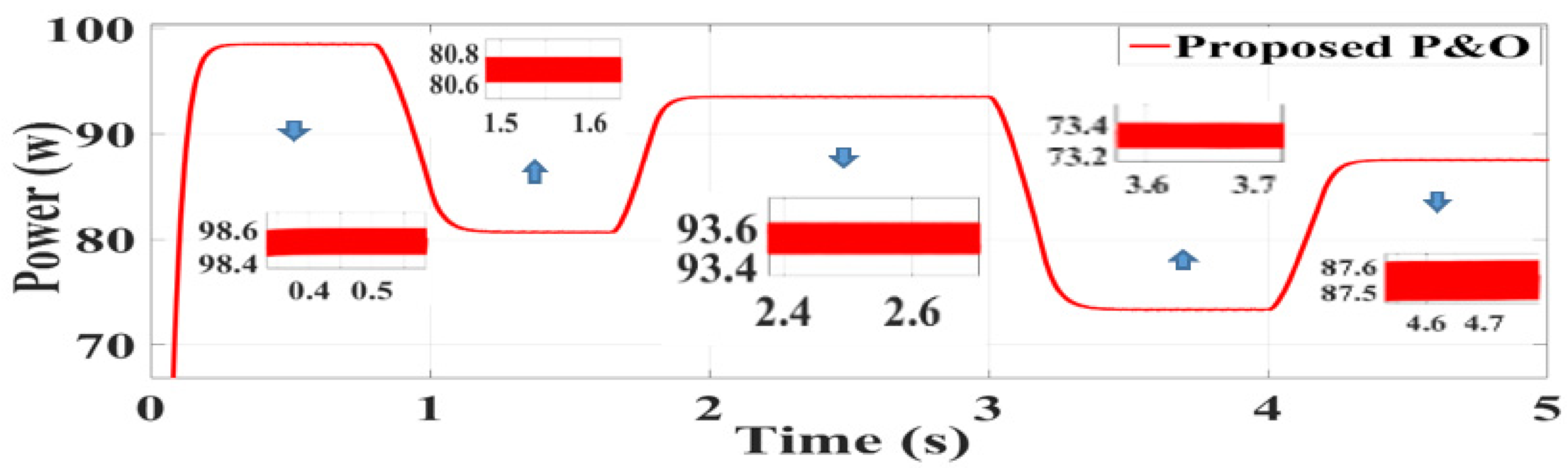
The results of the simulation were obtained with MATLAB/Simulink software. The PV module used in this study is Green Energy Technology GET-100A-1. The PV array was formed by connecting a module in series and a module in parallel. Figure 8 shows the conditions for the first part of the simulation, according to which 25 °C was selected for both methods, and the simulation was performed at five different radiation intensities of 800, 850, 900, 950, and 1000 W/m2. Figure 8 shows the radiation changes in Figure 9, Figure 10 and Figure 11. Figure 9, Figure 10 and Figure 11 show the output power for the proposed SPInC and conventional InC algorithms and proposed P&O algorithm in [36], respectively. Fsw = 5 kHz.
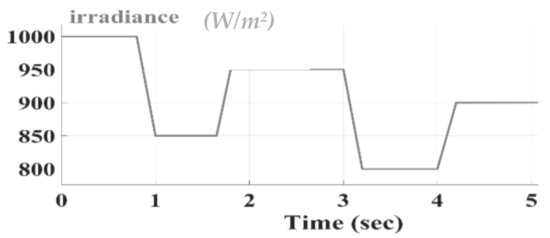
Figure 8.
Insolation change pattern in ramped manner.
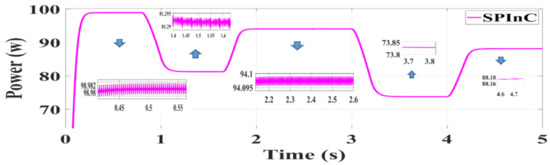
Figure 9.
Simulation result of the SPInC algorithm.
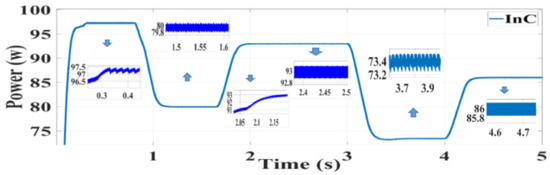
Figure 10.
Simulation result of the InC algorithm.
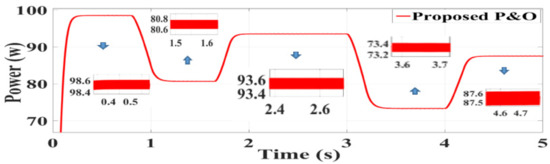
Figure 11.
Simulation result of the proposed perturb and observe (P&O) algorithm [36].
According to Figure 9, Figure 10 and Figure 11, it can be concluded that in different radiations, all three algorithms, namely, the conventional InC, SPInC, and the proposed P&O, detected maximum peak power at a good speed but with different accuracies. Figure 9, Figure 10 and Figure 11 show the output power of the system for five different levels of radiation in a transient and steady state for SPInC and the conventional InC and proposed P&O algorithm, respectively. According to Table 2, the efficiency of SPInC for all radiation intensities is higher than that of the conventional InC and proposed P&O methods, and the output power ripple for SPInC is lower than that of the conventional InC and proposed P&O methods. In general, the SPInC algorithm accurately detects the maximum power point, and, at all moments, has higher efficiency and less power ripple than the conventional InC. Furthermore, the SPInC algorithm does not lose the tracking path due to the selection of the appropriate at any given moment. However, in the conventional case, according to the simulation results, the algorithm lost the tracking path and found the correct path after several iterations. Table 2 compares the performance of the three algorithms for different radiations at a constant temperature.

Table 2.
Comparison of performance indicators of the SPInC and InC methods under irradiance changes.
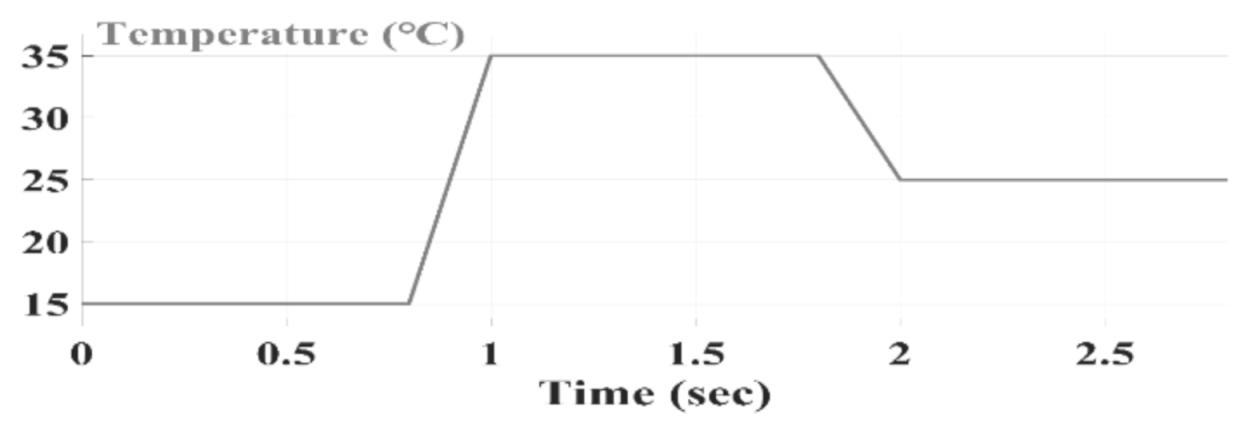
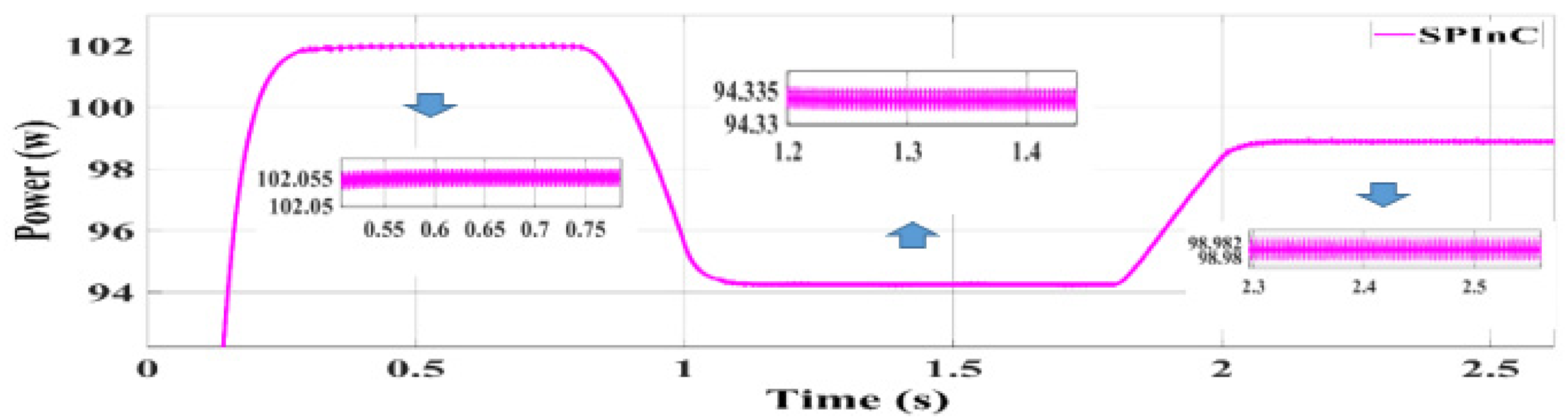
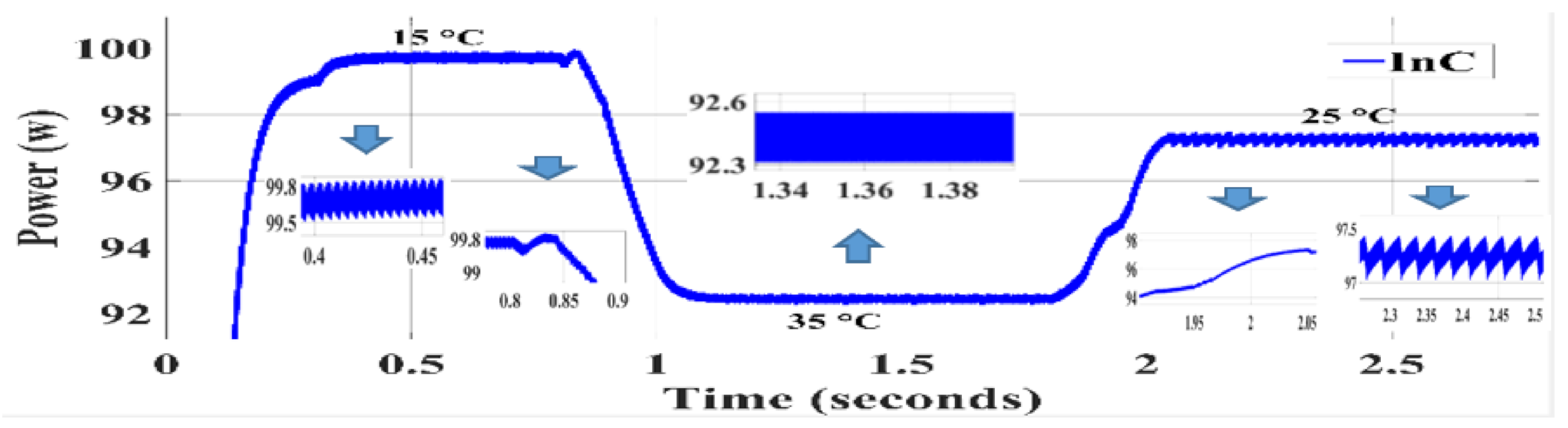
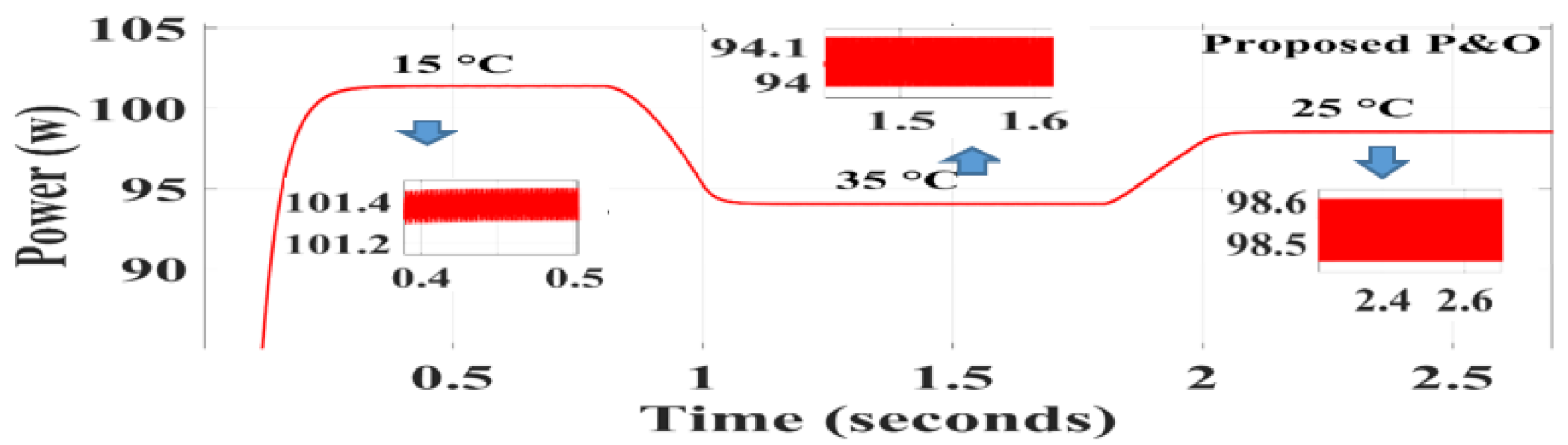
Figure 12 shows the conditions for the second part of the simulation. For the three methods, radiation intensity 1000 W/m2 was selected, and simulations were performed at three different temperatures, 15, 35, and 25 °C. Figure 12 shows the temperature changes in Figure 13, Figure 14 and Figure 15. Figure 13, Figure 14 and Figure 15 show the output power for the SPInC and conventional InC and proposed P&O algorithms, respectively.
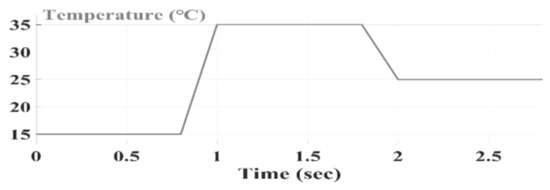
Figure 12.
Insolation change pattern in ramped manner.
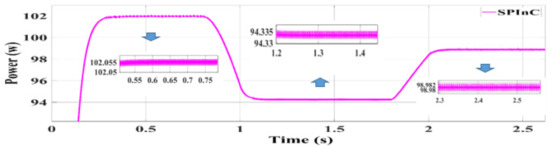
Figure 13.
Simulation result of SPInC algorithm.
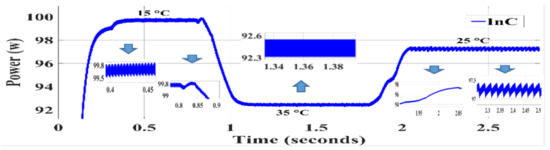
Figure 14.
Simulation result of InC algorithm.
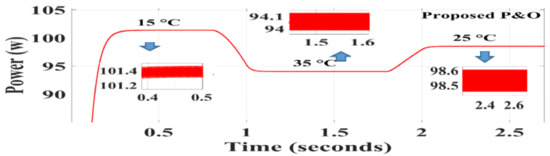
Figure 15.
Simulation result of proposed P&O algorithm [36].
Table 3 compares the energy generated by the three algorithms for the power output under the radiation changes in Figure 8.

Table 3.
Energy generated as a function of MPPT technique and irradiance input.
According to Figure 13, Figure 14 and Figure 15, it can be concluded that in temperature changes, all three techniques, namely, conventional InC, SPInC and the proposed P&O method, detected the maximum power point at a good speed but with different accuracies. Figure 13, Figure 14 and Figure 15 show the output power of the system for three different temperatures in a transient and steady state for SPInC and the conventional and proposed P&O algorithms, respectively. According to Table 4, the SPInC output for all three temperatures is higher than the conventional InC and proposed P&O algorithm, and the output power ripple for the SPInC is lower than that for the conventional InC and proposed P&O methods. In general, the SPInC algorithm accurately detects the maximum power point, and at all moments, it has higher efficiency and less power ripple than the conventional InC. Furthermore, the SPInC algorithm does not lose the tracking path due to selection of the appropriate at any time. However, in the conventional InC, according to simulation results, for example, at t = 0.8 s, the algorithm loses the tracking path and finds the correct path after several iterations. Table 4 compares the performance of the three algorithms for different temperatures in constant irradiation.

Table 4.
Comparison of performance indicators of the SPInC and InC methods under temperature changes.
Table 5 compares the energy generated by the three algorithms for the power output under the temperature changes in Figure 12. In Table 6, the SPInC method is compared with several valid articles. According to the results, SPInC has a lower power ripple and higher efficiency. Furthermore, system implementation is simplified by removing the division operations from the algorithm structure. The results show that SPInC is able to compete with the modified algorithms presented in recent popular articles.

Table 5.
Energy generated as a function of MPPT technique and temperature input.

Table 6.
Comparison between the SPInC technique and several valid articles.
6. Conclusions
This paper introduces an improved SPInC algorithm. The SPInC algorithm, by recognition of the operation region and selection of the appropriate size of ∆d for each region, reduced the output power ripple and increased the efficiency of the system. SPInC can detect sudden changes in radiation and temperature, and choosing the appropriate size of the ∆d in each moment, it can receive the maximum power from the panel. Furthermore, by elimination of the division operation from the conventional InC algorithm, the implementation of the algorithm was simplified. The results of the simulation show that the efficiency of SPInC in any condition is higher than that of the conventional InC and proposed P&O algorithm, and it has a smaller output power ripple. Finally, comparing SPInC with recent popular articles, it has been proven that this algorithm can compete with algorithms which that recently been presented in reputable papers. The study of the degradation of solar panels based on the proposed algorithm will be investigated in our future research.
Author Contributions
Conceptualization, investigation, and writing—original draft preparation, S.J.Z. and N.E.; writing—review and editing and supervision, S.M. and K.-H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Breeze, P. Power Generation Technologies; Newnes: Oxford, UK, 2019. [Google Scholar]
- Gross, M.; Rüdiger, M. Renewable Energies; Routledge: Abingdon, UK, 2014. [Google Scholar]
- Oncel, S.S. Green energy engineering: Opening a green way for the future. J. Clean. Prod. 2017, 142, 3095–3100. [Google Scholar] [CrossRef]
- Zadeh, M.J.Z.; Fathi, S.H. A new approach for photovoltaic arrays modeling and maximum power point estimation in real operating conditions. IEEE Trans. Ind. Electron. 2017, 64, 9334–9343. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K. Variable perturbation size adaptive P&O MPPT algorithm for sudden changes in irradiance. IEEE Trans. Sustain. Energy 2014, 5, 718–728. [Google Scholar]
- Moon, S.; Yoon, S.G.; Park, J.H. A new low-cost centralized MPPT controller system for multiply distributed photovoltaic power conditioning modules. IEEE Trans. Smart Grid 2015, 6, 2649–2658. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2015, 7, 181–188. [Google Scholar] [CrossRef]
- Liu, C.; Wu, B.; Cheung, R. Advanced algorithm for MPPT control of photovoltaic systems. In Proceedings of the Canadian Solar Buildings Conference, Montreal, QC, Canada, 20–24 August 2004; Volume 8, pp. 20–24. [Google Scholar]
- Faranda, R.; Leva, S. Energy comparison of MPPT techniques for PV Systems. Wseas Trans. Power Syst. 2008, 3, 446–455. [Google Scholar]
- Bahari, M.I.; Tarassodi, P.; Naeini, Y.M.; Khalilabad, A.K.; Shirazi, P. Modeling and simulation of hill climbing MPPT algorithm for photovoltaic application. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Capri, Italy, 22–24 June 2016; pp. 1041–1044. [Google Scholar]
- Kjær, S.B. Evaluation of the “hill climbing” and the “incremental conductance” maximum power point trackers for photovoltaic power systems. IEEE Trans. Energy Convers. 2012, 27, 922–929. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An enhanced adaptive P&O MPPT for fast and efficient tracking under varying environmental conditions. IEEE Trans. Sustain. Energy 2018, 9, 1487–1496. [Google Scholar]
- Ahmed, J.; Salam, Z. A modified P&O maximum power point tracking method with reduced steady-state oscillation and improved tracking efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the perturb-and-observe and incremental conductance MPPT methods for PV systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Mei, Q.; Shan, M.; Liu, L.; Guerrero, J.M. A novel improved variable step-size incremental-resistance MPPT method for PV systems. IEEE Trans. Ind. Electron. 2010, 58, 2427–2434. [Google Scholar] [CrossRef]
- Necaibia, S.; Kelaiaia, M.S.; Labar, H.; Necaibia, A.; Castronuovo, E.D. Enhanced auto-scaling incremental conductance MPPT method, implemented on low-cost microcontroller and SEPIC converter. Sol. Energy 2019, 180, 152–168. [Google Scholar] [CrossRef]
- Zakzouk, N.E.; Elsaharty, M.A.; Abdelsalam, A.K.; Helal, A.A.; Williams, B.W. Improved performance low-cost incremental conductance PV MPPT technique. IET Renew. Power Gener. 2016, 10, 561–574. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified incremental conductance algorithm for photovoltaic system under partial shading conditions and load variation. IEEE Trans. Ind. Electron. 2014, 61, 5384–5392. [Google Scholar]
- Guo, Y.; Sun, H.; Zhang, Y.; Liu, Y.; Li, X.; Xue, Y. Duty-Cycle Predictive Control of Quasi-Z-Source Modular Cascaded Converter Based Photovoltaic Power System. IEEE Access 2020, 8, 172734–172746. [Google Scholar] [CrossRef]
- Thangavelu, A.; Vairakannu, S.; Parvathyshankar, D. Linear open circuit voltage-variable step-size-incremental conductance strategy-based hybrid MPPT controller for remote power applications. IET Power Electron. 2017, 10, 1363–1376. [Google Scholar] [CrossRef]
- Elbaset, A.A.; Ali, H.; Abd-El Sattar, M.; Khaled, M. Implementation of a modified perturb and observe maximum power point tracking algorithm for photovoltaic system using an embedded microcontroller. IET Renew. Power Gener. 2016, 10, 551–560. [Google Scholar] [CrossRef]
- Sokolov, M.; Shmilovitz, D. A modified MPPT scheme for accelerated convergence. IEEE Trans. Energy Convers. 2008, 23, 1105–1107. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Self-adaptive incremental conductance algorithm for swift and ripple-free maximum power harvesting from PV array. IEEE Trans. Ind. Inform. 2017, 14, 2031–2041. [Google Scholar] [CrossRef]
- Rezk, H.; Aly, M.; Al-Dhaifallah, M.; Shoyama, M. Design and Hardware Implementation of New Adaptive Fuzzy Logic-Based MPPT Control Method for Photovoltaic Applications. IEEE Access 2019, 7, 106427–106438. [Google Scholar] [CrossRef]
- Behera, T.K.; Behera, M.K.; Nayak, N. Spider monkey based improve P&O MPPT controller for photovoltaic generation system. In Proceedings of the 2018 Technologies for Smart-City Energy Security and Power, Bhubaneswar, India, 28–30 March 2018; pp. 1–6. [Google Scholar]
- Hsieh, G.C.; Hsieh, H.I.; Tsai, C.Y.; Wang, C.H. Photovoltaic power-increment-aided incremental-conductance MPPT with two-phased tracking. IEEE Trans. Power Electron. 2012, 28, 2895–2911. [Google Scholar] [CrossRef]
- Belkaid, A.; Colak, I.; Isik, O. Photovoltaic maximum power point tracking under fast varying of solar radiation. Appl. Energy 2016, 179, 523–530. [Google Scholar] [CrossRef]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; e Melo, G.D.A.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2012, 60, 1156–1167. [Google Scholar] [CrossRef]
- Sekhar, P.C.; Mishra, S. Takagi–Sugeno fuzzy-basedincremental conductance algorithm for maximum powerpoint tracking of a photovoltaic generating system. IET Renew. Power Gener. 2014, 8, 900–914. [Google Scholar] [CrossRef]
- Motahhir, S.; El Ghzizal, A.; Sebti, S.; Derouich, A. Modeling of Photovoltaic System with Modified Incremental Conductance Algorithm for Fast Changes of Irradiance. Int. J. Photoenergy 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Fesharaki, V.J.; Sheikholeslam, F.; Jahed Motlagh, M.R. Maximum power point tracking with constraint feedback linearization controller and modified incremental conductance algorithm. Trans. Inst. Meas. Control 2018, 40, 2322–2331. [Google Scholar] [CrossRef]
- Jiang, Y.; Qahouq, J.A.A.; Haskew, T.A. Adaptive step size with adaptive-perturbation-frequency digital MPPT controller for a single-sensor photovoltaic solar system. IEEE Trans. Power Electron. 2012, 28, 3195–3205. [Google Scholar] [CrossRef]
- Nasiri, M.; Mobayen, S.; Zhu, Q.M. Super-Twisting Sliding Mode Control for Gearless PMSG-Based Wind Turbine. Complex 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Bingöl, O.; Burçin, Ö. Analysis and comparison of different PV array configurations under partial shading conditions. Sol. Energy 2018, 160, 336–343. [Google Scholar] [CrossRef]
- Ammar, H.H.; Azar, A.T.; Shalaby, R.; Mahmoud, M.I. Metaheuristic Optimization of Fractional Order Incremental Conductance (FO-INC) Maximum Power Point Tracking (MPPT). Complex 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Ali, A.I.; Sayed, M.A.; Mohamed, E.E. Modified efficient perturb and observe maximum power point tracking technique for grid-tied PV system. Int. J. Electr. Power Energy Syst. 2018, 99, 192–202. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).