Impact of Tube Bundle Placement on the Thermal Charging of a Latent Heat Storage Unit
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Model Description
2.2. Governing Equations
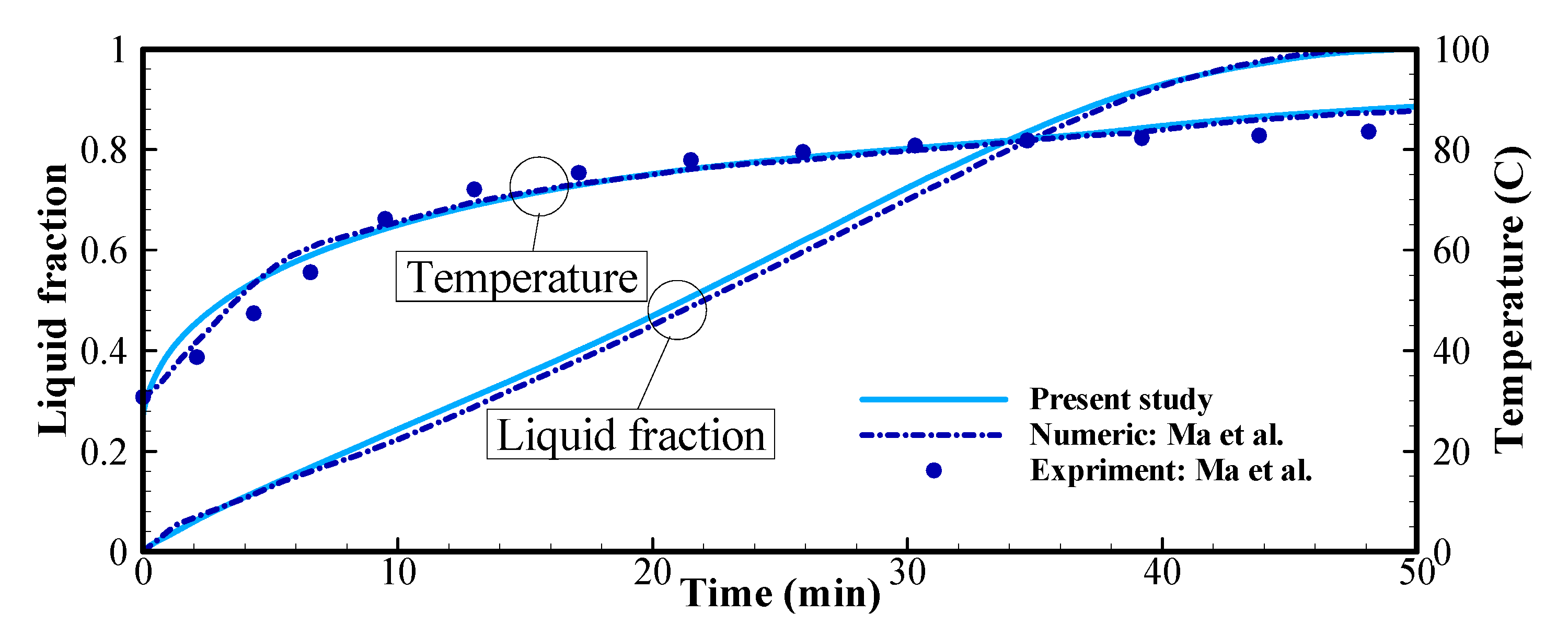
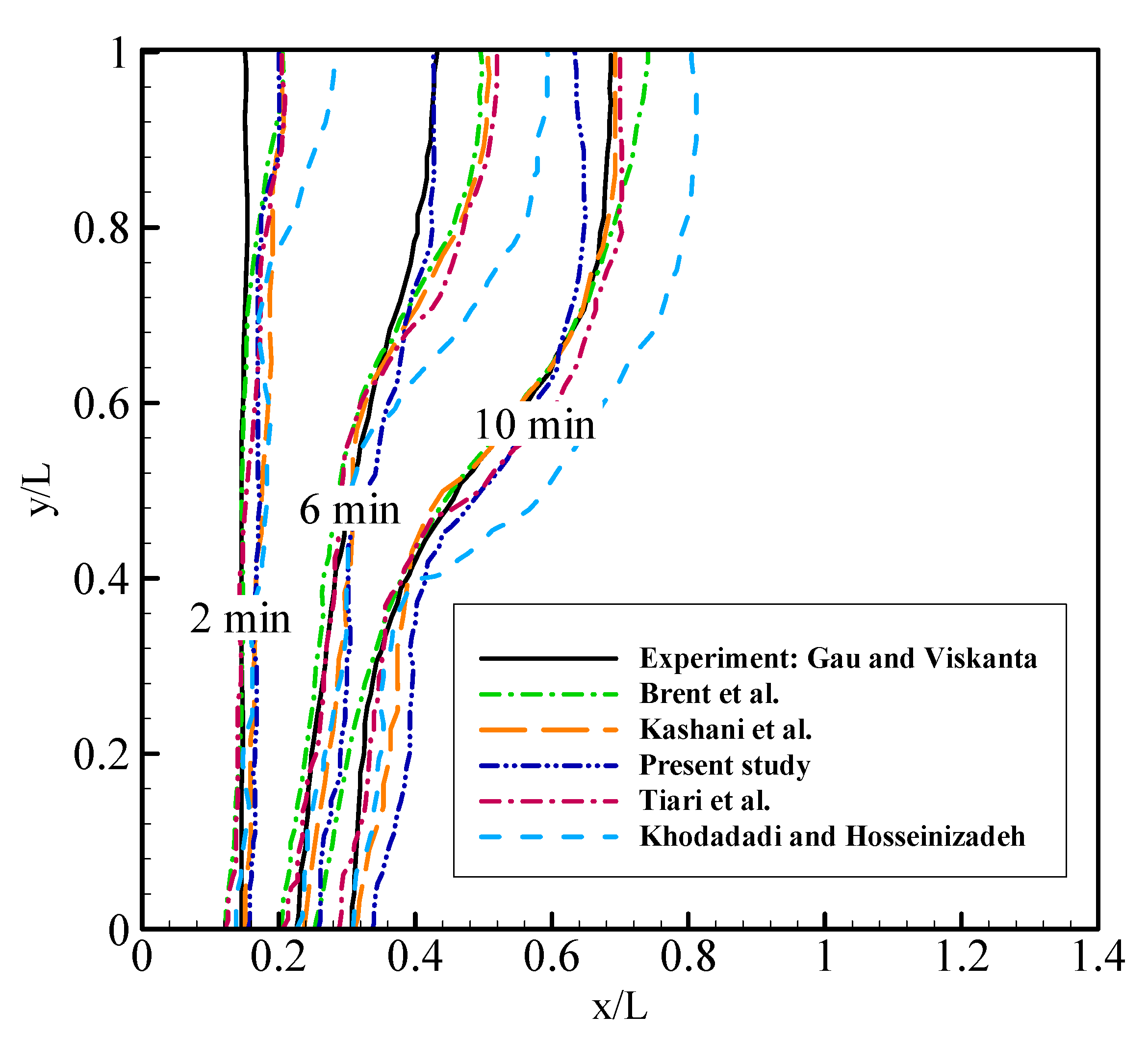
3. Numerical Method and Validation
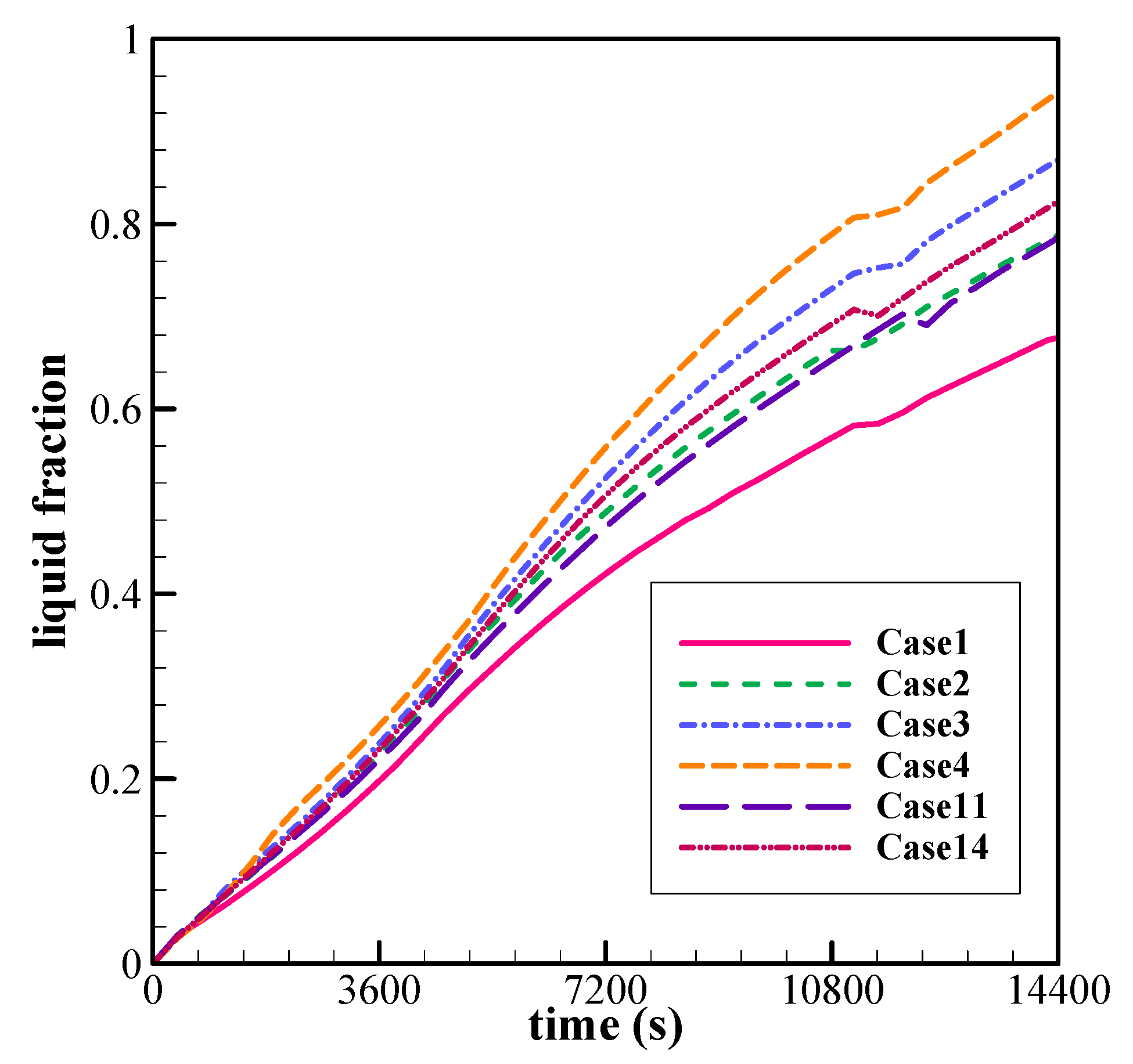
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dincer, I. On thermal energy storage systems and applications in buildings. Energy Build. 2002, 34, 377–388. [Google Scholar] [CrossRef]
- Ghoneim, A. Comparison of theoretical models of phase-change and sensible heat storage for air and water-based solar heating systems. Sol. Energy 1989, 42, 209–220. [Google Scholar] [CrossRef]
- Keshtkar, M.M.; Talebizadeh, P. Multi-objective optimization of cooling water package based on 3E analysis: A case study. Energy 2017, 134, 840–849. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, Y.; He, Y.-L. Effects of PCM arrangement and natural convection on charging and discharging performance of shell-and-tube LHS unit. Int. J. Heat Mass Transf. 2017, 115, 99–107. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Lohrasbi, S.; Ganji, D.D.; Nsofor, E.C. Simultaneous energy storage and recovery in the triplex-tube heat exchanger with PCM, copper fins and Al2O3 nanoparticles. Energy Convers. Manag. 2019, 180, 949–961. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.; Mohammad, A.T. Experimental study of melting and solidification of PCM in a triplex tube heat exchanger with fins. Energy Build. 2014, 68, 33–41. [Google Scholar] [CrossRef]
- Memon, Z.Q.; Pao, W.; Hashim, F.M.; Ali, H.M. Experimental investigation of two-phase separation in T-Junction with combined diameter ratio. J. Nat. Gas Sci. Eng. 2020, 73, 103048. [Google Scholar] [CrossRef]
- Sajawal, M.; Rehman, T.-u.; Ali, H.M.; Sajjad, U.; Raza, A.; Bhatti, M.S. Experimental thermal performance analysis of finned tube-phase change material based double pass solar air heater. Case Stud. Therm. Eng. 2019, 15, 100543. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Nsofor, E.C. Solidification enhancement in a triplex-tube latent heat energy storage system using nanoparticles-metal foam combination. Energy 2017, 126, 501–512. [Google Scholar] [CrossRef]
- Sardari, P.T.; Mohammed, H.I.; Giddings, D.; Gillott, M.; Grant, D. Numerical study of a multiple-segment metal foam-PCM latent heat storage unit: Effect of porosity, pore density and location of heat source. Energy 2019, 189, 116108. [Google Scholar] [CrossRef]
- Sharifi, N.; Faghri, A.; Bergman, T.L.; Andraka, C.E. Simulation of heat pipe-assisted latent heat thermal energy storage with simultaneous charging and discharging. Int. J. Heat Mass Transf. 2015, 80, 170–179. [Google Scholar] [CrossRef] [Green Version]
- Mahdi, J.M.; Nsofor, E.C. Melting of PCM with Nanoparticles in a Triplex-Tube Thermal Energy Storage System. Ashrae Trans. 2016, 122, 215–224. [Google Scholar]
- Singh, R.P.; Kaushik, S.; Rakshit, D. Melting phenomenon in a finned thermal storage system with graphene nano-plates for medium temperature applications. Energy Convers. Manag. 2018, 163, 86–99. [Google Scholar] [CrossRef]
- Gatea, M.A.; Jawad, H.A. Thermoplasmonic of single Au@ SiO2 and SiO2@ Au core shell nanoparticles in deionized water and poly-vinylpyrrolidonematrix. Baghdad Sci. J. 2019, 16, 376–381. [Google Scholar]
- Mahdi, J.M.; Mohammed, H.I.; Hashim, E.T.; Talebizadehsardari, P.; Nsofor, E.C. Solidification enhancement with multiple PCMs, cascaded metal foam and nanoparticles in the shell-and-tube energy storage system. Appl. Energy 2020, 257, 113993. [Google Scholar] [CrossRef]
- Sadeghi, H.M.; Babayan, M.; Chamkha, A. Investigation of using multi-layer PCMs in the tubular heat exchanger with periodic heat transfer boundary condition. Int. J. Heat Mass Transf. 2020, 147, 118970. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.; Khodadadi, J. Numerical simulation of the effect of the size of suspensions on the solidification process of nanoparticle-enhanced phase change materials. J. Heat Transf. 2013, 135. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Lohrasbi, S.; Nsofor, E.C. Hybrid heat transfer enhancement for latent-heat thermal energy storage systems: A review. Int. J. Heat Mass Transf. 2019, 137, 630–649. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Esapour, M.; Hosseini, M.; Ranjbar, A.; Bahrampoury, R. Numerical study on geometrical specifications and operational parameters of multi-tube heat storage systems. Appl. Therm. Eng. 2016, 109, 351–363. [Google Scholar] [CrossRef]
- Esen, M. Thermal performance of a solar-aided latent heat store used for space heating by heat pump. Sol. Energy 2000, 69, 15–25. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Chen, H.; Zhang, G. Thermal performance and optimized thickness of active shape-stabilized PCM boards for side-wall cooling and under-floor heating system. Indoor Built Environ. 2016, 25, 1279–1295. [Google Scholar] [CrossRef]
- Kibria, M.; Saidur, R.; Al-Sulaiman, F.; Aziz, M.M.A. Development of a thermal model for a hybrid photovoltaic module and phase change materials storage integrated in buildings. Sol. Energy 2016, 124, 114–123. [Google Scholar] [CrossRef]
- Eisapour, M.; Eisapour, A.H.; Hosseini, M.J.; Talebizadehsardari, P. Exergy and energy analysis of wavy tubes photovoltaic-thermal systems using microencapsulated PCM nano-slurry coolant fluid. Appl. Energy 2020, 266, 114849. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, X.; Zhao, X.; Li, P.; Ali, S. Experimental investigation of the energy performance of a novel Micro-encapsulated Phase Change Material (MPCM) slurry based PV/T system. Appl. Energy 2016, 165, 260–271. [Google Scholar] [CrossRef]
- Bazai, H.; Moghimi, M.; Mohammed, H.I.; Babaei-Mahani, R.; Talebizadehsardari, P. Numerical study of circular-elliptical double-pipe thermal energy storage systems. J. Energy Storage 2020, 30, 101440. [Google Scholar] [CrossRef]
- Talebizadehsardari, P.; Mohammed, H.I.; Mahdi, J.M.; Gillott, M.; Walker, G.S.; Grant, D.; Giddings, D. Effect of airflow channel arrangement on the discharge of a composite metal foam-phase change material heat exchanger. Int. J. Energy Res. 2020, 45, 2593–2609. [Google Scholar] [CrossRef]
- GmbH, R.T. RT35 data sheet. Available online: https://www.rubitherm.eu/en/index.php/productcategory/organische-pcm-rt (accessed on 10 November 2020).
- Talebizadeh Sardari, P.; Walker, G.S.; Gillott, M.; Grant, D.; Giddings, D. Numerical modelling of phase change material melting process embedded in porous media: Effect of heat storage size. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Huang, Y.; Li, C.; Peng, Z.; Ding, Y. Thermal energy charging behaviour of a heat exchange device with a zigzag plate configuration containing multi-phase-change-materials (m-PCMs). Appl. Eng. 2015, 142, 328–336. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Internal and external fin heat transfer enhancement technique for latent heat thermal energy storage in triplex tube heat exchangers. Appl. Therm. Eng. 2013, 53, 147–156. [Google Scholar] [CrossRef]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal–external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]
- Kashani, S.; Ranjbar, A.; Abdollahzadeh, M.; Sebti, S. Solidification of nano-enhanced phase change material (NEPCM) in a wavy cavity. Heat Mass Transf. 2012, 48, 1155–1166. [Google Scholar] [CrossRef]
- Brent, A.; Voller, V.R.; Reid, K. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. Part A Appl. 1988, 13, 297–318. [Google Scholar]
- Tiari, S.; Qiu, S.; Mahdavi, M. Numerical study of finned heat pipe-assisted thermal energy storage system with high temperature phase change material. Energy Convers. Manag. 2015, 89, 833–842. [Google Scholar] [CrossRef]
- Khodadadi, J.; Hosseinizadeh, S. Nanoparticle-enhanced phase change materials (NEPCM) with great potential for improved thermal energy storage. Int. Commun. Heat Mass Transf. 2007, 34, 534–543. [Google Scholar] [CrossRef]



| Property | RT35 |
|---|---|
| Solidus temperature (°C) | 29 |
| Liquidus temperature (°C) | 35 |
| Viscosity (Pas) | 0.023 |
| Heat of fusion (kJ/kg) | 170 |
| Density (kg/m3) | 815 |
| Thermal expansion coefficient (1/K) | 0.0006 |
| Specific heat (kJ/kgK) | 2 |
| Thermal conductivity (W/mK) | 0.2 |
| Factors | Description | Levels | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| A | HL0/D (height of the first tube) | 1.2 | 1.8 | 2.4 | 3.0 |
| B | HL1/D (height of the second tube) | 1.2 | 1.8 | 2.4 | 3.0 |
| C | HL2/D (height of the third tube) | 1.2 | 1.8 | 2.4 | 3.0 |
| C | HL3/D (height of the fourth tube) | 1.2 | 1.8 | 2.4 | 3.0 |
| Experiment Number | Control Parameters | MVF after Four Hours | |||
|---|---|---|---|---|---|
| HL0/D | HL1/D | HL2/D | HL3/D | ||
| 1 | 1.2 | 1.2 | 1.2 | 1.2 | 0.68 |
| 2 | 1.2 | 1.8 | 1.8 | 1.8 | 0.79 |
| 3 | 1.2 | 2.4 | 2.4 | 2.4 | 0.87 |
| 4 | 1.2 | 3.0 | 3.0 | 3.0 | 0.94 |
| 5 | 1.8 | 1.2 | 1.8 | 2.4 | 0.79 |
| 6 | 1.8 | 1.8 | 1.2 | 3.0 | 0.81 |
| 7 | 1.8 | 2.4 | 3.0 | 1.2 | 0.85 |
| 8 | 1.8 | 3.0 | 2.4 | 1.8 | 0.87 |
| 9 | 2.4 | 1.2 | 2.4 | 3.0 | 0.83 |
| 10 | 2.4 | 1.8 | 3.0 | 2.4 | 0.85 |
| 11 | 2.4 | 2.4 | 1.2 | 1.8 | 0.79 |
| 12 | 2.4 | 3.0 | 1.8 | 1.2 | 0.81 |
| 13 | 3.0 | 1.2 | 3.0 | 1.8 | 0.82 |
| 14 | 3.0 | 1.8 | 2.4 | 1.2 | 0.82 |
| 15 | 3.0 | 2.4 | 1.8 | 3.0 | 0.87 |
| 16 | 3.0 | 3.0 | 1.2 | 2.4 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghalambaz, M.; Eisapour, A.H.; Mohammed, H.I.; Islam, M.S.; Younis, O.; Sardari, P.T.; Yaïci, W. Impact of Tube Bundle Placement on the Thermal Charging of a Latent Heat Storage Unit. Energies 2021, 14, 1289. https://doi.org/10.3390/en14051289
Ghalambaz M, Eisapour AH, Mohammed HI, Islam MS, Younis O, Sardari PT, Yaïci W. Impact of Tube Bundle Placement on the Thermal Charging of a Latent Heat Storage Unit. Energies. 2021; 14(5):1289. https://doi.org/10.3390/en14051289
Chicago/Turabian StyleGhalambaz, Mohammad, Amir Hossein Eisapour, Hayder I. Mohammed, Mohammad S. Islam, Obai Younis, Pouyan Talebizadeh Sardari, and Wahiba Yaïci. 2021. "Impact of Tube Bundle Placement on the Thermal Charging of a Latent Heat Storage Unit" Energies 14, no. 5: 1289. https://doi.org/10.3390/en14051289









