The Power Losses in Cable Lines Supplying Nonlinear Loads

Abstract

This paper presents the skin effect impact on the active power losses in the sheathless single-core cables/wires supplying nonlinear loads. There are significant conductor losses when the current has a distorted waveform (e.g., the current supplying diode rectifiers). The authors present a new method for active power loss calculation. The obtained results have been compared to the IEC-60287-1-1:2006 + A1:2014 standard method and the method based on the Bessel function. For all methods, the active power loss results were convergent for small-cable cross-section areas. The proposed method gives smaller power loss values for these cable sizes than the IEC and Bessel function methods. For cable cross-section areas greater than 185 mm², the obtained results were better than those for the other methods. There were also analyses of extra power losses for distorted currents compared to an ideal 50 Hz sine wave for all methods. The new method is based on the current penetration depth factor calculated for every considered current harmonics, which allows us to calculate the precise equivalent resistance for any cable size. This research is part of our work on a cable thermal analysis method that has been developed.

1. Introduction

Power losses in transmission lines (cable lines, overhead wires) always occur depending on different physical phenomena. Among the power losses sources in the lines, the basic one is caused by the conductor heating while the current flows. The energy is released as Joules of heat [1,2]. The character and power of loads supplied by the transmission line in the design stage should avoid cable overloading. Mostly, there should be highlighted nonlinear loads which generate higher current harmonics to the supply network. These load types have a negative influence on the transmission line. Higher harmonics significantly impact the power losses and cause the cable conductor temperature to increase [3,4]. Assume that conductors work in these conditions for a long time. This may lead to insulation degradation and severe damage to the supplying cables. Supply equipment failure affects the economic losses in production enterprises due to unplanned demurrage and off-switching. It also generates additional costs linked with installation repairing. The costs and times of repair, especially for underground cable lines, are very high, so their occurrence should be minimized.

This article presents a simplified method for the calculation of active power losses and correlates it to the IEC-60287-1-1:2006 + A1:2014 standard method and the second one using the Bessel function. The obtained results may constitute a starting point to calculate the temperature distribution for different thermal backfills or determine the cable conductor’s optimal diameter and insulation.

The common element for all used methods [5] concerning active power loss calculations in power cables determines the resultant resistance, $R_{AC}\left(h\right)$, for a given current harmonic order (h). In each method, both skin and proximity effects are considered. The first method is based on the Bessel function. It allows finding a solution to the equation in polar coordinate systems associated with wave propagation and spherical potentials. In calculations the conductor resistance variation caused by the skin effect is considered as a correction factor for resistance, $R_{DC}$. The second method allows obtaining active power losses using the resultant surface resistance, considering the current penetration depth for uniform current flowing through a cross-section that is deep and wide. The next one is analytically described by the French researcher Levasseur based on skin effect observation and using frequency changes in the Kelvin effect calculations [6]. The most popular active power loss calculation method is described in the IEC-60287-1-1:2006 + A1:2014 standard. This method uses factors correlating to the skin effect.

In the currently used methods [5,7], the increase in resistance for the fundamental frequency is considered no matter what the cable cross-section area is. In such small cross-sections (e.g., 25 mm²), the depth of the current penetration—resulting from the skin effect—is greater than the radius of the low-voltage cable’s conductor. Hence, the conclusion is that the skin effect does not occur in this case and that the previously mentioned methods introduce an error in calculating the value of active power losses. However, in the authors’ new method the penetration depth factor concerning the radius of the considered cable conductor is considered.

It is difficult to carry out a laboratory experiment because of the relatively high RMS current values and current total harmonic distortion (THD_I) needed for a wide range of low-voltage cable cross-section areas. Therefore, in this article power losses due to skin effect are used only for theoretical calculations for the comparison of different methods.

The main contribution of this work can be summarized as follows:

• Presentation of a new active power loss calculation method based on the current penetration depth (CPD) factor depending on the analyzed current frequency.
• Comparison of the new method to already-existing methods.
• The active power loss increment for distorted currents is compared to the ideal 50 Hz sine wave for three calculation methods.

2. The Influence of Current Distortion on Power Cable Core Parameters

The current harmonic sources in the supply lines are nonlinear loads. Examples of nonlinear loads used by residential consumers are LED lights and power supplies for computers, TV sets, mobile and tablet chargers, and other electronic equipment. Thus, the universal usage of such loads is visible. They have an insignificant influence on the power network due to the low power of individual devices. However, the adverse impact increases if those devices work in bigger groups.

The opposite situation can be noticed for industrial consumers. Single loads have significant power (from several dozen kW to a few MW). In the power system infrastructure, the economy can be planned without considering important reserve factors for these loads. Such a situation can be acceptable for linear cases, because usually for this type of issue calculations are performed when planning the electrical systems. The current distortion level has a pivotal influence on the power cables’ real load value, supplying receivers for nonlinear loads. Among nonlinear high-power loads, we can highlight in particular power electronic converters such as rectifiers (full-bridge, six-pulse, twelve-pulse), frequency converters, and arc furnaces [8,9,10].

The higher harmonics appearing in the current frequency spectrum for nonsinusoidal waveforms can be described as [11,12,13]:

$$i_0\left(t\right)=A_0+B_1\sin \omega t+C_1\cos \omega t+{{\displaystyle \sum }}_{n=2}^{\infty }{B}_n\sin \left(n\omega t\right)+{{\displaystyle \sum }}_{n=2}^{\infty }{C}_n\cos \left(n\omega t\right),$$

(1)

where:

• $A_0$ is the DC component of the load current,
• $B_1\sin \omega t$ is the active current component,
• $C_1\cos \omega t$ is the reactive current component,
• ${{\displaystyle \sum }}_{n=2}^{\infty }{B}_n\sin \left(n\omega t\right)$ is the active current component of the higher harmonics,
• ${{\displaystyle \sum }}_{n=2}^{\infty }{C}_n\cos \left(n\omega t\right)$ is the reactive current component of the higher harmonics.

In relation to the standards [14], the current harmonics are considered up to 40 order. The authors took into account these requirements and conducted a power loss analysis according to these guidelines (up to the 40th order).

Total harmonic distortion (THD) is a parameter describing the current deformation level and can be expressed by Equation (2):

$$TH{D}_I=\frac{\sqrt{{{\displaystyle \sum }}_{n=1}^{40}{I}_n^2}}{I_1},$$

(2)

where:

• $I_1$ is the effective value of the signal of the fundamental component,
• $I_n$ is the effective value of the signal of the n-th harmonic.

The significant participation of higher current harmonics can negatively affect the rest loads installed in the same power system due to the voltage deformation, further interaction, and increase in the current and voltage higher harmonic levels [15,16,17,18,19].

Power cables are used widely in power systems, especially in industry. The cables must meet the following requirements:

−

Electrical (current carrying capacity, short-circuit durability, high insulation resistance);

−

Mechanical (special working conditions, environmental conditions, non-flammability, cable routing).

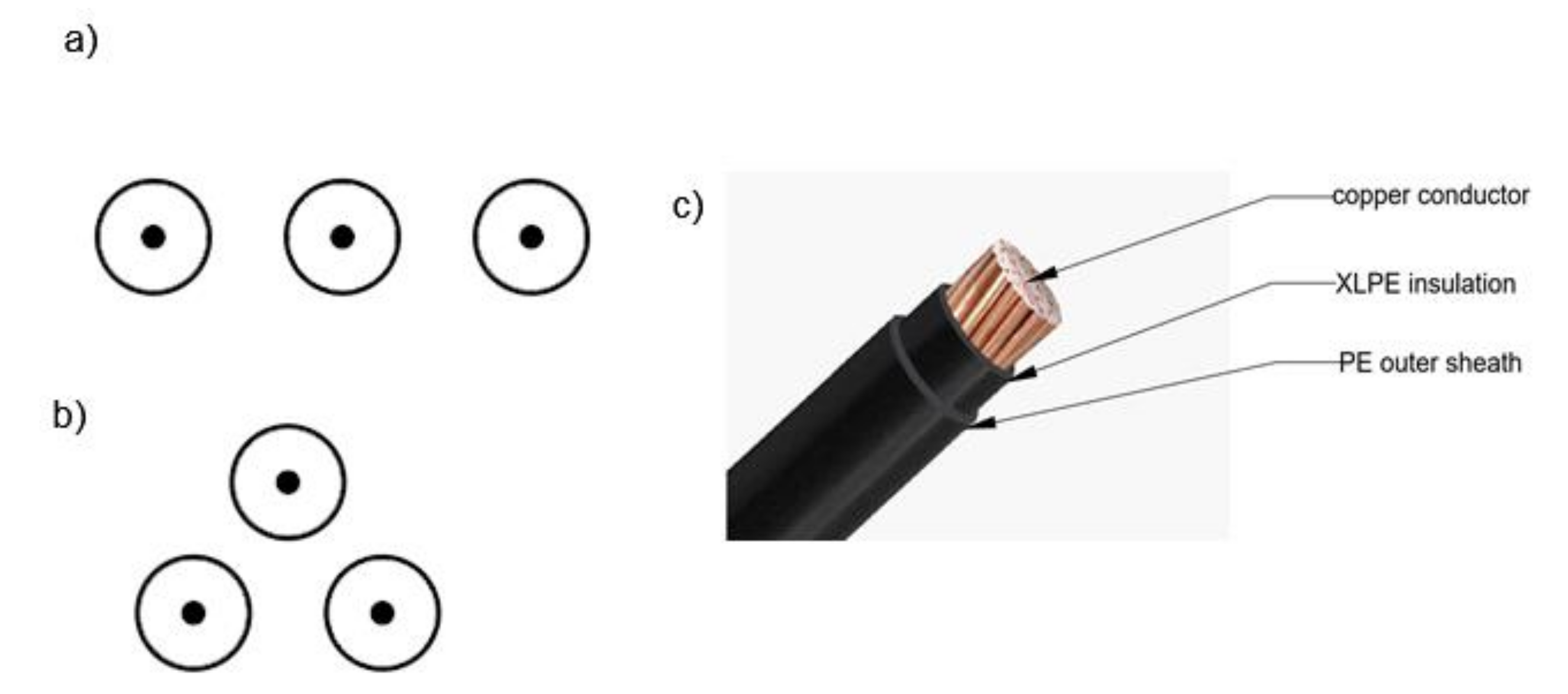
Due to this, the comprehensive requirements should be taken into account during the design process. Figure 1 presents possible cable arrangement methods (flat or trefoil) for three single-core cables and cable construction.

The highest operating temperatures for different cable insulation types, according to PN-HD 60364-5-52:2011 [20], are:

−

polyvinyl chloride (PVC): 70 °C;

−

cross-linked polyethylene (XLPE) and ethylene-propylene rubber: 90 °C.

Both construction and the used materials have a significant influence on cable heating. The cable core material determines the conductivity. The insulation material and its thickness impact the electric strength, mechanical durability, and cable heating (temperature distribution). An example of this is that cables with XLPE insulation increase the cable’s optimal operating temperature compared to PVC or PE insulation. Along with insulating properties, it exhibits chemical stability and is leak-proof.

Additionally, when the cable is equipped with a shield on each core in the case of multi-core cable or single-core cables, the sheath levels the proximity effect. The low-voltage cables that are mostly used are not shielded, so this effect cannot be neglected in these construction types. Increasing the accuracy of calculations can contribute to lowering the cost of building cable lines.

Cable routing and their backfill have non-negligible effects on the temperature distribution and maximal permissible load current. The most popular thermal backfills used in cables laid in the ground are dry sand, a sand-bentonite mixture (SCM), sand, and Portland cement (with a 12:1 ratio) [21,22,23]. There are also advantages of new materials, such as geopolymers, which have better thermal conductivity properties and safer for the environment [24]. Backfill’s higher thermal conductivity allows conducting the cable’s heat during current flow. The use of backfill also reduces the formation of dry zones around cables, which harm heat dissipation. When the cable temperature rises, the electric conductivity decreases due to the decrease in the electrons’ mobility in the metal conductor. Aluminum cables/wires are most often used in power systems, including AsXSn, steel-aluminum (AFL), and aluminum alloys AlMgSi (BLX-T). This directly affects the lower conductivity value compared to copper cores.

The two-dimensional temperature distribution in the steady state for cables in the thermal backfill can be calculated independently for a chosen cable routing according to [25]:

$$\frac{\partial }{\partial x}\left[k\left(T\right)\frac{\partial T}{\partial x}\right]+\frac{\partial }{\partial y}\left[k\left(T\right)\frac{\partial T}{\partial y}\right]=-q_v,$$

(3)

where:

• $T$ denotes the temperature at any point in the $x-y$ plane around the underground cable,
• $k\left(T\right)$ is the temperature-dependent thermal conductivity,
• $q_v$ is the volumetric heat source per unit volume.

It should be noticed that the skin effect causes an irregular current intensity distribution in the cable conductor. The highest current density appears at the outer layer of the conductor cable. Therefore, a significant temperature increase occurs. The temperature changes inside the cable core, which can be calculated from Equation (3); intensifies the resistance increase; and, therefore, effects the equivalent resistance changes and power losses in nonlinear loads. This impact is illustrated in Figure 2 [7].

In this article, the temperature effect on the resistance value was skipped to highlight in particular the skin effect on the cable working conditions.

3. Active Power Losses

When the current is flowing through the conductor, power losses are generated as heat. This phenomenon was observed and described independently by Joule and Lenz in the 19th century and is known as Joule-Lenz heat.

The equation for the conductor heat losses is given by [26]:

$$\Delta P=R{I}^2,$$

(4)

where:

• $R$ is the conductor resistance, in $\left[\mathsf{\Omega }\right]$,
• $I$ is the RMS current value in $\left[A\right]$.

For nonsinusoidal current flow in the conductor, the power loss calculation is more complicated because it requires the consideration of the skin effect and the proximity effect [5,27,28,29]. The proximity effect can be neglected for a sufficiently large distance between each cable core or shielded cables. For a distorted current, the total active power losses in a cable are equal to the sum of each current harmonic power loss and can be expressed as:

$$\Delta P={{\displaystyle \sum }}_{n=1}^{\infty }{R}_n{\left(I_{\%n}·I_{1h}\right)}^2,$$

(5)

where:

• $I_{1h}$ is the amplitude of the current fundamental harmonic,
• $I_{\%n}$ is the percent value of the n-th harmonic.

The $R_n$ resistance for any harmonic can be calculated based on the current penetration depth. According to this, we can calculate the resistance value for each current harmonic:

$$R_n=\frac{l}{\gamma ·s_n},$$

(6)

where:

• $l$ is the wire length in $\left[\mathrm{m}\right]$,
• $s_n$ is the equivalent of cross-section area including the skin depth effect in $\left[{\mathrm{mm}}^2\right]$.

In the case of a circular cross area, the effective area is described as:

$$s_n=\pi r^2-\pi {\left(r-{\delta }_n\right)}^2.$$

(7)

The current penetration depth (expressed by Equation (8)) describes how far (counting from the external edge) the current flows [5]. In this way, it is easy to notice that the effective conductor cross-area through which a current of a given frequency flows is lower than the area resulting from the conductor’s geometric dimensions (Figure 3):

$${\delta }_n=\frac{1}{\sqrt{\pi n{f}_{1h}{\mu }_0{\mu }_r\gamma }},$$

(8)

where:

• $n$ is the harmonic order number in $\left[-\right]$,
• $f_{1h}$ is the basic harmonic frequency in $\left[\mathrm{Hz}\right]$,
• ${\mu }_0$ is the vacuum permeability in $\left[\mathrm{Vs}/\mathrm{Am}\right]$,
• ${\mu }_r$ is the relative permeability in $\left[-\right]$,
• $\gamma$ is the conductivity of the material in $\left[\mathrm{m}/\left(\mathsf{\Omega }·{\mathrm{mm}}^2\right)\right]$.

Resistance calculations were performed using the superposition method for a chosen current frequency (Figure 4). This approach allows for each harmonic to determine the cable power losses by creating an equivalent circuit.

In turn, the IEC-60287-1-1:2006 + A1:2014 [30] standard shows the calculation methodology for the resistance variations as a result of the skin effect as follows:

$$R_{AC}=R\left[1+{\gamma }_s+{\gamma }_p\right],$$

(9)

where:

$${\gamma }_s=\frac{X_s^4}{192+0.8X_s^4},$$

(10)

$$X_s^2=\frac{8\pi f}{R}{10}^{-7}·k_s.$$

(11)

• $R_{AC}$ is the AC resistance of the conductor in $\left[\mathsf{\Omega }\right]$,
• $R$ is the DC resistance of the conductor in $\left[\mathsf{\Omega }\right]$,
• ${\gamma }_s$ is a skin effect factor in $\left[-\right],$
• ${\gamma }_p$ is a proximity effect factor in $\left[-\right],$
• $k_s$ is the coefficient depending of the number of cable cores (for a single-core cable $k_s=1$) in $\left[-\right]$.

The Bessel function were used as a third method [31,32,33] according to the formulas:

$$k_{b }=Re\left[ \frac{Z_s J_0\left(Z_s\right)}{2 J_1\left(Z_s\right)}\right],$$

(12)

where:

$$Z_s=e^{\left(j\frac{3\pi }{4}\right)}·\sqrt{2{\mu }_0{\mu }_r\gamma n{f}_{1h}}.$$

(13)

$J_0, J_1$ are Bessel functions of the first kind of the zeroth and first order, respectively.

The calculated resistance value as a frequency function is obtained as:

$$R_{B_{AC}}=R{k}_b.$$

(14)

Active power loss calculations for cable cases were conducted for the three described methods, skipping the proximity effect (${\gamma }_p$ value used in Equation (9) was equal to 0) to show only the influence of the skin effect.

4. Simulation Model

With the use of the Matlab software (MathWorks Inc., Natick, MA, USA), we developed a model allowing us to compare the three calculation methods generating the active power losses in the power cables considering the skin effect. The first model was completed using the IEC-60287-1-1:2006+A1:2014 [30] standard guidelines, and the second one was completed using the Bessel function. Both methods’ results were compared to those of the third one, which was developed by the authors (the algorithm presents the method in Figure 5).

An algorithm illustrating the third one that was developed according to the authors’ proposition is presented in Figure 5. This model was realized with the current penetration depth (CPD) method used for the given frequencies.

This is a description of the authors’ method:

• Based on the measured distorted current waveform, we calculated the harmonic spectrum (using FFT analysis) to obtain the percentage magnitude values for each frequency (concerning the first harmonic order $I_{\%n}$
• For a given cable, the calculation conductor resistances suitable for the given harmonics (estimated based on Equations (6)–(8)) were based on the current penetration depth.
• We multiplied the current I_%n² vector and the resistance $R_n$ vector.
• We summarized the obtained values to achieve the total active power losses for the whole current harmonics spectrum (Equation (5)).

All the described methods were used to determine the power losses for three chosen nonsinusoidal currents:

−

Distorted current waveform measured for bridge rectifier load in the real-life laboratory arrangement (${\mathrm{THD}}_{\mathrm{I}}= 76\%$),

−

Measured waveform (from 1st point) with the added in-phase sinusoidal wave with a magnitude equal to half the basic harmonic of the distorted waveform (${\mathrm{THD}}_{\mathrm{I}}= 41\%$),

−

Measured waveform (from 1st point) with added shifted 90° sinusoidal wave with a magnitude equal to half the basic harmonic of the distorted waveform (${\mathrm{THD}}_{\mathrm{I}}= 32\%$).

An example waveform and its harmonic spectrum is shown in Figure 6.

All the calculations were carried out for cables from $25$ to $400{ \mathrm{mm}}^2$ in a flat arrangement and the distances between each phase cable were equal to 2d (where d is the diameter). These calculations were conducted for the copper conductor and PVC insulation. For each cross-sectional area, the long-term current carrying capacity data were taken from the manufacturer’s catalogue. There were three calculation series for the current equal to $25$, $50,$ and $75\%$ of the maximum current-carrying capacity for a unitary cable length equal to 1 m [34].

5. Research Results

This chapter presents the numerical calculations of the power loss values generated in the power cables, taking into account the skin effect for the described methods. The first one is based on the IEC-60287-1-1:2006 + A1:2014 [30] standard, the second is based on the Bessel function, and the third is illustrated by the algorithm proposed by the authors. The results calculated for the different power cables and current shapes are presented in

Table 1. The cable power losses for the 25% rated cable current.

AWG	ΔP for THDI Equal:			ΔPIEC for THDI Equal:			ΔPBessel for THDI Equal:
	32%	41%	76%	32%	41%	76%	32%	41%	76%
[mm2]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]
25	2.089	2.210	2.986	2.091	2.212	2.992	2.090	2.212	2.990
35	2.205	2.333	3.153	2.209	2.338	3.163	2.206	2.335	3.159
50	2.155	2.280	3.082	2.162	2.289	3.102	2.159	2.285	3.097
70	2.365	2.504	3.393	2.379	2.520	3.423	2.375	2.516	3.417
95	2.498	2.649	3.615	2.520	2.672	3.644	2.516	2.667	3.634
120	2.594	2.757	3.800	2.625	2.786	3.817	2.621	2.780	3.797
150	2.652	2.826	3.943	2.695	2.865	3.951	2.688	2.853	3.910
185	2.781	2.971	4.190	2.816	2.998	4.168	2.800	2.975	4.091
240	3.061	3.279	4.674	3.049	3.257	4.583	3.010	3.201	4.425
300	3.289	3.530	5.067	3.219	3.447	4.908	3.141	3.344	4.643
400	3.559	3.826	5.534	3.414	3.668	5.295	3.250	3.465	4.840

Note: $I=0.25I_{dd}$, $\Delta P$ is the calculated power losses for the proposed method, $\Delta P_{IEC}$ for the IEC standard method, $\Delta P_{Bessel}$ for the Bessel function method.

,

Table 2. The cable power losses for the 50% rated cable current.

AWG	ΔP for THDI Equal:			ΔPIEC for THDI Equal:			ΔPBessel for THDI Equal:
	32%	41%	76%	32%	41%	76%	32%	41%	76%
[mm2]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]
25	8.355	8.840	11.946	8.363	8.850	11.967	8.361	8.847	11.959
35	8.820	9.332	12.611	8.836	9.352	12.654	8.825	9.340	12.638
50	8.619	9.120	12.329	8.649	9.157	12.407	8.634	9.142	12.390
70	9.459	10.015	13.571	9.515	10.079	13.691	9.499	10.063	13.670
95	9.993	10.596	14.458	10.080	10.687	14.574	10.066	10.670	14.536
120	10.377	11.029	15.199	10.498	11.143	15.269	10.482	11.118	15.190
150	10.606	11.304	15.772	10.780	11.459	15.803	10.751	11.412	15.641
185	11.122	11.884	16.760	11.263	11.994	16.672	11.201	11.899	16.366
240	12.245	13.116	18.695	12.198	13.026	18.331	12.041	12.805	17.699
300	13.157	14.118	20.269	12.876	13.789	19.632	12.564	13.375	18.571
400	14.237	15.305	22.138	13.654	14.671	21.179	13.000	13.859	19.358

Note: $I=0.50I_{dd}$, $\Delta P$ is the calculated power losses for the proposed method, $\Delta P_{IEC}$ for the IEC standard method, $\Delta P_{Bessel}$ for the Bessel function method.

and

Table 3. The cable power losses for the 75% rated cable current.

AWG	ΔP for THDI Equal:			ΔPIEC for THDI Equal:			ΔPBessel for THDI Equal:
	32%	41%	76%	32%	41%	76%	32%	41%	76%
[mm2]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]	[W]
25	18.799	19.891	26.878	18.816	19.912	26.925	18.813	19.907	26.908
35	19.845	20.998	28.375	19.880	21.041	28.471	19.856	21.015	28.435
50	19.393	20.521	27.739	19.460	20.603	27.916	19.427	20.569	27.877
70	21.283	22.533	30.534	21.409	22.678	30.804	21.374	22.642	30.757
95	22.484	23.842	32.532	22.679	24.046	32.792	22.648	24.007	32.706
120	23.349	24.815	34.197	23.621	25.072	34.355	23.585	25.016	34.177
150	23.864	25.435	35.487	24.256	25.783	35.556	24.190	25.677	35.193
185	25.025	26.739	37.711	25.342	26.986	37.513	25.202	26.773	36.823
240	27.551	29.512	42.064	27.445	29.310	41.245	27.092	28.812	39.823
300	29.604	31.766	45.606	28.970	31.024	44.172	28.269	30.095	41.784
400	32.034	34.436	49.810	30.722	33.009	47.653	29.250	31.183	43.556

Note: $I=0.75I_{dd}$, $\Delta P$ is the calculated power losses for the proposed method, $\Delta P_{IEC}$ for the IEC standard method, $\Delta P_{Bessel}$ for the Bessel function method.

.

The results were obtained for a unitary cable length equal to 1 m. For the longer line lengths, the active power losses are proportional to the length.

There is no effect of the current value on the voltage supply deformation in the presented methodology and, therefore, on the current deformation. Hence, for three loads the active power losses change with the current load square. For the active power losses calculation prepared for sinewave current, it is assumed that the current flows through the whole conductor cross-section. Therefore, the skin effect (for 50 Hz, the penetration depth is 9.6 mm) is not considered.

Additionally, the difference between each compared method is illustrated in Figure 7 (the results received for $0.5I_{dd}$ and $0.75I_{dd}$ exhibit similar tendencies, therefore we illustrated only one case).

The differences between the analyzed methods are dependent on the cable cross-section area. For cables, the 25, 35, 50, 70 mm² obtained results for the unitary power losses are very similar. The differences are maximally equal to 0.1 W—the skin effect is limited due to the small cable radius. If the CPD is smaller than the cable radius, the effective resistance for each harmonic increases. It is easier to understand power losses dependence for small cross-sections. The presented methods gave more divergent values for cross-sections higher than 185 mm².

Figure 8 shows the percentage of active power losses calculated for distorted currents compared to the ideal sinusoidal wave for a 50 Hz frequency and the same RMS value. For small cable cross-sectional areas (lower than 50 mm²), the relative active power loss growth is less than 1% for all the analyzed current distortion cases. For cross-section areas higher than 50 mm², the percentage of power loss rises. For a 400 mm² cable and a current THD equal to 76%, the highest increments (27.6% for the IEC method, 16.6% for the Bessel function method, and 33.3% for the method proposed by the authors) are observed. The power losses calculated by the IEC method achieved the highest values, except for the highest distortion case and the cable with a cross-sectional area higher than 150 mm².

The power loss values influence the cable operating temperature and maximum current-carrying capacity. It is crucial to consider the effect of temperature change on the cable conductors’ resistance.

For the “IEC method”, we observed higher power losses for the same reference distorted current. This is a consequence of the assumption that for small cable cross-sections, the current does not flow through the entire cross-section area (this results in higher resistance values compared to the “penetration coefficient methods” for the lowest cross-sections of the series). The new method presented in this article allows for the fact that even for high frequencies of the considered harmonics the current penetration depth is large. In this case, for relatively small values of cable cross-section areas the current flows through their entire cross-section (resulting in lower resistance values compared to the IEC method). For this reason, in Figure 7 and Figure 8 at the cross-section of 150 mm², the trend lines cross. Comparing the results to the Bessel functions method, there is a similar tendency, but the trend lines cross for 95 mm² (above this size, the CPD method gives more significant power loss values). 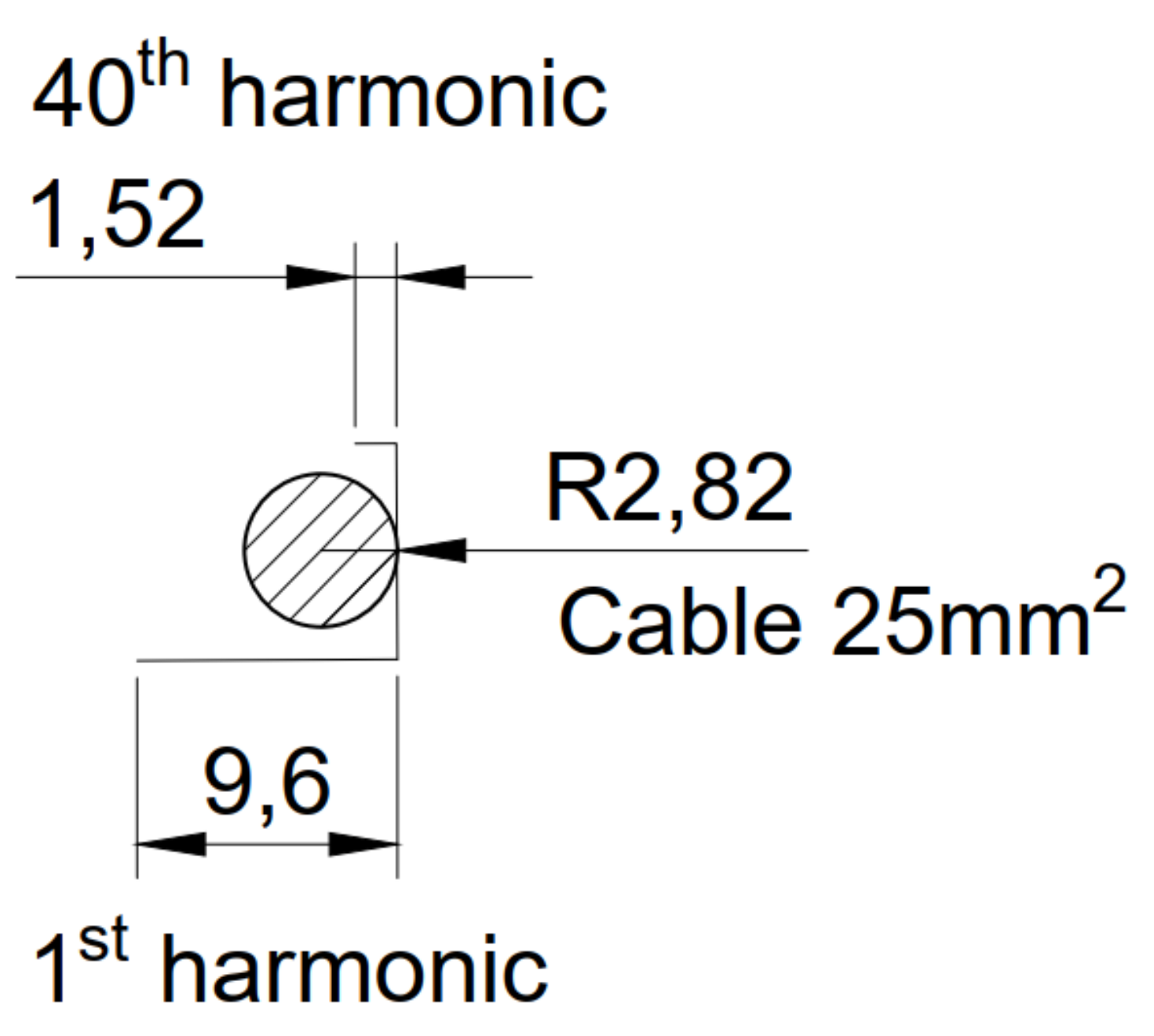Figure 9 shows the penetration depths for the 1st and 40th current harmonics based on the 25 mm² cable conductor background. In the currently used methods [5,7], the increase in resistance for the fundamental frequency is considered no matter what the cable cross-section area is. For small cable cross-sectional areas such as 25 mm², the depth of the current penetration—resulting from the skin effect—is greater than the radius of the low-voltage cable’s conductor. Hence, we conclude that the skin effect does not occur in this case and that the previously mentioned methods introduce an error in calculating the value of active power losses. However, in the authors’ new method the penetration depth factor concerning the radius of the considered cable conductor is taken into account.

For the total cable lengths used in the systems, the active power losses caused by the skin effect can obtain high values. Therefore, economic functioning aspects are significantly affected. It should be underlined that the operating THD factor has many possible current waveform shapes for the same THD value. Therefore, for any distorted case there is a need for individual analysis.

For low frequencies and small cable cross-sections, the electric current’s penetration depth is greater than the conductor’s radius. For this case, the proposed method does not consider the skin effect impact in contrast to the IEC standard. Thus, the active power losses have lower values (the IEC standard method predicts higher losses than the authors’ proposed method). The high loss value causes discrepancies in the obtained results for the fundamental (first) current harmonic obtained in the IEC method. However, in the authors’ method the losses are small for low THDI values and small cable cross-sections.

6. Conclusions

The assumed analysis of active power losses, which only considers the skin effect, determines the degree of power losses, which are often neglected during the design process. This problem becomes even more critical in the case of currents distorted from the sine wave pattern. Due to higher harmonics, the losses become even more significant, directly affecting electricity costs.

As the power consumed by a given nonlinear loads increases, the THD coefficient decreases as a result of an increase in the amplitude of the fundamental current harmonic. As a result, for higher values of the load current, even at relatively low values of the THD_I coefficient the skin effect may significantly affect the power cable’s resistance when supplying the considered loads. Additionally, in the case of the algorithm proposed by the authors, each separate value of each current harmonic is taken into account, so the result is burdened with a lower error. The filtering systems can solve active power losses in systems with nonsinusoidal (distorted) currents. The filter examples for current distortion reduction are passive filters (classic LC filters), active filters, or hybrid solutions [35,36,37,38,39,40]. However, these devices’ application also needs to be analyzed in detail based on the difference in filter installation costs and the potential gains achieved by reducing the current THD. The increase in the power losses caused by the flow of a significantly distorted current shown in the article highlights a serious problem related to the possibility of thermal damage to the cable. This problem becomes apparent when supplying high-power loads that use the phenomenon of an electric arc during operation—e.g., arc furnaces (EAF). Neglecting the skin effect may result in damage to the cable line and consequently high repair costs. Unfortunately, due to the required high distortion and RMS values of the flowing currents for a wide cable size range, it is impossible to prepare laboratory tests for the considered scenarios. The authors presented that the method can be used for optimisation-designed power lines supplying highly nonlinear power loads (especially for high power ones). The method proposed by the authors can be used to determine the temperature distribution both inside and outside power cables.

The presented calculation was prepared for unitary cable length equal to 1 m. Therefore, for different cable lengths, the active power losses are assumed to have higher values proportional to the line length.

Nevertheless, compared to existing for many years (Bessel function method and IEC standard method), the new method allows for the accepted proposed algorithm of power loss calculations.

The proposed method uses the CPD factor taken for described well-known skin effect in electrical conductors. Additionally, due to the proposed method, it is possible to mark the conductor’s current density off.

It should be noted that the approach presented in the article does not take into account the effect of the deformed load current on the supply voltage distortion, which results in a greater distortion of the load current. Hence, for the three variants of the considered loads, the power losses change with the current square.

To sum up:

−

The presented method for cross-section areas of up to 70 mm² gives convergent results compared to other methods.

−

Contrary to other compared methods, the proposed algorithm considers the real physical phenomenon of current penetration depth.

−

The proposed solution allows determining the temperature distribution both inside and outside for each electrical environmental condition.

−

The proposed method can be used for the optimal design of power cable lines. This issue will be considered in further research.