AC Current Ripple in Three-Phase Four-Leg PWM Converters with Neutral Line Inductor
Abstract
:1. Introduction
2. Basic Assumptions and Modulation Principle
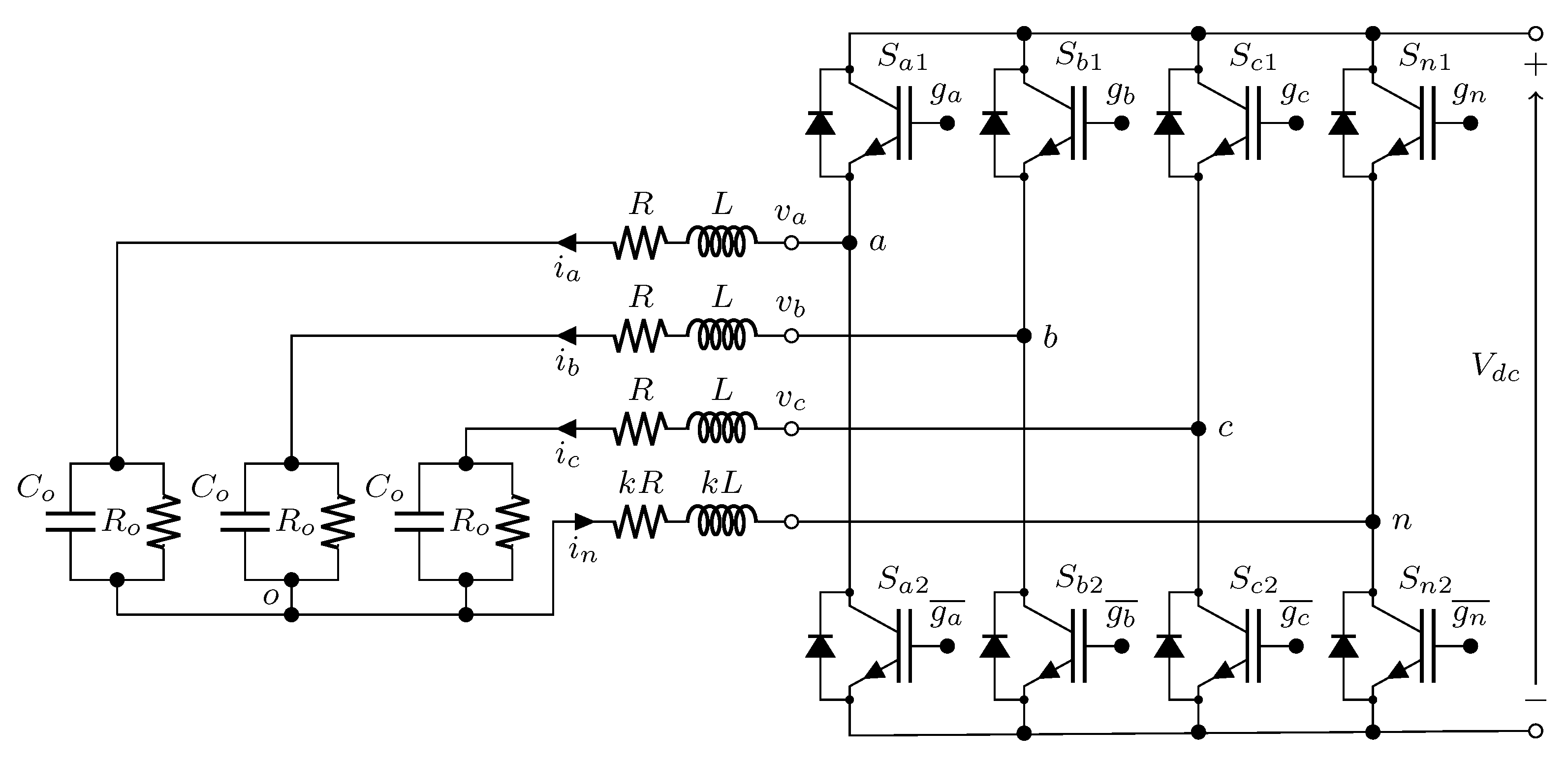
2.1. Converter Model and Current Ripple Definition
2.2. Carrie-Based Sinusoidal Pulse-Width Modulation (SPWM)
3. Analysis of Phase Currents Ripple
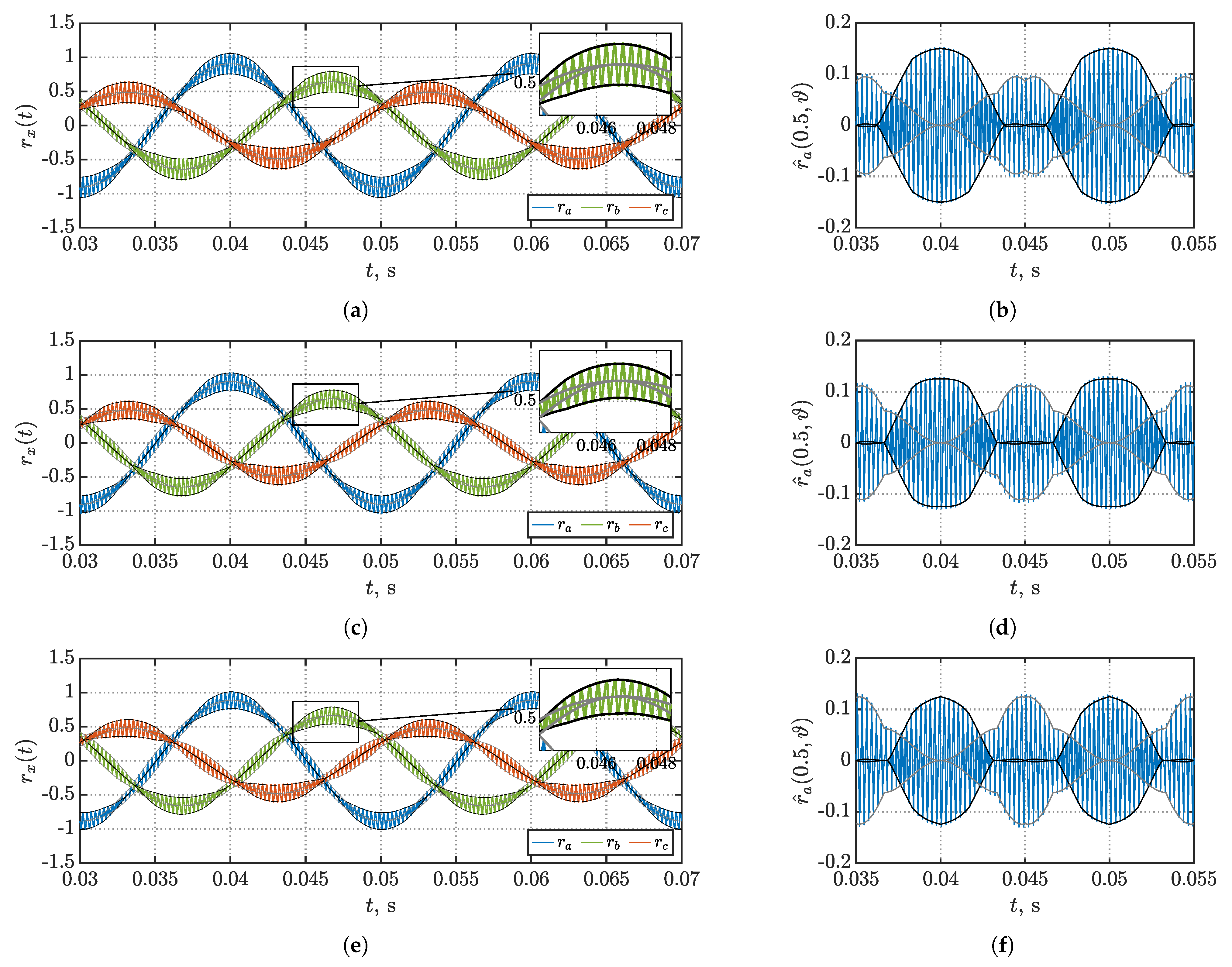
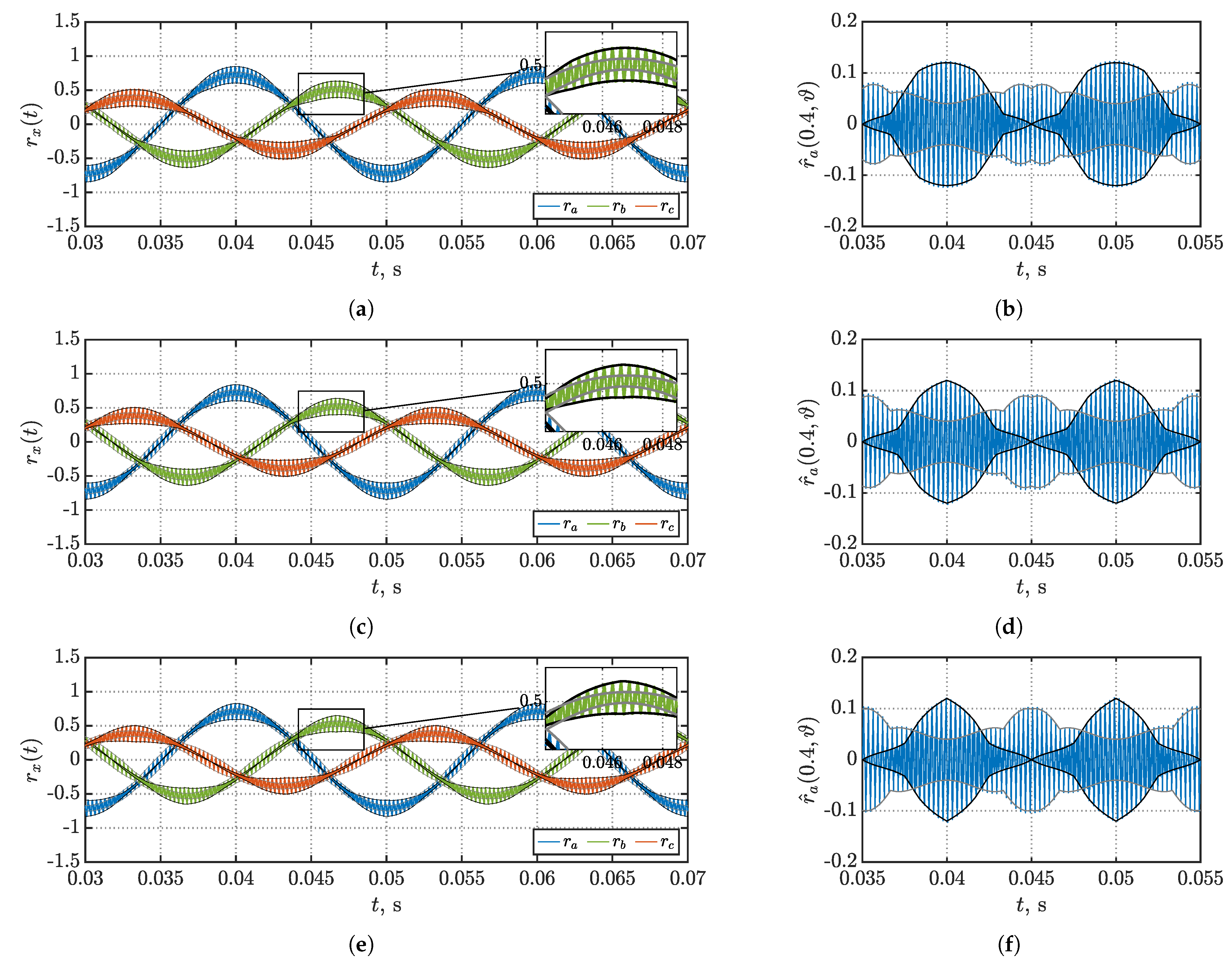
3.1. Phase Current Ripple Waveform
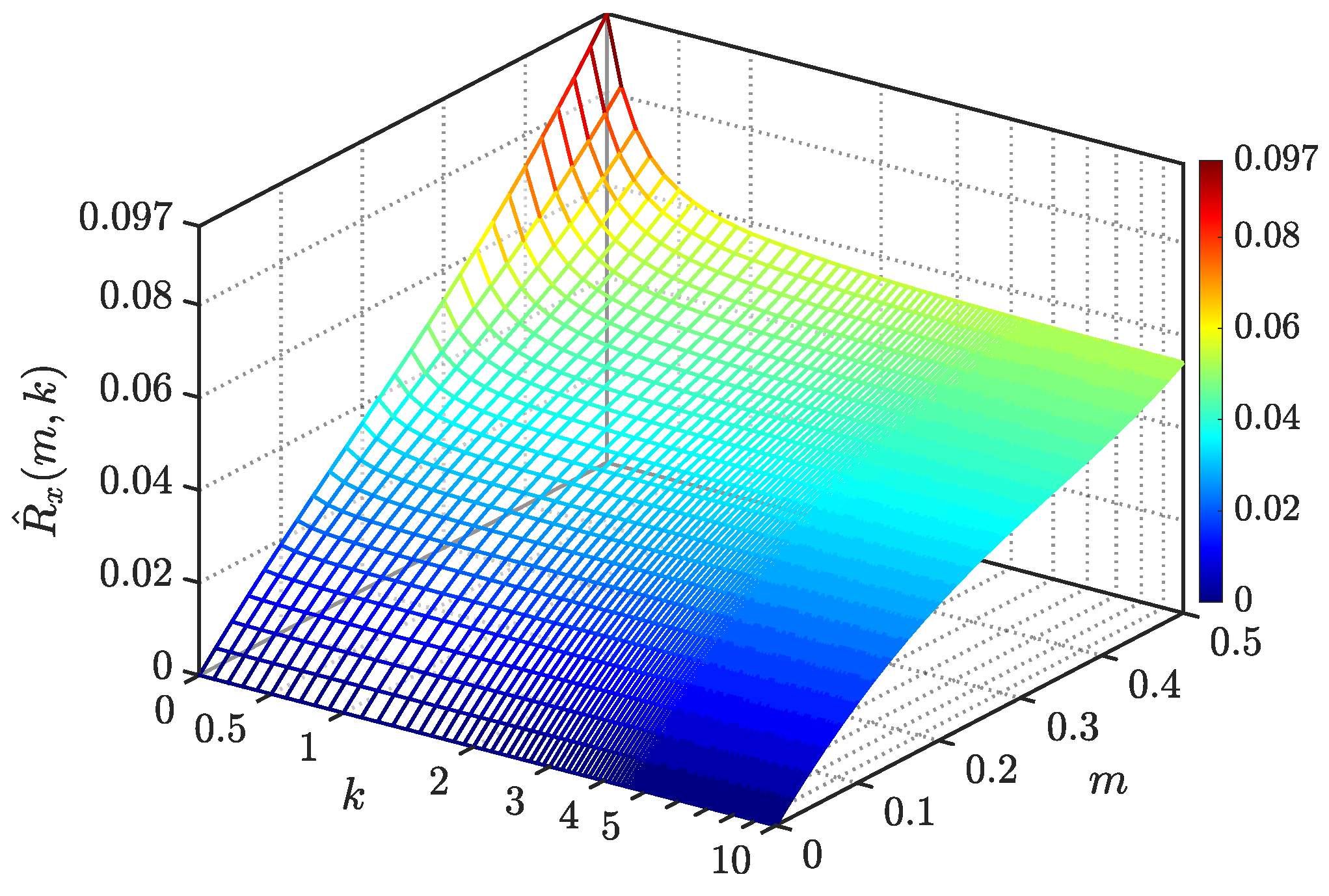
3.2. Phase Current Ripple RMS
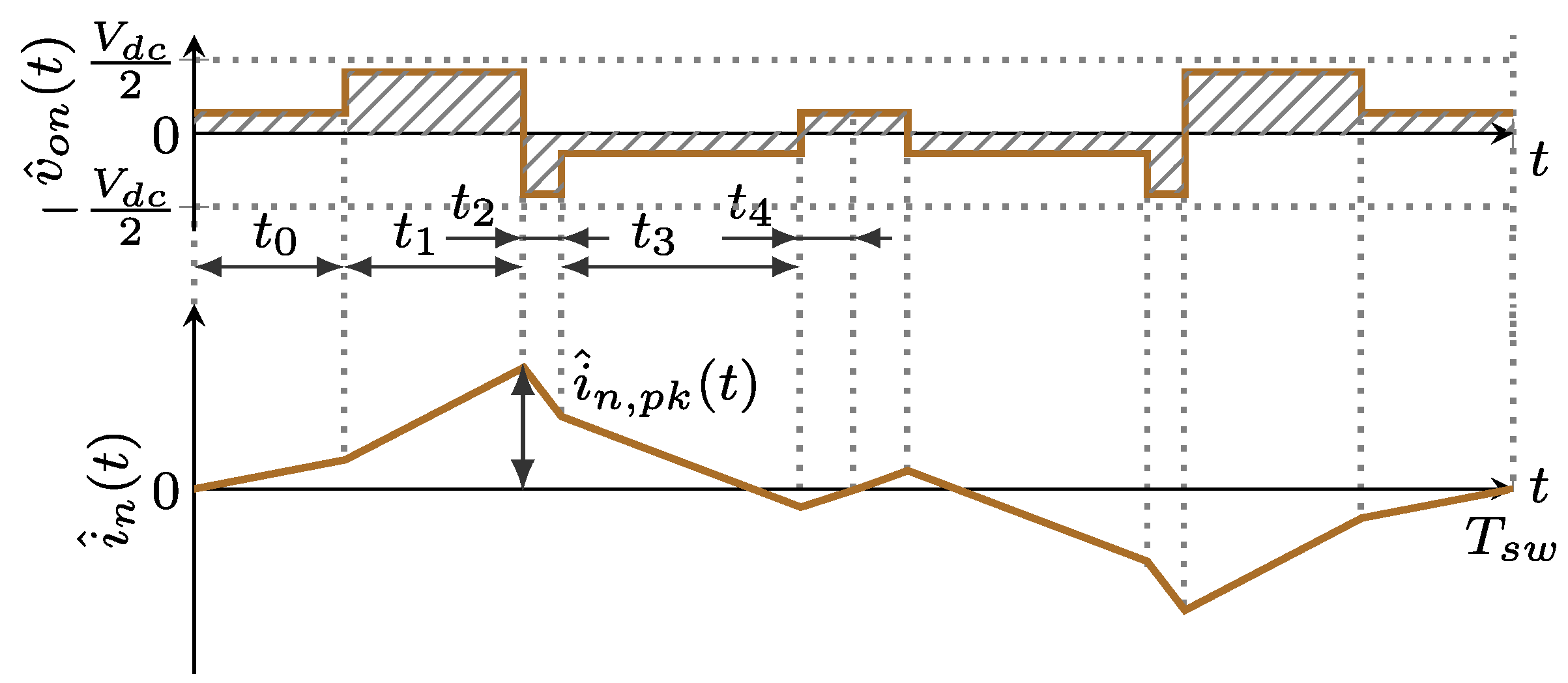
4. Analysis of Neutral Current Ripple
4.1. Neutral Current Ripple Waveform
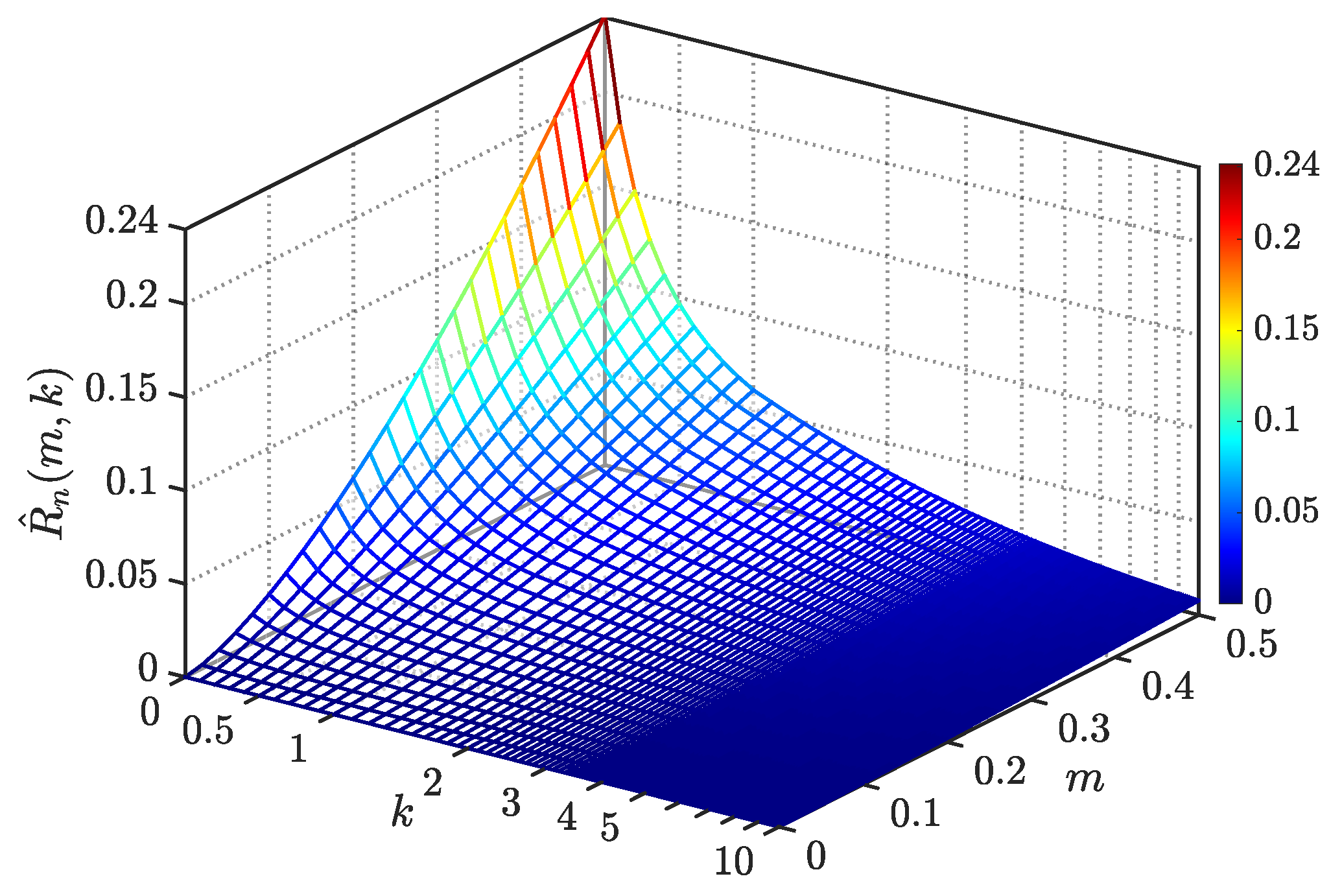
4.2. Neutral Current Ripple RMS
5. Performance Comparison and Design Example
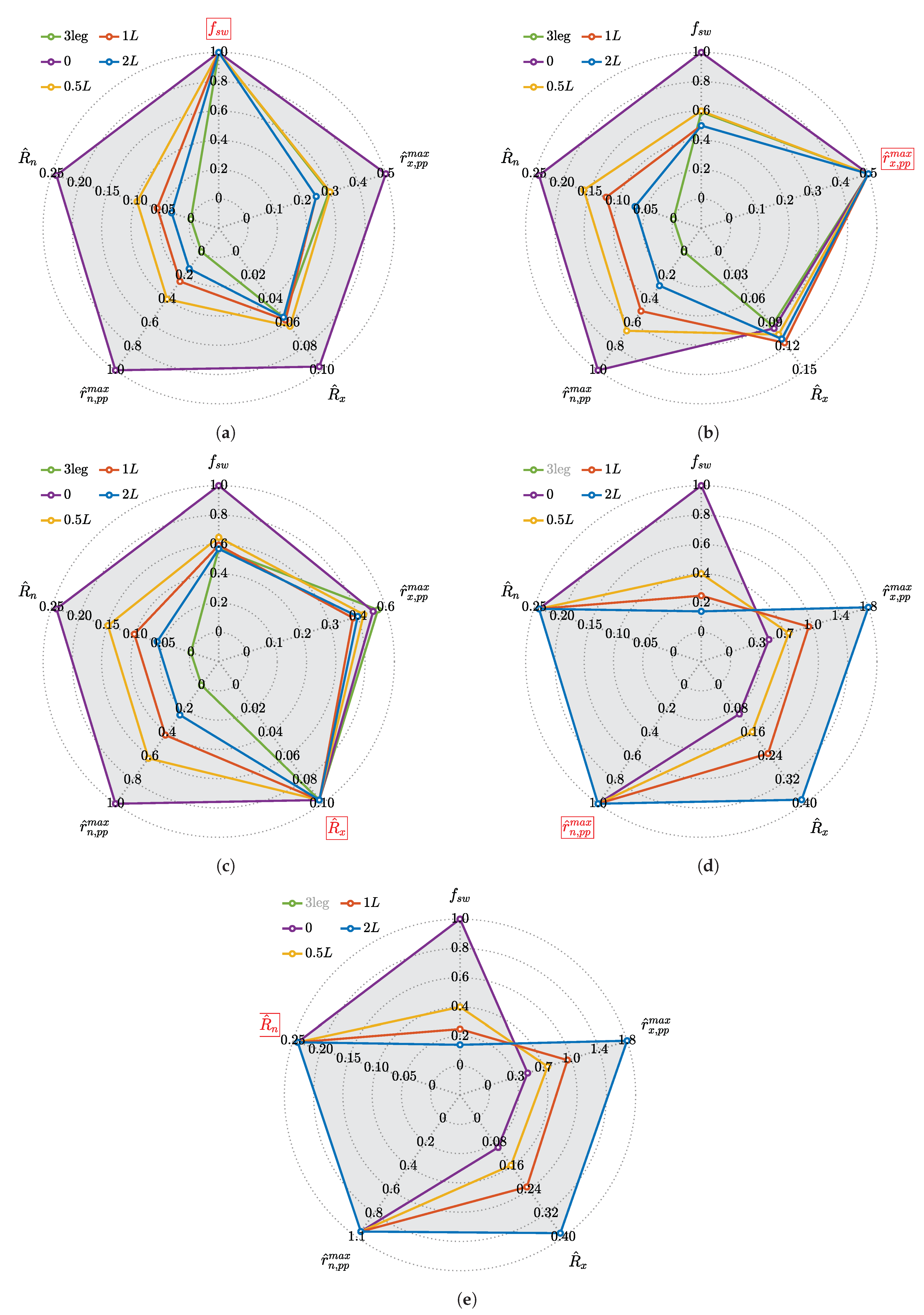
5.1. Performance Comparison
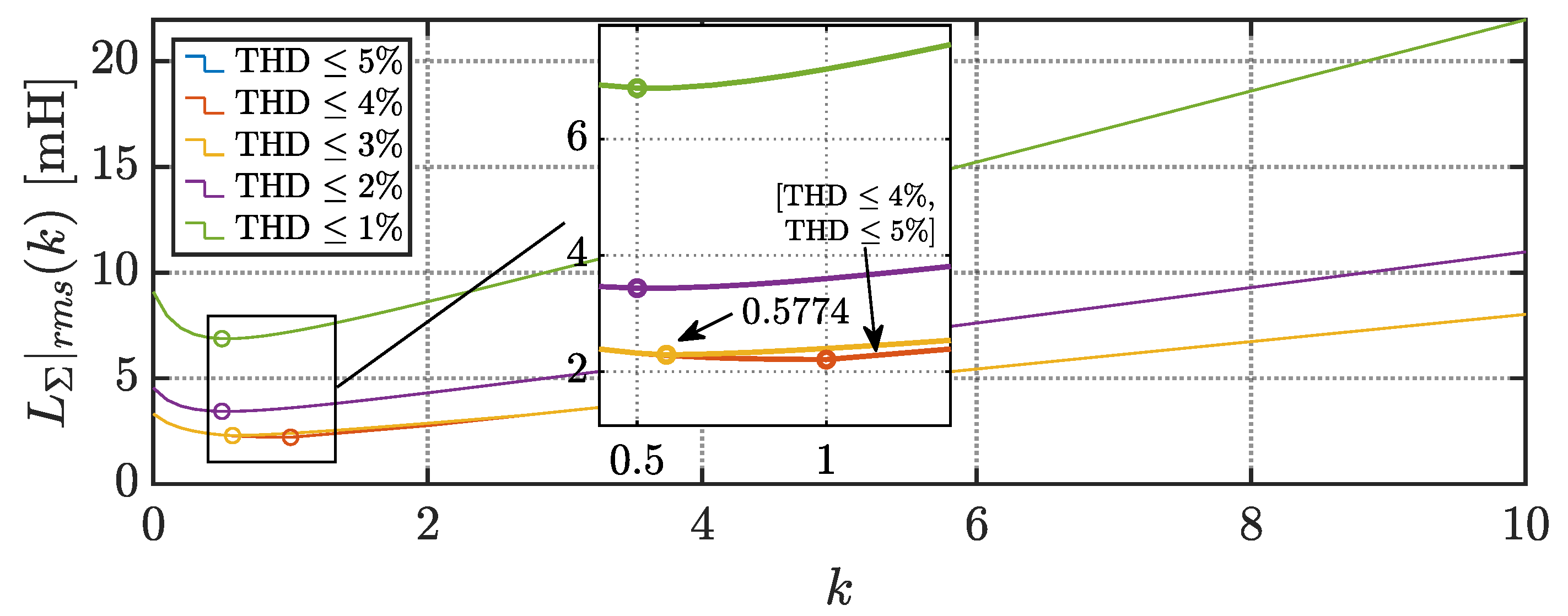
5.2. Design Example
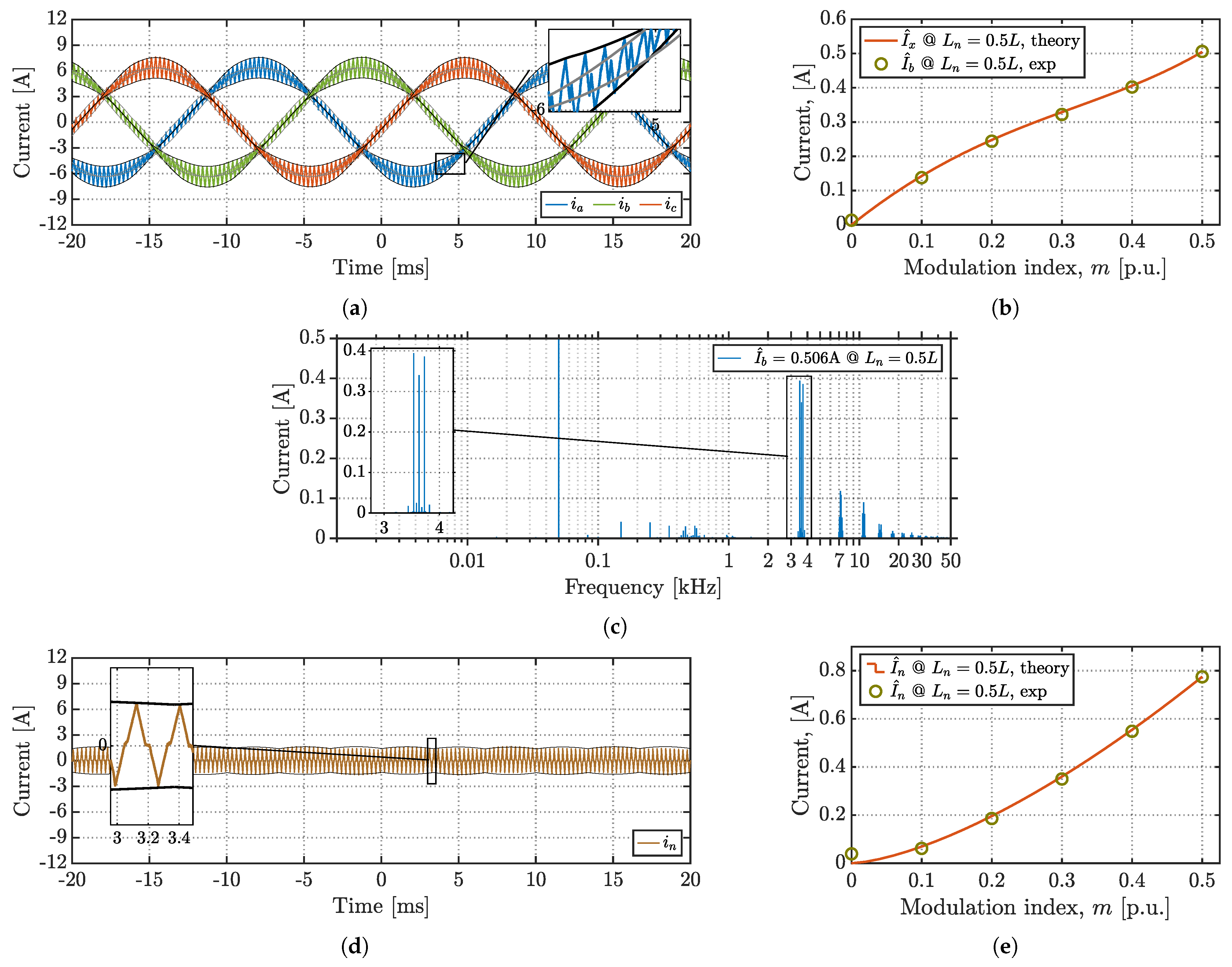
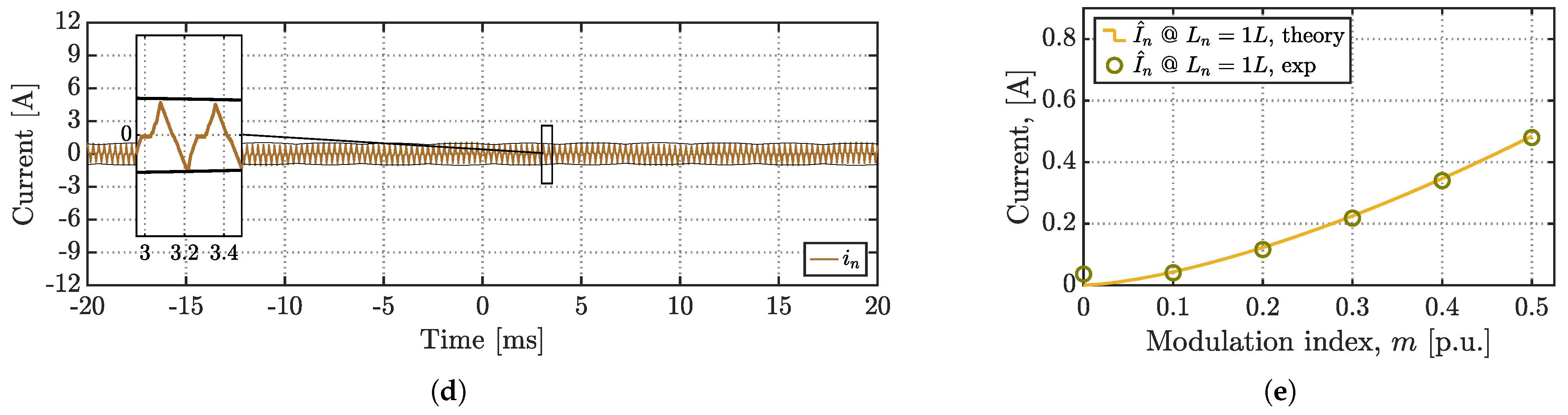
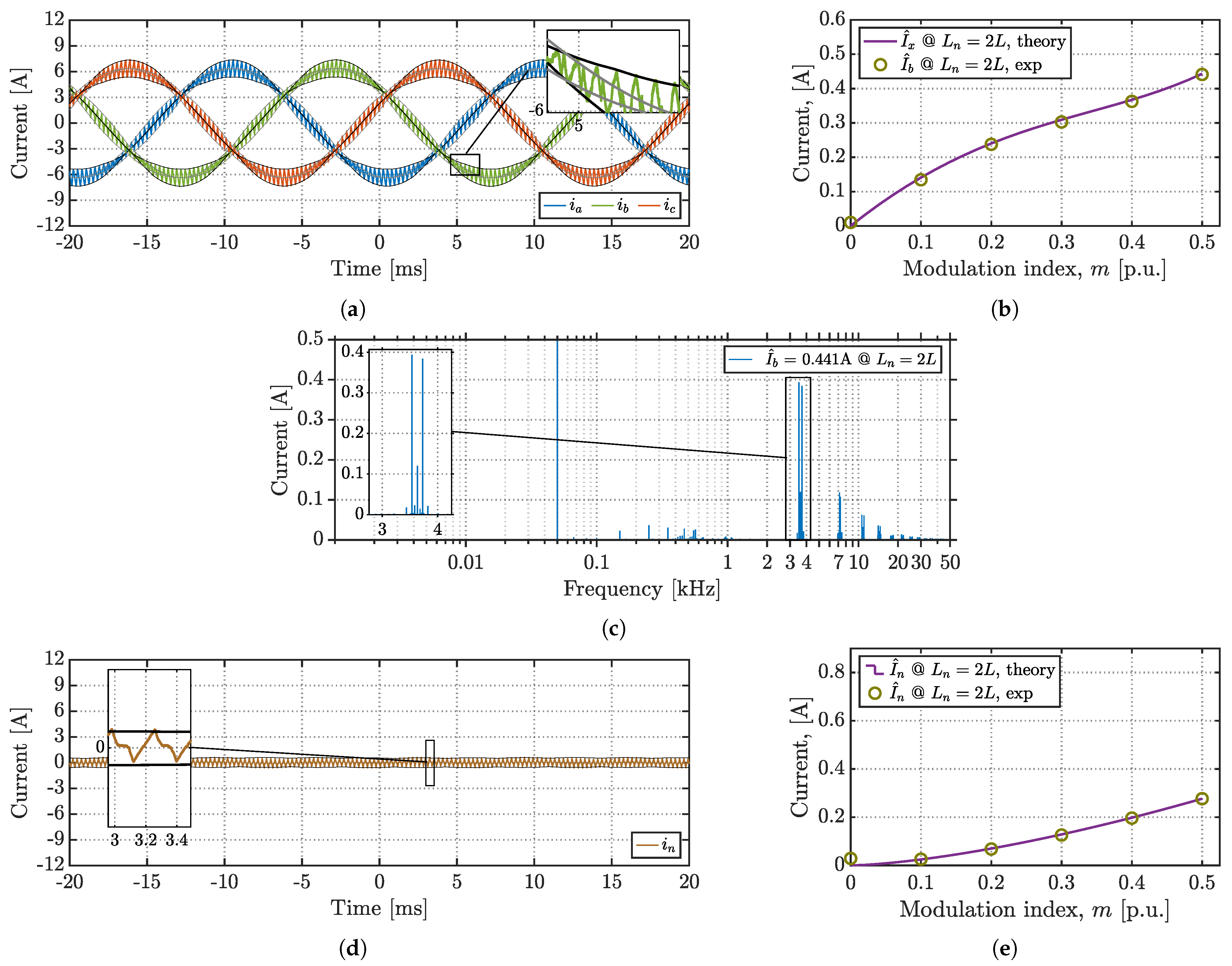
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, Q.-C. Power-Electronics-Enabled Autonomous Power Systems: Architecture and Technical Routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Brenna, M.; Foiadelli, F.; Leone, C.; Longo, M. Electric Vehicles Charging Technology Review and Optimal Size Estimation. J. Electr. Eng. Technol. 2020, 15, 2539–2552. [Google Scholar] [CrossRef]
- Dong, G.; Ojo, O. Current Regulation in Four-Leg Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 2095–2105. [Google Scholar] [CrossRef]
- Shekari, T.; Golshannavaz, S.; Aminifar, F. Techno-Economic Collaboration of PEV Fleets in Energy Management of Microgrids. IEEE Trans. Power Syst. 2016, 32, 3833–3841. [Google Scholar] [CrossRef]
- Viatkin, A.; Hammami, M.; Grandi, G.; Ricco, M. Analysis of a Three-Phase Four-Leg Front-End Converter for EV Chargers with Balanced and Unbalanced Grid Currents. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 3442–3449. [Google Scholar]
- Lin, Z.; Ruan, X.; Jia, L.; Zhao, W.; Liu, H.; Rao, P. Optimized Design of the Neutral Inductor and Filter Inductors in Three-Phase Four-Wire Inverter With Split DC-Link Capacitors. IEEE Trans. Power Electron. 2019, 34, 247–262. [Google Scholar] [CrossRef]
- Nascimento, C.F.; Diene, O.; Watanabe, E.H. Analytical model of three-phase four-wire VSC operating as grid forming power converter under unbalanced load conditions. In Proceedings of the 2017 IEEE 12th International Conference on Power Electronics and Drive Systems (PEDS), Honolulu, HI, USA, 12–15 December 2017; pp. 1219–1224. [Google Scholar]
- Hintz, A.; Prasanna, U.R.; Rajashekara, K. Comparative Study of the Three-Phase Grid-Connected Inverter Sharing Unbalanced Three-Phase and/or Single-Phase systems. IEEE Trans. Ind. Appl. 2016, 52, 5156–5164. [Google Scholar] [CrossRef]
- Zhao, W.; Ruan, X.; Yang, D.; Chen, X.; Jia, L. Neutral Point Voltage Ripple Suppression for a Three-Phase Four-Wire Inverter With an Independently Controlled Neutral Module. IEEE Trans. Ind. Electron. 2017, 64, 2608–2619. [Google Scholar] [CrossRef]
- Fu, Y.; Li, Y.; Huang, Y.; Lu, X.; Zou, K.; Chen, C.; Bai, H. Imbalanced Load Regulation Based on Virtual Resistance of A Three-Phase Four-Wire Inverter for EV Vehicle-to-Home Applications. IEEE Trans. Transp. Electrif. 2018, 5, 162–173. [Google Scholar] [CrossRef]
- Zhang, R.; Prasad, V.; Boroyevich, D.; Lee, F. Three-dimensional space vector modulation for four-leg voltage-source converters. IEEE Trans. Power Electron. 2002, 17, 314–326. [Google Scholar] [CrossRef]
- Hava, A.; Kerkman, R.; Lipo, T. Carrier-based PWM-VSI overmodulation strategies: Analysis, comparison, and design. IEEE Trans. Power Electron. 1998, 13, 674–689. [Google Scholar] [CrossRef] [Green Version]
- Hava, A.M.; Kerkman, R.J.; A Lipo, T. Simple analytical and graphical methods for carrier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Jiang, D.; Wang, F. Current-Ripple Prediction for Three-Phase PWM Converters. IEEE Trans. Ind. Appl. 2013, 50, 531–538. [Google Scholar] [CrossRef]
- Grandi, G.M.; Loncarski, J. Evaluation of current ripple amplitude in three-phase PWM voltage source inverters. In Proceedings of the 2013 International Conference-Workshop Compatibility And Power Electronics, Ljubljana, Slovenia, 5–7 June 2013; pp. 156–161. [Google Scholar]
- Jiang, D.; Wang, F. Study of analytical current ripple of three-phase PWM converter. In Proceedings of the 2012 Twen-ty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2020; pp. 1568–1575. [Google Scholar]
- Grandi, G.; Loncarski, J.; Seebacher, R. Effects of current ripple on dead-time distortion in three-phase voltage source inverters. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 207–212. [Google Scholar]
- Hammami, M.; Ricco, M.; Viatkin, A.; Mandrioli, R.; Grandi, G. Evaluation of AC Current Ripple in case of SplitCapacitor Three-Phase Four Wires Inverters. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 128–132. [Google Scholar]
- Cai, W.; Shen, Y.; Xiao, X.; Wang, W.; Zhang, W.; Li, K.; Zhang, C.; Zhao, Z. Design of the Neutral Line Inductor for Three-phase Four-leg Inverters. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 2455–2460. [Google Scholar]
- Jahns, T.; De Doncker, R.; Radun, A.; Szczesny, P.; Turnbull, F. System design considerations for a high-power aerospace resonant link converter. IEEE Trans. Power Electron. 1993, 8, 663–672. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Li, J. Modeling, Analysis, and Mitigation of Load Neutral Point Voltage for Three-Phase Four-Leg Inverter. IEEE Trans. Ind. Electron. 2012, 60, 2010–2021. [Google Scholar] [CrossRef]
- Viatkin, A.; Mandrioli, R.; Hammami, M.; Ricco, M.; Grandi, G. Theoretical Analysis of the AC Current Ripple in Three-Phase Four-Leg Sinusoidal PWM Inverters. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 796–801. [Google Scholar]
- Mandrioli, R.; Viatkin, A.; Hammami, M.; Ricco, M.; Grandi, G. A Comprehensive AC Current Ripple Analysis and Performance Enhancement via Discontinuous PWM in Three-Phase Four-Leg Grid-Connected Inverters. Energies 2020, 13, 4352. [Google Scholar] [CrossRef]











| Parameter | Value |
|---|---|
| Rated DC voltage, Vdc (V) | 100 |
| Ac-link inductor parameters: L (mH), R (Ω) | 1.73, 0.727 |
| Passive load parameters: Co (μF), Ro (Ω) | |
| - balanced | 45, 6.6 |
| - unbalanced (ph. a/b/c) | 51, 5.9/21, 9.2/11, 12.4 |
| Power factor (50 Hz) | 1 |
| Switching frequency, fsw (kHz) | 3.6 |
| VSC Architecture | Label | |||||
|---|---|---|---|---|---|---|
| Three-leg, Ln = ∞ | 3leg | 1 | 0.2887 | 0.054 | - | - |
| Four-leg without neutral line inductor | 0 | 1 | 0.5 | 0.0969 | 1 | 0.2414 |
| Four-leg with neutral line inductor, Ln = 0.5L | 0.5L | 1 | 0.3 | 0.0628 | 0.4 | 0.0965 |
| Four-leg with neutral line inductor, Ln = 1L | 1L | 1 | 0.25 | 0.0576 | 0.25 | 0.0603 |
| Four-leg with neutral line inductor, Ln = 2L | 2L | 1 | 0.25 | 0.0552 | 0.1429 | 0.0345 |
| Parameter | Value |
|---|---|
| Rated active power, P (kW) | 11 |
| Rated RMS value of grid line-to-line voltage, Vac (V) | 400 |
| Dc voltage range, Vdc (V) | 700–1000 |
| Switching frequency, fsw (kHz) | 100 |
| Maximum peak-to-peak phase current ripple, (% of fundamental) | 10 |
| VSC Architecture | Label | |||||
|---|---|---|---|---|---|---|
| Three-leg, Ln = ∞ | 3leg | 637.9 | 2.64 | 637.9 | 2.64 | - |
| Four-leg without neutral line inductor | 0 | 1104.9 | 2.74 | 1104.9 | 2.74 | - |
| Four-leg with neutral line inductor, Ln = 0.5L | 0.5L | 662.9 | 2.96 | 662.9 | 2.96 | 331.5 |
| Four-leg with neutral line inductor, Ln = 1/√3L | 0.5774L | 637.9 | 3.01 | 640.6 | 3.0 | 369.9 |
| Four-leg with neutral line inductor, Ln = 1L | 1L | 552.4 | 3.26 | 600.1 | 3.0 | 600.1 |
| Four-leg with neutral line inductor, Ln = 2L | 2L | 552.4 | 3.12 | 575 | 3.0 | 1150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viatkin, A.; Mandrioli, R.; Hammami, M.; Ricco, M.; Grandi, G. AC Current Ripple in Three-Phase Four-Leg PWM Converters with Neutral Line Inductor. Energies 2021, 14, 1430. https://doi.org/10.3390/en14051430
Viatkin A, Mandrioli R, Hammami M, Ricco M, Grandi G. AC Current Ripple in Three-Phase Four-Leg PWM Converters with Neutral Line Inductor. Energies. 2021; 14(5):1430. https://doi.org/10.3390/en14051430
Chicago/Turabian StyleViatkin, Aleksandr, Riccardo Mandrioli, Manel Hammami, Mattia Ricco, and Gabriele Grandi. 2021. "AC Current Ripple in Three-Phase Four-Leg PWM Converters with Neutral Line Inductor" Energies 14, no. 5: 1430. https://doi.org/10.3390/en14051430










