1. Introduction
In recent years, the energy industry has showed significant interest in the digitization of well construction processes for improved safety and cost reduction. To achieve that, robust and accurate modeling of physical processes is essential, and especially modeling cuttings transport is important to safely and successfully drill wells.
Most commonly, mechanistic models are used to estimate the cuttings concentration in wellbores. These models are used during the design and execution phases of operations. Based on the simulation results from the mechanistic model, several decisions can be made to alleviate potential hole cleaning problems. For example, the pump’s flow rate and the drill string’s rotation speed can be adjusted to mitigate nonproductive time (NPT) events. An NPT event can be a pack-off leading to a stuck pipe due to elevated cuttings accumulation around the bottomhole assembly (BHA), or it can be induced lost circulation due to elevated equivalent circulating density (ECD) in the presence of high concentrations of cuttings. Lost circulation can easily transform into a catastrophic blowout event. Therefore, it is important to model and monitor the cuttings concentration in the wellbore.
Up until now, these mechanistic models were useful; however, there are some inherent shortcomings to these models. First, a mechanistic model can be inaccurate because it is unlikely to perfectly model the complex physical interactions associated with cuttings transport. These include the effects of pipe rotation, eccentricity, inclination, chemical interactions, fluid and cuttings properties, etc. Additionally, mechanistic models frequently require updating the input parameters. Some of these parameters, such as geometry, trajectory, and fluid properties, may be extracted from daily drilling reports. However, there are a lot of manual measurement steps required to collect these inputs and a human operator is needed to input and maintain the model parameters [
1]. This manual process is a major challenge that prevents streamlining well construction operations.
In this study, an alternative, data-driven modeling approach is taken with the aim to overcome the shortcomings of mechanistic models. After various trials, an artificial neural network model is used. The model is applied to the experimental datasets collected at The University of Tulsa—Drilling Research Projects (TUDRP). These datasets were collected through the experimental research projects conducted in the last 40 years, which include a wide spectrum of wellbore and pipe sizes, inclinations, rate-of-penetration (ROP) values, pipe rotation speeds, flow rates, and fluid and cuttings properties. The performance of the proposed model is compared with existing mechanistic models by comparing the results with the experimental datasets. The results show that, especially for this particular research area, the data-driven model performs significantly better. Finally, using this model, a genetic algorithm is applied to determine the optimal flow rate and pipe rotation speed. The decision is made considering the minimum required energy for this process.
Data-driven models are more practical to implement and show the potential to overcome the disadvantages of the mechanistic model by providing better accuracy and requiring fewer manual inputs. Therefore, data-driven models can be a better candidate in the act of digitizing the well construction process. In addition, to the best of the authors’ recollection, there is no optimization attempt reported in the literature regarding flow rate and rotation speed considering cuttings transport performance based on a quantitative function defined to be minimized using a machine learning technique.
The paper structure is organized as follows: After this brief introduction, existing relevant studies in the literature are presented in the Literature Review section along with machine learning and genetic algorithm-related topics. The results are analyzed and discussed in the Results and Discussions section. Finally, the conclusions are provided in the last section. In the Appendix, basic working structures of neural networks and genetic algorithms are introduced along with the particular network parameters used in the study.
2. Literature Review
Mechanistic and computational fluid dynamics (CFD) models for cuttings transport are very important because there is no direct measurement of cuttings deposition during drilling wells. The cuttings deposition is usually inferred by interpreting a multitude of sensory measurements (i.e., standpipe pressure, hook load, etc.), which are prone to human error. Therefore, the operations need to rely on simulations from these models. However, there is only a limited amount of literature, especially about data-driven models for cuttings transport. In this section, some literature about various modeling approaches for cuttings transport is presented.
Cayeux et al. [
2] proposed a real-time, transient cuttings transport model that can calculate the distribution of cuttings along the wellbore. They applied this model to datasets that are from actual drilling operations and demonstrated the model’s usability cases with these two case studies. A good match between the surface measurements, observations, and model’s prediction was attained.
Erge and van Oort [
3] introduced a new cuttings transport modeling approach including the effects of rotation and eccentricity. The proposed model was developed by constructing 3D velocity profiles and by comparing the local velocities to a local critical velocity definition to estimate the cuttings deposition along the trajectory of the wellbore. Then, they introduced time-dependency into the proposed model and demonstrated the model’s capabilities using an actual drilling dataset with a stuck pipe event that occurred due to cuttings pack-off. The results showed fair agreement between the model’s prediction and the data [
4,
5].
Ozbayoglu et al. [
6] conducted a comparative analysis using physics-based and data-driven models for estimating the frictional pressure losses in an annulus. The results showed that the data-driven model more accurately captured the complex dynamics especially while the drill string was compressed and rotating.
Ozbayoglu et al. [
7] developed a new cuttings-transport mechanistic model that includes the effects of drill-pipe rotation and eccentricity. The model can estimate the volumetric distribution phases in three-phase flow and the pressure losses in the horizontal sections. Additionally, they conducted experiments involving three-phase flow and compared the results from the mechanistic model to the experimental data. They noted a good agreement between them.
Ozbayoglu et al. [
8] conducted cuttings transport experiments for a wide range of flow rates, cuttings injection rates, and inner pipe rotation speeds. Additionally, they recorded these experiments via a high-speed digital camera. They implemented an image processing algorithm to extract some characteristic information about cuttings transport during these experiments, such as the concentration of moving particles, their relative transport velocities, etc. These parameters were used as inputs to the mechanistic model and, in doing so, the performance of the mechanistic model improved significantly.
Tombul et al. [
9] applied several data-driven models (linear and nonlinear regression, support vector regression (SVR), support vector machine (SVM), and artificial neural networks (ANN)) to predict the velocity and direction of the cuttings using experimental data collected via a particle image velocimeter. The experimental test matrix included a distinct rate of penetration values, inclinations, rotation speeds, and flow rates. They noted that SVM performed better when estimating the direction of the cuttings and that SVR better predicted velocity.
Zamora et al. [
10] and, later, Friedheim and Contreras [
11] presented a cuttings transport model that combines an analytical model, a fuzzy logic technique, and experimental data. The results of their model were presented under four categories ranging from “very good” to “poor” hole cleaning. They stated that this type of data-driven modeling is well suited for implementation and use during real-time operations, which is also verified in this present study.
Aggwu et al. [
12] presented a comprehensive literature review of experimental, numerical, and artificial intelligence (AI) modeling studies on cuttings settling velocity research. They concluded that AI techniques provide a unique way to model the cuttings settling velocity and that a variety should be investigated to determine the most relevant technique for this field of research. In a more recent study, Aggwu et al. [
13] applied ANN to estimate the cuttings settling velocity considering the cuttings shape, size, and density and the drilling fluid’s viscosity and density. They mentioned that, generally, physics-based models assume cuttings shape to be a perfect sphere. This assumption causes the model to be inaccurate in actual conditions. In contrast, they demonstrated that the ANN model can capture the effect of the cuttings shape and can provide more accurate estimations of cuttings settling velocity in comparison to physics-based, correlation-type models.
Al-Azani et al. [
14] used SVM to estimate the cuttings concentration in the wellbore by correlating it with the drilling fluid properties and the drilling parameters such as the pump rate, rotation speed, etc. In a later study [
15], they extended the initial work by incorporating ANN models. They trained the models using the data published by Yu et al. [
16]. It is shown that SVM provided a higher accuracy in comparison to both the ANN model and Yu et al.’s empirical correlation. They also emphasized the benefits of using data-driven approaches as being a good fit for real-time applications and providing better accuracy.
Krishna et al. [
17] investigated several modeling approaches for the detection and prediction of lost circulation events that can be caused due to various reasons including ineffective hole cleaning. They concluded that the AI-based predictive models show varying performance based on the scenarios and that no model simply outperforms all others. A hybrid of AI-based models was recommended to improve the adaptability to varying conditions and computational speed.
Kumar et al. [
18] compared the pressure drop prediction performance of several machine learning methods for the flow of Herschel–Bulkley fluids in eccentric and concentric annuli. These methods include ANN, Bayesian neural network (BNN), random forest (RF), and SVM. They showed that RF and BNN provided a superior prediction performance in comparison to ANN and SVM for the dataset used in their study.
Erge and van Oort [
19] proposed a new hybrid modeling approach that combines the physics-based and data-driven models to predict the standpipe pressure in well construction. Several data-driven models (ANN, deep learning, and Gaussian process (GP)) were evaluated with an actual drilling dataset. The hybrid model was developed using a rule-based stochastic hidden Markov model, which outperformed the results from purely physics-based or data-driven models.
Xiang [
20] trained an Least Squares Support Vector Machine (LS-SVM) using two different datasets from the cuttings transport literature [
21,
22]. The results show good agreement with the datasets, with an ≈8.6 relative root mean square error (RMSE).
Yongwang et al. [
23] applied an ant colony algorithm to solve a two-layer cuttings transport model with a nonlinear set of equations. Solving these equations with discrete Newton’s method and obtaining accurate results requires good estimation of the initial values. In contrast, the ant colony algorithm does not require the initial values and provides an easier and more stable solution of the equations. They showed that this approach offers fairly accurate results as well.
Shirangi et al. [
24] developed a CFD model for flow in annuli including the effects of geometry changes, drilling parameters, fluid properties, cuttings bed height, and inner pipe rotation. They ran about 55,000 simulations covering a wide parameter space and used these data points to train several data-driven models such as linear models, decision tree, SVR, neural network, and ensemble methods. With this data-driven modeling approach, the computationally expensive CFD simulations were replaced, and fast and accurate predictions were achieved.
Muftuoglu [
25] developed a fuzzy logic model for cuttings bed thickness estimation during the sediment transport in annuli. It was shown that the stationary bed thickness could be estimated with an error of about 6.81% using this approach.
Sorgun et al. [
26] conducted cuttings transport experiments at a flow loop, using water as the drilling fluid with various flow rates, inclinations, rotation speeds, and rates of penetration. They trained a fuzzy logic model using the data points collected at the experiments that can estimate the cuttings bed thickness. The results from the model showed good agreement with the experiments.
Jondahl and Viumdal [
27] used ultrasonic attenuation to characterize the drilling fluid properties, such as the density, plastic viscosity, and gel strength. An ANN was trained using these noninvasive acoustic measurements for 11 different fluids. The results from this study showed that ANN performed better when predicting the density and did not perform as well when predicting the viscosity or the gel strength, which is attributed to their nonlinear behavior. To overcome this challenge, the researchers outlined their next steps as extending the test matrix and analyzing different machine learning techniques such as SVM.
Kelin et al. [
28] presented a detailed review of cuttings transport studies from universities, research institutes, and service and research companies. They summarized their analysis into a set of rule of thumbs to optimize cuttings transport effectiveness for drilling operations.
Rooki et al. [
29] evaluated the use of ANN and multiple linear regression methods to predict the cuttings concentration in a wellbore during foam drilling applications. They compared these two data-driven methods to a mechanistic model and showed that ANN provided an overall better accuracy with predictions. In a later study, Rooki and Rakhshkhorshid [
30] presented a radial basis function network (RBFN) method to predict the cuttings concentration during underbalanced drilling. They compared RBFN to a more conventional backpropagation neural network (BPNN). According to their study, RBFN outperformed RBNN in terms of accuracy, training speed, and simplicity. In a more recent study, Rooki et al. [
31] developed an evolutionary fuzzy system (EFS) based on the genetic learning algorithm to estimate the cuttings concentration in a wellbore while drilling with foam. Sixty out of the 77 experimental data points were used in training, and the results showed that EFS outperformed the ANN, adaptive neuro-fuzzy inference system (ANFIS), and multiple linear regression methods in the remaining 17 data points that the algorithms were tested on.
Saini et al. [
32] proposed a digital twinning and reinforcement learning application for the hole cleaning challenge. A digital twin was developed by programming a hydraulics and a cuttings transport model that allows for rapid simulations considering the state and drilling parameter variation in time. Given the current state, several scenarios were evaluated with the digital twin simulations and an optimized action was selected based on the maximum reward using a Markov reward process.
Han et al. [
33] presented a state-of-the-art real-time 3D cuttings sensing system that allows a user to monitor the condition of the wellbore. They prototyped the system and showed that it could track the size, shape, and distribution of the cuttings. The system could also be used to detect the cavings, which is very important for early detection and mitigation any NPT event related to cuttings transport and wellbore instability.
Singh et al. [
34] evaluated some machine learning regression techniques to predict the pressure losses in a narrow annulus. The models were trained with the experimental data collected at the University of Tulsa. Their results show that Lasso and Ridge regression outperformed the principal component analysis and partial least squares regression.
Another application of ANN for wellbore hydraulics was presented by Wang and Salehi [
35]. They trained the ANN using the surface measurements and some meta-information from 3 different wells to predict the pump pressures during drilling. The results showed a good match between the measured and estimated pump pressures.
There are numerous studies published estimating cuttings concentration and frictional pressure losses during cuttings transport in wells using mechanistic models as well as empirical approaches. However, there is very limited published information available regarding the optimization of flow rate and pipe rotation speed considering hole cleaning. For example, Larsen et al. [
36] presented an empirical model aimed at determining the minimum required flow rate for directional wells to prevent cuttings accumulation in a wellbore. However, the model ignores the effect of pipe rotation. Bassal [
37] proposed empirical correlations that estimate the contribution of pipe rotation on cuttings transport.
Genetic algorithms and neural networks have been used together extensively in a variety of applications. In the majority of implementations, a genetic algorithm is utilized to find the optimal hyperparameters of the underlying neural network, as presented in [
38]. This is a natural implementation of a genetic algorithm to find the optimal solution to a particular problem; in this case, the problem was neural network optimal hyperparameter tuning.
However, in a handful of studies in the literature, neural networks were embedded into the genetic algorithm as the fitness functions [
39,
40,
41,
42,
43,
44,
45,
46]. In one study [
39], the authors used a neural network to find the suitability of the application of a beam through a certain angle to find the optimal set of angles for cancer patients during the application of intensity-modulated radiotherapy treatment. Using neural networks as the fitness function was also adopted in machining research, where the researchers of [
41] used the neural network embedded genetic algorithm to find the optimal energy efficiency during the milling process. It was also investigated in the product form design process in the application of automatic industrial design [
42], optimization of the determination of the amount of dye in ultrasound assisted-dispersive liquid–liquid micro-extraction coupled with derivative spectrophotometry [
43], optimization of the pulverized coal combustion performance [
44], enhancement of the overall performance of constructed wetlands in urban areas [
45], and engine optimization of efficiency and NOx emission [
46]. In a slightly different research, the authors used neural networks to find the best fitness function for the genetic algorithm for the machine programming problem in automatic software generation [
40].
The researchers in these vastly different study areas preferred neural networks to perform as the fitness function for the genetic algorithm due to a lack of appropriate representation of the optimization problem with a satisfactory empirical or mechanistic model. Our motivation in this study also aligns with this approach: to find the optimal drilling operational values for flow rate and rotation speed (rpm) for different working conditions. To the best of our knowledge, we have not encountered any study in the drilling research literature that focused on finding the optimal flow rate and rpm (or any other control parameters, for that matter) using neural network-driven genetic algorithms (or any other evolutionary algorithm). Thus, this paper attempts to provide a methodology to optimize the flow rate and pipe rotation speed, using a genetic algorithm as a decision tool, but uses artificial neural networks as the basis to estimate frictional losses and cuttings concentration while considering cuttings transport phenomena inside the wellbore.
In this paper, after providing a theoretical background regarding the machine learning techniques used in this study, followed by cuttings concentration and frictional loss estimations using mechanistic models and ANN, a methodology using a genetic algorithm to optimize the flow rate and pipe rotation speed is presented.
2.1. Theoretical Background
In this section, theoretical information about the models used in this study is presented briefly, including artificial neural networks, the genetic algorithm, and mechanistic models.
The data that were used for training and optimization were collected in TUDRP from various cuttings transport-related projects. Hence, temporal factors such as varying operating conditions, equipment state, sensor quality, and measurement noise were all implicitly factored into the data. This phenomena provides a safety net for the overall input and data quality, since some of the collected data might have experienced operational or systemic issues during data collection, which alone would not have a significant effect on the rest of the data.
The selected data inputs are among the most commonly preferred features used throughout the literature. Our aim was not only to precisely estimate the output parameters, namely cuttings concentration () and pressure drop (ΔP/ΔL), but also to assist the predictor model in obtaining a general understanding of the dynamics of the process and in making satisfactory and acceptable predictions under all circumstances within the operating range.
2.1.1. Artificial Neural Networks
In this study, 2 separate multilayer perceptron neural networks were developed with 11 inputs and 1 output. Each network had 1 hidden layer with 10 neurons. “tanh” was preferred as the activation function for ANN models. Both networks used the following inputs: pipe outer diameter, eccentricity, fluid density,
θ600,
θ300, cuttings size, cuttings density, flow rate, wellbore inclination, rate of penetration, and pipe rotation. Since wellbore diameter was constant for all data points considered in this study, it was not taken into consideration for ANN models. The general structure of ANN is provided in
Appendix A.1.
Network 1 was developed to predict the cuttings concentration value; therefore, the output neuron was associated with that value. In contrast, Network 2 was developed to predict the frictional pressure loss value.
After both networks were trained using a backpropagation learning algorithm, the predictions of cuttings concentration and frictional pressure loss from any given set of inputs were acquired and the system was able to perform a fairly robust and accurate forecasting. Since there was limited data to generate the prediction model, creating an unnecessarily complex model that would have better chances of overfitting was not desirable. Thus, a relatively simple and universal model was preferred. We decided to keep only one hidden layer. Moreover, 10, 15, and 20 neurons were used, and using 10 neurons resulted in the best performance. Therefore, we decided to use 1 hidden layer with 10 neurons. However, each topology was run several times and stored the one with the best cross validation performance to make sure a generalized, not overfit model was acquired. Early stop of the training was applied as soon as the cross validation (CV) error started to increase; hence, we ensured that the proposed prediction model would behave the same for new data. The final weights and other network topology parameters are provided in
Appendix B.1.
We used two neural networks, one for estimating the cuttings concentration and the other for pressure drop estimation. Each neural network had 11 inputs, 10 hidden neurons, and 1 output neuron. We chose the default training parameters that Matlab preconfigured for the fitting tool. We used Levenberg–Marquard learning for error backpropagation, which is a relatively fast gradient descent algorithm. Since we used cross validation for overfitting prevention, the training sessions were short. The number of epocs had a span of 5–20 in all attempts. We trained the model 10–15 times until we were satisfied with the training, cross validation, and testing error values. Hence, our time complexity was proportional with the number of neurons used, i.e., , where k represents the number of epocs for training, c represents the number of training sessions, and n represents the number of neurons in the neural network. After the training process, for the testing stage, the process was much faster, only a single forward pass through the network for each prediction. Hence, the time complexity was much smaller; , where n represents the number of neurons in the neural network.
2.1.2. Genetic Algorithm
In the second phase of the system, a genetic algorithm-based optimization tool was developed that takes cuttings concentration and frictional pressure loss values acquired from an ANN model and tunes them to find the optimal flow rate and rpm settings for any given drilling process. In
Appendix A.2. the general structure of genetic algorithms are presented.
The reason cuttings concentration and frictional pressure loss values for fine tuning and optimizing the flow rate and rpm are used is due to the fact that cuttings concentration and frictional pressure loss values are dependent variables of the system. Their values can be altered by adjusting the flow rate and rpm along with other controllable parameters; however, the relation between the controllable parameters of the process (neural network inputs) and the dependent variables (cuttings concentration and frictional pressure loss) is not easily represented through a simple function. However, the neural network comes to the rescue at this point. Hence, the cuttings concentration and frictional pressure loss values are able to be identified fairly accurately at any given point.
Meanwhile, since we attempted to find the optimal flow rate and rpm values, the cuttings concentration and frictional pressure loss values have to be associated with the flow rate and rpm values. For that purpose, the genetic algorithm is used with the following fitness function:
where
and
are constants and defined based on the experimental data. The genetic algorithm tries to minimize the
y value, hence aiming to find the best cuttings concentration and frictional pressure loss (
and Δ
P/Δ
L) pairs that force
y to be minimal. However, there are 2 major issues here: (i) both
and Δ
P/Δ
L cannot be lowered at the same time. When
is lowered below a certain threshold, either Δ
P/Δ
L may increase or the overall process may become unsustainable. Similarly, if Δ
P/Δ
L is decreased, there are sustainability issues. Hence, some trade-off is needed. (ii)
and Δ
P/Δ
L are not control parameters. Their values cannot be set arbitrarily. They are dependent on network inputs including flow rate and pipe rotation speed along with other process parameters. In this particular study, only optimization of flow rate and pipe rotation speed is of interest. In future work, the other control parameters (i.e., fluid properties, eccentricity, etc.) can also be optimized. As a result,
and Δ
P/Δ
L can be obtained through the neural network forecaster by giving different flow rate and pipe rotation speed values.
and Δ
P/Δ
L are well associated with flow rate and pipe rotation speed; hence, minimizing
y makes sense from a process perspective.
and are coefficients that need to be tuned for the particular process requirements. They can also be optimized; however, in this preliminary study, we set and . Hence, the flow rate (Q) and rpm can be optimized based on these fixed coefficient values.
The chromosome structure used in this study consists of 2 genes (one storing the Q value and the other one storing the rpm value). Since there are only 2 genes, there is only one cutoff point that can be implemented in the crossover operation (between Q and rpm genes). In addition, mutation can change the value of Q or rpm randomly depending on the mutation rate. During implementation, the following hyperparameter settings for the genetic algorithm were used:
Chromosome size: 2 genes;
Population size: 500;
Maximum number of generations: 100;
Crossover rate: 0.7;
Mutation rate: 0.001;
Elitism rate: 0.1;
Fitness function: as given in Equation (1).
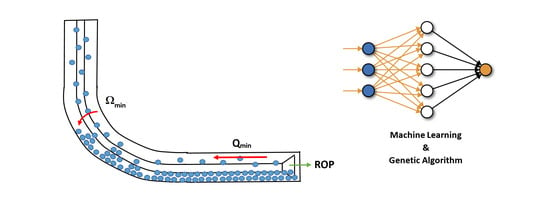
A schematic of the genetic algorithm process is presented in
Figure 1.
It is crucial to obtain a general model for and ΔP/ΔL predictions, since these are the two parameters (genes) that are used by the genetic algorithm for flow rate and rpm optimization. If and ΔP/ΔL predictions are adequately generalizable, i.e., the neural network is not overfit or underfit, and the optimization process will also be successful.
For the genetic algorithm, the chromosome consists of the flow rate and rpm values and the fitness function is the linear combination of two neural network predictors (one for cuttings concentration and one for pressure drop). The population size was chosen as 500 or 1000. The maximum number of generations was chosen as 100. Hence, the total time complexity of the genetic algorithm is , where and n represents the number of neurons in each neural network.
For most practical purposes, the genetic algorithm found the optimal flow rate and rpm values fairly quickly, since the overall time complexity was linear. Hence, it is possible to use such a system in real-time. The genetic algorithm Matlab code that is developed for this study is presented in
Appendix B.2.
2.1.3. Mechanistic Models
The mechanistic models used to compare the performance between the neural network models include Zhang’s model [
47] and Ozbayoglu’s model [
48]. Both models were based on the conservation of mass and momentum, and the solution was provided by using certain constitutive equations related to hydrodynamics. In addition, the models consider all wellbore inclinations from vertical to horizontal and the effect of pipe rotation on hole cleaning. The major differences between these models include the methodology to determine the flow patterns and the friction coefficients used. For the sake of not inflating the size of this paper, detailed information regarding these models are not presented here, but they can be found in the literature.