Optimization of a Small Wind Power Plant for Annual Wind Speed Distribution
Abstract
1. Introduction
2. Determination of Turbine Parameters
- ηg—mechanical gear efficiency;
- ηG—generator efficiency.
- pv—power transmitted by the wind at speed v, expressed as a relative percentage to attend the annual wind speed distribution in a particular location;
- Pv—the power of the wind speed v per unit of area;
- ΣPi—total wind power with speeds included in the annual distribution per unit of area;
- Nv—number of hours in the year of wind speed v;
- ev—percentage of energy supplied by wind speed v in the total energy supplied by winds with speeds included in the annual distribution.
- S = πr2—turbine working surface;
- R—turbine radius;
- P—turbine output power;
- Cp (λ) = 0.4 power coefficient for a three-blade turbine;
- Λ—tip-speed ratio;
- ρ = 1.225 kg/m3—air density.
- K = n2/n1—ratio of mechanical gears;
- n1—turbine speed;
- n2—generator speed.
3. Mathematical Model of the Generator
- D—losses factor;
- ik—phase current;
- J—moment of inertia;
- Rk—phase resistance;
- Te—electromagnetic torque;
- Tm—torque of the turbine;
- vk—phase voltage;
- θ—rotor position angle;
- Ψk (θ, ik)—magnetic flux of the phase.
- VS—supply voltage;
- vT SD—transistor saturation voltage;
- vD AC—diode forward voltage.
4. Optimizations of the Generators
- Tm—the calculated generator torque value;
- Tmexp—the expected torque value (at rated or at maximum generator speed);
- Ps+—average power supplied to the power source;
- Ps-—average power drawn from the power source;
- Pcu—power losses in the generator windings;
- PEE—power losses in the power electronic system;
- I—phase current the root mean square (RMS) value;
- S—cross-sectional area of the winding wire.
- TmN—torque of the turbine at rated speed;
- TmC—torque of the turbine at cut-off speed;
- ηN—drive efficiency at rated speed;
- TmGN—torque of the generator at rated speed;
- TmGC—torque of the generator at maximum speed.
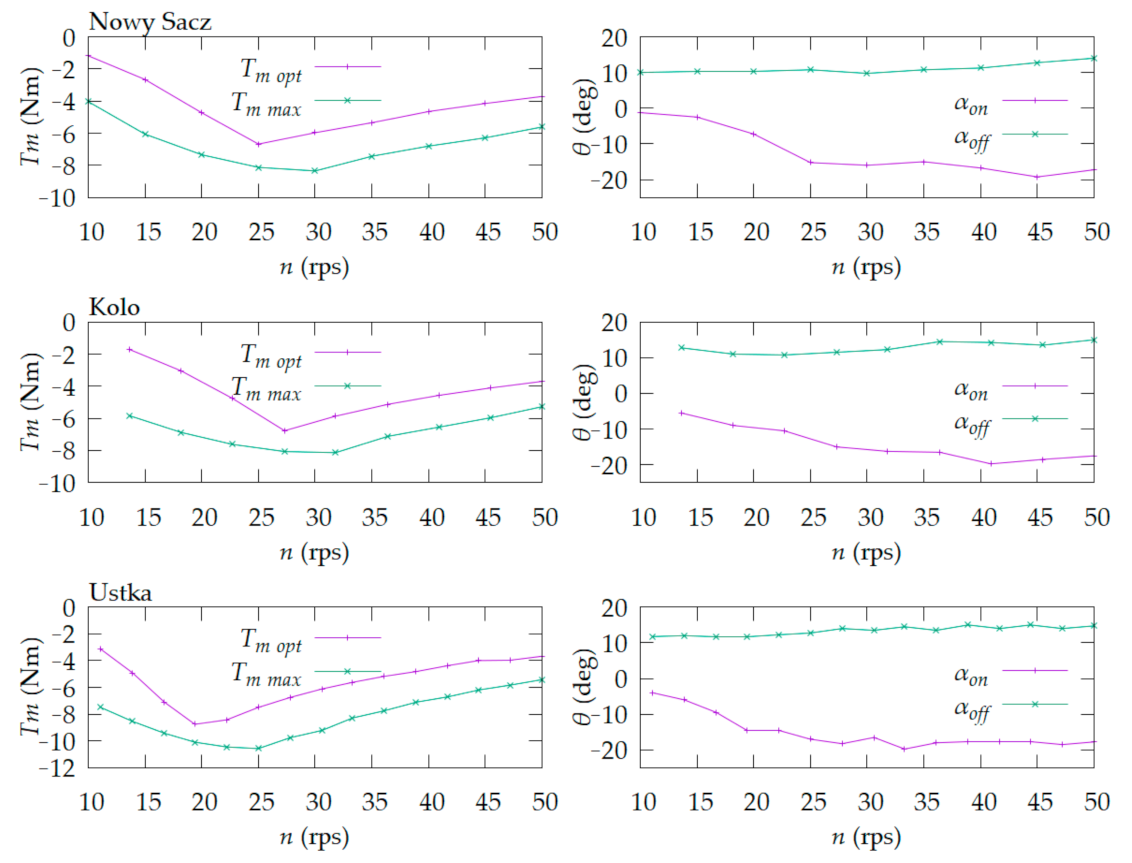
5. Optimization Results
- Nv—duration of winds with speed v;
- nv—generator rotational speed at wind speed v;
- Tmv—torque on the generator at wind speed v;
- ηv—generator efficiency at wind speed v.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klink, K. Climatological mean and interannual variance of United States surface wind speed, direction and velocity. Royal Meteorological Society. Int. J. Climatol. J. R. Meteorol. Soc. 1999, 19, 471–488. [Google Scholar] [CrossRef]
- Salmon, J.R.; John, L.W. A two-site correlation model for wind speed, direction and energy estimates. J. Wind Eng. Ind. Aerodyn. 1999, 79, 233–268. [Google Scholar] [CrossRef]
- Aikawa, M.; Hiraki, T.; Eiho, J. Grouping and representativeness of monitoring stations based on wind speed and wind direction data in urban areas of Japan. Environ. Monit. Assess. 2008, 136, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, O.; Guo, Y.; Yang, Z.; Zhang, L. An investigation of wind direction and speed in a featured wind farm using joint probability distribution methods. Sustainability 2018, 10, 4338. [Google Scholar] [CrossRef]
- Nouri, A.; Babram, M.A.; Elwarraki, E.; Enzili, M. Moroccan wind farm potential feasibility. Case study. Energy Convers. Manag. 2016, 122, 39–51. [Google Scholar] [CrossRef]
- Ozay, C.; Melih, S.C. Statistical analysis of wind speed using two-parameter Weibull distribution in Alaçatı region. Energy Convers. Manag. 2016, 121, 49–54. [Google Scholar] [CrossRef]
- Parajuli, A. A statistical analysis of wind speed and power density based on Weibull and Rayleigh models of Jumla, Nepal. Energy Power Eng. 2016, 8, 271–282. [Google Scholar] [CrossRef]
- Li, P.; Hu, W.; Hu, R.; Huang, Q. Strategy for wind power plant contribution to frequency control under variable wind speed. Renew. Energy 2019, 130, 1226–1236. [Google Scholar] [CrossRef]
- Qais, M.H.; Hany, M.H.; Saad, A. Low voltage ride-through capability enhancement of grid-connected permanent magnet synchronous generator driven directly by variable speed wind turbine: A review. J. Eng. 2017, 13, 1750–1754. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.; Daniel, M.T.; Ramos-Ruiz, J.; Enjeti, P.; Liu, L.; Aeloiza, E. Isolated AC–DC converter using medium frequency transformer for off-shore wind turbine DC collection grid. IEEE Trans. Ind. Electron. 2017, 64, 8939–8947. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Shimada, S.; Kozai, K. Assessment of the offshore wind resource in Japan with the ASCAT microwave scatterometer. Int. J. Remote Sens. 2019, 40, 1200–1216. [Google Scholar] [CrossRef]
- Akbari, N.; Dylan, J.; Richard, T. A cross-European efficiency assessment of offshore wind farms: A DEA approach. Renew. Energy 2020, 151, 1186–1195. [Google Scholar] [CrossRef]
- Feng, J.; Wen, Z.S. Design optimization of offshore wind farms with multiple types of wind turbines. Appl. Energy 2017, 205, 1283–1297. [Google Scholar] [CrossRef]
- Irawan, C.A.; Ouelhadj, D.; Jones, D.; Stålhane, M.; Sperstad, I.B. Optimisation of maintenance routing and scheduling for offshore wind farms. Eur. J. Oper. Res. 2017, 256, 76–89. [Google Scholar] [CrossRef]
- Ziemba, P.; Watrobski, J.; Ziolo, M.; Karczmarczyk, A. Using the PROSA method in offshore wind farm location problems. Energies 2017, 10, 1755. [Google Scholar] [CrossRef]
- Chipindula, J.; Botlaguduru, V.S.V.; Du, H.; Kommalapati, R.R.; Huque, Z. Life Cycle Environmental Impact of Onshore and Offshore Wind Farms in Texas. Sustainability 2018, 10, 2022. [Google Scholar] [CrossRef]
- Castro-Santos, L.; Diaz-Casas, V. Floating Offshore Wind Farms; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kotur, D.; Stefanov, P. Optimal power flow control in the system with offshore wind power plants connected to the MTDC network. Int. J. Electr. Power Energy Syst. 2019, 105, 142–150. [Google Scholar] [CrossRef]
- Petrović, P.; Curley, M. Detection inhomogeneities in wind direction and speed data. In Proceedings of the Fifth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 26–30 May 2008. [Google Scholar]
- Salahaddin, A.A.; Meeran, A.O. Surface Wind Characteristics and Wind Direction Estimation for “Kalar Region/Sulaimani-North Iraq”. Sci. J. Univ. Zakho 2013, 1, 882–890. [Google Scholar]
- Dore, A.J.; Fournier, N.; Weston, K.J.; Vieno, M. Development of a new wind-rose for the British Isles using radiosonde data, and application to an atmospheric transport model. Q. J. R. Meteorol. Soc. J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2006, 132, 2769–2784. [Google Scholar] [CrossRef]
- Pishgar-Komleh, S.H.; Akram, A. Evaluation of wind energy potential for different turbine models based on the wind speed data of Zabol region, Iran. Sustain. Energy Technol. Assess 2017, 22, 34–40. [Google Scholar] [CrossRef]
- Errami, Y.; Ouassaid, M.; Maaroufi, M. Control of a PMSG based wind energy generation system for power maximization and grid fault conditions. Energy Procedia 2013, 42, 220–229. [Google Scholar] [CrossRef]
- Xianguo, L. Diversification and localization of energy systems for sustainable development and energy security. Energy Policy 2005, 33, 2237–2243. [Google Scholar]
- Dizdarevic, N.; Majstrovic, M.; Zutobradic, S. Power quality in a distribution network after wind power plant connection. IEEE PES Power Syst. Conf. Expo. 2004, 2, 913–918. [Google Scholar]
- Muljadi, E.; Butterfield, C.P.; Ellis, A.; Mechenbier, J.; Hocheimer, J.; Young, R.; Miller, N.; Delmerico, R.; Zavadil, R.; Smith, J.C. Equivalencing the collector system of a large wind power plant. In In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Munoz, C.; Sauma, E.; Contreras, J.; Aguado, J.A. Impact of high wind power penetration on transmission network expansion planning. IET Gener. Transm. Distrib. 2012, 6, 1281–1291. [Google Scholar] [CrossRef]
- Pagnetti, A.; Ezzaki, M.; Anqouda, I. Impact of wind power production in a European Optimal Power Flow. Electr. Power Syst. Res. 2017, 152, 284–294. [Google Scholar] [CrossRef]
- Alsmadi, Y.M.; Xu, L.; Blaabjerg, F.; Ortega, A.P.; Abdelaziz, A.Y.; Wang, A.; Albataineh, Z. Detailed investigation and performance improvement of the dynamic behavior of grid-connected DFIG-based wind turbines under LVRT conditions. IEEE Trans. Ind. Appl. 2018, 54, 4795–4812. [Google Scholar] [CrossRef]
- Gilmanur, R.; Mohd, H.A. Nonlinear control-based modified BFCL for LVRT capacity enhancement of DFIG-based wind farm. IEEE Trans. Energy Convers. 2016, 32, 284–295. [Google Scholar]
- Conroy, J.F.; Watson, R. Low-voltage ride-through of a full converter wind turbine with permanent magnet generator. IET Renew. Power Gener. 2007, 1, 182–189. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F. Low voltage ride-through capability control for single-stage inverter-based grid-connected photovoltaic power plant. Sol. Energy 2018, 159, 665–681. [Google Scholar] [CrossRef]
- Ravikiran, H.; Moger, T. Comprehensive review on low voltage ride through capability of wind turbine generators. Int. Trans. Electr. Energy Syst. 2020, 30, e12524. [Google Scholar]
- Pengxiang, X.; Fu, L.; Wang, G.; Wang, Y. A compositive control method of low-voltage ride through for PMSG-based wind turbine generator system. IET Gener. Transm. Distrib. 2017, 12, 117–125. [Google Scholar]
- Abdelkrim, B.; Khiat, M.; Allaouiand, T.; Denai, M. Power quality improvement and low voltage ride through capability in hybrid wind-PV farms grid-connected using dynamic voltage restorer. IEEE Access 2018, 6, 68634–68648. [Google Scholar]
- Chang-Hyun, P.; Jang, G. Voltage quality assessment considering low voltage ride-through requirement for wind turbines. IET Gener. Transm. Distrib. 2016, 10, 4205–4212. [Google Scholar]
- Ogawa, K.; Yamamura, M.; Ishda, M. Study for Small Size Wind Power Generating System Using Switched Reluctance Generator. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 1510–1515. [Google Scholar]
- Narla, S.; Sozer, Y.; Husain, I. Switched Reluctance Generator Controls for Optimal Power Generation and Battery Charging. IEEE Trans. Ind. Appl. 2012, 48, 1452–1459. [Google Scholar] [CrossRef]
- Cardenas, R.; Pena, R.; Perez, M.; Clare, J.; Asher, G.; Wheeler, P. Control of a switched reluctance generator for variable-speed wind energy applications. IEEE Trans. Energy Convers. 2005, 20, 781–791. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Deng, X. Control for Power Converter of Small-Scale Switched Reluctance Wind Power Generator. IEEE Trans. Ind. Electron. 2021, 68, 3148–3158. [Google Scholar] [CrossRef]
- Barazarte, R.Y.; Gonzalez, G.; Hall, E. Comparison of Electrical Generators used for Wind Power Generation. IEEE Lat. Am. Trans. 2011, 9, 1040–1044. [Google Scholar] [CrossRef]
- Iwanaga, T.; Fukumoto, S.; Higuchi, T.; Yokoi, Y.; Abe, T. Analysis of a segment type switched reluctance generator for wind power generation. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–4. [Google Scholar]
- Korkosz, M.; Powrozek, A. The influence of control parameters on energy efficiency of switched reluctance generator for vehicle applications. E3S Web Conf. 2017, 14, 01037. [Google Scholar] [CrossRef]
- Ziapour, M.; Afjei, E.; Yousefi, M. Optimum commutation angles for voltage regulation of a high speed switched reluctance generator. In Proceedings of the 4th Annual International Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 13–14 February 2013; pp. 271–276. [Google Scholar]
- Sikder, C.; Husain, I.; Sozer, Y. Switched Reluctance Generator Control for Optimal Power Generation with Current Regulation. IEEE Trans. Ind. Appl. 2014, 50, 307–316. [Google Scholar] [CrossRef]
- Le-Huy, H.; Chakir, M. Optimizing the performance of a switched reluctance generator by simulation. In Proceedings of the XIX International Conference on Electrical Machine―ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Nassereddine, M.; Rizk, J.; Nagrial, M. Study on excitation control of Switched Reluctance Generator for wind energy conversion. In Proceedings of the 2008 Australasian Universities Power Engineering Conference, Sydney, Australia, 14–17 December 2008; pp. 1–5. [Google Scholar]
- Cardenas, R.; Pena, R.; Perez, M.; Asher, G.; Clare, J.; Wheeler, P. Control system for grid generation of a switched reluctance generator driven by a variable speed wind turbine. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society, Busan, Korea, 2–6 November 2004; pp. 1879–1884. [Google Scholar]
- Dos Santos Neto, P.J.; Dos Santos Barros, T.A.; De Paula, M.V.; De Souza, R.R.; Filho, E.R. Design of Computational Experiment for Performance Optimization of a Switched Reluctance Generator in Wind Systems. IEEE Trans. Energy Convers. 2018, 33, 406–419. [Google Scholar] [CrossRef]
- Dranca, M.A.; Zaharia, M.V.; Radulescu, M.M. Modelling and transient analysis of a three-phase low-speed switched reluctance micro-wind generator. In Proceedings of the 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; pp. 196–200. [Google Scholar]
- Faradjizadeh, F.; Tavakoli, M.R.; Salehnia, M.; Afjei, E. C-Dump converter for Switched Reluctance Generator. In Proceedings of the 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), Tehran, Iran, 5–6 February 2014; pp. 597–603. [Google Scholar]
- Meiqin, M.; Jianhui, S.; Chang, L.; Guorong, Z.; Yuzhu, Z. Controller for 1kW-5kW wind-solar hybrid generation systems. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008; pp. 001175–001178. [Google Scholar]
- Louie, H. Experiences in the construction of open source low technology off-grid wind turbines. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Wang, T.; He, D.; Wang, Q.; Huo, Y.; Lu, L.; Li, J. Power balance control for switched reluctance generator integrated in DC microgrid. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems (ICAMechS), Beijing, China, 22–24 August 2015; pp. 594–598. [Google Scholar]
- Gebraad, P.; Thomas, J.J.; Ning, A.; Fleming, P.; Dykes, K. Maximization of the annual energy production of wind power plants by optimization of layout and yaw-based wake control. Wind Energy 2017, 20, 97–107. [Google Scholar] [CrossRef]
- Maalawi, K.Y.; Badr, M.A. A practical approach for selecting optimum wind rotors. Renew. Energy 2003, 28, 803–822. [Google Scholar] [CrossRef]
- Yang, K. Geometry Design Optimization of a Wind Turbine Blade Considering Effects on Aerodynamic Performance by Linearization. Energies 2020, 13, 2320. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Afshar, P.A.N.; Ahmadizadeh, M.; Wood, D. Aero-structural design and optimization of a small wind turbine blade. Renew. Energy 2016, 87, 837–848. [Google Scholar] [CrossRef]
- Perkin, S.; Garrett, D.; Jensson, P. Optimal wind turbine selection methodology: A case-study for Búrfell. Iceland. Renew. Energy 2015, 75, 165–172. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H. Optimization of wind turbine energy and power factor with an evolutionary computation algorithm. Energy 2010, 35, 1324–1332. [Google Scholar] [CrossRef]
- Yahia, H.; Liouane, N.; Dhifaoui, R. Differential evolution method-based output power optimisation of switched reluctance generator for wind turbine applications. IET Renew. Power Gener. 2014, 8, 795–806. [Google Scholar] [CrossRef]
- Fan, Z.; Zhu, C. The optimization and the application for the wind turbine power-wind speed curve. Renew. Energy 2019, 140, 52–61. [Google Scholar] [CrossRef]
- Heidarian, M.; Ganji, B.A. Dynamic simulation model based on finite element method for switched reluctance generator. In In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Capri, Italy, 22–24 June 2016; pp. 1427–1432. [Google Scholar]
- Choi, D.; Byun, S.; Cho, Y.A. Study on the Maximum Power Control Method of Switched Reluctance Generator for Wind Turbine. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Ichinokura, O.; Kikuchi, T.; Nakamura, K.; Watanabe, T.; Guo, H.J. Dynamic simulation model of switched reluctance generator. IEEE Trans. Magn. 2003, 39, 3253–3255. [Google Scholar] [CrossRef]
- Yueying, Z.; Chuantian, Y.; Chengwen, Z. Multi-Objective Optimization of Switched Reluctance Generator for Electric Vehicles. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 1903–1907. [Google Scholar]
- Dos Santos, B.T.A.; Dos Santos, N.P.J.; Filho, P.S.N.; Moreira, A.B.; Filho, E.R. An Approach for Switched Reluctance Generator in a Wind Generation System with a Wide Range of Operation Speed. IEEE Trans. Power Electron. 2017, 32, 8277–8292. [Google Scholar]



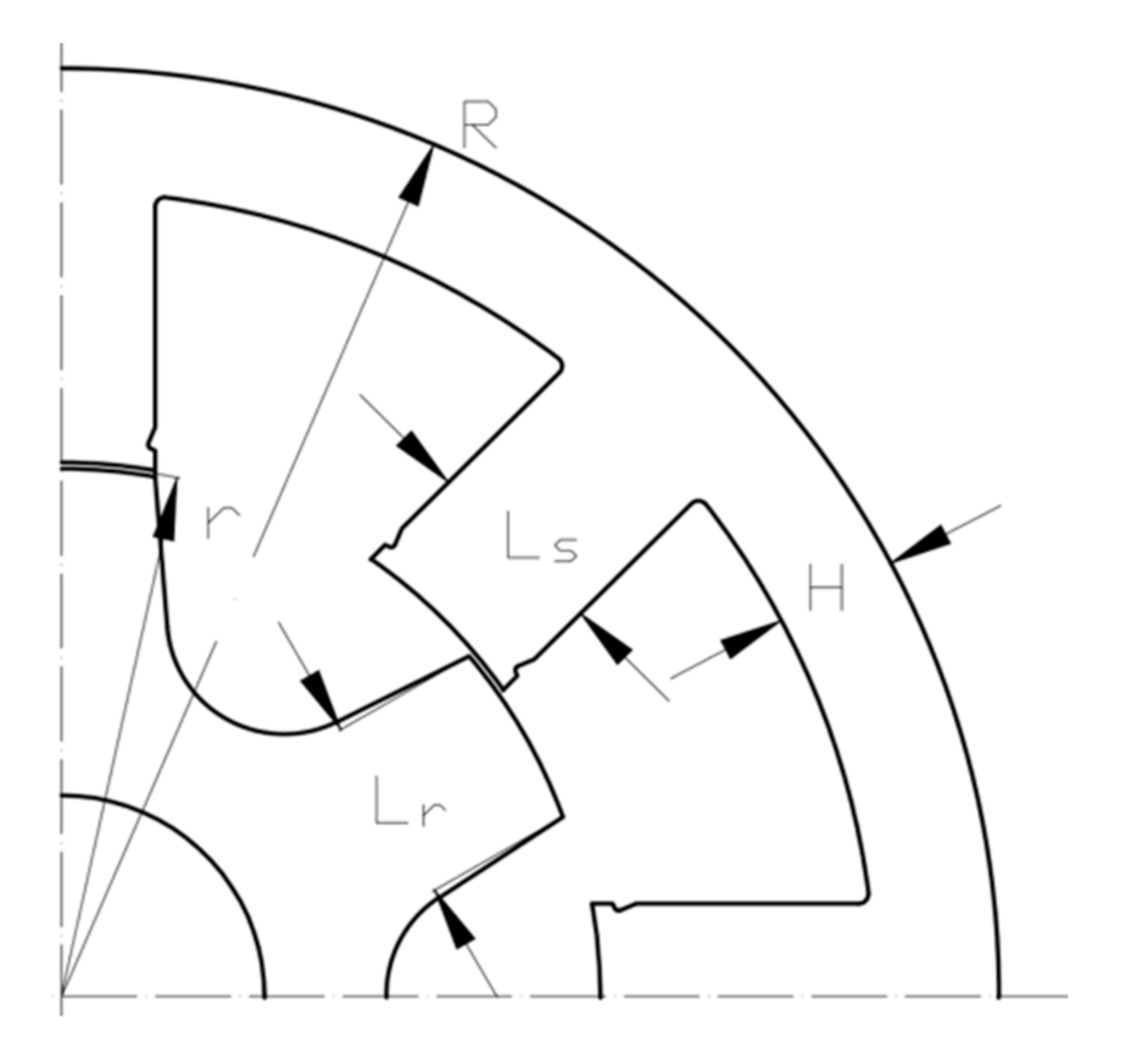

| Location | Rated Wind Speed (mps) | Turbine Radius (m) | Turbine Rated Rotational Speed (rps) | Cutoff Turbine Speed (rps) | Ratio of Mechanical Gears (n2/n1) |
|---|---|---|---|---|---|
| Ustka | 7 | 2.15 | 3.63 | 9.33 | 5.36 |
| Kolo | 6 | 2.70 | 2.48 | 4.54 | 11.01 |
| Nowy Sacz | 5 | 3.55 | 1.57 | 3.14 | 15.92 |
| Nowy Sacz | ||||||
|---|---|---|---|---|---|---|
| v (mps) | Tm (Nm) | Pm (W) | n (rps) | Pe (W) | Eexp (kWh) | Eexp_std (kWh) |
| 2 | 1.20 | 75 | 10 | 64 | 115 | 0 |
| 3 | 2.70 | 254 | 15 | 216 | 210 | 0 |
| 4 | 4.79 | 602 | 20 | 512 | 258 | 33 |
| 5 | 7.49 | 1176 | 25 | 999 | 244 | 31 |
| 6 | 6.25 | 1177 | 30 | 1000 | 112 | 25 |
| 7 | 5.35 | 1177 | 35 | 1000 | 37 | 13 |
| 8 | 4.68 | 1177 | 40 | 1000 | 16 | 8 |
| 9 | 4.16 | 1177 | 45 | 1000 | 7 | 5 |
| 10 | 3.75 | 1177 | 50 | 1000 | 2 | 2 |
| Expected annual energy production | 1001 | 117 | ||||
| Kolo | ||||||
|---|---|---|---|---|---|---|
| vw (mps) | Tm (Nm) | Pm (W) | n (rps) | Pe (W) | Eexp (kWh) | Eexp_std (kWh) |
| 3 | 1.72 | 147 | 13.6 | 125 | 271 | 0 |
| 4 | 3.05 | 348 | 18.2 | 296 | 429 | 94 |
| 5 | 4.76 | 680 | 22.7 | 578 | 498 | 109 |
| 6 | 6.86 | 1175 | 27.3 | 999 | 519 | 114 |
| 7 | 5.89 | 1177 | 31.8 | 1000 | 279 | 97 |
| 8 | 5.15 | 1177 | 36.4 | 1000 | 146 | 76 |
| 9 | 4.58 | 1177 | 40.9 | 1000 | 47 | 35 |
| 10 | 4.12 | 1177 | 45.5 | 1000 | 20 | 20 |
| 11 | 3.75 | 1177 | 50 | 1000 | 1 | 1 |
| Expected annual energy production | 2210 | 546 | ||||
| Ustka | ||||||
|---|---|---|---|---|---|---|
| vw (mps) | Tm (Nm) | Pm (W) | n (rps) | Pe (W) | Eext (kWh) | Eexp_std (kWh) |
| 4 | 3.16 | 221 | 11.1 | 188 | 317 | 109 |
| 5 | 4.94 | 431 | 13.9 | 367 | 480 | 165 |
| 6 | 7.12 | 745 | 16.7 | 633 | 546 | 188 |
| 7 | 9.64 | 1177 | 19.4 | 1000 | 593 | 206 |
| 8 | 8.43 | 1177 | 22.2 | 1000 | 336 | 174 |
| 9 | 7.49 | 1177 | 25.0 | 1000 | 279 | 206 |
| 10 | 6.75 | 1177 | 27.8 | 1000 | 158 | 158 |
| 11 | 6.13 | 1177 | 30.6 | 1000 | 149 | 149 |
| 12 | 5.62 | 1177 | 33.3 | 1000 | 88 | 88 |
| 13 | 5.19 | 1177 | 36.1 | 1000 | 61 | 61 |
| 14 | 4.82 | 1177 | 38.9 | 1000 | 26 | 26 |
| 15 | 4.50 | 1177 | 41.7 | 1000 | 18 | 18 |
| 16 | 4.22 | 1177 | 44.4 | 1000 | 14 | 14 |
| 17 | 3.97 | 1177 | 47.2 | 1000 | 8 | 8 |
| 18 | 3.75 | 1177 | 50.0 | 1000 | 2 | 2 |
| Expected annual energy production | 3033 | 1572 | ||||
| Control | Measured | Simulated | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| αon (deg) | αoff (deg) | n (rpm) | Tm (Nm) | Is av (A) | Iph av (A) | Iph max (A) | Tm (Nm) | Is av (A) | Iph av (A) | Iph max (A) |
| −26 | −6 | 33.79 | 1.02 | 12.20 | 7.28 | 18.38 | 1.04 | 11.40 | 7.14 | 18.6 |
| −26 | −6 | 24.02 | 2.04 | 17.05 | 9.89 | 25.32 | 1.98 | 15.91 | 9.65 | 25.7 |
| −26 | −6 | 19.61 | 3.03 | 20.95 | 11.84 | 30.51 | 2.95 | 19.94 | 11.60 | 31.0 |
| −26 | −6 | 16.90 | 4.06 | 24.62 | 13.53 | 35.01 | 4.01 | 24.10 | 13.38 | 35.6 |
| −26 | −6 | 14.87 | 5.07 | 27.69 | 15.30 | 39.72 | 5.28 | 28.68 | 15.19 | 40.0 |
| −26 | −6 | 13.39 | 6.03 | 30.28 | 17.29 | 46.26 | 6.69 | 33.46 | 16.98 | 44.2 |
| −27 | −7 | 36.15 | 1.01 | 12.74 | 7.15 | 19.32 | 1.08 | 12.55 | 7.17 | 20.6 |
| −27 | −7 | 25.30 | 2.08 | 18.02 | 9.87 | 26.93 | 2.12 | 17.77 | 9.85 | 28.7 |
| −27 | −7 | 20.94 | 2.99 | 21.74 | 11.67 | 32.09 | 3.05 | 21.74 | 11.69 | 34.2 |
| −27 | −7 | 17.90 | 4.05 | 25.70 | 13.43 | 36.94 | 4.19 | 26.29 | 13.58 | 39.5 |
| −27 | −7 | 15.72 | 5.09 | 29.06 | 15.21 | 41.80 | 5.54 | 31.25 | 15.49 | 44.5 |
| −27 | −7 | 14.12 | 6.01 | 31.51 | 17.19 | 46.86 | 6.58 | 34.29 | 16.75 | 46.4 |
| −30 | −5 | 31.52 | 2.045 | 22.71 | 12.48 | 30.01 | 2.17 | 23.15 | 12.86 | 34.1 |
| −30 | −5 | 25.95 | 2.985 | 27.63 | 14.83 | 35.81 | 3.13 | 28.49 | 15.25 | 40.7 |
| −30 | −5 | 22.11 | 4.055 | 32.66 | 17.04 | 41.27 | 4.23 | 33.83 | 17.45 | 46.1 |
| −30 | −5 | 18.62 | 5.035 | 35.18 | 18.46 | 45.33 | 5.06 | 35.37 | 18.82 | 46.5 |
| −30 | −5 | 14.72 | 6.04 | 35.01 | 19.31 | 50.07 | 6.59 | 38.29 | 20.97 | 46.8 |
| Mean squared error for the presented series of calculations | δTm | δIs av | δIph av | δIph m | ||||||
| 3.6% | 4.5% | 1.3% | 6.1% | |||||||
| Dimensions of the Generators | Symbol | Unit | Nowy Sacz | Kolo | Ustka |
|---|---|---|---|---|---|
| stator outside radius | R | mm | 63.4 | 65.4 | 69.7 |
| stator yoke thickness | H | mm | 7 | 7 | 7 |
| stator tooth width | Ls | mm | 6.7 | 6.3 | 7.3 |
| rotor tooth width | Lr | mm | 9.8 | 9.3 | 9.8 |
| radius of air gap | R | mm | 32.1 | 30.7 | 31.5 |
| thickness of air gap | D | mm | 0.4 | 0.4 | 0.4 |
| stator tooth height | Hs | mm | 24.1 | 27.5 | 31 |
| rotor tooth height | Hr | mm | 20 | 20 | 20 |
| Location of the Power Plant | Eexp (MWh) | Esim (MWh) | Esim/Eexp (%) |
|---|---|---|---|
| Nowy Sacz | 1.00 | 0.91 | 91.0 |
| Kolo | 2.21 | 2.10 | 95.0 |
| Ustka | 3.07 | 2.86 | 93.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wrobel, K.; Tomczewski, K.; Sliwinski, A.; Tomczewski, A. Optimization of a Small Wind Power Plant for Annual Wind Speed Distribution. Energies 2021, 14, 1587. https://doi.org/10.3390/en14061587
Wrobel K, Tomczewski K, Sliwinski A, Tomczewski A. Optimization of a Small Wind Power Plant for Annual Wind Speed Distribution. Energies. 2021; 14(6):1587. https://doi.org/10.3390/en14061587
Chicago/Turabian StyleWrobel, Krzysztof, Krzysztof Tomczewski, Artur Sliwinski, and Andrzej Tomczewski. 2021. "Optimization of a Small Wind Power Plant for Annual Wind Speed Distribution" Energies 14, no. 6: 1587. https://doi.org/10.3390/en14061587
APA StyleWrobel, K., Tomczewski, K., Sliwinski, A., & Tomczewski, A. (2021). Optimization of a Small Wind Power Plant for Annual Wind Speed Distribution. Energies, 14(6), 1587. https://doi.org/10.3390/en14061587






