Numerical Study of Fluid Flow and Heat Transfer Characteristics in a Cone-Column Combined Heat Sink
Abstract
:1. Introduction
2. Heat Sink Structure
3. Numerical Models and Boundary Conditions
3.1. Governing Equation
3.2. Boundary Conditions
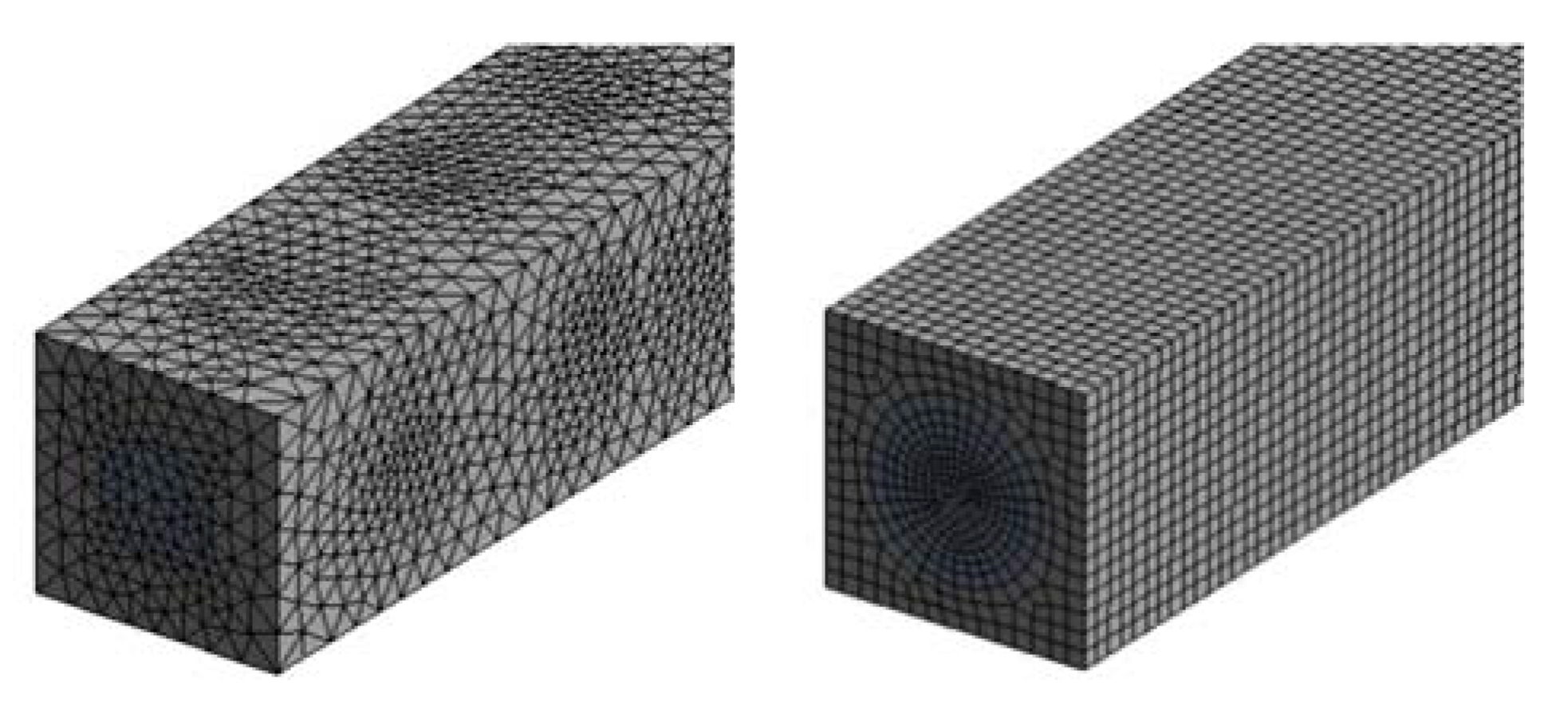
3.3. Meshing and Model Verification
4. Data Processing
5. Results
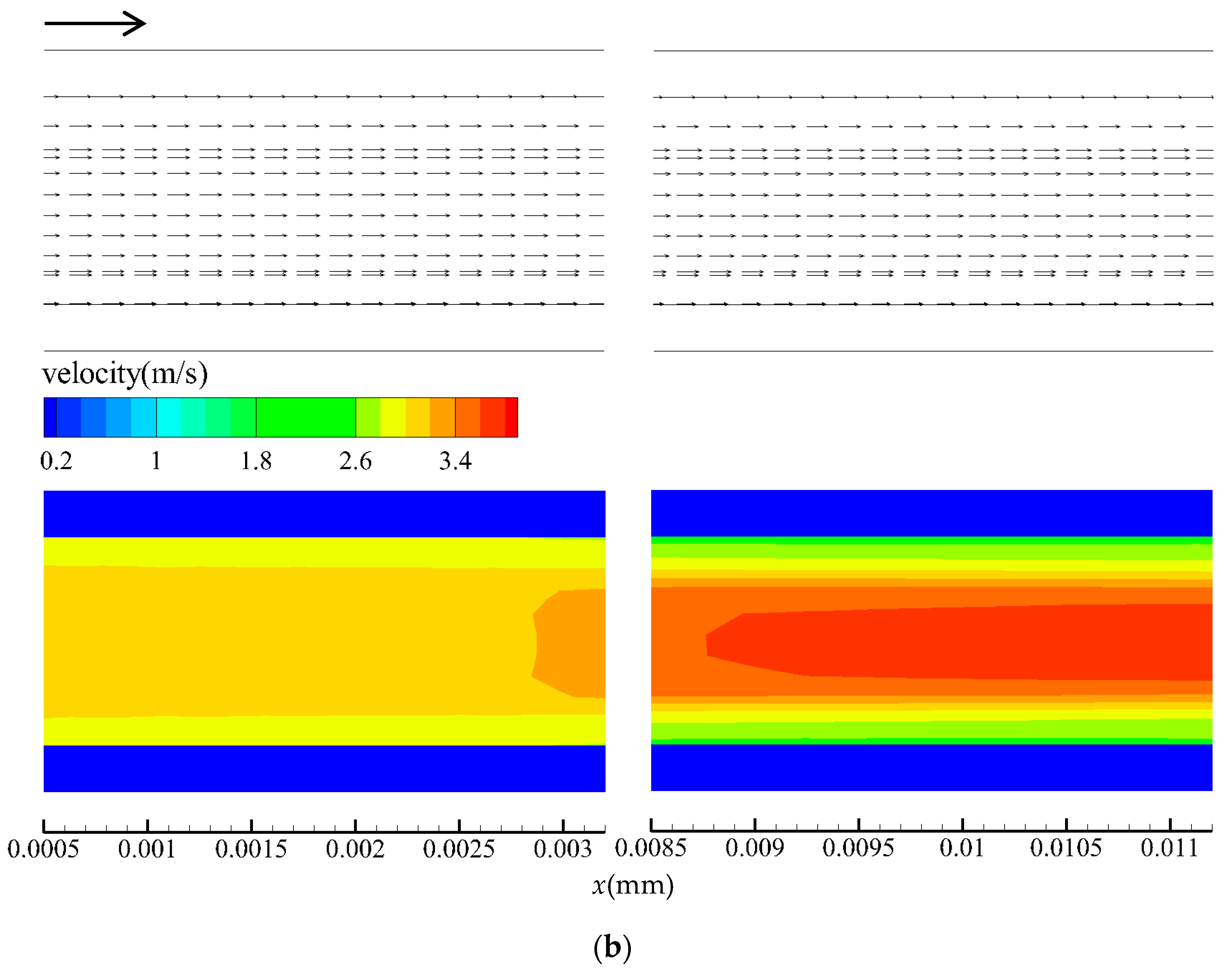
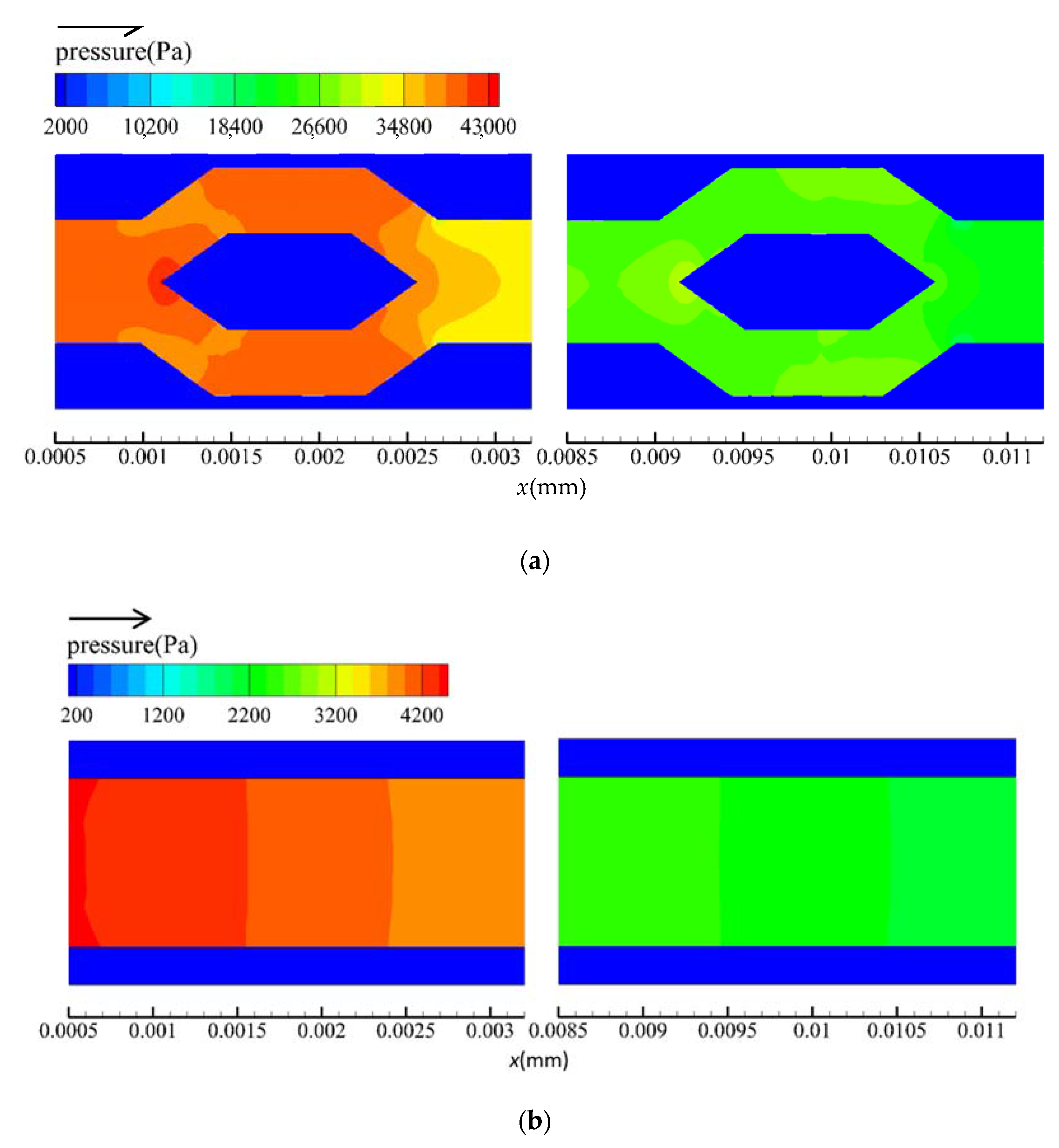
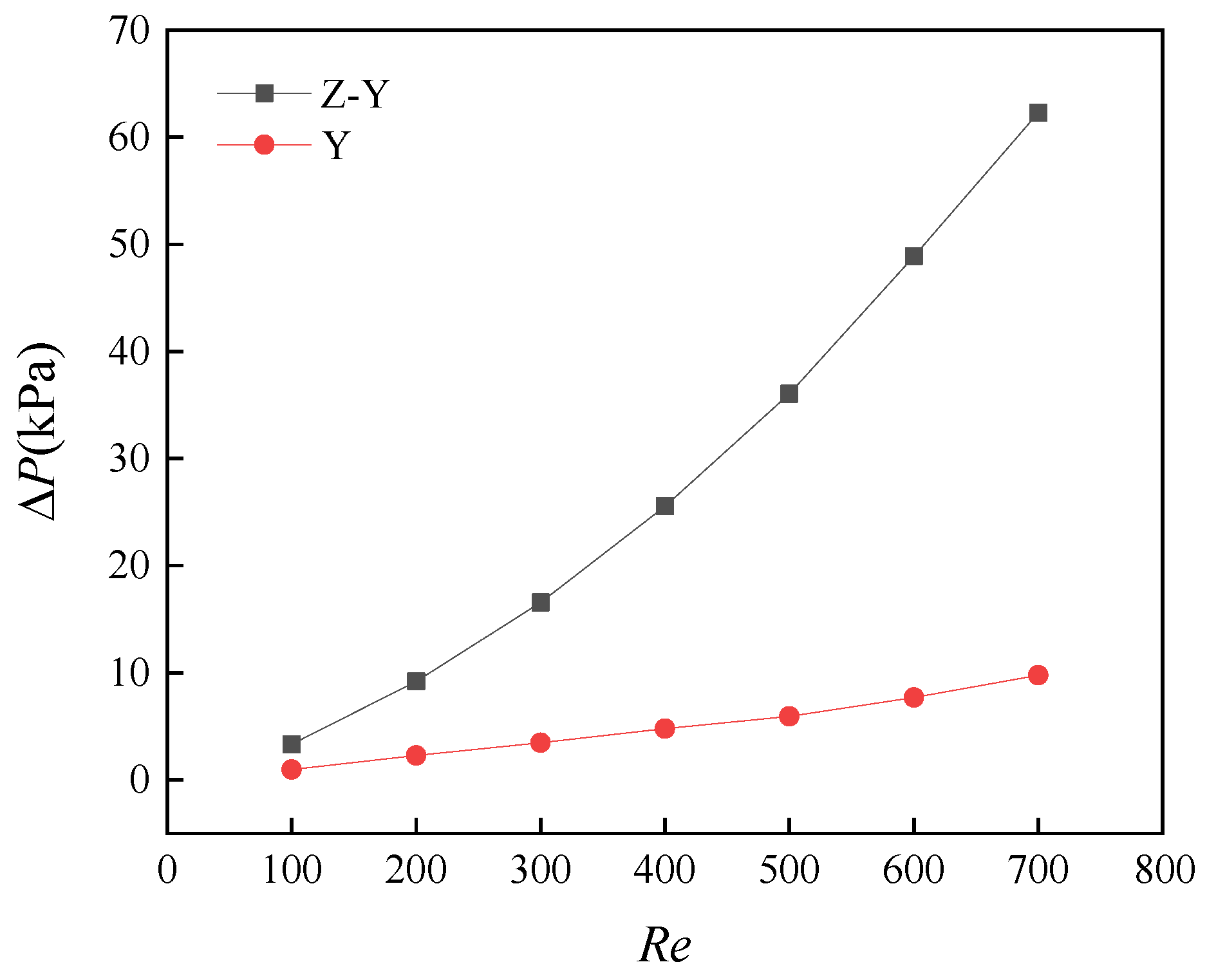
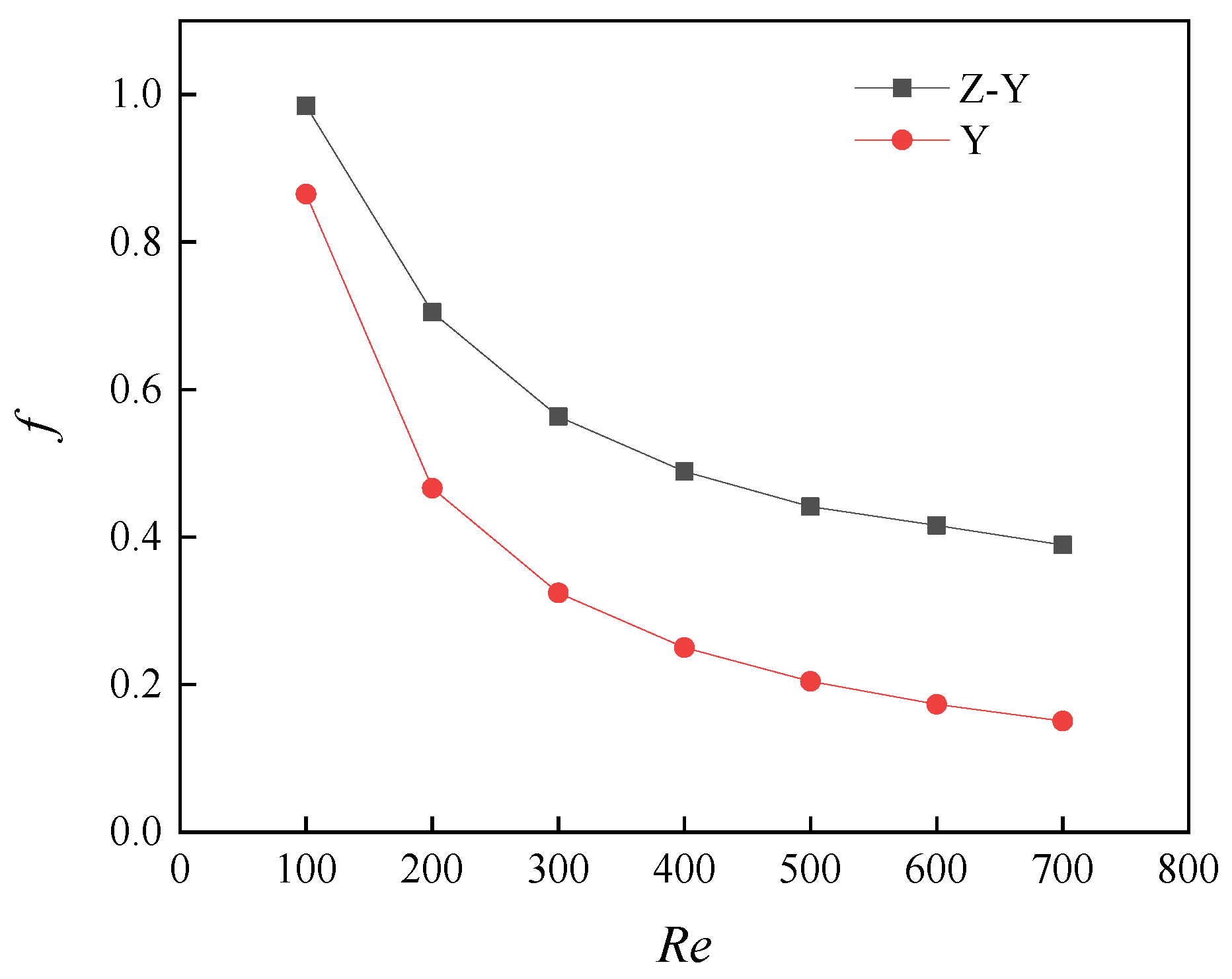
5.1. Flow Characteristics
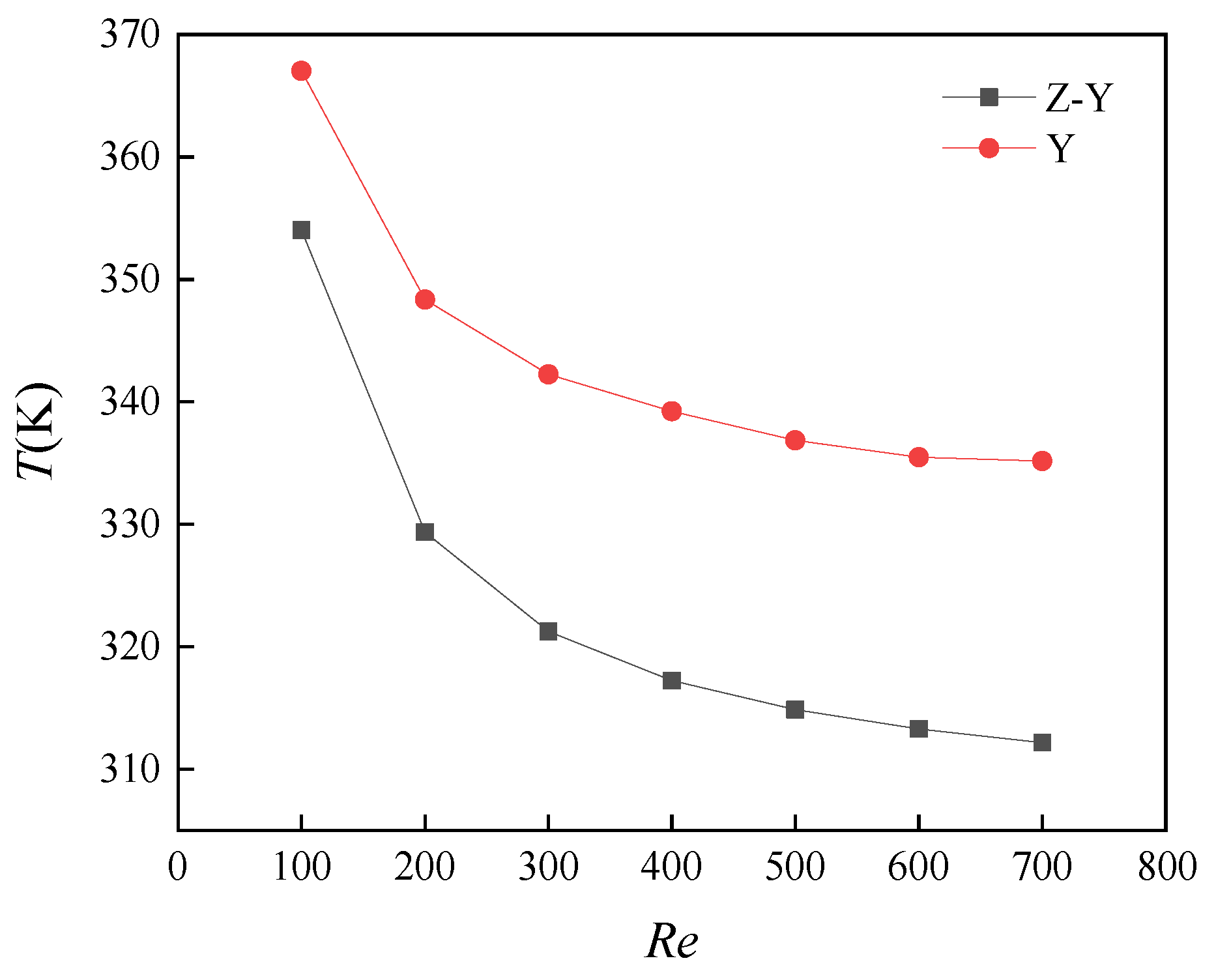
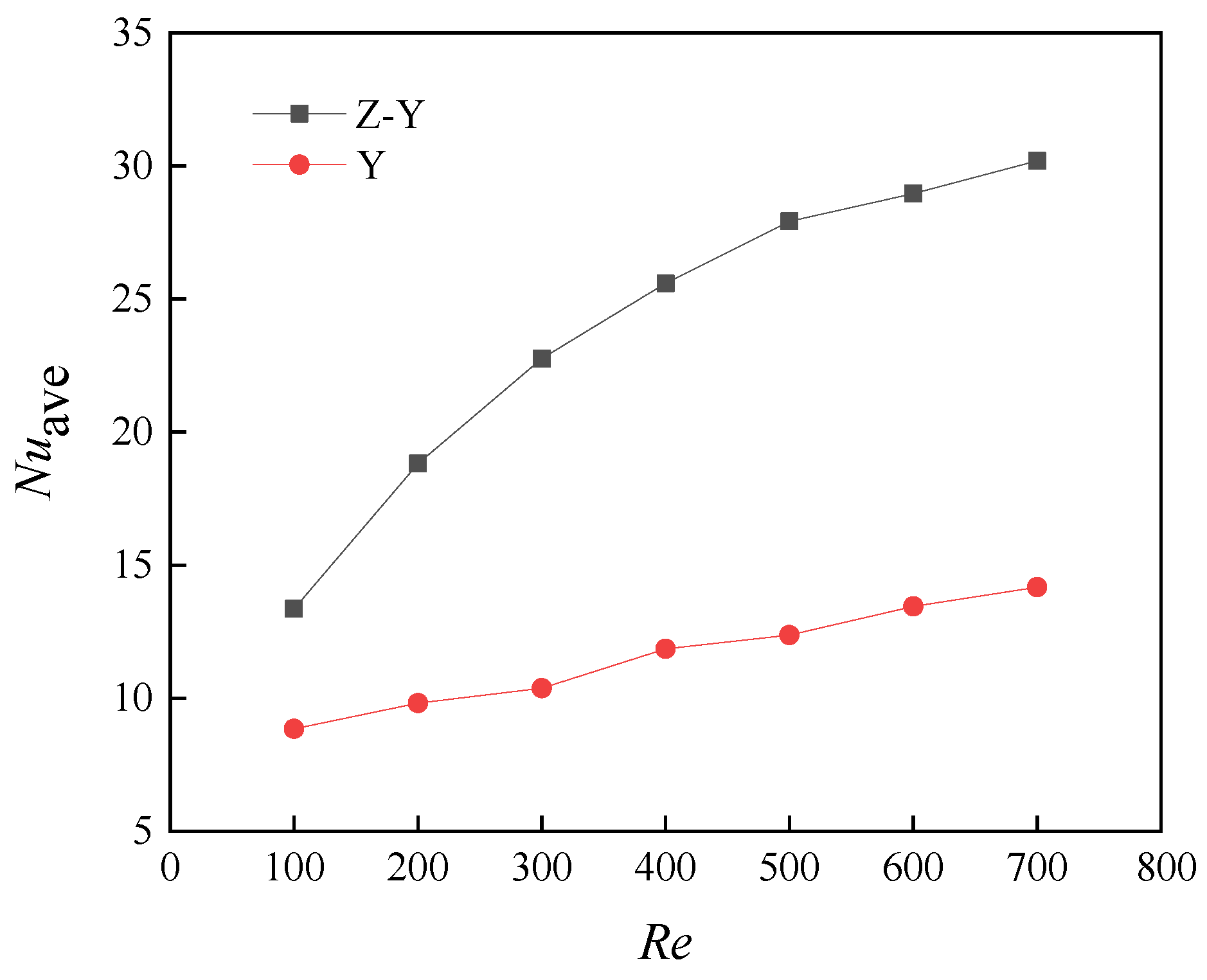
5.2. Heat Transfer Characteristics
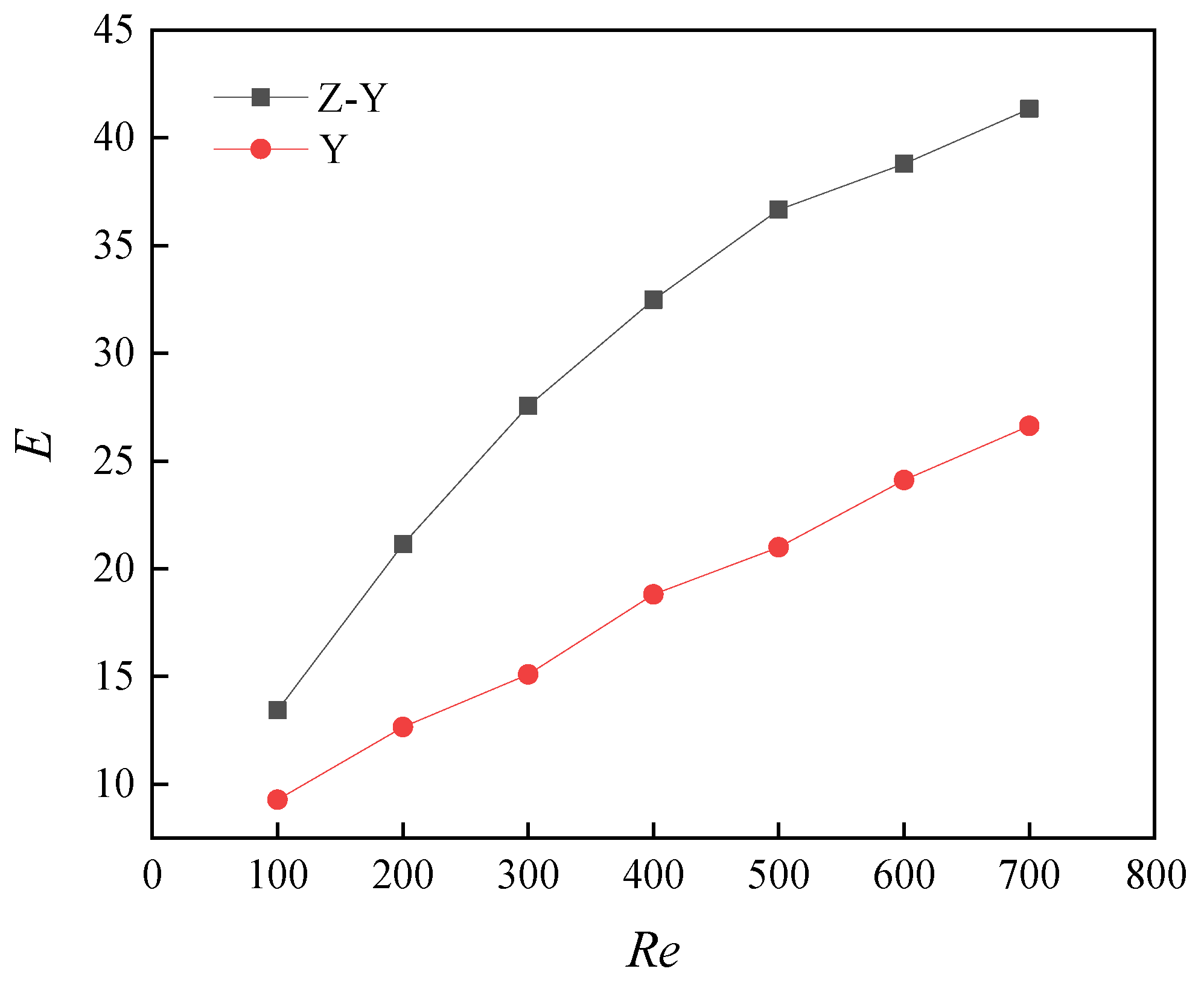
5.3. Comprehensive Performance Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-sectional area of a single channel, m2 |
| Ac | heat exchange contact area between fluid and solid, m2 |
| Cp | specific heat capacity of the cooling medium, J/(kg·K) |
| Dh | hydraulic diameter of microchannel, mm |
| E | enhanced heat transfer factor |
| f | apparent friction factor |
| H | microchannel height, mm |
| hf | energy loss along the path in the microchannel system |
| have | average convective heat transfer coefficient, W/(m2·K) |
| ks | thermal conductivity of the solid interface, W/(m·K) |
| kf | thermal conductivity of the liquid interface, W/(m·K) |
| L | length of microchannel, mm |
| La | cone-column length, mm |
| N | number of channels |
| Nuave | average Nusselt number |
| Pin | fluid inlet pressure, Pa |
| Pout | fluid outlet pressure, Pa |
| ΔP | pressure drop at the inlet and outlet of the channel, Pa |
| ΔPin | inlet pressure loss, Pa |
| ΔPout | outlet pressure loss, Pa |
| q | heat flux density, 106 W·m−2 |
| qm | mass flow rate of fluid, kg/s |
| Q | heat exchange, J |
| Qv | volume flow, m3/s |
| Re | Reynolds number |
| ΔT | the temperature difference between the fluid and the wall of the microchannel, K |
| Tin | fluid inlet temperature, 293 K |
| Tout | outlet fluid temperature, K |
| Ts | solid interface temperature, K |
| Tf | fluid interface temperature, K |
| Tw | heating surface temperature, K |
| u | velocity components in X direction, m/s |
| uin | liquid inlet flow rate, m/s |
| um | the average flow velocity of the liquid, m/s |
| v | velocity components in Y direction, m/s |
| w | velocity components in Z direction, m/s |
| W | microchannel cross-sectional area width, mm |
| Wa | cone-column combined heat sink inlet diameter, mm |
| Wb | cone-column width, mm |
| Wc | shunt channel width, mm |
| Wd | shunt outer diameter, mm |
| We | circular microchannel heat sink inlet diameter, mm |
| θ | cone angle, ° |
| ρ | density of the cooling medium, kg/m3 |
| η | dynamic viscosity of the cooling medium, Pa·s |
| λ | thermal conductivity, W/(m·K) |
| λl | coefficient of friction of the inner wall of the channel |
| sum of local drag coefficients |
References
- Chai, L.; Xia, G.D.; Wang, H.S. Numerical study of laminar flow and heat transfer in microchannel heat sink with offset ribs on sidewalls. Appl. Therm. Eng. 2016, 92, 32–41. [Google Scholar] [CrossRef]
- Hung, T.-C.; Yan, W.-M.; Wang, X.-D.; Huang, Y.-X. Optimal design of geometric parameters of double-layered microchannel heat sinks. Int. J. Heat Mass Transf. 2012, 55, 3262–3272. [Google Scholar] [CrossRef]
- Davarpanah, A.; Zarei, M.; Valizadeh, K.; Mirshekari, B. CFD design and simulation of ethylene dichloride (EDC) thermal cracking reactor. Energy Sources Part A Recover. Util. Environ. Eff. 2018, 41, 1573–1587. [Google Scholar] [CrossRef]
- Xie, G.; Li, Y.; Zhang, F.; Sundén, B. Analysis of micro-channel heat sinks with rectangular-shape-d flow obstructions. Numer. Heat Transf. Part A Appl. 2016, 69, 335–351. [Google Scholar] [CrossRef]
- Ambreen, T.; Kim, M.-H. Effect of fin shape on the thermal performance of nanofluid-cooled micro pin-fin heat sinks. Int. J. Heat Mass Transf. 2018, 126, 245–256. [Google Scholar] [CrossRef]
- Kuppusamy, N.R.; Saidur, R.; Ghazali, N.; Mohammed, H. Numerical study of thermal enhancement in micro channel heat sink with secondary flow. Int. J. Heat Mass Transf. 2014, 78, 216–223. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Zhou, M.; Li, J. Numerical simulation of fluid flow and heat transfer in a microchannel heat sink with offset fan-shaped re-entrant cavities in sidewall. Int. Commun. Heat Mass 2011, 38, 577–584. [Google Scholar] [CrossRef]
- Zhao, J. Flow and Heat Transfer Characteristics and Thermal Stress Analysis of Micro-Channel Heat Sink. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2015. [Google Scholar]
- Drofenik, U.; Stupar, A.; Kolar, J.W. Analysis of theoretical limits of forced-air cooling usin-g advanced composite materials with high thermal conductivities. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 528–535. [Google Scholar] [CrossRef]
- Tuckerman, D.; Pease, R. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Wei, Z.; Jianjun, S.; Tao, N.; Chenbo, M.; Qiuping, Y.; Yuyan, Z.; Zheng, W.; Sun, J.; Niu, T.; Ma, C.; et al. Structural optimization and heat transfer performance analysis of a cone-column combined heat sink. J. Heat Transf. 2020, 142, 044504. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Yang, J.; Liu, H. Thermal and hydraulic characteristics of microchannel heat sinks with cavities and fins based on field synergy and thermodynamic analysis. Appl. Therm. Eng. 2020, 175, 115348. [Google Scholar] [CrossRef]
- Xia, G.; Wang, Z.; Ma, D. The characteristics of fluid flow and heat transfer in a double-layer channel of a double-layer heat source. J. B Univ. Technol. 2018, 44, 455–462. [Google Scholar]
- Wang, Z.; Xia, G.; Ma, D.; Yang, Z. Study on fluid flow and heat transfer characteristics in single-layer and double-layer mi-crochannels. J. Eng. Thermophys 2019, 40, 1126–1130. [Google Scholar]
- Bhandari, P.; Prajapati, Y.K. Thermal performance of open microchannel heat sink with variable pin fin height. Int. J. Therm. Sci. 2021, 159, 106609. [Google Scholar] [CrossRef]
- Zhang, J.-F.; Jia, L.; Yang, W.-W.; Taler, J.; Oclon, P. Numerical analysis and parametric optimization on flow and heat transfer of a microchannel with longitudinal vortex generators. Int. J. Therm. Sci. 2019, 141, 211–221. [Google Scholar] [CrossRef]
- Zarei, M.; Davarpanah, A.; Mokhtarian, N.; Farahbod, F. Integrated feasibility experimental investigation of hydrodynamic, geometrical and, operational characterization of methanol conversion to formaldehyde. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 42, 89–103. [Google Scholar] [CrossRef]
- Valizadeh, K.; Farahbakhsh, S.; Bateni, A.; Zargarian, A.; Davarpanah, A.; Alizadeh, A.; Zarei, M. A parametric study to simulate the non-Newtonian turbulent flow in spiral tubes. Energy Sci. Eng. 2019, 8, 134–149. [Google Scholar] [CrossRef] [Green Version]
- Benedetto, A.D.; Sarli, V.D.; Russo, G. Effect of geometry on the thermal behavior of catalytic micro-combustors. Catal. Today 2010, 155, 116–122. [Google Scholar] [CrossRef]
- Sarli, V.D.; Trofa, M.; Benedetto, A.D. A novel catalytic micro-combustor inspired by the nasal geometry of reindeer: CFD modeling and simulation. Catalysts 2020, 10, 606. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Ahmadi, A.; Rosen, M.A.; Davarpanah, A. Thermodynamic optimization of a geothermal power plant with a genetic algorithm in two stages. Processes 2020, 8, 1277. [Google Scholar] [CrossRef]
- Li, J.; Peng, H.; Ling, X. Numerical study and experimental verification of transverse direction type serrated fins and field synergy principle analysis. Appl. Therm. Eng. 2013, 54, 328–335. [Google Scholar] [CrossRef]
- Morini, G.L. Single-phase convective heat transfer in microchannels: A review of experimental results. Int. J. Therm. Sci. 2004, 43, 631–651. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Viscous dissipation effects in microtubes and microchannels. Int. J. Heat Mass Transf. 2004, 47, 3159–3169. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Wang, L.; Zhou, M.; Cui, Z. Heat transfer enhancement in microchannel heat sinks with periodic expansion–constriction cross-sections. Int. J. Heat Mass Transf. 2013, 62, 741–751. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Ahmed, M.I. Optimum thermal design of triangular, trapezoidal and rectangular grooved microchannel heat sinks. Int. Commun. Heat Mass Transf. 2015, 66, 47–57. [Google Scholar] [CrossRef]
- Li, P.; Zhang, D.; Xie, Y.; Xie, G. Flow structure and heat transfer of non-Newtonian fluids in microchannel heat sinks with dimples and protrusions. Appl. Therm. Eng. 2016, 94, 50–58. [Google Scholar] [CrossRef]
- Service, R.F. Labs on a chip: Coming Soon: The pocket DNA sequencer. Science 1998, 282, 399–401. [Google Scholar] [CrossRef]
- Mital, M. Semi-analytical investigation of electronics cooling using developing nanofluid flow in rectangular microchannels. Appl. Therm. Eng. 2013, 52, 321–327. [Google Scholar] [CrossRef]
- Moghari, R.M.; Akbarinia, A.; Shariat, M.H.; Talebi, F.; Laur, R. Two phase mixed convection Al2O3–water nanofluid flow in an annulus. Int. J. Multiph. Flow 2011, 37, 585–595. [Google Scholar] [CrossRef]
- Xia, G.; Chai, L.; Qi, J. Research on fluid flow and heat transfer characteristics of trapezoidal silicon-based microchannel heat sink. J. B Univ. Technol. 2011, 37, 1079–1084. [Google Scholar]
- Hung, T.C.; Huang, Y.X.; Yan, W.M. Thermal performance analysis of porous-microchannel heat sinks with different con-figuration designs. Int. J. Heat. Mass Transf. 2013, 66, 235–243. [Google Scholar] [CrossRef]
- Wang, R.-J.; Wang, J.-W.; Lijin, B.-Q.; Zhu, Z.-F. Parameterization investigation on the microchannel heat sink with slant rectangular ribs by numerical simulation. Appl. Therm. Eng. 2018, 133, 428–438. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Xia, G.; Liu, X.; Wang, J. Characteristics of entropy generation and heat transfer in double-layered micro heat sinks with complex structure. Energy Convers. Manag. 2015, 103, 477–486. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhong, G.; Li, Z. The influence of structure on the heat transfer performance of double-layer microchannel heat sink. J. Aeronaut. Dyn. 2018, 33, 565–571. [Google Scholar]
- Zhai, Y.; Xia, G.; Liu, X.; Li, Y. Heat transfer in the microchannels with fan-shaped reentrant cavities and different ribs based on field synergy principle and entropy generation analysis. Int. J. Heat Mass Transf. 2014, 68, 224–233. [Google Scholar] [CrossRef]
- Li, Y.; Xia, G.; Ma, D.; Wang, J. Field synergy and entropy generation of convective heat transfer in complex microchannels. J. Aeronaut. Dyn. 2019, 34, 1471–1482. [Google Scholar]
- Li, J.; Zhu, Z.; Zhao, L.; Peng, H. Experimental investigation of the heat transfer and flow characteristics of microchannels with microribs. Int. J. Heat Mass Transf. 2019, 143, 118482. [Google Scholar] [CrossRef]
- Webb, R. Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design. Int. J. Heat Mass Transf. 1981, 24, 715–726. [Google Scholar] [CrossRef]
- Zhai, Y.; Xia, G.; Cui, Z. Numerical simulation of the flow and heat transfer of the spaced fan-shaped cavity microchannels. J. B Univ. Technol. 2014, 40, 627–633. [Google Scholar]
- Ghani, I.A.; Sidik, N.A.C.; Mamat, R.; Najafi, G.; Ken, T.L.; Asako, Y.; Japar, W.M.A. Heat transfer enhancement in microchannel heat sink using hybrid technique of ribs and secondary channels. Int. J. Heat. Mass Transf. 2017, 114, 640–655. [Google Scholar] [CrossRef]
- Fadzin, K.A.; Lee, A. Heat transfer enhancement in microchannel using nanofluids. Appl. Mech. Mater. 2013, 465–466, 536–540. [Google Scholar] [CrossRef]

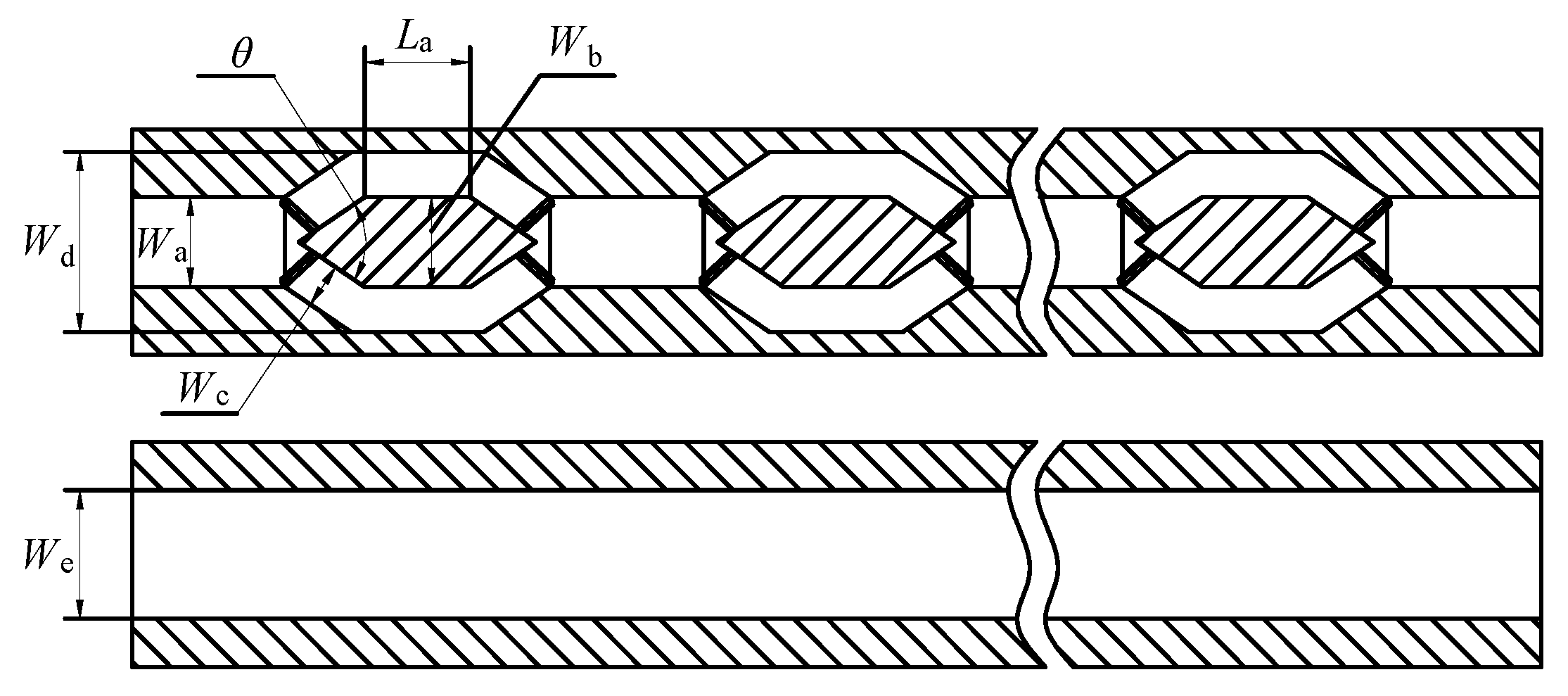

| Microchannel | Wa/mm | Wb/mm | Wc/mm | Wd/mm | We/mm | La/mm | θ/° |
|---|---|---|---|---|---|---|---|
| Z-Y | 0.7 | 0.55 | 0.35 | 1.3 | / | 0.7 | 72 |
| Y | / | / | / | / | 1.3 | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Sun, J.; Ma, C.; Yu, Q.; Zhang, Y.; Niu, T. Numerical Study of Fluid Flow and Heat Transfer Characteristics in a Cone-Column Combined Heat Sink. Energies 2021, 14, 1605. https://doi.org/10.3390/en14061605
Zheng W, Sun J, Ma C, Yu Q, Zhang Y, Niu T. Numerical Study of Fluid Flow and Heat Transfer Characteristics in a Cone-Column Combined Heat Sink. Energies. 2021; 14(6):1605. https://doi.org/10.3390/en14061605
Chicago/Turabian StyleZheng, Wei, Jianjun Sun, Chenbo Ma, Qiuping Yu, Yuyan Zhang, and Tao Niu. 2021. "Numerical Study of Fluid Flow and Heat Transfer Characteristics in a Cone-Column Combined Heat Sink" Energies 14, no. 6: 1605. https://doi.org/10.3390/en14061605
APA StyleZheng, W., Sun, J., Ma, C., Yu, Q., Zhang, Y., & Niu, T. (2021). Numerical Study of Fluid Flow and Heat Transfer Characteristics in a Cone-Column Combined Heat Sink. Energies, 14(6), 1605. https://doi.org/10.3390/en14061605






