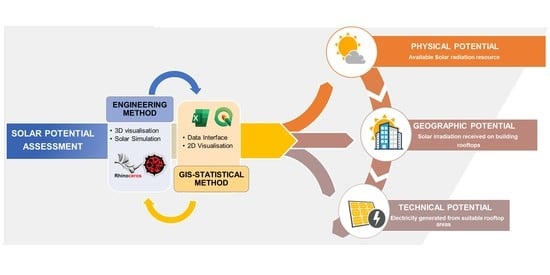
Combined Engineering—Statistical Method for Assessing Solar Photovoltaic Potential on Residential Rooftops: Case of Laghouat in Central Southern Algeria

Abstract

Solar energy planning becomes crucial to develop adaptive policies ensuring both energy efficiency and climate change mitigation. Cities, particularly building’s rooftops, constitute a promising infrastructure for enabling the use of locale solar resources. This study proposes a combined engineering–statistical methodology to assess the photovoltaic potential of residential rooftops. Using validated algorithms for solar simulation and geographical information system (GIS) for spatial dissemination, the proposed methodology deals with the lack of data and allows an accurate investigation of the geographical and technical potential. Applied to the municipality of Laghouat, the results reveal that suitable rooftops areas for PV installations in the examined typologies were approximately between 18 and 35%. Moreover, the deployment of distributed PV systems on residential rooftops provides significant technical potential, which could cover up to 55% of the annual electricity needs. These original findings offer a realistic assessment of the usable solar potential within municipalities, which helps decision-makers establish energy efficiency strategies by reducing energy consumption and increasing the share of renewable electricity production. Additionally, the discussion offers valuable insight into energy management and investigates eventual energy sharing among residential buildings to achieve a net-zero energy balance at the municipal level.

1. Introduction

Nowadays, photovoltaic (PV) distributed systems are increasingly catching the attention of professionals and policymakers, particularly after the significant drop in PV technology prices. According to the International Energy Agency’s (IEA) forecast, distributed PV applications accounted for almost half of the total PV growth worldwide in 2018 and it is expected to double by 2024, reaching thereby 530 gigawatts (GW) [1].

Solar installations on residential, commercial and industrial roofs are being privileged worldwide as an operative way to reduce the increasing electricity consumption. Therefore, their integration creates new challenges for electricity producers, energy system professionals and urban policymakers [2]. International experiences have shown that the integration of PV technologies in cities is mostly confronted by planning barriers and, more specifically, the lack of awareness of stockholders regarding local renewable energy resources [3]. Otherwise, the successful deployment of PV distributed systems requires a higher engagement through assessment tools that help to enhance the knowledge of their planning and applications in urban areas [4]. Indeed, the identification of solar potential in urban areas has a crucial role in promoting adaptive policies, financing programs and progressively moving cities toward a low-carbon energy transition [5].

The Energy transition is considered a national priority for public authorities in Algeria. Over the last decade, the government launched an ambitious program of energy efficiency and renewable energy development. The program aspires to reach twenty-seven per cent (27%) of the renewable energy share in electricity production to save almost 200 million tons of carbon dioxide (CO₂) emissions by 2030. Yet, nine years after the program launch, a meagre progress rate of 2% was reached. Indeed, the strategy adopted by the government privileges the photovoltaic utility-scale as an economic alternative in the long term [6]. However, their actual implantation has been hindered by several funding barriers. Simultaneously, electricity use in the residential sector in the country has doubled between 2009 and 2017, reaching up to 43% of the global electricity consumption [7]. For this purpose, PV distributed systems on residential roofs constitute an attractive option to overcome such growing needs.

In the literature, the estimation and improvement of solar potential have been applied to multiple study scales varying from the continental scale [8,9], city-scale [10,11,12] to the urban block scale [13,14,15,16,17,18]. A review of the various methodological approaches indicates that both scale and available data are of key importance [19,20,21]. Thus, depending on the end goal, multiple technologies and tools have been employed, from solar constant-methods with simple 2D visualization maps to the most sophisticated 3D modelling and web-based solar [22].

At a micro level, the neighbourhood scale was frequently used for solar assessment. On the one hand, some scholars examined solar exposure and daylighting to highlight the passive gains and the building’s performances [23,24,25,26]. On the other hand, other researchers focused on solar active gains by studying the impact of urban form parameters on solar irradiation availability and, consequently, the energy generated through PV or Solar thermal (ST) [27,28,29]. More recently, the net-zero energy (NZE) concept has highly influenced academic dialogue on solar assessment at the urban scale. Many researchers appraise the photovoltaic solar electricity potential compared to the consumption patterns, which brings a balance in supply and demand to achieve nearly net-zero energy (NZE) [30,31,32].

At the macroscale level, predicting solar radiation in cities becomes more prominent; Izquierdo et al. [19] have considerably shaped research in urban renewable resources assessment by introducing a three-level hierarchical approach: (i) the physical potential, which refers to the amount of solar radiation received; (ii) the geographic potential, which encompasses solar energy reaching the spatial areas of the building; and (iii) the technical potential, which concerns the amount of electricity that is generated depending on PV system characteristics.

The major complexity of solar assessment at this scale refers to the roof areas determination. In this regard, three major methodological approaches are depicted. These are the manual selection methods, geographic information systems (GIS) and statistical methods [10,33]. First, manual methods are highly accurate, yet they are time-consuming since they require the collection of a significant amount of data [34]. In contrast, GIS-based methodology alongside with remote sensing technology, such as Lidar and photogrammetry, have together propelled further research because they offer automatic rooftops computing [17,35,36,37,38]. However, this methodology requires high-cost equipment, which is often not available to local public authorities. Finally, the statistical method suggests ratios based on data issued from national standards, normative values or literature bases [39,40,41]. Indeed, by examining a targeted sample area, advanced data-mining techniques and statistics enable a comprehensive analysis of building characteristics [42,43,44]. These methodologies do not analyse multiple building features simultaneously; rather, they delimitate buildings to extract the needed quality indices.

The primary focus of this paper is to determine the physical, geographical and technical solar potential in urban areas. Due to the lack of data, this study builds on an alternative method that quantifies the residential rooftop area and its suitability for PV applications, based on their typology, using free and available public data. Moreover, this study contributes to existing knowledge by providing a reliable utilization factor for PV installations on residential roofs, which can be replicated in further research in the region. The outcomes will help to inform decision-makers of planning improvements for energy saving or achieving energy balance.

The rest of the paper is structured as follows: Section 2 provides an overview of the methodology and the tools used. It draws a detailed description of each method of assessment of PV potential. Section 3 presents the case of the study and summarizes the required data set. In Section 4, results are presented and discussed progressively, starting from geographic to the technical potential. Finally, Section 5 concludes and presents some perspectives and recommendations for future policy and planning development.

2. Materials and Methods

As mentioned above, the solar potential assessment requires high resources and accurate data, which is often not available. In order to create a valid method, a bottom-up approach is developed to assess geographical and technical PV potential on residential buildings’ rooftops.

The proposed methodology is mainly based on two major parts as it combines engineering and statistical methods. First, the engineering method refers to a solar simulation performed for 3D residential typologies. This approach helps to assess solar irradiation, shadowing losses and the coverage ground ratio based on PV panels’ performance under different tilt. The next step uses the statistical method. The results are extrapolated at a municipal scale for spatial dissemination. The following figure illustrates an overview of the methodology and each of its successive step (Figure 1).

2.1. The Engineering Method

This part is mainly based on a series of simulations that are performed on the selected residential typologies. Rhinoceros^® is used as a principal software for 3D modelling, which is recommended in the professional and academic fields. Within Rhinoceros^®, the visual algorithm program Grasshopper offers a list of plug-in adds and environmental features, helping to perform the desired solar and PV simulations. Among them, ladybug plugins were selected since it performs environmental simulation based on valid simulation engines. Moreover, the tool systemizes the analysis process, accelerates the calculations and provides comprehensible graphical visualizations in the Rhino/Grasshopper interface [45]. The employed algorithms are explained below and illustrated (see Supplementary Materials Figure S1).

2.1.1. Characterization

One important step in this study is to test the roof suitability and the utilization capacity for PV installation. In this sense, residential typologies and their probable urban surroundings are modelled using Rhinoceros^®. The characterization concerns a series of descriptors, namely: the roof area, the roof occupancy and the number of floors. Additional information about the household occupancy rate and yearly electric consumption is also required. In the Algerian residential context, we distinguish two residential types. The necessary data are extracted from various official national documents:

• Multi-story apartments are mainly built by public structure (namely, Office de Promotion et de Gestion Immobilière (OPGI)), under different formulas partly financed by the government. In this regard, their construction is regulated according to specifications predefined at a regional level. Thus, the projects are set according to urban and architectural prescriptions related to the spatial and functional organization and the construction system.
• Single-family houses generally refer to self-constructions and vary from traditional to modern buildings. Due to the absence of accurate data, the study selects only individual buildings built within land subdivision operations, which are regulated by the public municipality or under the Master urban plan. These documents establish guidelines in terms of the plots’ size, their built coverage and the authorized height.

2.1.2. Radiation Analysis

The solar radiation analysis is based on Typical Meteorological Year data (TMY). This dataset is available within the ladybugtool in EnergyPlus weather format (EPW). The Solar analysis component in ladybug uses Radiance’s engine in order to generate Cumulative Sky radiance distribution based on the weather file of the selected location [46]. The cumulative sky calculates the sky’s radiation for the whole year and represents it by a coloured sky dome patch (see Supplementary Materials Figure S1). The annual solar radiation received on roofs is expressed in a numerical value per square meter as kWh/m² and the intensity could even be perceptible through a coloured mesh in Rhino.

2.1.3. Sunlight Hours Analysis

The incorporation of shadings losses from permanent roof elements (evacuation shaft, stairwell) or the neighbourhood environment is needed for an accurate PV potential assessment. This coefficient varies significantly depending on building type, the constraints on roofs and the country. Since the methodology used in this study, is based on the 3D model, we argue being accurate by running shading patterns in various building orientation combinations with random and uniform heights. The results are expected to reflect the relative shadowing fraction on all the rooftops of residential typologies.

Using the sunlight hours analysis component from Ladybug, a 3D sun-path is created based on on-site location and weather data. The sun path provides a range of sun vectors of the desired hourly and daily data on the sun-path. The analysis is performed on solstice winter vectors (21 December) to conduct the assessment under the worst shadows conditions and calculates the number of hours of direct sunlight received by roofs. These vectors are recorded into the component and allow generating outline curves representing shadows on the roof area (see Supplementary Materials Figure S1).

2.1.4. Coverage Ground Ratio

On flat roofs, shadows might also occur between PV panel arrays. Latitude and climate are the crucial factors for choosing the appropriate layouts allowing to minimize panels’ self-shadowing. The coverage ground ratio (CGR) refers to the PV arrays area divided by the roof area after considering the setback ratio (SBR). The (SBR), for its part, represents the horizontal gap between PV arrays divided by the vertical height of PV panels, which is related to the tilt angle and the resulting shadow [47]. Therefore, for a given location, the CGR depends, namely, on these principal variables: PV panels dimensions, minimal array spacing, tilt angle and azimuth (See Figure 2).

Based on the climatic file of the studied case, “The Tilt and Orientation Factor” (TOF) component (see Supplementary Materials Figure S1) from ladybug is used to indicate the optimal tilt that receives the highest amount of solar radiation with the minimal spacing between panels, avoiding thereby self-shadowing. Finally, the CGR and SBR are then calculated according to the equations below:

SBR = d/h

(1)

CGR = 1/(cos β + SBR × sinβ)

(2)

where d is the spacing between panels and h is the vertical height depending on the tilt angle; β is the tilt angle.

2.2. GIS Statistical Method

The objective of this study is to provide the required scientific data helping policymakers in solar energy planning. All the considered simulations should be extendable and available for the whole municipality to give more insight and strategic vision. Hence, the engineering analysis results are extrapolated and mapped across the city following these steps.

2.2.1. Total Roof Area

Firstly, the study estimates the available roof area on the municipality-level. The required dataset is extracted from the Laghouat urban Master Plan (PDAU Laghouat, 2009). It consists of the number of housing as well as statistical data about the selected buildings.

For the multi-story buildings, the available roof area (A_MS._roofs) is calculated per building type according to the following equations (Equations (3) and (4)):

A_MS._Roofs = (A_app/f (1 + A_circ)) × Nr_bui

(3)

where  Aapp/f = A_app × Nr_app/f

(4)

A_app/f is the total residential area per floor, A_circ is the mean area of horizontal and vertical circulation, Nr_bui is the number of multi-story buildings; A_app is the area of one apartment, Nr_app/f is the number of apartments per floor.

For single-family housing, the available data concerns the Plot area, the coverage ratio. the roof areas (A_SF._roofs) is calculated as follow:

A_SF._roofs = (A_plot × CR) × Nr_plot

(5)

where A_{plot is} the plot’s area, CR is the regulatory coverage ground and Nr_plot is the number of plots.

2.2.2. Geographical Potential Map

The geographic potential refers to the yearly solar radiation, which is received on the residential buildings’ rooftops. It is calculated by multiplying the total roof area and the solar intensity. The total roof area has already been estimated in the previous step and the yearly intensity of solar radiation is carried out in the engineering part. Using the geographic information system “Quantum GIS”, the result can be visualized on a geographic map.

2.2.3. Utilization Factor

Based on the engineering results, the utilization factor (UF) can be identified for each typology. It represents the effective fraction of the usable roof area for PV installation after eliminating the shadowing losses, array spacing and roof occupation. It is calculated according to the following equation (Equation (6)):

UF = ((A_Roofs × (1 − (Ob_R + Sh_L)) × CGR

(6)

where A_Roofs is the total roofs area which could refer to A_SF in the case of single-family houses and A_MS in the case of multi-story apartments; Ob_R and Sh_L are the fractions of roofs occupation and shadows losses of each typology, respectively. CGR is the coverage ground ratio.

2.2.4. Technical Potential Maps

The technical potential refers to the amount of electricity generation over roofs. The calculation implies considering the effective suitable roof area, the solar irradiation, PV modules and the system efficiency. In this study, we assume a simplified module setting with an average efficiency of 17%. The PV yield is calculated according to the following equation:

Technical_p = (A_total × GR) × UF × PR × Me

(7)

where A_total is the total roof area, GR is the annual global solar radiation, PR is a ratio that considers the energy losses PR = 75%, Me is the module efficiency rate under standard test conditions Me = 17% and UF is the utilization factor.

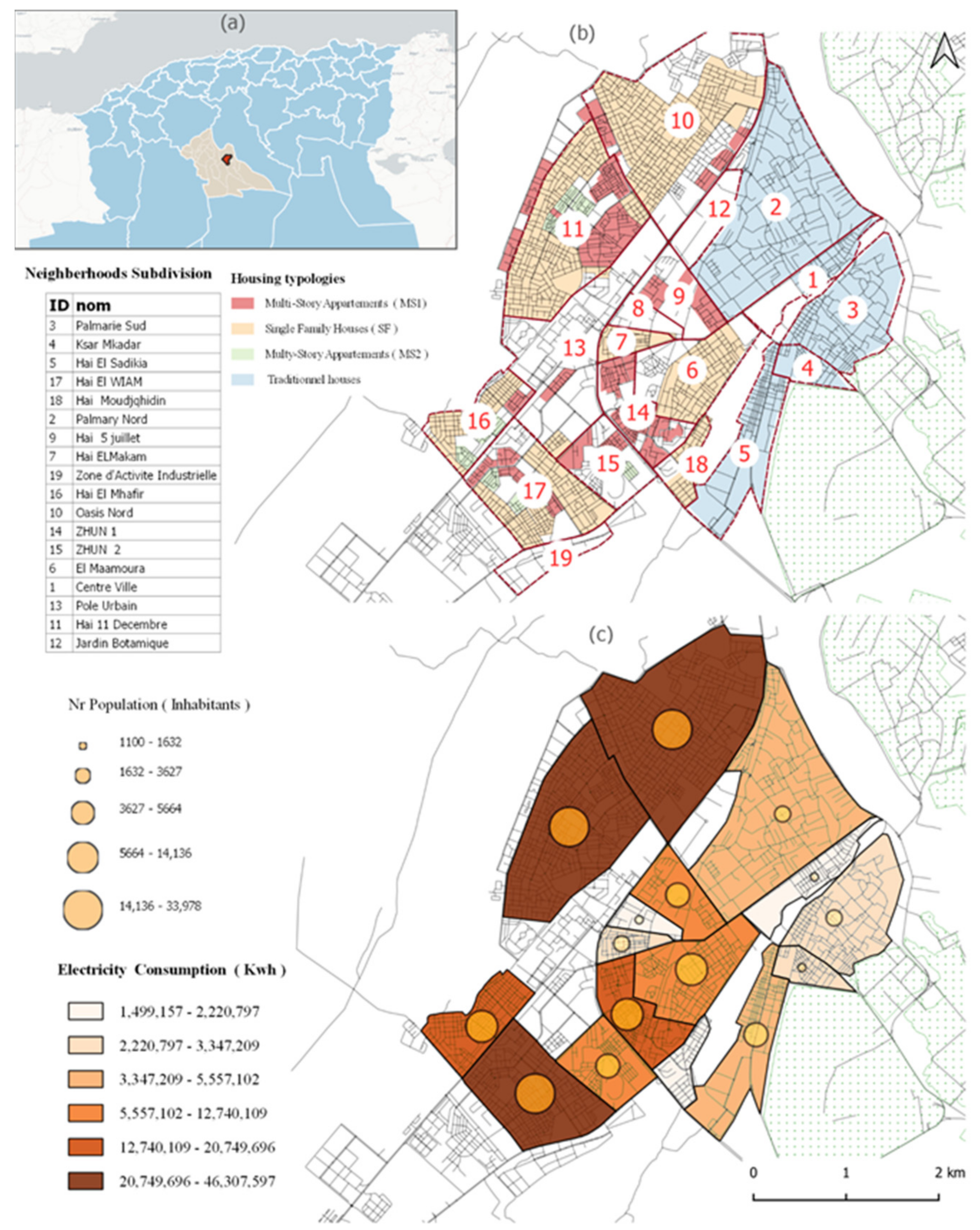
3. Case of Study

The methodological process presented is applied to the case of Laghouat. Laghouat is a province located in the central-southern part of Algeria, characterized by a hot-arid climate (see Figure 3a). The city is considered to be a vital energetic province as it contains an important Gas field and in Africa. In addition, Laghouat is home to the biggest solar photovoltaic plant in Algeria producing a total capacity of 60 megawatts (MW).

According to the latest local census conducted in 2012, the municipality is home to almost 180 thousand inhabitants. The housing stock was estimated at 26,170 dwellings in 2013, with an occupancy rate of six persons per habitation. The city is characterized by rapid urbanization as new housing programs are currently under construction to amortize the alarming deficit. The spatial pattern of Laghouat shows a mono-functional zone surrounding the city’s principal equipment with residential neighbourhoods, all aligned following one main road (Figure 3b).

The average per capita consumptions of electricity in Algeria’s residential sector is estimated at 1362.87 kWh/inhabitants. Given that the electricity consumption is correlated with the number of population, the total electricity consumption at the municipality level is presented in the map below (see Figure 3c). The analysis of electricity consumption per neighbourhood shows that higher consumption is noticed in individual housing neighbourhoods with higher population density. In contrast, the lowest density neighbourhoods are related to the traditional housing area.

4. Results and Discussion

The results are presented and discussed following a hierarchical process of solar assessment.

4.1. Physical and Geographic Potential

4.1.1. Total Roof Area

The residential buildings are composed, as mentioned, of two main types: single-family houses and multi-story apartments. As for the single-family houses, the parcel size varies between 150–350 m² with a coverage ratio of about 0.7. The number of floors ranges from 1 to 2 levels. Due to the absence of digitalized spatial data, all individual houses are considered to have a uniform height of 2 floors (see Figure 4).

For the multi-story apartment type, two typologies can be identified: multi-story apartment type 1 (MS1), which refers to mid-rise collective apartments, and multi-story apartment type 2 (MS2), which corresponds to semi-collective apartments (see Figure 4). All the data were gathered from the 2008 national consensus, which is the latest official national record. The footprint of a multi-story apartment, for its part, is extracted from Open Street Map (OSM).

The residential area in Laghouat presents a total roof area of about 1,852,730.324 m². Predominated by single-family roofs, it represents about 84% of the total rooftop compared to only 15% of multi-story roofs.

4.1.2. Radiation Analysis

The solar simulation results show that all horizontal surfaces, with no shading obscuration, receive yearly the amount of 1996.04 kWh/m². This value is extended to the rest of the city. Results for radiation are mapped all over the available footprint (see Supplementary Materials Figure S2).

4.2. Utilization Factor

The estimated roof area must be adjusted to determine the effective area for the PV electricity generation. For this purpose, the utilization factor depends on three main aspects: roof occupation, shadow losses and CGR.

4.2.1. Roof Occupation

In the absence of a detailed configuration of roofs for all the residential typologies, possible spatial obstacles have been identified using Google Earth images as indicated on the table. All the probable roof objects are summarized and categorized according to their nature, structural elements or equipment. The service area is an additional surface that refers to a peripheral path dedicated to maintenance or installation issues. The mean area of each one is estimated according to standards data (see

Table 1. The obstacles identified on a residential roof.

Roof Obstacles	Structural Element		Equipment			Service
	Stair	Evacuation Shaft	Water Tank	Parabolic Antenna	AC Unit	Safety Perimeter
Mean % Area	4%	0.40%	1.90%	0.30%	0.7%	9.10%
Single-family houses	X	X	X	X	X	X
Multi-story Apartments	-	X	-	-	-	X

).

4.2.2. Shadow Losses

A sunlight hours analysis was performed to identify the most effective rate of shadows losses on roofs resulting from their occupancy elements, as well as their neighbourhood. The simulation is executed on each single building typology in random and uniform neighbourhood height. Concerning their occupancy, it is considered that only structural obstacles could produce permanent shadows on rooftop surfaces. In the case of uniform heights, the average losses for single-family buildings are about 51% with a variation that ranges from 1% to 12% due to the orientation. In the case of random heights, the rate could reach more than 70% of the whole surface, which could eliminate the building from receiving any PV installation. In multifamily buildings, the shadow losses are estimated to about 20% (Figure 5). Indeed, the variability of shadows fractions depends highly on the roof’s configurations; the roofs in single-family houses are usually accessible and more crowded than multi-story apartment roofs. The results that are reported here should be understood with specific consideration to some limitations. According to Karteris et al. [14], the rooftop shape, structural elements position and orientation have a huge influence on the shading effects.

Due to the lack of data, the building shape and the stairwell position are simplified and identified according to the most commonly met situations.

4.2.3. Coverage Ground Ratio (CGR)

As stated in Section 2.1.4, the CGR depends on latitude and climatic conditions. Hence, for choosing the appropriate PV layout, the analysis determines the optimal tilt, which relates PV system performance to the solar irradiation intensity. First, the results illustrate the impact of the angle on solar radiation intensity and suggest the optimal tilt for each season (Figure 6). Then, we proceed to a comparison of the PV electricity profiles resulting from PV panel installed under the optimal tilt in each season (Figure 7).

The variation between the different profiles is detailed on each season as presented below:

• Tilts of 13.4° and 18° receive the maximal intensity of the solar radiation during summer and spring. In winter and autumn, the panels receive 80–90% of solar irradiation, consequently producing 23% less electricity, when considering 10% of annual shading.
• Tilts of 45–49.5° receive the maximal intensity of solar irradiation also during winter and autumn. In summer, it receives 80–90% of the total irradiation. Accordingly, the PV production decreases on average by 16%.

Nevertheless, it is worth mentioning that tilts at greater angles require more spacing between PV arrays to minimize self-shadowing. Consequently, the result shows a lower CGR. In parallel, decreasing the tilt angle to enhance the CGR would require a higher investment in term of installation and maintenance.

The comparison of PV yield profiles (see

Table 2. Impact of the tilt angle on CGR (Coverage Ground Ratio).

Tilt Angle	Minimal Spacing (m2)	CGR
49.5°	4.01	0.41
45°	3.9	0.42
31.5°	3.43	0.48
18°	2.76	0.6
13.4°	2.5	0.67

) demonstrates a low reduction of the annual PV production when the tilt angle is close to the optimal. For this reason, the average tilt is estimated at 31.5°, considering an SBR equal to 3/1, which means that CGR used for the study is 0.48. When combining the calculations presented in the previous Section 2.1.1, Section 2.1.2 and Section 2.1.3, the utilization factors are calculated according to Equation (4) for each typology. It indicates that the single-family houses and multi-story apartments have a UF equal to 0.18 and 0.35, respectively. This result presents a considerable contribution to knowledge since no previous research has been done in this specific context. Moreover, it could be easily replicated in other municipalities with the same residential typologies to estimate their technical PV potential.

The utilisation factor (UF) is mainly influenced by architectural and solar suitability. In the literature, we found different UF expressed as reduction coefficients. On the one hand, architectural reductions refer to the construction obstacles (heating and air conditioning installations, elevators, etc.), shading effects and, in some cases, other restriction due to historically protected buildings. On the other hand, the solar availability considers the solar irradiation intensity depending on the building orientation, roof inclination and the separation among PV panels which vary according to the geographic location. Indeed, all these reductions coefficients are fully or partially considered depending on the research goals.

Within this paper, we selected only coefficients that we consider essential in addressing the studied case’s specificity. The UF on residential buildings is less investigated compared to the commercial, industrial and public buildings. Moreover, the values that are found in the literature show a high variability according to the residential typology. Hence, to provide a notable comparison, the present study draws reference only from authors who provide UF with similar typologies (see

Table 3. Utilization factor compared to the literature review.

	Utilisation Factor
Residential Flat Roofs	This study	[48]	[14]	[20]	[34]
Single-family Houses Multi-Story Apartments	0.18	0.2	-	0.35	0.51
	0.35	-	0.25 0.5	0.48	0.54

). For instance, the solar suitability of residential roofs in Delhi is estimated at 0.2 [48]. In Greece, Karteris et al. [14] have distinguished between multifamily and multi-story buildings. In this regard, they found a variation in the utilization factor ranging from 0.25 to 0.5. Similarly, in the Canary Islands, the utilization factor is determined according to residential typologies (apartment buildings, semidetached and detached houses) and roofing characteristic. Therefore, the value varies (0.35–0.48) [20]. Another study in Spain, Ordóñez et al. [34] found higher utilization factors in Andalusia varying from (0.51; 0.53; 0.54) in townhouses, detached houses and high-rise buildings, respectively.

The utilization factors found in the present study are relatively poor compared to the values that are drawn from the literature. These lower results can be explained by the nature and the configuration of the roofs, which has a more cluttered character in the studied case. However, the amount of solar irradiation received annually is still more important (see Section 4.1.2). Consequently, the efficiency of the panels is greatest.

4.3. Technical Potential

In parallel to the centralized solar plants, the results reveal that Laghouat could be a leading municipality in energy efficiency with the highest renewable energy share in the country. Indeed, the suitable roof area for PV panels, considering the UF of each typology, is about 383,709.2 m². The annual electricity production achieved by installing the PV system on this area is evaluated at 90,148,816.32 kWh. Such an amount of annual electricity yield could replace 55% of the total electricity residential consumption, which is normally generated from fossil fuel energy sources.

Overall, the engineering analysis demonstrates that multi-story apartments of type 1(MS1) and type 2 (MS2) can cover 20–24% and 43% of their annual electricity needs, respectively. The electric consumption per multi-story building depends on the number of apartments, while the PV production depends on the roof size. In order to improve the energy balance in this typology, lateral façades, when well oriented, could also be used for PV generation [49].

Single-family housing is closer to achieve energy balance. The parcel sizes in Laghouat vary between 150–350 m². A parcel of 250 m² is the optimal size to meet 91% of the annual electricity needs. The size of 350 m² could be relevant to encourage PV connected buildings in the future. Nonetheless, these results are interpreted with caution because the electricity consumption is based on the national census indicating the rate of occupancy per dwelling and the rate of consumption per inhabitant, while the roof size does not correlate necessarily with the residents’ number. The purpose of estimating a technical potential is to offer an analytical vision, which would help to develop energy policy at the municipal level. Thus, the results are summarized per neighbourhood. Based on the aggregated results in

Table 4. Yearly technical potential per neighbourhood.

ID	Housing Type/Number/Percentage			Population	Yearly Consumption (kWh)	Total Area (m2)	UF	Suitable Area (m2)	Yearly PV Potential (kWh)
10	(SF)	2556	67%	15,336	20,900,974.32	626,220.00	0.18	112,719.60	26,482,396.50
	(MS1)	1240	33%	7440	10,139,752.80	26,997.98	0.35	9449.29	2,220,020.99
11	(SF)	1803	32%	10,818	14,743,527.66	315,525.00	0.18	56,794.50	13,343,326.88
	(MS2)	854	15%	5124	6,983,345.88	36,210.00	0.35	12,673.50	2,977,518.13
	(MS1)	3006	53%	18,036	24,580,723.32	47,100.51	0.35	16,485.18	3,873,035.36
14	(MS2)	148	9%	888	1,210,228.56	6290.00	0.35	2201.50	517,221.46
	(MS1)	1482	91%	8892	12,118,640.04	33,345.00	0.35	11,670.75	2,741,931.56
15	(MS2)	144	15%	864	1,177,519.68	6120.00	0.35	2,142.00	503,242.50
	(MS1)	800	85%	4800	6,541,776.00	24,848.59	0.35	8697.01	2,043,278.85
16	(SF)	888	38%	5328	7,261,371.36	93,240.00	0.18	16,783.20	3,943,053.00
	(MS2)	784	33%	4704	6,410,940.48	33,320.00	0.35	11,662.00	2,739,875.83
	(MS1)	684	29%	4104	5,593,218.48	17,468.90	0.35	6114.12	1,436,453.09
17	SF	1177	88%	7062	9,624,587.94	123,585.00	0.18	22,245.30	5,226,321.38
	(MS2)	168	11%	1008	1,373,772.96	7140.00	0.35	2499.00	587,116.25
	(MS1)	1374	86%	8244	11,235,500.28	37,161.61	0.35	13,006.56	3,055,768.47
18	(SF)	231	100%	1386	1,888,937.82	56,595.00	0.18	10,187.10	2,393,362.13
6	(SF)	1558	100%	9348	12,740,435.38	272,656.99	0.18	49,078.26	11,530,469.35
7	(SF)	331	100%	1986	2,706,659.82	69,510.00	0.18	12,511.80	2,939,528.25
9	(MS1)	750	100%	4500	6,132,915.00	19,395.75	0.35	6788.51	1,594,896.36

. This study concludes that neighbourhoods composed of individual housing only (ID: 6.7.18) are the most energy productive as they reach even more than 100% of the yearly electricity consumption. On the other hand, neighbourhoods composed of only multi-storey apartments (ID: 9.14.15) have less potential covering only 24–33% (Figure 8).

In terms of energy policy, these results suggest an interesting model of a net zero energy neighbourhood. The model promotes, technically and socially, an optimal mix of residential typologies. By sharing and matching energy, a neighbourhood composed of 14% of residential Type 1 (MS1), 14% of residential Type 2 (MS2) and 71% of a single-family could be self-sufficient. Indeed, smart energy management offers the possibility of PV energy-sharing among residential buildings. This scenario is expected to enhance energy efficiency and optimize the energy control between inter-connected buildings to achieve the net zero neighbourhood [30,50] (Figure 9).

Finally, the proposed master plan (see Figure 10) represents a crucial tool to reveal the benefit of distributed PV generation to municipal actors, from decision-makers to the general. It helps to inform decision-makers about the strategic option for energy balance and net zero neighbourhood improvements. Moreover, it offers investors and individual electricity consumers insights into optimal rooftops configurations, which would help to receive the full benefit of its available roof area and gain high investment profits.

5. Conclusions and Future Developments

Estimating the solar potential in urban rooftops is a complex task, particularly with the lack of resources and missing data. In this regard, the present study offers a reliable approach based on an engineering–statistical combined method in order to assess solar PV potential on residential rooftop using free and available public data.

Laghouat is one of the leading Algerian regions in electricity generation from renewable sources. However, the engineering methodology performed on each residential typology reveals that, for single-family typology, only 18% of the roof area could be used for PV installation. Investment in this area could cover 55–127% of the electricity needs, depending on the roof size.

For multi-story typology, 35% of the roof area is suitable for PV installation, which could cover 24–43% of the buildings’ need, depending on the number of apartments.

The analysis is limited to residential typologies. Yet, it provides a valuable result regarding the utilization factor in the residential sector. The reliable utilization factor for PV installations on residential roofs can be replicated in further research in other regions with similar building types or climatic conditions.

Moreover, the development of geographical and technical potential maps is extremely helpful for solar energy planning. Overall, the technical potential of residential rooftops in Laghouat municipality is estimated to be 90,148,816.32 kWh, which allows achieving 55% gains of the city-wide electricity from photovoltaic, on an annual base. Additionally, when aggregated per neighbourhoods, some of them are expected to cover from 24% reaching even more than 100% of the yearly electricity consumption.

These results offer significant insight for decision-makers as it helps them to develop different solar planning scenarios for energy savings and net zero neighbourhood projects at the municipal scale. In addition, it offers investors and individual electricity consumers recommendations for optimal rooftops configurations to maximise the benefit from the available roof area, hence, gain high investment profits.

Nonetheless, technical potential assessment is only the first step to support the development of solar energy. The road maps for PV integration in the built environment include multiples challenges that are sought to be addressed. Therefore, further research should focus on the economic and social implications of PV installations on residential roofs.