A Data-Driven Approach for Online Inter-Area Oscillatory Stability Assessment of Power Systems Based on Random Bits Forest Considering Feature Redundancy
Abstract
:1. Introduction
- In this paper, a data-driven scheme that can improve the OSM assessment accuracy, provide rapid data processing speed and reduce the computing time of the real-time OSA is proposed.
- A compositive feature selection unit is specially proposed to facilitate OSA. Not only can the pivotal features be selected to enhance the computational efficiency of the scheme, but the problem of feature redundancy is also effectively mitigated.
- To improve the robustness of the integrated scheme for the unseen network topologies, an update stage is proposed in the scheme considering the impacts of variations in system topology, distribution among generators and loads, and peak and minimum load.
- This paper analyzes the advantages of the proposed compositive feature selection unit by the comparisons with several other feature selection techniques. Tests of the robustness of the scheme to missing data are reported and discussed. Moreover, comparisons with other methods illustrate the applicability and superiority of the integrated scheme.
2. Problem Formulation and Supporting Methods
2.1. Problem Formulation of Oscillatory Stability Margin (OSM)
2.2. Introduction of Supporting Methods
- The value of MICe falls between 0 and 1.
- A stronger correlation tends to be assigned a higher score.
- A correlation between statistically independent variables tends to be assigned a score of 0.
3. Proposed Integrated Scheme for Estimating Oscillatory Stability Margin (OSM)
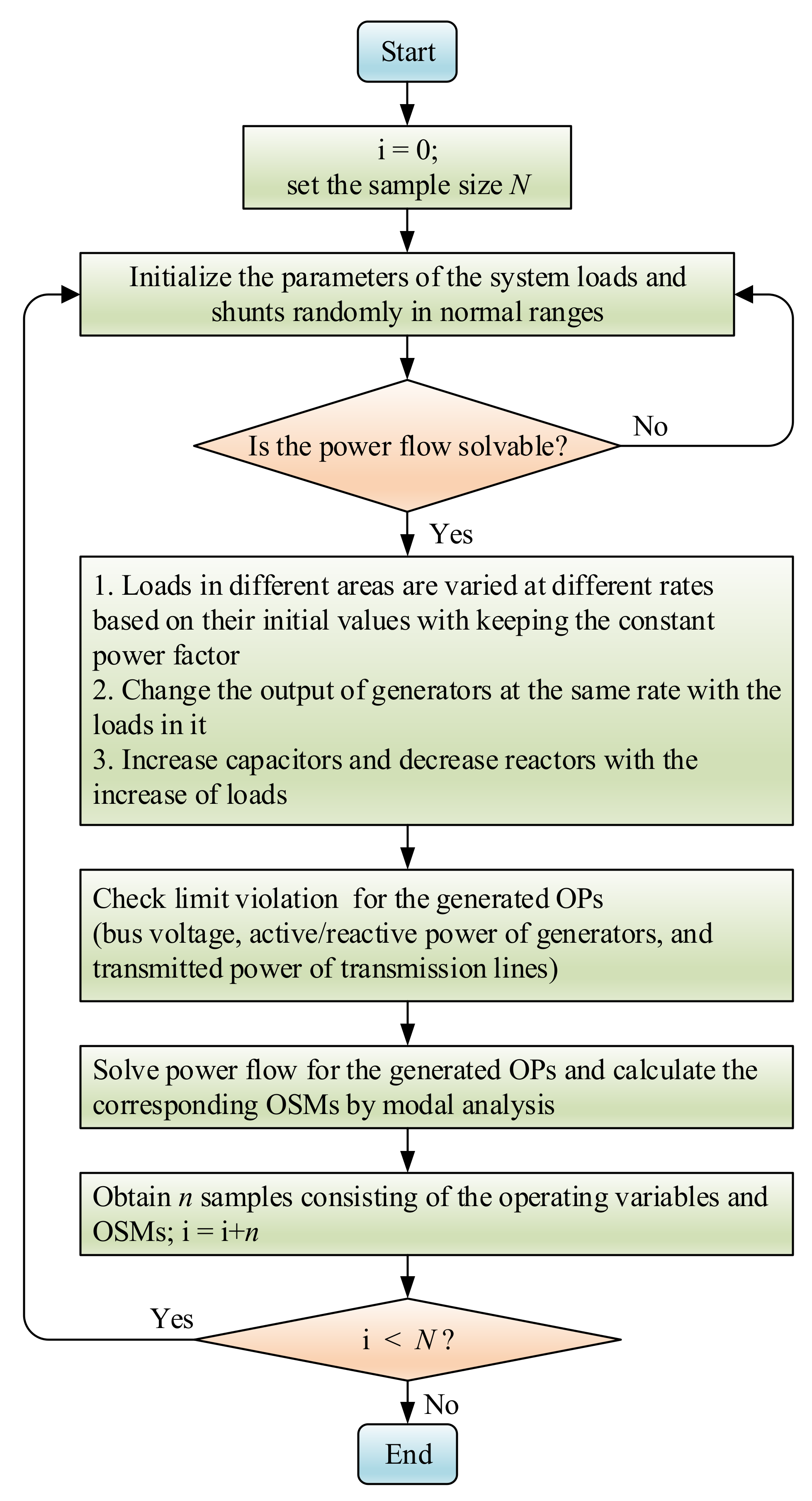
3.1. Process Flow of the Integrated Scheme
- Randomly initialize the parameters of the system loads and shunts in their normal ranges by introducing reasonable perturbations in the corresponding parameters.
- Iteratively change the system load level. Loads in different areas are varied with different rates based on their initial values while keeping a constant power factor. Concurrently, the balance of the load variations mainly relies on the generators in the same area.
- Increase capacitors and decrease reactors with the increase in loads to simulate the practical operating condition of the systems.
- Consider various factors influencing the operation of the system during database creation, including variations in system topology, distribution among generators and loads, and peak and minimum load. Contingencies, scheduled maintenance, and economic dispatch can lead to topology change. Optimal power flow considerations may produce the variation of distribution among generators and loads. The peak and minimum load values tend to be different in different seasons, especially between winter and summer. In practice, the system operating condition hardly stays the same because of such influence factors, and large condition variations may result in an unacceptable decrease in the assessment accuracy of data-driven methods [22]. To accommodate new operating conditions, the retraining using new samples corresponding to the new conditions is usually considered necessary [23]. Nevertheless, retraining is more or less time-consuming and may not meet the requirements for seamless estimation of OSM. Usually, a credible list of possible system operating conditions can be acquired from historical operating information collected and stored by utility companies. Thus, a recommended solution is to prepare an abundant database that includes multiple sample sets corresponding to potential system operating conditions on the basis of the credible list, and then use the prepared sample sets to train a series of RBF candidates beforehand in the offline stage.
3.2. Compositive Feature Selection Unit
4. Application to the IEEE 39-Bus System
4.1. Feature Selection Process
4.2. Oscillatory Stability Assessment (OSA) Performance Test
5. Performance Test in a 1648-Bus System
5.1. Data Processing Speed
5.2. Impact of Missing Data
5.3. Impact of Noise Data
- Noise is added only to the test set.
- Noise is added to both the training set and test set.
5.4. Comparisons with Other Methods
5.5. Tests for Variations in System Topology, Distribution among Generators and Loads, and Peak and Minimum Load
5.6. Additional Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liao, S.; Xu, J.; Sun, Y.; Bao, Y.; Tang, B. Control of energy-intensive load for power smoothing in wind power plants. IEEE Trans. Power Syst. 2018, 33, 6142–6154. [Google Scholar] [CrossRef]
- Tang, F.; Wang, B.; Liao, Q.; Pisani, C. Research on forced oscillations disturbance source locating through an energy approach. Int. Trans. Electr. Energy Syst. 2016, 26, 192–207. [Google Scholar] [CrossRef]
- Chung, C.Y.; Wang, L.; Howell, F.; Kundur, P. Generation rescheduling methods to improve power transfer capability constrained by small-signal stability. IEEE Trans. Power Syst. 2004, 19, 524–530. [Google Scholar] [CrossRef]
- Ma, J.; Wang, S.; Gao, X.; Wang, Z. Contribution factors based optimal selection of wide-area signals for power system damping control. Elect. Power Compon. Syst. 2014, 42, 935–944. [Google Scholar] [CrossRef]
- Teeuwsen, S.P.; Erlich, I.; El-Sharkawi, M.A.; Bachmann, U. Genetic algorithm and decision tree-based oscillatory stability assessment. IEEE Trans. Power Syst. 2006, 21, 746–753. [Google Scholar] [CrossRef]
- Krismanto, A.U.; Mithulananthan, N.; Kamwa, I. Oscillatory stability assessment of microgrid in autonomous operation with uncertainties. IET Renew. Power Gener. 2017, 12, 494–504. [Google Scholar] [CrossRef]
- Wang, T.; Bi, T.; Wang, H.; Liu, J. Decision tree based online stability assessment scheme for power systems with renewable generations. CSEE J. Power Energy Syst. 2015, 1, 53–61. [Google Scholar] [CrossRef]
- Preece, R.; Milanovic, J.V. Risk-based small-disturbance security assessment of power systems. IEEE Trans. Power Deliv. 2015, 30, 590–598. [Google Scholar] [CrossRef]
- Ma, J.; Dong, Z.Y.; Zhang, P. Comparison of BR and QR eigenvalue algorithms for power system small signal stability analysis. IEEE Trans. Power Syst. 2006, 21, 1848–1855. [Google Scholar] [CrossRef]
- Ma, J.; Wang, S.; Wang, Z.; Thorp, J.S. Power system small-signal stability region calculation method based on the guardian map theory. IET Gener. Transm. Distrib. 2014, 8, 1479–1488. [Google Scholar] [CrossRef]
- Rueda, J.L.; Colome, D.G.; Erlich, I. Assessment and enhancement of small signal stability considering uncertainties. IEEE Trans. Power Syst. 2009, 24, 198–207. [Google Scholar] [CrossRef]
- Kundur, P.; Wong, G.J.; Wang, D.Y.; Lauby, M. A comprehensive computer program package for small signal stability analysis of power systems. IEEE Trans. Power Syst. 1990, 5, 1076–1083. [Google Scholar] [CrossRef]
- Zheng, C.; Malbasa, V.; Kezunovic, M. Regression tree for stability margin prediction using synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 1978–1987. [Google Scholar] [CrossRef]
- Tan, B.; Yang, J.; Pan, X.; Li, J.; Xie, P.; Zeng, C. Representational learning approach for power system transient stability assessment based on convolutional neural network. J. Eng. 2017, 2017, 1847–1850. [Google Scholar] [CrossRef]
- Mohammadi, H.; Khademi, G.; Dehghani, M.; Simon, D. Voltage stability assessment using multi-objective biogeography-based subset selection. Int. J. Electr. Power Energy Syst. 2018, 103, 525–536. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.Y.; Zhao, J.H.; Zhang, P.; Wong, K.P. A reliable intelligent system for real-time dynamic security assessment of power systems. IEEE Trans. Power Syst. 2012, 27, 1253–1263. [Google Scholar] [CrossRef]
- Sun, M.; Konstantelos, I.; Strbac, G. A deep learning-based feature extraction framework for system security assessment. IEEE Trans. Smart Grid 2019, 10, 5007–5020. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Z.; Ma, Z.; Guo, P.; Shao, K.; Quan, S. Real-time approach for oscillatory stability assessment in large-scale power systems based on MRMR classifier. IET Gener. Transm. Distrib. 2019, 13, 4431–4442. [Google Scholar] [CrossRef]
- Reshef, Y.A.; Reshef, D.N.; Finucane, H.K.; Sabeti, P.C.; Mitzenmacher, M. Measuring dependence powerfully and equitably. J. Mach. Learn. Res. 2016, 17, 1–63. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, Y.; Wen, K.; Shugart, Y.Y.; Xiong, M.; Jin, L. Random bits forest: A strong classifier/regressor for big data. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, Y.; Liu, S.; Qin, L.; Li, H.; Qiu, H. A novel online estimation scheme for static voltage stability margin based on relationships exploration in a large data set. IEEE Trans. Power Syst. 2015, 30, 1380–1383. [Google Scholar] [CrossRef]
- Liu, S.; Liu, L.; Fan, Y.; Zhang, L.; Huang, Y.; Zhang, T.; Cheng, J.; Wang, L.; Zhang, M.; Shi, R.; et al. An integrated scheme for online dynamic security assessment based on partial mutual information and iterated random forest. IEEE Trans. Smart Grid. 2020, 11, 3606–3619. [Google Scholar] [CrossRef]
- Wang, B.; Fang, B.; Wang, Y.J.; Liu, H.S.; Liu, Y.L. Power system transient stability assessment based on big data and the core vector machine. IEEE Trans. Smart Grid. 2016, 7, 2561–2570. [Google Scholar] [CrossRef]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, C.A.; El-Sharkawi, M.A.; Marks, R.J. Power system security assessment using neural networks: Feature selection using fisher discrimination. IEEE Trans. Power Syst. 2001, 16, 757–763. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Liu, L.; Yang, N.; Mao, D.; Zhang, L.; Cheng, J.; Xue, T.; Liu, L.; Yan, G.; Qiu, L.; et al. A data-driven approach for online dynamic security assessment with spatial-temporal dynamic visualization using random bits forest. Int. J. Electr. Power 2021, 124, 106316. [Google Scholar] [CrossRef]
- Liu, S.; Shi, R.; Huang, Y.; Li, X.; Li, Z.; Wang, L.; Mao, D.; Liu, L.; Liu, S.; Zhang, M.; et al. A data-driven and data-based framework for online voltage stability assessment using partial mutual information and iterated random forest. Energies 2021, 14, 715. [Google Scholar] [CrossRef]
- PSS/E Users Manual; Shaw Power Technologies: Baton Rouge, LA, USA, 2004.
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Saraf, P.; Venayagamoorthy, G.K.; Luitel, B. Online oscillation monitoring of synchronous generators using Parallel-Prony analysis. In Proceedings of the 2014 IEEE Power & Energy Society Innovative Smart Grid Technologies, Washington, DC, USA, 19–22 February 2014; pp. 19–22. [Google Scholar]
- Yalcin, N.A.; Vatansever, F. A new hybrid method for signal estimation based on Haar transform and Prony analysis. IEEE Trans. Instrum. Meas. 2021, 70, 6501409. [Google Scholar] [CrossRef]
- González, J.P.; Roque, A.M.S.M.S.; Pérez, E.A. Forecasting functional time series with a new hilbertian ARMAX model: Application to electricity price forecasting. IEEE Trans. Power Syst. 2018, 33, 545–556. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, L.; Pan, Z.; Bai, F.; Liu, Y.; Liu, Y.; Patel, M.; Farantatos, E.; Bhatt, N. ARMAX-based transfer function model identification using wide-area measurement for adaptive and coordinated damping control. IEEE Trans. Smart Grid. 2017, 8, 1105–1115. [Google Scholar] [CrossRef]
- Shi, G. On the nonconvergence of the vector fitting algorithm. IEEE Trans. Circuits Syst. II 2016, 63, 718–722. [Google Scholar] [CrossRef]
- Górniak, P.; Bandurski, W. A new universal approach to time-domain modeling and simulation of UWB channel containing convex obstacles using vector fitting algorithm. IEEE Trans. Antenn. Propag. 2014, 62, 6394–6405. [Google Scholar] [CrossRef]








| Test System | ||
|---|---|---|
| IEEE 39-bus | 0.9831 | 0.00187 |
| 1648-bus | 0.9643 | 0.00179 |
| Test System | Offline Training | New Case Estimation |
|---|---|---|
| IEEE 39-bus | 89.18 s (2252 case) | 1.07 s (564 cases) |
| 1648-bus | 857.12 s (7310 cases) | 3.84 s (1828 cases) |
| Scenario | IEEE 39-Bus System | 1648-Bus System | ||
|---|---|---|---|---|
| RMSE | ||||
| Scenario 1 | 0.9613 | 0.00221 | 0.9534 | 0.00253 |
| Scenario 2 | 0.9724 | 0.00195 | 0.9608 | 0.00186 |
| Out of Service | Type | ||
|---|---|---|---|
| Line 683–711 | N-1 | 0.00197 | 0.00176 |
| G 202 | N-1 | 0.00211 | 0.00182 |
| G 1515 and Line 1218–1220 | N-2 | 0.00232 | 0.00185 |
| G 398 and Shunt 1306 | N-2 | 0.00219 | 0.00178 |
| G 749, Line 315–317 and Line 635–804 | N-3 | 0.00257 | 0.00180 |
| G 303, Line 535–546 and Shunt 561 | N-3 | 0.00247 | 0.00174 |
| Variation Range of the Distribution Relative to the Original Distribution | ||
|---|---|---|
| 70–110% | 0.00227 | 0.00179 |
| 75–115% | 0.00243 | 0.00175 |
| 85–125% | 0.00249 | 0.00181 |
| 90–130% | 0.00236 | 0.00185 |
| Minimum Load to Peak Load | ||
|---|---|---|
| 60–120% | 0.00208 | 0.00183 |
| 65–125% | 0.00221 | 0.00182 |
| 75–135% | 0.00214 | 0.00173 |
| 80–140% | 0.00231 | 0.00186 |
| Method | Data Processing Speed | RMSE |
|---|---|---|
| Proposed Integrated Scheme | 0.0021 s/case | 0.00179 |
| Prony | 0.0019 s/case | 0.00214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Mao, D.; Xue, T.; Tang, F.; Li, X.; Liu, L.; Shi, R.; Liao, S.; Zhang, M. A Data-Driven Approach for Online Inter-Area Oscillatory Stability Assessment of Power Systems Based on Random Bits Forest Considering Feature Redundancy. Energies 2021, 14, 1641. https://doi.org/10.3390/en14061641
Liu S, Mao D, Xue T, Tang F, Li X, Liu L, Shi R, Liao S, Zhang M. A Data-Driven Approach for Online Inter-Area Oscillatory Stability Assessment of Power Systems Based on Random Bits Forest Considering Feature Redundancy. Energies. 2021; 14(6):1641. https://doi.org/10.3390/en14061641
Chicago/Turabian StyleLiu, Songkai, Dan Mao, Tianliang Xue, Fei Tang, Xin Li, Lihuang Liu, Ruoyuan Shi, Siyang Liao, and Menglin Zhang. 2021. "A Data-Driven Approach for Online Inter-Area Oscillatory Stability Assessment of Power Systems Based on Random Bits Forest Considering Feature Redundancy" Energies 14, no. 6: 1641. https://doi.org/10.3390/en14061641
APA StyleLiu, S., Mao, D., Xue, T., Tang, F., Li, X., Liu, L., Shi, R., Liao, S., & Zhang, M. (2021). A Data-Driven Approach for Online Inter-Area Oscillatory Stability Assessment of Power Systems Based on Random Bits Forest Considering Feature Redundancy. Energies, 14(6), 1641. https://doi.org/10.3390/en14061641






