Study on the Sensitivity of a Gyroscope System Homing a Quadcopter onto a Moving Ground Target under the Action of External Disturbance
Abstract
:1. Introduction
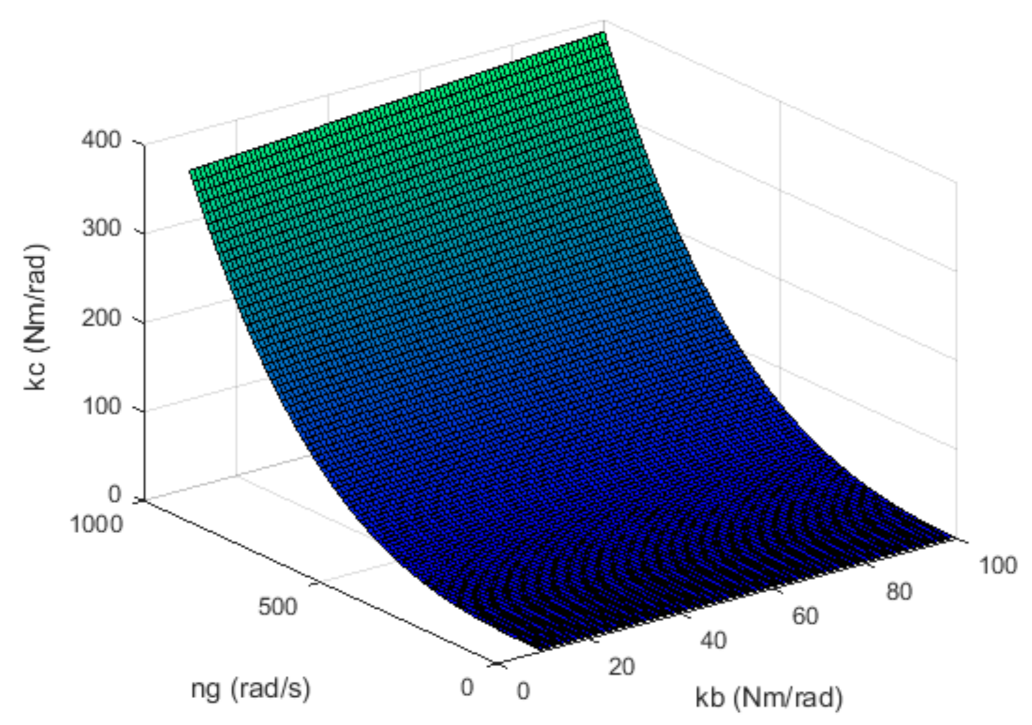
2. Determining Optimal Parameters for a Controlled Gyroscope System
- —state vector, —control vector,
- —state matrix, —control matrix,
- , , , ,
- —angles defining the position of the GS axis in space,
- —control moments,
- —damping coefficients in GS frame suspension bearings,
- —moment of inertia of a GS rotor relative to the longitudinal axis,
- —moment of inertia of a GS rotor relative to the transverse axis,
- —rotary speed of the GS rotor.
3. Test Results
3.1. Test Results Regarding the Sensitivity of a Gyroscope System during Tracking and Laser Illumination of a Ground Target
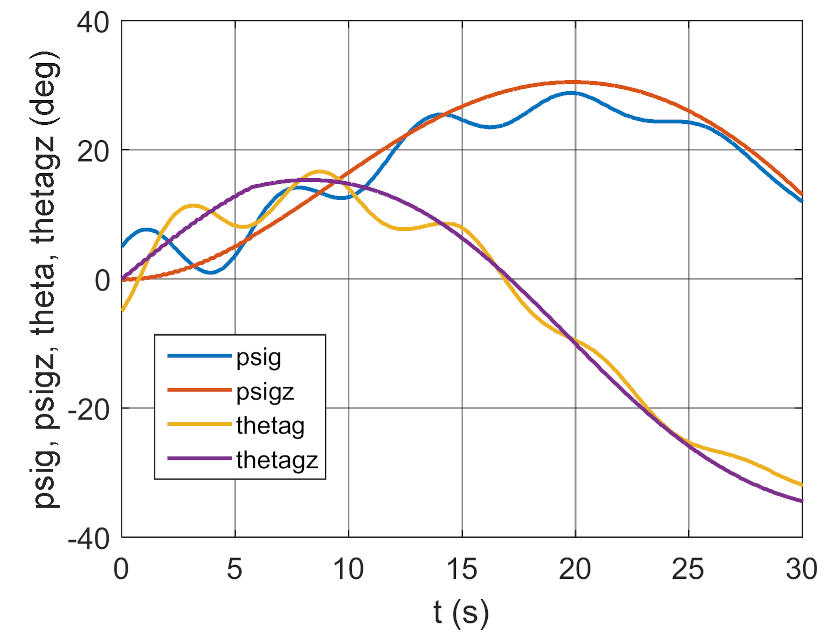
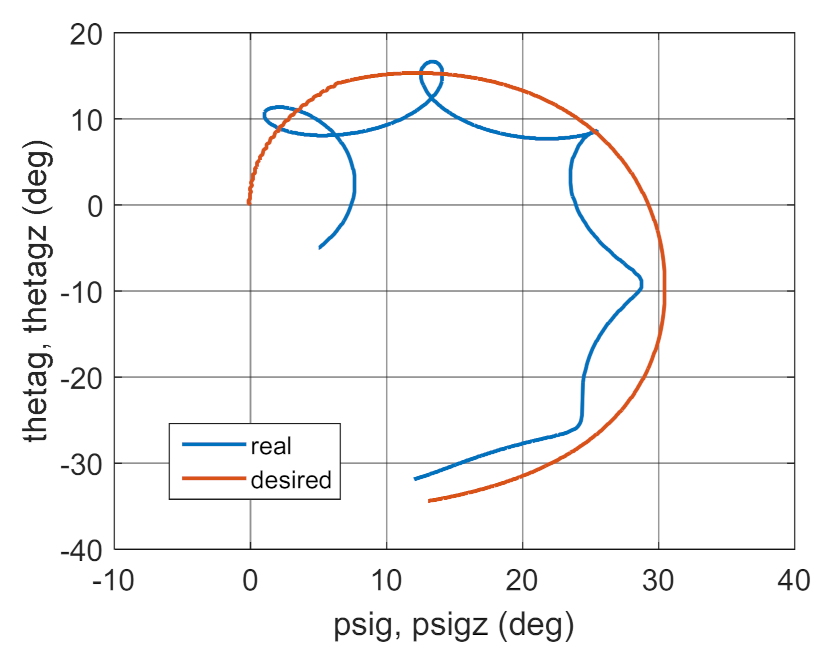
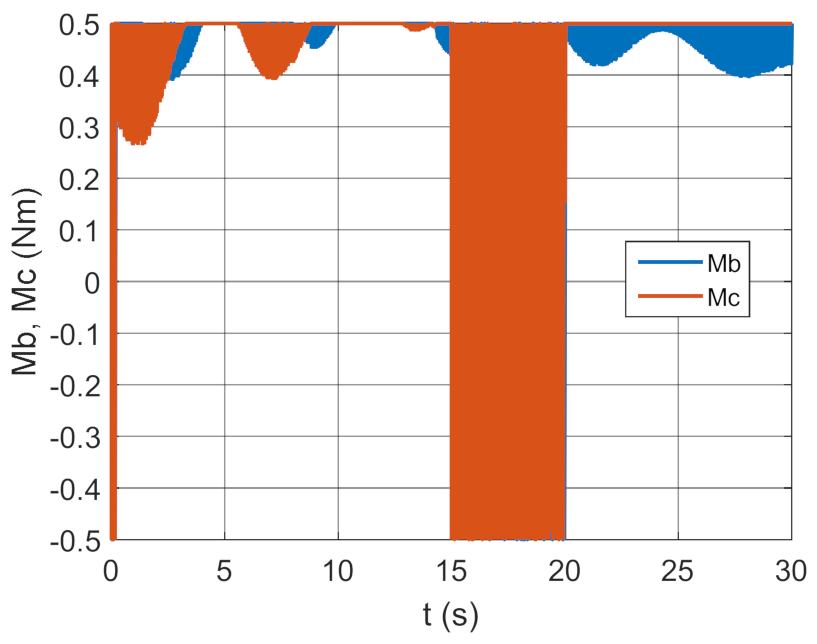
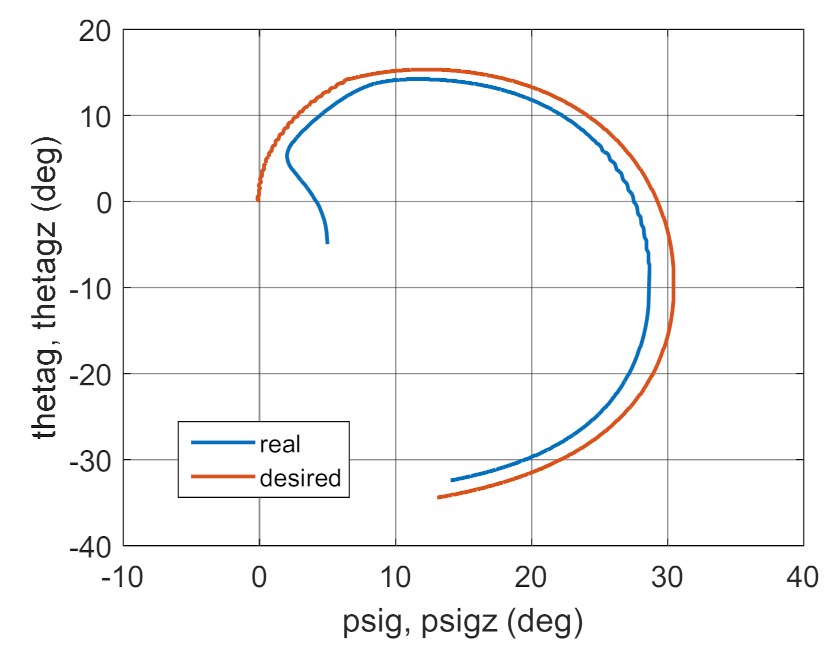
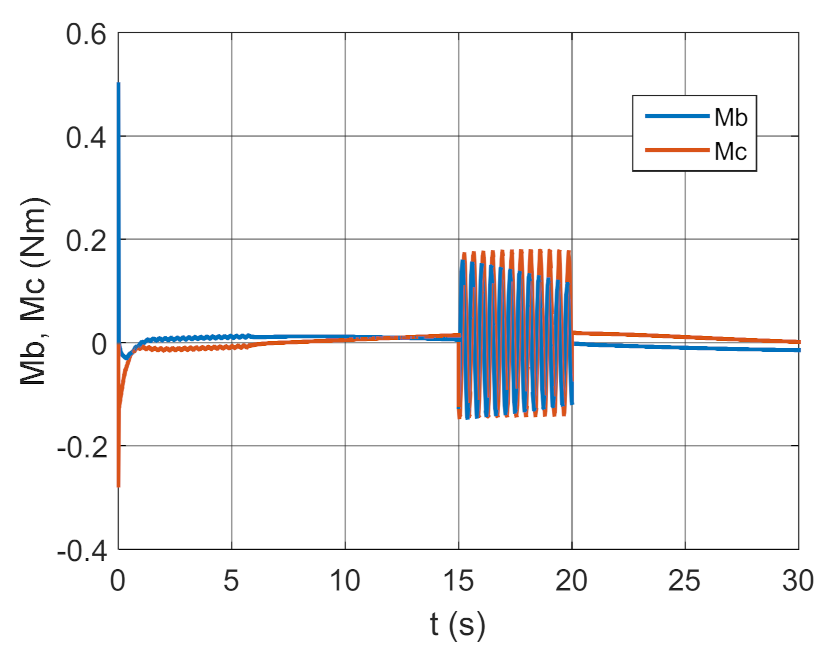
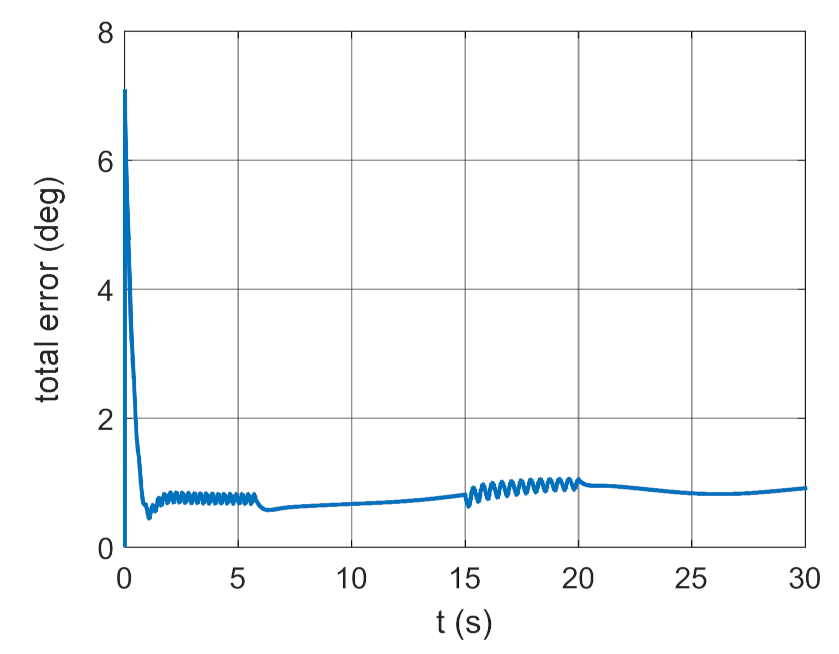
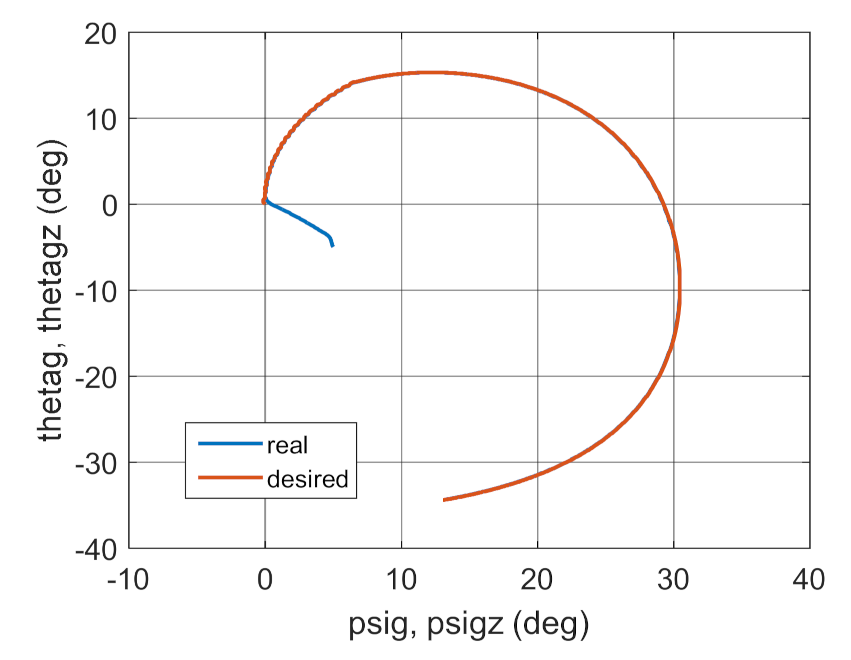
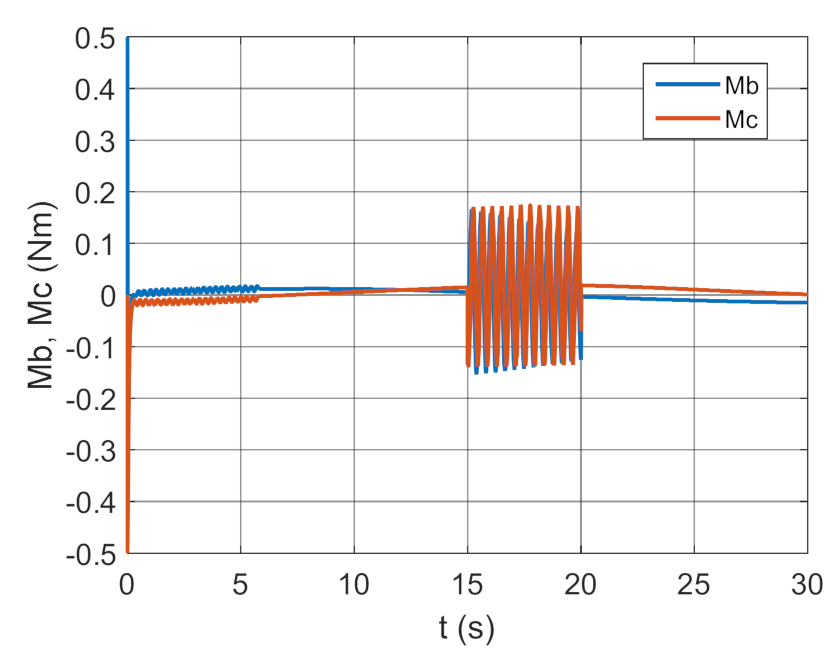
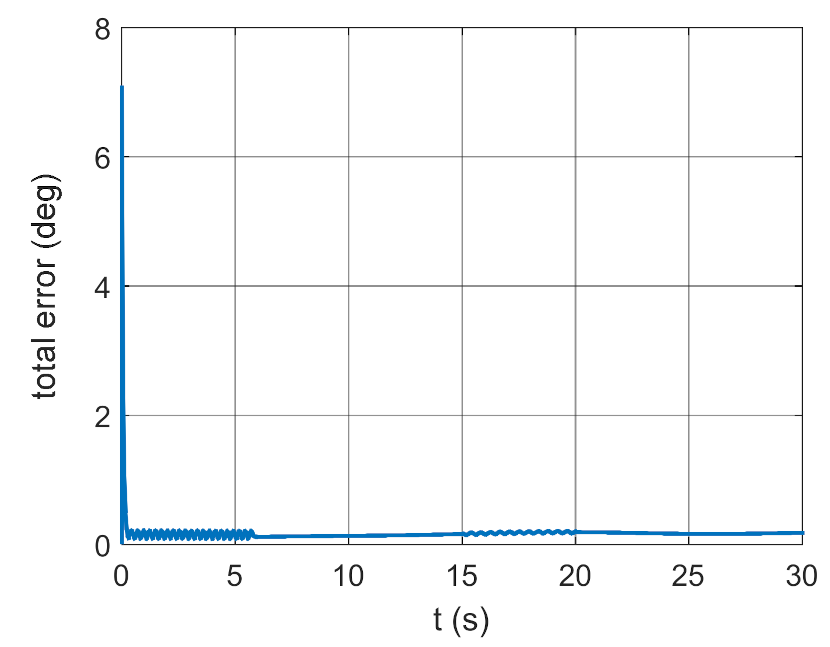
3.2. Simulation Studies Involving the Control over an Optimum Gyroscope System for Homing onto a Ground Target from Onboard a Quadcopter
- IAE (Integral Absolute Error) quality indicator:where:
- 2.
- ISSC (Integral Square State and Control) quality indicator:where:
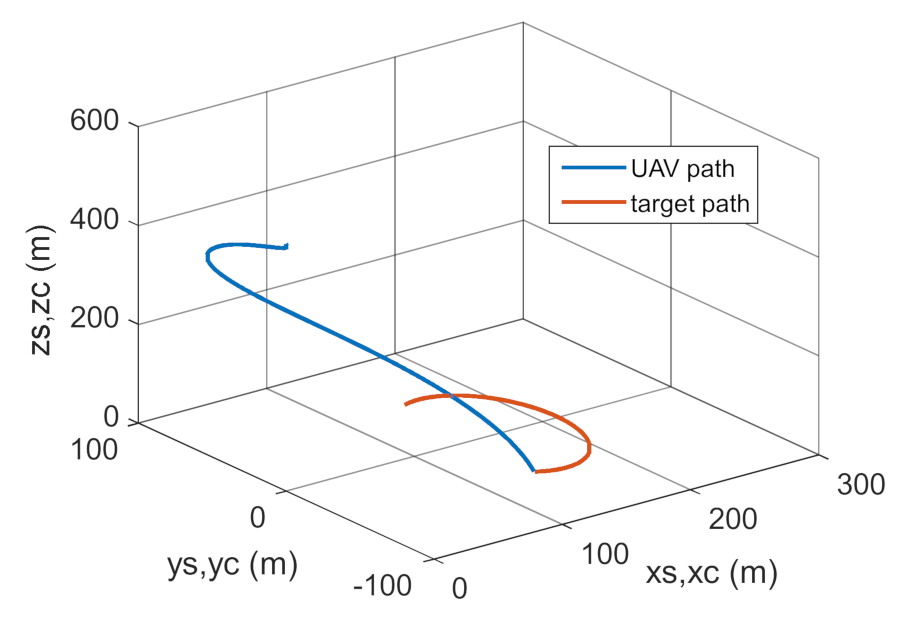

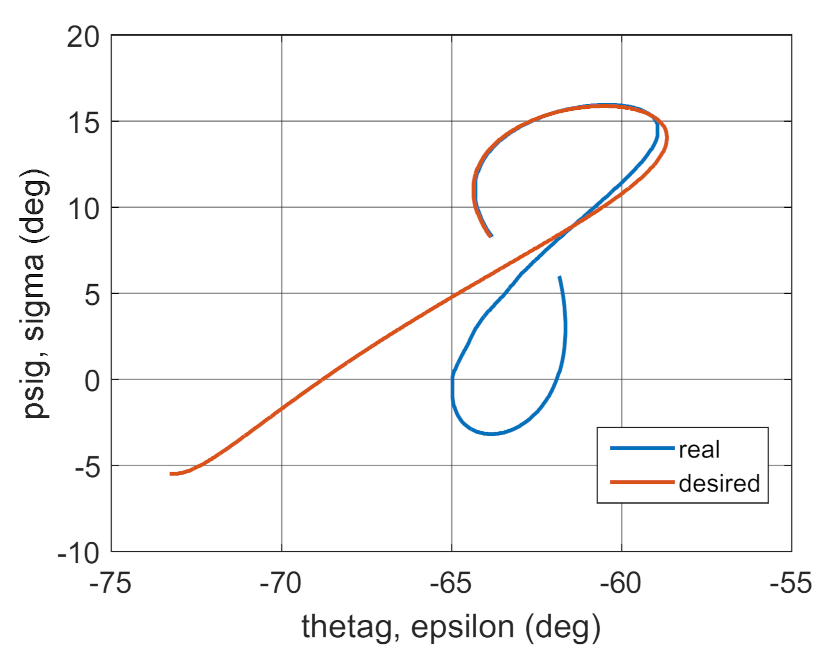
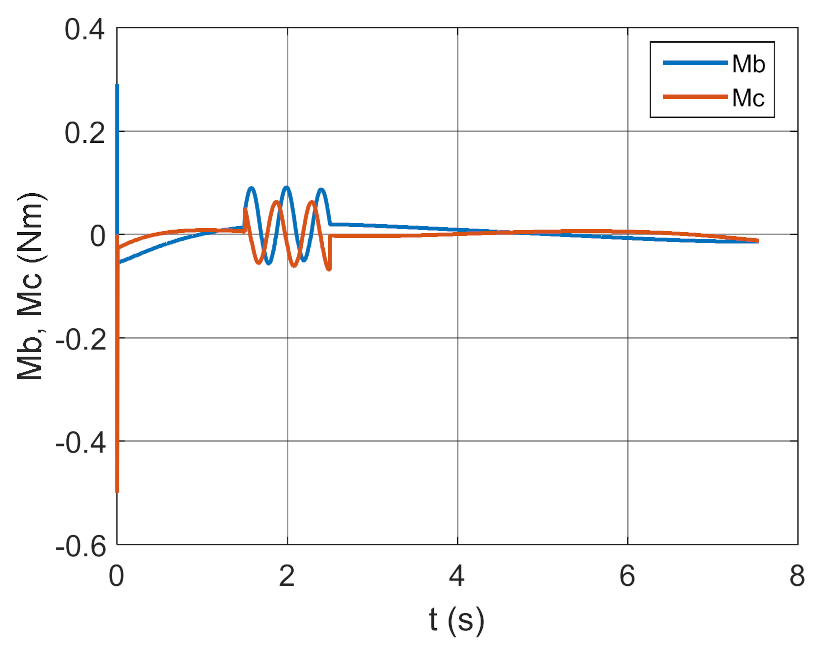
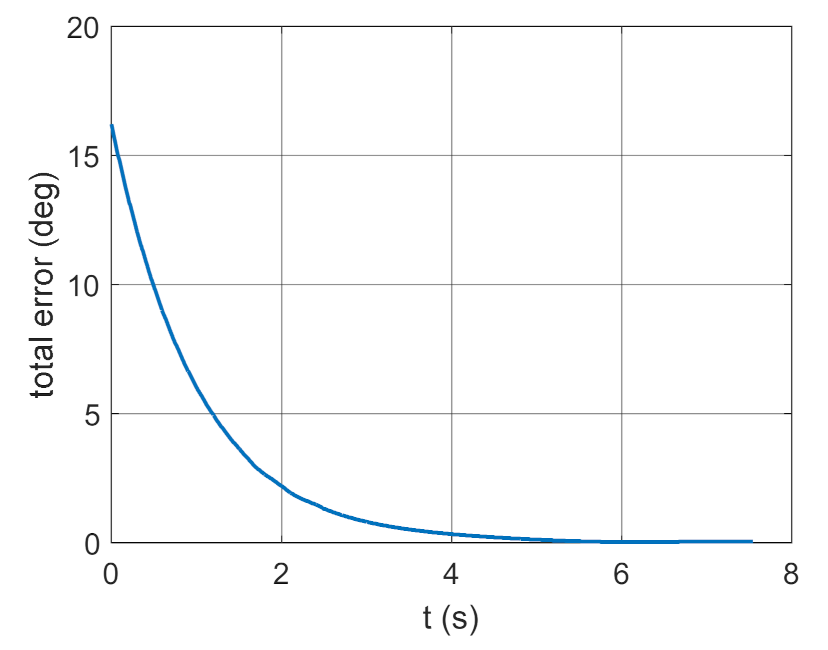



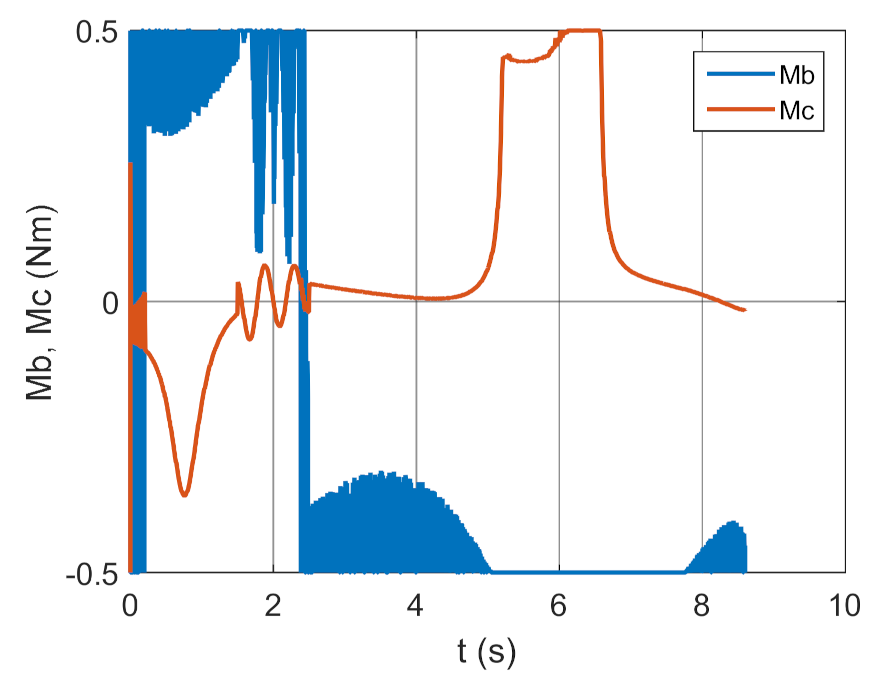

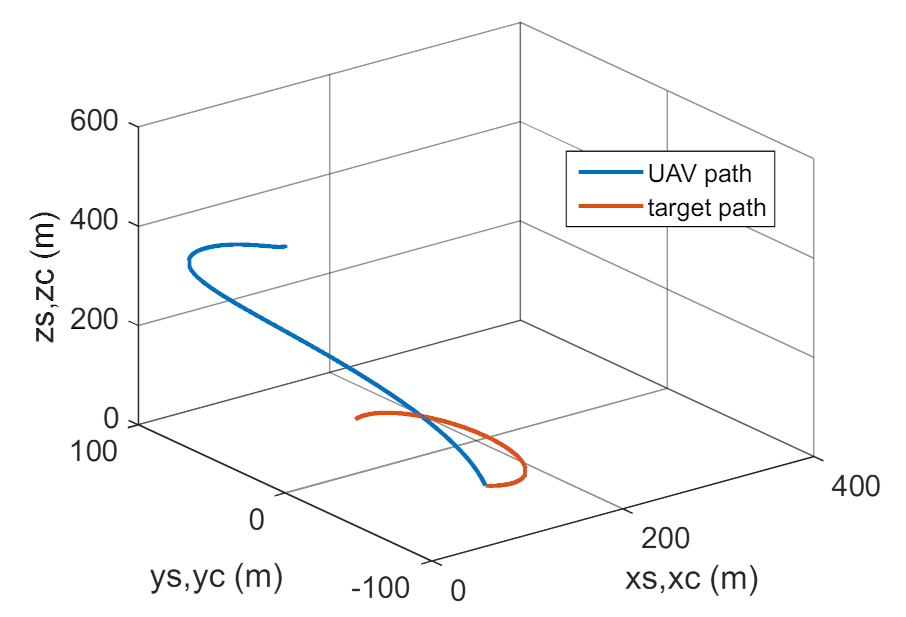
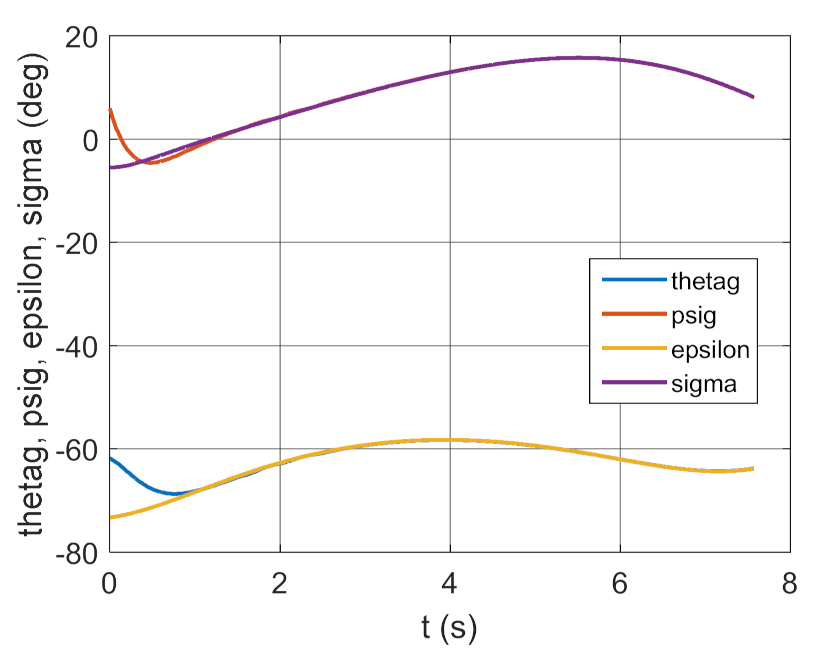
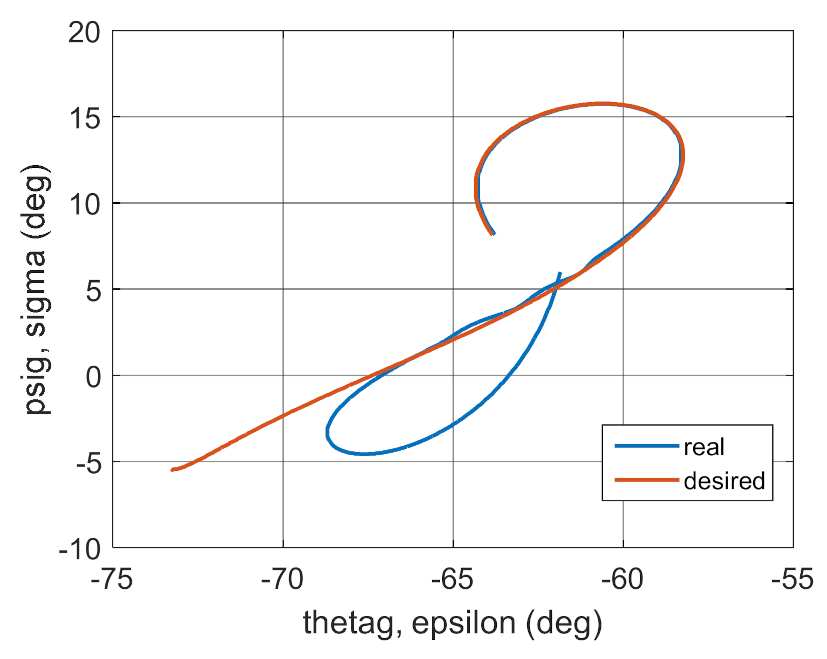

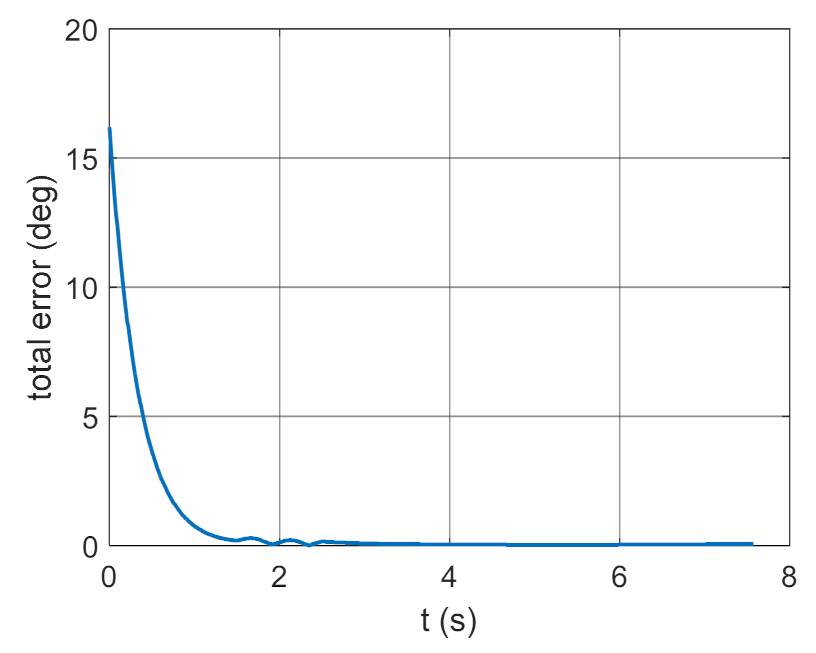
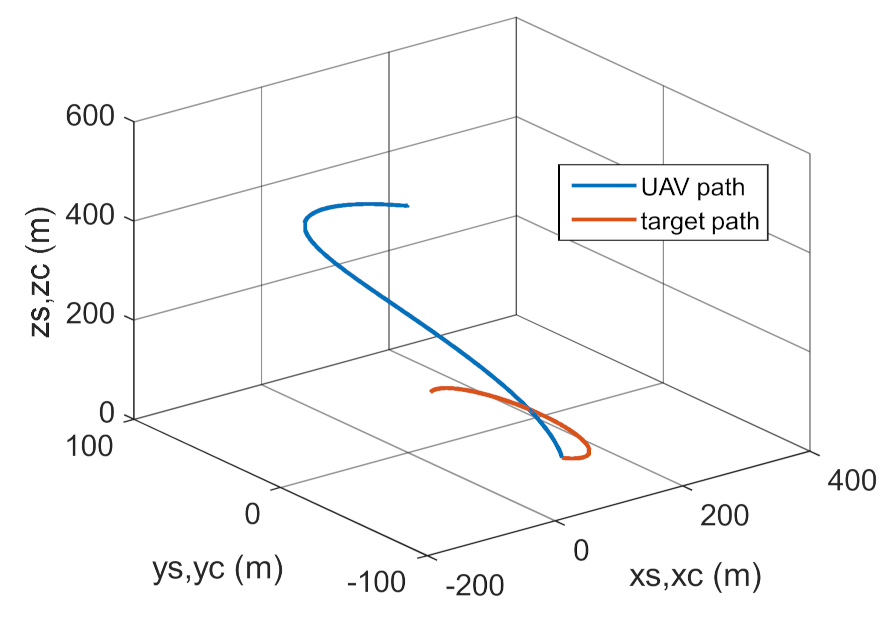

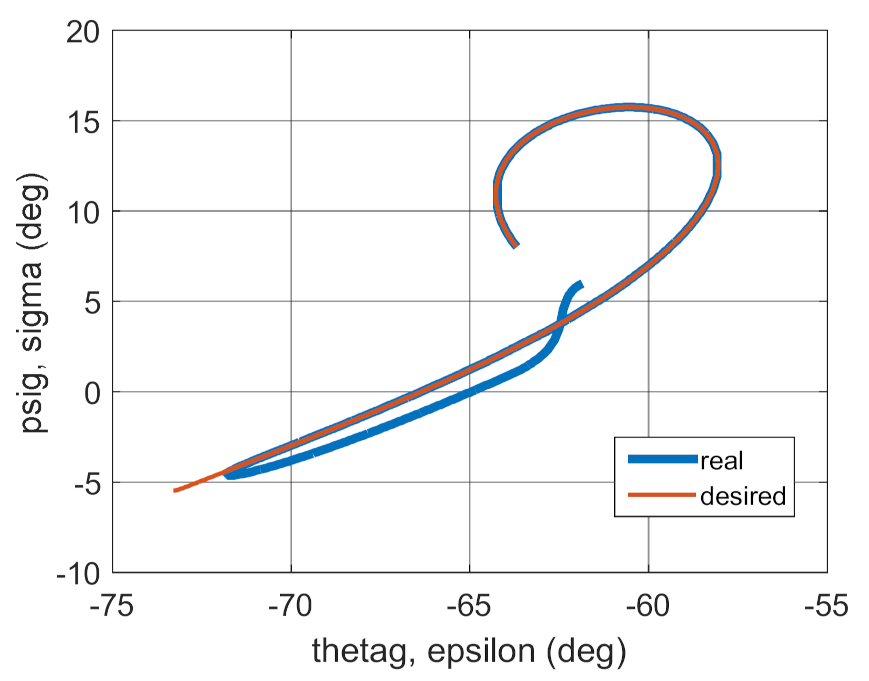
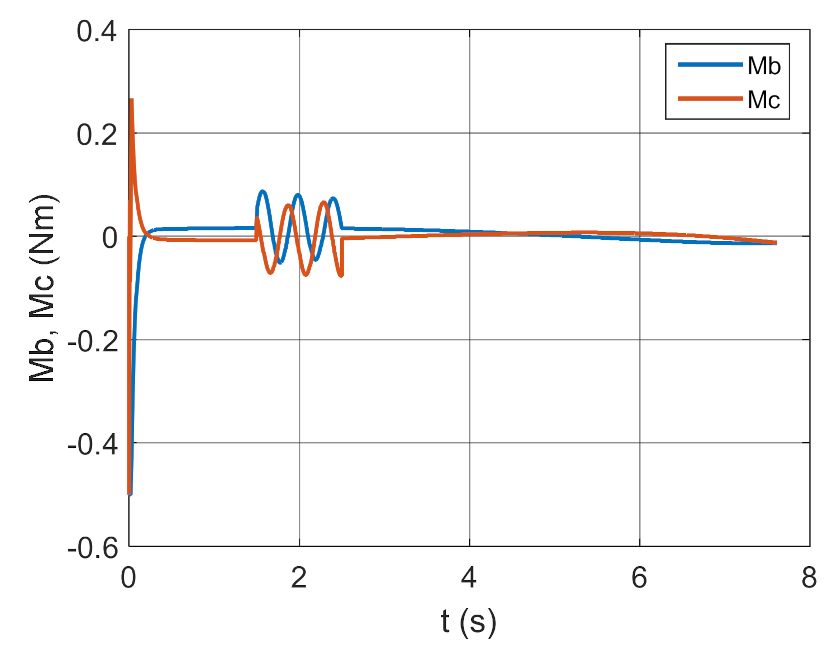
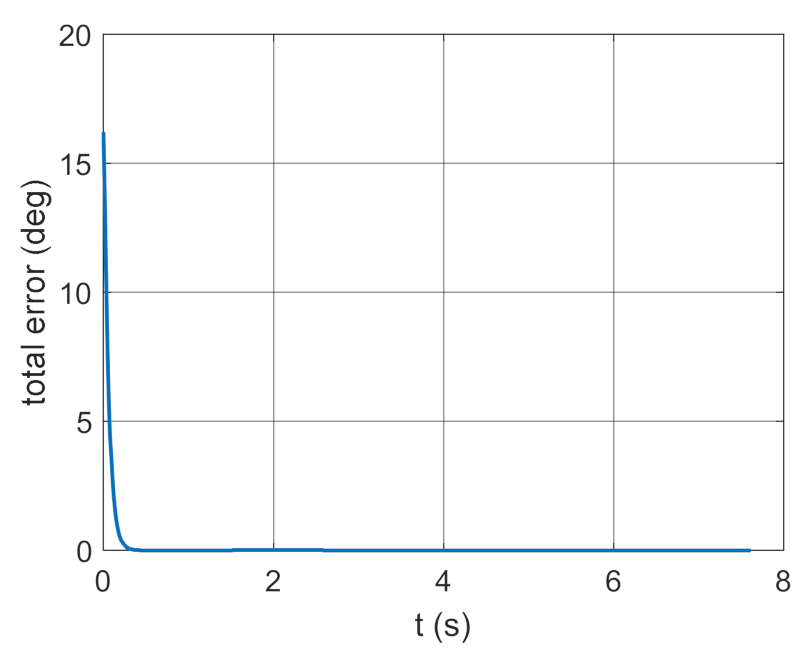
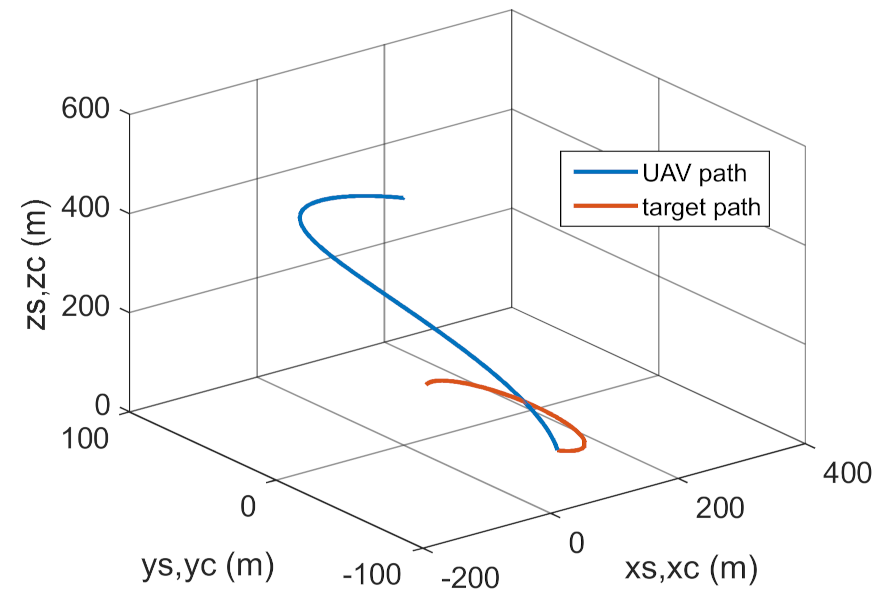

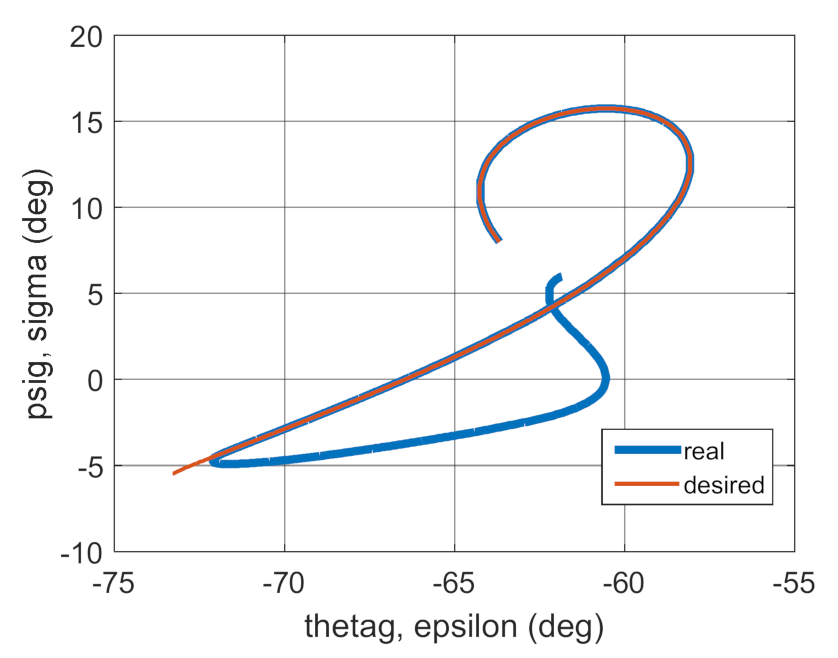
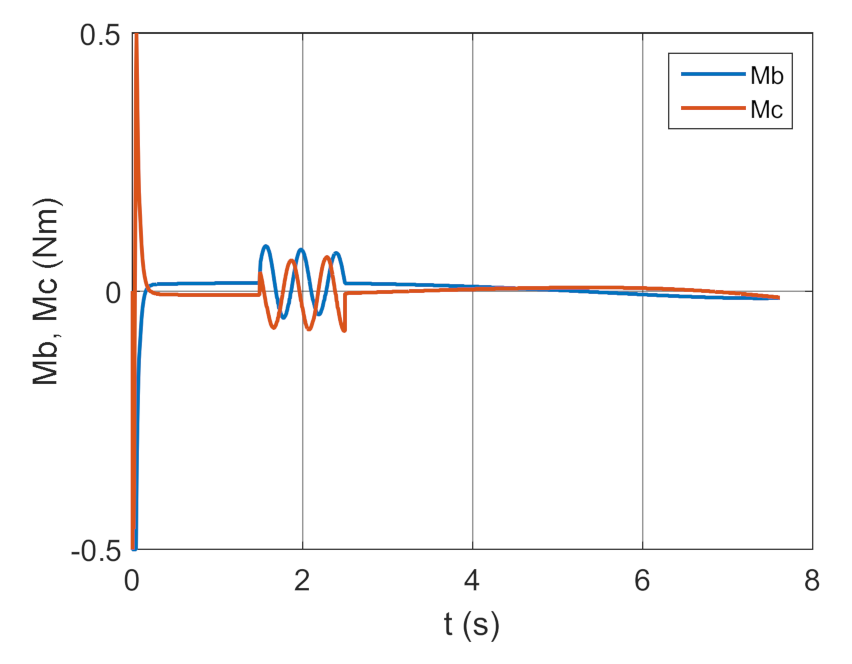
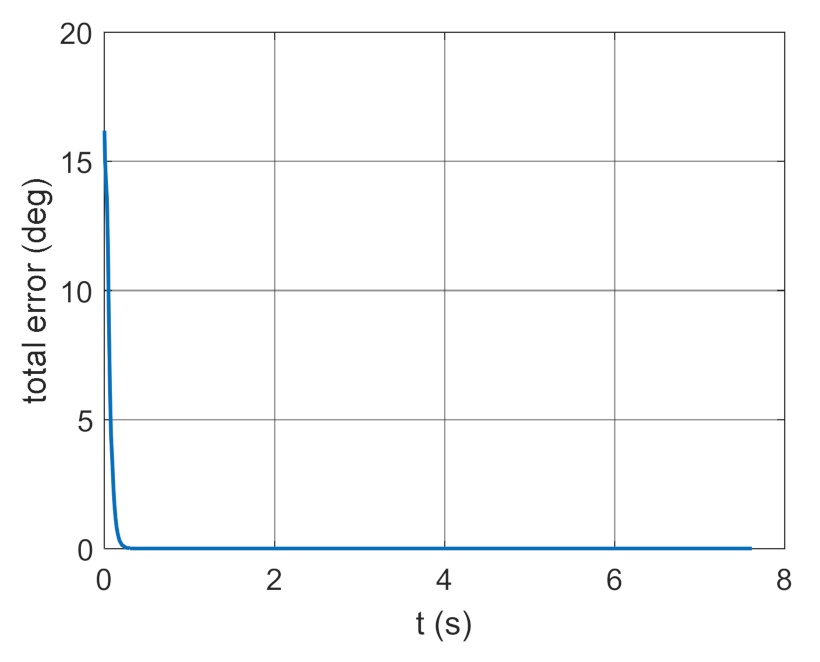

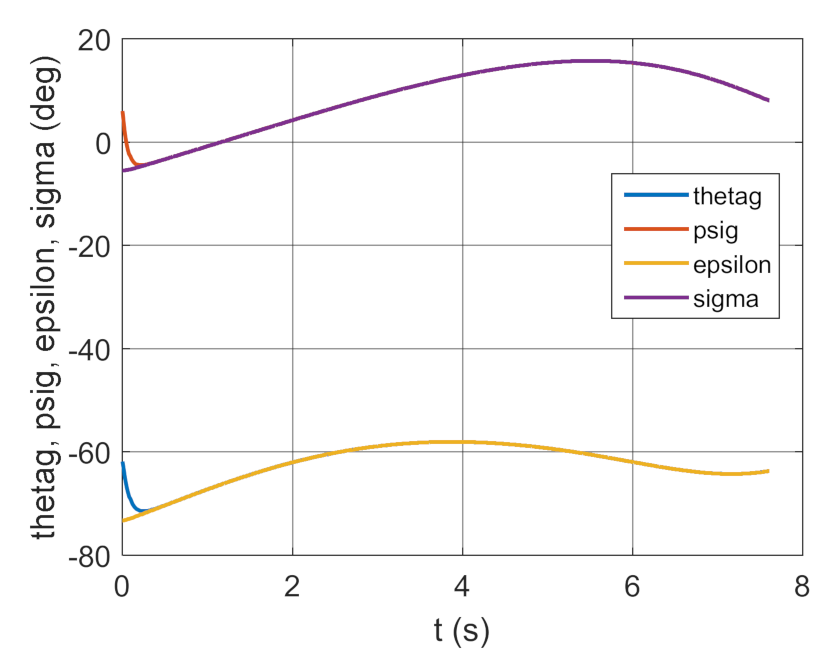
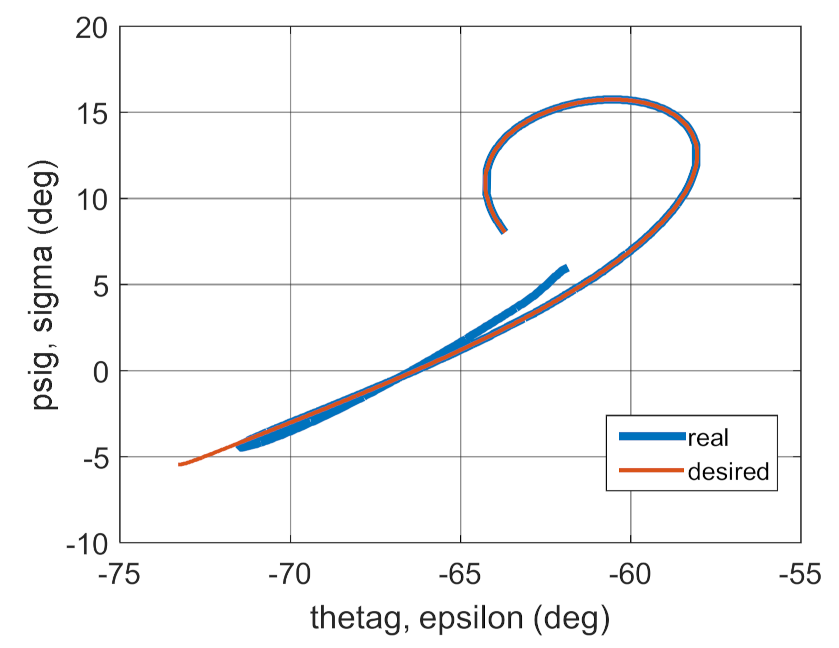


4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gapinski, D.; Krzysztofik, I. The process of tracking an air target by the designed scanning and tracking seeker. In Proceedings of the 2014 15th International Carpathian Control Conference (ICCC), Velke Karlovice, Czech Republic, 28–30 May 2014; IEEE: New York, NY, USA; pp. 129–134. [Google Scholar] [CrossRef]
- Stefański, K.; Koruba, Z. Analysis of the guiding of bombs on ground targets using a gyroscope system. J. Theor. Appl. Mech. 2012, 50, 967–973. [Google Scholar]
- Chodnicki, M.; Bartnik, K.; Nowakowski, M.; Kowaleczko, G. Design and analysis of a feedback loop to regulate the basic parameters of the unmanned aircraft. Aircr. Eng. Aerosp. Technol. 2018, 92, 318–328. [Google Scholar] [CrossRef]
- Kowaleczko, G.; Pietraszek, M.; Słonkiewicz, Ł. Analysis of the Impact of the Target Illumination Time on the Effectiveness of the Flight Trajectory Correction System. J. Konbin 2019, 49, 229–253. [Google Scholar] [CrossRef] [Green Version]
- Hasseni, S.; Abdou, L. Decentralized PID Control by Using GA Optimization Applied to a Quadrotor. J. Autom. Mob. Robot. Intell. Syst. 2018, 12, 33–44. [Google Scholar] [CrossRef]
- Praveen, V.; Pillai, A.S. Modeling and simulation of quadcopter using PID controller. Int. J. Control Theory Appl. 2016, 9, 7151–7158. [Google Scholar]
- Zulu, A.; John, S. A Review of Control Algorithms for Autonomous Quadrotors. Open J. Appl. Sci. 2014, 4, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Xuan-Mung, N.; Hong, S.K. Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer. Appl. Sci. 2019, 9, 5184. [Google Scholar] [CrossRef] [Green Version]
- Xuan-Mung, N.; Hong, S.K.; Nguyen, N.P.; Ha, L.N.N.T.; Le, T.-L. Autonomous Quadcopter Precision Landing Onto a Heaving Platform: New Method and Experiment. IEEE Access 2020, 8, 167192–167202. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.-K. Improved Altitude Control Algorithm for Quadcopter Unmanned Aerial Vehicles. Appl. Sci. 2019, 9, 2122. [Google Scholar] [CrossRef] [Green Version]
- Xuan-Mung, N.; Hong, S.-K. A Multicopter Ground Testbed for the Evaluation of Attitude and Position Controller. Int. J. End. Technol. 2018, 7, 65–73. [Google Scholar]
- Shi, X.; Lu, L.; Jin, G.; Tan, L. Research on the attitude of small UAV based on MEMS devices. AIP Conf. Proc. 2017, 1839, 020094. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Praveen, B.; Nisanth, U.; Hemanth, M. Development of Auto Stabilization Algorithm for UAV Using Gyro Sensor. Int. J. Eng. Res. Technol. 2017, 5, 1–3. [Google Scholar]
- Awrejcewicz, J.; Koruba, Z. Classical Mechanics. Applied Mechanics and Mechatronics; Springer: New York, NY, USA, 2012; Volume 30. [Google Scholar]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tewari, A. Modern Control Design with Matlab and Simulink; John Wiley & Sons: Chichester, UK, 2002. [Google Scholar]
- Kaczorek, T.; Dzieliński, A.; Dąbrowski, W.; Łopatka, R. Fundamentals of Control Theory; WNT: Warsaw, Poland, 2013. [Google Scholar]
- Krzysztofik, I.; Takosoglu, J.; Koruba, Z. Selected methods of control of the scanning and tracking gyroscope system mounted on a combat vehicle. Annu. Rev. Control 2017, 44, 173–182. [Google Scholar] [CrossRef]
- Baranowski, L. Effect of the mathematical model and integration step on the accuracy of the results of computation of artillery projectile flight parameters. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 475–484. [Google Scholar] [CrossRef] [Green Version]
- Grzyb, M.; Stefanski, K. Turbulence impact on the control of guided bomb unit. In Proceedings of the 23rd International Conference Engineering Mechanics 2017, Svratka, Czech Republic, 15–18 May 2017; Brno University of Technology: Brno, Czech Republic; pp. 358–361. [Google Scholar]
- Kowaleczko, G.; Żyluk, A. Influence of atmospheric turbulence on bomb release. J. Theor. Appl. Mech. 2009, 47, 69–90. [Google Scholar]



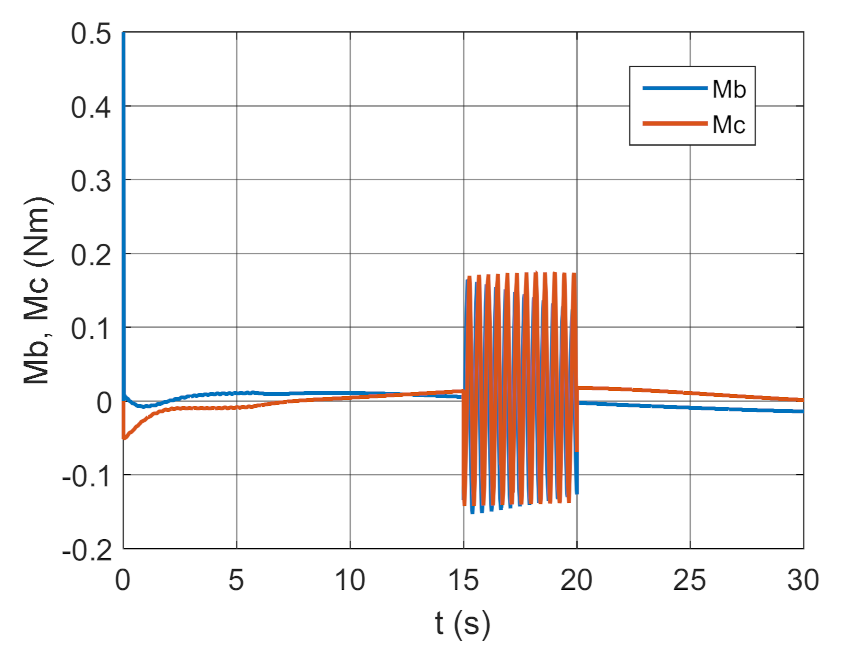
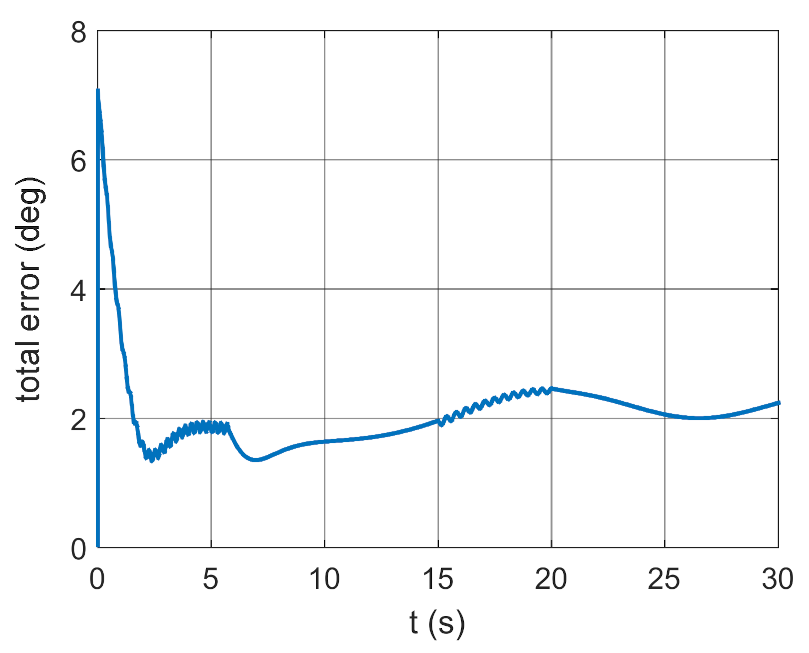
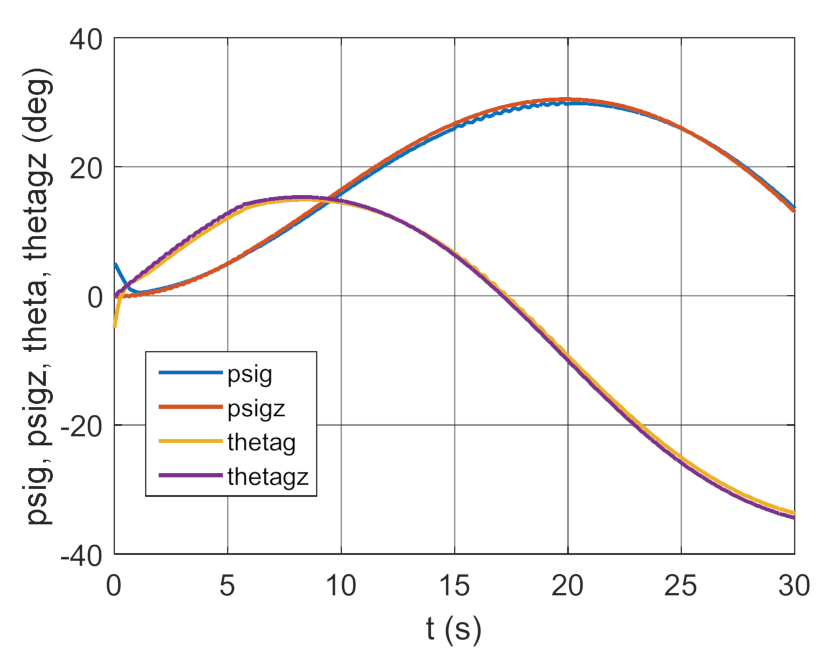
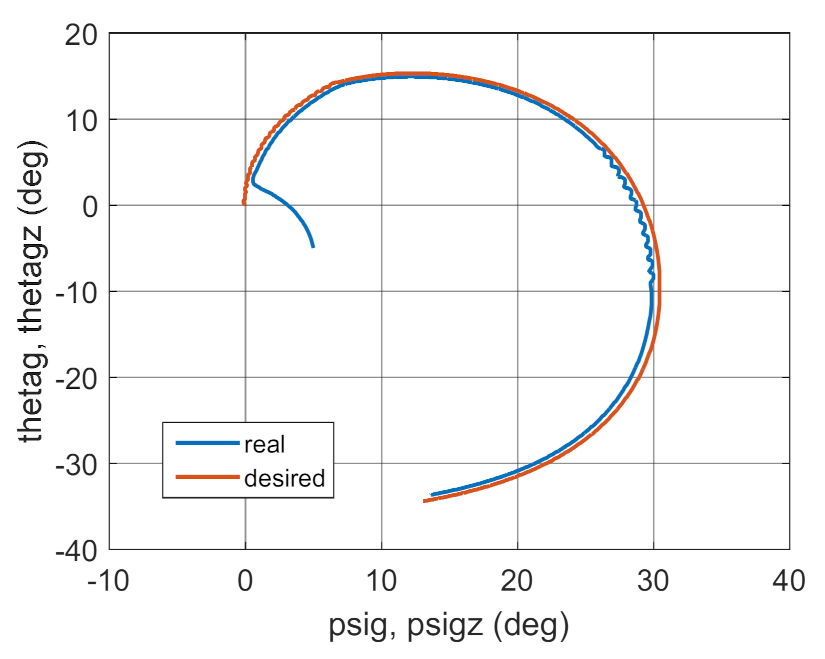

| Variant | Regulator Parameters | ISSC | IAE |
|---|---|---|---|
| 1 | 9.2403 × 108 | 5.3726 × 103 | |
| 2 | 9.6861 × 108 | 7.2331 × 103 | |
| 3 | − optimum | 1.1070 × 109 | 4.3352 × 103 |
| 4 | − optimum | 1.6691 × 109 | 1.7290 × 103 |
| 5 | 1.6845 × 109 | 1.8137 × 103 | |
| 6 | 1.6263 × 109 | 1.9237 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krzysztofik, I.; Koruba, Z. Study on the Sensitivity of a Gyroscope System Homing a Quadcopter onto a Moving Ground Target under the Action of External Disturbance. Energies 2021, 14, 1696. https://doi.org/10.3390/en14061696
Krzysztofik I, Koruba Z. Study on the Sensitivity of a Gyroscope System Homing a Quadcopter onto a Moving Ground Target under the Action of External Disturbance. Energies. 2021; 14(6):1696. https://doi.org/10.3390/en14061696
Chicago/Turabian StyleKrzysztofik, Izabela, and Zbigniew Koruba. 2021. "Study on the Sensitivity of a Gyroscope System Homing a Quadcopter onto a Moving Ground Target under the Action of External Disturbance" Energies 14, no. 6: 1696. https://doi.org/10.3390/en14061696
APA StyleKrzysztofik, I., & Koruba, Z. (2021). Study on the Sensitivity of a Gyroscope System Homing a Quadcopter onto a Moving Ground Target under the Action of External Disturbance. Energies, 14(6), 1696. https://doi.org/10.3390/en14061696







