Abstract
Worst-case execution time (WCET) is an important metric in real-time systems that helps in energy usage modeling and predefined execution time requirement evaluation. While basic timing analysis relies on execution path identification and its length evaluation, multi-thread code with critical section usage brings additional complications and requires analysis of resource-waiting time estimation. In this paper, we solve a problem of worst-case execution time overestimation reduction in situations when multiple threads are executing loops with the same critical section usage in each iteration. The experiment showed the worst-case execution time does not take into account the proportion between computational and critical sections; therefore, we proposed a new worst-case execution time calculation model to reduce the overestimation. The proposed model results prove to reduce the overestimation on average by half in comparison to the theoretical model. Therefore, this leads to more accurate execution time and energy consumption estimation.
1. Introduction
One of the metrics defining programming code efficiency is the execution time, that is, task execution speed. The execution time is highly important in real-time systems where strict bounds for task execution time might be applied. Safety-critical real-time embedded systems need to be functionally correct, meet timing deadlines requirement of low energy consumption, and conform to the increasing demand for computing power. It is a necessary step in the development and validation process for real-time embedded systems.
One of the reasons to predict and assure programming code execution time bounds is energy consumption. In battery-powered systems, the code execution time should be adjusted to battery replacement or charging times. Since it is also based on the code execution time, the energy consumption amount can be predicted. However, real experiments for code execution time bound estimation in most cases is not appropriate because of expensive resource (and energy) usage. Therefore, it is important to estimate the possible ranges of the code execution time in advance, without executing it. While the best-case (minimal) execution time indicates the ideal situation, the more important is the worst-case execution time (WCET). The WCET is important for the evaluation of software safety and the optimization of energy consumption.
WCET estimation is performed by analyzing possible paths and variations in the code. Traditional WCET takes into account the code flow (operations, conditions, loops, etc.) and resource (memory, critical sections, etc.) usage. WCET in multi-thread, multi-core systems are even more challenging because it requires estimation of interaction between threads. Multi-thread code leads to WCET unpredictability when two or more threads request access to the same critical section at an identical moment in time. This increases the worst-case execution time because at least one thread must wait while the resource will be released. The increased WCET can cause missing the hard deadlines, consequently resulting in system failure [1], and it is very challenging to tightly predict the worst-case resource usage at compile time [2].
In WCET analysis, the goal is to come as close as possible to the real execution time bounds, but not below, the execution time on the target hardware. Due to different reasons, the overestimation of the WCET is unavoidable; however, it should be as close as possible to the real execution time in order to economize on resource and energy usage.
The aim of this paper is to reduce the WCET overestimation in multi-thread loops with critical section usage.
The structure of the paper is as follows. Related research in the area of WCET estimation is overviewed in Section 2. In Section 3, existing WCET estimation model for multi-thread code is adapted for loop usage in order to highlight its overestimation problem. A new WCET estimation model for multi-thread code, with executed loops and critical section usage in it, is also proposed in Section 3. The proposed model is applied and validated in Section 4 to indicate the reduction of the overestimation problem.
The proposed WCET estimation model is new and takes into account the distribution of computational and critical section blocks both of an analyzed and other threads. The proposed model proves to reduce the overestimation on average by half in comparison to the existing theoretical model.
2. Related Research
In design or real-time and embedded systems, the execution time is an important parameter. Execution time allows the prediction of system performance bounds and at the same time impacts the energy consumption. Minimization of energy consumption is an important problem and a key factor in sustainable production and operation. Therefore, the energy consumption analysis and prediction problems are solved in these software and hardware decisions such as wireless sensor networks, cloud/distributed system computing, battery-powered real-time systems, and high-performance computing [3,4,5,6].
The landscape of energy consumption prediction solutions varies. One area is worst-case response energy consumption (WCRE) based on hardware usage. Wagemann et al. [7] proposed a SysWCEC solution, which takes into account different hardware activation and swathing off. Another area is WCET prediction. By knowing the WCET value or modeling it for different situations, the tradeoff between the program performance and energy consumption can be estimated [8]. Therefore, accurate estimation of WCET leads to more accurate energy consumption estimation.
Commonly, there are two main methods of finding WCET—measurement-based methods and static methods. In measurement-based methods, the execution time is measured either through direct measurement or simulation of the code by giving different inputs. The level of granularity at which these measurements can be performed varies for different processor architectures. While most current processor architectures support hardware performance counters, these counters can only provide a limited level of accuracy and care must be taken to obtain accurate measurements [9]. Zoubek and Trommler [10] highlight that the measurement-based method is not safe for critical systems. There are concerns that not all factors are taken into account—the state changes in the underlying hardware cache line being evicted, a pipeline being totally flushed out, etc. [11].
Another WCET estimation method type is static timing analysis. These techniques estimate the execution time of a program without actually executing any code. They are mainly used to determine the WCET of a program, meaning a conservative estimate or upper bound for the execution time of a program. Static methods are safe, from generalized perspectives, but safety comes at the cost of a possible over-approximation. As can be seen, static estimation tries to find an upper bound to the WCET by approaching from higher times, for instance, classifying cache hits that are guaranteed to be applied in every case of execution [12,13,14].
The more active research activity in the field of parallel programming code WCET analysis started from 2011. Then, multiple papers on static timing analysis to derive safe bounds of parallel software were published [15,16,17,18,19,20,21]. Since nowadays hardware solutions are mostly multi-cores, some additional challenges arise in timing analysis. Accurate WCET analysis must take into account multi-thread solutions, shared cache/shared bus usage, concurrently reading and/or writing shared data, etc. All these issues are raised in the field of WCET estimation for independent threads running concurrently [22,23].
A systematic literature analysis was executed in Web of Science: Science Citation Index Expanded (Clarivate), Scopus (Elsevier), Association for Computing Machinery (ACM) Digital Library, and Google Scholar systems to find papers in the field of WCET analysis in modern, parallel systems, loop situations, or critical sections. Most databases were referencing the same scientific papers; therefore, we summarize the main results of the research. The results of the analysis (see Table 1) present the most related WCET research papers, devoted to improving the accuracy of WCET estimates.

Table 1.
Summary of worst-case execution time (WCET) estimation-related research papers.
The summary of research papers in the field of WCET in parallel systems revealed a variety of different research areas. All the papers investigate some specific architectures and situations of solution. This indicates the timing analysis problem modernity because every new architecture or programming code implementation solution requires appropriate models for its timing analysis.
3. WCET Estimation in Parallel Threads, Executing Loop Actions with Critical Section Usage
The calculation of worst-case execution time in parallel applications is difficult because of critical section usage, which can be used only by one thread at one time moment. If the critical section is locked (used by another thread), another thread(s) has to wait until the resource will be released. In situations such as this one, the code execution time cannot be estimated precisely, because it is difficult to predict when different threads will request for a critical section and when they will receive it. The order of critical section execution by different threads has also a big influence on the thread scheduling. Therefore, WCET calculation for each thread must take into account the worst possible order of the critical section usage by different threads.
In Section 3.1, we formalize the existing WCET models by applying them to parallel thread execution in a loop with critical sections. In Section 3.2, we compare the existing models to brute-force situations, representing real WCET values. Based on the insight, a new model for WCET calculation is presented in Section 3.3.
3.1. Theoretical Background for WCET Calculation in Parallel Threads, Executing Loop Actions with Critical Sections
The WCET for each thread can be calculated as a sum of worst-case calculation time (WCCT) and worst-case waiting time (WCWT). This is possible when computational (comp) and critical section (cs) blocks of all threads have performance limits (maximum and minimum possible execution values).
The WCCT for thread X can be calculated easily because no additional influencing factors are influencing it. It is equal to the sum of all computational and critical section blocks maximum sizes. Adapting the idea for a multi-thread loop, it should be calculated by adding maximum execution time values of all n computational blocks and all m critical section blocks in each loop iterations. When maximum block values are the same in each loop iteration the sum of maximum execution time for computational (comp_max) and critical section (cs_max) blocks in one iteration should be multiplied by the number of iterations N in the loop (see Equation (1)).
Equation (1) can be used to obtain WCET in the best-case scenario in which no conflicts exist between different threads. However, it is unrealistic to expect WCCT to be the same as WCET in cases of multiple threads in the loop using the same critical section. The probability of using the same critical section at the same time exists and some additional delay will be added to WCCT.
The worst-case waiting time analysis model, proposed by Ozaktas et al. [23], assumes critical section block in one thread will arrive at the same time as in other threads. In this situation, the thread will be placed into a queue and will be granted access to the critical section as the last thread, after all other threads release it. Taking into account the maximum execution times of these critical sections, the worst-case waiting time of one thread WCWTX can be calculated by adding the maximum value of the critical section in all other threads than this (there are P threads in total) for each iteration. Therefore, if we want to calculate the WCWT for one thread X out of P treads, we need to sum the maximum critical section block size of each m critical sections of each iteration of N iteration loop. The critical section blocks should also be of all other threads rather than the thread itself because the thread does not need to wait for critical section, occupied by itself. Therefore, we sum up critical section block sizes of threads from 1 to P, except the thread X itself (see Equation (2)). In the case in which all iterations of the loop have the same maximum execution time values of critical sections, the sum of all critical section execution times in other threads than this one has to be added and multiplied by the number of iterations in the loop.
To calculate the total WCET of the loop with N iterations and P threads, there have to be taken the WCET value of the thread, which has the maximum WCCTX + WCWTX value (see Equation (3)). It is important to assign the WCET to the maximum sum of WCCTX + WCWTX because it defines when the slowest thread will finish its execution. The program execution will finish only when the last thread finishes its execution.
From now on in this paper, we assume each thread in one loop iteration has just one computational and one critical section. In most cases, the minimum and maximum possible values of computational and critical section blocks are the same for each iteration. This simplifies the problem and reduces some additional variations. Taking into account those assumptions and the presented theoretical background of the situation, the WCET calculation for P parallel threads, executing the same actions in the loop with N iterations can be simplified. The simplified form is different in the expression of WCET value in each iteration of the loop—WCET of one iteration is equal to the sum of the maximum size of its computational block and the worst case for waiting time when the thread must wait for other threads to release the critical section. The maximum critical section execution time for this thread should also be added to obtain the WCCT. Therefore, the WCET of one iteration for thread k is expressed as the sum of the maximum critical section size of each P thread in the system plus the maximum computational size of the thread (Equation (4)).
This formula would be equal to the WCET estimation by Ozaktas et al. [23], adapted for the loop situation. We named this WCET value as theoretical.
3.2. Experiments for WCET Overestimation Estimation
To estimate how the theoretical WCET estimation method is precise, series of experiments were executed. During the experiments, all possible combinations of computational and critical section distribution in time were modeled and called brute-force WCET. In this experiment, a case of two threads was analyzed. Each of the threads executed five loop iterations. The time of all critical sections varied from one to two cycles, while computational block time in the first thread varied from 96 to 97 cycles.
The computational block time of the second thread was modeled to have different values to present different proportions between those two threads CpP (computational time of thread two divided by computational time of thread one). In order to evaluate the impact of the ratio between computational and critical sections, the computational block size of the second thread was changed to obtain 20 different situations. For the second thread, the computational block size started from values of 1–2 cycles and was increased by five cycles for each situation up to 96–97 cycles’ value.
The size of computational and critical sections was selected as cycles in order to use discrete modeling. Due to the huge number of analyzed situations (for this situation, 1,048,576 code block distribution combinations were generated), the discrete event modeling is not suitable for real-time calculations. It also takes time to brute force all possible combinations based on the implementation because it might require additional memory to store all intermediate states.
For comparison of theoretical WCET to modeled, brute-force WCET values were compared to calculated WCCT and WCET values based on the presented equations in Section 3.1.
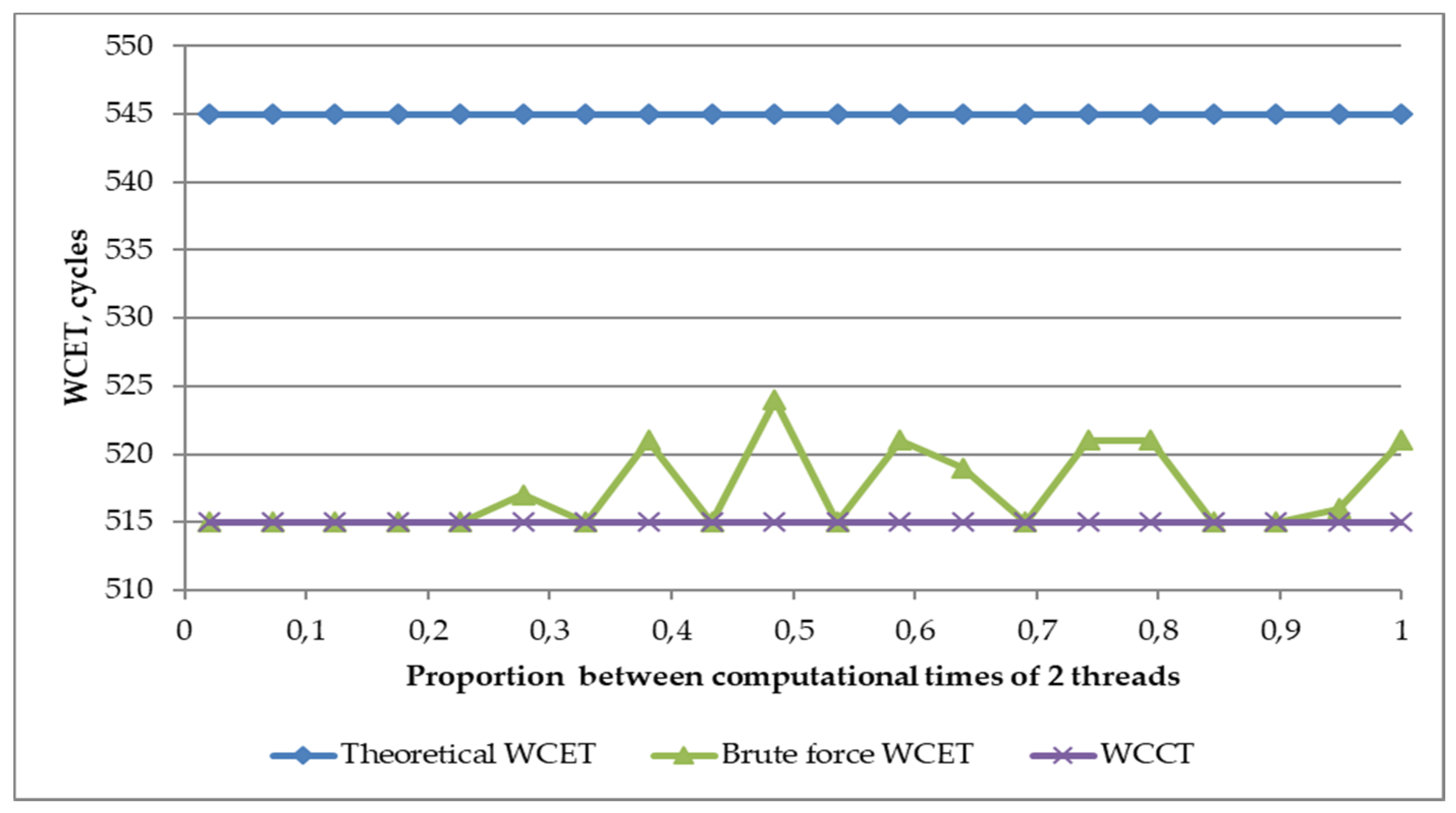
The modeling results revealed that if the critical section maximum size is smaller than the computational section size, the WCWT in most cases is at least two times smaller than the model by Ozaktas et al. [23], predicted and described in the theoretical model (see Figure 1).
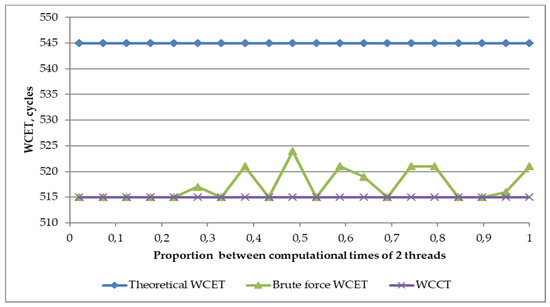
Figure 1.
Experimental results with two threads, illustrating the theoretical WCET value to brute-force WCET to highlight the overestimation problem.
In the given example, the WCCT is equal to 515 cycles. It does not depend on the proportion between the computational time of two threads CpP because for WCCT, we take the longer thread only. This value defines the fastest possible execution time.
As the proposed model by Ozaktas et al. [23] for WCET calculation to WCCT adds maximum critical section execution times of all other threads, the value is constant and independent from the proportion between the computational time of two threads CpP—it is equal to 545 in this example situation.
The area between WCCT and theoretical WCWT in the range where actual execution times might appear. Discrete event modeling results prove its values fit into the defined value range; however, it shows the WCWT calculation might be reduced to be closer to the real (brute-force) WCET—the modeled maximum WCET is equal to 524, which is just one-third of the dedicated range. This is influenced by the fact there are no collisions in every iteration; therefore, the thread maximum waiting time does not have to be added in each iteration. This proves a model for more accurate WCET calculation is needed in order to reduce the overestimation.
3.3. Proposed Model for WCET Overestimation Reduction
To highlight how WCWT can be reduced, an example of a situation with three threads of the same priority are executed in one loop with N iterations and have only one computational and one critical section in one iteration.
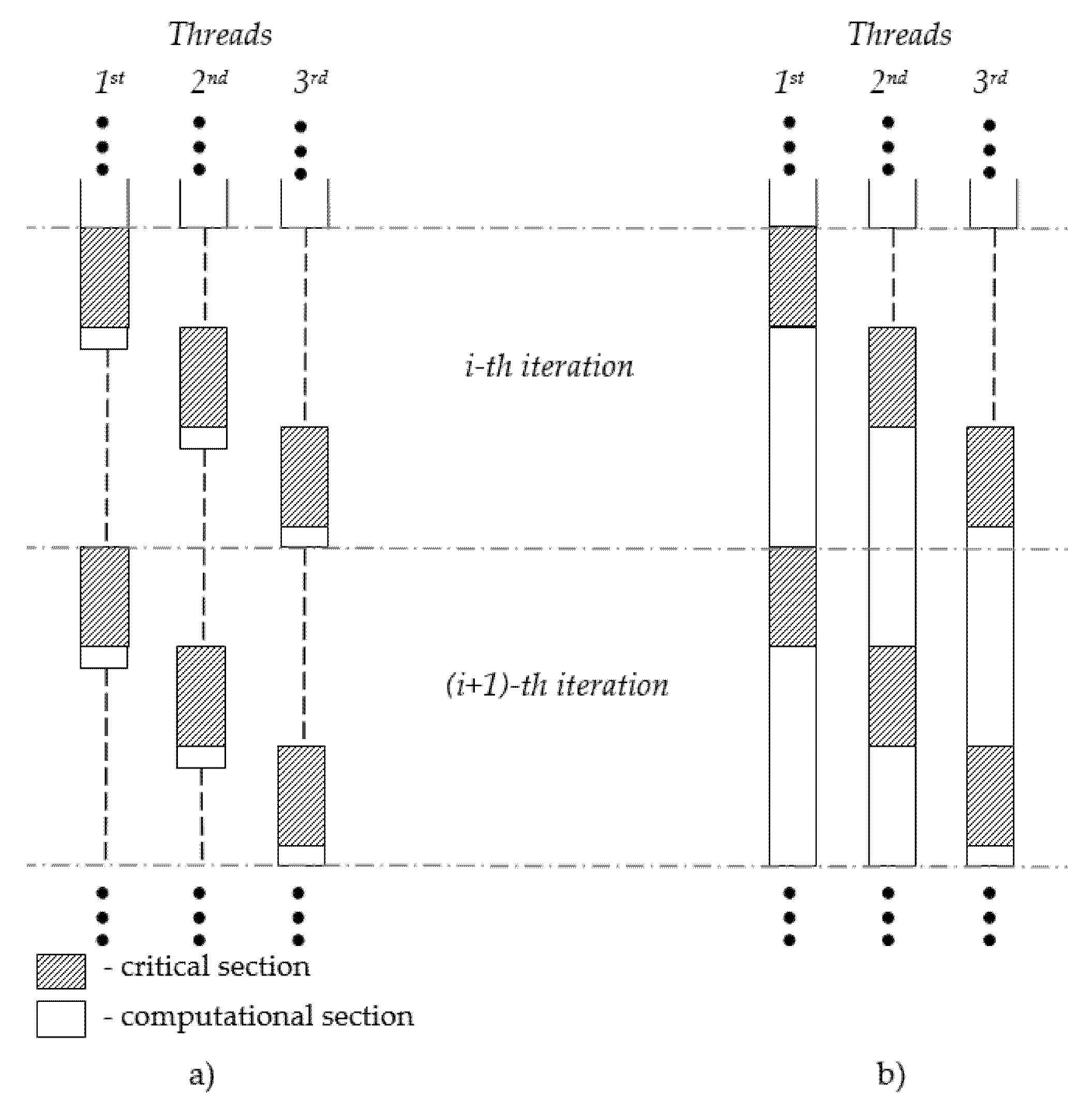
As shown in Figure 2, if all threads would such as to enter a critical section at the same time (the beginning of ith iteration) one of the threads (third thread) would be forced to wait while all others would leave the critical section. This is the worst-case waiting time scenario for the third thread in this loop iteration, which can be obtained by Equation (2). If the maximum value of all computational blocks would be close to zero, all threads would be waiting for a locked resource every time they requested it. Therefore, the real WCET for all threads would be very close to WCET, calculated by Equation (2).
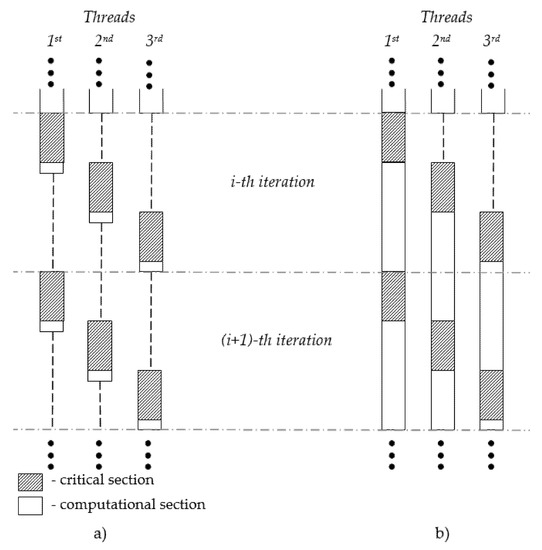
Figure 2.
Example of situations for (a) worst-case waiting time and (b) best-case waiting time.
However, by increasing the size of the computational block, the waiting time can be decreased, while instead of waiting for the critical section, the thread will execute different computations and potentially will request for the critical section block after it will be released by other threads. The ideal situation could be achieved by meeting two conditions—(a) all computational blocks and critical section blocks should be exactly the same length in all threads and (b) the computational block in each thread should be at least as big as the sum of critical section blocks in all the rest threads. When all threads start at the same time, in the same iteration, there would be a delay because of the occupied critical section. In the next iteration, once the first thread releases the critical section, the second thread will take it, and after the second thread release the critical section, the third thread will request for it, etc.
This example and an experiment we described earlier (see Figure 1) shows that the WCWT is dependable on the proportion of computational and critical section size and on computational and critical section size proportion of one thread compared to other threads. Therefore, for WCET calculation overestimation reduction, it is important to find out how many iterations can be executed with no collision in a row after a collision has happened.
Modeling and theoretical assumptions revealed that if the length of the computational section of one thread is shorter than a critical section of another thread, there will be a collision between these threads in every iteration because there is no chance to execute the computational block in one thread with no delay while the second thread is in a critical section. Therefore, if for one thread, the minimal possible computational block length compmin is shorter than the maximum possible critical section length csmax in another thread, the frequency of collisions of threads X with thread Y (cfX->Y) is equal to 1.
If the minimal possible computational block length compmin in one thread is longer than the length of maximum possible critical section length csmax in another thread, at least one full iteration (compmax + csmax) of the shorter thread will be executed during the computational time of the longer thread. This means there would be no collision in this iteration for the shorter thread. The simplest way to find out what is the maximum frequency of collisions between two threads is to calculate how many full iterations of the shorter thread can be fitted into the minimum possible computational time of the longer thread. To do this, we need to take the minimal computational size of the longer thread and divide it from the sum of maximum computational and critical section times. As we calculate how many full iterations might fit into one computational size of another thread, the obtained value should be cast to obtain the integer part of it only. (see Equation (5)).
where compY_min means the minimum possible computational time of the longer thread, compY_min is the maximum possible computational time of the shorter thread, and csY_min is the maximum possible critical section time of the shorter thread.
If both cfX->Y and cfY->X are equal to 1, it means that both threads will have a collision in all iterations. However, if one of these frequencies is smaller than 1 (only one can be smaller than 1), it means multiple iterations of one thread will fit into one iteration of another thread, and there will be no collisions in each iteration of the thread. Naturally, the thread with a shorter loop size will finish earlier compared to the thread with a longer iteration time. Therefore, the longer thread for a certain number of iterations will have no collisions because it will be the only thread of these two that did not finish all iterations of the loop. Therefore, for the first iterations, the delay on one iteration WCWTi will be equal to the maximum value of other thread, while for the rest iterations, the waiting time of one iteration WCWTi will be equal to 0.
The minimal collision frequency of two threads c (see Equation (6)) is important for both the shorter and longer thread WCWT calculation because for the shorter thread, it will define how often the iteration will have a collision in it, while for the longer thread, it can be used to find out how many iterations will be left after the shorter thread is finished.
If there are two threads with known minimum and maximum possible computational times and maximum possible critical section times, the WCET for thread X (WCETX) can be calculated according to Equation (7). In this equation, we calculate how many iterations will have a coalition between those two threads (the WCET of this iteration will be equal to the sum of the maximum computational block size of the thread and the sum of the maximum critical section execution time of both threads) and how many iterations will be collision free (therefore, a maximum critical section block size of the other thread is not needed).
If there are more than two threads, it is not enough to calculate the collision frequency with all other threads and to choose the biggest one. Collisions in one pair of threads influence other pairs as well. Therefore, to ensure the real WCWT will not be longer than the calculated one, all possible combinations between threads have to be taken into account. For each pair, the collision frequency has to be evaluated. This is performed by calculating how many iterations of one thread would fit into the minimal possible computational time of another thread. The iteration execution time of the later thread is calculated by simulating a situation in which it will be the last one in the queue to receive access to the critical section. Therefore, the thread will have to wait for the critical section to be released by all other threads in the queue (see Equation (8)).
As in the two-thread case, Equation (6) is used to obtain the collision coefficient, which defines what part of iterations will have a collision or will be free of collisions.
When more than two threads are used, each thread may have collisions with more than one other thread in the same iterations. Therefore, the collision coefficient for thread X is the maximum collision coefficient between thread X and all the other threads (see Equation (9)).
Accordingly, Equation (7) has to be changed (see Equation (10)) to obtain a more universal form suitable for any number of threads, rather than two only.
The proposed WCET estimation model takes into account the proportion between computational and critical sections in one specific thread and the proportion of threads’ computational block size to all the other threads. The model requires multiple calculations to obtain all interactions between different threads; however, the calculation is not costly and its implementation and execution complexity are much easier in comparison to discrete event modeling.
4. Validation of the Proposed Model
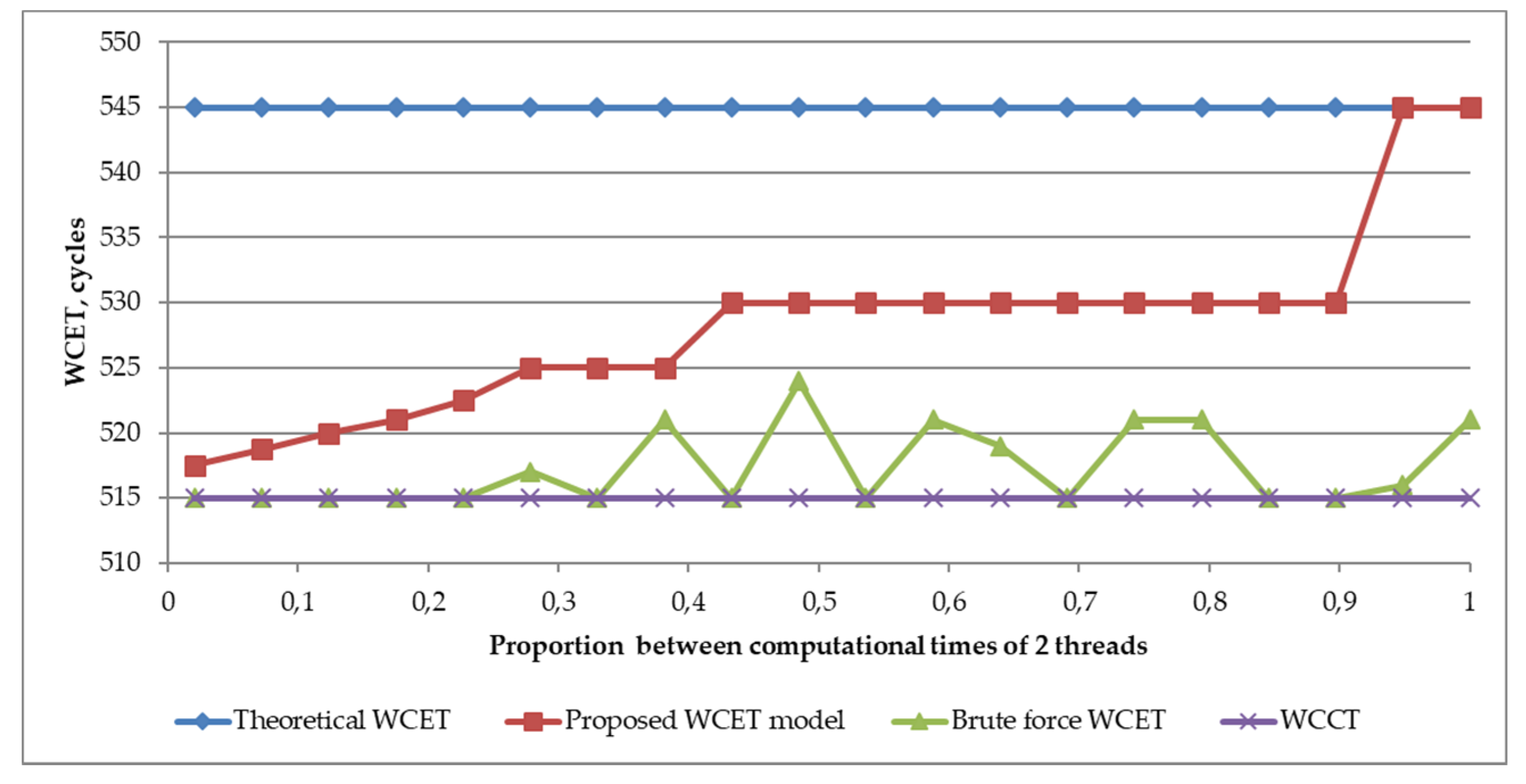
The proposed WCET model was validated by extending the experiment, described in Section 3.2. The same parameters were used to calculate WCET values with the proposed model. The experiment with two-thread results showed the proposed model presents the WCET values more realistically (see Figure 3). In the analyzed situation, the proposed model allowed the reduction of the overestimation of the WCET up to 10 times in situations when the size between computational times of two threads was very different.
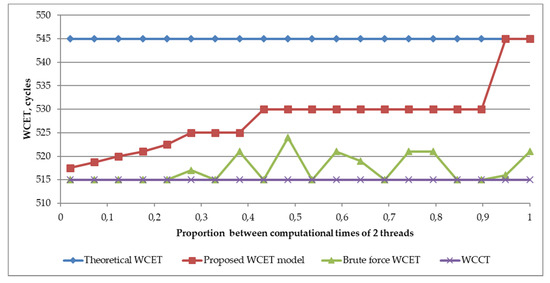
Figure 3.
Extended results of Section 3.2 experiment results with two threads, illustrating the position of the proposed WCET model results in comparison to theoretical and realistic values.
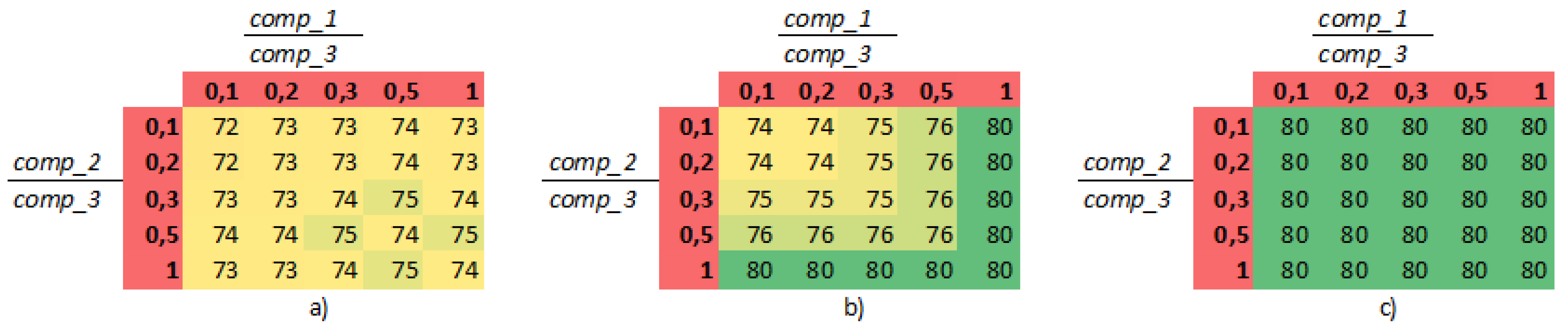
By inspecting how the proposed model meets the brute-force modeled situation with more than two threads, an analysis of three thread and four iteration loops for each of them was executed. Five possible variants of computational and critical section blocks for each thread was modeled by using discrete event modeling (see Figure 4a), calculated by using our proposed WCET model (see Figure 4b), and calculated by using theoretical WCET model, based on the model by Ozaktas et al. [23] (see Figure 4c).
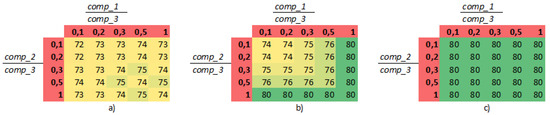
Figure 4.
Results of WCET in three threads and four iteration loops situation, obtained by (a) brute-force modeled WCET (b) proposed WCET model, and (c) theoretical WCET model.
As discrete event modeling has limitations, all threads had a critical section of one cycle to reduce the model complexity. Computational blocks of the third thread varied from 16 to 17 cycles, while computational times of first and second threads had values [1;2], [2;3], [4;8], [8;9], and [16;17]. The variations allowed us to evaluate how the WCET depends on the ratio of maximum computational times in the first and second threads (comp_1, comp_2) to the third thread’s maximum computational time (comp_3). Critical block size in all threads was constant, and the third thread’s computational block size was also constant; therefore, we analyzed 25 different combinations by changing the computational block sizes of thread 1 ad thread 2 (five different values for each of the two threads). In Figure 4, all 25 combinations are represented as intersections of proportion between computational blocks of first and third threads and the proportion between computational blocks of second and third threads. As characteristic to the theoretical model based on Ozaktas et al. study(Figure 4c), all WCET values are identical, even though the proportion between computational blocks and this situation is equal to 80 cycles, while the modeled value has a different pattern, and the WCET value varies from 72 to 75 cycles (Figure 4a). The results of our proposed model are in between those two solutions (Figure 4b), where the WCET values vary from 74 to 80 cycles. It does not mimic the pattern of modeled WCET, however, reduces the overestimation of the theoretical model.
Results of this experiment show that the proposed WCET model is closer (the overestimation varies from 1% to 10% and on average is 4%) to the brute force modeled results and more closely mimics the distribution of the WCET values in comparison to the theoretical model (the overestimation varies from 7% to 11% and on average is 9%).
To evaluate whether the changes are significant in comparison to the theoretical WCET model, t distribution and a significance value (p-value) were used. The difference between the calculated WCET value and modeled execution time value for all 25 cases was analyzed. The difference for the theoretical model is 6.4 (standard deviation equal to 0.866), while for the proposed is 3.253 (standard deviation equal to 2.354). Based on these numbers, the calculated p-value is < 0.0001. This means a significant value and 95% confidence interval of the difference between results of these two models, i.e., the two means are significantly different.
The proposed model was also applied to multiple different situations in a range of brute force-based discrete event modeling tools possibilities in order to estimate whether it guarantees that the real (modeled) WCET value does not increase the calculated WCET value. All situations proved the calculated WCET value is greater or equal to the modeled WCET value and, at the same time, is less or equal to the calculated theoretical WCET value.
5. Conclusions
Sustainable development encourages the reduction of energy consumption in all possible areas. System programing code execution timing analysis is one of the factors used for system energy consumption modeling and prediction. While information technologies are changing over time, the timing analysis methods must follow to assure accurate energy consumption modeling and prediction results. Multi-thread systems are widely used; however, existing WCET estimation models are not accurate for timing analysis of multiple threads with the usage of the same critical section—in our analyzed situations the overestimation in average reaches 5%. Therefore, modifications to existing solutions should be performed to achieve more realistic WCET results.
Discrete event modeling revealed the WCET depends on the proportion of computational blocks between each thread in the loop. Therefore, for accurate WCET estimation in multi-thread loops, WCET for each thread should be evaluated by taking into account both critical sections and computational blocks of other threads—WCWT estimation based on critical section size of other threads leads to an overestimation of the WCET.
A newly proposed WCET estimation model allows reduction of overestimation—the overestimation was reduced almost twice (from 5% to 2% in analyzed two-thread situations and from 9% to 4% in three-thread situations) in comparison to the theoretical, existing model. This is a statistically significant change and decreases the overestimation problem. However, there is room for improvement because discrete event modeled WCET proves the proposed model also has an overestimation problem.
Author Contributions
Conceptualization, S.R.; methodology, S.R.; software, S.R. and A.S. (Andrius Stankevicius); validation, S.R., A.S. (Asta Slotkiene), and I.S.; formal analysis, S.R. and S.V.; investigation, S.R., A.S. (Asta Slotkiene), and K.T.; resources, A.S. (Asta Slotkiene), K.T., I.S., A.S. (Andrius Stankevicius), and S.V.; data curation, S.R. and A.S. (Asta Slotkiene); writing—original draft preparation, S.R., and A.S. (Asta Slotkiene); writing—review and editing, S.R., A.S. (Asta Slotkiene), K.T., I.S., A.S. (Andrius Stankevicius), and S.V.; visualization, S.R.; supervision, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work would not be performed without COST Action IC1202—Timing Analysis on Code-Level (TACLe) support which funded the short-term scientific mission to Institut de Recherche en Informatique de Toulouse (IRIT). The authors especially thank Christine Rochange for the inspiration and scientific support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- El Sayed, M.A.; El Sayed, M.S.; Aly, R.F.; Habashy, S.M. Energy-Efficient Task Partitioning for Real-Time Scheduling on Multi-Core Platforms. Computers 2021, 10, 10. [Google Scholar] [CrossRef]
- Reder, S.; Masing, L.; Bucher, H.; ter Braak, T.; Stripf, T.; Becker, J. A WCET-Aware Parallel Programming Model for Predictability Enhanced Multi-core Architectures. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition, Dresden, Germany, 19–23 March 2018. [Google Scholar]
- Meng, F.; Su, X. Reducing WCET Overestimations by Correcting Errors in Loop Bound Constraints. Energies 2017, 10, 2113. [Google Scholar] [CrossRef]
- Shiraz, M.; Gani, A.; Shamim, A.; Khan, S.; Ahmad, R.W. Energy Efficient Computational Offloading Framework for Mobile Cloud Computing. J. Grid Comput. 2015, 13, 1–18. [Google Scholar] [CrossRef]
- Shaheen, Q.; Shiraz, M.; Khan, S.; Majeed, R.; Guizani, M.; Khan, N.; Aseere, A.M. Towards Energy Saving in Computational Clouds: Taxonomy, Review, and Open Challenges. IEEE Access 2019, 6, 29407–29418. [Google Scholar] [CrossRef]
- Khan, M.K.; Shiraz, M.; Ghafoor, K.Z.; Khan, S.; Sadig, A.S.; Ahmed, G. EE-MRP: Energy-efficient multistage routing protocol for wireless sensor networks. Wirel. Commun. Mob. Comput. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Wägemann, P.; Dietrich, C.; Distler, T.; Ulbrich, P.; Schröder-Preikschat, W. Whole-system worst-case energy-consumption analysis for energy-constrained real-time systems. In Proceedings of the 30th Euromicro Conference on Real-Time Systems (ECRTS 2018), Barcelona, Spain, 3–6 July 2018. [Google Scholar]
- Wang, Z.; Gu, Z.; Shao, Z. WCET-aware energy-efficient data allocation on scratchpad memory for real-time embedded systems. IEEE Trans. 2014, 23, 2700–2704. [Google Scholar] [CrossRef]
- Zaparanuks, D. Accuracy of performance counter measurements. In Performance Analysis of Systems and Software; IEEE: New York, NY, USA, 2009. [Google Scholar]
- Zoubek, C.; Trommler, P. Overview of worst case execution time analysis in single- and multicore environments. In Proceedings of the ARCS 2017—30th International Conference on Architecture of Computing Systems, Vienna, Austria, 3–6 April 2017. [Google Scholar]
- Lokuciejewski, P.; Marwedel, P. Worst-Case Execution Time Aware Compilation Techniques for Real-Time Systems—Summary and Future Work; Springer: Berlin/Heidelberg, Germany, 2011; pp. 229–234. [Google Scholar]
- Mushtaq, H.; AI-Ars, Z.; Bertels, K. Accurate and efficient identification of worst-case execution time for multi-core processors: A survey. In Proceedings of the 8th IEEE Design and Test Symposium, Marrakesh, Morocco, 16–18 December 2013. [Google Scholar]
- Bygde, S.; Ermedahl, A.; Lisper, B. An efficient algorithm for parametric WCET calculation. J. Syst. Archit. 2011, 57, 614–624. [Google Scholar] [CrossRef]
- Cassé, H.; Ozaktas, H.; Rochange, C. A Framework to Quantify the Overestimations of Static WCET Analysis. In 15th International Workshop on Worst-Case Execution Time Analysis; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2015. [Google Scholar]
- Gustavsson, A.; Gustafsson, J.; Lisper, B. Toward static timing analysis of parallel software. In 12th International Workshop on Worst-Case Execution Time Analysis; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2012; Volume 23, pp. 38–47. [Google Scholar]
- Rochange, C.; Bonenfant, A.; Sainrat, P.; Gerdes, M.; Wolf, J.; Ungerer, T.; Petrov, Z.; Mikulu, F. WCET analysis of a parallel 3D multigrid solver executed on the MERASA multi-core. In International Workshop on Worst-Case Execution Time Analysis; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2010; Volume 15. [Google Scholar]
- Gerdes, M.; Wolf, J.; Guliashvili, I.; Ungerer, T.; Houston, M.; Bernat, G.; Schnitzler, S.; Regler, H. Large drilling machine control code—parallelization and WCET speedup. In Proceedings of the Industrial Embedded Systems (SIES), 2011 6th IEEE International Symposium on, Vasteras, Sweden, 15–17 June 2011. [Google Scholar]
- Gustavsson, A.; Ermedahl, A.; Lisper, B.; Pettersson, P. Towards WCET analysis of multi core architectures using UPPAAL. In 10th International Workshop on Worst-Case Execution Time Analysis; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2010. [Google Scholar]
- Pellizzoni, R.; Betti, E.; Bak, S.; Yao, G.; Criswell, J.; Caccamo, M.; Kegley, R. A predictable execution model for COTS-based embedded systems. In Proceedings of the 2011 17th IEEE Real-Time and Embedded Technology and Applications Symposium, Chicago, IL, USA, 11–14 April 2011; pp. 269–279. [Google Scholar]
- Sun, J.; Guan, J.; Wang, W.; He, Q.; Yi, W. Real-Time Scheduling and Analysis of OpenMP Task Systems with Tied Tasks. In Proceedings of the 38th IEEE Real-Time Systems Symposium, Paris, France, 5–8 December 2017. [Google Scholar]
- Segarra, J.; Cortadella, J.; Tejero, R.G.; Vinals-Yufera, V. Automatic Safe Data Reuse Detection for the WCET Analysis of Systems With Data Caches. IEEE Access 2020, 8, 192379–192392. [Google Scholar] [CrossRef]
- Casini, D.; Biondi, A.; Buttazzo, G. Analyzing Parallel Real-Time Tasks Implemented with Thread Pools. In Proceedings of the 56th ACM/ESDA/IEEE Design Automation Conference (DAC 2019), Las Vegas, NV, USA, 2–6 June 2019. [Google Scholar]
- Ozaktas, H.; Rochange, C.; Sainrat, P. Automatic WCET Analysis of Real-Time Parallel. In 13th International Workshop on Worst-Case Execution Time Analysis; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2013. [Google Scholar]
- Alhammad, A.; Pellizzoni, R. Time-predictable execution of multithreaded applications on multicore systems. In Proceedings of the 2014 Design, Automation and Test in Europe Conference and Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar]
- Schlatow, J.; Ernst, R. Response-Time Analysis for Task Chains in Communicating Threads. In Proceedings of the 2016 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Vienna, Austria, 11–14 April 2016. [Google Scholar]
- Rouxel, R.; Derrien, S.; PuautI, I. Tightening Contention Delays While Scheduling Parallel Applications on Multi-core Architectures. ACM Trans. Embed. Comput. Syst. 2017, 16, 1–20. [Google Scholar] [CrossRef]
- Zhang, Q.; Huangfu, Y.; Zhang, W. Statistical regression models for WCET estimation. Qual. Technol. Quant. Manag. 2019, 16, 318–332. [Google Scholar] [CrossRef]
- Rouxel, R.; Skalistis, S.; Derrien, S.; PuautI, I. Hiding Communication Delays in Contention-Free Execution for SPM-Based Multi-Core Architectures. In Proceedings of the 31st Euromicro Conference on Real-Time Systems (ECRTS’19), Stuttgart, Germany, 9–12 July 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).