Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction
Abstract
:1. Introduction
- Investigation of numerical errors of the DP algorithm in implementing an optimal control strategy for hybrid vehicles.
- Comprehensive rule extraction from DP results to establish a near optimal rule-based strategy for multi-objective (many objectives).
- Establish additional rules to overcome shortcomings of the useful strategies extracted from DP results.
- A systematic methodology to develop an easy to implement, real time, near optimal power management strategy for parallel hybrid three-wheelers.
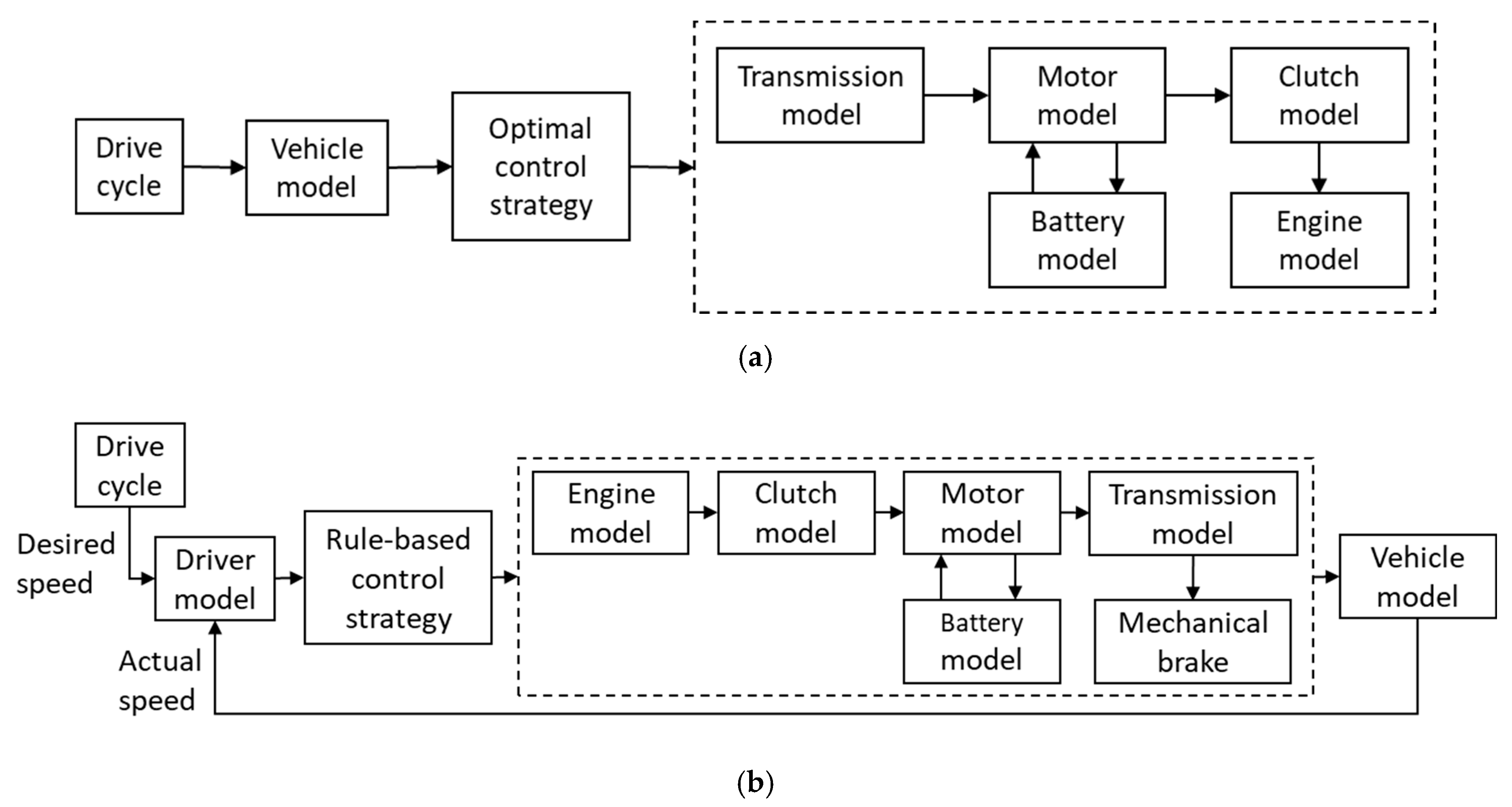
2. Hybrid Electric Three-Wheeler Models
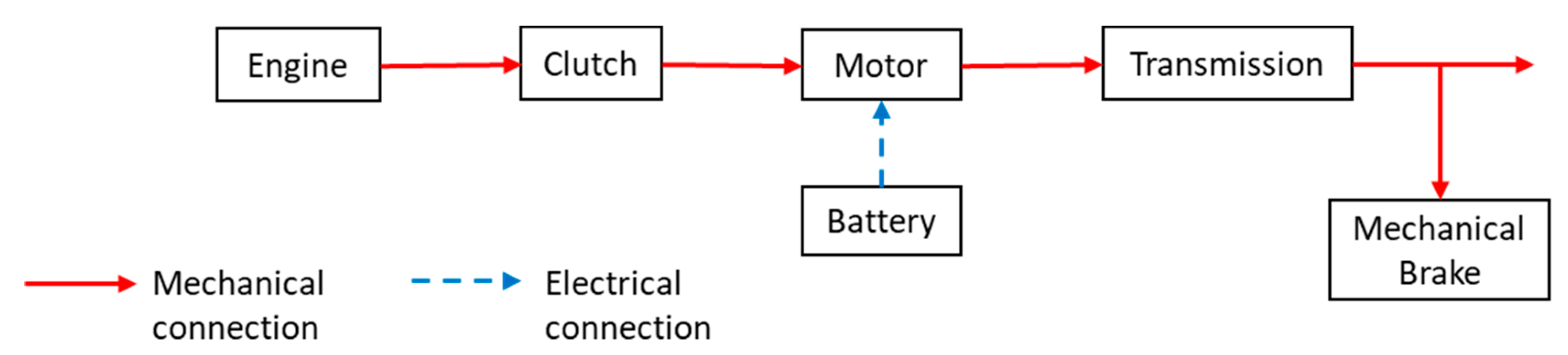
2.1. Parallel Hybrid Electric Powertrain Model
2.1.1. Longitudinal Vehicle Model
2.1.2. Transmission Model
- , gear downshift.
- , gear upshift.
- , maintain the current gear.
2.1.3. Clutch Model
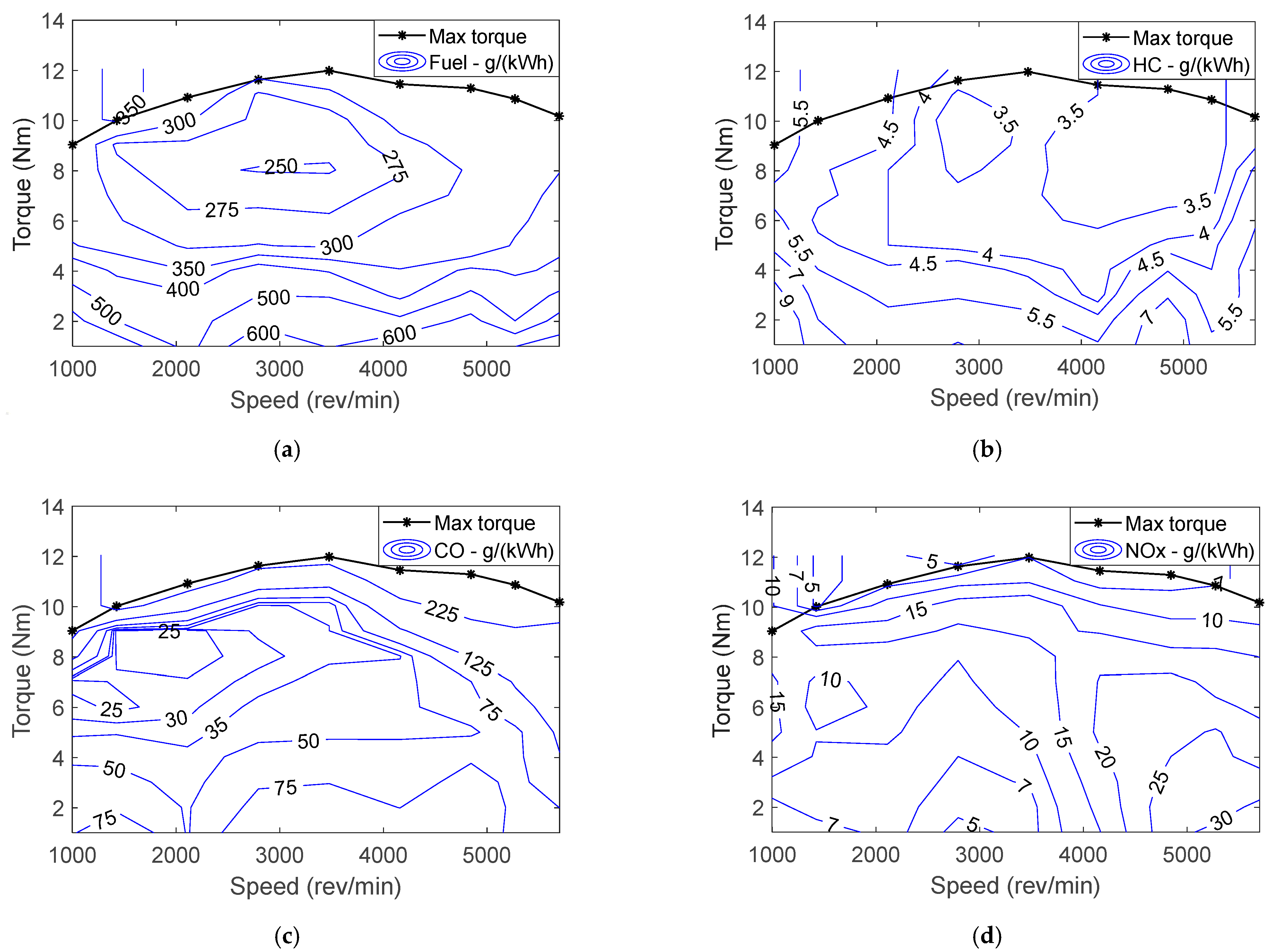
2.1.4. Internal Combustion Engine Model
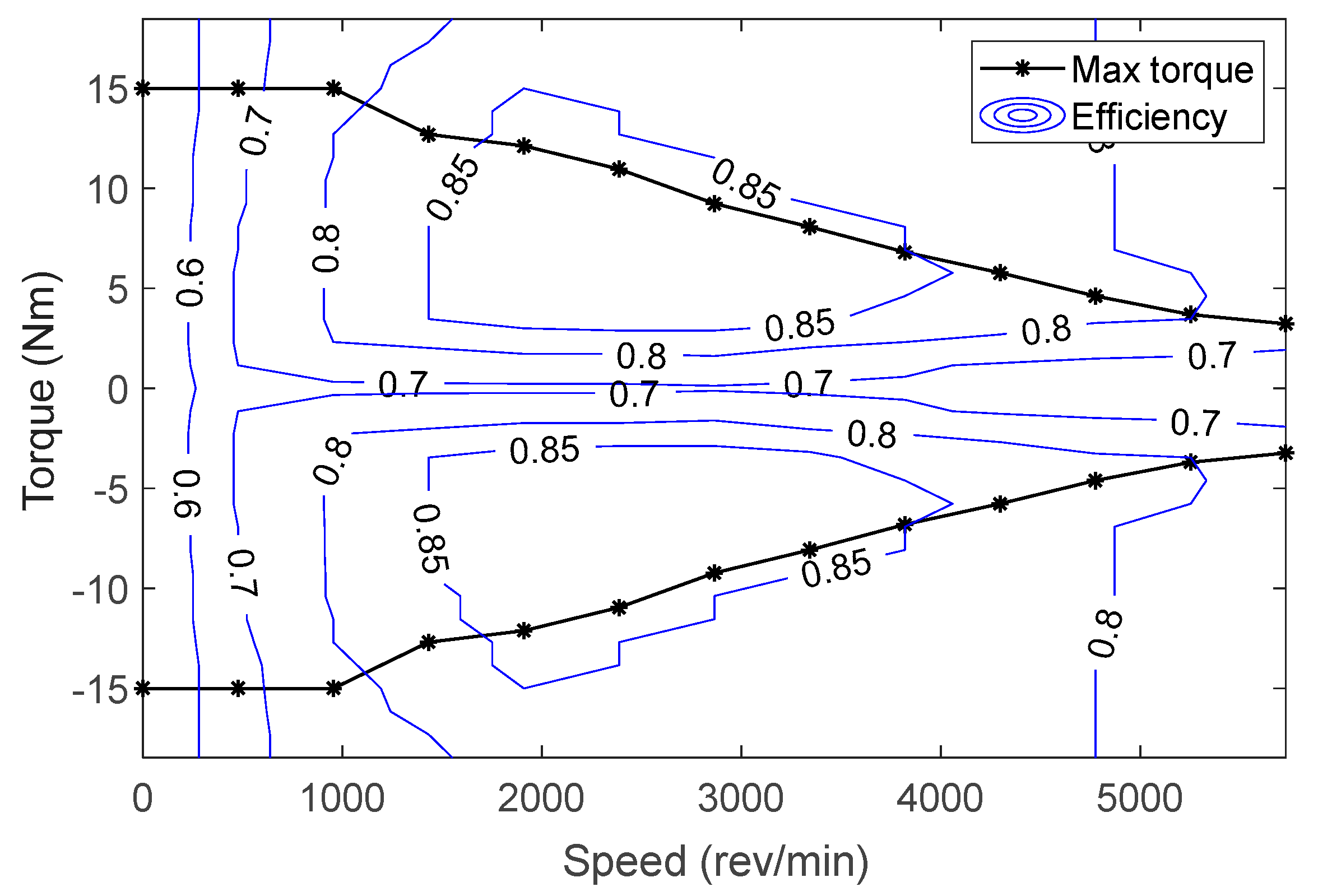
2.1.5. Electric Motor Model
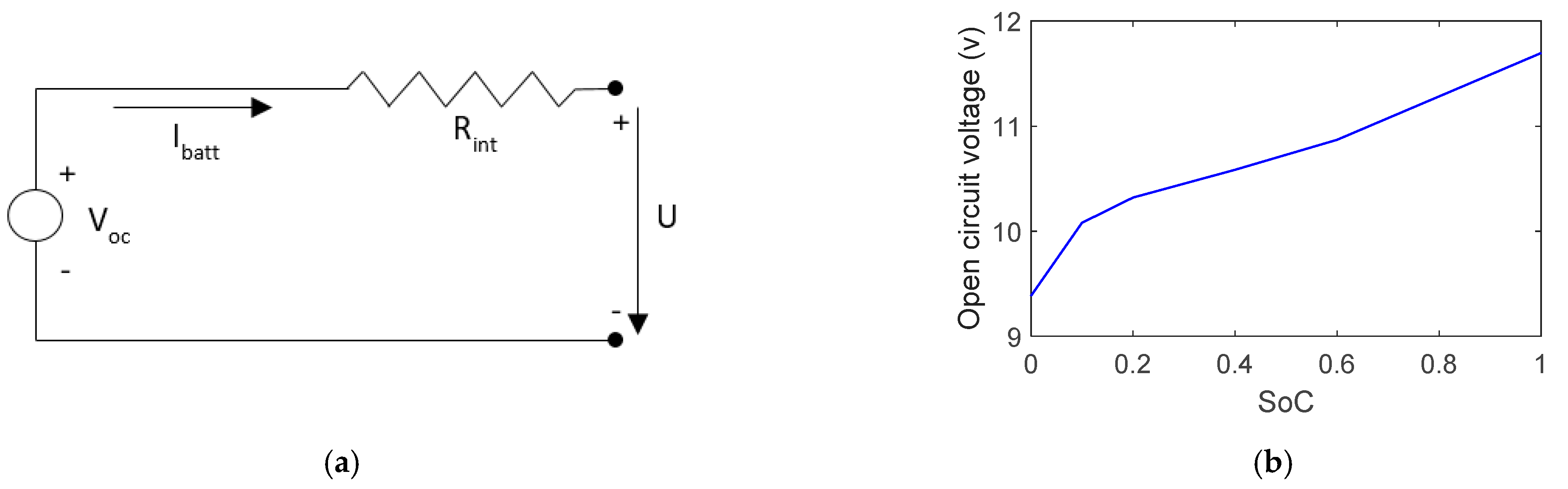
2.1.6. Battery Model
2.2. Quasi-Static Hybrid Electric Vehicle Models
- , only the motor provides necessary torque or full brake energy recuperation;
- , both the motor and engine provide the necessary torque;
- , only the engine provides the necessary torque;
- , engine provides surplus torque and motor is in generator mode;
- , engine provides surplus torque and motor is in maximum generator mode (full recharge).
3. Global Optimal Control Strategy Based on DP
3.1. Implementation of DP
3.2. Problem Formulation
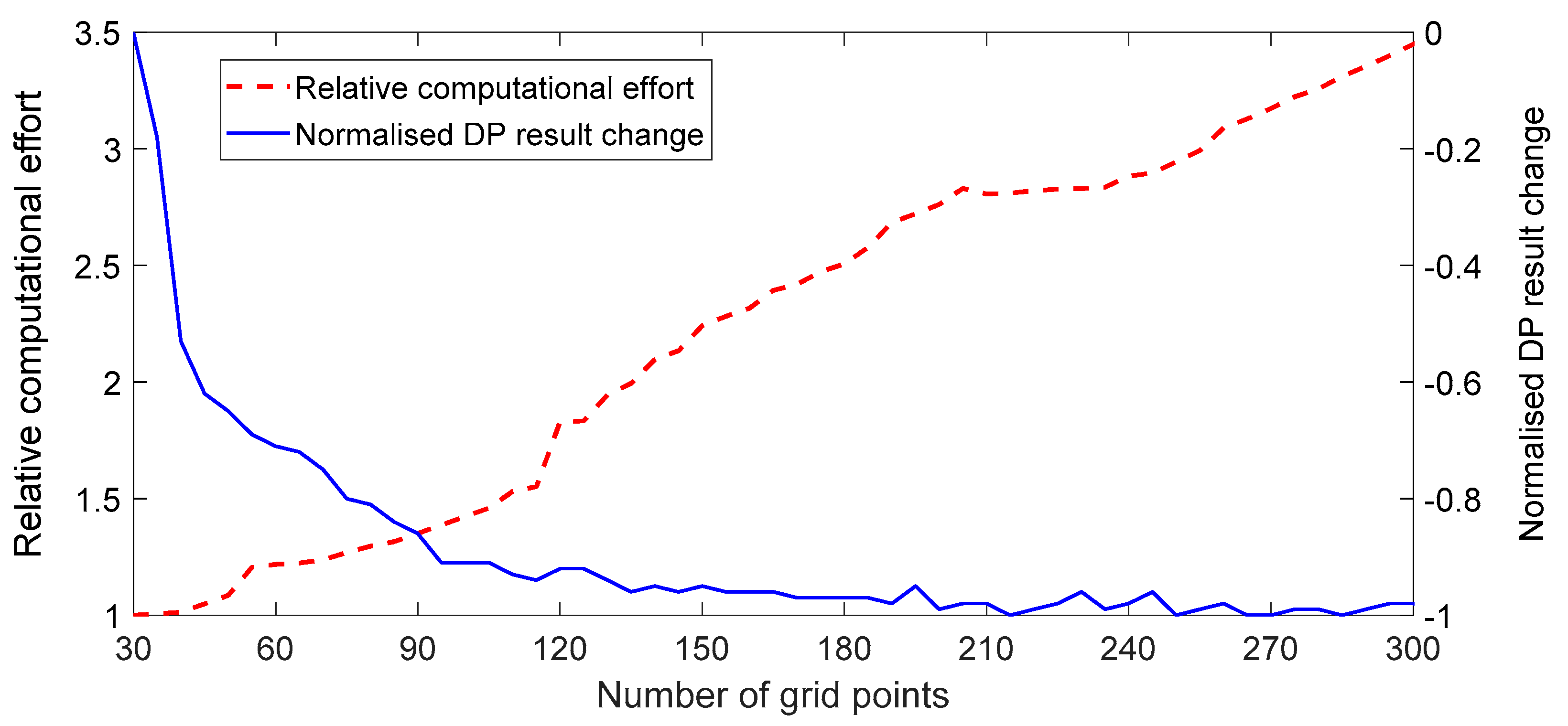
3.3. Numerical Issues of DP
3.3.1. Boundary Issue and Resolution of the Study
3.3.2. Resolution of State Variable
3.3.3. Resolution of Control Variable
3.4. Results of DP Based Control Strategy
4. Rule-Based Power Management Strategy
4.1. Rule Extraction from DP Based Control Strategy
4.1.1. Power Configuration Selection Strategy
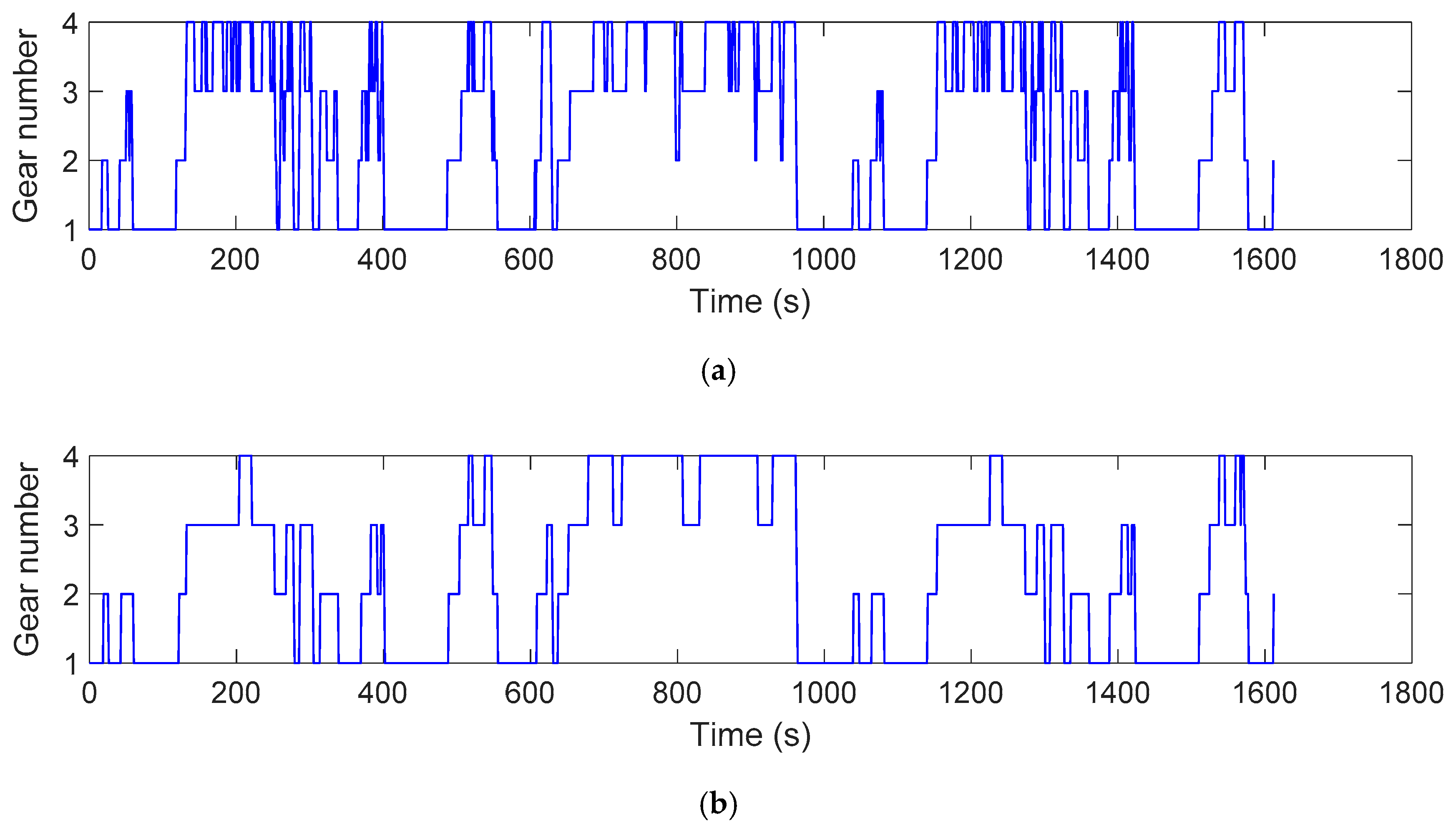
4.1.2. Gear Shift Logic
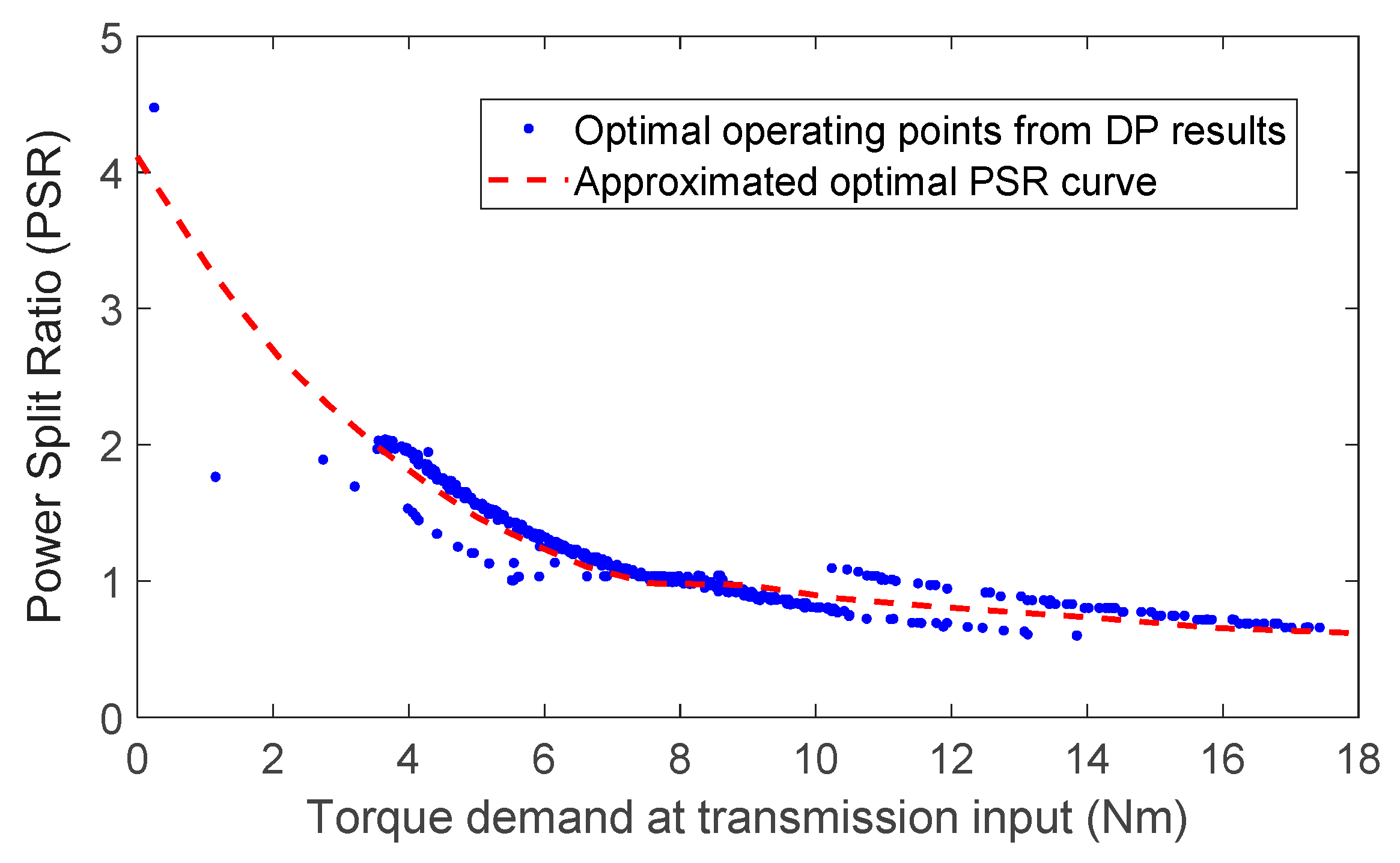
4.1.3. Power Split Logic
- PSR = 0, only the motor provides the demanded power (EV mode);
- PSR = 1, only the engine provides the demanded power (engine only mode);
- 0 < PSR < 1, both engine and motor provide the demanded power (engine assist mode);
- PSR > 1, the engine provides surplus power and motor acts as a generator (recharge mode).
4.2. Proposed Rule-Based Strategy
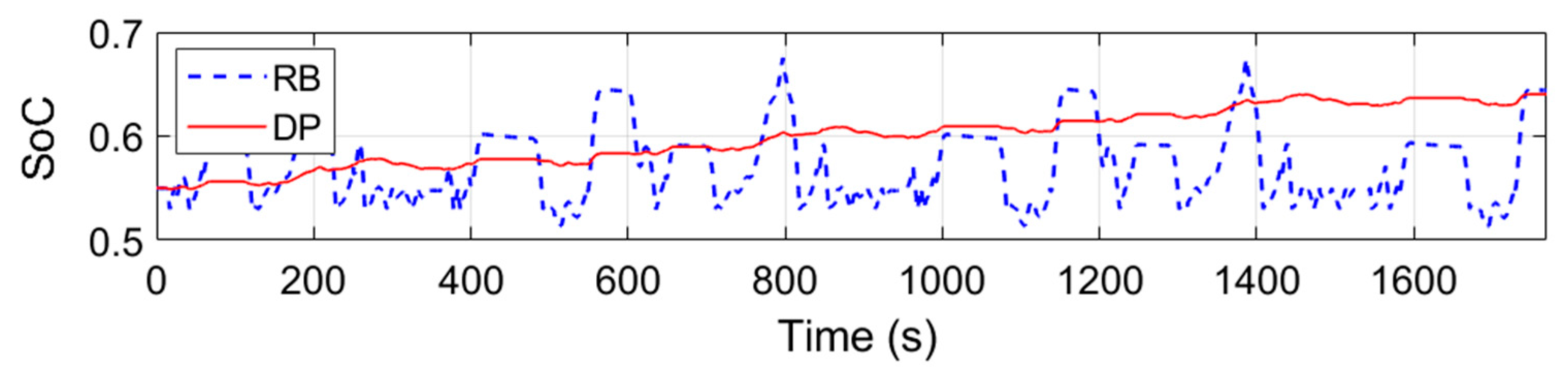
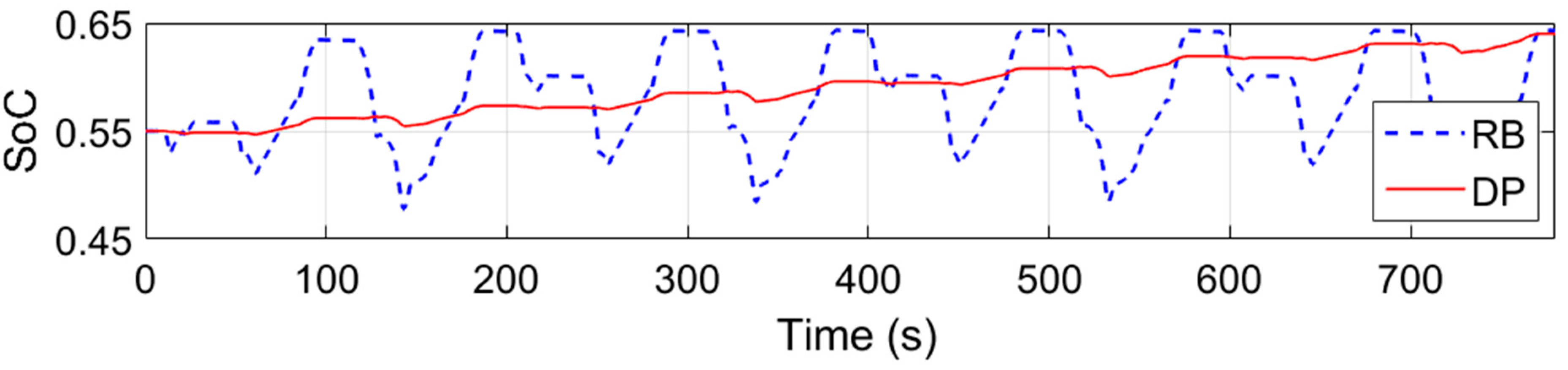
4.3. Comparison of Proposed Rule-Based and DP Based Control Strategy
5. Conclusions
- Numerical issues were observed during the DP optimization procedure. Thus, the effect of discretization resolution of the state and control variables were investigated. Results show that computational effort and accuracy of the optimal result from the DP optimization procedure increase with higher discretization resolutions of the state and control variables.
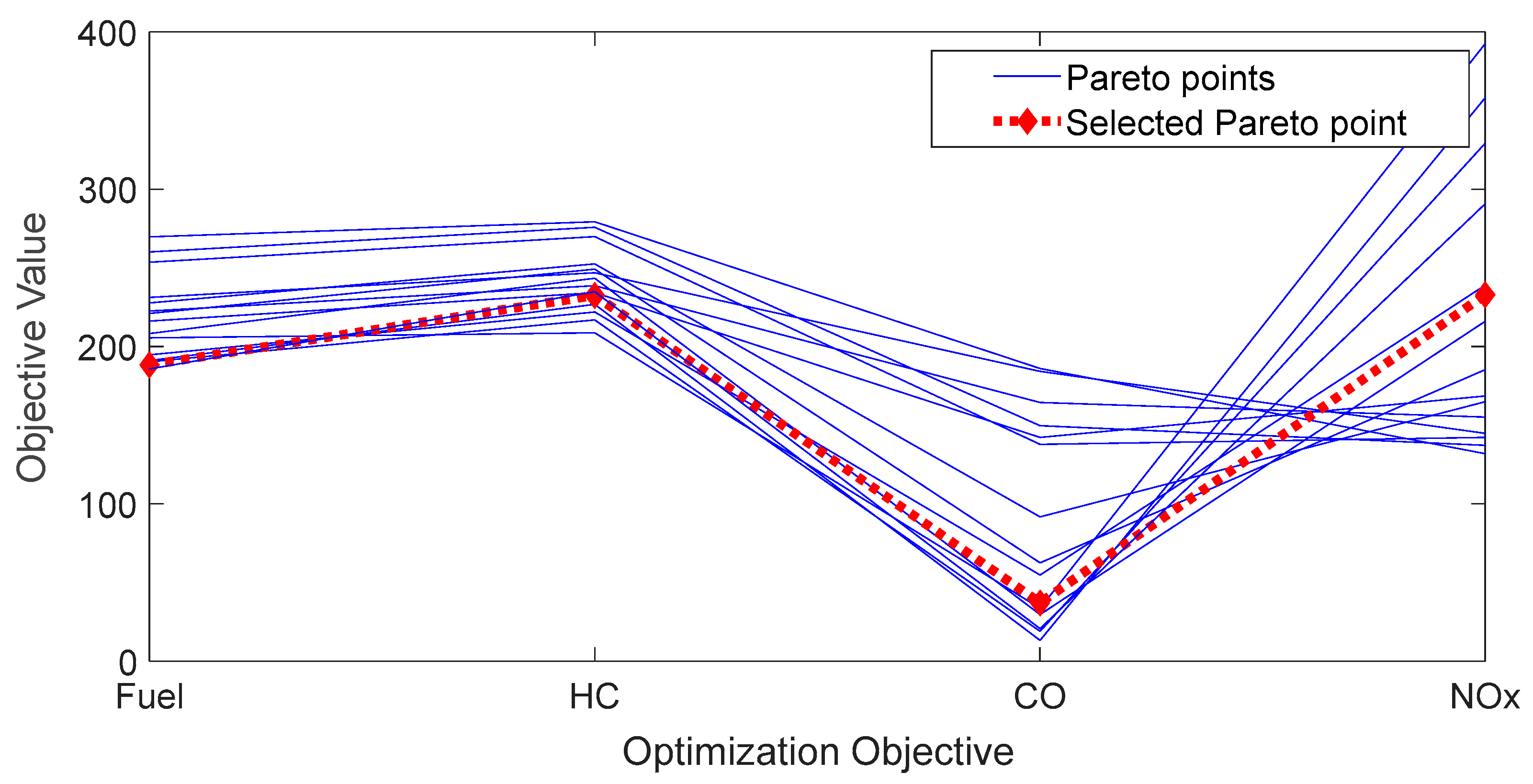
- The cost function of the optimization problem considered multiple objectives: fuel consumption, emissions and gear shift strategy. Results showed that gear shift strategy and remaining objectives behaved uniquely; contradictory to fuel and emission objectives, frequency of gear shift increased with lower weighting factors and vice versa. Moreover, within the engine model used in the present study, a higher degree of conflict was observed between NOx and remaining objectives (i.e., fuel, HC and CO).
- Three main useful strategies were extracted from DP results, i.e., full EV mode on/off threshold, gear shift and power-split strategy to develop the rule-based algorithm. The rule-based strategy-maintained fuel consumption and emissions within 10% of the DP results for WLTC and NEDC drive cycles. The proposed control strategy is computationally less demanding, easy-to-implement on a vehicle and near-optimal; thus, a viable option to control a hybrid electric three-wheeler operating in densely populated urban roads.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| BSFC | Brake Specific Fuel Consumption |
| CNG | Compressed Natural Gas |
| CPU | Central Processing Unit |
| DC | Direct Current |
| DP | Dynamic Programming |
| EV | Electric Vehicle |
| GPS | Global Positioning System |
| IC | Internal Combustion |
| LPG | Liquefied Petroleum Gas |
| NEDC | New European Drive Cycle |
| PSR | Power Split Ratio |
| RAM | Random Access Memory |
| RB | Rule-Based |
| SI | Spark Ignition |
| SoC | State of Charge |
| UDC | Urban Drive Cycle |
| WLTC | Worldwide Harmonized Light Vehicles Test Cycle |
References
- Ghosh, A. Possibilities and challenges for the inclusion of the electric vehicle (EV) to reduce the carbon footprint in the transport sector: A review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Saxena, S.N. Revolution in growth of three-wheeler electric vehicles in India. J. Glob. Tour. Res. 2019, 4, 117–126. [Google Scholar] [CrossRef]
- Overview Information of the Bajaj RE 4s Three-Wheeler. Available online: https://www.globalbajaj.com/global/english/brands/intracity/re/re-4s/overview/ (accessed on 14 October 2020).
- Kokate, V.L.; Uttekar, S.S.; Karandikar, P.B.; Holmukhe, R.M. Retrofitting of Auto Rickshaw to E-Rickshaw—A Feasibility Study. In Proceedings of the First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 229–234. [Google Scholar]
- Hofman, T.; van der Tas, S.G.; Ooms, W.; van Meijl, E.W.P.; Laugeman, B.M. Development of a Micro-Hybrid System for a Three-Wheeled Motor Taxi. World Electr. Veh. J. 2009, 3, 572–580. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, D.; Jash, T. Merits and Challenges of E-Rickshaw as An Alternative form of Public Road Transport System: A Case Study in the State of West Bengal in India. Energy Procedia 2015, 79, 307–314. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, L.; Yip, A.; Fowler, M.; Young, S.B.; Fraser, R.A. Environmental feasibility of re-use of electric vehicle batteries. Sustain. Energy Technol. Assess. 2014, 6, 64–74. [Google Scholar] [CrossRef]
- Rajper, S.Z.; Albrecht, J. Prospects of Electric Vehicles in the Developing Countries: A Literature Review. Sustainability 2020, 12, 1906. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.; Ali, Y.; Khan, A.U. Sustainable hybrid electric vehicle selection in the context of a developing country. Air Qual. Atmos. Health 2020, 13, 489–499. [Google Scholar] [CrossRef]
- Vezzini, A.; Sharan, H.; Umanand, L. Low-pollution three-wheeler autorickshaw with power-assist series hybrid and novel variable DC-link voltage system. J. Indian Inst. Sci. 2005, 85, 105–118. [Google Scholar]
- Amjad, S.; Rudramoorthy, R.; Neelakrishnan, S.; Gurusubramanian, S.; Raja, J.D.; Mathew, R.; Sundaravel, M. Plug-in hybrid conversion of three wheeler using a novel drive strategy. Int. J. Altern. Propuls. 2012, 2, 148. [Google Scholar] [CrossRef]
- Jijith, R.V.; Indulal, S. Hybrid Electric Three-Wheeler with ANN Controller. In Proceedings of the International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, 21–22 December 2018; pp. 1–5. [Google Scholar]
- Padmanaban, V.; Ramasubramanian, A.; Subramaniam, T. Investigation on use of plug—In hybrid electric vehicle (PHEV) technology using renewable energy for an autorickshaw. J. KONES. Powertrain Transp. 2012, 19, 383–394. [Google Scholar] [CrossRef]
- Maddumage, W.U.; Abeyasighe, K.Y.; Perera, M.S.M.; Attalage, R.A.; Kelly, P. Comparing Fuel Consumption and Emission Levels of Hybrid Powertrain Configurations and a Conventional Powertrain in Varied Drive Cycles and Degree of Hybridization. Sci. Technol. 2020, 19, 20–33. [Google Scholar] [CrossRef]
- Biasini, R.; Onori, S.; Rizzoni, G. A near-optimal rule-based energy management strategy for medium duty hybrid truck. Int. J. Powertrains 2013, 2, 232. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C. Modelling and control of hybrid electric vehicles (A comprehensive review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar] [CrossRef] [Green Version]
- Sudhakaran, S.; Indulal, S.; Lal Priya, P.S. Fuzzy Logic Controller Design for Retrofitted Three-wheeled Hybrid Electric Vehicle. In Proceedings of the 2020 First IEEE International Conference on Measurement, Instrumentation, Control and Automation (ICMICA), Kurukshetra, India, 24–26 June 2020; pp. 1–5. [Google Scholar]
- Lin, C.C.; Peng, H.; Grizzle, J.W.; Kang, J.M. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar] [CrossRef] [Green Version]
- Kum, D.; Peng, H.; Bucknor, N.K. Supervisory Control of Parallel Hybrid Electric Vehicles for Fuel and Emission Reduction. J. Dyn. Syst. Meas. Control 2011, 133, 1–10. [Google Scholar] [CrossRef]
- Lin, C.-C.; Filipi, Z.; Wang, Y.; Louca, L.; Peng, H.; Assanis, D.N.; Stein, J. Integrated, Feed-Forward Hybrid Electric Vehicle Simulation in SIMULINK and its Use for Power Management Studies. SAE Tech. Pap. 2001, 1. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Shi-jie, H.; Dong-ge, L.; Wei, G.; Hu, X. Optimal Energy Control Strategy Design for a Hybrid Electric Vehicle. Discret. Dyn. Nat. Soc. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Sundström, O.; Guzzella, L.; Soltic, P. Optimal Hybridization in Two Parallel Hybrid Electric Vehicles using Dynamic Programming. IFAC Proc. Vol. 2008, 41, 4642–4647. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Lukic, S.M. Dynamic programming technique in hybrid electric vehicle optimization. In Proceedings of the IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–8. [Google Scholar]
- Lin, C.-C.; Filipi, Z.; Louca, L.; Peng, H.; Assanis, D.; Stein, J. Modelling and control of a medium-duty hybrid electric truck. Int. J. Heavy Veh. Syst. 2004, 11, 349. [Google Scholar] [CrossRef] [Green Version]
- Asghar, M.; Bhatti, A.I.; Izhar, T. Benchmark fuel economy for a parallel hybrid electric three-wheeler vehicle (rickshaw). Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Xing, Z.; Du, K. Emission factors of air pollutants from CNG-gasoline bi-fuel vehicles: Part II. CO, HC and NOx. Sci. Total Environ. 2016, 565, 698–705. [Google Scholar] [CrossRef] [PubMed]
- Wallington, T.J.; Sullivan, J.L.; Hurley, M.D. Emissions of CO2, CO, NOx, HC, PM, HFC-134a, N2O and CH4 from the global light duty vehicle fleet. Meteorol. Z. 2008, 17, 109–116. [Google Scholar] [CrossRef]
- Ram, N.S.M. Trends in Automotive Electronics in Two and Three Wheeled Vehicles. SAE Tech. Pap. 2003. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; Li, B.; Ji, J.; Zhao, K.; Hu, C. A review of power management strategies and component sizing methods for hybrid vehicles. Renew. Sustain. Energy Rev. 2018, 96, 132–144. [Google Scholar] [CrossRef]
- Arsie, I.; Graziosi, M.; Pianese, C. Optimization of supervisory control strategy for parallel hybrid vehicle with provisional load estimate. In Proceedings of the 7th International Symposium on Advanced Vehicle Control (AVEC), Arnhem, The Netherlands, 23–27 August 2004; pp. 483–488. [Google Scholar]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Di Cairano, S. MPC-Based Energy Management of a Power-Split Hybrid Electric Vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Lei, Z.; Li, W.; Qin, D.; Chen, Z. An Adaptive Equivalent Consumption Minimization Strategy for Plug-In Hybrid Electric Vehicles Based on Energy Balance Principle. IEEE Access 2019, 7, 67589–67601. [Google Scholar] [CrossRef]
- Cheng, R.; Rodemann, T.; Fischer, M.; Olhofer, M.; Jin, Y. Evolutionary Many-Objective Optimization of Hybrid Electric Vehicle Control: From General Optimization to Preference Articulation. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Tulpule, P.; Marano, V.; Rizzoni, G. Effects of different PHEV control strategies on vehicle performance. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3950–3955. [Google Scholar]
- Wei, X. Modeling and Control of a Hybrid Electric Drivetrain for Optimum Fuel Economy, Performance and Driveability. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2004. [Google Scholar]
- Wang, X.; He, H.; Sun, F.; Sun, X.; Tang, H. Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles. Energies 2013, 6, 5656–5675. [Google Scholar] [CrossRef]
- He, H.; Sun, F.; Zhang, J. Application Study on the Dynamic Programming Algorithm for Energy Management of Plug-in Hybrid Electric Vehicles. Energies 2015, 8, 3225–3244. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy Management for a Power-Split Plug-in Hybrid Electric Vehicle Based on Dynamic Programming and Neural Networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Markel, T.; Simpson, A. Cost-Benefit Analysis of Plug-In Hybrid Electric Vehicle Technology. World Electr. Veh. J. 2007, 1, 294–301. [Google Scholar] [CrossRef] [Green Version]
- Markel, T.; Smith, K.; Pesaran, A.A. Improving Petroleum Displacement Potential of PHEVs Using Enhanced Charging Scenarios. In Electric and Hybrid Vehicles; Elsevier: Amsterdam, The Netherlands, 2010; pp. 211–225. ISBN 9780444535658. [Google Scholar]
- Chan, C.C.; Bouscayrol, A.; Chen, K. Electric, Hybrid, and Fuel-Cell Vehicles: Architectures and Modeling. IEEE Trans. Veh. Technol. 2010, 59, 589–598. [Google Scholar] [CrossRef]
- Denis, N.; Dubois, M.R.; Trovao, J.P.F.; Desrochers, A. Power Split Strategy Optimization of a Plug-in Parallel Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 315–326. [Google Scholar] [CrossRef]
- Nguyễn, B.-H.; Trovão, J.P.F.; German, R.; Bouscayrol, A. Real-Time Energy Management of Parallel Hybrid Electric Vehicles Using Linear Quadratic Regulation. Energies 2020, 13, 5538. [Google Scholar] [CrossRef]
- Karaoğlan, M.U.; Kuralay, N.S.; Colpan, C.O. The effect of gear ratıos on the exhaust emıssıons and fuel consumptıon of a parallel hybrid vehicle powertrain. J. Clean. Prod. 2019, 210, 1033–1041. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Zhang, Y.; Wu, Y.; Chen, Z.; Ye, M. Rule learning based energy management strategy of fuel cell hybrid vehicles considering multi-objective optimization. Energy 2020, 207, 118212. [Google Scholar] [CrossRef]
- Assadian, F.; Mohan, G.; Longo, S. Comparative analysis of forward-facing models vs backward-facing models in powertrain component sizing. In Proceedings of the Hybrid and Electric Vehicles Conference (HEVC), London, UK, 6–7 November 2013; Volume 2013, pp. 1–6. [Google Scholar]
- Elbert, P.; Ebbesen, S.; Guzzella, L. Implementation of Dynamic Programming for n-Dimensional Optimal Control Problems with Final State Constraints. IEEE Trans. Control Syst. Technol. 2013, 21, 924–931. [Google Scholar] [CrossRef]
- Sundstrom, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the IEEE International Conference on Control Applications, St. Petersburg, Russia, 8–10 July 2009; pp. 1625–1630. [Google Scholar]
- Sundström, O.; Ambühl, D.; Guzzella, L. On Implementation of Dynamic Programming for Optimal Control Problems with Final State Constraints. Oil Gas Sci. Technol. Rev. l’IFP 2010, 65, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Du, W.; Qian, F. An Adaptive Multi-Objective Differential Evolution Algorithm for Solving Chemical Dynamic Optimization Problems. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2015; Volume 37, pp. 821–826. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Jakob, W.; Blume, C. Pareto Optimization or Cascaded Weighted Sum: A Comparison of Concepts. Algorithms 2014, 7, 166–185. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S. Multi-Objective Optimization. In Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; pp. 197–211. ISBN 9780124167438. [Google Scholar]
- Fleming, P.J.; Purshouse, R.C.; Lygoe, R.J. Many-Objective Optimization: An Engineering Design Perspective. In Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, 2005; Volume 3410, pp. 14–32. [Google Scholar]
- Liang, J.; Walker, P.D.; Ruan, J.; Yang, H.; Wu, J.; Zhang, N. Gearshift and brake distribution control for regenerative braking in electric vehicles with dual clutch transmission. Mech. Mach. Theory 2019, 133, 1–22. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, N.; Walker, P.; Zhou, X.; Zhan, W.; Wei, Y.; Ke, N. Gear shift schedule design for multi-speed pure electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 70–82. [Google Scholar] [CrossRef]
- Minister of Transport, S.L. Motor Traffic (Speed Limits) Regulations, No. 1 of 2012. In Gazette Extraordinary No. 1763/26 of June 22, 2012; Department of Government Printing: Colombo, Sri Lanka, 2012; pp. 1A–2A. [Google Scholar]
- Specifications—Bajaj RE 4S Twin Spark 4-Stroke DTSi Three-Wheeler. Available online: https://www.globalbajaj.com/global/english/brands/intracity/re/re-4s/specifications/ (accessed on 13 October 2020).
- President, S.L. Vehicular exhaust emission standards for importation, manufacturing or assembling of vehicles. In Gazette Extraordinary No. 2079/42 of July 12, 2018; Department of Government Printing: Colombo, Sri Lanka, 2018; p. 3A. [Google Scholar]








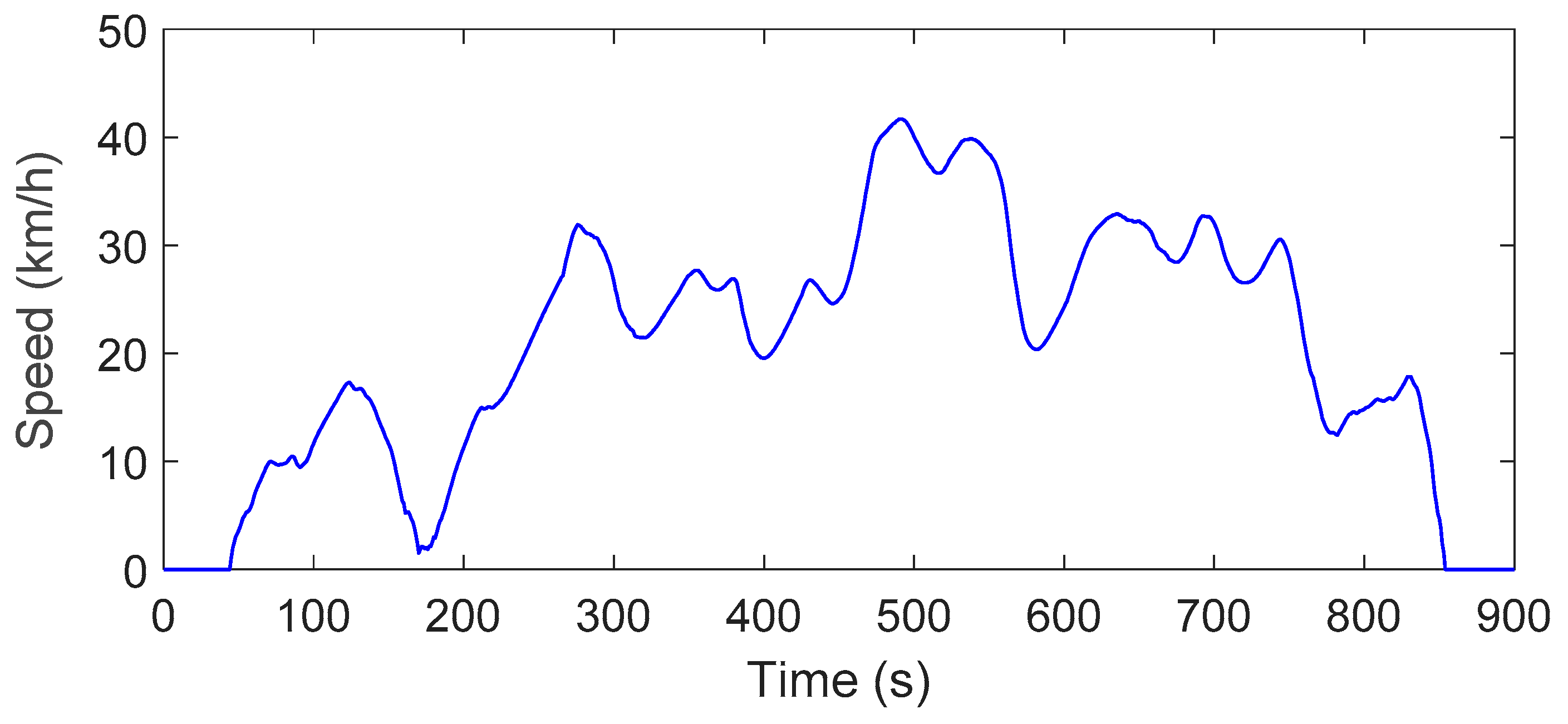
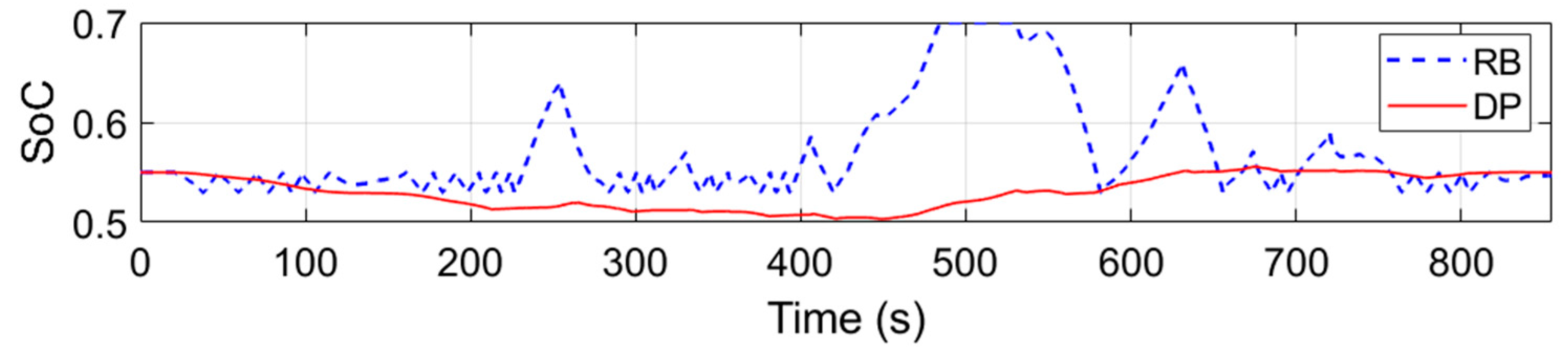
| Powertrain | Parameter | Value |
|---|---|---|
| Engine | Maximum power (kW) | 6 |
| Electric motor | Maximum power (kW) | 3 |
| Battery | No. of Modules | 6 |
| Capacity (Ah) | 6 | |
| Nominal voltage (volt/module) | 10.8 | |
| Vehicle | Frontal area (m2) | 1.86 |
| Tire radius (m) | 0.2 | |
| Coefficient of drag | 0.44 | |
| Rolling resistance coefficient | 0.015 | |
| Glider mass–without propulsion (kg) | 280 | |
| Curb weight (kg) | 448 |
| Variables | Grid | |
|---|---|---|
| Stage (k) | Time | 0:1:1612 |
| State (x) | SoC Gear number | 0.4:0.0027:0.7 1, 2, 3, 4 |
| Control (u) | Torque split factor Gear shift command | −1:0.028:1 −1, 0, 1 |
| Controller | Fuel (l/100 km) | HC (g/km) | CO (g/km) | NOx (g/km) |
|---|---|---|---|---|
| DP | 1.32 | 0.142 | 1.096 | 0.405 |
| Rule Based | 1.38 | 0.145 | 1.151 | 0.408 |
| Deviation | +4.92% | +2.09% | +5.02% | +0.68% |
| Controller | Fuel (l/100 km) | HC (g/km) | CO (g/km) | NOx (g/km) |
|---|---|---|---|---|
| DP | 1.53 | 0.162 | 2.264 | 0.438 |
| Rule-Based | 1.59 | 0.157 | 2.485 | 0.474 |
| Deviation | +4.01% | −2.87% | +9.76% | +8.16% |
| Controller | Fuel (l/100 km) | HC (g/km) | CO (g/km) | NOx (g/km) |
|---|---|---|---|---|
| DP | 1.15 | 0.124 | 0.801 | 0.309 |
| Rule-Based | 1.26 | 0.135 | 0.989 | 0.327 |
| Deviation | +9.61% | +8.59% | +23.50% | +5.86% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maddumage, W.; Perera, M.; Attalage, R.; Kelly, P. Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction. Energies 2021, 14, 1833. https://doi.org/10.3390/en14071833
Maddumage W, Perera M, Attalage R, Kelly P. Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction. Energies. 2021; 14(7):1833. https://doi.org/10.3390/en14071833
Chicago/Turabian StyleMaddumage, Waruna, Malika Perera, Rahula Attalage, and Patrick Kelly. 2021. "Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction" Energies 14, no. 7: 1833. https://doi.org/10.3390/en14071833
APA StyleMaddumage, W., Perera, M., Attalage, R., & Kelly, P. (2021). Power Management Strategy of a Parallel Hybrid Three-Wheeler for Fuel and Emission Reduction. Energies, 14(7), 1833. https://doi.org/10.3390/en14071833







