Humidity in Power Converters of Wind Turbines—Field Conditions and Their Relation with Failures
Abstract
:1. Introduction
- to characterize the climatic conditions in converter cabinets of WT based on humidity and temperature data collected in turbines on three different continents,
- to relate these to the ambient climatic conditions and the WT operating conditions,
- to identify potential dependencies on the converter cooling concept and position and
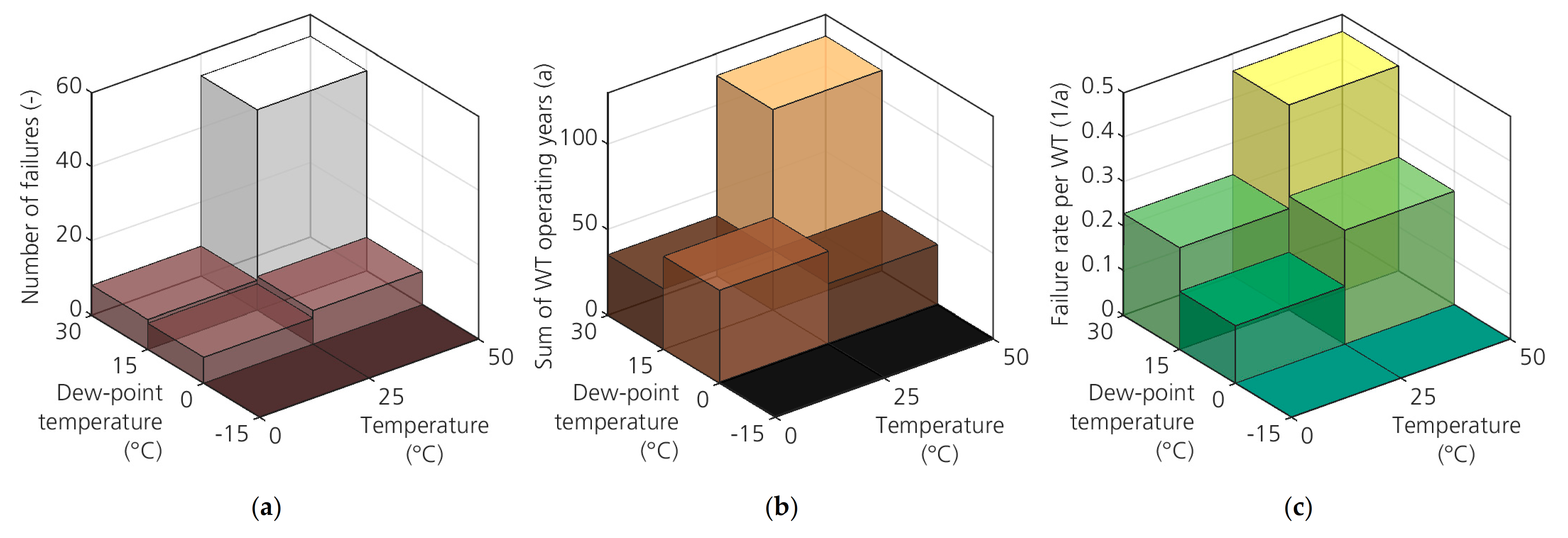
- to shed light on the question why different seasonal failure patterns are observed in air-cooled and liquid-cooled converters of WT [4].
2. Materials and Methods
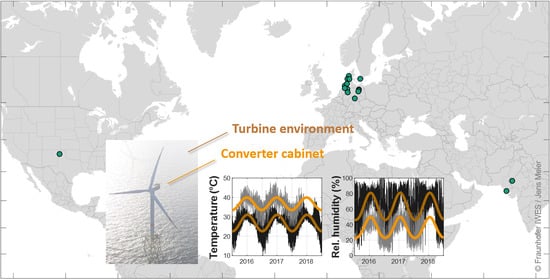
2.1. Temperature and Humidity Measurement Campaigns
2.2. Supplementary Site-Specific Environmental Data (ERA5)
2.3. Methods of Analysis
- The starting point is the analysis of visualized measured temperature and humidity time series along with the ambient climatic conditions in the wind farm (site-specific ERA5 data) and with the WT operating point (i.e., active power fed to the grid normalized with the rated power of the WT). Note that due to the direct transferability of dew-point temperature into absolute humidity and vice versa, we limit the presentation in this paper to only one of these quantities. In the presentation and discussion of results, it should be understood that statements on one of these quantities apply in the same way to the second one.
- The temperature and humidity conditions inside the converter cabinets are characterized by means of two-dimensional histograms showing the range of values and distributions of these signals.
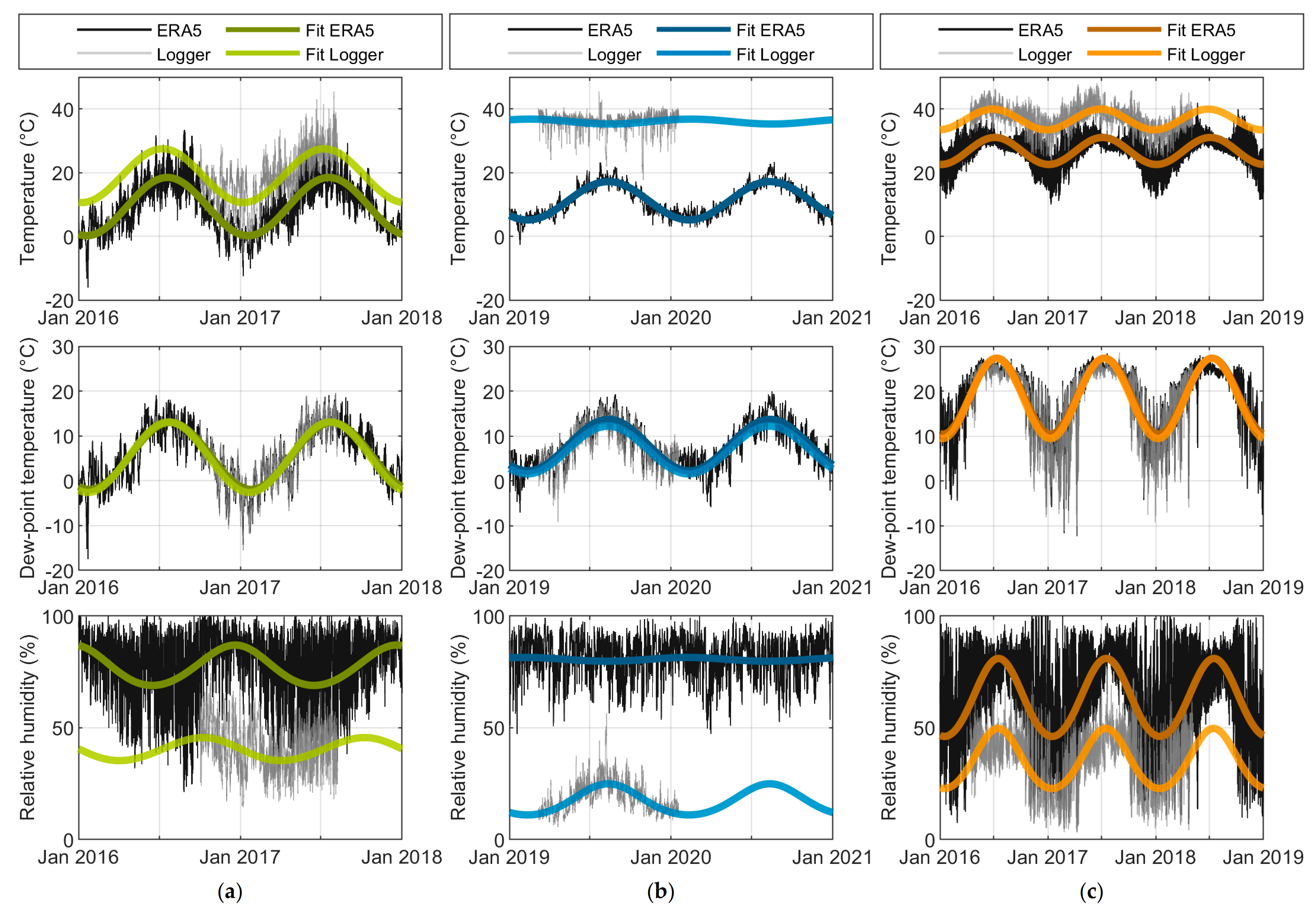
- Based on the periodicities observed in the data, sinusoidal functions are fitted to the temperature and humidity time series by means of nonlinear regression, similarly to the procedure presented in [27] for the case of ambient climatic data:A simple comparison of some aggregated descriptive statistics (e.g., measures of location or dispersion) of the temperature and humidity would lead to misleading results due to the pronounced seasonal variations in climatic conditions and the different lengths of measurement periods, which typically deviate from full-year periods. In this situation, the fitting of sinusoidal functions to the WT-internal and WT-external climatic time series is a suitable method to allow a systematic comparative analysis across different sites, WT types and measurement periods.
- Scatterplots of the estimated parameters of the sinusoidal regression functions (e.g., the constant terms, the amplitudes and phase shifts) are used to reveal similarities and differences of the WT under analysis and identify how design factors such as the converter position in the WT or the cooling concept of the converter influence the climatic conditions in the converter cabinets.
3. Results and Discussion
3.1. Seasonal Converter Failure Patterns and Relation with Ambient Conditions
3.2. Climatic Conditions in Converter Cabinets of Wind Turbines
- an onshore WT with an air-cooled converter in the tower base located in the federal state of Thuringia in Germany,
- an offshore WT in the German North Sea with a liquid-cooled converter in the nacelle, and
- an onshore WT located in India with a liquid-cooled converter in the tower base.
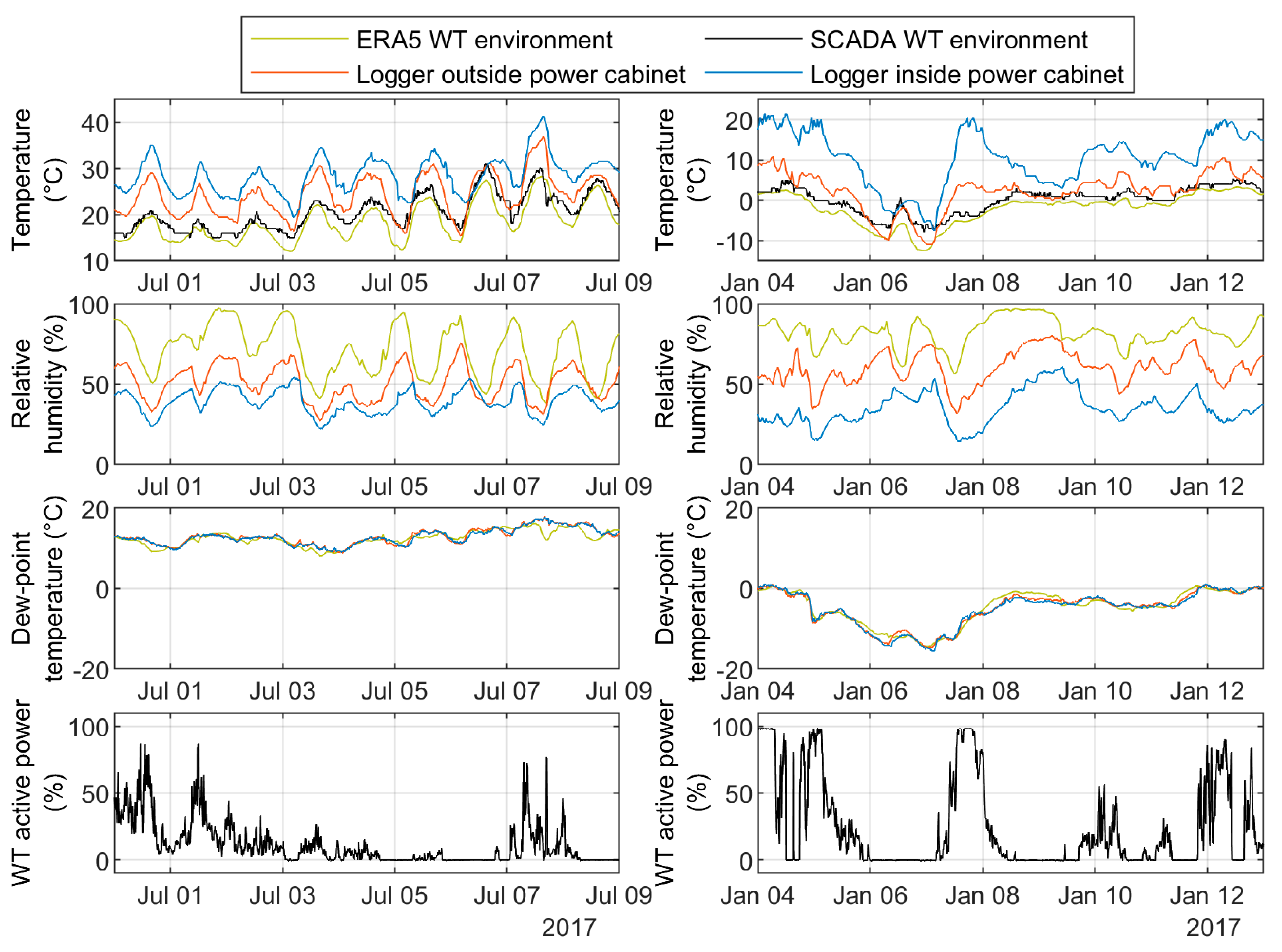
3.2.1. Example 1: Onshore WT in Germany with Air-Cooled Converter in the Tower Base
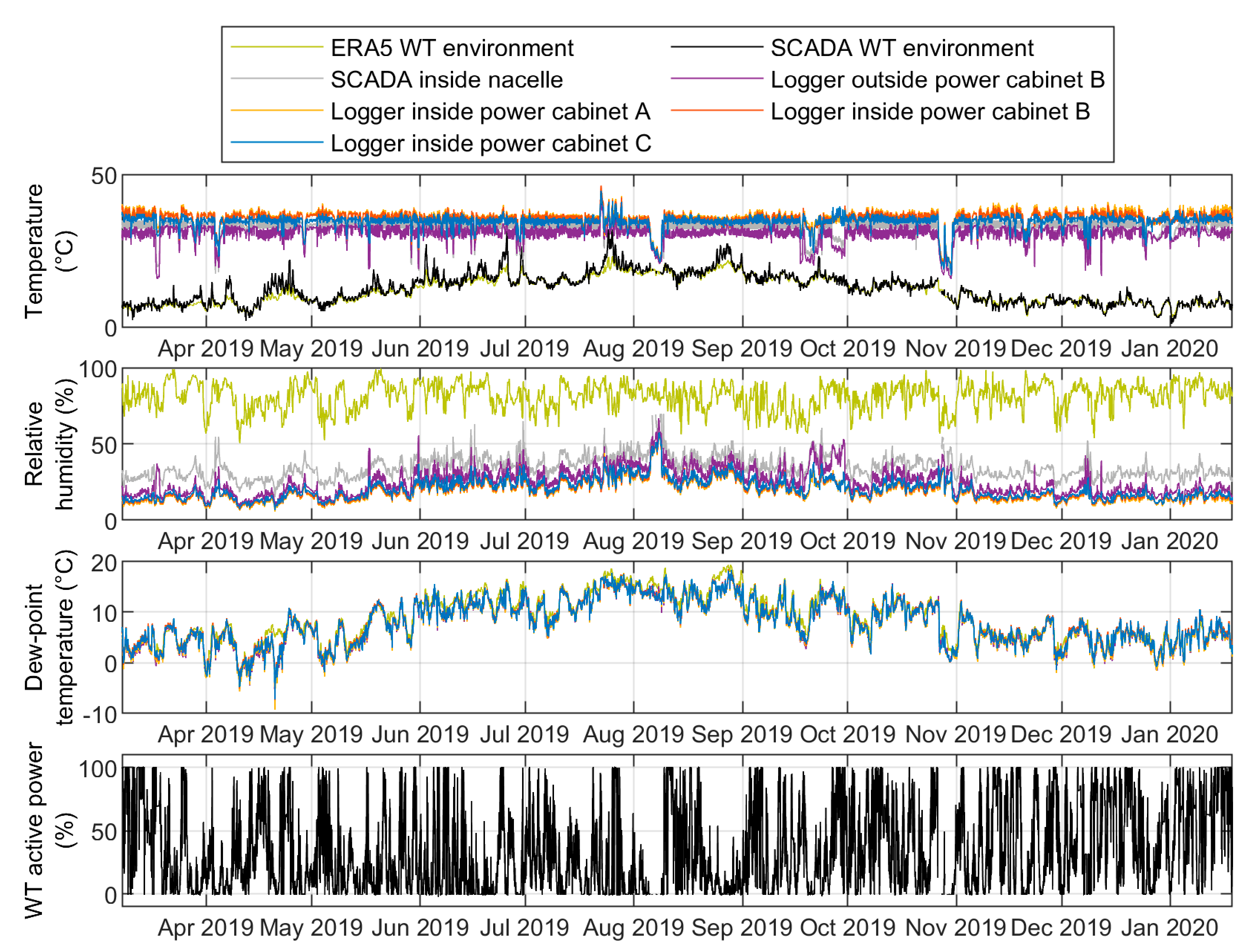
3.2.2. Example 2: Offshore WT in the German North Sea with Liquid-Cooled Converter in the Nacelle
3.2.3. Example 3: Onshore WT in India with Liquid-Cooled Converter in the Tower Base
3.3. Characterization of Climatic Conditions inside WT Converter Cabinets
3.3.1. Description of Cabinet Climate by Means of 2D Frequency Distributions
3.3.2. Influence of Sampling Rates Used in Climatic Measurement Campaigns
3.3.3. Ranges of Cabinet-Internal Temperature and Humidity According to Field Measurements on 31 Wind Turbines
3.4. Role of Converter Position and Cooling Concept for Cabinet-Internal Climatic Conditions
- As observed already in the in-depth analysis of WT1 in Section 3.2, the average temperature levels (A0) show a notable difference of, in this case, approximately 10 K.
- The amplitudes of the annual temperature cycles A1 are similar inside and outside, i.e., they are only slightly lower inside the air-cooled converter cabinet in the tower base of this turbine than in the WT environment.
- The annual temperature cycles are nearly “in phase”, with the maxima being shifted by not more than 11 days.
- While the thermal coupling between the converter-cabinet air and the air surrounding the turbine is similarly close in WT3 as in WT1, the temperature conditions inside WT2 appear to be decoupled from those surrounding the turbine (cf. also Section 3.2).
- As the diagrams for the dew-point temperature in the middle part of Figure 15a–c show, the fit functions confirm the close agreement of the cabinet-internal and WT-external dew-point temperature and absolute humidity, respectively, that was previously observed in Section 3.2.
- It is interesting to note that the annual maximum of the resulting relative humidity inside the converter cabinet does not necessarily coincide with that of the dew-point temperature, as the case of WT1 reveals. This is related to the fact that an increase in temperature has a reverse effect on RH compared to an increase in the dew-point temperature. Considering, e.g., the first quarter of the year, the increase in moisture content of the cabinet air expressed in the increase in dew-point temperature is overcompensated by the even stronger increasing cabinet temperature in this period, resulting in a decreasing RH.
4. Conclusions
4.1. Summary and Main Conclusions of the Present Work
4.2. Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gayo, J.B. Final Publishable Summary of Results of Project ReliaWind (Project Final Report). Available online: https://cordis.europa.eu/project/id/212966/reporting (accessed on 30 January 2019).
- Lin, Y.; Tu, L.; Liu, H.; Li, W. Fault analysis of wind turbines in China. Renew. Sustain. Energy Rev. 2016, 55, 482–490. [Google Scholar] [CrossRef]
- SPARTA Portfolio Review 2016; System Performance, Availability and Reliability Trend Analysis. Available online: www.sparta-offshore.com/SpartaHome#downloads (accessed on 19 January 2019).
- Fischer, K.; Pelka, K.; Puls, S.; Poech, M.-H.; Mertens, A.; Bartschat, A.; Tegtmeier, B.; Broer, C.; Wenske, J. Exploring the Causes of Power-Converter Failure in Wind Turbines based on Comprehensive Field-Data and Damage Analysis. Energies 2019, 12, 593. [Google Scholar] [CrossRef] [Green Version]
- Fischer, K.; Stalin, T.; Ramberg, H.; Wenske, J.; Wetter, G.; Karlsson, R.; Thiringer, T. Field-Experience Based Root-Cause Analysis of Power-Converter Failure in Wind Turbines. IEEE Trans. Power Electron. 2015, 30, 2481–2492. [Google Scholar] [CrossRef]
- Fischer, K.; Pelka, K.; Bartschat, A.; Tegtmeier, B.; Coronado, D.; Broer, C.; Wenske, J. Reliability of Power Converters in Wind Turbines: Exploratory Analysis of Failure and Operating Data From a Worldwide Turbine Fleet. IEEE Trans. Power Electron. 2019, 34, 6332–6344. [Google Scholar] [CrossRef]
- Tavner, P.; Greenwood, D.M.; Whittle, M.W.G.; Gindele, R.; Faulstich, S.; Hahn, B. Study of weather and location effects on wind turbine failure rates. Wind. Energy 2012, 16, 175–187. [Google Scholar] [CrossRef]
- Su, C.; Hu, Z. Reliability assessment for Chinese domestic wind turbines based on data mining techniques. Wind. Energy 2018, 21, 198–209. [Google Scholar] [CrossRef]
- Reder, M. Reliability Models and Failure Detection Algorithms for Wind Turbines. Ph.D. Thesis, CIRCE Universidad Zaragoza, Zaragoza, Spain, 2017. [Google Scholar]
- Tanaka, N.; Ota, K.; Iura, S.; Kusakabe, Y.; Nakamura, K.; Wiesner, E.; Thal, E. Robust HVIGBT Module Design against High Humidity. In Proceedings of the Power Conversion and Intelligent Motion (PCIM) Conference 2015, Nuremberg, Germany, 19–21 May 2015; pp. 368–373. [Google Scholar]
- SEMIKRON Application Note 16-001 Effect of Humidity and Condensation on Power Electronics Systems. Available online: www.semikron.com/dl/service-support/downloads/download/semikron-application-note-effect-of-humidity-and-condensation-on-power-electronics-systems-en-2016-07-15-rev-00/ (accessed on 24 October 2020).
- Zorn, C.; Kaminski, N.; Piton, M. Impact of Humidity on Railway Converters. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management (PCIM Europe 2017), Nuremberg, Germany, 16–18 May 2017; VDE Verlag: Berlin, Germany, 2017; pp. 715–722. [Google Scholar]
- ECPE European Center for Power Electronics Programme of ECPE Workshop Humidity in Power Electronics-Degradation Mechanisms and Lifetime Modelling. Available online: https://www.ecpe.org/events/workshops-tutorials/all/details/evt/mdl/ed/0/134/ (accessed on 16 March 2021).
- Ambat, R. Humidity and Intrinsic Aspects of PCBA Causing Climatic Reliability Issues in Electronics. In Proceedings of the CELCORR Seminar on Climatic Reliability of Electronics, Lyngby, Denmark, 20–21 March 2019. [Google Scholar]
- Piotrowska, K.; Ambat, R. Residue-Assisted Water Layer Build-Up Under Transient Climatic Conditions and Failure Occurrences in Electronics. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1617–1635. [Google Scholar] [CrossRef]
- Laska, B. Semiconductor Reliability of Worldwide Operated Traction Converter. In Proceedings of the ECPE Workshop Humidity in Power Electronics—Degradation Mechanisms and Lifetime Modelling, Bremen, Germany, 5–6 June 2019. [Google Scholar]
- Fischer, K.; Stalin, T.; Ramberg, H.; Thiringer, T.; Wenske, J.; Karlsson, R. Investigation of Converter Failure in Wind Turbines, Elforsk Report 12:58. Available online: http://publica.fraunhofer.de/dokumente/N-349544.html (accessed on 26 March 2021).
- Bartschat, A.; Broer, C.; Coronado, D.; Fischer, K.; Kucka, J.; Mertens, A.; Meyer, R.; Moriße, M.; Pelka, K.; Tegtmeier, B.; et al. Zuverlässige Leistungselektronik für Windenergieanlagen. In Abschlussbericht zum Fraunhofer-Innovationscluster Leistungselektronik für Regenerative Energieversorgung; Fraunhofer-Verlag: Stuttgart, Germany, 2018; ISBN 978-3-8396-1326-9. [Google Scholar]
- Fischer, K. Humidity in Power Converters of Wind Turbines-Field Conditions and Impact on Reliability. In Proceedings of the ECPE Workshop Humidity in Power Electronics—Degradation Mechanisms and Lifetime Modelling, Bremen, Germany, 5–6 June 2019. [Google Scholar]
- Brunko, A.; Holzke, W.; Groke, H.; Orlik, B.; Kaminski, N. Model-Based Condition Monitoring of Power Semiconductor Devices in Wind Turbines. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–6 September 2019. [Google Scholar]
- Lascar Electronics, Datasheet EasyLog EL-USB-2 Temperature, Humidity and Dew Point Data Logger. 2020. Available online: www.lascarelectronics.com/media/7272/easylog-data-logger_el-usb-2_iss16_02-2021.pdf (accessed on 27 March 2021).
- E+E Elektronik Datasheet EE16 Series Humidity / Temperature Transmitter for HVAC Applications. 2020. Available online: https://downloads.epluse.com/fileadmin/data/product/ee16/datasheet_EE16.pdf (accessed on 27 March 2021).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef] [Green Version]
- European Centre for Medium-Range Weather Forecasts Computation of Near-Surface Humidity and Snow Cover. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation#ERA5:datadocumentation-Computationofnear-surfacehumidityandsnowcover (accessed on 15 February 2021).
- IFS Documentation CY41R2, Part IV Physical Processes. Available online: https://www.ecmwf.int/en/elibrary/16648-ifs-documentation-cy41r2-part-iv-physical-processes (accessed on 15 February 2021).
- Schilling, O.; Lassmann, M. Humidity Requirement Engineering-Standards and Real Climatic Data. In Proceedings of the ECPE Workshop Humidity and Condensation in Power Electronic Systems—Degradation Mechanisms and Lifetime Modelling, Bremen, Germany, 5–6 June 2019. [Google Scholar]
- Snell, J.; Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers. J. R. Stat. Soc. Ser. A Stat. Soc. 1995, 158, 355. [Google Scholar] [CrossRef]
- Fuchs, F.; Mertens, A. Steady State Lifetime Estimation of the Power Semiconductors in the Rotor Side Converter of a 2 MW DFIG Wind Turbine via Power Cycling Capability Analysis. In Proceedings of the 14th European Conference on Power Electronics and Applications (EPE 2011), Birmingham, UK, 30 August–1 September 2011; pp. 1–8. [Google Scholar]
- IEC 60721-3-3:2019 Classification of Environmental Conditions-Part 3-3: Classification of Groups of Environmental Parameters and Their Severities–Stationary Use at Weatherprotected Locations; International Standard: Geneva, Switzerland, 2019.
- Wintrich, A.; Nicolai, U.; Tursky, W.; Reimann, T. SEMIKRON Application Manual Power Semiconductors; ISLE Verlag: Ilmenau, Germany, 2015; ISBN 978-3-938843-83-3. [Google Scholar]
- Infineon AN2009-08 V2.0 Application and Assembly Notes for PrimePACKTM Modules. Available online: www.infineon.com/dgdl/Infineon-Application_and_Assembly_Notes_PrimePACK_Modules-ApplicationNotes-v02_00-EN.pdf?fileId=db3a30431375fb1a011376a24657002d (accessed on 14 November 2020).
- Piotrowska, K.; Jellesen, M.S.; Ambat, R. Water film formation on the PCBA surface and failure occurrence in electronics. In Proceedings of the 2018 IMAPS Nordic Conference on Microelectronics Packaging (NordPac), Oulu, Finland, 12–14 June 2018; pp. 72–76. [Google Scholar]
- Piotrowska, K.; Din, R.U.; Grumsen, F.B.; Jellesen, M.S.; Ambat, R. Parametric Study of Solder Flux Hygroscopicity: Impact of Weak Organic Acids on Water Layer Formation and Corrosion of Electronics. J. Electron. Mater. 2018, 47, 4190–4207. [Google Scholar] [CrossRef]
- Piotrowska, K.; Grzelak, M.; Ambat, R. No-Clean Solder Flux Chemistry and Temperature Effects on Humidity-Related Reliability of Electronics. J. Electron. Mater. 2018, 48, 1207–1222. [Google Scholar] [CrossRef]
- Hatori, K. The Reliability of IGBT Modules against Humidity and Condensation. In Proceedings of the ECPE Workshop Humidity and Condensation in Power Electronic Systems–Degradation Mechanisms and Lifetime Modelling, Bremen, Germany, 5–6 June 2019. [Google Scholar]









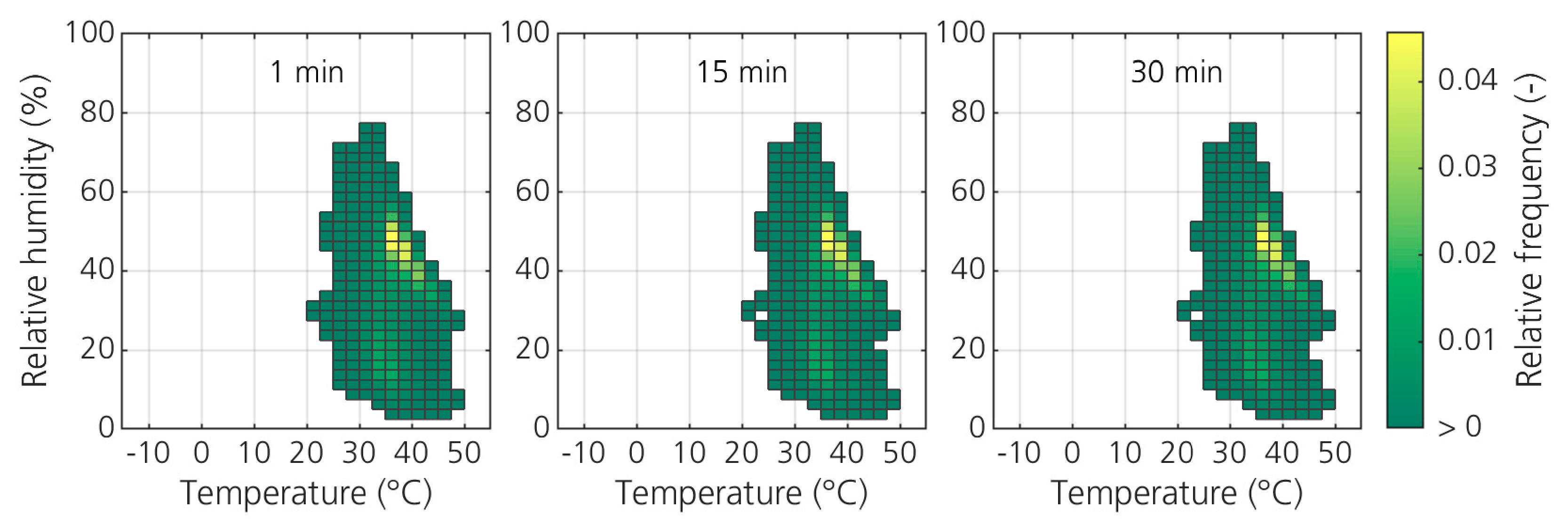


| Range Inside Converter Cabinet (Measured) | Range in WT Environment (ERA5) | |||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| Temperature | −7.5 °C | 78.0 °C | −17.5 °C | 48.8 °C |
| Relative Humidity | 0% | 83.4% | 2.0% | 100% |
| Absolute Humidity | 0 g/m³ | 27.7 g/m³ | 0.7 g/m³ | 28.0 g/m³ |
| Dew-Point Temperature | −32.3 °C | 28.6 °C | −22.5 °C | 28.8 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, K.; Steffes, M.; Pelka, K.; Tegtmeier, B.; Dörenkämper, M. Humidity in Power Converters of Wind Turbines—Field Conditions and Their Relation with Failures. Energies 2021, 14, 1919. https://doi.org/10.3390/en14071919
Fischer K, Steffes M, Pelka K, Tegtmeier B, Dörenkämper M. Humidity in Power Converters of Wind Turbines—Field Conditions and Their Relation with Failures. Energies. 2021; 14(7):1919. https://doi.org/10.3390/en14071919
Chicago/Turabian StyleFischer, Katharina, Michael Steffes, Karoline Pelka, Bernd Tegtmeier, and Martin Dörenkämper. 2021. "Humidity in Power Converters of Wind Turbines—Field Conditions and Their Relation with Failures" Energies 14, no. 7: 1919. https://doi.org/10.3390/en14071919
APA StyleFischer, K., Steffes, M., Pelka, K., Tegtmeier, B., & Dörenkämper, M. (2021). Humidity in Power Converters of Wind Turbines—Field Conditions and Their Relation with Failures. Energies, 14(7), 1919. https://doi.org/10.3390/en14071919