Optimization and Influence of Micro-Chamfering on Oil Film Lubrication Characteristics of Slipper/Swashplate Interface within Axial Piston Pump
Abstract
:1. Introduction
2. Lubrication Model and Coupling Algorithm
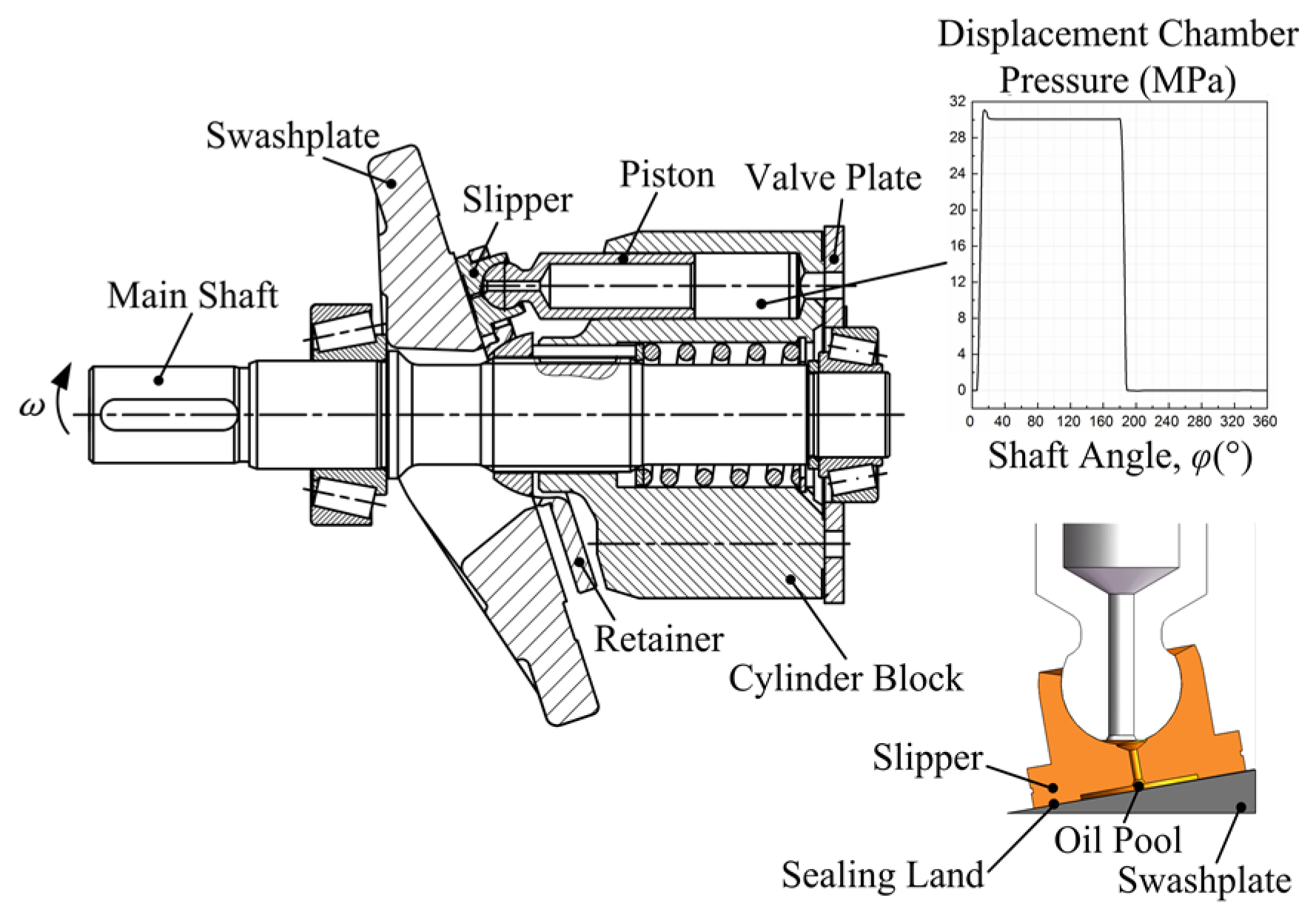
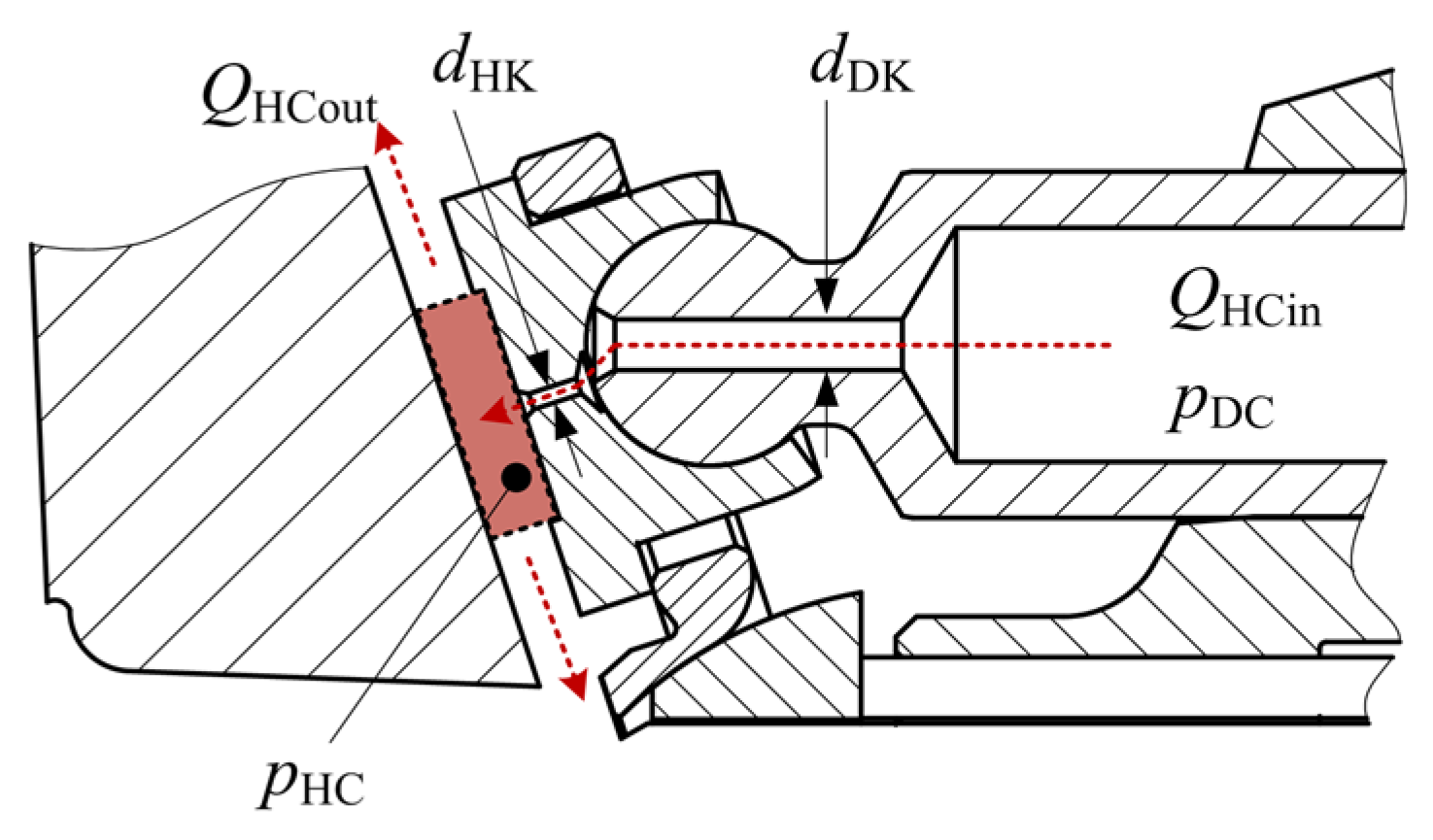
2.1. Axial Piston Pump Structure
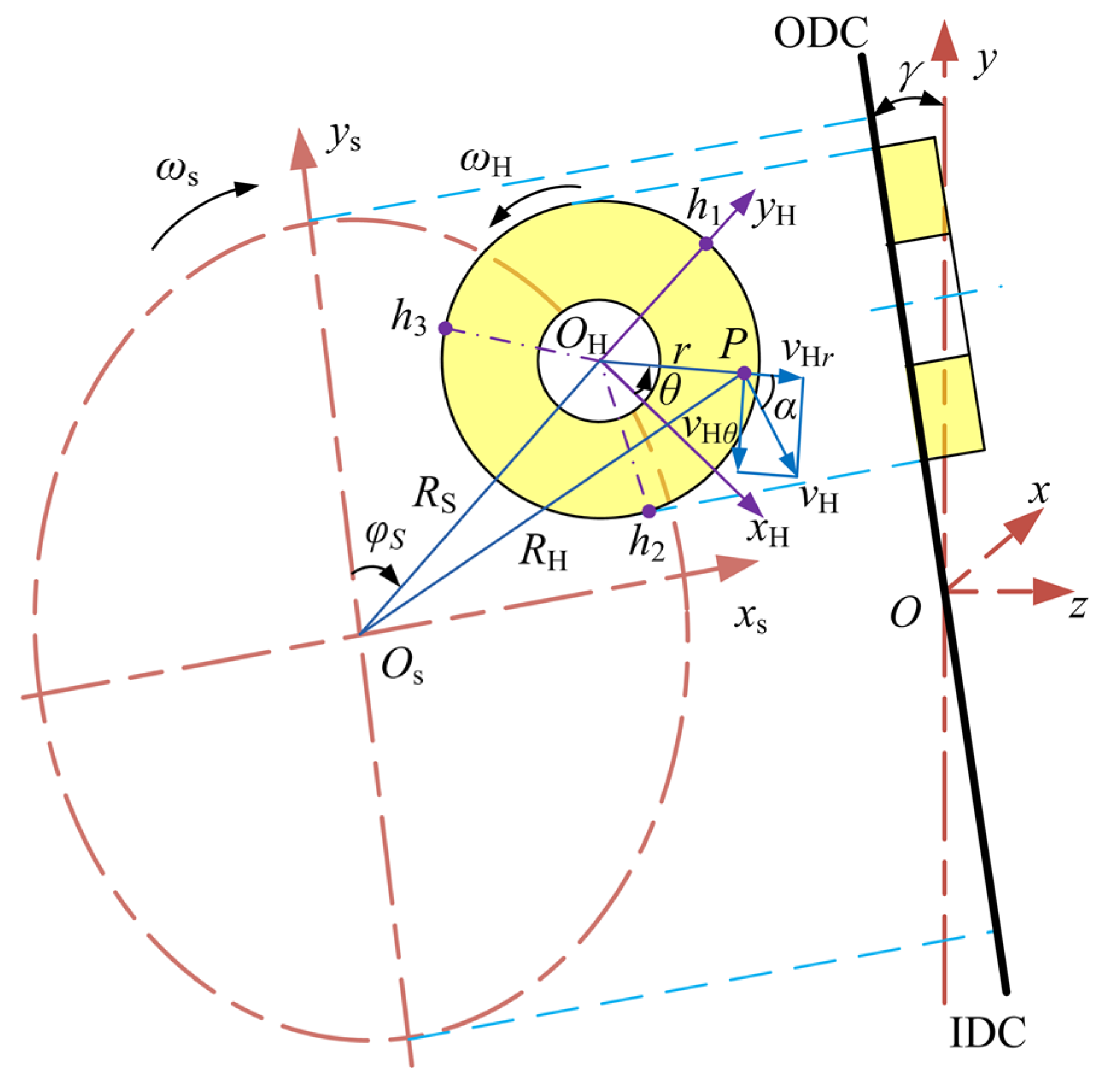
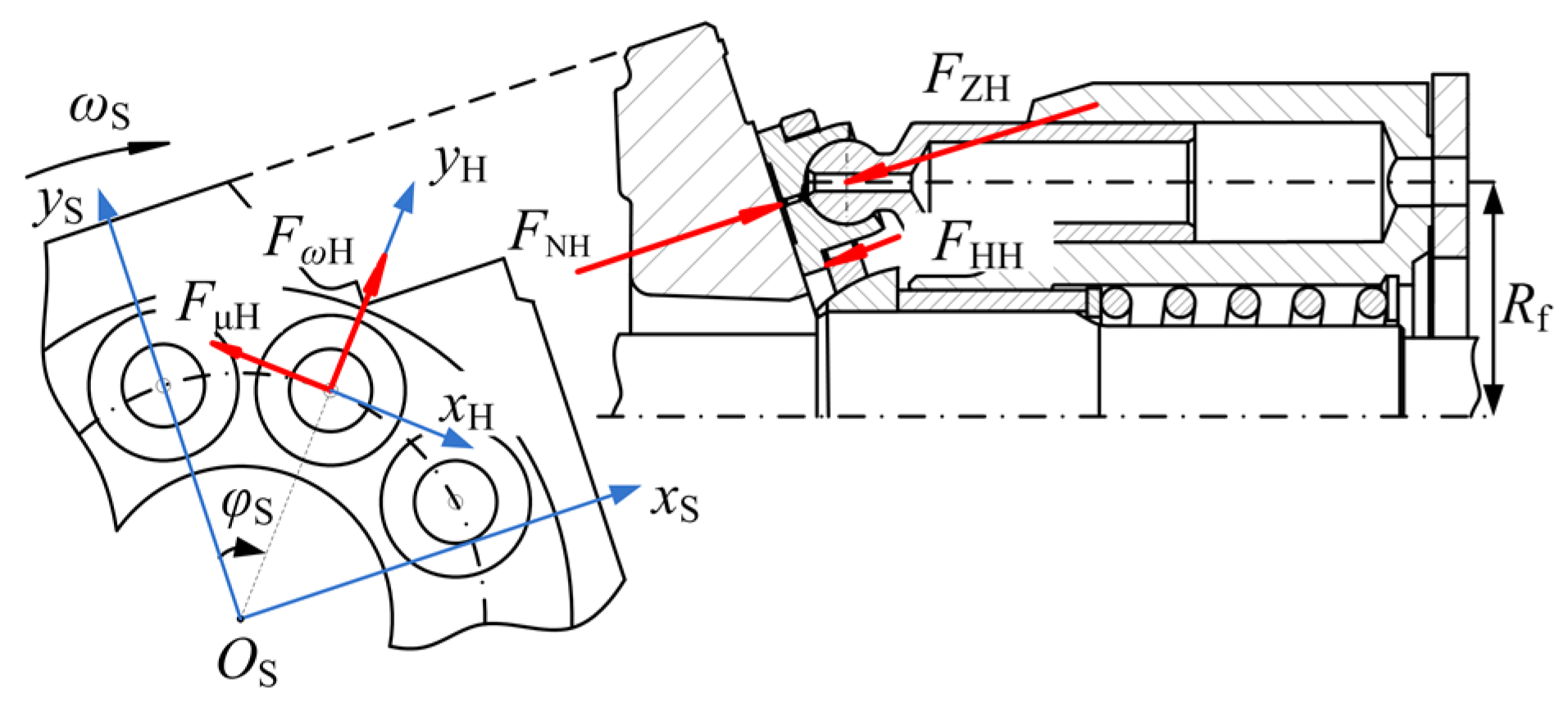
2.2. Kinetic and Force Analysis of Slipper
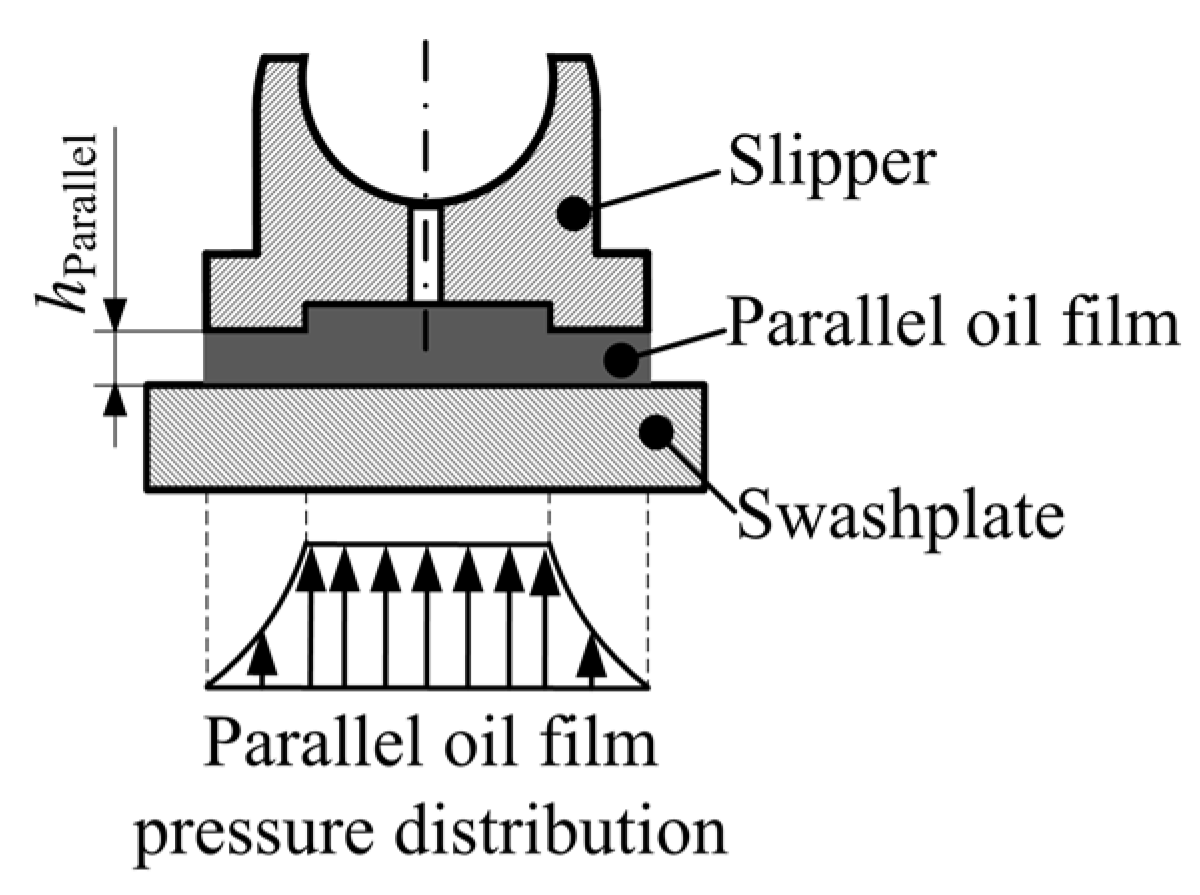
2.3. Pressure and Power Loss Models
- (1)
- The fluid in the oil film is the incompressible and Newtonian one;
- (2)
- The fluid velocity on the boundary is the same as the velocity of the working surface;
- (3)
- Because the oil film thickness is micron level, the fluid flow can be considered to be the laminar one.
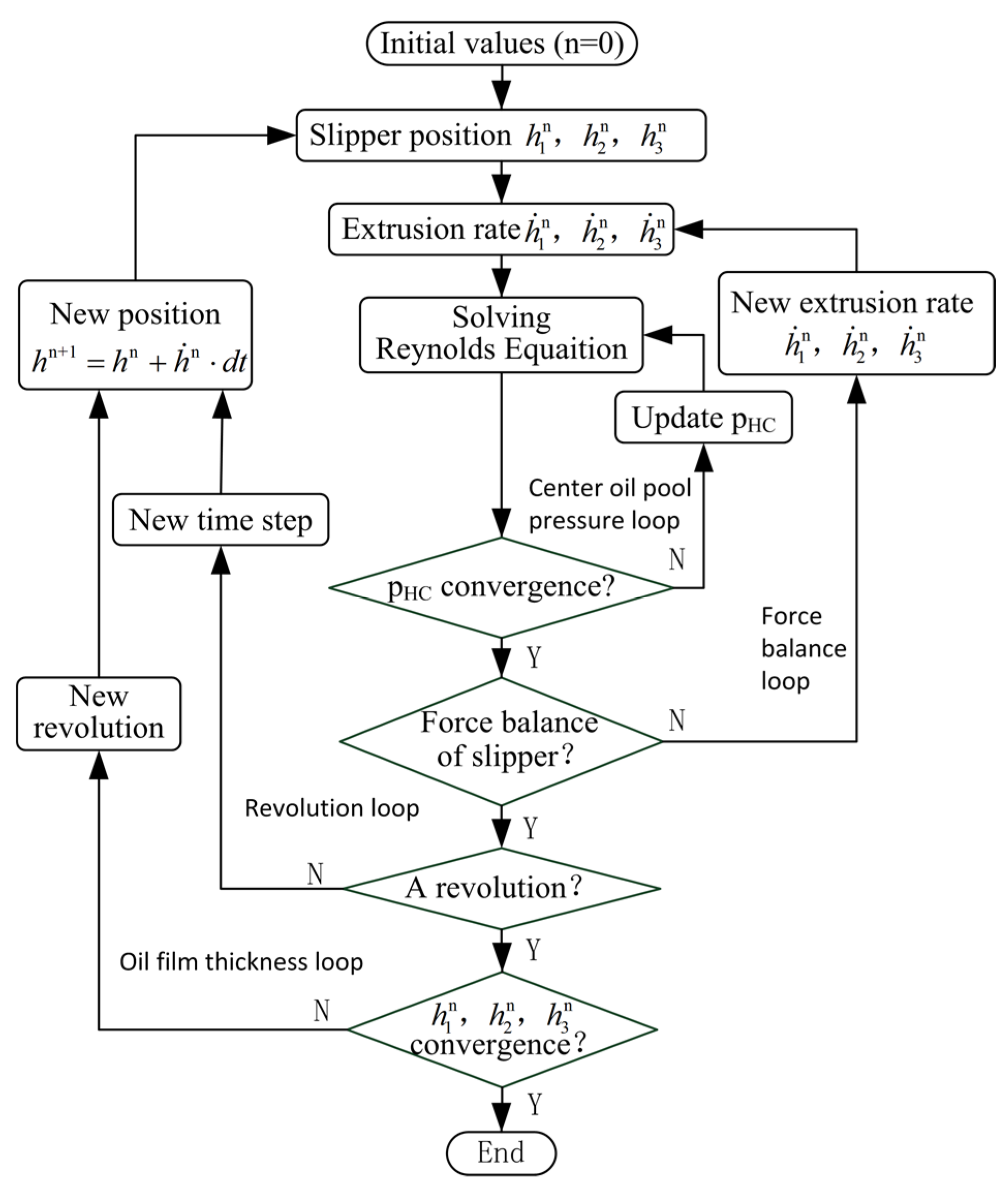
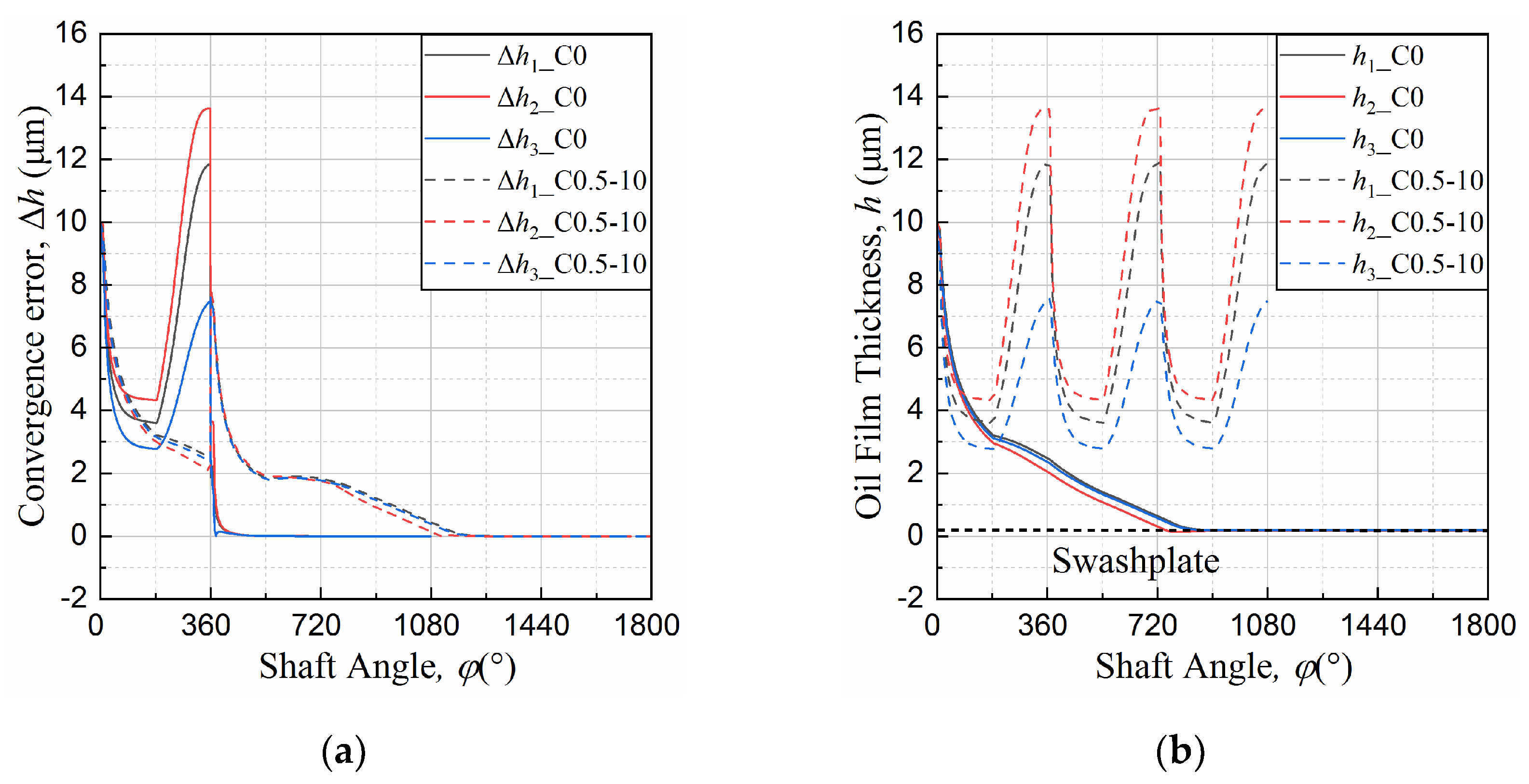
2.4. Coupling Algorithm
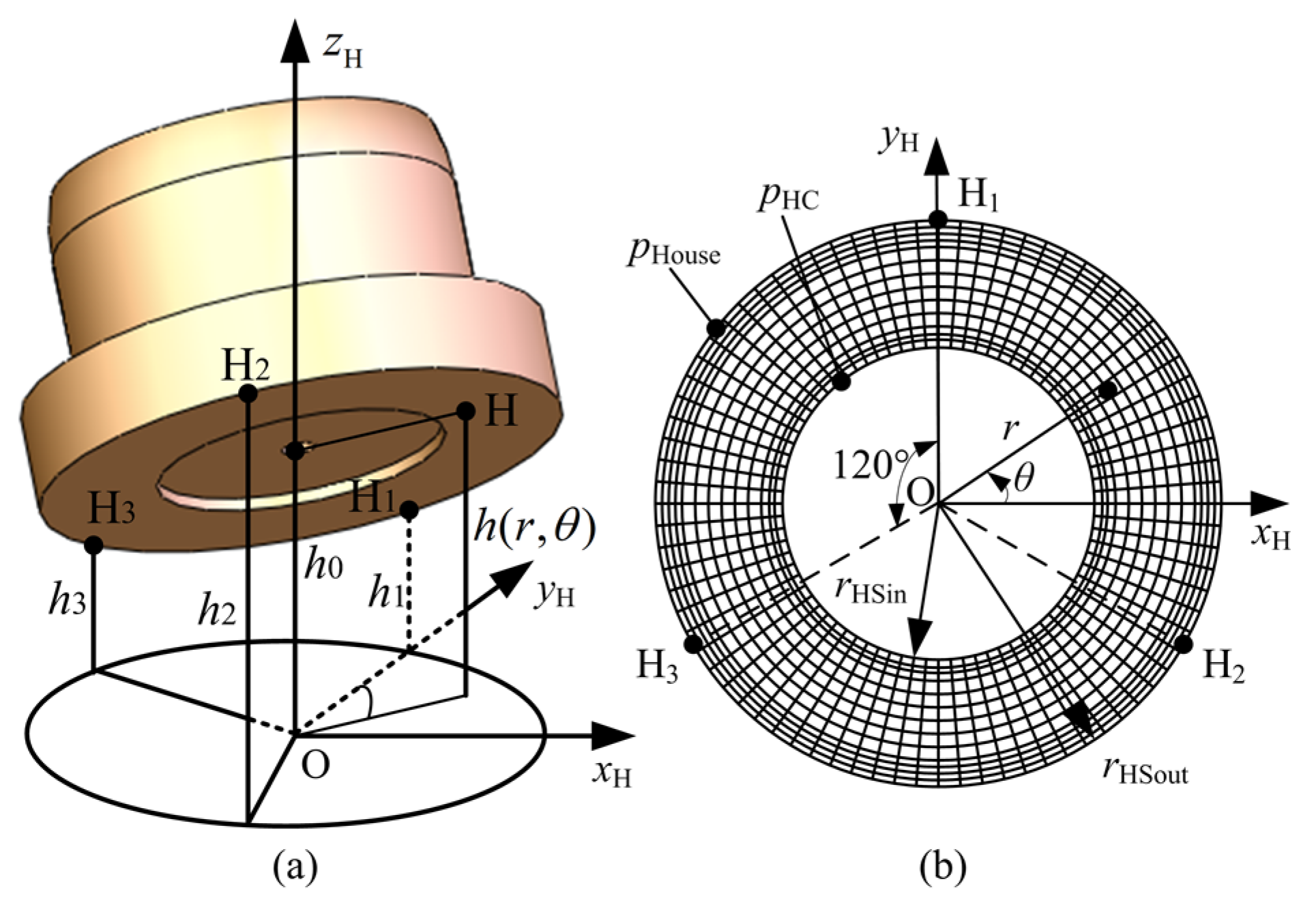
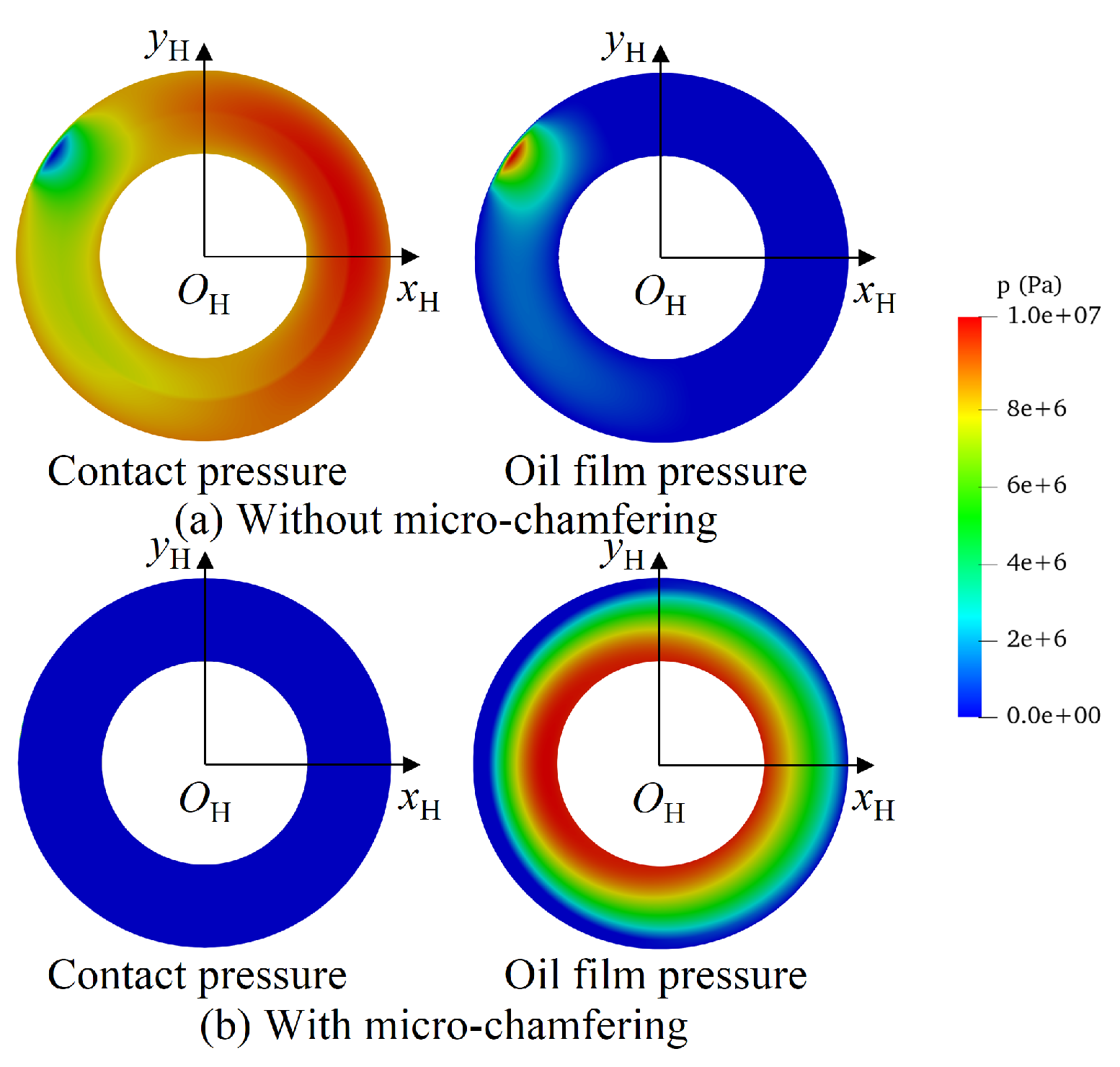
3. Impact of Micro-Chamfering on Oil Film Lubrication
4. Optimization of Micro-Chamfering Parameters
4.1. Working Conditons Selected of Optimization
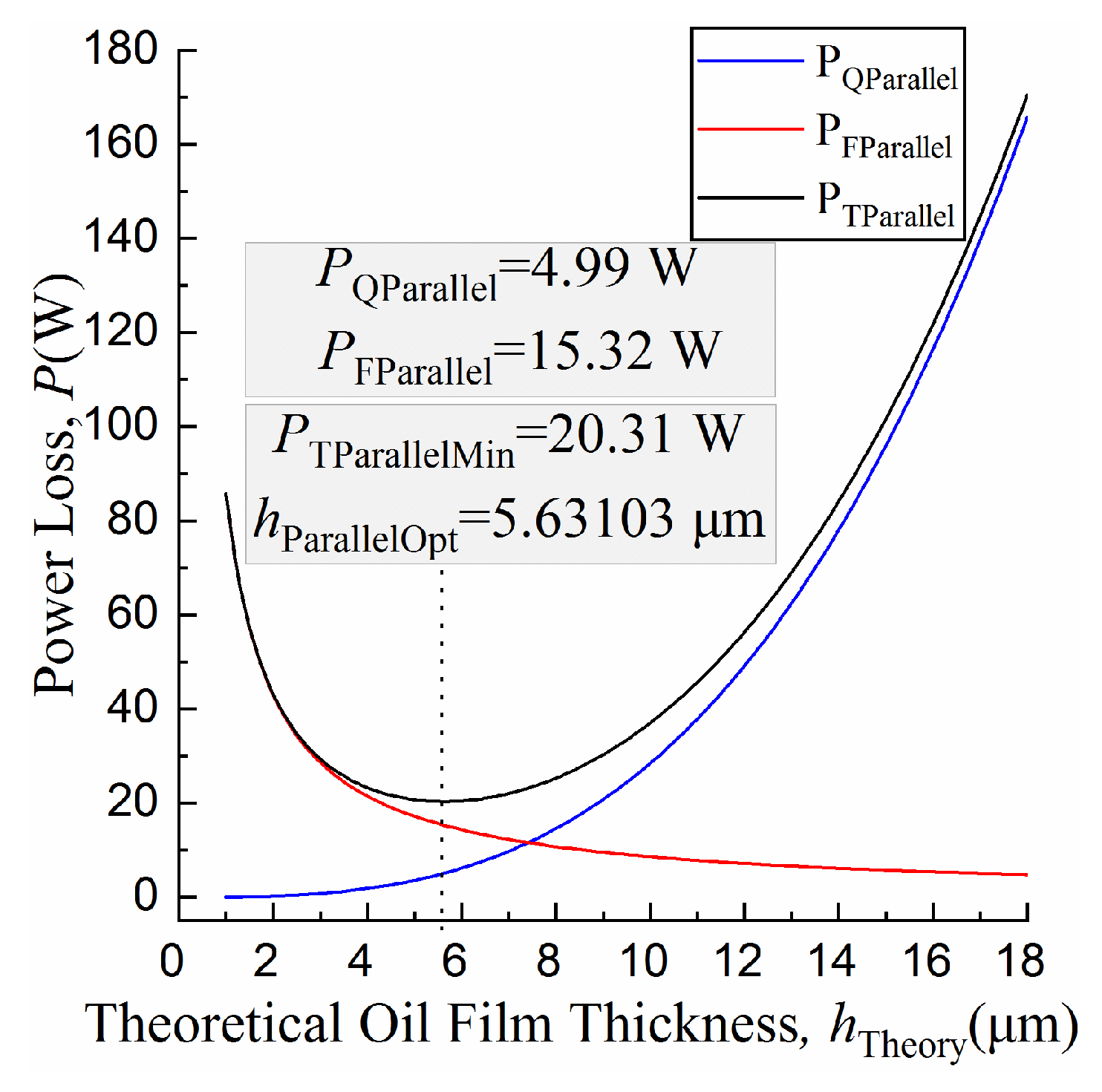
4.2. Optimization Objective
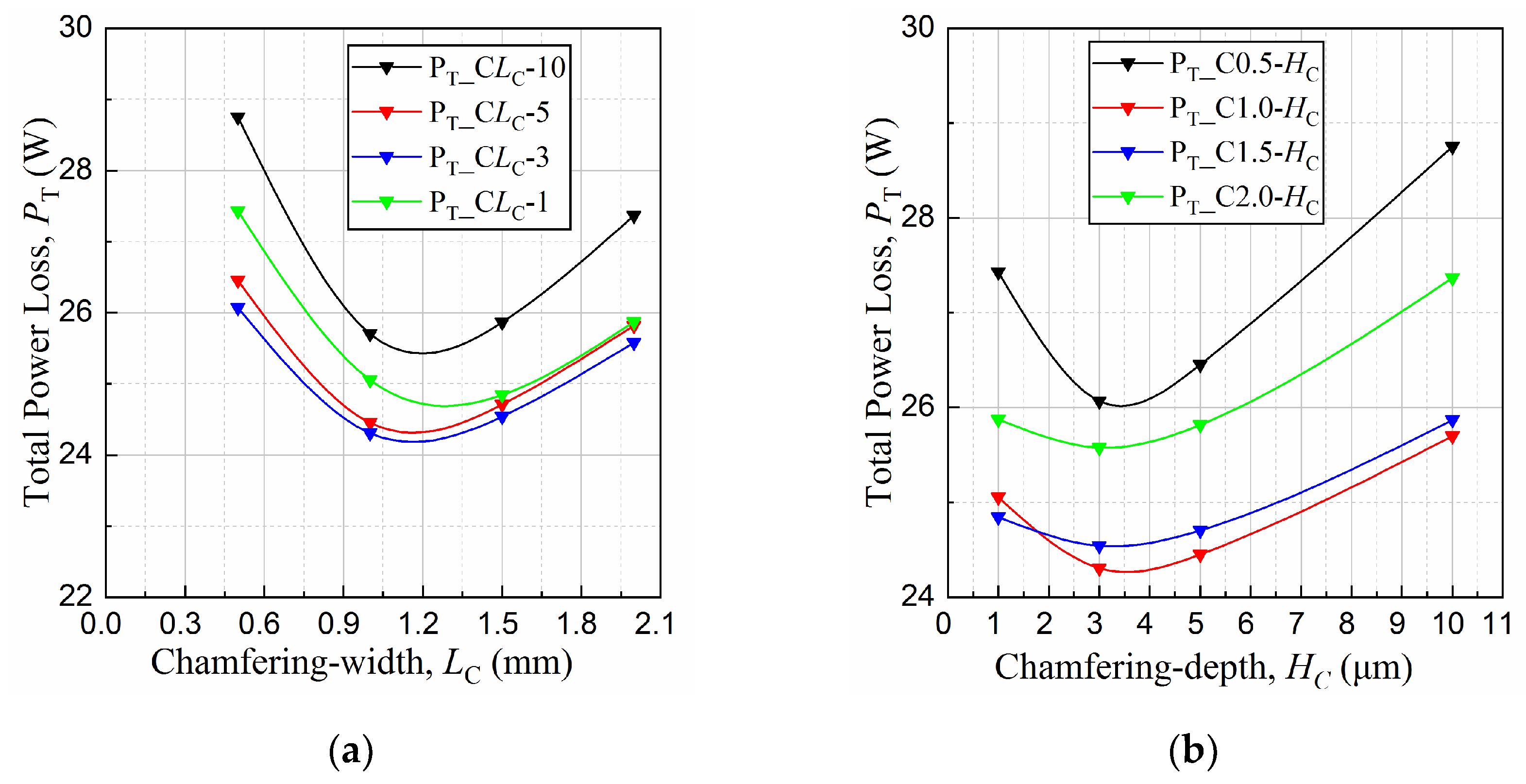
4.3. Optimization of Micro-Chamfering
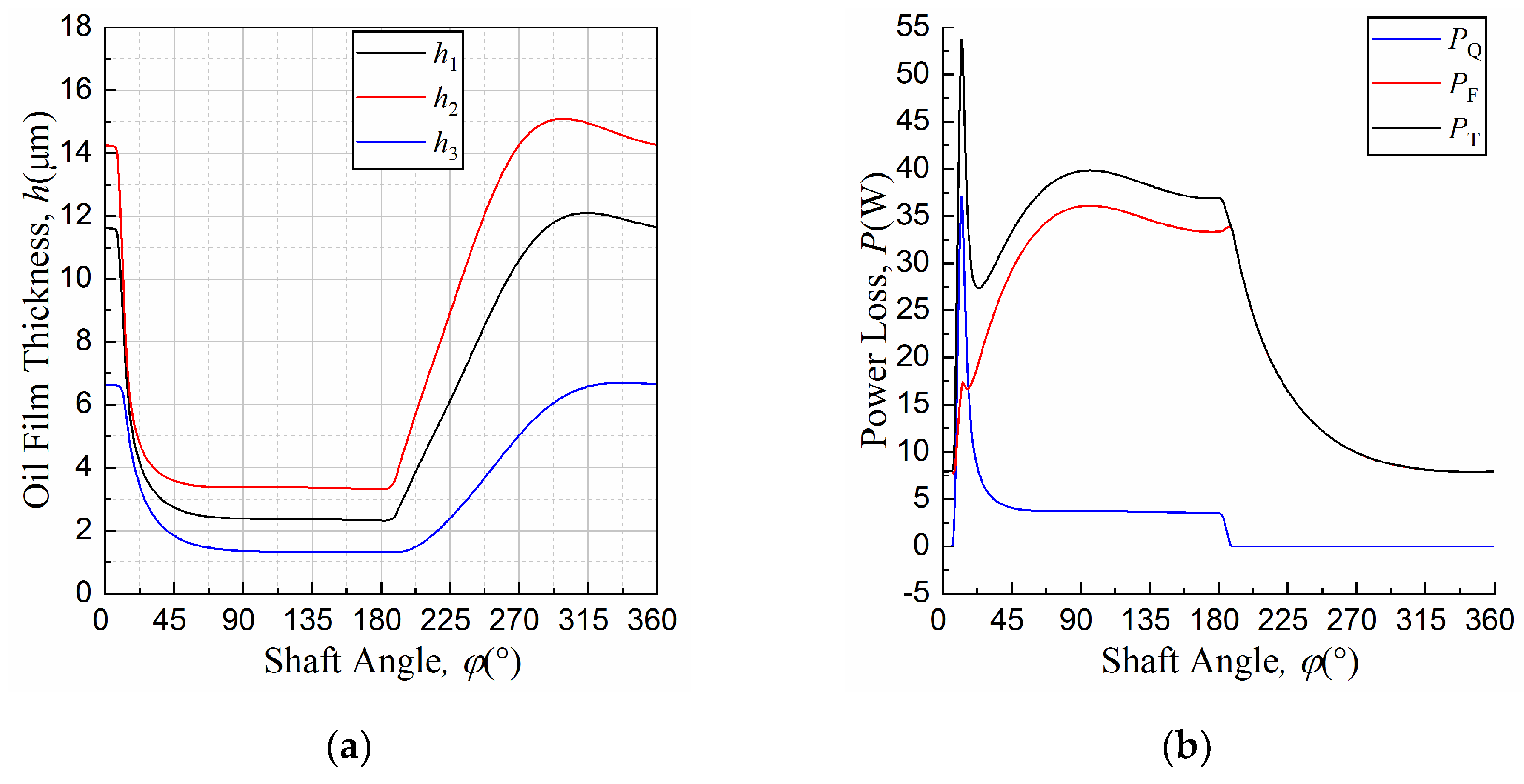
4.4. Lubrication Perfomance Analysis with Optimal Micro-Chamfering
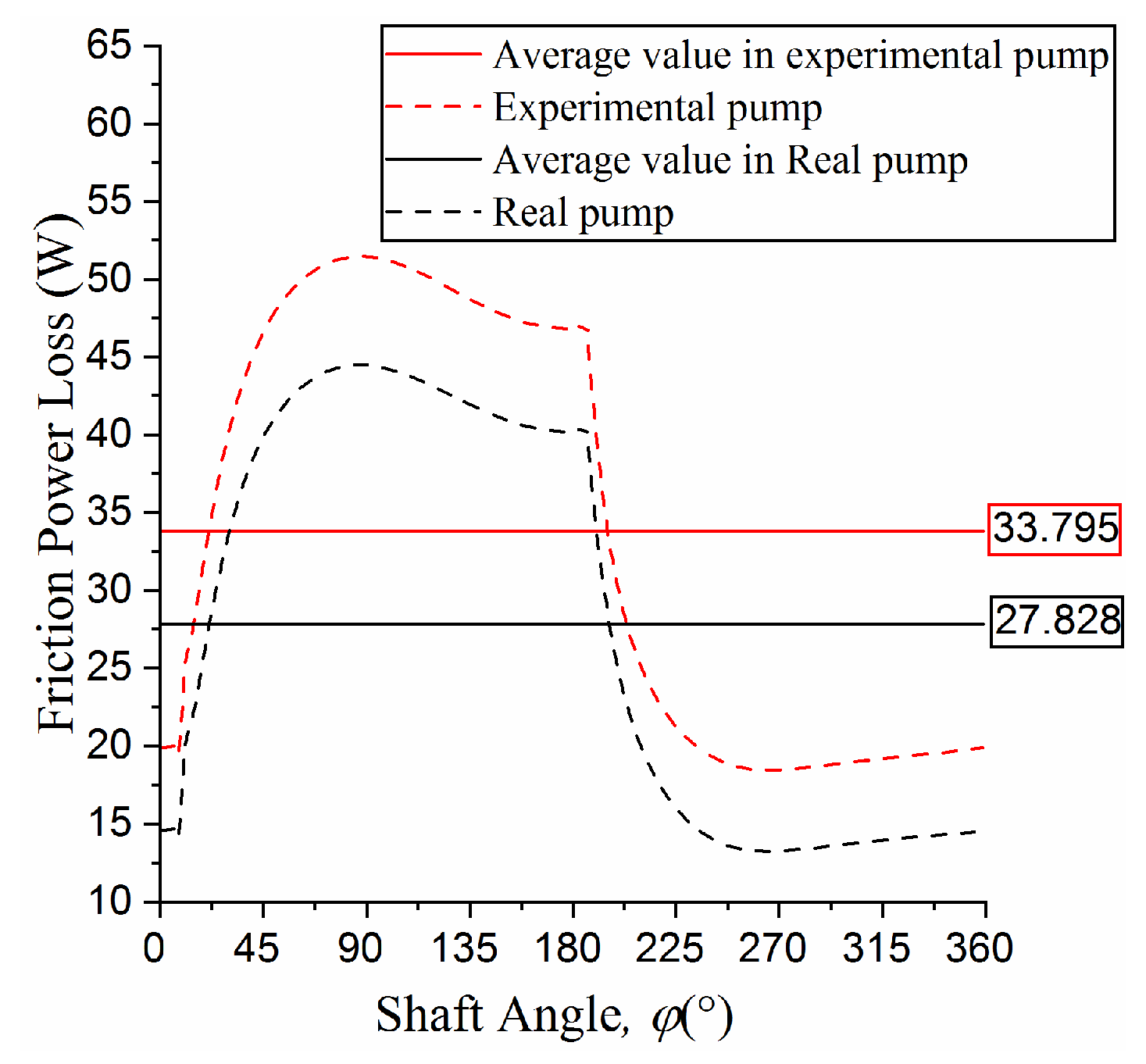
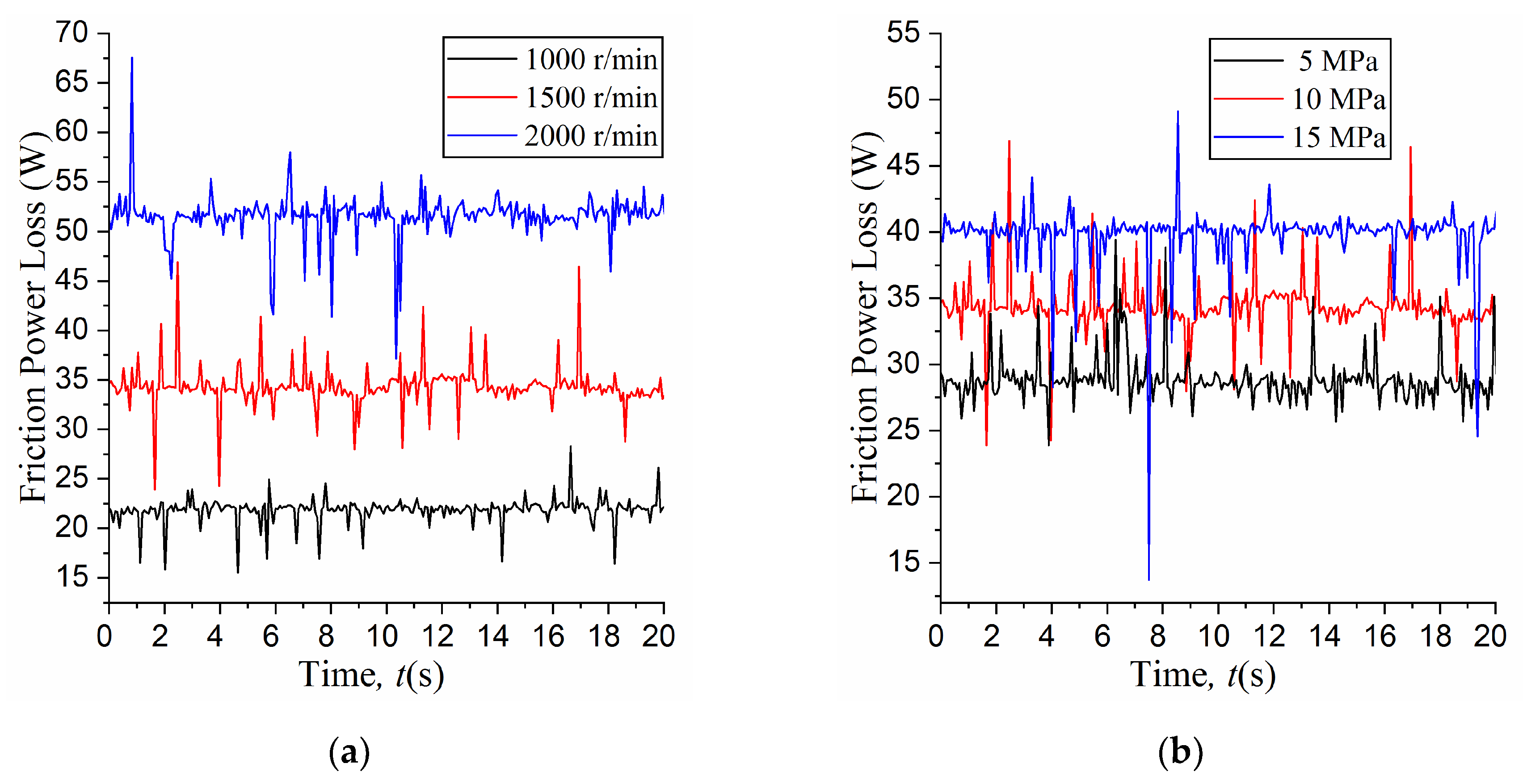
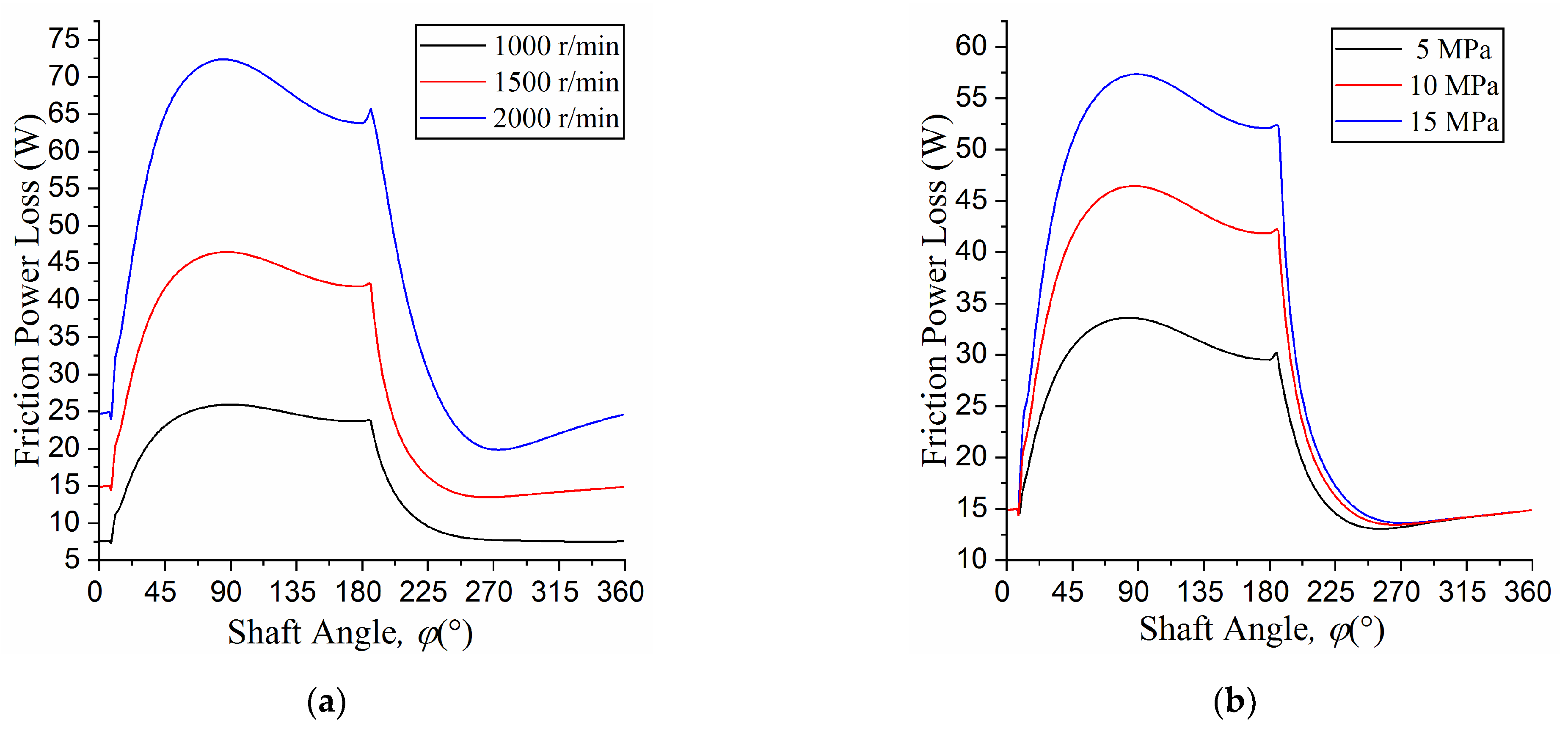
5. Experiments
6. Conclusions
- (1)
- The oil film thickness decreases with the increase in the working pressure and the swashplate inclination angle, but it increases with the increase in the shaft speed and the pump house pressure.
- (2)
- Micro-chamfering is conducive to generate the oil film lubrication and to reduce the power loss between the slipper and swashplate.
- (3)
- The minimum total power loss can be taken as the optimization objective. The optimal parameter group of micro-chamfering is the width of 1.2 mm and the depth of 3.5 μm or C1.2-3.5.
- (4)
- The simulation results of the optimal parameter group of micro-chamfering are approximately equal to the analytical ones. The experimental results of the power loss of the slipper/swashplate interface are also essentially consistent with the simulation one. The coupling lubrication numerical model and the optimization are proved to be correct and effective to provide a basis for further optimization design of axial piston pumps.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, S.R.; Chen, J.H.; Lu, Y.L. Hydraulic piston pump in civil aircraft: Current status, future directions and critical technologies. Chin. J. Aeronaut. 2019, 33, 16–30. [Google Scholar] [CrossRef]
- Shen, W.; Huang, H.; Pang, Y. Review of the energy saving hydraulic system based on common pressure rail. IEEE Access 2017, 5, 655–669. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, R.; Sarkar, B.K. Condition monitoring of hydraulic transmission system with variable displacement axial piston pump and fixed displacement motor. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Xiong, S.P.; Wilfong, G.; Lumkes, J. Components sizing and performance analysis of hydro-mechanical power split transmission applied to a wheel loader. Energies 2019, 12, 1613. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, J.H.; Xu, B. Multi-objective optimization of micron-scale surface textures for the cylinder/valve plate interface in axial piston pumps. Tribol. Int. 2019, 138, 316–329. [Google Scholar] [CrossRef]
- Song, Y.H.; Ma, J.M.; Zeng, S.K. A numerical study on influence of temperature on lubricant film characteristics of the piston/cylinder interface in axial piston pumps. Energies 2018, 11, 1842. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.H.; Li, Y.; Xu, B. Experimental study on the influence of the rotating cylinder block and pistons on churning losses in axial piston pumps. Energies 2017, 10, 662. [Google Scholar] [CrossRef] [Green Version]
- Lan, Y.; Hu, J.W.; Huang, J.H. Fault diagnosis on slipper abrasion of axial piston pump based on Extreme Learning Machine. Measurement 2018, 124, 378–385. [Google Scholar] [CrossRef]
- Haidak, G.; Wang, D.Y.; Lisiane, E.A.E. Modelling of deformation and failure of slipper-retainer assembly in axial piston machine. Eng. Fail. Anal. 2020, 111, 104490. [Google Scholar] [CrossRef]
- Haidak, G.; Wang, D.Y. The impact of the deformation phenomenon on the process of lubricating and improving the efficiency between the slipper and swashplate in axial piston machines. IEEE Access 2019, 7, 69393–69409. [Google Scholar] [CrossRef]
- Wang, Y.J. Pressure distribution characteristics in slipper pad bearing of axial piston pump. Drain. Irrig. Eng. 2014, 32, 1–5. [Google Scholar]
- Hashemi, S.; Kroker, A.; Bobach, L. Multibody dynamics of pivot slipper pad thrust bearing in axial piston machines incorporating thermal elastohydrodynamics and mixed lubrication model. Tribol. Int. 2016, 96, 57–76. [Google Scholar] [CrossRef]
- Ye, S.G.; Tang, H.S.; Ren, Y. Study on the load-carrying capacity of surface textured slipper bearing of axial piston pump. Appl. Math. Model 2020, 77, 554–584. [Google Scholar] [CrossRef]
- Zhou, J.J.; Zhou, J.C.; Jing, C.B. Experimental Research on the Dynamic Lubricating Performance of Slipper/Swash Plate Interface in Axial Piston Pumps. Chin. J. Mech. Eng. 2020, 33, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wieczorek, U.; Ivantysynova, M. Computer aided optimization of bearing and sealing gaps in hydrostatic machines—The simulation tool CASPAR. Int. J. Fluid Power 2002, 3, 7–20. [Google Scholar] [CrossRef]
- Shang, L.Z.; Ivantysynova, M. Scaling Criteria for Axial Piston Machines Based on Thermo-Elastohydrodynamic Effects in the Tribological Interfaces. Energies 2018, 11, 3210. [Google Scholar] [CrossRef] [Green Version]
- Schenk, A.; Ivantysynova, M. A Transient Thermoelastohydrodynamic Lubrication Model for the Slipper/Swashplate in Axial Piston. J. Tribol. 2015, 137, 1–10. [Google Scholar] [CrossRef]
- Złoto, T.; Kowalski, K. Load of the slipper-swash plate kinematic pair of an axial piston pump. MATEC Web Conf. 2018, 157, 08013. [Google Scholar] [CrossRef]
- Xu, B.; Li, Y.B.; Zhang, B. Numerical simulation of overturning phenomenon of axial piston pump slipper pair. J. Mech. Eng. 2010, 46, 161–168. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.H.; Yang, H.Y. Investigation on structural optimization of anti-overturning slipper of axial piston pump. Sci. China (Tech. Sci.) 2012, 55, 3010–3018. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Q.N.; Zhang, J.H. Effect of case drain pressure on slipper/swashplate pair within axial piston pump. J. Zhejiang Univ.-Sci. A (Appl. Phys. Eng.) 2015, 16, 1001–1014. [Google Scholar] [CrossRef]
- Qun, C.; Zhang, J.H.; Xu, B. Multi-position measurement of oil film thickness within the slipper bearing in axial piston pumps. Measurement 2018, 122, 66–72. [Google Scholar]
- Tang, H.S.; Yan, Y.B.; Li, J. Characteristics of clearance leakage and friction torque of slipper pair in axial piston pump. J. South China Univ. Tech. (Nat. Sci. Ed.) 2014, 42, 74–79. [Google Scholar]
- Tang, H.S.; Li, J.; Yan, Y.B. Power loss characteristics of slipper/swash plate pair in axial piston pump. J. Cent. South Univ. (Sci. Tech.) 2017, 48, 361–369. [Google Scholar]
- Nie, S.L.; Huang, G.H.; Li, Y.P. Tribological study on hydrostatic slipper bearing with annular orifice damper for water hydraulic axial piston motor. Tribol. Int. 2006, 39, 1342–1354. [Google Scholar] [CrossRef]
- Ma, J.M.; Shen, Y.Y.; Li, Q.L. Oil Film Analysis of Swash Plate/slipper pair based on CFD. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 265–272. [Google Scholar]
- Chen, J.; Ma, J.M.; Li, J. Performance optimization of grooved slippers for aero hydraulic pumps. J Chin. J. Aeronaut. 2016, 29, 814–823. [Google Scholar] [CrossRef] [Green Version]
- Borghi, M.; Specchia, E.; Zardin, B. Numerical analysis of the dynamic behavior of axial piston pumps and motors slipper bearing. SAE Int. J. Passeng. Cars-Mech. Syst. 2009, 2, 1285–1302. [Google Scholar] [CrossRef]
- Hooke, C.J.; Kakoullis, Y.P. The effect of non-flatness on the performance of slippers in axial piston pumps. Proc. Inst. Mech. Engrs. 1983, 197, 239–247. [Google Scholar] [CrossRef]
- Koc, E.; Hooke, C.J. Considerations in the design of partially hydrostatic slipper bearings. Tribol. Int. 1997, 30, 815–823. [Google Scholar] [CrossRef]
- Manring, N.D.; Wray, C.L.; Dong, Z.L. Experimental studies on the performance of slipper bearings within axial-piston pumps. ASME J. Tribol. 2004, 126, 511–518. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, J.H.; Liu, C.Q. Oil film characteristics and power consumption of slipper pair under redundant pressing force. J. South China Univ. Tech. (Nat. Sci. Ed.) 2011, 39, 111–116. [Google Scholar]
- Wang, K.L.; Jiang, J.H.; Wang, Z.B. Micro-motion of piston/cylinder interface and the influence of micro chamfering on it. J. Huangzhong Univ. Sci. Tech. (Nat. Sci. Ed.) 2019, 47, 46–51. [Google Scholar]
- Sharma, S.C.; Yadav, S.K. Performance analysis of a fully textured hybrid circular thrust pad bearing system operating with non-Newtonian lubricant. Tribol. Int. 2014, 77, 50–64. [Google Scholar] [CrossRef]





| Symbols | Value | Units |
|---|---|---|
| Rf | 33.5 | mm |
| rHSin | 5.9 | mm |
| rHSout | 10.7 | mm |
| lHK | 2.9 | mm |
| dHK | 0.8 | mm |
| lHC | 0.9 | mm |
| Cq | 0.63 | - |
| K | 2 | GPa |
| μ | 0.02784 | N·s/m2 |
| γ | 18 | ° |
| pHouse | 0.1 | MPa |
| pL | 10 | MPa |
| ω | 1500 | r/min |
| Width | LC (mm) | ||||
|---|---|---|---|---|---|
| Depth | 0.5 | 1.0 | 1.5 | 2.0 | |
| HC (μm) | 1 | C0.5-1 | C1.0-1 | C1.5-1 | C2.0-1 |
| 3 | C0.5-3 | C1.0-3 | C1.5-3 | C2.0-3 | |
| 5 | C0.5-5 | C1.0-5 | C1.5-5 | C2.0-5 | |
| 10 | C0.5-10 | C1.0-10 | C1.5-10 | C2.0-10 | |
| Parameters | Analytical Results | Simulation Results |
|---|---|---|
| h (μm) | 5.63103 | 5.80803 |
| PQ (W) | 4.99 | 2.57 |
| PF (W) | 15.32 | 22.07 |
| PT (W) | 20.31 | 24.64 |
| Shaft Speed (r/min) | Average Friction Power Loss (W) | |
|---|---|---|
| Experimental Results | Simulation Results | |
| 1000 | 21.864 | 21.104 |
| 1500 | 34.372 | 33.795 |
| 2000 | 51.555 | 50.748 |
| Working Pressure (MPa) | Average Friction Power Loss (W) | |
|---|---|---|
| Experimental Results | Simulation Results | |
| 5 | 28.823 | 27.611 |
| 10 | 34.372 | 33.795 |
| 15 | 39.777 | 38.938 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Wang, Z. Optimization and Influence of Micro-Chamfering on Oil Film Lubrication Characteristics of Slipper/Swashplate Interface within Axial Piston Pump. Energies 2021, 14, 1961. https://doi.org/10.3390/en14071961
Jiang J, Wang Z. Optimization and Influence of Micro-Chamfering on Oil Film Lubrication Characteristics of Slipper/Swashplate Interface within Axial Piston Pump. Energies. 2021; 14(7):1961. https://doi.org/10.3390/en14071961
Chicago/Turabian StyleJiang, Jihai, and Zebo Wang. 2021. "Optimization and Influence of Micro-Chamfering on Oil Film Lubrication Characteristics of Slipper/Swashplate Interface within Axial Piston Pump" Energies 14, no. 7: 1961. https://doi.org/10.3390/en14071961
APA StyleJiang, J., & Wang, Z. (2021). Optimization and Influence of Micro-Chamfering on Oil Film Lubrication Characteristics of Slipper/Swashplate Interface within Axial Piston Pump. Energies, 14(7), 1961. https://doi.org/10.3390/en14071961






