Regional Pole Placers of Power Systems under Random Failures/Repair Markov Jumps
Abstract
:1. Introduction
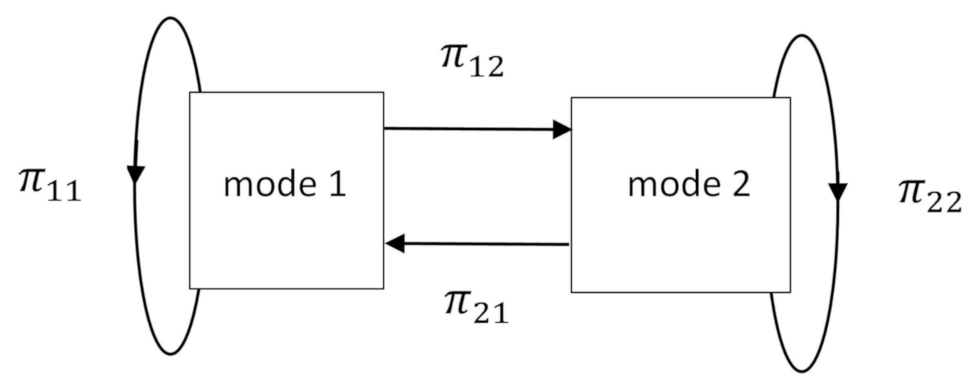
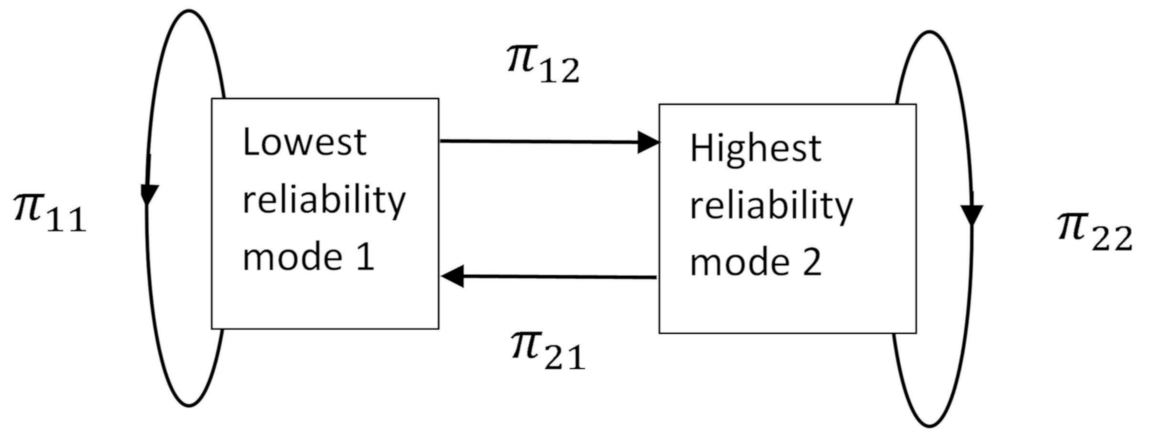
- Two extreme cases, such as the most reliable and the least reliable modes of a SMIB system, are considered. The transition probability matrix of the SMIB system is obtained from the practical results of line/transformer failure repair rates.
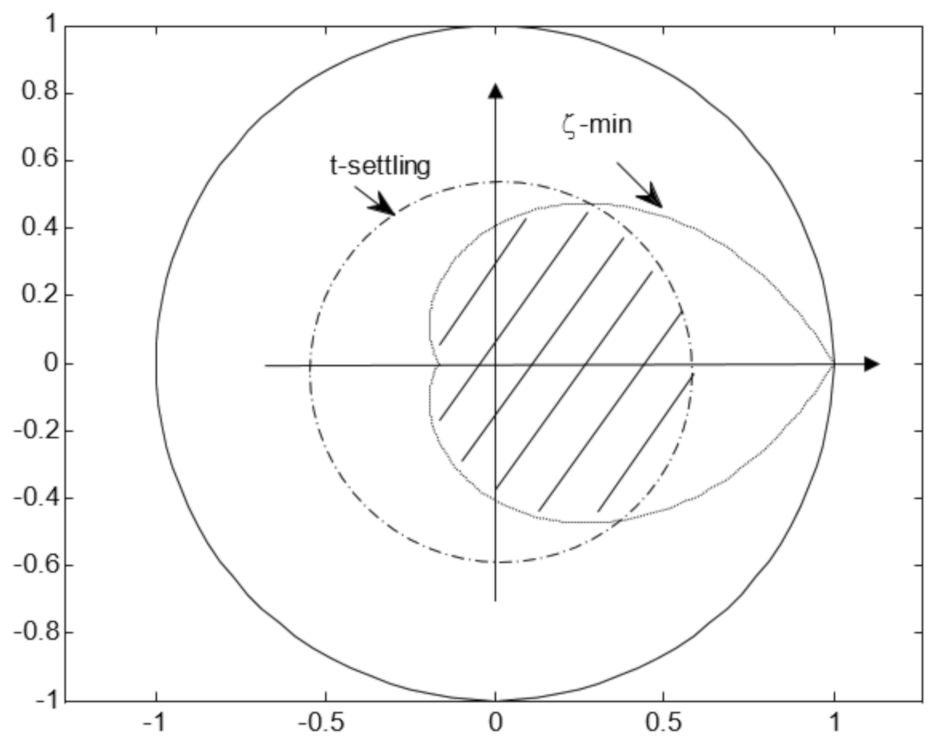
- A simple state feedback PSS design is developed in the framework of LMI to achieve stochastic stability in terms of settling time and damping ratio (regional pole placement for the discrete-time system).
- For each of the two modes (failure/ repair), a stabilizer is designed to achieve the control target. The design avoids losing stability during the switching between the two controllers.
- This is the first time multi-controllers are designed based on the practical failure/ repair rates.
2. Problem Statements
- For matrices , the norm-bounded uncertainty can be eliminated using the fact: .
- The nonlinear matrix equation can be linearized using the Schur complement: .
3. Proposed Methodology
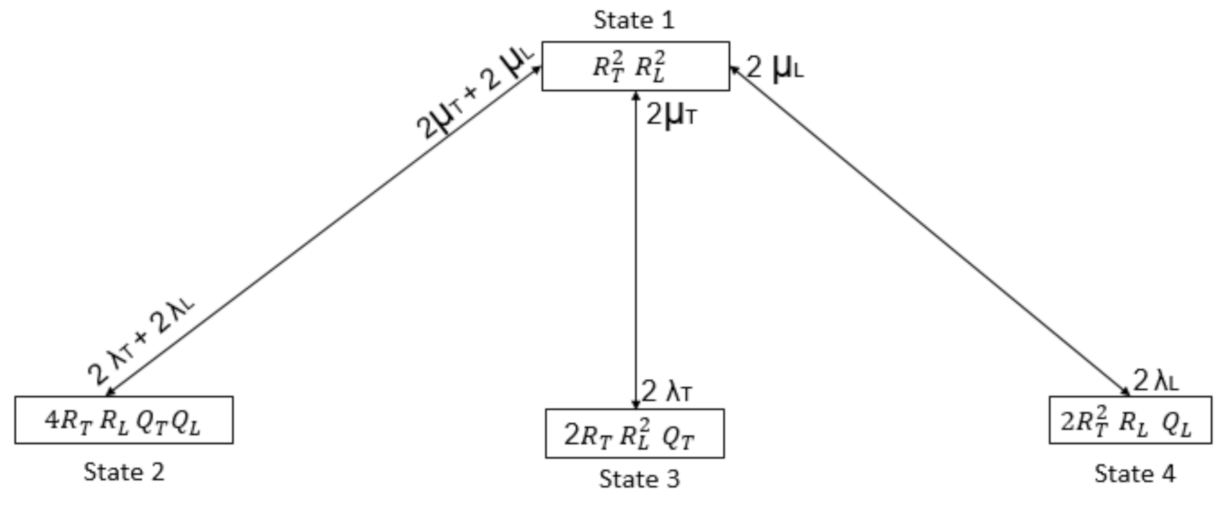
3.1. Markov Reliability Evaluation
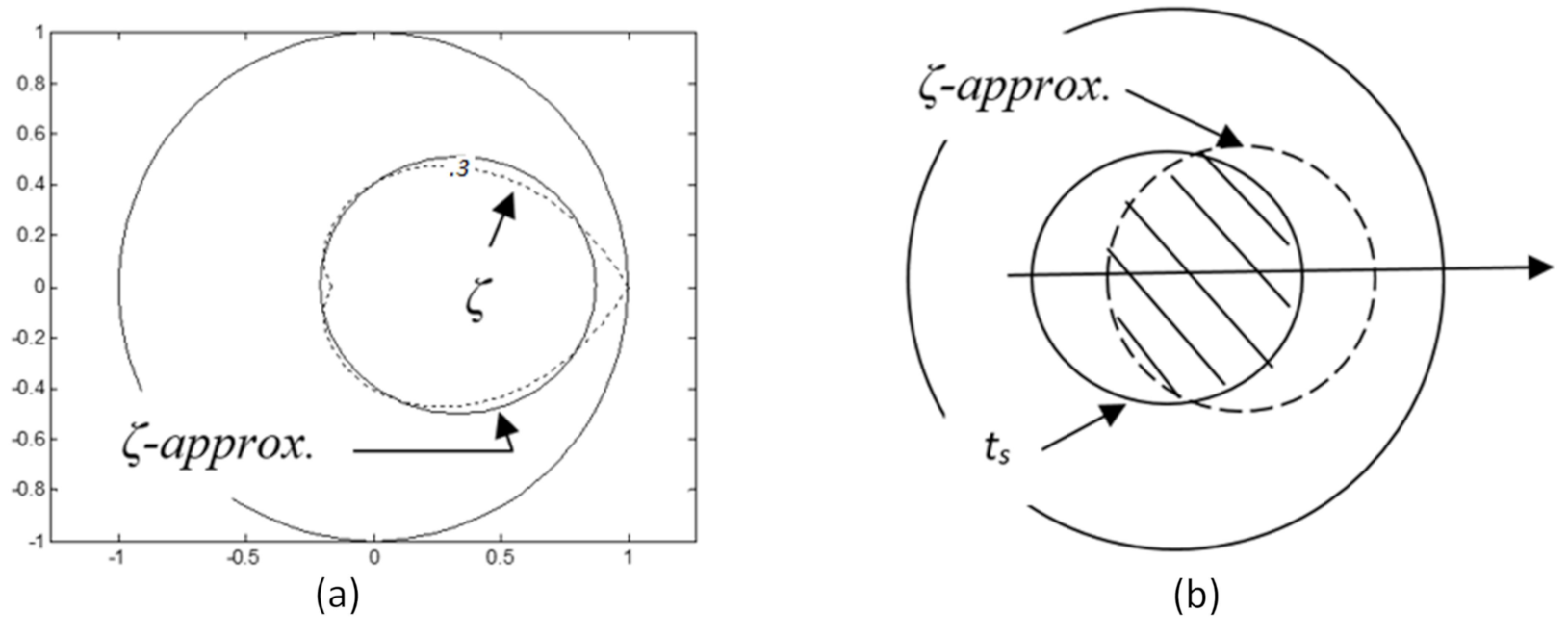
3.2. Regional Pole Placer Design for Power Systems under Markov Jumps
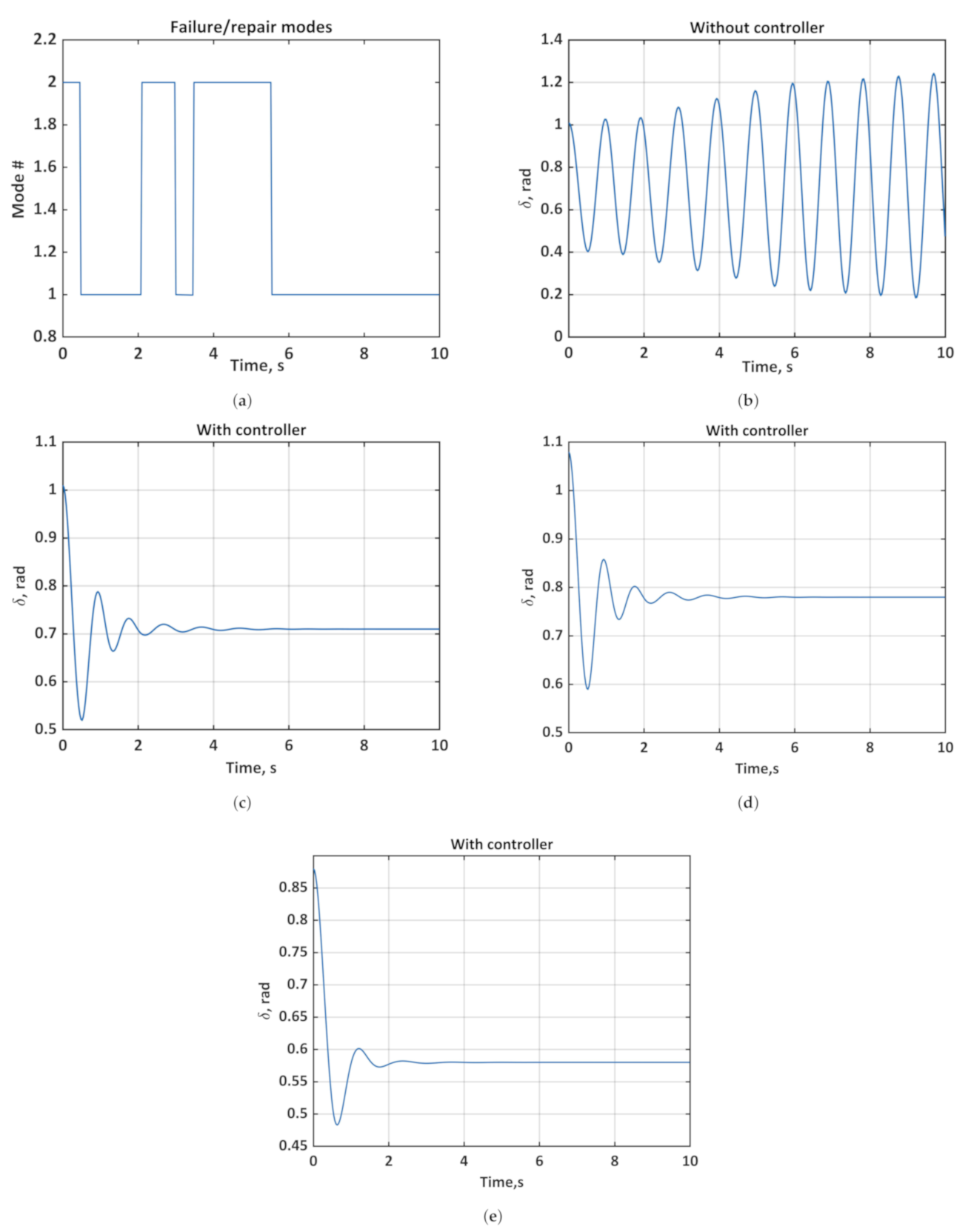
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. The Uncertain Discrete-Time Model of SMIB SYSTEM
Appendix B. Design of Regional Pole Placer
References
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics Stability and Control, 3rd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Farahan, M.; Ganjefar, S. Intelligent power system stabilizer design using adaptive fuzzy sliding mode controller. Neurocomputing 2017, 226, 135–144. [Google Scholar] [CrossRef]
- Sarita, K.; Kumar, S.; Vardhan, A.S.S.; Elavarasan, R.M.; Saket, R.K.; Shafiullah, G.M.; Hossain, E. Power enhancement with grid stabilization of renewable energy-based generation system using UPQC-FLC-EVA technique. IEEE Access 2020, 8, 207443–207464. [Google Scholar] [CrossRef]
- Salgotra, A.; Pan, S. Model based PI power system stabilizer design for damping low frequency oscillations in power systems. ISA Trans. 2018, 76, 110–121. [Google Scholar] [CrossRef] [PubMed]
- Soliman, H.M.; Ghommam, J.R. Reliable Control of Power Systems; Chapter in the book Diagnosis, Fault Detection & Tolerant Control; Springer: Berlin/Heidelberg, Germany, March 2020. [Google Scholar]
- Hossain, E.; Hossain, J.; Un-Noor, F. Utility grid: Present challenges and their potential solutions. IEEE Access 2018, 6, 60294–60317. [Google Scholar] [CrossRef]
- Hu, W.; Liang, J.; Jin, Y.; Wu, F. Model of Power System Stabilizer Adapting to Multi-Operating Conditions of Local Power Grid and Parameter Tuning. Sustainability 2018, 10, 2089. [Google Scholar] [CrossRef] [Green Version]
- Konara, A.I.; Annakkage, U.D. Robust Power System Stabilizer Design Using Eigenstructure Assignment. IEEE Trans. Power Syst. 2016, 31, 1845–1853. [Google Scholar] [CrossRef]
- Ahshan, R.; Iqbal, M.T.; Mann, G.K.; Quaicoe, J.E. Microgrid reliability evaluation considering the intermittency effect of renewable energy sources. Int. J. Smart Grid Clean Energy 2017, 6, 252–268. [Google Scholar] [CrossRef]
- Urgun, D.; Singh, C. A hybrid monte carlo simulation and multi label classification method for composite system reliability evaluation. IEEE Trans. Power Syst. 2018, 34, 908–917. [Google Scholar] [CrossRef]
- Huda, A.N.; Živanović, R. Accelerated distribution systems reliability evaluation by multilevel Monte Carlo simulation: Implementation of two discretisation schemes. IET Gener. Transm. Distrib. 2017, 11, 3397–3405. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Engineering Systems: Concepts and Techniques, 2nd ed.; Springer Science and Business Media: New York, NY, USA, 1992. [Google Scholar]
- Elmakias, D. New Computational Methods in Power System Reliability; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hou, K.; Jia, H.; Xu, X.; Liu, Z.; Jiang, Y. A continuous time Markov chain based sequential analytical approach for composite power system reliability assessment. IEEE Trans. Power Syst. 2015, 31, 738–748. [Google Scholar] [CrossRef]
- Lisnianski, A.; Elmakias, D.; Laredo, D.; Haim, H.B. A multi-state Markov model for a short-term reliability analysis of a power generating unit. Reliab. Eng. Syst. Saf. 2012, 98, 1–6. [Google Scholar] [CrossRef]
- Soliman, H.; Shafiq, M. Robust stabilisation of power systems with random abrupt changes. IET Gener. Transm. Distrib. 2015, 9, 2159–2166. [Google Scholar] [CrossRef]
- Ray, P.K.; Paital, S.R.; Mohanty, A.; Eddy, F.Y.; Gooi, H.B. A robust power system stabilizer for enhancement of stability in power system using adaptive fuzzy sliding mode control. Appl. Soft Comput. 2018, 73, 471–481. [Google Scholar] [CrossRef]
- Ugrinovskii, V.; Pota, H.R. Decentralized control of power systems via robust control of uncertain Markov jump parameter systems. Int. J. Control 2005, 78, 662–677. [Google Scholar] [CrossRef]
- Ma, J.; Wang, S.; Qiu, Y.; Li, Y.; Wang, Z.; Thorp, J.S. Angle Stability Analysis of Power System With Multiple Operating Conditions Considering Cascading Failure. IEEE Trans. Power Syst. 2017, 32, 873–882. [Google Scholar] [CrossRef]
- Wu, W.; Wen, F.; Xue, Y.; Zhao, X.; Hu, R. A Markov chain based model for forecasting power system cascading failures. Dianli Xitong Zidonghua (Autom. Electr. Power Syst.) 2013, 37, 29–37. [Google Scholar]
- Soliman, H.M.; Elshafei, A.L.; Shaltout, A.A.; Morsi, M.F. Robust power system stabiliser. IEE Proc. Gener. Transm. Distrib. 2000, 147, 285–291. [Google Scholar] [CrossRef]
- Passrba, J. Analysis and Control of Power System Oscillations; Technical Brochure 111. 1996. Available online: https://e-cigre.org/publication/111-analysis-and-control-of-power-system-oscillations (accessed on 2 April 2021).
- Benzaouia, A. Saturated Switching Systems; Springer: London, UK, 2012. [Google Scholar]
- Haddad, W.M.; Bernstein, D.S. Controller design with regional pole constraints. IEEE Trans. Autom. Control 1992, 37, 54–69. [Google Scholar] [CrossRef]


| Elements | Parameters | Values |
|---|---|---|
| Synchronous machine | 1.6 | |
| 0.32 | ||
| 1.55 | ||
| rad/s | ||
| 6 s | ||
| H | 5 s | |
| Exciter + amplifier | 25 | |
| s | ||
| Transmission line + transformer | 0.8 | |
| Nominal load (at infinite bus) | P | 0.7 |
| Q |
| Loading Condition | P (Per Unit) | Q (Per Unit) |
|---|---|---|
| Heavy | 1 | 0.5 |
| Nominal | 0.7 | 0.3 |
| Light | 0.4 | 0.1 |
| Elements | Calculation |
|---|---|
| Transformers | Failure rate failure/year failure/h |
| Repair time h | |
| Average annual outage time Unreliability | |
| Reliability | |
| Repair rate repair/h | |
| Transmission lines | Failure rate failure/year failure/h |
| Repair time h | |
| Average annual outage time Unreliability | |
| Reliability | |
| Repair rate repair/h |
| UP States | Condition | State Probability |
|---|---|---|
| 1 | 2T(UL(U) | 0.9818509 |
| 2 | 1T(UL(UT(DL(D) | 0.00001935 |
| 3 | 1T(UL(UT(D) | 0.0011219 |
| 4 | 2T(UL(UL(D) | 0.0169344 |
| System Reliability Condition | Mode 1 | Mode 2 |
|---|---|---|
| Maximum (Mode 1) | 0.826 | 0.174 |
| Minimum (Mode 2) | 0.00116 | 0.99884 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Sheikhi, F.A.; Soliman, H.M.; Ahshan, R.; Hossain, E. Regional Pole Placers of Power Systems under Random Failures/Repair Markov Jumps. Energies 2021, 14, 1989. https://doi.org/10.3390/en14071989
El-Sheikhi FA, Soliman HM, Ahshan R, Hossain E. Regional Pole Placers of Power Systems under Random Failures/Repair Markov Jumps. Energies. 2021; 14(7):1989. https://doi.org/10.3390/en14071989
Chicago/Turabian StyleEl-Sheikhi, Farag Ali, Hisham M. Soliman, Razzaqul Ahshan, and Eklas Hossain. 2021. "Regional Pole Placers of Power Systems under Random Failures/Repair Markov Jumps" Energies 14, no. 7: 1989. https://doi.org/10.3390/en14071989







