Model Predictive Control with Adaptive Building Model for Heating Using the Hybrid Air-Conditioning System in a Railway Station
Abstract
:1. Introduction
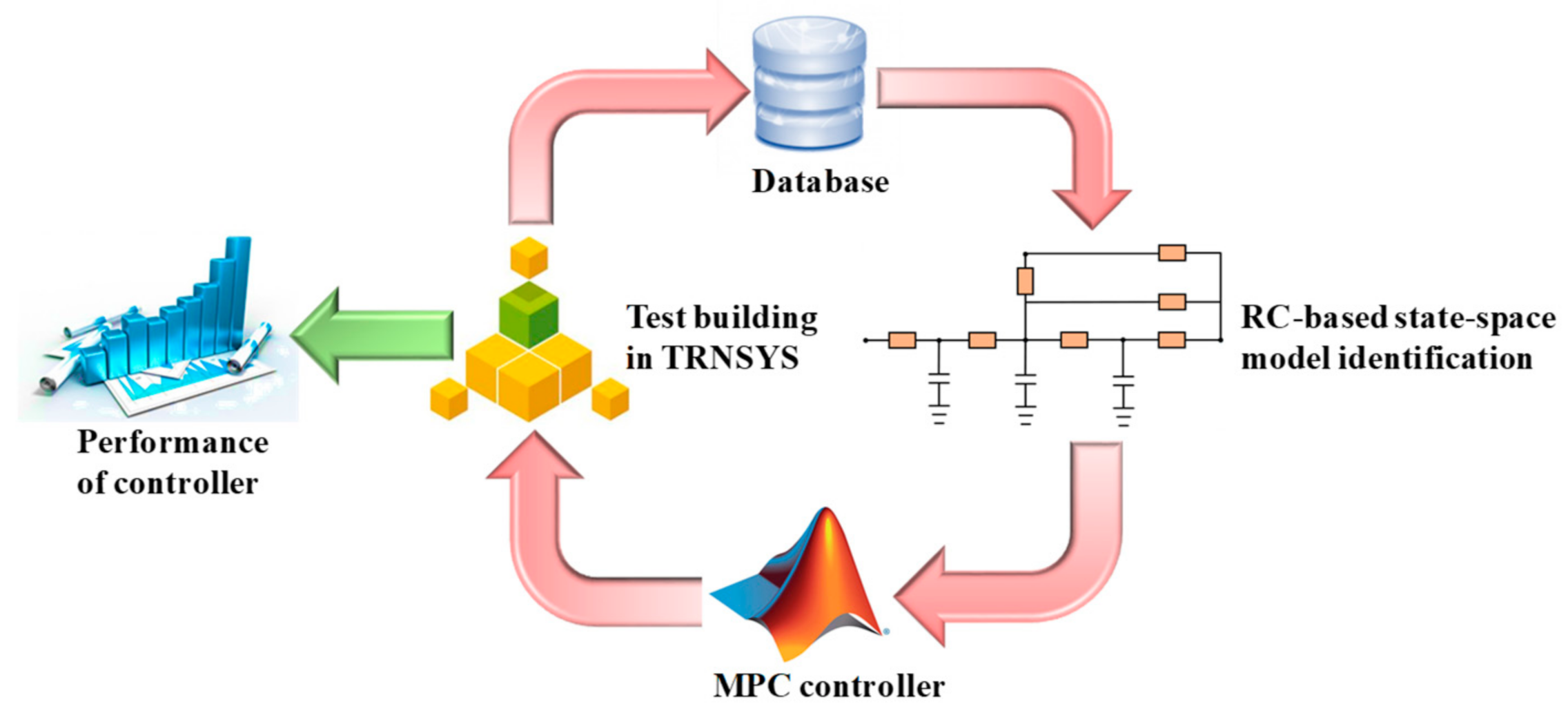
2. The Overview of Research Methodology
3. MPC Controller Design
3.1. Dynamic Thermal Model for Building
3.1.1. Model of All-Air System
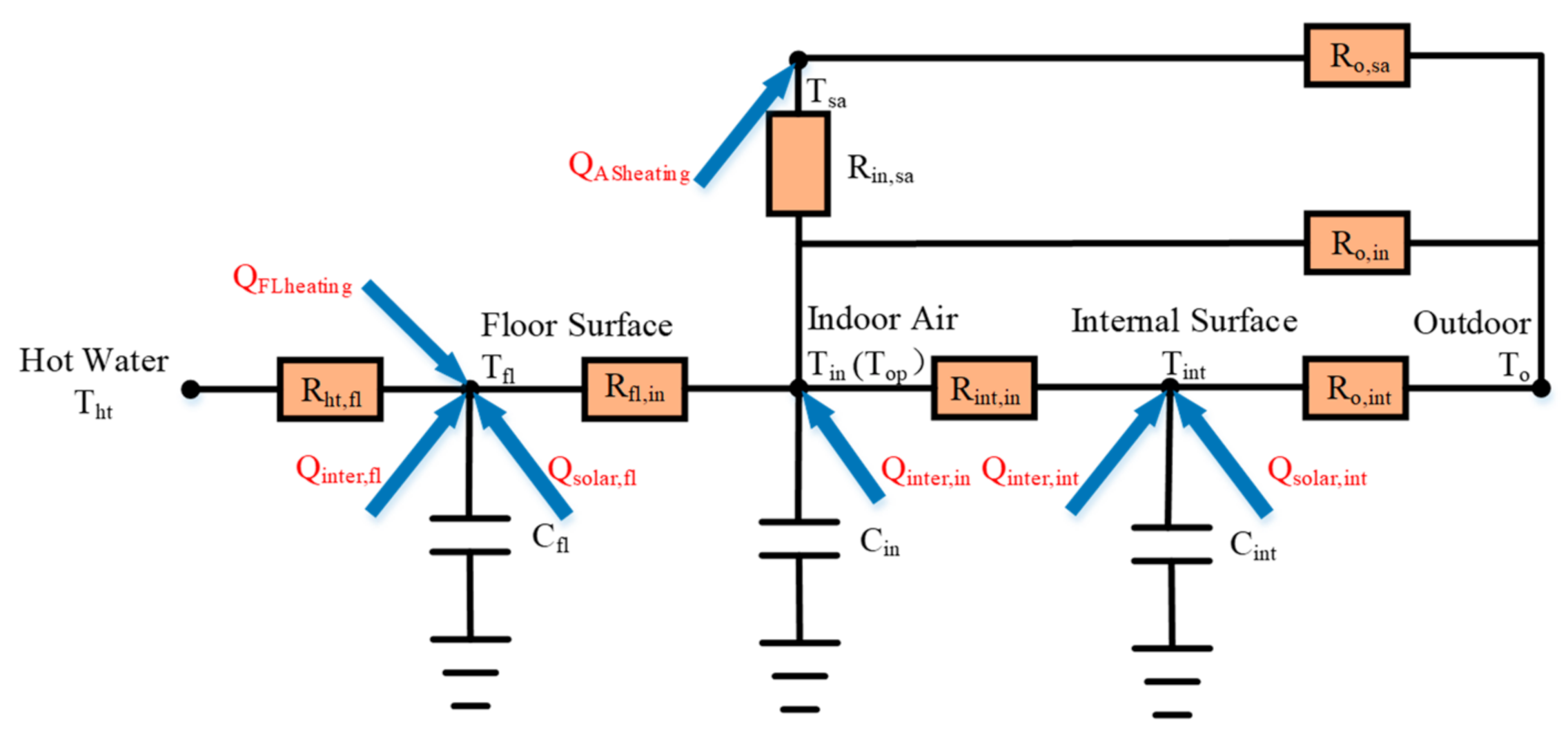
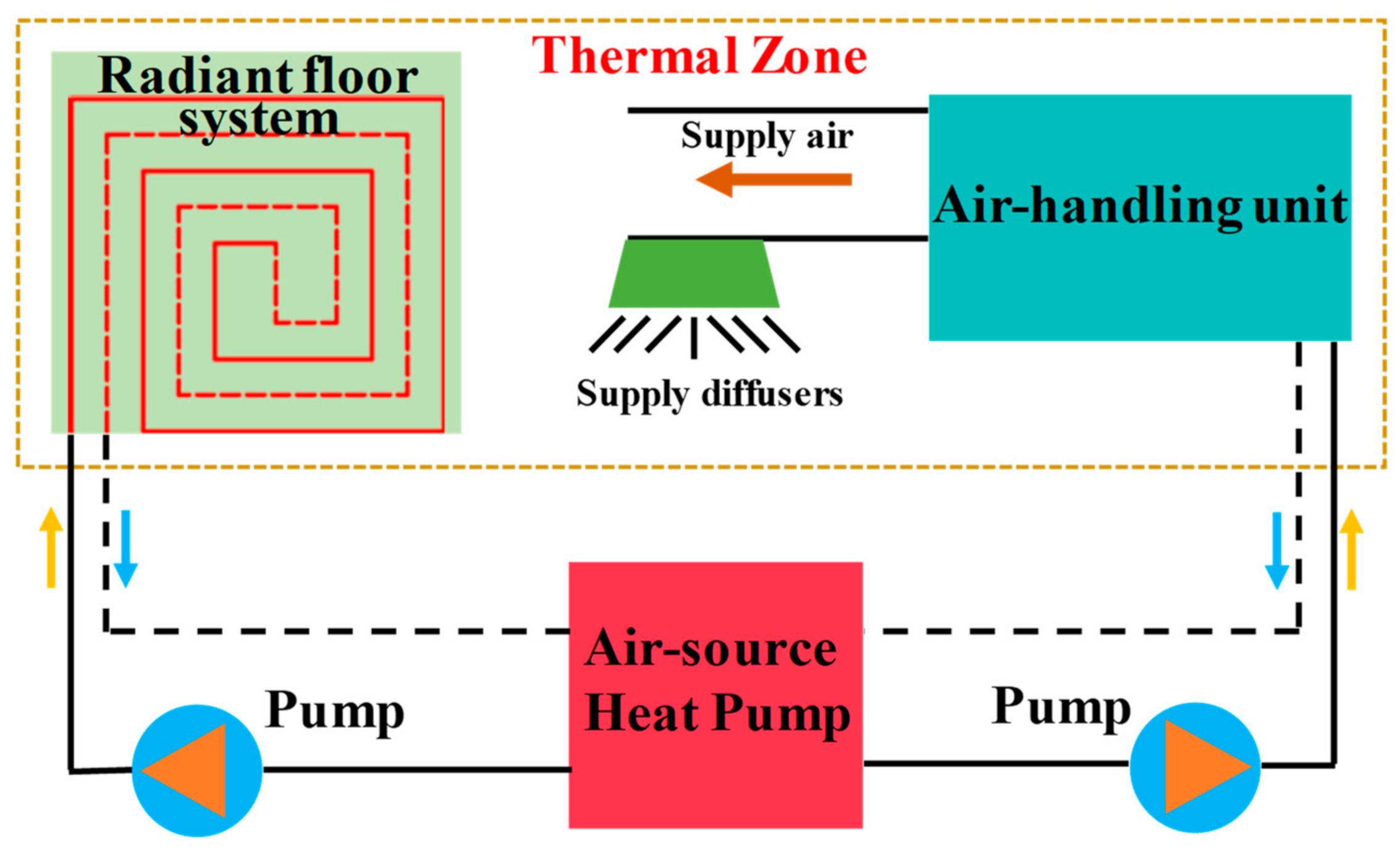
3.1.2. Model of Zone with the Hybrid Air Conditioning System
3.2. Model Transformation
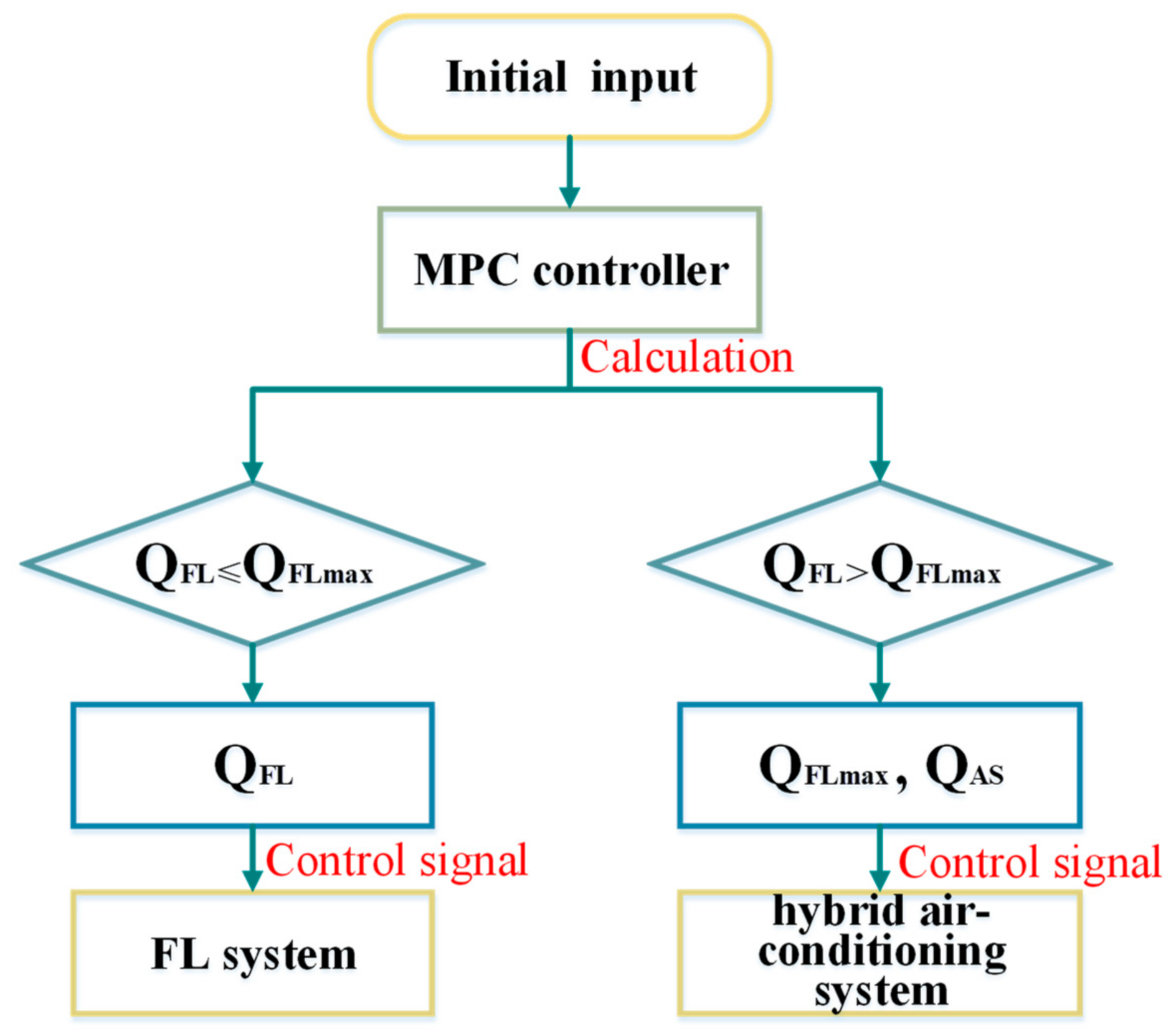
3.3. The Objective Function and Constraints
3.4. The Solution of Optimization Problem
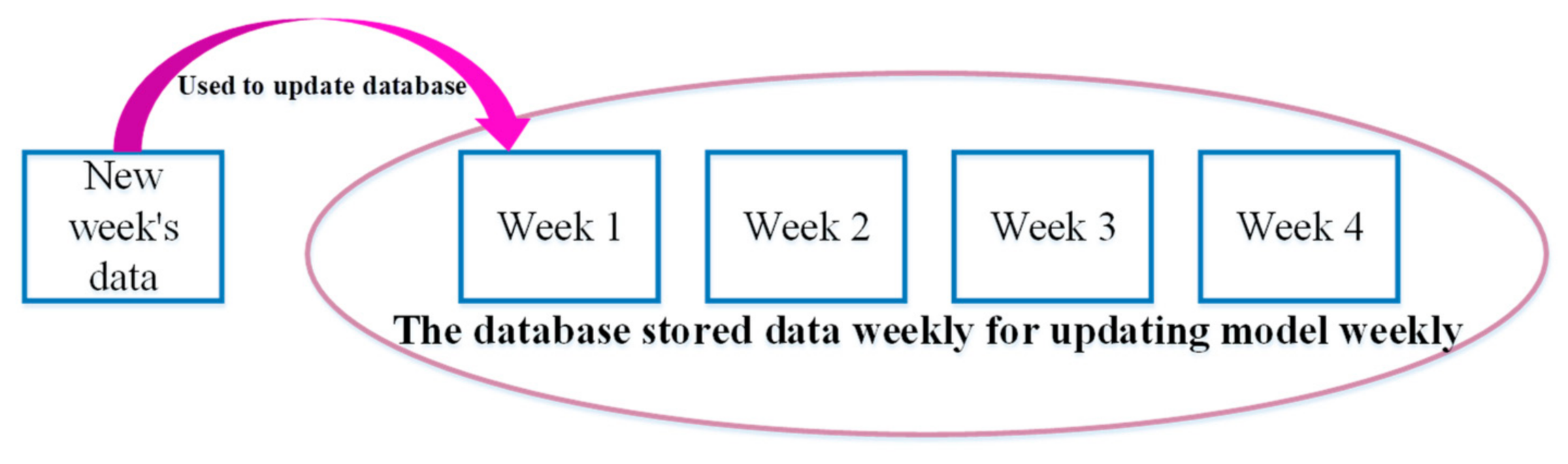
3.5. Update the Building Dynamics Model Regularly
4. Case Study
4.1. Target Building
4.2. Geometrical and Envelope Description
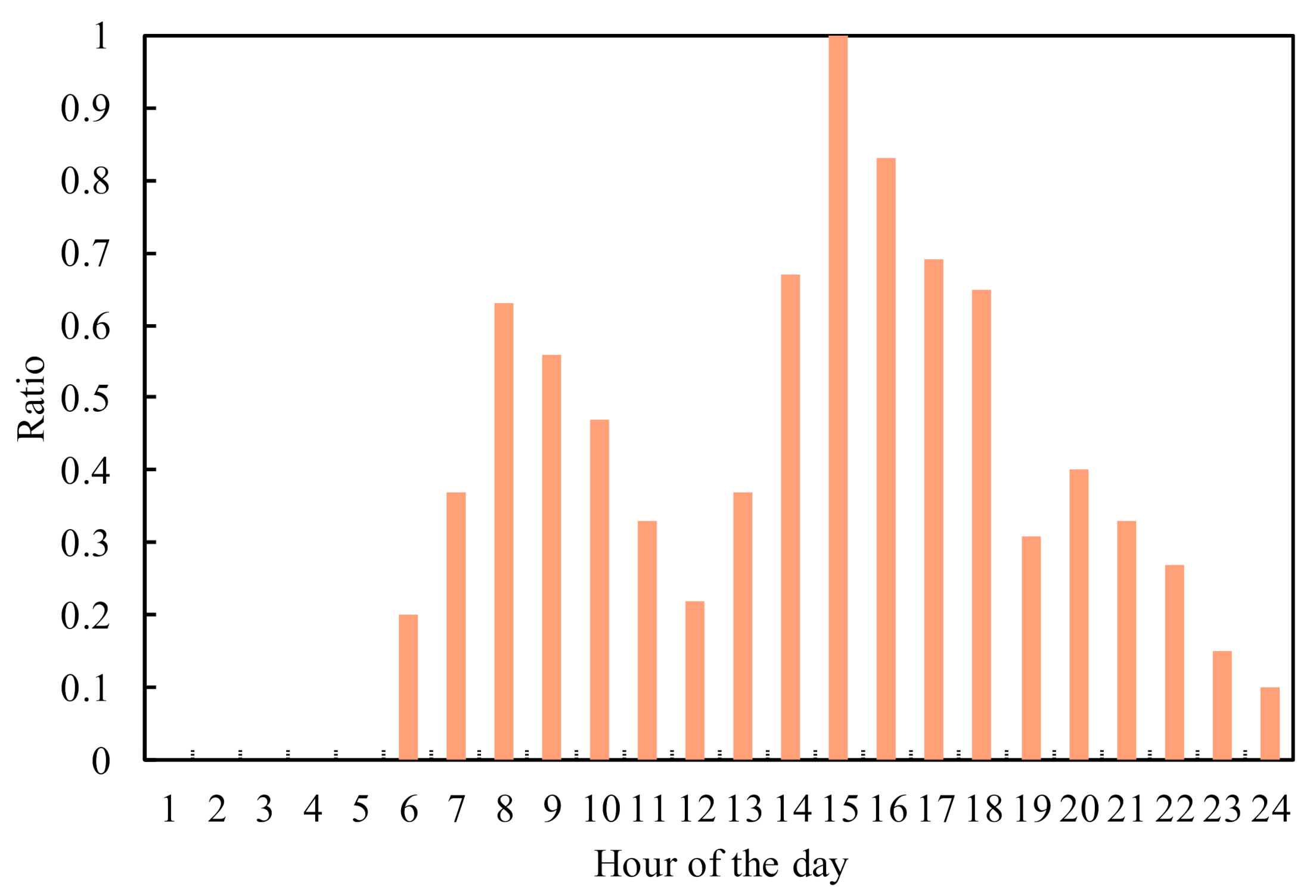
4.3. Internal Heat Gains
4.4. Air Infiltration
4.5. Heating System
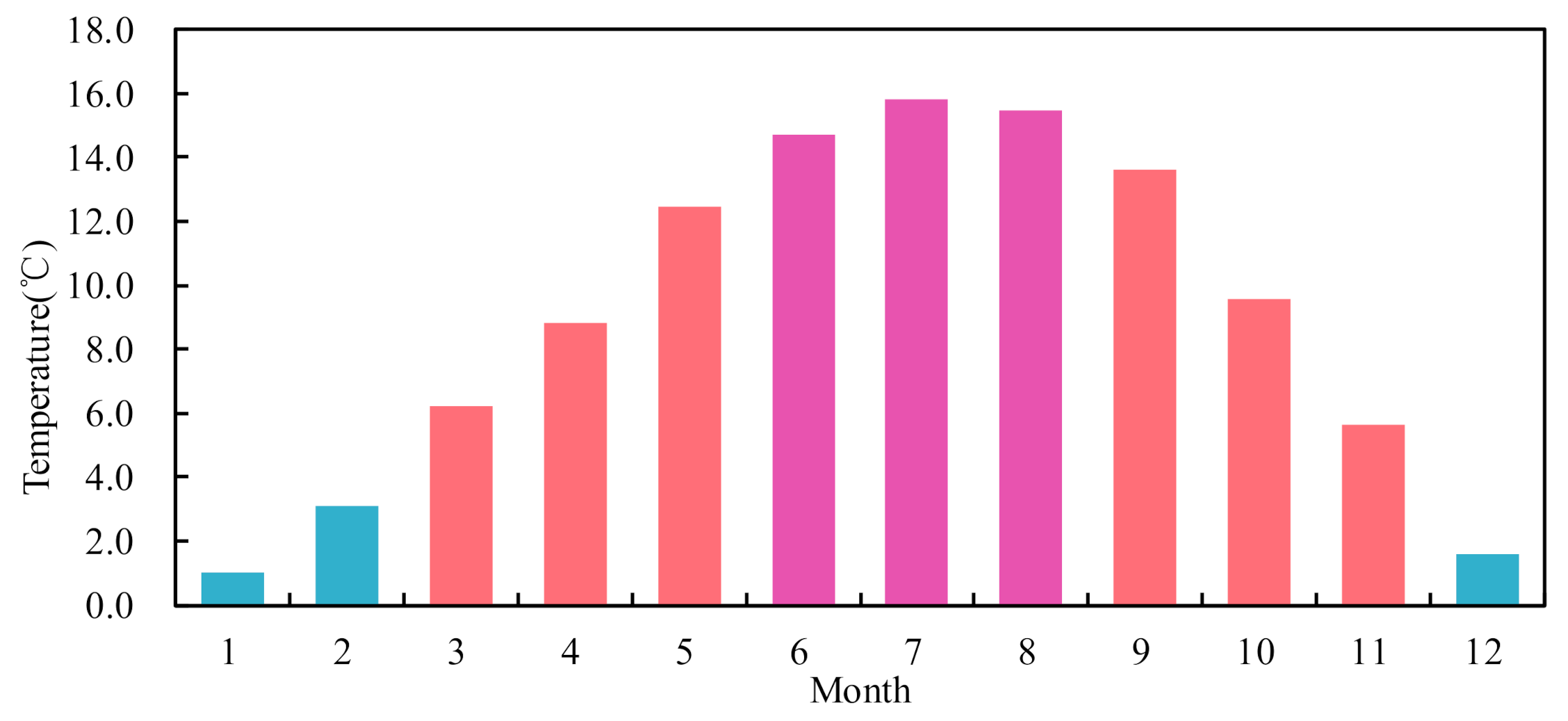
4.6. Determination of Indoor Design Parameter
4.7. Determination of System Energy Consumption
4.7.1. Power Consumption of ASHP
4.7.2. Power Consumption of Pump and Fan
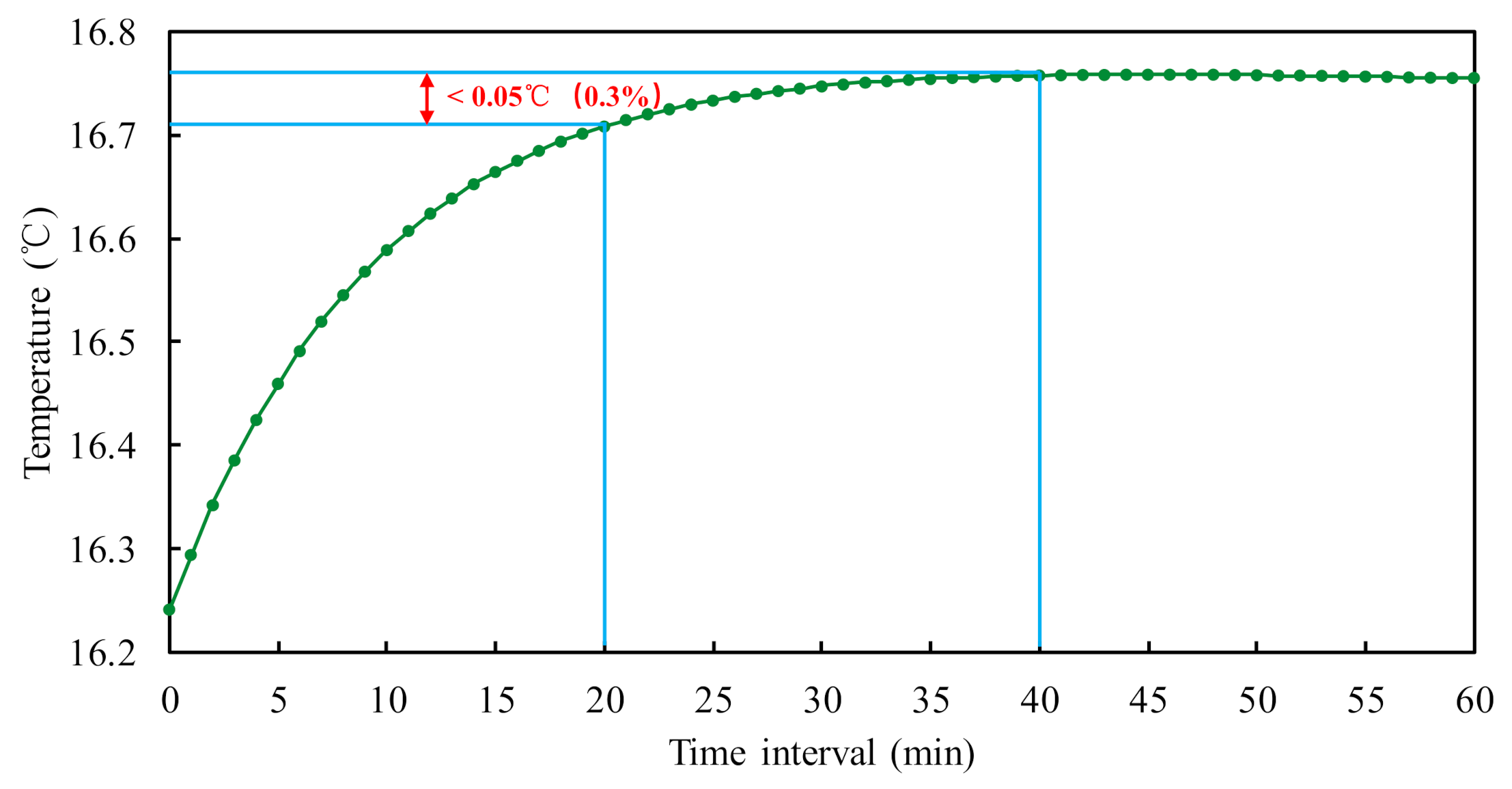
4.8. Determination of Sampling Time and Prediction Horizon
4.9. Parameter Substitution
4.10. Data Acquisition and Identification
4.11. Prediction of Weather Data and Occupancy
5. Simulation Results and Discussion
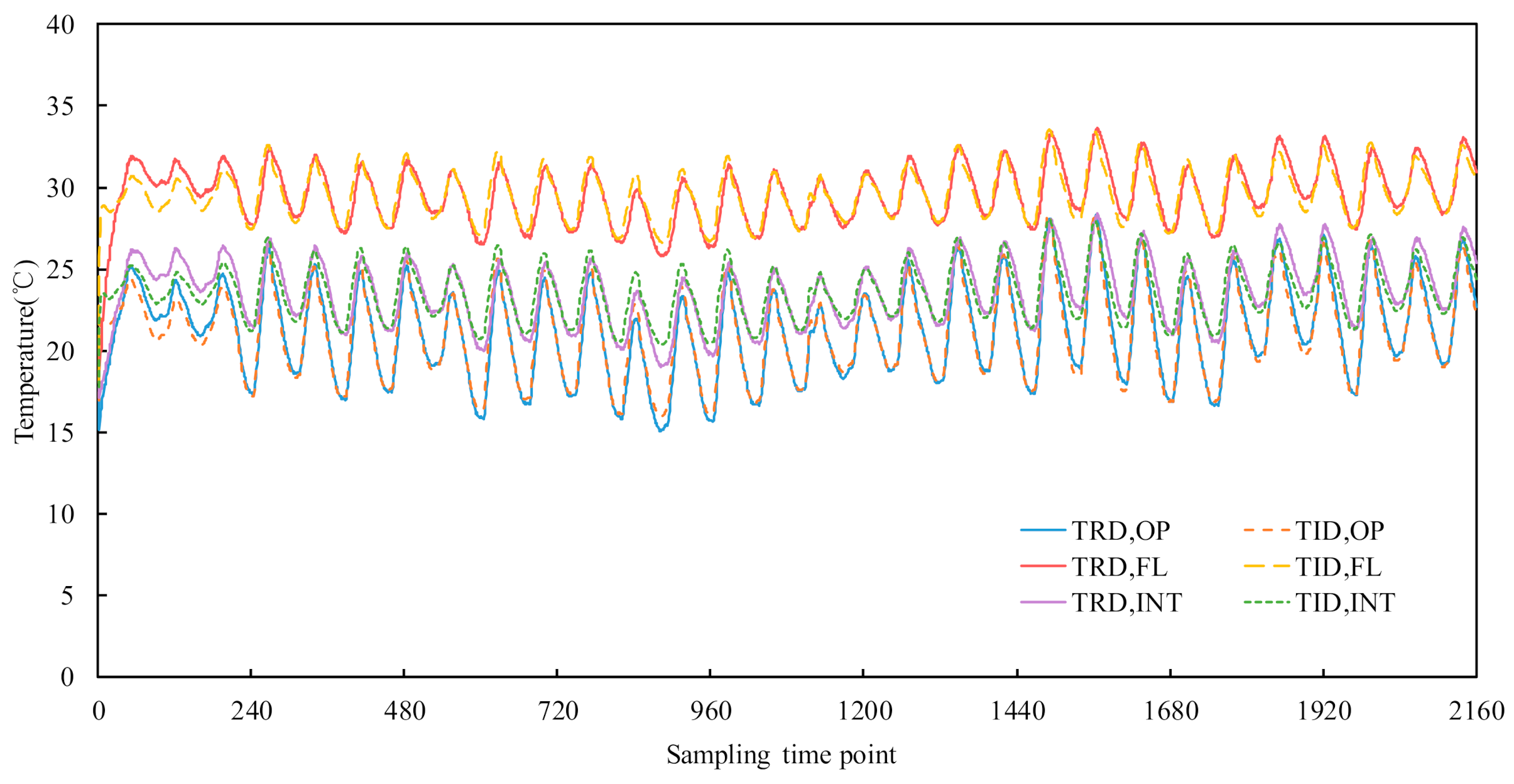
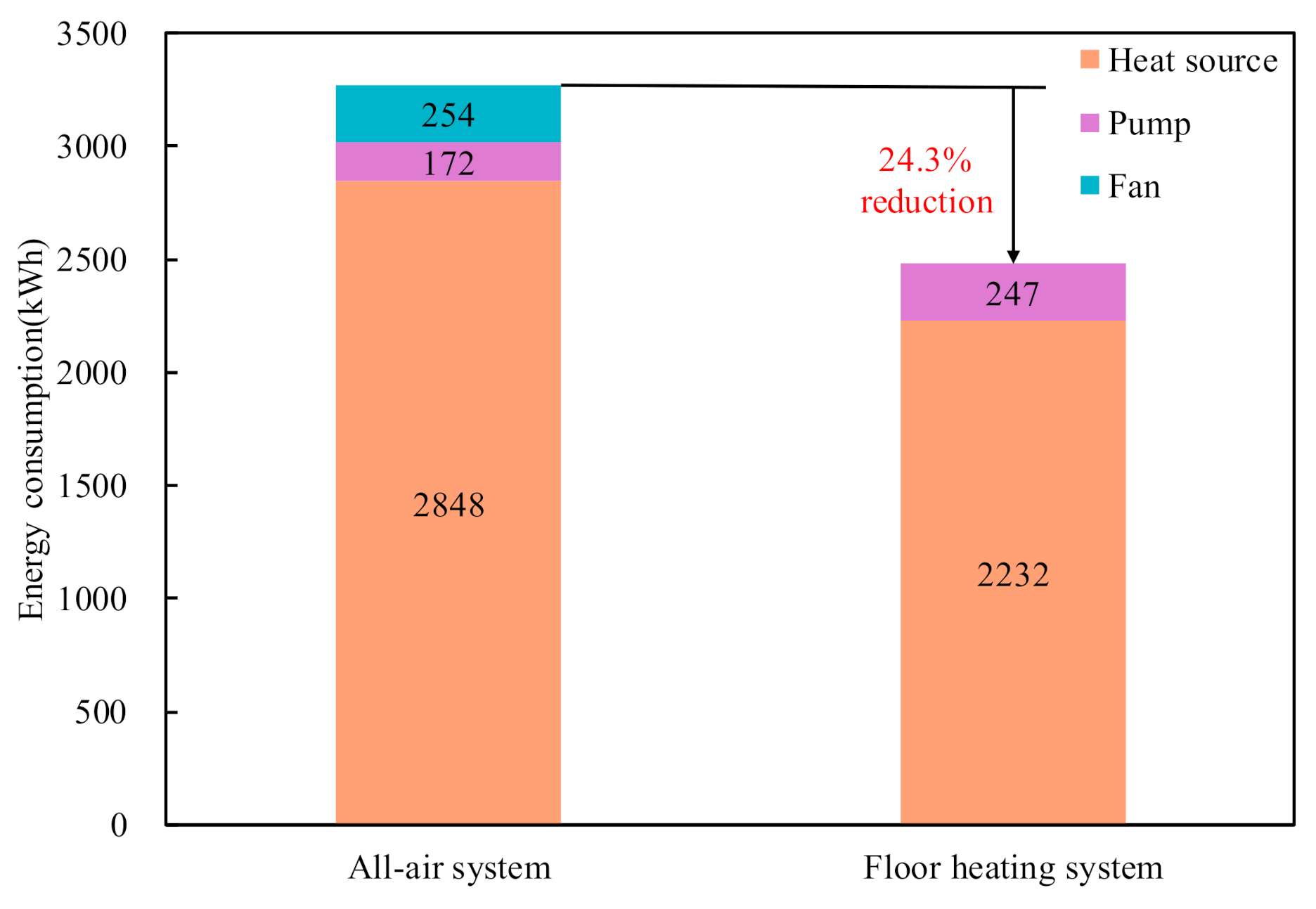
5.1. Comparison of Performance between Radiant Floor Heating and All-Air System
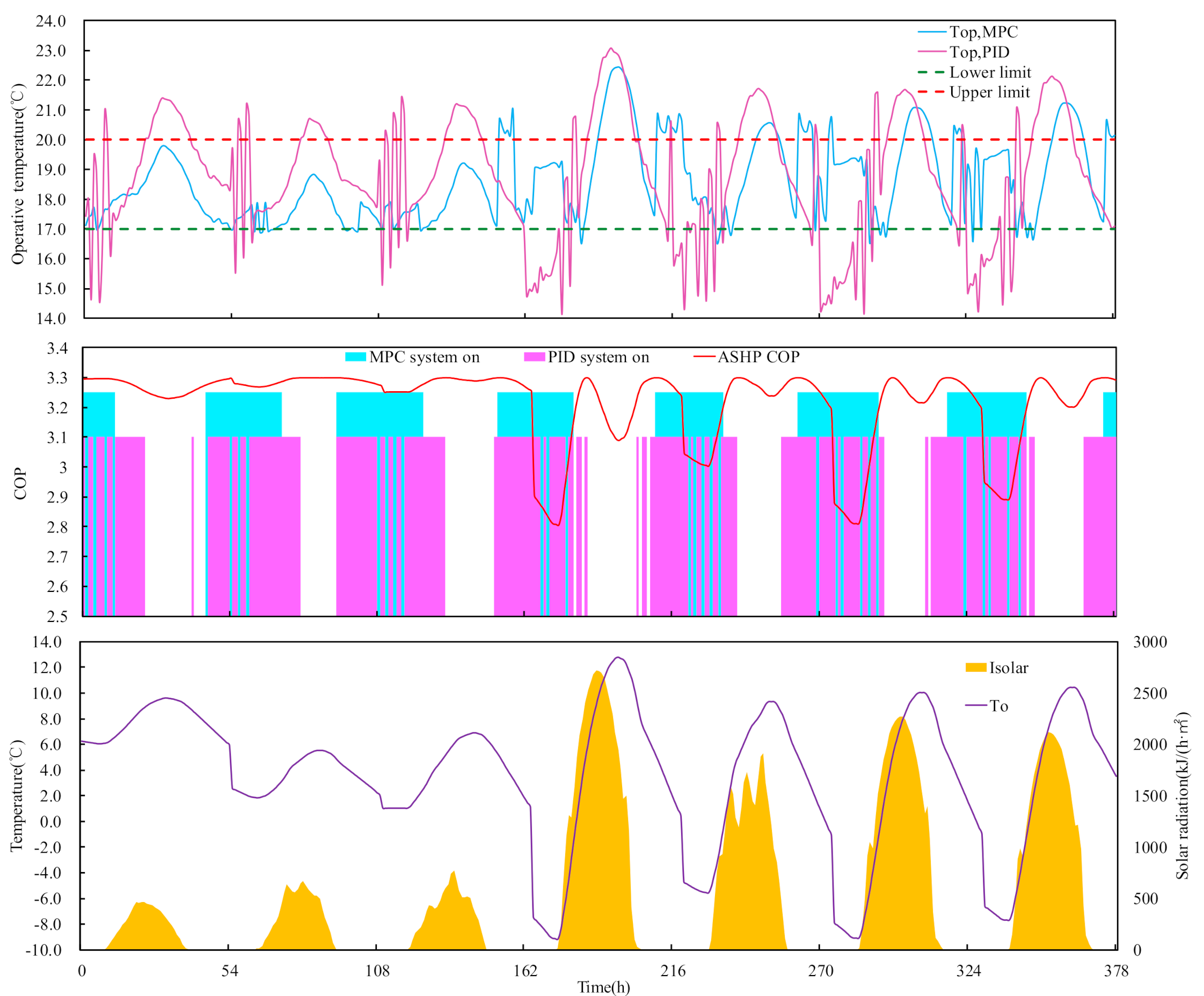
5.2. Comparison of Performance between the Adaptive MPC and PID Control
5.3. Comparison of Performance between the Adaptive MPC and Initial MPC
6. Conclusions
- For the hybrid air conditioning system, the preferential use of radiant floor heating has greater energy saving potential than the preferential use of all-air system based on the MPC strategy.
- In terms of thermal comfort, the adaptive MPC achieves 90.5% indoor operative temperature satisfaction rate with lower temperature fluctuations benefited by the solution of time delay, whereas the PID control could only achieve 79.8%.
- In terms of energy-saving, the adaptive MPC achieves 22.2% energy consumption reduction as compared to the PID control for the system. It can be demonstrated that the MPC is superior to the PID control in temperature control and energy saving due to its advanced optimal control algorithm.
- The adaptive MPC achieves better indoor thermal comfort and 11.5% energy-saving as compared to the initial MPC with more accurate forecasting models which clarify the importance of updating the control model in time.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area (m2) |
| A | system matrix in state—space model |
| B | input matrix in state—space model |
| C | equivalent overall thermal capacitance (J/K) |
| C | output matrix in state—space model |
| d | disturbance vector |
| E | disturbance matrix in state—space model |
| E | disturbance matrix in state—space model |
| F | conversion coefficients for heat gains |
| H | height (m) |
| h | coefficient of heat transfer (W/(m2·°C) |
| I | global solar radiation (W/m2) |
| J | objection function |
| K | Kalman gain |
| L | length (m) |
| m | volume flow rate (m3/h) |
| N | prediction horizon |
| N | variation of passenger flow |
| P | covariance matrix of state estimate error |
| Q | heating amount (kW) |
| Q | covariance matrix of process noise |
| R | equivalent overall thermal resistance (K/W) |
| R | covariance matrix of measurement noise |
| T | temperature (°C) |
| u | input vector |
| W | energy consumption (kWh) |
| W | weighting factor |
| W | width (m) |
| x | system state vector |
| y | observed output vector in state—space model |
| Greek symbols | |
| process noise | |
| measurement noise | |
| slack variable | |
| Subscripts | |
| AS | all—air system |
| c | continuous—time |
| co | convective heat transfer |
| d | discrete—time |
| FL | radiant floor heating system |
| fl | floor surface |
| ht | hot water |
| in | indoor air |
| int | inner suface of wall |
| inter | internal heat gains |
| k | time step |
| o | outdoor air |
| op | operative temperature |
| r | radiant heat transfer |
| sa | supply air |
| solar | incident solar radiation |
| t | current time |
| win | window |
| Abbreviations | |
| AHU | air—handling unit |
| ASHP | air—source heat pump |
| COP | coefficient of performance |
| MPC | model predictive control |
| PID | proportional-integral-derivative |
| PMV | Predicted Mean Vote |
| RC | resistance-capacitance model |
References
- Annual Development Report of China’s Building Energy Efficiency in 2020; Building Energy Conservation Research Center, Tsinghua University: Beijing, China, 2020.
- Li, L.; Ma, W.; Chen, Z. Energy Consumption Factors Analysis and Energy Saving Measures Research of Modern Railway Passenger Station; China’s Railway Ministry Press: Beijing, China, 2010.
- Shengwei, W.; Zhenjun, M. Supervisory and optimal control of building HVAC systems: A review. HVAC&R Res. 2008, 14, 3–32. [Google Scholar]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Martin, K.; Michal, K. MPC-Based Reference Governors; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Zhang, D.; Huang, X.; Gao, D.; Cui, X.; Cai, N. Experimental study on control performance comparison between model predictive control and proportion-integral-derivative control for radiant ceiling cooling integrated with underfloor ventilation system. Appl. Therm. Eng. 2018, 143, 130–136. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Jorgensen, J.B.; Li, R. Price-responsive model predictive control of floor heating systems for demand response using building thermal mass. Appl. Therm. Eng. 2019, 153, 316–329. [Google Scholar] [CrossRef]
- Joe, J.; Karava, P. A model predictive control strategy to optimize the performance of radiant floor heating and cooling systems in office buildings. Appl. Energy 2019, 245, 65–77. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Ng, B.F.; Zhang, T.; Babu, S.; Zhang, Z.; Chen, W.; Dubey, S. A state-space thermal model incorporating humidity and thermal comfort for model predictive control in buildings. Energy Build. 2018, 170, 25–39. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Supervisory model predictive controller (MPC) for residential HVAC systems: Implementation and experimentation on archetype sustainable house in Toronto. Energy Build. 2017, 154, 268–282. [Google Scholar] [CrossRef]
- Sturzenegger, D.; Gyalistras, D.; Morari, M.; Smith, R.S. Model Predictive Climate Control of a Swiss Office Building: Implementation, Results, and Cost-Benefit Analysis. IEEE Trans. Control Syst. Technol. 2016, 24, 1–12. [Google Scholar] [CrossRef]
- Aswani, A.; Master, N.; Taneja, J.; Culler, D.; Tomlin, C. Reducing Transient and Steady State Electricity Consumption in HVAC Using Learning-Based Model-Predictive Control. Proc. IEEE 2012, 100, 240–253. [Google Scholar] [CrossRef]
- Huang, H.; Chen, L.; Hu, E. A new model predictive control scheme for energy and cost savings in commercial buildings: An airport terminal building case study. Build. Environ. 2015, 89, 203–216. [Google Scholar] [CrossRef]
- O’Dwyer, E.; Cychowski, M.; Kouramas, K.; De Tomasi, L.; Lightbody, G. Scalable, Reconfigurable Model Predictive Control for Building Heating Systems. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2248–2253. [Google Scholar]
- Ferreira, P.M.; Ruano, A.E.; Silva, S.; Conceicao, E.Z.E. Neural networks based predictive control for thermal comfort and energy savings in public buildings. Energy Build. 2012, 55, 238–251. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhao, T.; Zhang, J.; Chen, T. Predication control for indoor temperature time-delay using Elman neural network in variable air volume system. Energy Build. 2017, 154, 545–552. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, Z.; Kusiak, A. Predictive modeling and optimization of a multi-zone HVAC system with data mining and firefly algorithms. Energy 2015, 86, 393–402. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Gray-box modeling and validation of residential HVAC system for control system design. Appl. Energy 2015, 137, 134–150. [Google Scholar] [CrossRef]
- Derakhtenjani, A.S.; Candanedo, J.A.; Chen, Y.; Dehkordi, V.R.; Athienitis, A.K. Modeling approaches for the characterization of building thermal dynamics and model-based control: A case study. Sci. Technol. Built. Environ. 2015, 21, 824–836. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Wang, Y.; Liu, J. Numerical and experimental analysis of floor heat storage and release during an intermittent in-slab floor heating process. Appl. Therm. Eng. 2014, 62, 398–406. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, M.; Geng, Y.; Lin, B.; Zhu, Y. A model to compare convective and radiant heating systems for intermittent space heating. Appl. Energy 2018, 215, 211–226. [Google Scholar] [CrossRef]
- Afram, A.; Fung, A.S.; Janabi-Sharifi, F.; Raahemifar, K. Development of an accurate gray-box model of ubiquitous residential HVAC system for precise performance prediction during summer and winter seasons. Energy Build. 2018, 171, 168–182. [Google Scholar] [CrossRef]
- O'Dwyer, E.; De Tommasi, L.; Kouramas, K.; Cychowski, M.; Lightbody, G. Modelling and disturbance estimation for model predictive control in building heating systems. Energy Build. 2016, 130, 532–545. [Google Scholar] [CrossRef]
- Zajic, I.; Larkowski, T.; Sumislawska, M.; Burnham, K.J.; Hill, D. Modelling of an Air Handling Unit: A Hammerstein-bilinear Model Identification Approach. In Proceedings of the 21st International Conference on Systems Engineering, Las Vegas, NV, USA, 16–18 August 2011; pp. 59–63. [Google Scholar]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Zhai, D. An adaptive robust model predictive control for indoor climate optimization and uncertainties handling in buildings. Build. Environ. 2019, 163, 106326. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 2020, 271, 115147. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Woolley, J.; Schiavon, S.; Bauman, F.; Raftery, P.; Pantelic, J. Side-by-side laboratory comparison of space heat extraction rates and thermal energy use for radiant and all-air systems. Energy Build. 2018, 176, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Karmann, C.; Schiavon, S.; Bauman, F. Thermal comfort in buildings using radiant vs. all-air systems: A critical literature review. Energy Build. 2017, 111, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hu, F.; Su, J.; Wei, X.; Qin, R. Comparisons on Kalman-Filter-Based Dynamic State Estimation Algorithms of Power Systems. IEEE Access 2020, 8, 51035–51043. [Google Scholar] [CrossRef]
- Xu, W. Technical Specification for Floor Radiant Heating and Cooling; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Lofberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Qian, B.; Yu, T.; Bi, H.; Lei, B. Measurements of Energy Consumption and Environment Quality of High-Speed Railway Stations in China. Energies 2020, 13, 1681. [Google Scholar] [CrossRef] [Green Version]
- Khorasanizadeh, H.; Sheikhzadeh, G.A.; Azemati, A.A.; Hadavand, B.S. Numerical study of air flow and heat transfer in a two-dimensional enclosure with floor heating. Energy Build. 2014, 78, 98–104. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hil: New York, NY, USA, 1972. [Google Scholar]
- ASHRAE. Thermal Environmental Conditions for Human Occupancy; ANSI/ASHRAE Standard 55-2017 2017; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- ASHRAE. ASHRAE Handbook of Fundamentals; ASHRAE: Atlanta, GA, USA, 2017. [Google Scholar]
- The Mathwork. System Identification Toolbox. Available online: https://www.mathworks.com/help/ident/index.html?s_tid=srchtitle (accessed on 3 January 2021).
- Verhaegen, M.; Deprettere, E. A Fast, Recursive MIMO State Space Model Identification Algorithm. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 1349–1354. [Google Scholar]

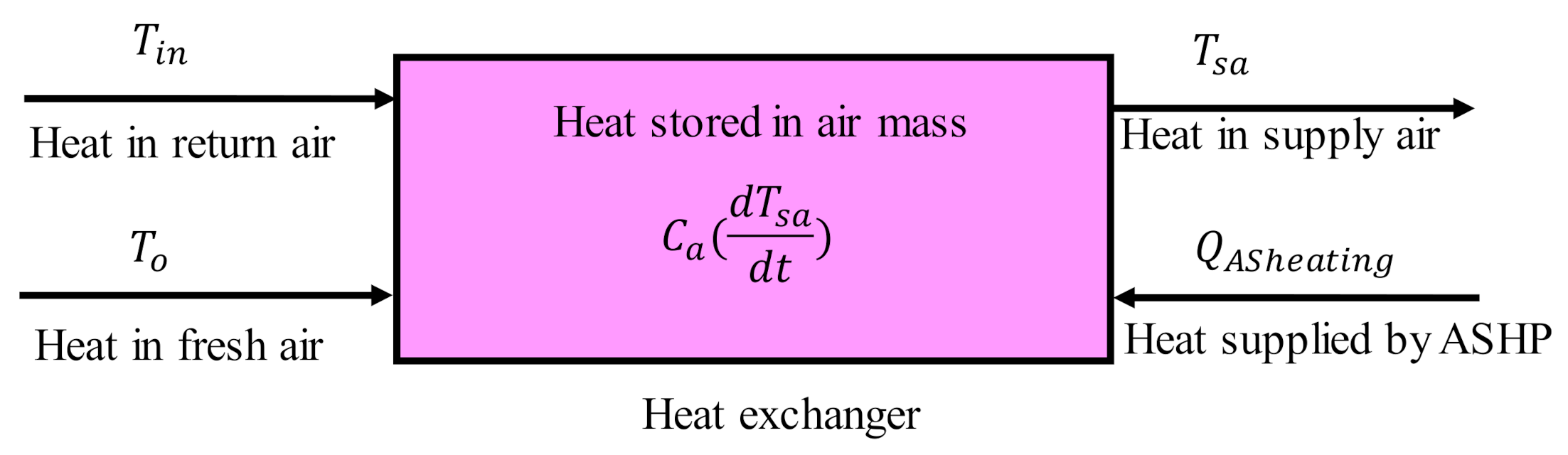







| Envelope | Constitutions | Total U-Value (W/(m2·K)) |
|---|---|---|
| External wall | Cement mortar 0.04 m | 0.32 |
| Insulating material 0.08 m | ||
| concrete hollow block 0.3 m | ||
| Internal wall | Cement mortar 0.04 m | 0.71 |
| Insulating material 0.04 m | ||
| Aerated concrete block 0.05 m | ||
| Overhead floorslab | Cement mortar 0.04 m | 0.67 |
| Reinforced concrete 0.2 m | ||
| Insulating material 0.04 m | ||
| Floor | Cement mortar 0.02 m | 0.12 |
| Insulating material 0.04 m | ||
| Reinforced concrete 0.12 m | ||
| compacted clay 0.2 m | ||
| Windows | Double glazing of 0.006 m width for | 2.4 |
| each glazing and 0.012 m air space | ||
| Glass curtain wall | Double low-E glazing of 0.006 m width for | 1.9 |
| each glazing and 0.012 m air space |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, R.; Yuan, Z.; Lei, B.; Zheng, J.; Luo, X. Model Predictive Control with Adaptive Building Model for Heating Using the Hybrid Air-Conditioning System in a Railway Station. Energies 2021, 14, 1996. https://doi.org/10.3390/en14071996
Lv R, Yuan Z, Lei B, Zheng J, Luo X. Model Predictive Control with Adaptive Building Model for Heating Using the Hybrid Air-Conditioning System in a Railway Station. Energies. 2021; 14(7):1996. https://doi.org/10.3390/en14071996
Chicago/Turabian StyleLv, Ruixin, Zhongyuan Yuan, Bo Lei, Jiacheng Zheng, and Xiujing Luo. 2021. "Model Predictive Control with Adaptive Building Model for Heating Using the Hybrid Air-Conditioning System in a Railway Station" Energies 14, no. 7: 1996. https://doi.org/10.3390/en14071996





