Ensemble Methods for Jump-Diffusion Models of Power Prices

Abstract

We propose a machine learning-based methodology which makes use of ensemble methods with the aims (i) of treating missing data in time series with irregular observation times and detecting anomalies in the observed time behavior; (ii) of defining suitable models of the system dynamics. We applied this methodology to US wholesale electricity price time series that are characterized by missing data, high and stochastic volatility, jumps and pronounced spikes. For missing data, we provide a repair approach based on the missForest algorithm, an imputation algorithm which is completely agnostic about the data distribution. To identify anomalies, i.e., turbulent movements of power prices in which jumps and spikes are observed, we took into account the no-gap reconstructed electricity price time series, and then we detected anomalous regions using the isolation forest algorithm, an anomaly detection method that isolates anomalies instead of profiling normal data points as in the most common techniques. After removing anomalies, the additional gaps will be newly filled by the missForest imputation algorithm. In this way, a complete and clean time series describing the stable dynamics of power prices can be obtained. The decoupling between the stable motion and the turbulent motion allows us to define suitable jump-diffusion models of power prices and to provide an estimation procedure that uses the full information contained in both the stable and the turbulent dynamics.

1. Introduction

Time series are occasionally observed at irregular observation times. Such irregular samples may occur naturally in climate research [1], in astronomy [2], in heart rate analysis [3] and even in financial time series [4]. The typical method applied to deal with irregular samples is to ignore them and literally close up the gaps. However, a missing values imputation (or gap filling) strategy can be informative and could provide fundamental knowledge for the subsequent stochastic analysis [5]. This is particularly true for financial time series. In such a case, although price time series are typically non stationary, log-return time series, computed as the difference in log-prices between two subsequent observations, have better behavior [6]. In the presence of missing data, log-returns computed over different time intervals may have different informative content. In fact, information affecting the dynamics of power prices can be released while the market is closed [7,8]. Moreover, we could encounter difficulties if we want to detect seasonality in market prices or compare markets with different closure day patterns.

In this paper, we will focus on the electricity prices of US power markets. US electricity price time series show irregular sampling (lack of daily data points) as a result of weekends, holidays and other missing data due to market specific reasons.

Existing methods for analyzing irregular time series can be categorized into three main directions [9]: (i) the repair approach in which missing observations are recovered via smoothing or imputation [10,11,12,13,14]—also implemented, especially in recent years, by machine learning methods [15,16,17,18]; (ii) the generalization of spectral analysis tools [19,20], such as wavelets [21,22,23,24]; (iii) kernel methods [25,26]. In this paper, we deal with a repair approach which uses an input preparation step based on machine learning. We work out this problem first by using a regular sampling grid layer over the original time series, and then by computing a value for each of new sampled point from the available samples, in order to have an equidistant missing-data problem [5]. For such an imputation process, we chose the missForest algorithm [27] that is completely agnostic about the data distribution. We verified that using this machine learning strategy for gap-filling, data quality did improve in a very efficient manner, especially compared to traditional methods. Therefore, being predominantly data-driven by design, we could rely just on training data and using very few parameters to reconstruct complete time series. Once the filling process of the observed power price time series is completed, the anomaly detection problem is addressed.

“An anomaly is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism” [28]. Electricity price time series are prone to have anomalies: they can occur as a consequences of excess demand, power outages, communication failures, activation of circuit breakers at substations, meter malfunctions and other reasons [29,30]. The liberalization process of the electricity sector has significantly increased the price volatility [31]. Looking at the time series of electricity prices, we can see some very erratic behavior. Power prices show, in fact, variable and unpredictable behavior with high and stochastic volatility; jumps and pronounced spikes; and a strong mean-reversion component, responsible for reducing prices after a jump or a spike has occurred [32]. Specifically, electricity price time series are characterized by normal stable periods in which they fluctuate around a long-run mean and turbulent price movements in which the dynamics are affected by jumps and short-lived spikes of large magnitude. This complex dynamics produces non-normal empirical distributions of log-returns with high volatility values and non-zero skewness and high kurtosis values [33].

In this paper we provide a general methodology to detect the stable price dynamics and decouple them from the turbulent dynamics in which jumps and spikes, i.e., anomalous price movements, occur. Our starting point is to consider the reconstructed no-gap time series, filled by the missForest algorithm, as affected by anomalies that we are going to identify and remove. The anomaly identification process is carried out on the filled original time series of electricity prices by using the isolation forest (or iForest) algorithm [34], an anomaly detection method that isolates anomalies instead of profiling normal data points, as in the most common techniques [35]. Using this unsupervised method, we can detect abrupt changes or novelty in prices time series without using a “universal” definition, considering that we cannot provide a “standard” reference for anomaly in electricity prices time series. As for the lack of “good” (non-anomalous) benchmark time series, we prefer an agnostic approach. Moreover, since we want to reduce to the minimum the impact of parameter setting on the anomaly detection process, iForest is a particularly suitable algorithm for this purpose [36,37,38]. Once identified, anomalies can be removed from the dynamics. At the end of this process, the additional gaps created by removing the anomalous regions of the dynamics will be newly filled by the missForest imputation algorithm. In this way, we obtain: (i) a complete and clean time series describing the stable dynamics of power prices; (ii) a separation between the stable dynamics and the turbulent dynamics to feed the stochastic analysis with. This is the first contribution of the present paper to the literature.

Several models have been proposed in the literature to describe the dynamics of power prices observed in real markets. Since the seminal paper by Lucia and Schwartz [39], the literature on this topic has grown exponentially. Mean-reverting jump-diffusion processes have been proposed [40,41] to account for the jumpy and spiky behavior of power prices. Regime-switching processes [42] have also been used with the aim of modeling the stable dynamics and the turbulent dynamics of power prices separately [43,44,45]. Compared to more complex regime-switching models, jump-diffusion models offer a good compromise between mathematical tractability and the physical description of the price dynamics. Their use can be considered as the simplest modeling methodology to describe non-Gaussian processes with stochastic volatility. However, the estimation procedure of jump-diffusion models on market data require some care in order to take into account in a proper way the various components of the dynamics [32]. When estimating a jump-diffusion model, the main difficulty is to determine which price variations are caused by jumps and which ones are caused by the diffusion component of the process. The easiest and most common way to deal with this problem is to fix a threshold according to which price variations are considered to be caused by jumps and spikes [44]. In this case, the threshold must be set according to some well defined (but arbitrary) criteria [46]. An alternative approach is to estimate the jump-diffusion model by maximum likelihood without filtering jumps first [40]. However, this technique allows one to reproduce the standard deviation of log-returns well but underestimates kurtosis [45]. The use of iForest algorithm is suitable for overcoming these difficulties. The decoupling of the price dynamics between the stable motion and the turbulent motion obtained by the machine learning techniques proposed in this paper, allows us to provide a suitable estimation procedure for both the diffusion component and the jump component of the model that makes use of the full information contained in both the stable and the turbulent dynamics. The estimation results show an interesting agreement with market data. This is the second contribution to the literature.

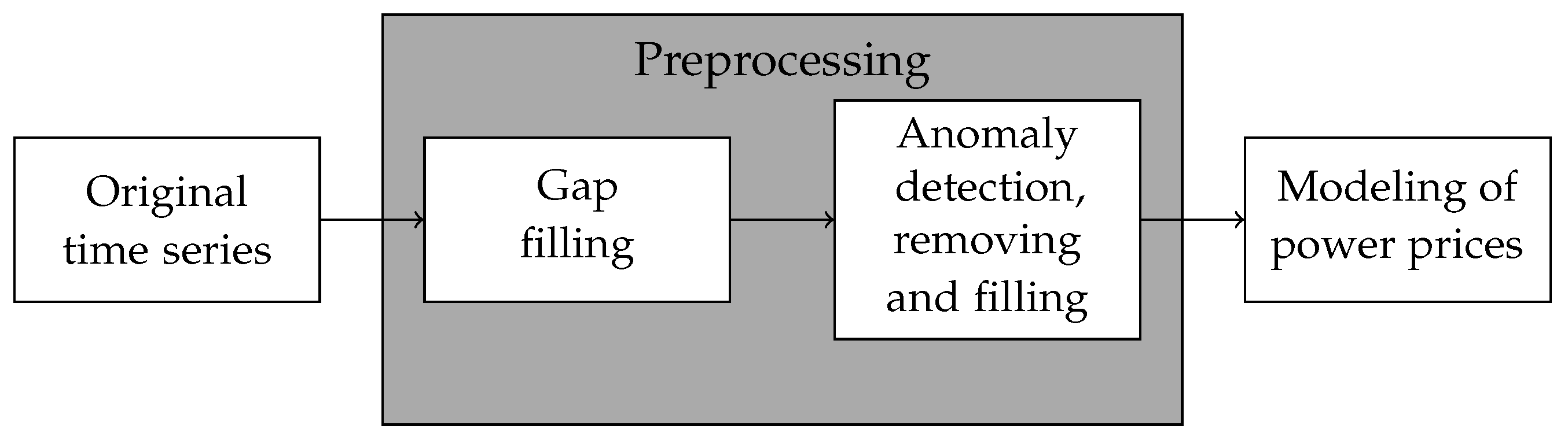
To our knowledge, this is the first study in which unsupervised machine learning techniques have been employed to detect jumps and spikes in power price time series, thereby allowing the possibility of accurately describing the observed dynamics using the jump-diffusion models. The workflow of the whole methodology is depicted in Figure 1.

The proposed approach has several advantages and potential applications. Specifically, our methodology offers the possibility to improve the data quality by using a data-driven approach, i.e., an unsupervised technique having as few parameters as possible, for the imputation of missing data and for the detections of anomalies in the dynamics [47,48,49]. Moreover, accurately modeling electricity price dynamics using simple models which can be easily calibrated on high quality data is essential for all the power market players [31]. The jump-diffusion model proposed in this paper is a short-term model and the short-term modeling of electricity prices is a central topic for both traders and producers in their attempts to hedge financial risk due to the unpredictability of power prices [50] by using power derivatives as well [51]. In this regard, having good short-term models of electricity prices capturing the first four central moments of log-return empirical distributions is of crucial importance for pricing power derivatives [52]. Moreover, modeling power prices over longer time horizons, ranging from a few years to decades, is strategically important for energy companies, in their efforts toward evaluating investments in capacity expansion and generating new technologies, and for policy makers involved in the energy planning decision making processes. In this regard, the proposed methodology can be employed as a long-term forecasting approach that allows us to derive the long-run behavior of power prices from their short-term dynamics. In the presence of a mean-reverting component, in fact, the probability distributions of power prices tend toward stationary long-run probability distributions [53]. In this way, the proposed approach also develops a robust link between the short-term and the long-term behavior of electricity prices.

The paper is organized as follows. Section 2 discusses the data processing methodology. Section 3 illustrates in some detail the mean-reverting jump-diffusion model used to describe the dynamics of power prices and the estimation procedure. Section 4 concludes. A comparison between the use of the missForest algorithm for gap filling purposes and a more traditional approach based on moving average techniques is provided in Appendix A.

2. The Data Processing Methodology

This section is devoted to discussing the data processing methodology. It is composed by two subsections in which we illustrate in detail all the steps of our procedure, namely, the filling process of the original wholesale time series of daily electricity prices, the anomaly detection process and the reconstruction of the stable motion time series.

2.1. Gap Filling

In our analysis we will consider daily electricity prices computed as weighted averages of the 24 hourly market prices. They are expressed in nominal dollars per megawatt-hour ($/MWh). Let us, therefore, denote by $p\left(t\right)$ the daily price at time t of 1 MWh of electricity and by M the number of observations of the original power price time series, one observation for each business day in which market data are available. We introduce, therefore, the following sets:

$$\begin{array}{c}\hfill p_{obs}=\{p\left({\overline{t}}_1\right),p\left({\overline{t}}_2\right),\cdots ,p\left({\overline{t}}_M\right)\}\end{array}$$

(1)

$$\begin{array}{c}\hfill {\mathbb{T}}_{obs}=\{{\overline{t}}_1,{\overline{t}}_2,\cdots ,{\overline{t}}_M\}\end{array}$$

(2)

where the set $p_{obs}$ contains the original power price time series and ${\mathbb{T}}_{obs}$ is the original time grid composed by M daily positions. Then, we use a complete daily grid that includes, in addition to business days, weekends, holidays and all the other days with missing market data—hereinafter, market-closure days. In this way we expand the cardinality of both sets from M to $N=M+C$, by introducing C additional elements corresponding to the number of market-closure days. We set, therefore,

$$\begin{array}{c}\hfill p=\{p\left(t_1\right),p\left(t_2\right),\cdots ,p\left(t_N\right)\}\end{array}$$

(3)

$$\begin{array}{c}\hfill \mathbb{T}=\{t_1,t_2,\cdots ,t_N\}\end{array}$$

(4)

$\mathbb{T}$ being the complete set of daily ordered time grid positions. This operation produces a set of missing observations in correspondence with market-closure days. Hence we can split the data points into two subsets, namely, the observation set, $p_{obs}$, and a set of missing values, $p_{mis}$, given by the set difference,

$$p_{mis}=p \backslash p_{obs},$$

(5)

defined on the time set difference

$${\mathbb{T}}_{mis}=\mathbb{T} \backslash {\mathbb{T}}_{obs}.$$

(6)

Now, to address the missing data problem in order to fill the gaps represented by the subset $p_{mis}$, we adopted an iterative imputation scheme based on the random forest technique [54]. In particular, we used the missForest algorithm [27] to fit a random forest model by taking the time series values belonging to $p_{obs}$ as the outcome variables and the time values belonging to the set ${\mathbb{T}}_{obs}$ as the input variables. After the fit, the missing values were imputed using prediction values from the fitted random forest algorithm, thereby determining the whole set p, i.e., the filled time series.

Our dataset consists of daily time series of electricity prices observed in four US power markets in the period 1 January 2001 to 24 March 2020. Two power markets, namely, SP15 and Palo Verde (PV), are located in the US Southwest region: respectively, in Southern California (SP15) and in the Southwest (PV). The remaining two, namely, PJM and Nepool (NE) power markets, are located in the US Northeast region. Data are freely downloadable at www.eia.gov/electricity/wholesale (accessed on 27 March 2020). Figure 2 shows, as an example, the original time series (in blue) and the parts filled (in red) by the missForest algorithm on a complete daily grid for the 4-month period of September 2014 to December 2014.

Table 1. Count of daily grid positions being empty (missing) or not (populated) in the period 1 January 2001 to 24 March 2020. Total grid positions: 7023.

	Populated	Missing
SP15	4638	2385
PV	4662	2361
PJM	4881	2142
NE	4493	2530

reports the number of days with missing data computed over the whole period under investigation, i.e., the period of 1 January 2001 to 24 March 2020.

Table 2. Mean and standard deviation (Std) values of the original and the filled time series empirical distribution.

	Original Mean	Filled Mean	Original Std	Filled Std
SP15	50.83	51.94	34.13	37.09
PV	44.01	46.57	28.82	35.26
PJM	50.06	50.05	27.09	26.49
NE	56.52	56.85	32.19	31.52

depicts the values of the mean and standard deviation of the original and the filled time series’ empirical distribution.

A comparison between the original time series empirical distribution and the filled time series empirical distribution is depicted in Figure 3.

We remark that this approach needs no tuning parameters, and hence it needs neither prior knowledge about the data nor assumptions about the distribution of the data of the variable domain [27]. Misztal [55] underlined the good performance of the missForest algorithm over generic missing patterns, including the case of Not missing at random (NMAR) data. According to Little and Rubin [56], there are three missing data mechanisms: missing completely at random (MCAR), missing at random (MAR) and not missing at random (NMAR). MCAR means that the probability of a piece of information being missing does not depend on $p_{mis}$ or $p_{obs}$; MAR means that the probability of a piece of information being missing does not depend on $p_{mis}$, but may depend on $p_{obs}$; MNAR means that the probability of a piece of information being missing does depend on $p_{mis}$. Obviously, there is a risk of having artificial and compromised numerical effects which are inherent to any imputation method and that may result in further spurious effects [57]. However, missForest outperforms many methods of imputation, especially if data are supposed to describe complex interactions in which non-linear relations are suspected [27]. Empirical and simulation studies confirm that missForest method perform well and can produce unbiased parameter estimates and standard errors [58,59,60,61].

2.2. Anomaly Detection, Removing and Filling

Before addressing the anomaly detection problem, we performed a decomposition of the filled time series in order to extract the stochastic component of the power price dynamics. To do this, let us pose:

$$s\left(t\right)=lnp\left(t\right),$$

(7)

the natural logarithm of the electricity price at time t. We assume that $s\left(t\right)$ is a linear superposition of a deterministic component, $f\left(t\right)$, accounting for trend and seasonality, and a random component, $x\left(t\right)$, namely,

$$s\left(t\right)=f\left(t\right)+x\left(t\right).$$

(8)

Typically, electricity prices are higher in winter time and lower in summer time, so the seasonal component must account for this semiannual periodicity. A trend must be taken into account for expected inflation and conceivably for a real escalation rate of power prices (positive or negative). We used the STL decomposition technique [62] to identify the deterministic component of the dynamics, $f\left(t\right)$. STL stands for “seasonal and trend decomposition using LOESS” and separates the time series into a trend, a seasonal and a residual, stochastic component. LOESS stands for “locally estimated scatterplot smoothing” and it is a seasonal-trend decomposition procedure. Many excellent and comprehensive presentations of the STL decomposition technique can be found in the literature (see, e.g., ref. [63] and references therein). Figure 4 depicts (from top to bottom) the deterministic components, respectively, trend and seasonality, and the residual stochastic component of the filled time series of daily electricity log-prices, obtained from the STL decomposition technique, in the case of SP15 and Palo Verde power markets for the period 1 January 2001 to 24 March 2020. In Figure 5 the time series STL decomposition is shown in the case of PJM and Nepool power log-prices during the same period.

The anomaly detection problem can be now addressed. In the approach we propose, turbulent price movements, i.e., jumps and spikes, are identified as anomalies in the power price time dynamics. The purpose of this analysis is to identify and isolate anomalies in the stochastic component of the dynamics in order to decouple the stable motion from the jumpy and spiky behavior. To detect anomalies, we use the isolation forest (or iForest) algorithm which is an unsupervised learning algorithm for anomaly detection that works on the principle of isolating anomalies [34,35]. This method uses two main characteristics of anomalies: (i) they are the smaller part of the dataset and (ii) they have values that are very different from those that are considered normal points. Anomalies are “few and different,” and these peculiarities allows us to isolate them with respect to normal data points. Being a technique that creates a data-induced random tree, called an isolation tree (or iTree), the data partitioning continues until the isolation of every instance has been obtained. As for their susceptibility to isolation, anomalies are more likely to be isolated closer to the root of the tree, while normal points stay more in depth. The iForest algorithm is characterized by high detection performances [34].

After detection, anomalies can be removed from the dynamics. At the end of this process, the additional gaps created by removing anomalies are newly filled by using the missForest imputation algorithm, thereby providing a new price time series describing the stable dynamics of electricity markets prices. We call this time series the “stable” time series. In this way, the stable motion can be decoupled from the turbulent motion in which jump and spikes are observed. Figure 6 shows both the stable dynamics (the red line) and the anomalous turbulent dynamics (the blue line) for the power markets under investigation. The analysis was performed in an unsupervised manner using the hyperparameters reported in

Table 3. iForest hyperparameter values.

iForest Hyperparameter	Value
Number of iTrees	1000
Contamination value	Find automatically
Max samples	256

. In Figure 7, we can see the detail for a 60 day time frame.

3. Modeling Electricity Price Dynamics

The reconstruction of the filled power price time series and the decoupling technique based on the machine learning algorithms are very useful for defining suitable stochastic models of the electricity price dynamics. Moreover, the decoupling between the stable motion and the turbulent motion allows us to introduce appropriate estimation techniques. In this section, we propose a mean-reverting jump-diffusion model of power prices and we discuss a two-step estimating technique of the model based on the information contained in both the stable time series and the turbulent dynamics.

3.1. A Mean-Reverting Jump-Diffusion Model of Power Prices

We focus on a mean-reverting jump-diffusion model in which the dynamics of $x\left(t\right)$ are described by the following stochastic differential equation:

$$dx\left(t\right)=-\alpha x\left(t\right)dt+\sigma dw\left(t\right)+Jdq\left(t\right),$$

(9)

where $w\left(t\right)$ is a Wiener process and $q\left(t\right)$ is a Poisson process with constant intensity $\lambda$. In Equation (9) the random variable J, describing the jump amplitude, is assumed to be distributed as a normal random variable with mean $\mu$ and standard deviation ${\sigma }_J$, i.e., $J\sim N(\mu ,{\sigma }_J^2)$. Moreover, we assumed that the Wiener process, the Poisson process and the jump amplitude, are mutually independent processes. Nevertheless, this analysis can be extended to account for jump amplitude with arbitrary probability distributions [53]. The decoupling technique discussed in this paper allows us to estimate the dynamic model using a two-step procedure that makes use of on the information contained in both the stable time series and the turbulent dynamics. We will show that the proposed model provides an interesting description of the power price dynamics observed in real markets, thereby offering a good compromise between mathematical tractability and the physical interpretation of the main stylized facts of power price dynamics. For this reason, it can be used for several financial applications ranging from the pricing of power derivatives and the hedging of financial risk [52], to the evaluation of long-term investments in power generating technologies [53].

3.2. The Empirical Analysis

Figure 8 reproduces the stochastic component of daily electricity prices, hereinafter, prices,

$$p_x\left(t\right)=exp\left(x\left(t\right)\right),$$

(10)

and the stochastic components of log-returns, hereinafter, log-returns,

$$\Delta x\left(t\right)=x(t+\Delta t)-x\left(t\right),$$

(11)

where $\Delta t$ is equal to one day, obtained from the original filled time series for the 15-year period 1 January 2004 to 31 December 2018 for the four power markets under investigation.

We note that in the power markets located in the same US region electricity prices show very similar patterns.

Table 4. Count of daily grid positions being empty (missing) or not (populated) for the period January 2004 to December 2018. Total grid positions: 5928.

	Populated	Missing
SP15	3628	1851
PV	3688	1791
PJM	3811	1668
NE	3555	1924

depicts the number of days with missing data in the 15-year period of 1 January 2004 to 31 December 2018.

3.2.1. A Short-Term Empirical Analysis

In this section we show an empirical analysis of the model in the 2-year time interval of 1 January 2017 to 31 December 2018. In all four markets, log-returns show large fluctuations with jumps and spikes, and non-normal, leptokurtic empirical distributions. The descriptive statistics of log-returns are displayed in

Table 5. Descriptive statistics of log-returns (2017–2018).

	Mean	St. Dev.	Skewness	Kurtosis
SP15	0.0001	0.1706	0.4441	11.5882
PV	0.0003	0.1768	0.3523	11.1401
PJM	0.0001	0.1585	−0.4177	18.4634
NE	−0.0004	0.1817	0.7832	8.7816

.

We estimated the dynamics described by Equation (9) on market data by using a two-step procedure. In the first step, the parameters of the diffusion component of the model, i.e., $\alpha$ and $\sigma$, were estimated. In the second step the parameters of the jump component of the model, i.e., $\lambda$, $\mu$ and ${\sigma }_J$ were estimated.

In the first step, the following Euler discretization of the diffusion component of Equation (9) with time-step $\Delta t$ equal to one day was used, namely,

$$\Delta x\left(t\right)=-\alpha x\left(t\right)\Delta t+\sigma \Delta w\left(t\right).$$

(12)

In order to account for the volatility due to the diffusion component of the model, without including the volatility of the jump component, the parameter $\sigma$ was determined by estimating Equation (12) on the stable time series (i.e., the red time series depicted in Figure 6) by maximum likelihood in the time interval 1 January 2017 to 31 December 2018. On the other hand, since the mean-reversion component must force back prices to fluctuate around the long-run mean after an anomalous price movement has occurred, the mean-reversion parameter, $\alpha$, was determined by estimating Equation (12) on the stochastic component of the filled original time series via maximum likelihood for the same time interval. Estimation results are depicted in

Table 6. Estimation results (2017–2018): step one. Standard errors are between parentheses.

	$\mathit{\alpha }$		$\mathit{\sigma }$
SP15	0.0838	(0.0097)	0.0778	(0.0021)
PV	0.0807	(0.0067)	0.0883	(0.0023)
PJM	0.1184	(0.0065)	0.0885	(0.0024)
NE	0.0852	(0.0064)	0.1051	(0.0027)

.

In the second step of the estimation procedure we determined the values of the jump parameters. The approach we followed is based on the simulated moments method [64,65] using Monte Carlo techniques [65,66]. For each triple of values $(\lambda ,\mu ,{\sigma }_J$) belonging to a suitable three dimensional grid, a sample of one thousand random paths was generated from Equation (9) by using Monte Carlo techniques with the estimated parameters, $\alpha$ and $\sigma$, determined in the first step. Along each path, the first central moments, in particular the standard deviation, the skewness and the kurtosis, of log-returns were computed and averaged over the sample. We assumed that a triple $(\lambda ,\mu ,{\sigma }_J$) offers a good fit if for each central moment, the difference between the sample average value and the observed value reported in Table 5 is less than one-fourth ($25\%$) of the sample standard deviation for that moment. Some good triples are reported in

Table 7. Estimation results (2017–2018): step two.

	$\mathit{\mu }$	${\mathit{\sigma }}_{\mathit{J}}$	$\mathit{\lambda }$
SP15	0.04	0.37	15.8%
PV	0.04	0.38	15.5%
PJM	−0.04	0.48	6.8%
NE	0.09	0.35	15.8%

.

Table 8. Statistics of simulated path log-returns (2017–2018). Sample standard deviations are between parentheses.

	Mean	St. Dev.	Skewness	Kurtosis
SP15	−0.0001	0.1708	0.4609	11.7550
	(0.0005)	(0.0113)	(0.5264)	(1.8673)
PV	0.0000	0.1767	0.4036	11.1325
	(0.0006)	(0.0113)	(0.5067)	(1.8445)
PJM	0.0002	0.1582	−0.4272	18.4418
	(0.0005)	(0.0121)	(0.9810)	(4.3313)
NE	0.0002	0.1813	0.7366	8.7964
	(0.0006)	(0.0101)	(0.3883)	(1.3830)

displays some statistical parameters of simulated paths. Such values are determined by averaging over one thousand randomly generated paths using the estimates obtained in the two-step procedure. The agreement with the descriptive statistics of log-returns shown in Table 5 is very interesting.

We recall the importance, in option pricing and in risk hedging methodologies, of a given model being able to capture the first four central moments of empirical distributions of log-returns, not only the standard deviation. Skewness is particularly related to the asymmetry between upward versus downward moves; the kurtosis describes the tails of the distribution. These parameters are particularly relevant in the case of power prices in which extreme events may occur [52].

3.2.2. A Long-Term Empirical Analysis

Accurately modeling the electricity price dynamics using short-term models is also a crucial task for describing the electricity price dynamics on longer time horizons. In the presence of a mean-reverting component, in fact, the probability distributions of power prices tend to stationary long-run probability distributions [53]. In this way, the long-term behavior of power prices can be derived by the short-term dynamics. However, for a long-run empirical analysis, the amplitude of the estimation time interval must be increased in order to get more significant values [6]. To this end, we considered the 15-year period 1 January 2004 to 31 December 2018. The descriptive statistics of log-returns are displayed in

Table 9. Descriptive statistics of log-returns (2004–2018).

	Mean	St. Dev.	Skewness	Kurtosis
SP15	0.0000	0.0960	0.4276	23.5549
PV	0.0000	0.0935	0.5753	28.2951
PJM	0.0000	0.1431	−0.4011	14.7284
NE	0.0000	0.1360	0.4508	12.4794

.

We used the same two-step procedure to estimate the jump-diffusion model described by Equation (9) over this fifteen-year time horizon too. Estimation results are depicted in

Table 10. Estimation results (2004–2018): step one. Standard errors are between parentheses.

	$\mathit{\alpha }$		$\mathit{\sigma }$
SP15	0.0475	(0.0036)	0.0613	(0.0007)
PV	0.0479	(0.0011)	0.0618	(0.0006)
PJM	0.1008	(0.0027)	0.0925	(0.0009)
NE	0.0622	(0.0012)	0.0886	(0.0009)

for the parameters of the diffusion component of the model, and in

Table 11. Estimation results (2004–2018): step two.

	$\mathit{\mu }$	${\mathit{\sigma }}_{\mathit{J}}$	$\mathit{\lambda }$
SP15	0.03	0.34	4.5%
PV	0.03	0.38	3.2%
PJM	−0.03	0.40	6.6%
NE	0.04	0.34	8.5%

for the parameters of the jump component of the model.

Table 12. Statistics of simulated path log-returns obtained using estimated parameters (2004–2018). Sample standard deviations are between parentheses.

	Mean	St. Dev.	Skewness	Kurtosis
SP15	0.0000	0.0960	0.4560	23.5352
	(0.0001)	(0.0034)	(0.4844)	(3.2481)
PV	0.0000	0.0932	0.6194	28.5322
	(0.0001)	(0.0034)	(0.5851)	(3.8200)
PJM	0.0000	0.1425	−0.4152	14.7151
	(0.0001)	(0.0037)	(0.3175)	(1.4268)
NE	0.0001	0.1356	0.4421	12.4323
	(0.0001)	(0.0032)	(0.2588)	(1.0766)

displays some statistical parameters computed from simulated log-return time series. Such values were determined by averaging over one thousand randomly generated paths using the estimates obtained in the two-step procedure. Additionally, in this case, the agreement with the descriptive statistics of observed log-returns shown in Table 9 is very interesting.

4. Concluding Remarks

In this paper we provided a general methodology to fill missing data in time series with irregular observation times and to detect anomalies in the dynamics. Our approach is based on machine learning ensemble techniques. In particular, the missForest imputation algorithm was used to fill in the gaps of the time series, and the isolation forest algorithm was used to detect anomalies in the time behavior. Moreover, the missForest algorithm was also used to fill the additional gaps originated by removing anomalies, in order to create a complete and clean time series describing the stable dynamics of power prices. The decoupling of the price dynamics between the stable motion and the turbulent motion allowed us to define a suitable mean-reverting jump-diffusion model of power prices and a two-step estimation procedure of the model parameters that uses the full information contained in both, the stable time series and the anomalous regions of the dynamics. The same two-step procedure was used to estimate both models, the short-term and the long-term.

The filling and decoupling technique proposed in this paper seems to be a powerful tool of analysis for investigating the features of the complex dynamics of power prices observed in real markets. It allows one to distinguish normal periods in which prices fluctuate around the long-run mean from turbulent movements of power prices characterized by jumps and spikes. Within this framework, the decoupling technique is a powerful tool for estimating jump-diffusion stochastic models of power prices in an accurate way. The obtained results show interesting agreement with empirical data.

Moreover, ensemble methods allowed us to put into evidence some similarities of the electricity price dynamics observed in different power markets. From this point of view, unsupervised machine learning techniques can be used to study the dynamics of the power markets prices as a whole, instead of taking them individually, thereby considering factors in common and similarities. We left those topics to future investigations.

Finally, let us remark that, although our analysis focused on power market prices, the proposed methodology is general and can be applied to very different contexts ranging from physical to social sciences.