A Method to Avoid Underestimated Risks in Seismic SUPSA and MUPSA for Nuclear Power Plants Caused by Partitioning Events

Abstract

Seismic probabilistic safety assessment (PSA) models for nuclear power plants (NPPs) have many non-rare events whose failure probabilities are proportional to the seismic ground acceleration. It has been widely accepted that minimal cut sets (MCSs) that are calculated from the seismic PSA fault tree should be converted into exact solutions, such as binary decision diagrams (BDDs), and that the accurate seismic core damage frequency (CDF) should be calculated from the exact solutions. If the seismic CDF is calculated directly from seismic MCSs, it is drastically overestimated. Seismic single-unit PSA (SUPSA) models have random failures of alternating operation systems that are combined with seismic failures of components and structures. Similarly, seismic multi-unit PSA (MUPSA) models have failures of NPPs that undergo alternating operations between full power and low power and shutdown (LPSD). Their failures for alternating operations are modeled using fraction or partitioning events in seismic SUPSA and MUPSA fault trees. Since partitioning events for one system are mutually exclusive, their combinations should be excluded in exact solutions. However, it is difficult to eliminate the combinations of mutually exclusive events without modifying PSA tools for generating MCSs from a fault tree and converting MCSs into exact solutions. If the combinations of mutually exclusive events are not deleted, seismic CDF is underestimated. To avoid CDF underestimation in seismic SUPSAs and MUPSAs, this paper introduces a process of converting partitioning events into conditional events, and conditional events are then inserted explicitly inside a fault tree. With this conversion, accurate CDF can be calculated without modifying PSA tools. That is, this process does not require any other special operations or tools. It is strongly recommended that the method in this paper be employed for avoiding CDF underestimation in seismic SUPSAs and MUPSAs.

1. Introduction

1.1. Multi-Unit Probabilistic Safety Assessments

Probabilistic safety assessments (PSAs) that calculate core damage frequency (CDF) are divided into single-unit PSAs (SUPSAs) and multi-unit PSAs (MUPSAs).

Many SUPSAs for nuclear power plants (NPPs) have been performed since the first PSA of WASH-1400 [1]. The initial MUPSA studies [2,3] were performed due to the gradually increasing concern regarding multi-unit nuclear accidents. After the Fukushima accident in 2011, many studies and reports on MUPSA [4,5,6,7,8,9,10,11,12,13,14,15,16] were published. In 2019, the International Atomic Energy Agency (IAEA) published a technical report [17] as part of a safety report series that provides comprehensive guidance for performing MUPSA. One method proposed for seismic MUPSA was converting correlated seismic failures into seismic common cause failures (CCFs) [18].

In MUPSA [17], multi-unit core damage frequency (MUCDF), site core damage frequency (SCDF), and single-unit core damage frequency (SUCDF) are defined as accident frequencies in which at least two NPPs, at least one NPP, and only one NPP are in a core damage state following an initiating event, respectively.

1.2. Alternating Operation Systems

Figure 1 shows a typical alternating operation system with two pump trains. One train is in an operational state, and the other train is in a standby state. Each train periodically switches its operation status between the operational and standby states. NPPs have alternating operation systems, such as the component cooling water system (CCWS), essential service water system (ESWS), essential chilled water system (ECWS), and chemical and volume control system (CVCS).

A Boolean equation for the failures in alternating operation systems can be expressed as Equation (1). The Boolean equation can be a fault tree or minimal cut sets (MCSs) that are calculated from the fault tree. In this paper, the operation fractions of ${\mathrm{X}}_1$ and ${\mathrm{X}}_2$ are defined as partitioning events. If one NPP has $\mathrm{S}$ alternating systems and each system has T partitioning events, the Boolean AND combination number of partitioning events in MCSs might be up to ${\mathrm{S}}^{\mathrm{T}}$. The other combinations, such as ${\mathrm{X}}_1{\mathrm{X}}_2,$ are not allowed in MCSs since they are mutually exclusive.

$$\begin{gathered} \mathrm{f}\left(X,B\right)={\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)+{\mathrm{X}}_2{\mathrm{f}}_2\left(B\right) \\ {\mathrm{X}}_1=\mathrm{Fraction} \mathrm{of} \mathrm{train} 1 \mathrm{operation} \\ {\mathrm{X}}_2=\mathrm{Fraction} \mathrm{of} \mathrm{train} 2 \mathrm{operation} \\ \left\{{\mathrm{f}}_1\left(B\right),{ \mathrm{f}}_2\left(B\right)\right\}=\mathrm{Operation} \mathrm{failures} \mathrm{during} \left\{{\mathrm{X}}_1,{ \mathrm{X}}_2\right\} \end{gathered}$$

(1)

Seismic SUPSA models have random failures of alternating operation systems that are combined with many seismic failures of components and structures. Furthermore, seismic MUPSA models have failures of NPPs that undergo alternating operations between full power and low power and shutdown (LPSD).

An NPP is in full-power operation for 1 or 2 years and in LPSD operation for 1 or 2 months to replace or reload nuclear fuels. That is, NPPs are a kind of alternating operation system. A Boolean equation to calculate the failures in alternating operation NPPs can be expressed as Equation (2). In this paper, the operation fractions of ${\mathrm{X}}_1$, ${\mathrm{X}}_2$, and ${\mathrm{X}}_3$ are also defined as partitioning events.

$$\begin{gathered} \mathrm{f}\left(X,B\right)={\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)+{\mathrm{X}}_2{\mathrm{f}}_2\left(B\right)+{\mathrm{X}}_3{\mathrm{f}}_3\left(B\right) \\ {\mathrm{X}}_1= \mathrm{Fraction} \mathrm{of} \mathrm{full}-\mathrm{power} \mathrm{operation} \\ {\mathrm{X}}_2= \mathrm{Fraction} \mathrm{of} \mathrm{LPSD} \mathrm{operation} \mathrm{with} \mathrm{nuclear} \mathrm{fuel} \\ {\mathrm{X}}_3= \mathrm{Fraction} \mathrm{of} \mathrm{LPSD} \mathrm{operation} \mathrm{without} \mathrm{nuclear} \mathrm{fuel} \\ \left\{{\mathrm{f}}_1\left(B\right), {\mathrm{f}}_2\left(B\right), {\mathrm{f}}_3\left(B\right)\right\}=\mathrm{Operation} \mathrm{failures} \mathrm{during} \left\{{\mathrm{X}}_1,{ \mathrm{X}}_2,{ \mathrm{X}}_3\right\} \end{gathered}$$

(2)

Thus, multiple NPPs in a single nuclear site are considered a group of alternating operation NPPs. Since the Kori nuclear site in Korea has nine NPPs and each LPSD PSA has 15 plant operating states (POSs), there might be ${16}^9$ combinations of plant-level partitioning events in the MCSs of MUPSA.

1.3. Seismic MCS Conversion to Exact Solutions

Probability calculation from MCSs can be categorized as follows: (1) If the MCS size is small, accurate probability can be calculated by converting MCSs into sum-of-disjoint products (SDPs) [19,20] or applying the inclusion–exclusion principle (IEP) [21] to MCSs. (2) If the MCS size is huge, accurate probability can be calculated by converting MCSs into a binary decision diagram (BDD) [21]. Here, SDP and BDD have Boolean solutions that have no intersections. (3) Regardless of MCS size, min-cut-upper-bound (MCUB) is popularly calculated from MCSs as an approximate probability.

Seismic SUPSA and MUPSA models have many non-rare events and complemented events. It is well known that CDFs are drastically overestimated if CDFs are directly calculated from MCSs without converting MCSs into exact solutions, such as a BDDs [21], and calculating CDFs from the exact solutions. That is, MCSs for seismic SUPSA and MUPSA should be converted into exact solutions, and seismic CDFs should be calculated from the exact solutions for best-estimate risk calculation. Thus, to calculate accurate seismic CDFs (SUCDF, MUCDF, and SCDF), (1) MCSs are calculated from the fault tree, (2) MCSs are converted to a BDD, and (3) accurate CDFs are calculated from the BDD by a dedicated tool [21]. Instead of MCS conversion to exact solutions, the probability p(f(X, B)) in Equations (1) and (2) can be calculated by applying the inclusion–exclusion equation (see Equation (5)) [19] to MCSs if the MCS is small.

The author of this paper developed the Advanced Cutset Upper Bound Estimator (ACUBE) tool [21] for the US Electric Power Research Institute (EPRI), which converts MCSs into a BDD and calculates the probability from the BDD. It has been actively used as a quantification standard for seismic PSA in the United States.

Efficient BDD algorithms [22,23,24] were developed to convert a fault tree or MCSs into a BDD that has Boolean solutions in the form of nested Shannon decomposition [25]. A great effort was made to develop practical BDD algorithms [26,27] that can solve huge fault trees in PSA.

Probability calculations with simple MCSs are illustrated in

Table 1. Probability calculations with simple minimal cut sets (MCSs).

	Case 1	Case 2
MCSs	BX + BY {A, X, Y} = basic events	BX + BY {A} = basic event {X, Y} = partitioning events /X = Y, /Y = X, XY = 0, and X + Y = 1
SDP	BX + B/XY	BX + BY = B
BDD	B(X + /XY)	B(X + Y) = B
MCUB	1 − (1 − p(BX))(1 − p(BY))	Not applicable
Probability by IEP	p(BX) + p(BY) − p(BXY)	p(BX) + p(BY) = p(B)
Probability by SDP	p(BX) + p(B/XY)	p(BX) + p(BY) = p(B)
Probability by BDD	p(B)(p(X) + p(/X)p(Y))	p(B)

(a) SDP is calculated by BX + BY = BX + /(BX)BY = BX + (/B + B/X)BY = BX + B/XY. (b) SDP and BDD have Boolean solutions that have no intersections. (c) IEP, SDP, and BDD probabilities in Case 1 are identical. (d) IEP, SDP, and BDD probabilities in Case 1 are smaller than those in Case 2. SDP: sum-of-disjoint product; BDD: binary decision diagram; MCUB: min-cut-upper-bound; IEP: inclusion–exclusion principle.

. Most PSA tools calculate probabilities in Case 1. If X and Y are partitioning events, these events satisfy the relations of /X = Y, /Y = X, XY = 0, and X + Y = 1. According to these relations, SDP and BDD probabilities should be p(B) as in Case 2. In this way, partitioning event combinations should be deleted during the probability calculation. However, the deletion of partitioning event combinations is impossible without modifying PSA tools.

1.4. Objectives of This Study

Seismic SUPSA models have random failures of alternating operation systems that are combined with many non-rare seismic failures. Furthermore, seismic MUPSA models have failures of NPPs that undergo alternating operations between full power and LPSD.

If combinations of mutually exclusive partitioning events are not eliminated in exact solutions, such as a BDD of MCSs, CDFs can be drastically underestimated (see Section 2, Section 3, Section 4, Section 5 and Section 6). It is impossible to eliminate intersections of mutually exclusive events without modifying tools for generating MCSs from fault trees and converting MCSs into exact solutions. This CDF underestimation is prohibited for regulatory purposes. For this reason, it is necessary to develop a new fault tree modeling method to avoid CDF underestimation and accurately calculate CDFs.

This paper is the first to report on this CDF underestimation problem caused by partitioning events, and subsequently, this work proposes a simple solution to avoid CDF underestimation that converts partitioning events into conditional events in fault trees.

2. Exclusive Modeling of One Group of Partitioning Events

If a system has n trains that are alternatively operated one by one or an NPP undergoes n full-power and LPSD operations periodically, a Boolean equation to calculate system failure can be expressed as Equation (3).

$$\mathrm{f}\left(X,B\right)={\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)+{\mathrm{X}}_2{\mathrm{f}}_2\left(B\right)+\cdots +{\mathrm{X}}_{\mathrm{n}}{\mathrm{f}}_{\mathrm{n}}\left(B\right)$$

(3)

where $X$ has n partitioning events and ${\mathrm{f}}_{\mathrm{i}}\left(B\right)$ can be a complex Boolean equation that consists of random failure events $B$. The fault tree in Equation (3) is a typical case. Usual fault trees can have Boolean AND combinations of ${\mathrm{X}}_{\mathrm{i}}$’s, and these Boolean AND combinations should be deleted in MCSs since they are mutually exclusive.

The partitioning events are mutually exclusive events that satisfy the following equations in Equation (4). They can be depicted by the Venn diagram in Figure 2 that has no intersections of mutually exclusive partitioning events.

$$\begin{gathered} {\mathrm{X}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{j}}=0, \mathrm{i}\ne \mathrm{j} \\ {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{X}}_{\mathrm{i}}=1 \end{gathered}$$

(4)

Here, 0 and 1 denote empty and union sets, respectively.

If members of $X$ are not mutually exclusive, $\mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)$ can be calculated by the inclusion–exclusion equation [19] in Equation (5).

$$\begin{gathered} \mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)=\mathrm{p}\left({\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)\right)+\mathrm{p}\left({\mathrm{X}}_2{\mathrm{f}}_2\left(B\right)\right)+\cdots \\ +{\left(-1\right)}^1\left[\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{f}}_1\left(B\right){\mathrm{f}}_2\left(B\right)\right)+\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_3{\mathrm{f}}_1\left(B\right){\mathrm{f}}_3\left(B\right)\right)+\cdots \right] \\ +{\left(-1\right)}^2\left[\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{X}}_3{\mathrm{f}}_1\left(B\right){\mathrm{f}}_2\left(B\right){\mathrm{f}}_3\left(B\right)\right)+\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{X}}_4{\mathrm{f}}_1\left(B\right){\mathrm{f}}_2\left(B\right){\mathrm{f}}_4\left(B\right)\right)+\cdots \right] \\ +\dots \\ +{\left(-1\right)}^{\mathrm{n}-1}\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{X}}_3\dots {\mathrm{X}}_{\mathrm{n}}{\mathrm{f}}_1\left(B\right){\mathrm{f}}_2\left(B\right){\mathrm{f}}_3\left(B\right)\dots {\mathrm{f}}_{\mathrm{n}}\left(B\right)\right) \end{gathered}$$

(5)

However, since ${\mathrm{X}}_1$, ${\mathrm{X}}_2$, … are mutually exclusive events, Equation (5) should be

$$\mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)=\mathrm{p}\left({\mathrm{X}}_1\right)\mathrm{p}\left({\mathrm{f}}_1\left(B\right)\right)+\mathrm{p}\left({\mathrm{X}}_2\right)\mathrm{p}\left({\mathrm{f}}_2\left(B\right)\right)+\cdots +\mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}\right)\mathrm{p}\left({\mathrm{f}}_{\mathrm{n}}\left(B\right)\right).$$

(6)

The probability in Equation (5) is much smaller than that in Equation (6). That is, if Boolean AND combinations of mutually exclusive partitioning events in a single group are not eliminated in the inclusion–exclusion equation or in the exact solutions, such as a BDD, the system failure probability or CDF would be underestimated. However, it is impossible to eliminate mutually exclusive event combinations without modifying calculation tools. Therefore, there is a great need to explicitly model the partitioning events in fault trees instead of revising such tools. This is an objective of this paper.

To accomplish this objective, partitioning events are expressed as shown in Equation (7). They can be confirmed by reflecting the terms on the right-hand side in Equation (7) into the Venn diagram in Figure 2.

$$\begin{gathered} {\mathrm{X}}_2=/{\mathrm{X}}_1{\mathrm{X}}_2 \\ {\mathrm{X}}_3=/{\mathrm{X}}_1/{\mathrm{X}}_2{\mathrm{X}}_3 \\ {\mathrm{X}}_{\mathrm{n}}=/{\mathrm{X}}_1/{\mathrm{X}}_2\dots /{\mathrm{X}}_{\mathrm{n}-1}{\mathrm{X}}_{\mathrm{n}} \end{gathered}$$

(7)

Here, the probabilities of Equation (7) can be expressed by employing the conditional probabilities as

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_2\right)=\mathrm{p}\left(/{\mathrm{X}}_1{\mathrm{X}}_2\right)=\mathrm{p}\left(/{\mathrm{X}}_1\right)\mathrm{p}({\mathrm{X}}_2|/{\mathrm{X}}_1) \\ \mathrm{p}\left({\mathrm{X}}_3\right)=\mathrm{p}\left(/{\mathrm{X}}_1/{\mathrm{X}}_2{\mathrm{X}}_3\right)=\mathrm{p}\left(/{\mathrm{X}}_1\right)\mathrm{p}(/{\mathrm{X}}_2|/{\mathrm{X}}_1)\mathrm{p}({\mathrm{X}}_3|/{\mathrm{X}}_1/{\mathrm{X}}_2) \\ \mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}\right)=\mathrm{p}\left(/{\mathrm{X}}_1/{\mathrm{X}}_2\dots /{\mathrm{X}}_{\mathrm{n}-1}{\mathrm{X}}_{\mathrm{n}}\right)=\mathrm{p}\left(/{\mathrm{X}}_1\right)\mathrm{p}(/{\mathrm{X}}_2|/{\mathrm{X}}_1)\dots \mathrm{p}({\mathrm{X}}_{\mathrm{n}}|/{\mathrm{X}}_1/{\mathrm{X}}_2\dots /{\mathrm{X}}_{\mathrm{n}-1}). \end{gathered}$$

(8)

Equation (8) shows that partitioning events are not independent events, since

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_2\right)\ne \mathrm{p}({\mathrm{X}}_2|/{\mathrm{X}}_1) \\ \mathrm{p}\left({\mathrm{X}}_3\right)\ne \mathrm{p}({\mathrm{X}}_3|/{\mathrm{X}}_1/{\mathrm{X}}_2) \\ \mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}\right)\ne \mathrm{p}({\mathrm{X}}_{\mathrm{n}}|/{\mathrm{X}}_1/{\mathrm{X}}_2\dots /{\mathrm{X}}_{\mathrm{n}-1}). \end{gathered}$$

(9)

In this paper, conditional events are intentionally defined as in Equation (10) to explicitly model partitioning events with explicit events $X^{\mathrm{c}}$ inside a fault tree.

$$\begin{gathered} {\mathrm{X}}_1^{\mathrm{c}}\equiv {\mathrm{X}}_1 \\ {\mathrm{X}}_2^{\mathrm{c}}\equiv {\mathrm{X}}_2|/{\mathrm{X}}_1 \\ {\mathrm{X}}_3^{\mathrm{c}}\equiv {\mathrm{X}}_3|/{\mathrm{X}}_1/{\mathrm{X}}_2 \\ {\mathrm{X}}_{\mathrm{n}}^{\mathrm{c}}\equiv {\mathrm{X}}_{\mathrm{n}}|/{\mathrm{X}}_1/{\mathrm{X}}_2\dots /{\mathrm{X}}_{\mathrm{n}-1} \end{gathered}$$

(10)

Then, probabilities of conditional events can be easily derived from the Venn diagram in Figure 2.

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_1^{\mathrm{c}}\right)=\mathrm{p}\left({\mathrm{X}}_1\right) \\ \mathrm{p}\left({\mathrm{X}}_2^{\mathrm{c}}\right)=\frac{\mathrm{p}\left({\mathrm{X}}_2\right)}{{{\displaystyle \sum }}_{\mathrm{i}=2}^{\mathrm{n}}\mathrm{p}\left({\mathrm{X}}_{\mathrm{i}}\right)}, \mathrm{p}\left(/{\mathrm{X}}_2^{\mathrm{c}}\right)=1-\frac{\mathrm{p}\left({\mathrm{X}}_2\right)}{{{\displaystyle \sum }}_{\mathrm{i}=2}^{\mathrm{n}}\mathrm{p}\left({\mathrm{X}}_{\mathrm{i}}\right)} \\ \mathrm{p}\left({\mathrm{X}}_3^{\mathrm{c}}\right)=\frac{\mathrm{p}\left({\mathrm{X}}_3\right)}{{{\displaystyle \sum }}_{\mathrm{i}=3}^{\mathrm{n}}\mathrm{p}\left({\mathrm{X}}_{\mathrm{i}}\right)}, \mathrm{p}\left(/{\mathrm{X}}_3^{\mathrm{c}}\right)=1-\frac{\mathrm{p}\left({\mathrm{X}}_3\right)}{{{\displaystyle \sum }}_{\mathrm{i}=3}^{\mathrm{n}}\mathrm{p}\left({\mathrm{X}}_{\mathrm{i}}\right)} \\ \mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}^{\mathrm{c}}\right)=1 \end{gathered}$$

(11)

Using the conditional events in Equations (10) and (11), partitioning events and their probabilities can be expressed as in Equations (12) and (13).

$$\begin{gathered} {\mathrm{X}}_2=/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}} \\ {\mathrm{X}}_3=/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{X}}_3^{\mathrm{c}} \\ {\mathrm{X}}_{\mathrm{n}}=/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}\dots /{\mathrm{X}}_{\mathrm{n}-1}^{\mathrm{c}}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{c}} \end{gathered}$$

(12)

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_2\right)=\mathrm{p}\left(/{\mathrm{X}}_1^{\mathrm{c}}\right)\mathrm{p}\left({\mathrm{X}}_2^{\mathrm{c}}\right) \\ \mathrm{p}\left({\mathrm{X}}_3\right)=\mathrm{p}\left(/{\mathrm{X}}_1^{\mathrm{c}}\right)\mathrm{p}\left(/{\mathrm{X}}_2^{\mathrm{c}}\right)\mathrm{p}\left({\mathrm{X}}_3^{\mathrm{c}}\right) \\ \mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}\right)=\mathrm{p}\left(/{\mathrm{X}}_1^{\mathrm{c}}\right)\mathrm{p}\left(/{\mathrm{X}}_2^{\mathrm{c}}\right)\dots \mathrm{p}\left(/{\mathrm{X}}_{\mathrm{n}-1}^{\mathrm{c}}\right)\mathrm{p}\left({\mathrm{X}}_{\mathrm{n}}^{\mathrm{c}}\right) \end{gathered}$$

(13)

Finally, $\mathrm{f}\left(X,B\right)$ in Equation (3) can be converted to Equation (14). Please note that the terms on the right-hand side in Equation (14) are explicitly mutually exclusive since ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}/{\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}=0$.

When converting MCSs of $\mathrm{f}\left(X,B\right)$ into exact solutions, any combination of the terms on the right-hand side in Equation (14) becomes an empty set since ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}/{\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}=0$. This is a strength of the method proposed in this paper.

$$\mathrm{f}\left(X,B\right)={\mathrm{X}}_1^{\mathrm{c}}{\mathrm{f}}_1\left(B\right)+/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{f}}_2\left(B\right)+\cdots +/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}\dots /{\mathrm{X}}_{\mathrm{n}-1}^{\mathrm{c}}{\mathrm{X}}_{\mathrm{n}}^{\mathrm{c}}{\mathrm{f}}_{\mathrm{n}}\left(B\right)$$

(14)

The Boolean equations in Equations (3) and (14) are identical. It should be noted that the partitioning events in Equation (3) can be modeled in the fault tree using conditional events as in Equation (14). If a fault tree has Boolean AND combinations of partitioning events and they are converted into conditional events, the MCS generation tool from the fault tree automatically deletes these AND combinations (e.g., ${\mathrm{X}}_2{\mathrm{X}}_3 = (/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}})(/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{X}}_3^{\mathrm{c}}) = 0)$ Furthermore, the MCS conversion tool to exact solutions automatically deletes similar combinations of conditional events. With this modeling, the underestimation of CDF can be avoided.

3. Exclusive Modeling of Multiple Group Partitioning Events

A system or NPP can have multiple groups of partitioning events as in Equation (15). Here, $X$, $Y$, and $Z$ are the first, second, and third groups of partitioning events, respectively. $B$ has regular basic events.

$$\begin{gathered} \mathrm{f}\left(X,B\right)={\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)+{\mathrm{X}}_2{\mathrm{f}}_2\left(B\right)+\cdots \\ \mathrm{g}\left(Y,B\right)={\mathrm{Y}}_1{\mathrm{g}}_1\left(B\right)+{\mathrm{Y}}_2{\mathrm{g}}_2\left(B\right)+\cdots \\ \mathrm{h}\left(Y,B\right)={\mathrm{Z}}_1{\mathrm{h}}_1\left(B\right)+{\mathrm{Z}}_2{\mathrm{h}}_2\left(B\right)+\cdots \end{gathered}$$

(15)

The partitioning events satisfy the following equations. This can be shown by using the Venn diagram in Figure 2.

$$\begin{gathered} {\mathrm{X}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{j}}={\mathrm{Y}}_{\mathrm{i}}{\mathrm{Y}}_{\mathrm{j}}={\mathrm{Z}}_{\mathrm{i}}{\mathrm{Z}}_{\mathrm{j}}=0, \mathrm{i}\ne \mathrm{j} \\ {\displaystyle \sum }_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{j}}{\mathrm{Y}}_{\mathrm{j}}={\displaystyle \sum }_{\mathrm{k}}{\mathrm{Z}}_{\mathrm{k}}=1 \end{gathered}$$

(16)

Similarly to the conversion in Section 3, all terms on the right-hand in Equation (15) can be exclusively converted to Equation (17). Please note that the terms on the right-hand side in Equation (17) are explicitly mutually exclusive. When calculating probabilities of $\mathrm{f}\left(X,B\right)$, $\mathrm{g}\left(Y,B\right)$, $\mathrm{h}\left(Y,B\right)$, $\mathrm{f}\left(X,B\right)\mathrm{g}\left(Y,B\right)\mathrm{h}\left(Z,B\right)$, and $\left(X,B\right)+\mathrm{g}\left(Y,B\right)+\mathrm{h}\left(Z,B\right)$, combinations that have ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}/{\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}$, ${\mathrm{Y}}_{\mathrm{j}}^{\mathrm{c}}/{\mathrm{Y}}_{\mathrm{j}}^{\mathrm{c}}$, or ${\mathrm{Z}}_{\mathrm{k}}^{\mathrm{c}}/{\mathrm{Z}}_{\mathrm{k}}^{\mathrm{c}}$ are automatically deleted since they have explicitly mutually exclusive event combinations. This is a strength of the new method presented in this paper.

$$\begin{gathered} \mathrm{f}\left(X,B\right)={\mathrm{X}}_1^{\mathrm{c}}{\mathrm{f}}_1\left(B\right)+/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{f}}_2\left(B\right)+\cdots \\ \mathrm{g}\left(Y,B\right)={\mathrm{Y}}_1^{\mathrm{c}}{\mathrm{g}}_1\left(B\right)+/{\mathrm{Y}}_1^{\mathrm{c}}{\mathrm{Y}}_2^{\mathrm{c}}{\mathrm{g}}_2\left(B\right)+\cdots \\ \mathrm{h}\left(Y,B\right)={\mathrm{Z}}_1^{\mathrm{c}}{\mathrm{h}}_1\left(B\right)+/{\mathrm{Z}}_1^{\mathrm{c}}{\mathrm{Z}}_2^{\mathrm{c}}{\mathrm{h}}_2\left(B\right)+\cdots \end{gathered}$$

(17)

4. Application to a Simple System

The new method was applied to the simple Boolean equation in Equation (18). Probabilities of partitioning events and regular basic events are shown in Equation (19).

$$\mathrm{f}\left(X,B\right)={\mathrm{X}}_1{\mathrm{B}}_1+{\mathrm{X}}_2{\mathrm{B}}_2+{\mathrm{X}}_3{\mathrm{B}}_3$$

(18)

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_1\right)=0.5, \mathrm{p}\left({\mathrm{X}}_2\right)=0.3, \mathrm{p}\left({\mathrm{X}}_3\right)=0.2 \\ \mathrm{p}\left({\mathrm{B}}_1\right)=\mathrm{p}\left({\mathrm{B}}_2\right)=\mathrm{p}\left({\mathrm{B}}_3\right)=0.9 \end{gathered}$$

(19)

The probability of a Boolean equation $\mathrm{f}\left(X,B\right)$ in Equation (18) can be calculated by the inclusion–exclusion equation [19] as in Equation (20). To avoid the underestimated $\mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)$ in Equation (20), the fourth to seventh terms on the right-hand side in Equation (20) should be deleted since they have partitioning event combinations. If an NPP has many alternating operation systems, the fault tree for this NPP would have multiple group partitioning events. In this case, it is difficult to find and delete complex combinations of partitioning events. Furthermore, there is no dedicated tool to delete these complex combinations of partitioning events.

$$\begin{gathered} \mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)=\mathrm{p}\left({\mathrm{X}}_1{\mathrm{B}}_1\right)+\mathrm{p}\left({\mathrm{X}}_2{\mathrm{B}}_2\right)+\mathrm{p}\left({\mathrm{X}}_3{\mathrm{B}}_3\right) \\ -\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{B}}_1{\mathrm{B}}_2\right)-\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_3{\mathrm{B}}_1{\mathrm{B}}_3\right)-\mathrm{p}\left({\mathrm{X}}_2{\mathrm{X}}_3{\mathrm{B}}_2{\mathrm{B}}_3\right) \\ +\mathrm{p}\left({\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{X}}_3{\mathrm{B}}_1{\mathrm{B}}_1{\mathrm{B}}_3\right)=0.67077 \end{gathered}$$

(20)

To explicitly avoid the underestimation of the probability of $\mathrm{f}\left(X,B\right)$, Equation (18) can be converted into Equation (21), which is similar to Equation (14). Here, the conditional events and their probabilities are shown via Equations (22) and (23).

$$\mathrm{f}\left(X,B\right)={\mathrm{X}}_1^{\mathrm{c}}{\mathrm{B}}_1+/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{B}}_2+/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{X}}_3^{\mathrm{c}}{\mathrm{B}}_3$$

(21)

where the conditional events are defined as

$$\begin{gathered} {\mathrm{X}}_1^{\mathrm{c}}\equiv {\mathrm{X}}_1 \\ {\mathrm{X}}_2^{\mathrm{c}}\equiv {\mathrm{X}}_2|/{\mathrm{X}}_1 \\ {\mathrm{X}}_3^{\mathrm{c}}\equiv {\mathrm{X}}_3|/{\mathrm{X}}_1/{\mathrm{X}}_2 \end{gathered}$$

(22)

and their probabilities are

$$\begin{gathered} \mathrm{p}\left({\mathrm{X}}_1^{\mathrm{c}}\right)=\mathrm{p}\left({\mathrm{X}}_1\right)=0.5 \\ \mathrm{p}\left({\mathrm{X}}_2^{\mathrm{c}}\right)=\frac{\mathrm{p}\left({\mathrm{X}}_2\right)}{\mathrm{p}\left({\mathrm{X}}_2\right)+\mathrm{p}\left({\mathrm{X}}_3\right)}=\frac{0.3}{0.3+0.2}=0.6 \\ \mathrm{p}\left({\mathrm{X}}_3^{\mathrm{c}}\right)=1 \end{gathered}$$

(23)

The accurate probability of $\mathrm{f}\left(X,B\right)$ can be calculated by Equation (24) without employing any other techniques or dedicated PSA tools. This is a great strength of the method proposed in this paper.

$$\begin{gathered} \mathrm{p}\left(\mathrm{f}\left(X,B\right)\right)=\mathrm{p}\left({\mathrm{X}}_1^{\mathrm{c}}{\mathrm{B}}_1\right)+\mathrm{p}\left(/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{B}}_2\right)+\mathrm{p}\left(/{\mathrm{X}}_1^{\mathrm{c}}/{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{X}}_3^{\mathrm{c}}{\mathrm{B}}_3\right) \\ =0.5 \times 0.9 + 0.5 \times 0.6 \times 0.9 + 0.5 \times 0.4 \times 1.0 \times 0.9 =0.9 \end{gathered}$$

(24)

5. Application to Simple NPPs

If one NPP U1 or U2 has three operating states (FP, LPSD with nuclear fuel, and LPSD without nuclear fuel), Boolean equations for MUCDF and SCDF can be expressed as in Equation (25), and their fault trees are depicted in Figure 3. Here, %I is a seismic initiating event that has a frequency unit. Since no nuclear fuel is loaded in NPPs during the operation period of ${\mathrm{X}}_3$ or ${\mathrm{Y}}_3$, core damage is impossible. Therefore, ${\mathrm{f}}_3\left(B\right)$ and ${\mathrm{g}}_3\left(B\right)$ are empty sets.

$$\begin{gathered} \mathrm{MUCDF}=\%\mathrm{I}\times \mathrm{U}1\times \mathrm{U}2 \\ \mathrm{S}\mathrm{CDF}=\%\mathrm{I}\times (\mathrm{U}1+\mathrm{U}2) \\ \mathrm{U}1={\mathrm{X}}_1{\mathrm{f}}_1\left(B\right)+{\mathrm{X}}_2{\mathrm{f}}_2\left(B\right)+{\mathrm{X}}_3{\mathrm{f}}_3\left(B\right) \\ \mathrm{U}2={\mathrm{Y}}_1{\mathrm{g}}_1\left(B\right)+{\mathrm{Y}}_2{\mathrm{g}}_2\left(B\right)+{\mathrm{Y}}_3{\mathrm{g}}_3\left(B\right) \\ {\mathrm{f}}_3\left(B\right)={\mathrm{g}}_3\left(B\right)=0 \end{gathered}$$

(25)

where

$$\begin{gathered} {\mathrm{X}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{j}}={\mathrm{Y}}_{\mathrm{i}}{\mathrm{Y}}_{\mathrm{j}}=0, \mathrm{i}\ne \mathrm{j} \\ {\mathrm{X}}_1+{\mathrm{X}}_2+{\mathrm{X}}_3={\mathrm{Y}}_1+{\mathrm{Y}}_2+{\mathrm{Y}}_3=1 \end{gathered}$$

(26)

To avoid MUCDF underestimation, Equation (25) can be converted into Equation (27) by replacing partitioning events of ${\mathrm{X}}_1,{ \mathrm{X}}_2,{ \mathrm{Y}}_1,$ and ${\mathrm{Y}}_2$ with conditional events of ${\mathrm{X}}_1^{\mathrm{c}}$,/${\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}$, ${\mathrm{Y}}_1^{\mathrm{c}}$, and/${\mathrm{Y}}_1^{\mathrm{c}}{\mathrm{Y}}_2^{\mathrm{c}}$, respectively. That is, the fault tree in Figure 3 can be converted to the fault tree in Figure 4.

$$\begin{gathered} \mathrm{MUCDF}=\%\mathrm{I}\times \mathrm{U}1\times \mathrm{U}2 \\ \mathrm{S}\mathrm{CDF}=\%\mathrm{I}\times (\mathrm{U}1+\mathrm{U}2) \\ \mathrm{U}1={\mathrm{X}}_1^{\mathrm{c}}{\mathrm{f}}_1\left(B\right)+/{\mathrm{X}}_1^{\mathrm{c}}{\mathrm{X}}_2^{\mathrm{c}}{\mathrm{f}}_2\left(B\right) \\ \mathrm{U}2={\mathrm{Y}}_1^{\mathrm{c}}{\mathrm{g}}_1\left(B\right)+/{\mathrm{Y}}_1^{\mathrm{c}}{\mathrm{Y}}_2^{\mathrm{c}}{\mathrm{g}}_2\left(B\right) \end{gathered}$$

(27)

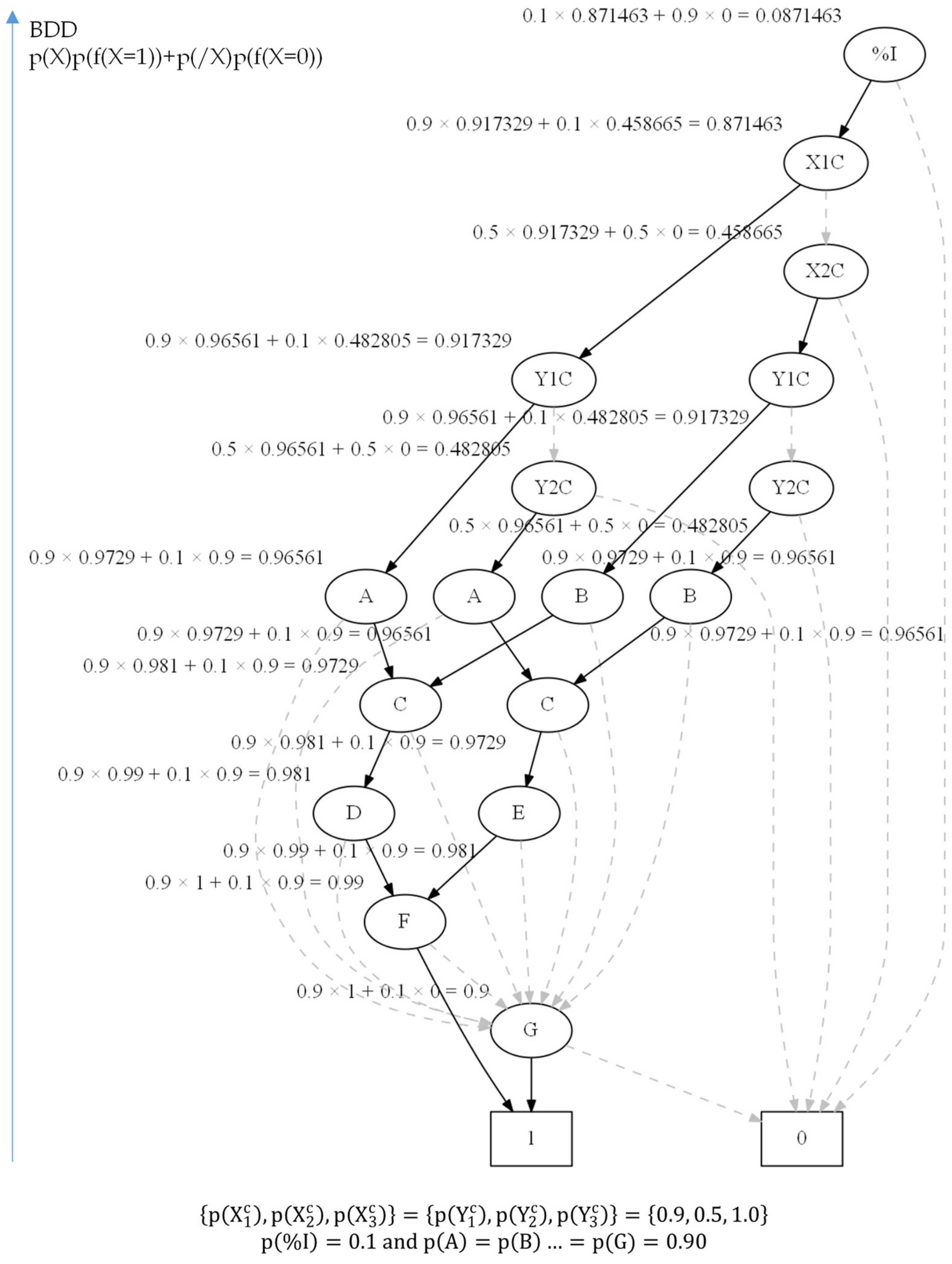
After generating MCSs from the original fault tree in Figure 3 and converting each MCS to a BDD, the underestimated MUCDF is calculated from the BDD in Figure 5. On the other hand, if a similar process is applied to the revised fault tree in Figure 4, the BDD in Figure 6 is created. During this process, the combinations of mutually exclusive partitioning events are automatically deleted since ${\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}/{\mathrm{X}}_{\mathrm{i}}^{\mathrm{c}}={\mathrm{Y}}_{\mathrm{j}}^{\mathrm{c}}/{\mathrm{Y}}_{\mathrm{j}}^{\mathrm{c}}=0$.

Sensitivity studies for MUCDF and SCDF were performed with the fault trees in Figure 3 and Figure 4 by increasing basic event probabilities from 0.01 to 0.99 with the fixed initiating event frequency and partitioning event probabilities in Equation (28).

$$\begin{gathered} \mathrm{p}\left(\%\mathrm{I}\right)=0.1 \\ \left\{\mathrm{p}\left({\mathrm{X}}_1\right), \mathrm{p}\left({\mathrm{X}}_2\right), \mathrm{p}\left({\mathrm{X}}_3\right)\right\}= \left\{\mathrm{p}\left({\mathrm{Y}}_1\right), \mathrm{p}\left({\mathrm{Y}}_2\right), \mathrm{p}\left({\mathrm{Y}}_3\right)\right\}=\left\{0.9, 0.05, 0.05\right\} \\ \left\{\mathrm{p}\left({\mathrm{X}}_1^{\mathrm{C}}\right), \mathrm{p}\left({\mathrm{X}}_2^{\mathrm{c}}\right), \mathrm{p}\left({\mathrm{X}}_3^{\mathrm{c}}\right)\right\} = \left\{\mathrm{p}\left({\mathrm{Y}}_1^{\mathrm{c}}\right), \mathrm{p}\left({\mathrm{Y}}_2^{\mathrm{c}}\right), \mathrm{p}\left({\mathrm{Y}}_3^{\mathrm{C}}\right)\right\}=\left\{0.9, 0.5, 1.0\right\} \end{gathered}$$

(28)

MCSs are calculated from the MUCDF and SCDF fault trees in Figure 3 and Figure 4, MCSs are converted into a BDD, and then MUCDF and SCDF are calculated from the BDD. The underestimated and accurate CDFs are compared in

Table 2. Comparison of MUCDFs and SCDFs.

MUCDF Comparison
p(A) = p(B) = … = p(G)	0.01	0.10	0.50	0.90	0.99
MUCDF from Figure 3a	8.190 × 10−4	8.198 × 10−3	4.364 × 10−2	7.914 × 10−2 (e)	8.187 × 10−2
MUCDF from Figure 4b	9.025 × 10−4	9.033 × 10−3	4.795 × 10−2	8.715 × 10−2 (f)	9.021 × 10−2
Underestimation error % (abs((b) − (a))/(b) × 100)	9.25%	9.24%	8.98%	9.19%	9.25%
SCDF Comparison
p(A) = p(B) =…= p(G)	0.01	0.10	0.50	0.90	0.99
SCDF from Figure 3c	1.010 × 10−3	1.160 × 10−2	7.005 × 10−2	9.849 × 10−2	9.909 × 10−2
SCDF from Figure 4d	1.919 × 10−3	2.071 × 10−2	1.188 × 10−1	1.864 × 10−1	1.900 × 10−1
Underestimation error % (abs((d) − (c))/(d) × 100)	47.37%	43.97%	41.01%	47.16%	47.83%

(e) specific MUCDF in Figure 5. (f) specific MUCDF in Figure 6.

. If partitioning events are ignored, both MUCDF and SCDF are underestimated in all calculations, and SCDF is much more underestimated than MUCDF.

6. Conclusions

There are several systems undergoing alternating operations in NPPs, and each NPP alternates between full power and LPSD. Therefore, complex Boolean AND combinations of mutually exclusive partitioning events should be eliminated when generating MCSs from a fault tree and converting MCSs into exact solutions.

For the correct probability calculation of a fault tree that has partitioning events, a proper modeling method of these events was proposed in Section 3, and the strength and simplicity of this modeling method were demonstrated by the applications in Section 4 and Section 5. If MCSs for seismic SUPSA and MUPSA are generated and converted into exact solutions without deleting combinations of mutually exclusive partitioning events, final CDFs (SUCDF, MUCDF, and SCDF) can be underestimated. Unfortunately, it is impossible to eliminate mutually exclusive event combinations without modifying PSA tools for generating MCSs from a fault tree and converting MCSs into a BDD.

Therefore, there is a great need to explicitly model the partitioning events in fault trees instead of revising PSA tools. This paper is the first to report on this problem and provide a solution to avoid CDF underestimation. If the partitioning events are modeled with conditional events in the seismic SUPSA and MUPSA fault trees with the method in this paper, accurate CDF calculation is possible using the existing PSA tools. This is the strength of the proposed method. The use of the method in this paper is strongly recommended for avoiding CDF underestimation in seismic SUPSA and MUPSA.

The failures of alternating operation systems are frequently modeled in internal, flooding, and fire event SUPSAs. Therefore, for calculating accurate CDF, it is also recommended that the modeling method of partitioning events in this paper be applied to any SUPSAs where the failures of alternating operation systems are modeled.