Energy and Exergy Analyses of Adsorption Chiller at Various Recooling-Water and Dead-State Temperatures
Abstract
:1. Introduction
- -
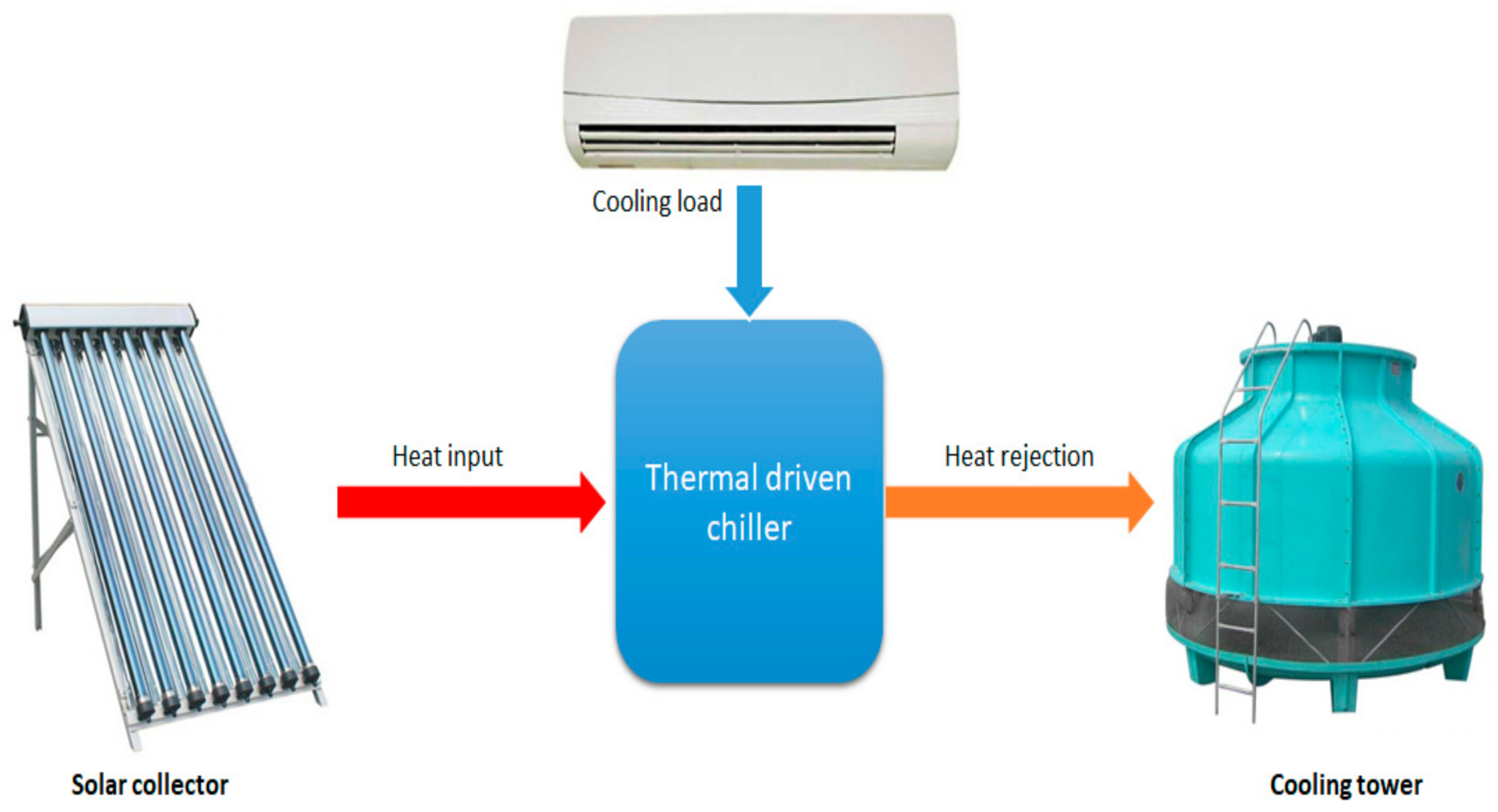
- The cold air is obtained as the heat is rejected from the chilled water in the evaporator of the chiller.
- -
- Heat input is the heat required in the generator to drive the process, which is delivered either by the solar system or by backup heat sources.
- -
- Heat rejection is ideally the summation of the useful load and driving heat; it can be dissipated normally by a cooling tower or dry cooler.
2. Methodology and Mathematical Model
2.1. Energy Performance
2.2. Exergy Analysis
- -
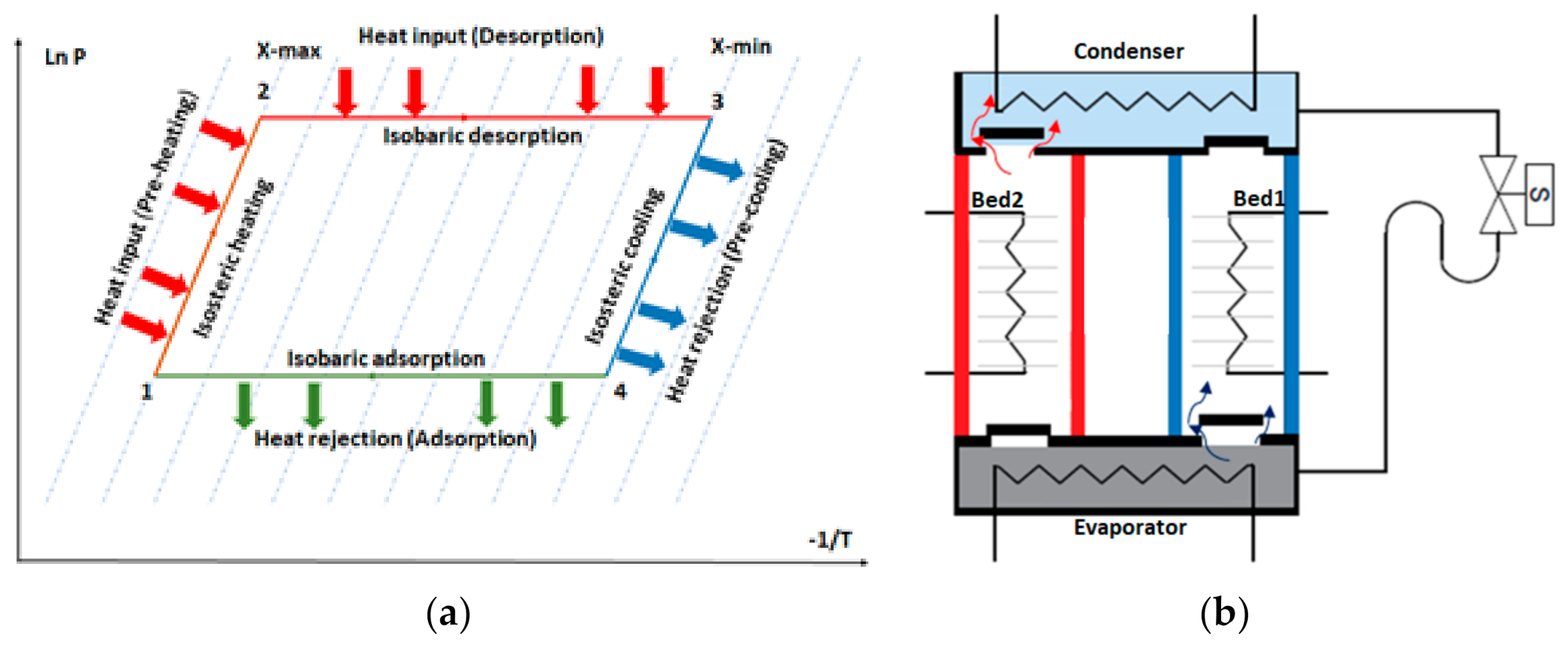
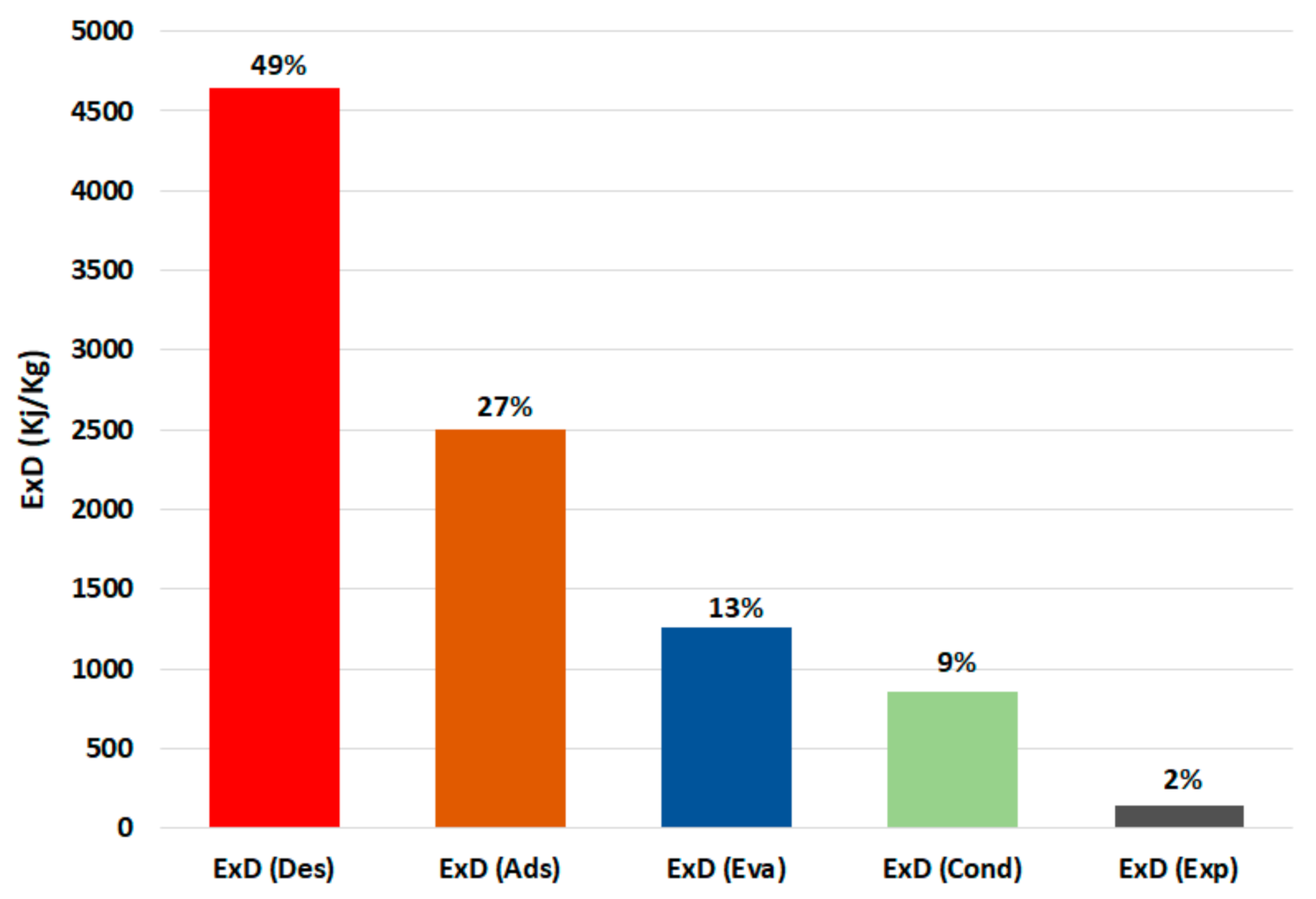
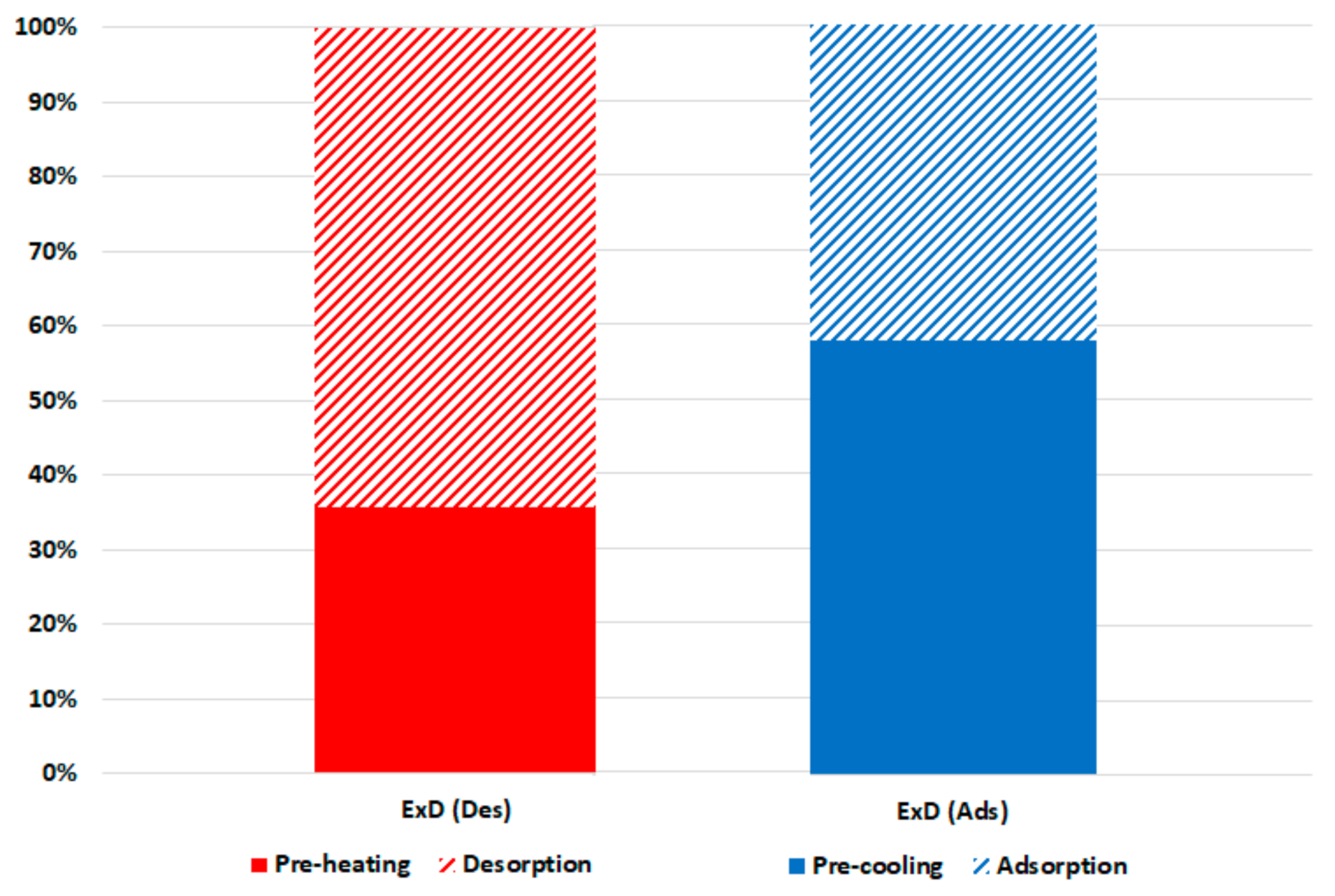
- Exergy destruction in the adsorber ():
- -
- Exergy destruction in the desorber ():
- -
- Exergy destruction in the condenser (:
- -
- Exergy destruction in the evaporator ():
- -
- Exergy destruction in the expansion (:
- -
- Total exergy destruction ():
- The water vapor (refrigerant) behaves as an ideal gas.
- The pressure and temperature inside the adsorbent bed are uniforms.
- Potential, kinetic, and chemical effects are neglected.
- The expansion process is isenthalpic.
- The pressure drop in the non-return values is neglected.
- The chiller is well insulated, and there are no heat losses to the surroundings.
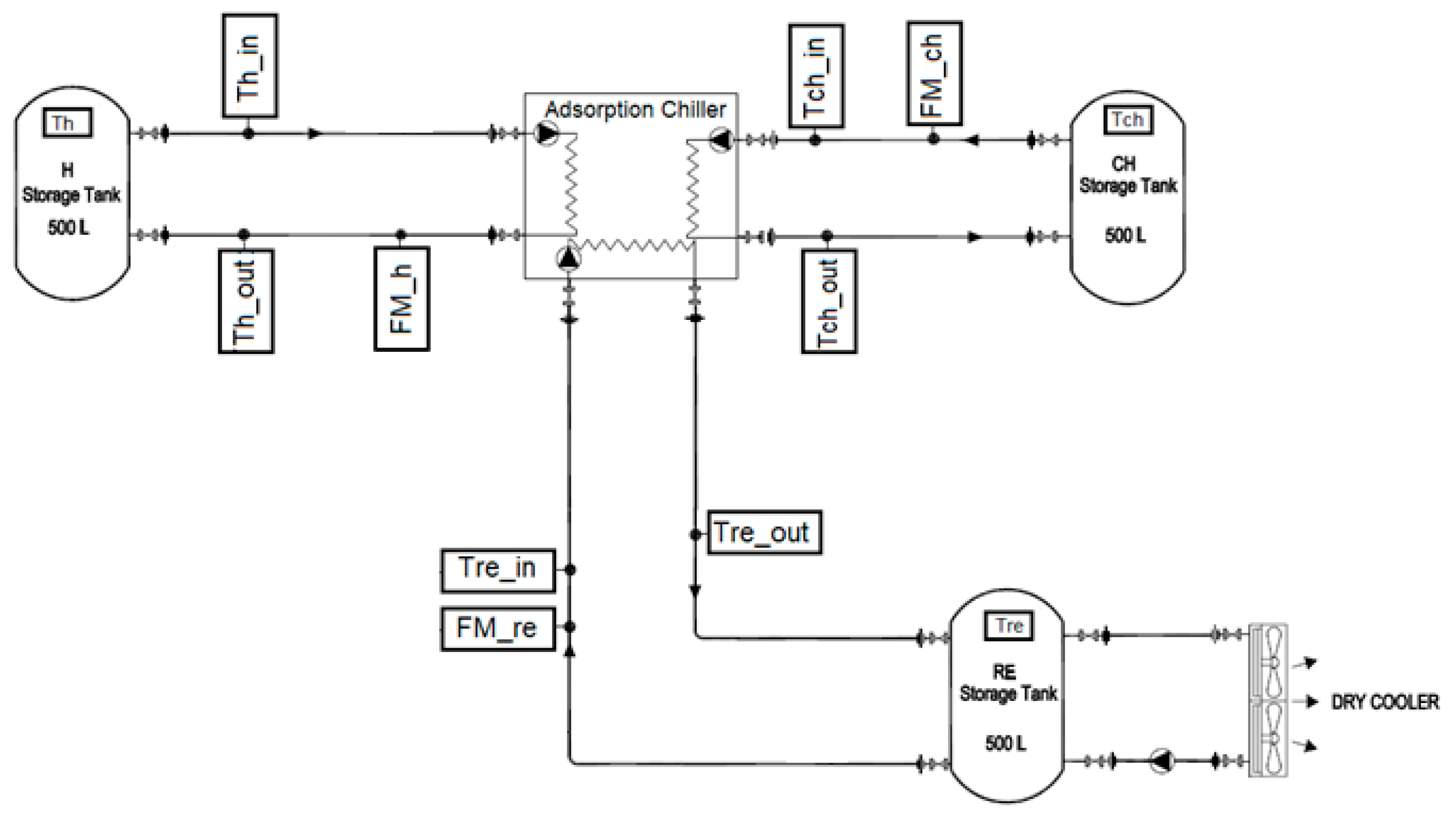
3. Experimental Setup
- Hot water inlet temperature (Th_in) of 90 0.5 °C maintained by an electric water heater.
- Recooling-water inlet temperature (Tre_in) of 30–45 °C maintained by a dry-cooler with a 100 L buffer tank.
- Chilled water inlet temperature (Tch_in) of 18 0.5 °C maintained by an electrical heater.
- Flow rates for hot, recooling, and chilled water are 1.2, 1.2, and 0.71 L/s, respectively.
- Cooling cycle time duration of 550 s.
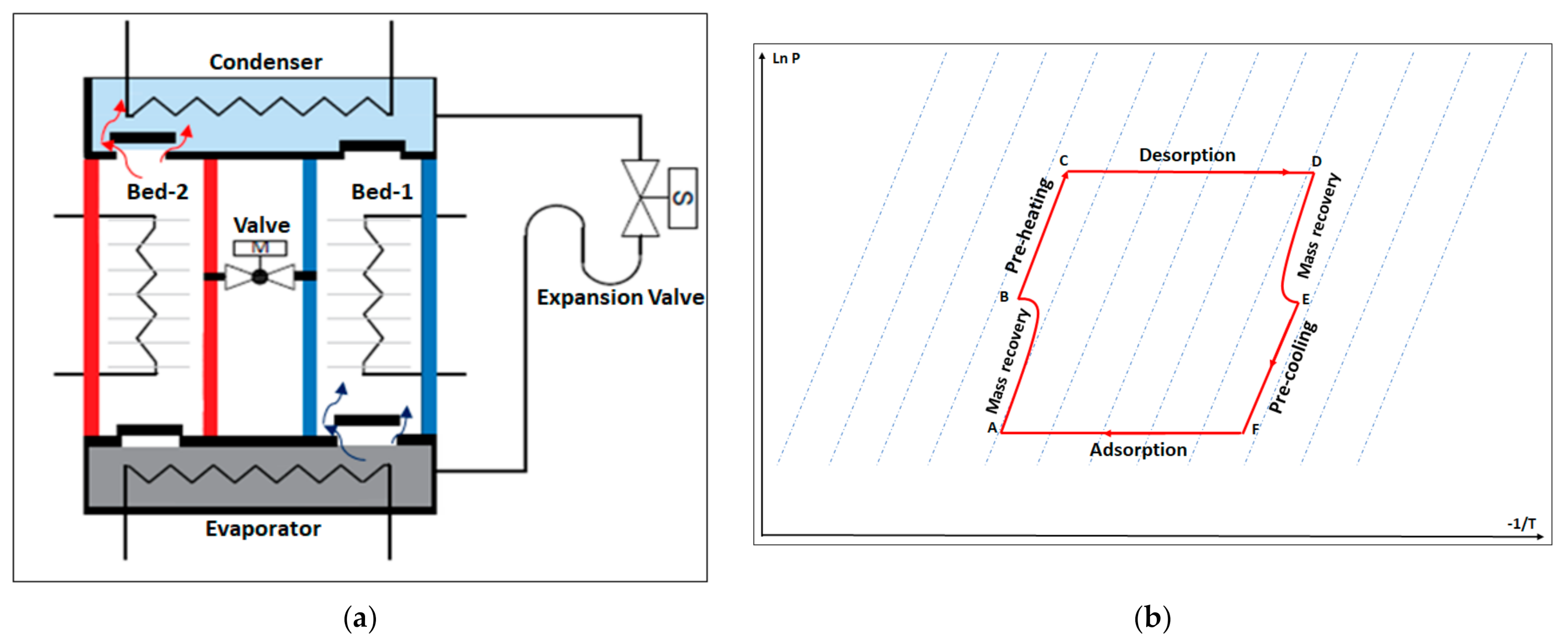
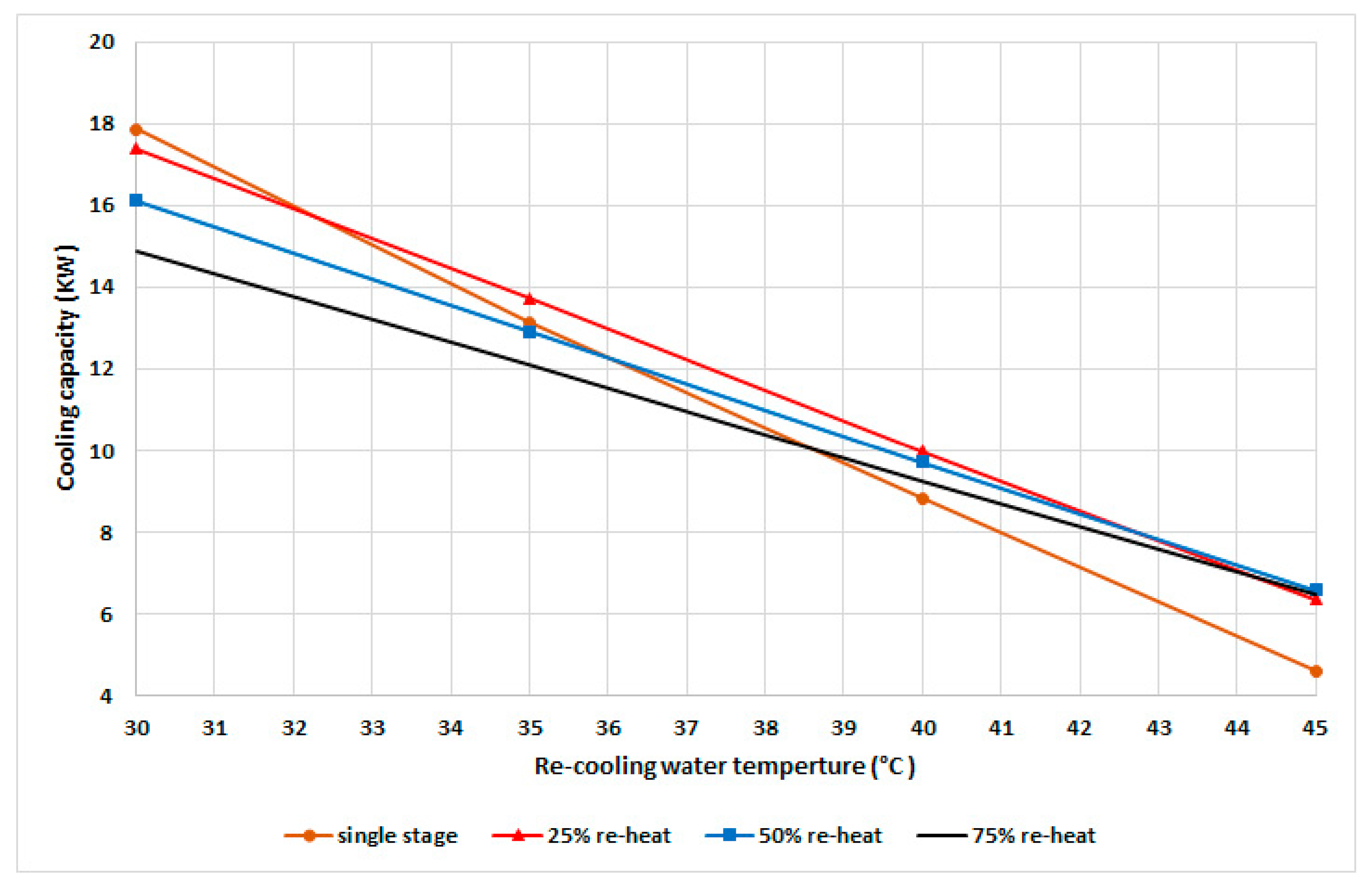
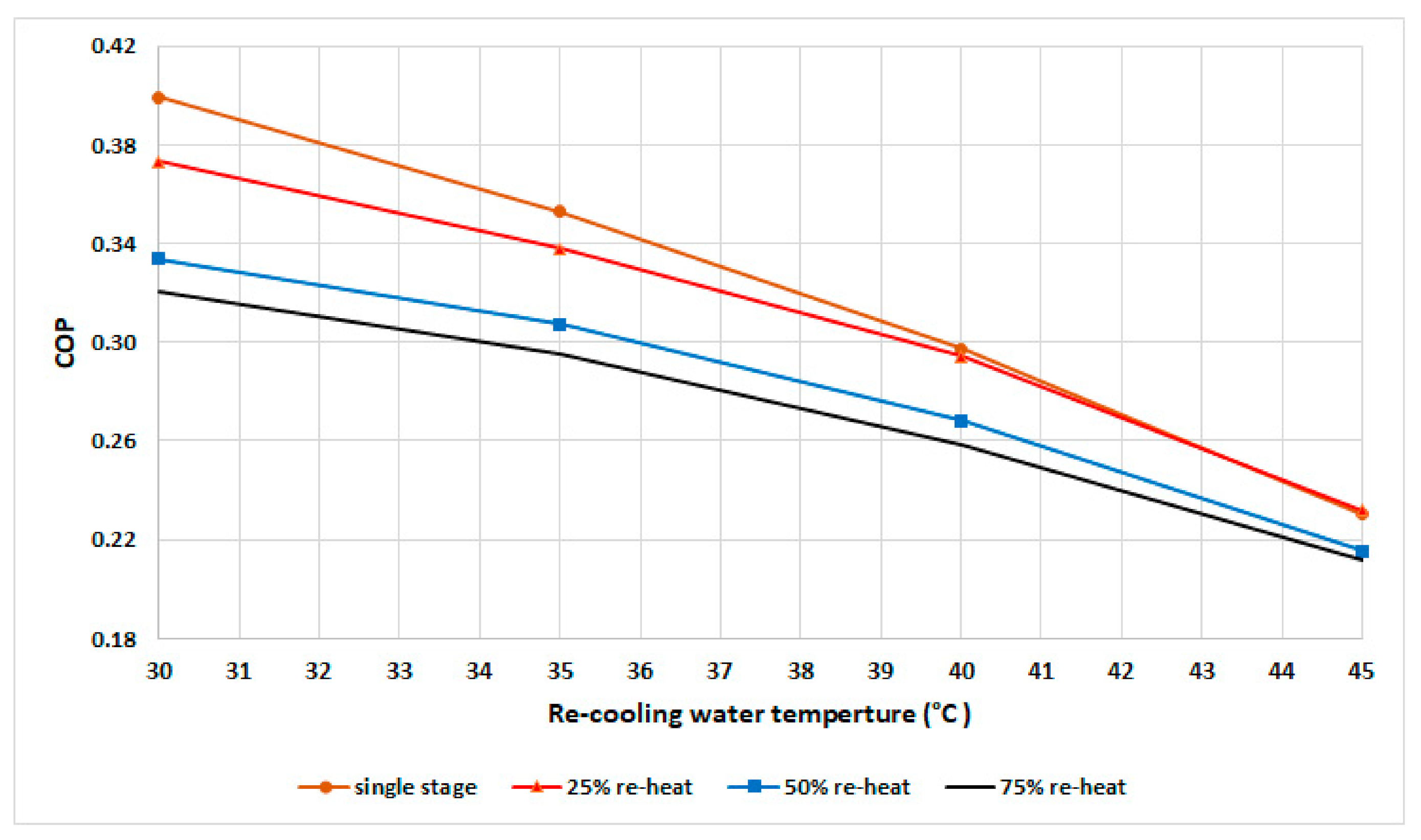
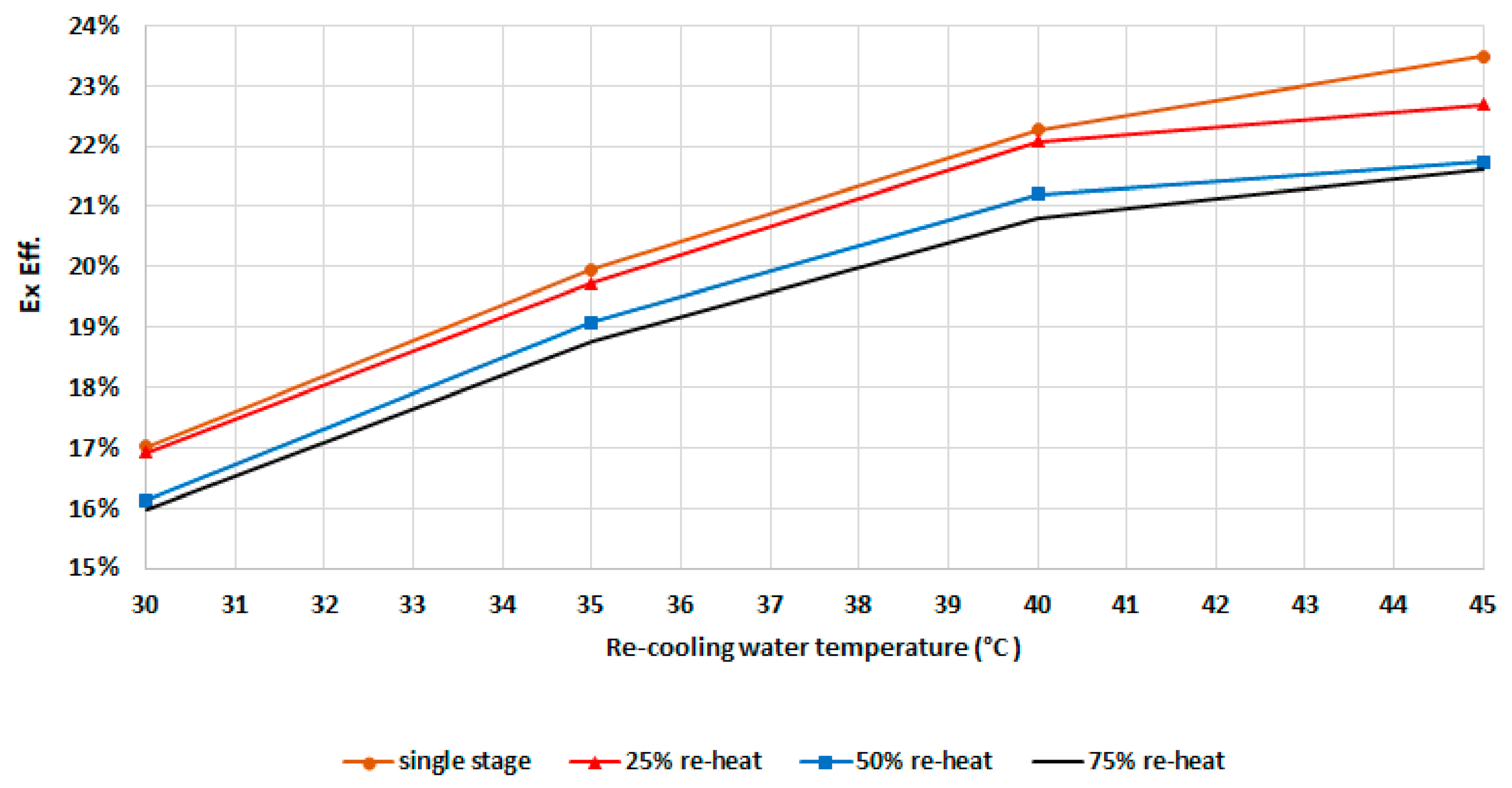
- Four modes were investigated: single-stage mode, 25% reheat cycle mode (25% mass recovery time of the cooling duration), 50% reheat cycle mode (50% mass recovery time of the cooling duration), and 75% reheat cycle mode (75% mass recovery time of the cooling duration)
- Three electromagnetic flowmeters (FM_h, FM_ch, and FM_re) (manufactured by ALIA GROUP) with accuracies of ± 0.4% were used to measure the water flow rate at the hot water loop, chilled water loop, and recooling-water loop, respectively.
- Eight platinum resistance thermometers (PT100 Class A, Pico Technology, St Neots, UK) with two temperature measuring data loggers (PT-104 is a four-channel logger) having a resolution of 0.001 °C and an accuracy of 0.015 °C were used to measure the inlet and outlet temperatures for the hot water, chilled water, and recooling water, in addition to the temperature of the storage tanks.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Cooling; IEA: Paris, France, 2020. [Google Scholar]
- Ayou, D.S.; Coronas, A. New Developments and Progress in Absorption Chillers for Solar Cooling Applications. Appl. Sci. 2020, 10, 4073. [Google Scholar] [CrossRef]
- Narayanan, R. Chapter Seven—Heat-Driven Cooling Technologies. In Clean Energy for Sustainable Development; Rasul, M.G., Azad, A.K., Sharma, S.C., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 191–212. [Google Scholar]
- Rucha, P.; Salibaa, S.; Onga, C.L.; Al-Shehrib, Y.; Al-Rihailib, A.; Al-Mogbelb, A.; Michela, B. Heat-Driven Adsorption Chiller Systems for Sustainable Cooling Applications. In Proceedings of the 11th IEA Heat Pump Conference 2014 Conference Proceedings, Montreal, QC, Canada, 12–16 May 2014. [Google Scholar]
- Thu, K. Adsorption Desalination: Theory & Experiments. Ph.D. Thesis, National University of Singapore, Singapore, 2010. [Google Scholar]
- Ambarita, H.; Kawai, H. Experimental study on solar-powered adsorption refrigeration cycle with activated alumina and activated carbon as adsorbent. Case Stud. Therm. Eng. 2016, 7, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Núñez, T.; Mittelbach, W.; Henning, H.-M. Development of an adsorption chiller and heat pump for domestic heating and air-conditioning applications. Appl. Therm. Eng. 2007, 27, 2205–2212. [Google Scholar] [CrossRef]
- Wang, R. Performance improvement of adsorption cooling by heat and mass recovery operation. Int. J. Refrig. 2001, 24, 602–611. [Google Scholar] [CrossRef]
- Restuccia, G.; Freni, A.; Vasta, S.; Aristov, Y. Selective water sorbent for solid sorption chiller: Experimental results and modelling. Int. J. Refrig. 2004, 27, 284–293. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S.; Wang, X. Comprehensive strategies for performance improvement of adsorption air conditioning systems: A review. Renew. Sustain. Energy Rev. 2019, 99, 138–158. [Google Scholar] [CrossRef]
- Ghilen, N.; Gabsi, S.; Benelmir, R.; El Ganaoui, M. Performance Simulation of Two-Bed Adsorption Refrigeration Chiller with Mass Recovery. J. Fundam. Renew. Energy Appl. 2017, 7. [Google Scholar] [CrossRef]
- Bhatia, S.C. (Ed.) 14—Geothermal power generation. In Advanced Renewable Energy Systems; Wood-Head Publishing India: Delhi, India, 2014; pp. 334–388. [Google Scholar]
- Evola, G.; Costanzo, V.; Marletta, L. Exergy Analysis of Energy Systems in Buildings. Buildings 2018, 8, 180. [Google Scholar] [CrossRef] [Green Version]
- Szargut, J.; Morris, D.; Steward, F. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes; Hemisphere Publishing Corporation: New York, NY, USA, 1988. [Google Scholar]
- Vijayaraghavan, S.; Goswami, D.Y. On Evaluating Efficiency of a Combined Power and Cooling Cycle. J. Energy Resour. Technol. 2003, 125, 221–227. [Google Scholar] [CrossRef]
- Baiju, V.; Muraleedharan, C. Exergy Assessment of Single Stage Solar Adsorption Refrigeration System Using ANN. ISRN Mech. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Baiju, V.; Muraleedharan, C. Energy and exergy analysis of solar hybrid adsorption refrigeration system. Int. J. Sustain. Eng. 2013, 6, 289–300. [Google Scholar] [CrossRef]
- Ogueke, N.; Ndeke, C. Exergy based performance analysis of a solid adsorption solar refrigerator. Int. J. Renew. Energy Res. 2014, 4, 363–370. [Google Scholar]
- Cao, N.V.; Duong, X.Q.; Lee, W.S.; Park, M.Y.; Lee, S.S.; Chung, J.D. Exergy Analysis of Advanced Adsorption Cooling Cycles. Entropy 2020, 22, 1082. [Google Scholar] [CrossRef] [PubMed]
- Rezaie, B.; Javan, S.; Mohammadi, V.; Ahmadi, P. Performance Assessment and Optimization of a Combined Cooling, Heating and Power (CCHP) System for Residential Application using Low Grade Heat of an Internal Combustion Engine. Curr. Altern. Energy 2017, 2, 1. [Google Scholar] [CrossRef]
- Cihan, A.; Hacıhafızogˇlu, O.; Kahveci, K. Energy-exergy analysis and modernization suggestions for a combined-cycle power plant. Int. J. Energy Res. 2006, 30, 115–126. [Google Scholar] [CrossRef]
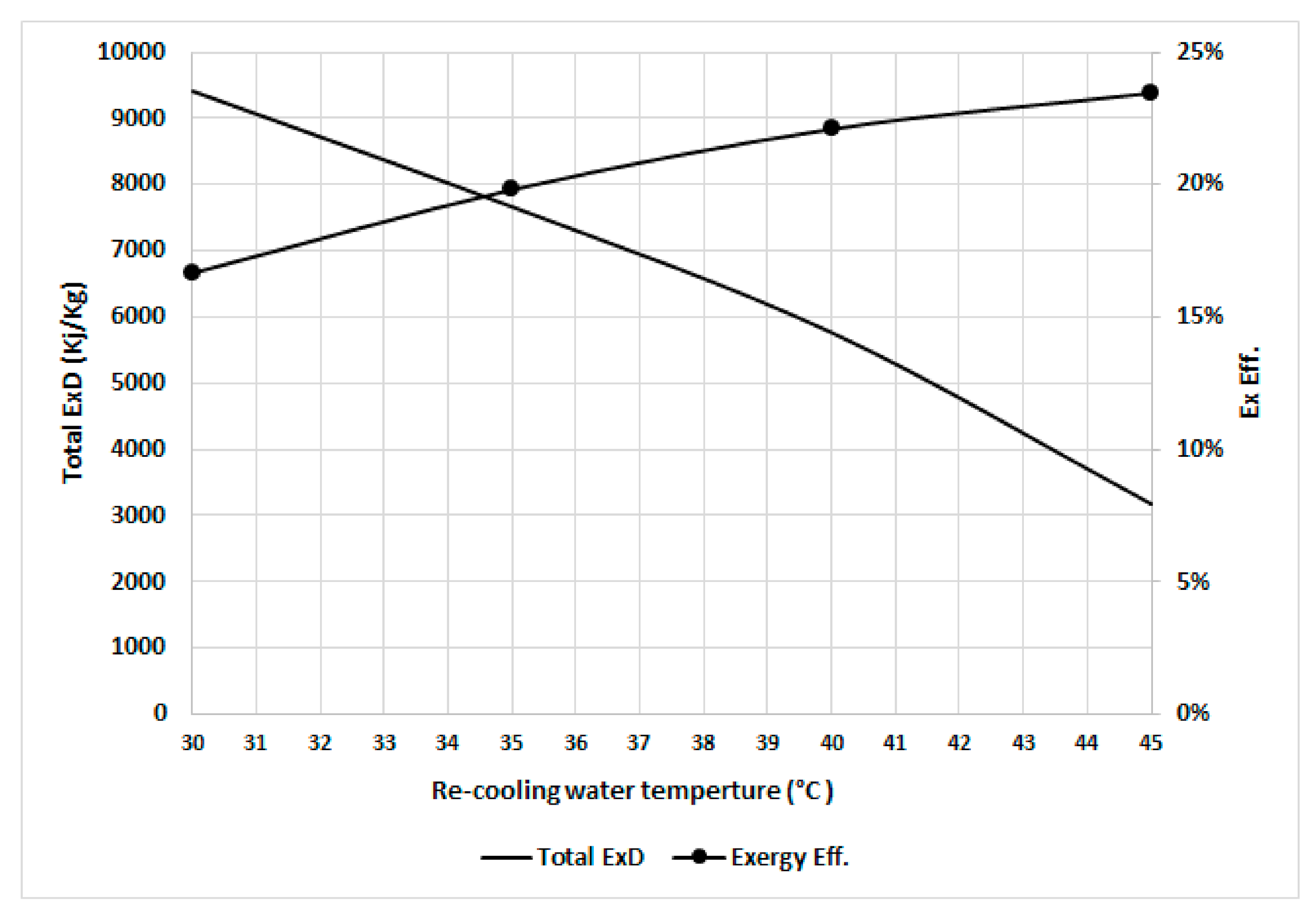
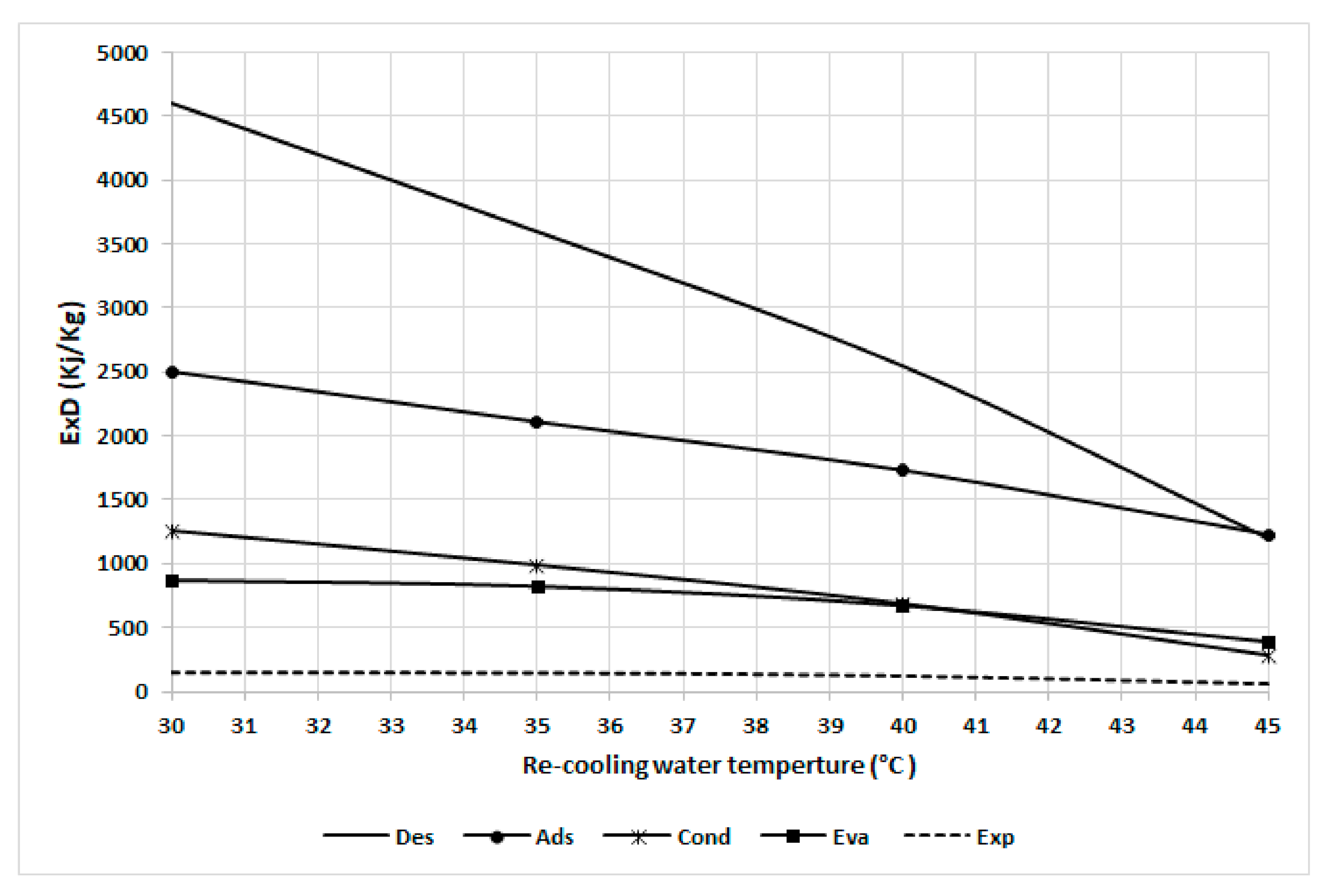
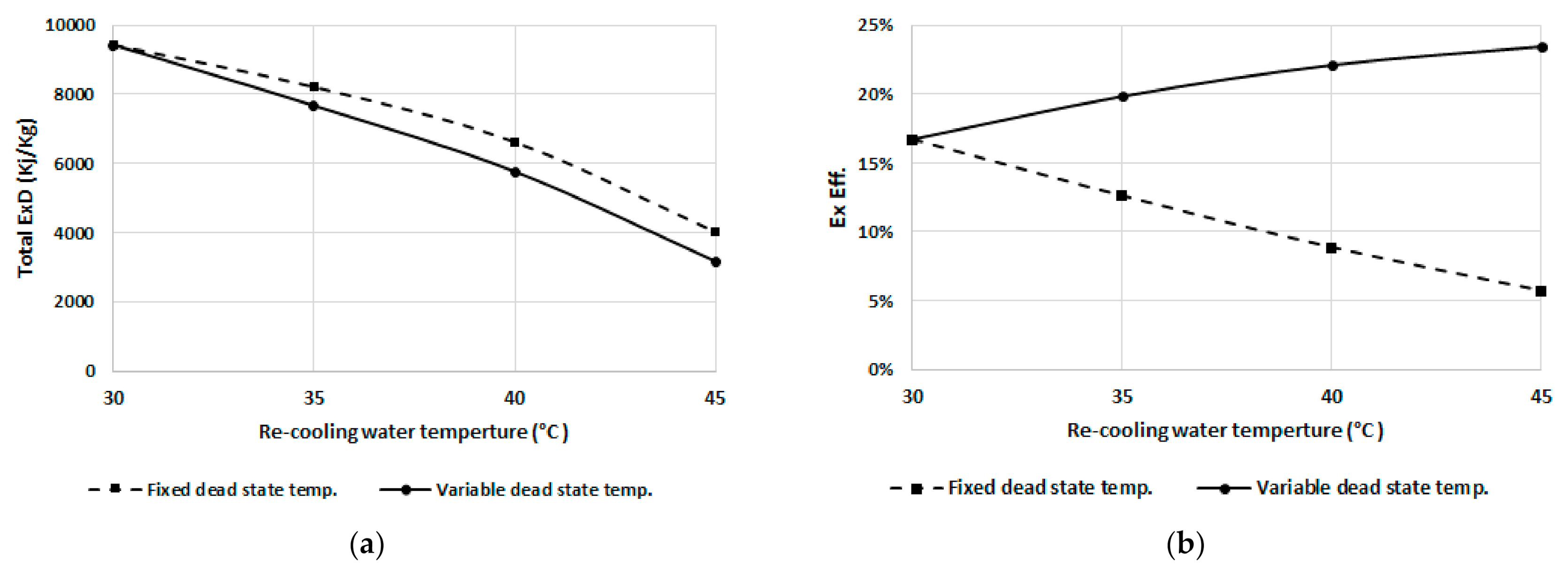
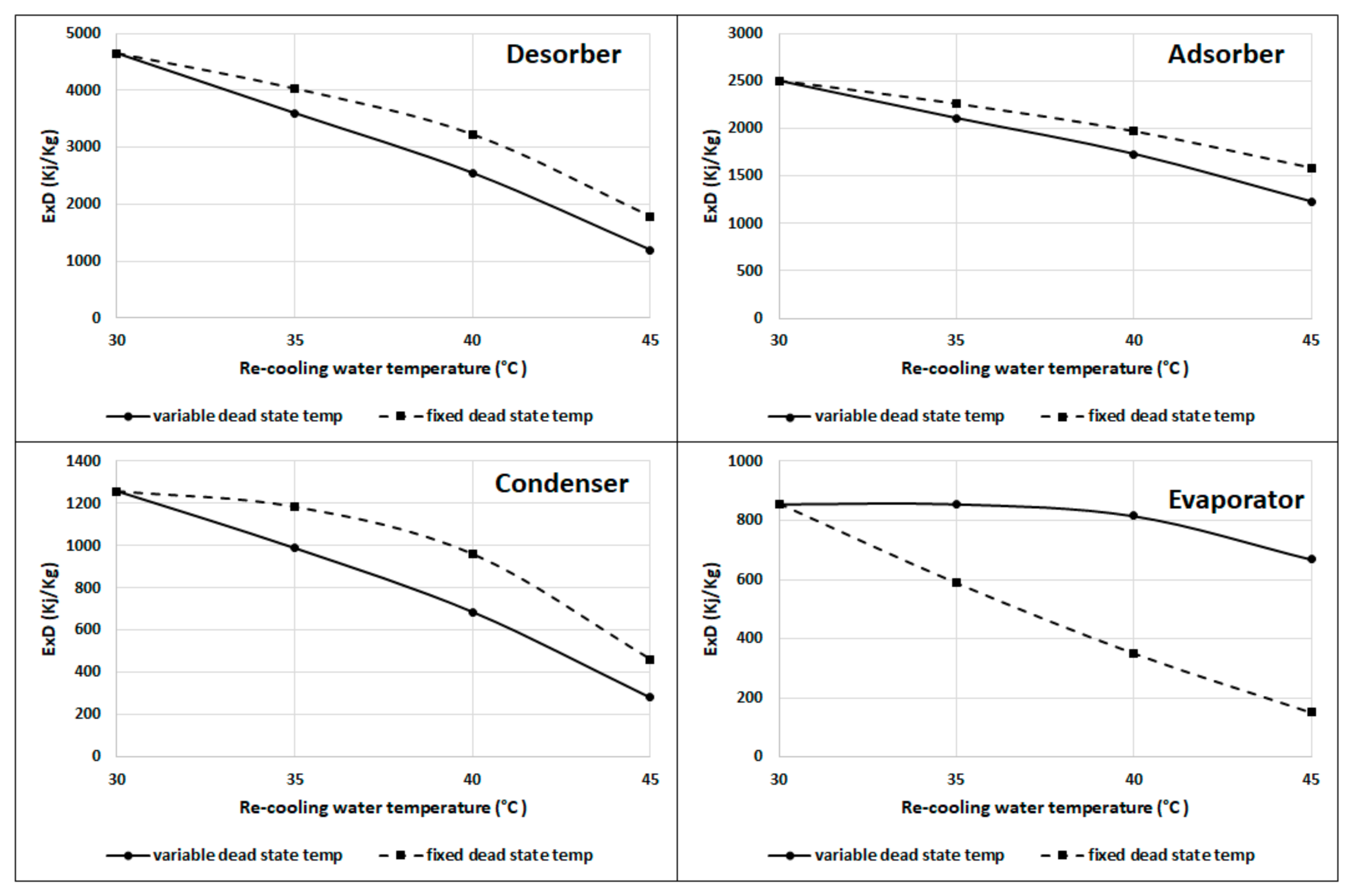
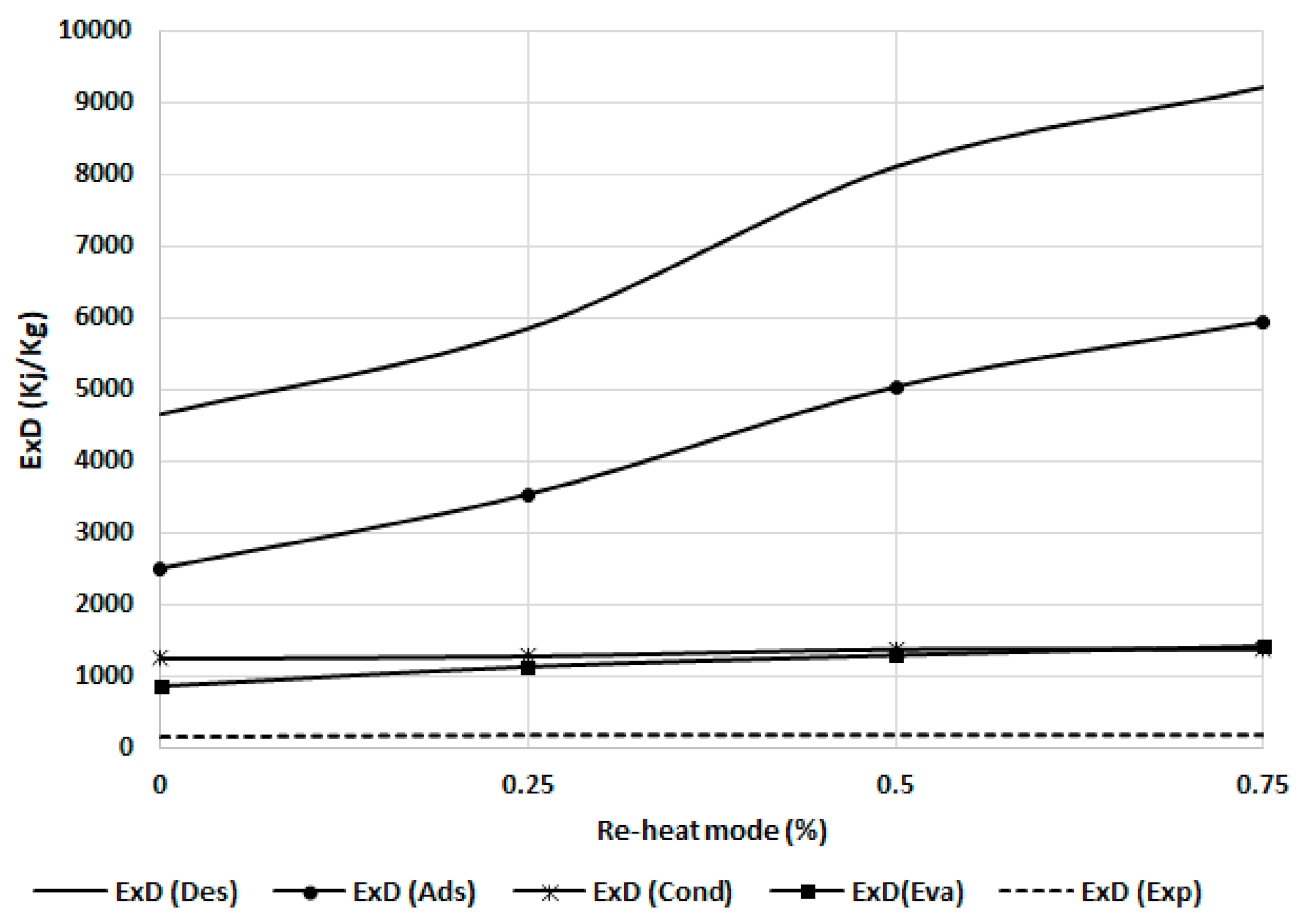
| Variable Dead State Temperature (5 °C Less Than the Recooling Water Temperature) | Fixed Dead State Temperature (25 °C) | |||
|---|---|---|---|---|
| Components | Exergy Destruction | Total Exergy Efficiency | Exergy Destruction | Total Exergy Efficiency |
| Adsorber | Decreasing | Increasing | Decreasing | Decreasing |
| Desorber | Decreasing | Decreasing | ||
| Condenser | Decreasing | Decreasing | ||
| Evaporator | Decreasing | Decreasing | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsarayreh, A.A.; Al-Maaitah, A.; Attarakih, M.; Bart, H.-J. Energy and Exergy Analyses of Adsorption Chiller at Various Recooling-Water and Dead-State Temperatures. Energies 2021, 14, 2172. https://doi.org/10.3390/en14082172
Alsarayreh AA, Al-Maaitah A, Attarakih M, Bart H-J. Energy and Exergy Analyses of Adsorption Chiller at Various Recooling-Water and Dead-State Temperatures. Energies. 2021; 14(8):2172. https://doi.org/10.3390/en14082172
Chicago/Turabian StyleAlsarayreh, Ahmad A., Ayman Al-Maaitah, Menwer Attarakih, and Hans-Jörg Bart. 2021. "Energy and Exergy Analyses of Adsorption Chiller at Various Recooling-Water and Dead-State Temperatures" Energies 14, no. 8: 2172. https://doi.org/10.3390/en14082172
APA StyleAlsarayreh, A. A., Al-Maaitah, A., Attarakih, M., & Bart, H. -J. (2021). Energy and Exergy Analyses of Adsorption Chiller at Various Recooling-Water and Dead-State Temperatures. Energies, 14(8), 2172. https://doi.org/10.3390/en14082172






