Linear Regression Analysis and Techno-Economic Viability of an Air Source Heat Pump Water Heater in a Residence at a University Campus
Abstract
:1. Introduction
2. Objectives
- i.
- To determine the reduction in the annual power, load factor and energy consumption after retrofitting an existing electric boiler with an ASHP unit.
- ii.
- To establish linear correlations of the daily volumes of hot water consumed to the electrical energy consumed by the electric boiler and the ASHP water heater in summer and winter.
- iii.
- To compare the daily volumes of hot water and electrical energy consumed by the electric boiler and the ASHP water heater, for both summer and winter using the Wilcoxon rank sum test.
- iv.
- To determine the annual cost saving and the payback period of the ASHP system.
- v.
- To conduct an ANOVA multiple comparison test to verify if any significant difference existed among the groups for average month-day volume of hot water and the electrical energy consumed by the heating devices during summer and winter.
3. Theory and Calculations
4. Uncertainty Analysis of the Measurements
5. Error Analysis
6. Statistical Tests
6.1. Wilcoxon Rank Sum Test
6.2. Wilcoxon Algorithms
6.3. One-Way ANOVA
- i.
- is an observation in which i represent the observation number and j represents a different group of the predictor variable y.
- ii.
- All are independent.
- iii.
- represents the population mean for the jth group.
- iv.
- is the random error, independent and normally distributed, with zero mean and constant variance, ().
- v.
- The model assumes that the columns of are the constant plus the error component .
6.4. ANOVA Table
7. Materials and Methods
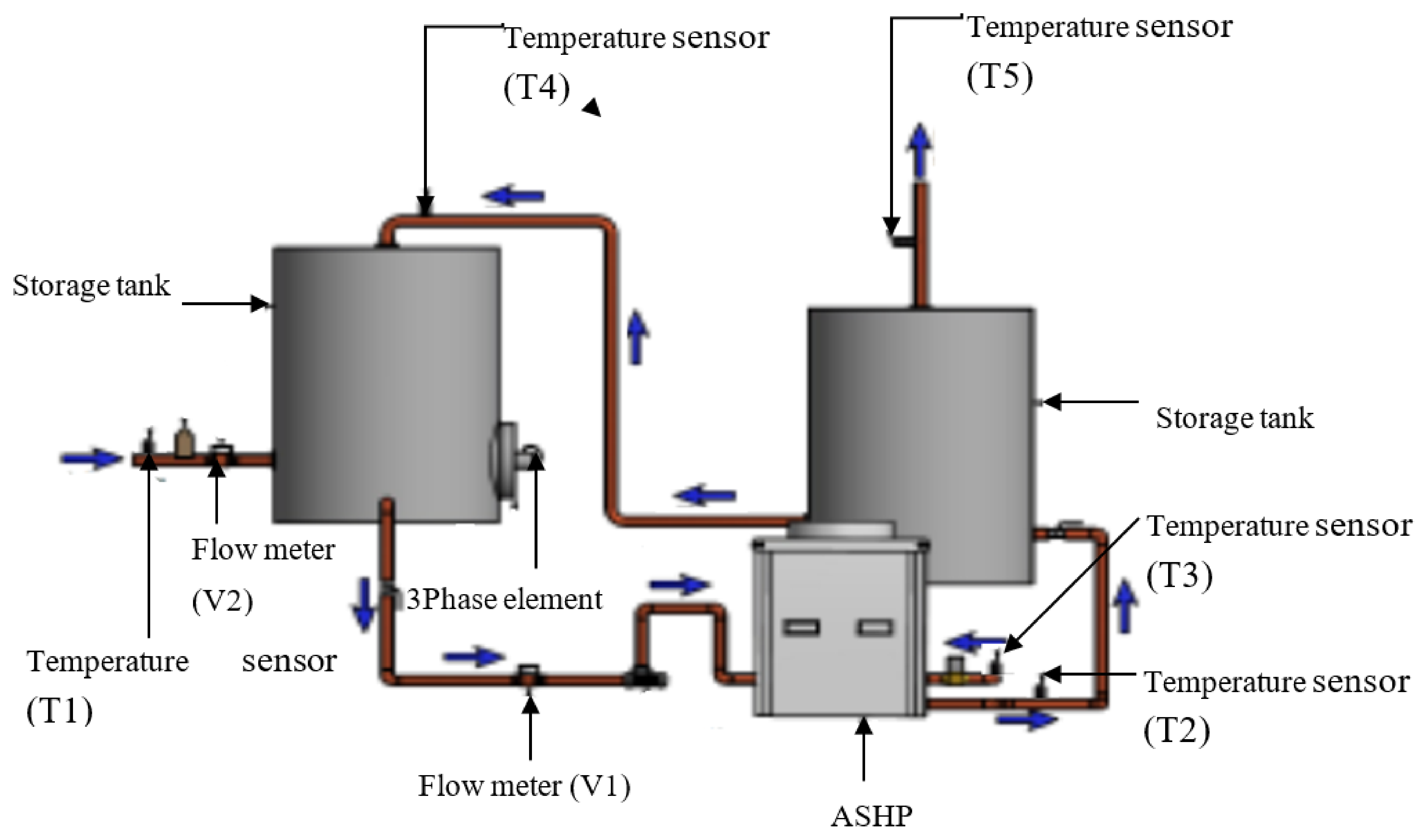
7.1. Materials
7.2. Experimental Setup
- i.
- The electrical energy and the volume of hot water consumed using the electric boiler and the ASHP water heater during the monitoring period.
- ii.
- The derivation of mathematical models for the two hot water devices and the conduction of a techno-economic analysis of the ASHP water heater.
8. Results and Discussion
8.1. Modelling the Daily Electrical Energy Consumed
8.1.1. Modelling the Daily Electrical Energy Consumed during the Summer Period
8.1.2. Modelling the Daily Electrical Energy Consumed during the Winter Period
8.2. Comparison of the Electrical Energy and Volumes Consumed by Both Systems
8.2.1. Comparison of the Daily Volumes and Energy Consumed Using Wilcoxon Rank Sum Test during the Summer Season
8.2.2. Comparison of the Volumes and Energy Consumed Using Wilcoxon Rank Sum Test during the Winter
8.3. Average Month-Day Performance of the Electric Boiler and ASHP Water Heater
- the electrical energy consumed,
- the volume of hot water consumed,
- the load factor,
- the maximum and average power, and
- the COP.
8.4. Monthly Electrical Energy Saving
8.5. Techno-Economic Cost Analysis of the Installed ASHP System
8.6. One-Way ANOVA Test among the Derived Groups Means
- The average month-day electrical energy consumed by the electric boiler during the summer (energy consumed by the boiler in summer),
- The average month-day electrical energy consumed by the ASHP water heater during the summer (energy consumed by the ASHP in summer),
- The average month-day electrical energy consumed by the electric boiler during the winter (energy consumed by the boiler in winter),
- The average month-day electrical energy consumed by the ASHP water heater during the winter (energy consumed by the ASHP in winter).
- The average month-day volume of hot water consumed from the electric boiler during the summer (volume consumed from the boiler in summer),
- The average month-day volume of hot water consumed from the ASHP water heater during the summer (volume consumed from the ASHP in summer),
- The average month-day volume of hot water consumed from the electric boiler during the winter (volume consumed from the boiler in winter),
- The average month-day volume of hot water consumed from the ASHP water heater during the winter (volume consumed from the ASHP in winter).
8.6.1. One-Way ANOVA Test among the Derived Groups’ Means of Electrical Energy Consumed
8.6.2. Multiple Comparison Test among the Derived Group Means of Electrical Energy Consumed
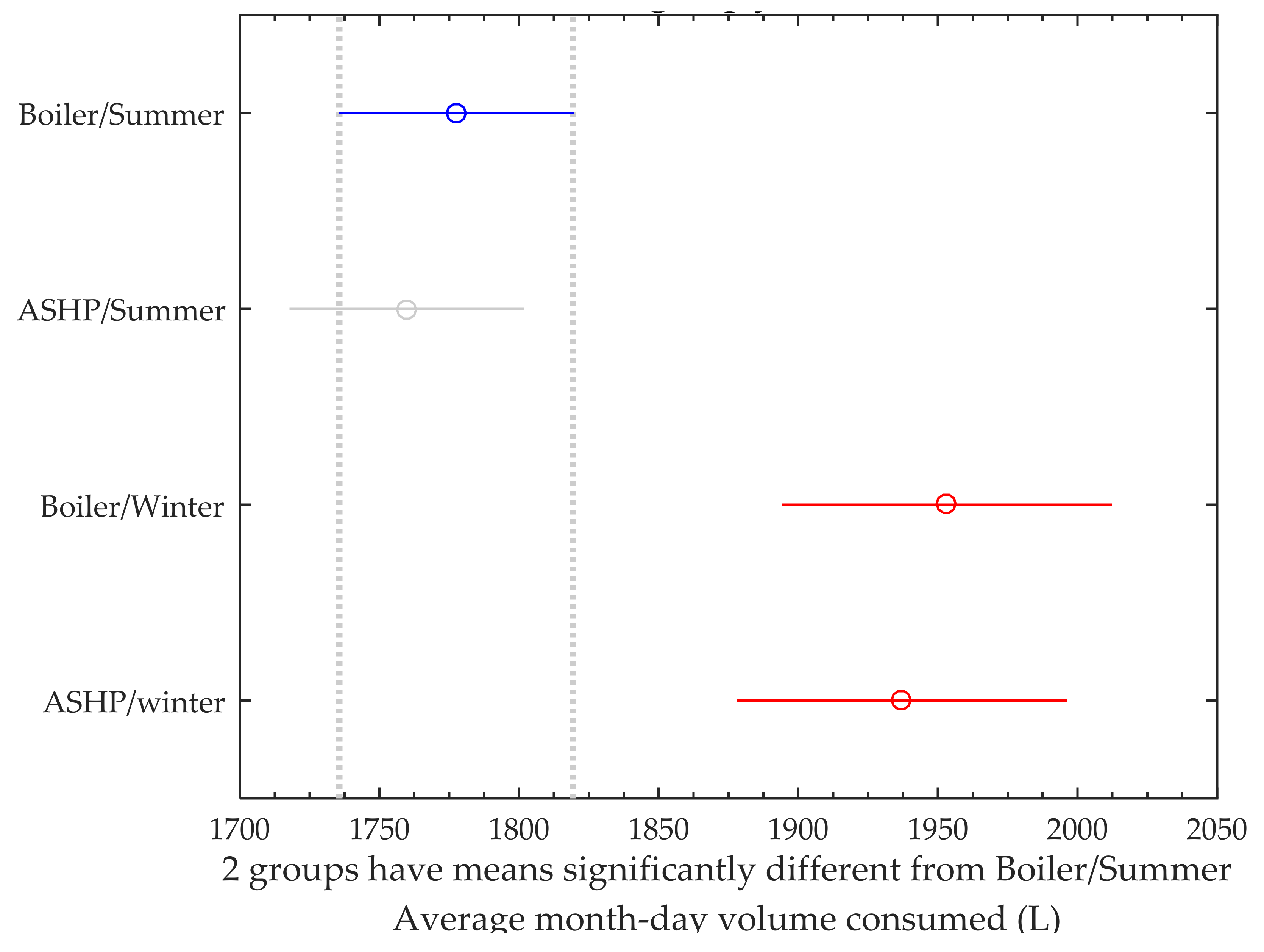
8.6.3. One-Way ANOVA Test among the Groups Means of Volume of Hot Water Consumed
8.6.4. Multiple Comparison Test among the Group Means of Volume of Water Consumed
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P | Average electrical power in kW |
| Pmax | Maximum electrical power consumed in kW |
| t | time taken in h |
| E | Electrical energy consumed in kWh |
| Q | Thermal energy consumed in kWh |
| T1 | Water temperature of the inlet of ASHP in °C |
| T2 | Water temperature of the outlet of ASHP in °C |
| m | Mass of water heated in kg |
| c | Specific heat capacity of water in kJ/kg °C |
| COP | Coefficient of performance |
| LF | Load factor |
| NPV | Net present value of money in Rand (R) |
| FV | Future value of money in Rand (R) |
| r | Annual rate of return in % |
| r2 | Determination coefficient |
| p-value | Probability of the F statistics |
| ANOVA1 | One-way analysis of variance |
| SST | Total sum of square among the group means |
| SSR | Sum of square between the group means |
| SSE | Sum of square within the group means |
| Ebs | Average month-day electrical energy consumed by electric boiler during summer in kWh |
| Eas | Average month-day electrical energy consumed by ASHP water heater during summer in kWh |
| Ebw | Average month-day electrical energy consumed by electric boiler during winter in kWh |
| Vbs | Average month-day volume of hot water consumed from electric boiler during summer in L |
| Vas | Average month-day volume of hot water consumed from ASHP water heater during summer in L |
| Vbw | Average month-day volume of hot water consumed from electric boiler during winter in L |
| Vaw | Average month-day volume of hot water consumed from ASHP water heater during winter in L |
References
- Bott, C.; Dressel, I.; Bayer, P. State-of-technology review of water-based closed seasonal thermal energy storage systems. Renew. Sustain. Energy Rev. 2019, 113, 109241. [Google Scholar] [CrossRef]
- Granade, H.C.; Creyts, J.; Derkach, A.; Farese, P.; Nyquist, S.; Ostrowski, K. Unlocking energy efficiency in the US economy. McKinsey Co. 2009, 1, 1–165. [Google Scholar]
- Willem, H.; Lin, Y.; Lekov, A. Review of energy efficiency and system performance of residential heat pump water heaters. Energy Build. 2017, 143, 191–201. [Google Scholar] [CrossRef] [Green Version]
- Tangwe, S.L. Demonstration of Residential Air Source Heat Pump Water Heaters Performance in South Africa: Systems Monitoring and Modelling. Ph.D. Thesis, University of Sunderland, Tyne and Wear, UK, 2018. [Google Scholar]
- Staffell, I.; Brett, D.; Brandon, N.; Hawkes, A. A review of domestic heat pumps. Energy Environ. Sci. 2012, 5, 9291–9306. [Google Scholar] [CrossRef]
- Morrison, G.L.; Anderson, T.; Behnia, M. Seasonal performance rating of heat pump water heaters. Sol. Energy 2004, 76, 147–152. [Google Scholar] [CrossRef]
- Mohanraj, M.; Belyayev, Y.; Jayaraj, S.; Kaltayev, A. Research and developments on solar assisted compression heat pump systems–A comprehensive review (Part A: Modeling and modifications). Renew. Sustain. Energy Rev. 2018, 83, 90–123. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A. Nonparametric Statistical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Proctor, C.R.; Dai, D.; Edwards, M.A.; Pruden, A. Interactive effects of temperature, organic carbon, and pipe material on microbiota composition and Legionella pneumophila in hot water plumbing systems. Microbiome 2017, 5, 130. [Google Scholar] [CrossRef] [PubMed]
- Simcock, N.; Thomson, H.; Petrova, S.; Bouzarovski, S. (Eds.) Energy Poverty and Vulnerability: A Global Perspective; Routledge: London, UK, 2017. [Google Scholar]
- Shin, H.C.; Park, J.W.; Kim, H.S.; Shin, E.S. Environmental and economic assessment of landfill gas electricity generation in Korea using LEAP model. Energy Policy 2005, 33, 1261–1270. [Google Scholar] [CrossRef]
- Chua, K.J.; Chou, S.K.; Yang, W.M. Advances in heat pump systems: A review. Appl. Energy 2010, 87, 3611–3624. [Google Scholar] [CrossRef]
- Mathioulakis, E.; Panaras, G.; Belessiotis, V. Artificial neural networks for the performance prediction of heat pump hot water heaters. Int. J. Sustain. Energy 2018, 37, 173–192. [Google Scholar] [CrossRef]
- Tangwe, S.; Simon, M.; Meyer, E. Mathematical modeling and simulation application to visualize the performance of retrofit heat pump water heater under first hour heating rating. Renew. Energy 2014, 72, 203–211. [Google Scholar] [CrossRef]
- Park, H.; Nam, K.H.; Jang, G.H.; Kim, M.S. Performance investigation of heat pump–gas fired water heater hybrid system and its economic feasibility study. Energy Build. 2014, 80, 480–489. [Google Scholar] [CrossRef]
- Pritchard, B.A.; Beckman, W.A.; Mitchell, J.W. Heat pump water heaters for restaurant applications. Int. J. Ambient Energy 1991, 12, 59–68. [Google Scholar] [CrossRef]
- Korolija, I.; Zhang, Y.; Marjanovic-Halburd, L.; Hanby, V.I. Regression models for predicting UK office building energy consumption from heating and cooling demands. Energy Build. 2013, 59, 214–227. [Google Scholar] [CrossRef]
- Rezaie, B.; Dincer, I.; Esmailzadeh, E. Energy options for residential buildings assessment. Energy Convers. Manag. 2013, 65, 637–646. [Google Scholar] [CrossRef]
- Available online: http://www.onsetcomp.com (accessed on 27 May 2013).
- Hohne, P.A.; Kusakana, K.; Numbi, B.P. A review of water heating technologies: An application to the South African context. Energy Rep. 2019, 5, 1–19. [Google Scholar] [CrossRef]
- Martinopoulos, G.; Papakostas, K.T.; Papadopoulos, A.M. Comparative analysis of various heating systems for residential buildings in Mediterranean climate. Energy Build. 2016, 124, 79–87. [Google Scholar] [CrossRef]
- Rankin, R.; Rousseau, P.G.; van Eldik, M. Demand side management for commercial buildings using an inline heat pump water heating methodology. Energy Convers. Manag. 2004, 45, 1553–1563. [Google Scholar] [CrossRef]
- Lloyd, C.R.; Kerr, A.S.D. Performance of commercially available solar and heat pump water heaters. Energy Policy 2008, 36, 3807–3813. [Google Scholar] [CrossRef]
- Keinath, C.M.; Garimella, S. An energy and cost comparison of residential water heating technologies. Energy 2017, 128, 626–633. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, Z.; Song, Y.; Yin, X.; Cao, F. Energy, exergy, economic and environmental analysis of refrigerant charge in air source transcritical carbon dioxide heat pump water heater. Energy Convers. Manag. 2020, 223, 113209. [Google Scholar] [CrossRef]
- Tangwe, S.L.; Simon, M. Quantification of the viability of residential air source heat pump water heaters as potential replacement for geysers in South Africa. J. Eng. Des. Technol. 2019, 17, 456–470. [Google Scholar] [CrossRef]
- Kukard, W.C. The Adaptive Predictive Control of an Energy Efficient Central Water Heating System Applied in the South African Commercial Sector. Ph.D. Thesis, North-West University, Vanderbair Park, South Africa, 2016. [Google Scholar]
- Tangwe, S.L.; Simon, M. Development of simplified benchmark models to predict the coefficient of performance of residential air source heat pump water heaters in South Africa. Energy Effic. 2019, 12, 1821–1835. [Google Scholar] [CrossRef]
- De Swardt, C.A.; Meyer, J.P. A performance comparison between an air-source and a ground-source reversible heat pump. Int. J. Energy Res. 2001, 25, 899–910. [Google Scholar] [CrossRef]
- Storesletten, K. Fiscal implications of immigration—A net present value calculation. Scand. J. Econ. 2003, 105, 487–506. [Google Scholar] [CrossRef] [Green Version]
- Tangwe, S.; Manyi-Loh, C. An Economic-Cost Analysis of Commercial Air Source Heat Pump Water Heater in the University Campus. In Proceedings of the AIUE 17th Industrial and Commercial Use of Energy (ICUE) Conference 2019, Cape Town, South Africa, 26 November 2019; ISBN 978-0-6399647-4-4. Available online: https://ssrn.com/abstract=3650487 (accessed on 20 July 2020). [CrossRef]
- Meyer, S.L. Data Analysis for Scientists and Engineers; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Tangwe, S.; Kusakana, K. A statistical methodology to compare the performance of residential air source heat pump water heaters. Int. J. Sustain. Energy 2020, 1–20. [Google Scholar] [CrossRef]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 5th ed.; Chapman & Hall/CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Tangwe, S.; Simon, M.; Meyer, E. March. Quantifying Residential Hot Water Production Savings by Retrofitting Geysers with Air Source Heat Pumps. In Proceedings of the 2015 International Conference on the Domestic Use of Energy (DUE), Cape Town, South Africa, 31 March–1 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 235–241. [Google Scholar]
- Kachelmeier, S.J.; Messier, W.F., Jr. An investigation of the influence of a nonstatistical decision aid on auditor sample size decisions. Account. Rev. 1990, 65, 209–226. [Google Scholar]
- Nahm, F.S. Nonparametric statistical tests for the continuous data: The basic concept and the practical use. Korean J. Anesthesiol. 2016, 69, 8. [Google Scholar] [CrossRef]





| Quantity | Type A Uncertainty | Type B Uncertainty | Combined Uncertainty |
|---|---|---|---|
| Ambient temperature (°C) | ±0.200 | ±0.120 | ±0.233 |
| Relative humidity (%) | ±0.250 | ±0.140 | ±0.286 |
| Water flow rates into inlet of the ASHP unit (L/min) | ±0.010 | ±0.006 | ±0.012 |
| Power consumed by the ASHP system (kW) | ±0.130 | ±0.003 | ±0.130 |
| Inlet water temperature of the ASHP (°C) | ±0.250 | ±0.120 | ±0.277 |
| Outlet water temperature of the ASHP (°C) | ±0.230 | ±0.120 | ±0.259 |
| Average month-day electrical energy consumed (kWh) | ±0.130 | ±0.025 | ±0.132 |
| Average month-day thermal energy gained (kWh) | ±0.190 | ±0.042 | ±0.195 |
| Average month-day COPs | ±0.260 | ±0.203 | ±0.330 |
| Source | Sum Square SS | Degree of Freedom df | Mean Square MS | F-Statistic | p-Value (Prob > F) |
|---|---|---|---|---|---|
| Group (between) | SSR | k − 1 | MSR = SSR/k − 1 | MSR/MSE | P(Fk − 1,N − k) > F |
| Error (within) | SSE | N − k | MSE = SSE/N − k | ||
| Total | SST | N − 1 |
| Materials | Quantity |
|---|---|
| Power meter | 1 |
| Flow meter | 2 |
| Temperature sensors | 5 |
| Ambient temperature and relative humidity sensor | 1 |
| 12 kW, 1000 L electric boiler with an additional 1000 L storage tank | 1 |
| 4.0 kW input ASHP unit | 1 |
| Water filter | 1 |
| Data logger | 1 |
| Waterproof enclosure | 1 |
| Input Parameter | Constants | Constant Symbols | Scaling Constant | Output Parameter | Mathematic Model |
|---|---|---|---|---|---|
| Volumes of water consumed from boiler in summer (Vbs) | Forcing Scaling | A B | −44 0.098 | Electrical energy consumed by boiler in summer (Ebs) | Ebs = A + B (Vbs) Ebs = −51 + 0.10 (Vbs) |
| Volumes of water consumed from ASHP in summer (Vas) | Forcing Scaling | A B | 0.49 0.02 | Electrical energy consumed by ASHP in summer (Eas) | Eas = A + B (Vas) Eas = 0.27 + 0.02 (Vas) |
| Volumes of water consumed from boiler in winter (Vbw) | Forcing Scaling | A B | −331.63 0.243 | Electrical energy consumed by boiler in winter (Ebw) | Ebw = A + B (Vbw) Ebw = −331 + 0.243 (Vbw) |
| Volumes of water consumed from ASHP in winter (Vaw) | Forcing Scaling | A B | 188.75 0.120 | Electrical energy consumed by ASHP in winter (Eaw) | Eaw = A + B (Vaw) Eaw = −188 + 0.12 (Vaw) |
| Month | Device | E/kWh | V/L | LF | Pmax/kW | P/kW | t/h | COP |
|---|---|---|---|---|---|---|---|---|
| January | Boiler | 126.70 | 1740.00 | 0.45 | 12.48 | 12.05 | 10.50 | |
| ASHP | 36.26 | 1700.00 | 0.37 | 4.70 | 4.40 | 8.24 | 3.40 | |
| February | Boiler | 125.40 | 1730.00 | 0.45 | 12.46 | 12.22 | 10.26 | |
| ASHP | 34.63 | 1705.00 | 0.36 | 4.67 | 4.33 | 8.00 | 3.52 | |
| March | Boiler | 127.10 | 1750.00 | 0.46 | 12.47 | 12.11 | 10.50 | |
| ASHP | 35.73 | 1720.00 | 0.37 | 4.67 | 4.41 | 8.10 | 3.46 | |
| April | Boiler | 137.85 | 1900.00 | 0.46 | 12.45 | 12.11 | 11.38 | |
| ASHP | 39.47 | 1885.00 | 0.37 | 4.67 | 4.34 | 9.10 | 3.00 | |
| May | Boiler | 140.10 | 1940.00 | 0.46 | 12.37 | 12.05 | 11.63 | |
| ASHP | 42.30 | 1920.00 | 0.38 | 4.67 | 4.42 | 9.57 | 2.85 | |
| June | Boiler | 134.82 | 1964.00 | 0.47 | 12.39 | 12.19 | 12.12 | |
| ASHP | 40.26 | 1961.00 | 0.35 | 4.67 | 4.19 | 10.18 | 2.88 | |
| July | Boiler | 138.63 | 1955.00 | 0.47 | 12.38 | 12.06 | 11.50 | |
| ASHP | 41.79 | 1930.00 | 0.37 | 4.67 | 4.41 | 9.50 | 2.97 | |
| August | Boiler | 137.85 | 1953.00 | 0.46 | 12.38 | 12.10 | 11.75 | |
| ASHP | 41.45 | 1937.00 | 0.37 | 4.67 | 4.34 | 9.75 | 2.90 | |
| September | Boiler | 138.20 | 1830.00 | 0.46 | 12.46 | 12.30 | 11.24 | |
| ASHP | 35.80 | 1810.00 | 0.37 | 4.67 | 4.42 | 8.10 | 3.12 | |
| October | Boiler | 138.70 | 1835.00 | 0.48 | 12.39 | 12.19 | 11.44 | |
| ASHP | 35.40 | 1830.00 | 0.36 | 4.67 | 4.40 | 8.05 | 3.14 | |
| November | Boiler | 122.58 | 1710.00 | 0.47 | 12.38 | 12.22 | 10.03 | |
| ASHP | 33.24 | 1700.00 | 0.37 | 4.67 | 4.43 | 7.50 | 3.48 | |
| December | Boiler | 122.40 | 1725.00 | 0.46 | 12.38 | 12.23 | 10.00 | |
| ASHP | 33.86 | 1720.00 | 0.37 | 4.67 | 4.44 | 7.63 | 3.39 | |
| Annual- | Boiler | 132.53 | 1836.00 | 0.46 | 12.41 | 12.15 | 11.03 | |
| average | ASHP | 37.52 | 1818.20 | 0.37 | 4.67 | 4.38 | 08.64 | 3.10 |
| Month | Boiler’s Electrical Energy/kWh | ASHP Electrical Energy/kWh | COP of ASHP | Saving /kWh |
|---|---|---|---|---|
| January | 3927.7 | 1124.06 | 3.4 | 2803.64 |
| February | 3511.2 | 969.64 | 3.52 | 2541.56 |
| March | 3940.1 | 1107.63 | 3.46 | 2832.47 |
| April | 4135.5 | 1184.1 | 3 | 2951.4 |
| May | 4343.1 | 1311.3 | 2.85 | 3031.8 |
| June | 4044.6 | 1207.8 | 2.88 | 2836.8 |
| July | 4297.53 | 1295.49 | 2.97 | 3002.04 |
| August | 4273.35 | 1284.95 | 2.9 | 2988.4 |
| September | 4146 | 1074 | 3.12 | 3072 |
| October | 4299.7 | 1097.4 | 3.14 | 3202.3 |
| November | 3677.4 | 997.2 | 3.48 | 2680.2 |
| December | 3794.4 | 1049.66 | 3.39 | 2744.74 |
| Annual total | 48,390.58 | 13,703.23 | 34,687.35 |
| Year | No of Year | Saving /kwh | TARRIF/6.5% Rise Per Year | FV /R | NPV /R | Cost Incurs /R | Cumulative Net Cost Saving/R |
|---|---|---|---|---|---|---|---|
| 2016 | 0.00 | 80,000.00 | 00000.00 | ||||
| 2017 | 1.00 | 34,805.94 | 1.575 | 54,819.36 | 51,473.57 | 0.00 | 54,819.36 |
| 2018 | 2.00 | 34,805.94 | 1.65375 | 57,560.32 | 50,748.59 | 0.00 | 105,568.0 |
| 2019 | 3.00 | 34,805.94 | 1.736438 | 60,438.34 | 50,033.82 | 0.00 | 155,601.8 |
| 2020 | 4.00 | 34,805.94 | 1.823259 | 63,460.26 | 49,329.12 | 1000.00 | 204,930.9 |
| 2021 | 5.00 | 34,805.94 | 1.914422 | 66,633.27 | 48,634.35 | 0.00 | 253,565.2 |
| 2022 | 6.00 | 34,805.94 | 2.010143 | 69,964.93 | 47,949.36 | 0.00 | 301,514.6 |
| 2023 | 7.00 | 34,805.94 | 2.110651 | 73,463.18 | 47,274.01 | 0.00 | 348,788.6 |
| 2024 | 8.00 | 34,805.94 | 2.216183 | 77,136.34 | 46,608.18 | 1000.00 | 395,396.8 |
| 2025 | 9.00 | 34,805.94 | 2.326992 | 80,993.16 | 45,951.73 | 0.00 | 441,348.5 |
| 2026 | 10.00 | 34,805.94 | 2.443342 | 85,042.81 | 45,304.52 | 0.00 | 486,653.0 |
| 2027 | 11.00 | 34,805.94 | 2.565509 | 89,294.95 | 44,666.43 | 0.00 | 531,319.5 |
| 2028 | 12.00 | 34,805.94 | 2.693784 | 93,759.7 | 44,037.32 | 1000.00 | 575,356.8 |
| 2029 | 13.00 | 34,805.94 | 2.828474 | 98,447.69 | 43,417.08 | 0.00 | 618,773.9 |
| 2030 | 14.00 | 34,805.94 | 2.969897 | 103,370.1 | 42,805.57 | 0.00 | 661,579.4 |
| 2031 | 15.00 | 34,805.94 | 3.118392 | 108,538.6 | 42,202.68 | 2000.00 | 703,782.1 |
| Source | Sum Square SS | Degree of Freedom df | Mean Square MS | F-Statistic | p-Value (Prob > F) |
|---|---|---|---|---|---|
| Group (between) | 56,295.8 | 3 | 18,765.3 | 805.66 | 5.12 × 10−21 |
| Error (within) | 465.8 | 20 | 23.3 | ||
| Total | 56,761.6 | 23 |
| Group | Group | Lower Confidence Interval | Estimate | Upper Confidence Interval |
|---|---|---|---|---|
| Energy consumed by boiler in summer | Energy consumed by ASHP in summer | 87.87 | 94.63 | 101.38 |
| Energy consumed by boiler in summer | Energy consumed by boiler in winter | −21.86 | −13.59 | −5.32 |
| Energy consumed by boiler in summer | Energy consumed by ASHP in winter | 77.68 | 85.95 | 94.22 |
| Energy consumed by ASHP in summer | Energy consumed by boiler in winter | −116.49 | −108.22 | −99.95 |
| Energy consumed by ASHP in summer | Energy consumed by ASHP in winter | −16.95 | −8.68 | −0.40 |
| Energy consumed by boiler in winter | Energy consumed by ASHP in winter | 89.99 | 99.54 | 109.09 |
| Source | Sum Square SS | Degree of Freedom df | Mean Square MS | F-Statistic | p-Value (Prob > F) |
|---|---|---|---|---|---|
| Group (between) | 167,817.8 | 3 | 55,939.3 | 16.02 | 1.52 × 10−5 |
| Error (within) | 9845.9 | 20 | 3492.3 | ||
| Total | 237,663.7 | 23 |
| Group | Group | Lower Confidence Interval | Estimate | Upper Confidence Interval |
|---|---|---|---|---|
| Volume consumed from boiler in summer | Volume consumed from ASHP in summer | −64.83 | 17.88 | 100.58 |
| Volume consumed from boiler in summer | Volume consumed from boiler in winter | −276.79 | −175.50 | −74.21 |
| Volume consumed from boiler in summer | Volume consumed from ASHP in winter | −260.79 | −159.50 | −58.21 |
| Volume consumed from ASHP in summer | Volume consumed from boiler in winter | −294.66 | −193.38 | −92.09 |
| Volume consumed from ASHP in summer | Volume consumed from ASHP in winter | −278.66 | −177.38 | −76.09 |
| Volume consumed by boiler in winter | Volume consumed from ASHP in winter | −100.96 | 16.00 | 132.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manyi-Loh, C.E.; Sikhonza, M.; Tangwe, S. Linear Regression Analysis and Techno-Economic Viability of an Air Source Heat Pump Water Heater in a Residence at a University Campus. Energies 2021, 14, 2280. https://doi.org/10.3390/en14082280
Manyi-Loh CE, Sikhonza M, Tangwe S. Linear Regression Analysis and Techno-Economic Viability of an Air Source Heat Pump Water Heater in a Residence at a University Campus. Energies. 2021; 14(8):2280. https://doi.org/10.3390/en14082280
Chicago/Turabian StyleManyi-Loh, Christy E., Mandlenkosi Sikhonza, and Stephen Tangwe. 2021. "Linear Regression Analysis and Techno-Economic Viability of an Air Source Heat Pump Water Heater in a Residence at a University Campus" Energies 14, no. 8: 2280. https://doi.org/10.3390/en14082280





