The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production
Abstract
:1. Introduction
2. Nomenclature
3. Materials and Methods
3.1. Mathematical Model
3.2. Physical Model
3.3. Economic Model
3.3.1. Gas in Place—GIP
3.3.2. Capital Expenditure—CAPEX
3.3.3. Recovery Factor—RF
3.3.4. Investment Recovery Factor—IRF
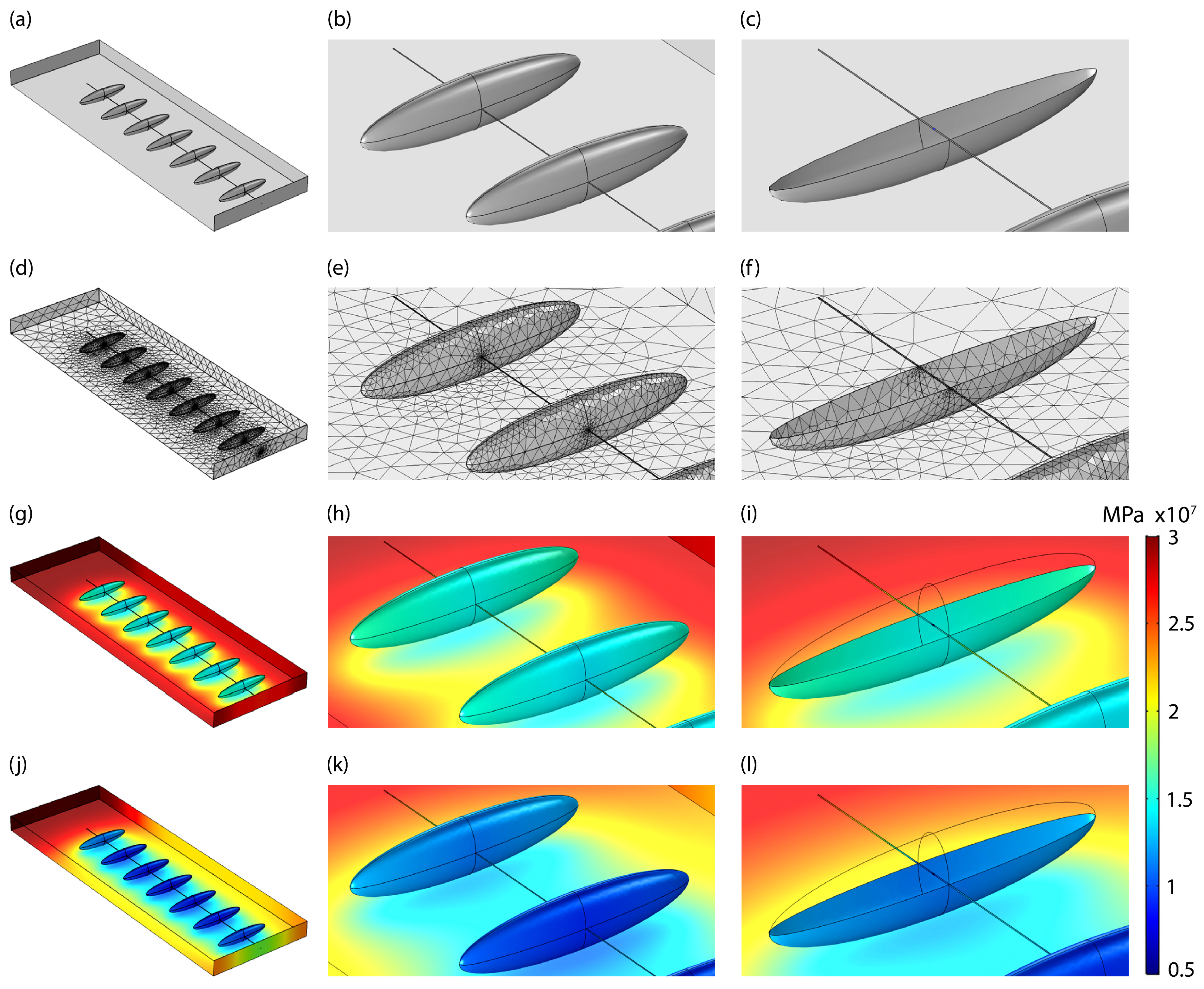
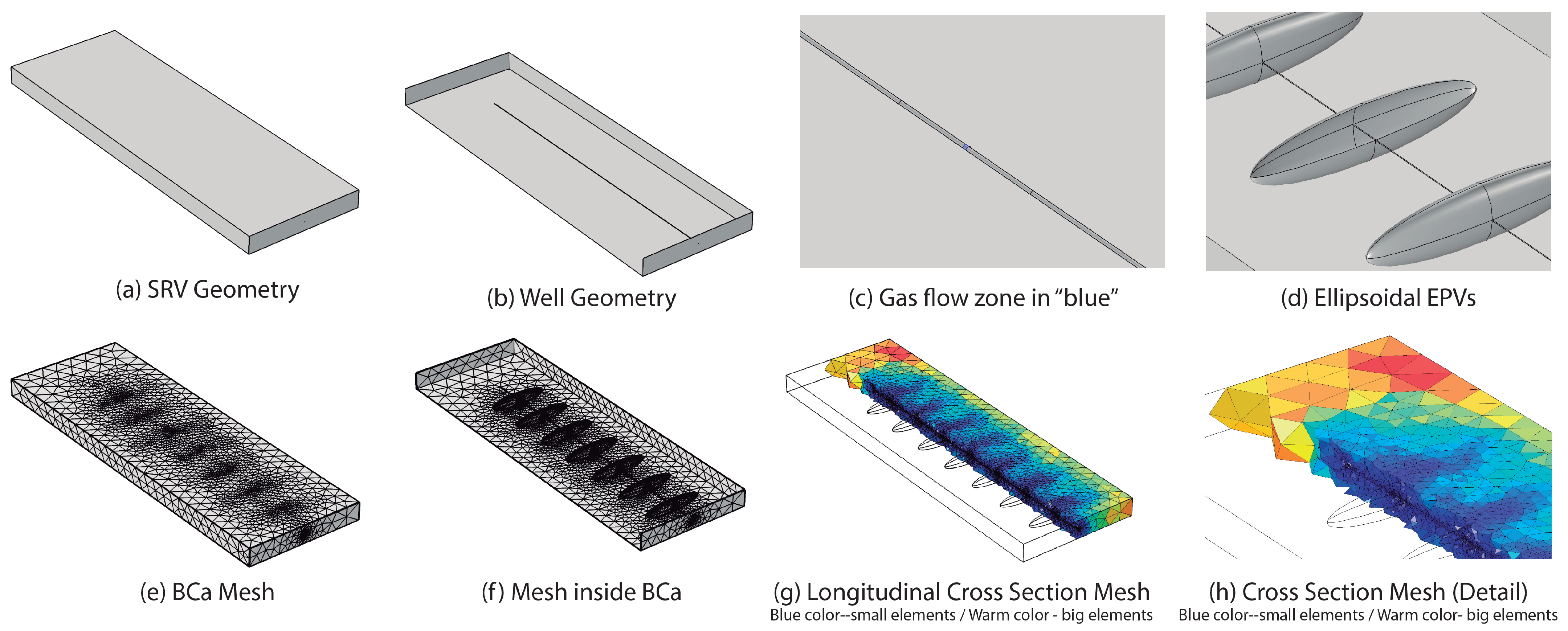
3.4. Numerical Model
- We define SRV geometry according to the dimensions that appear in the Table 2.
- We consider SRV outer contour numerically a no-flow boundary condition.
- We model the horizontal well as a horizontal cylinder. We erase this cylinder volume from the SRV generating an inner no-flow boundary condition. Physically, this no-flow contour corresponds to the placement of a metal casing.
- We generate seven sections in the horizontal well in which the contour is permeable and in which pressure Dirichlet-type condition is imposed (). These seven sections correspond to the points where the projectile launcher pierces the well casing.
- We create seven ellipsoidal volumes (EPVs) of high permeability according to the dimensions that appear in Table 2.
- We mesh the whole BCa with 155,561 tetrahedral element. The quality of the elements ranges from 0.08 to 0.63 on a dimensionless scale with the range 0–1.
- The simulation time is 10 years and the time step is 36.5 days.
3.5. Models Discussion
- The mathematical model is generalist and fully applicable to other shale gas wells. At the technological level, we have included the most relevant phenomena.
- The defined physical model is considered for a specific Base Case with a specific geometry. However, what we seek in this study is to qualitatively characterize the relative importance of the geometry of the EPVs in relation to other parameters (e.g., porosity). For this purpose, the physical model that we have presented is completely valid.
- The economic model is qualitative valid and generalize to other shale gas wells. Its quantitative results are limited by the assumption of the fixed gas price throughout the life of the shale gas well.
- The methodology to develop the 3D numerical model is applicable to any other shale gas well design.
4. Results and Discussion
4.1. Pressure State Analysis
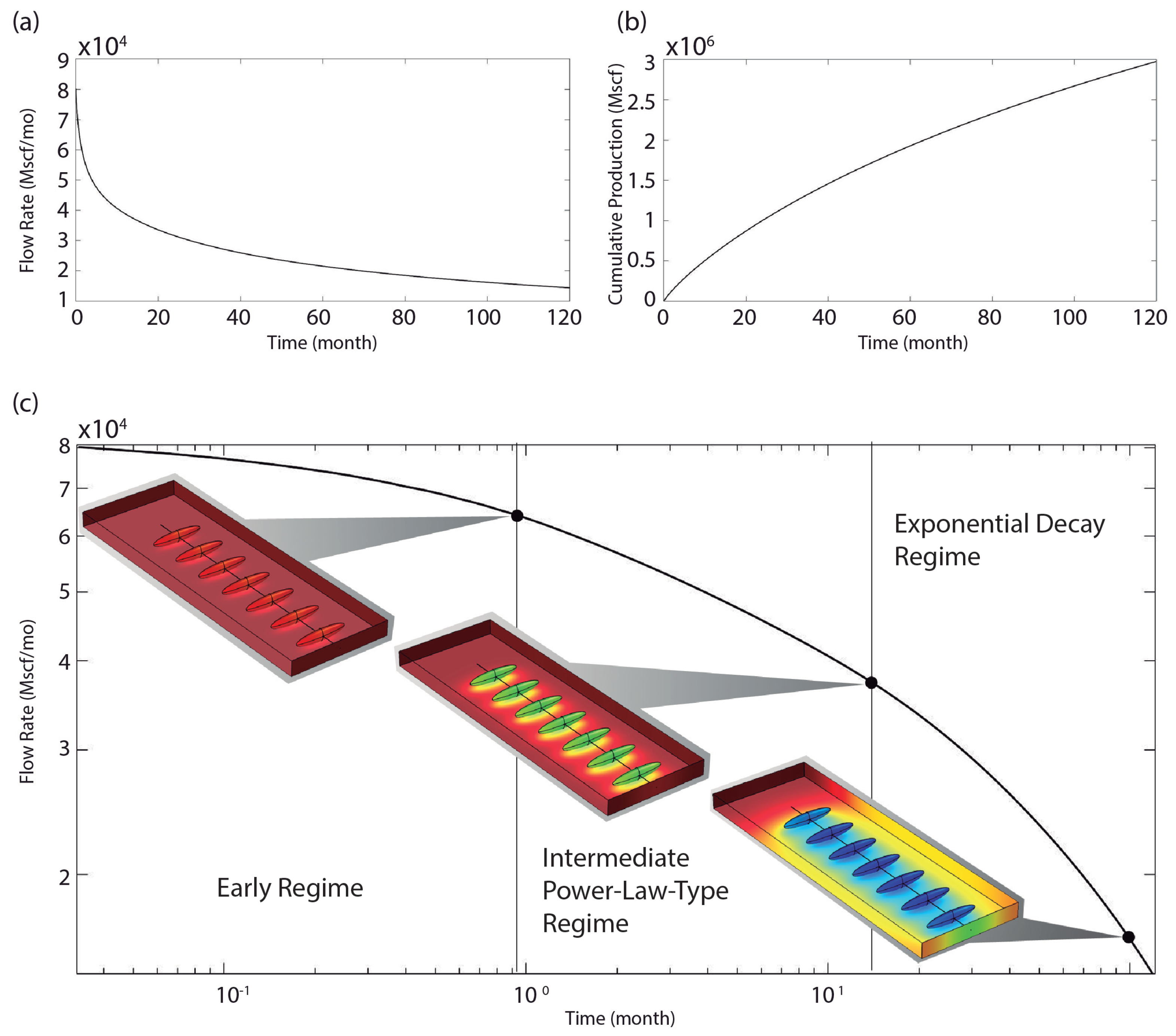
4.2. Methane Production Analysis and Economic Performance
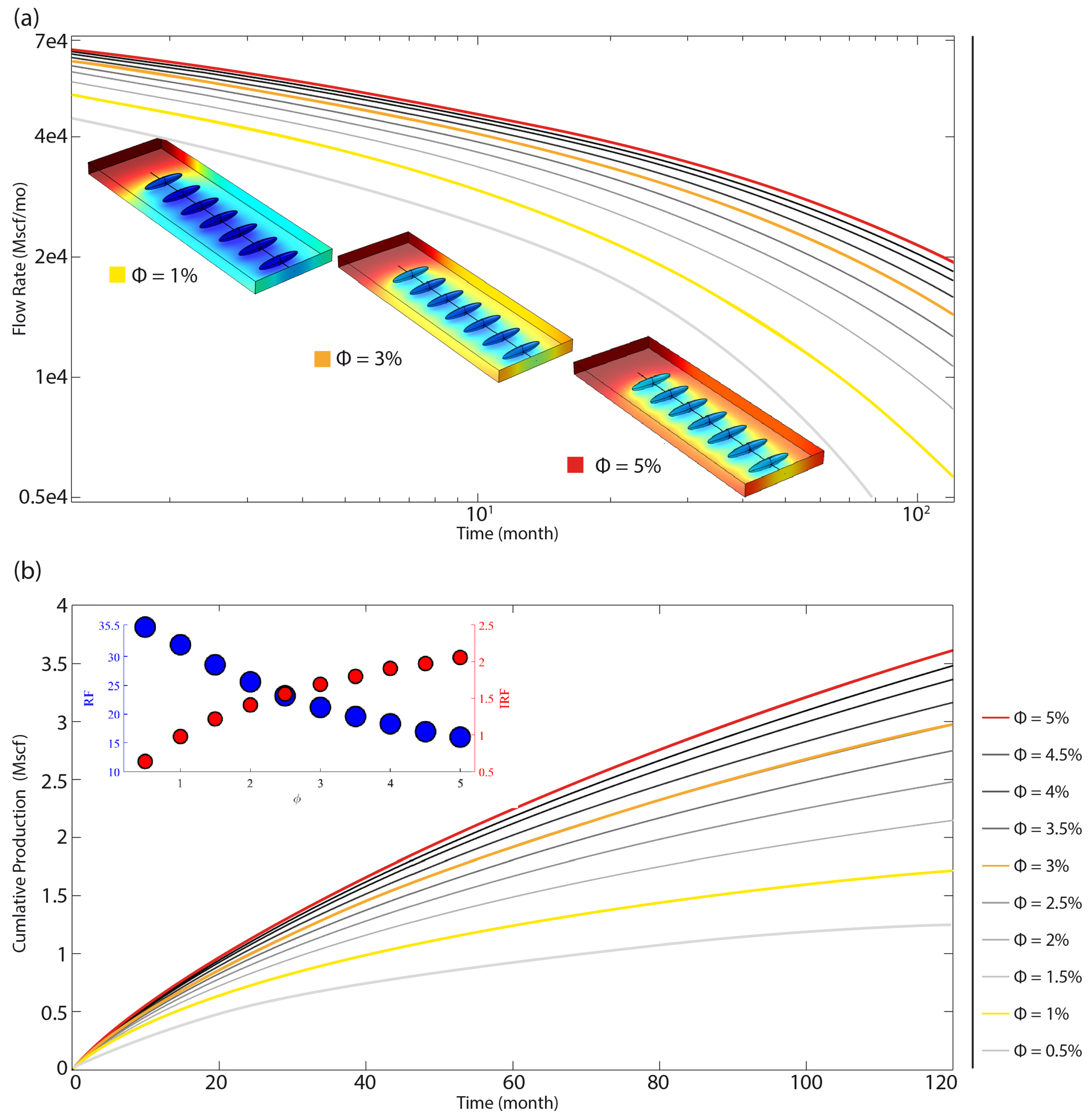
4.3. Economic Sensitivity Analysis, Comparison of the Variation of Porosity, Permeability and Kerogen
4.3.1. Porosity
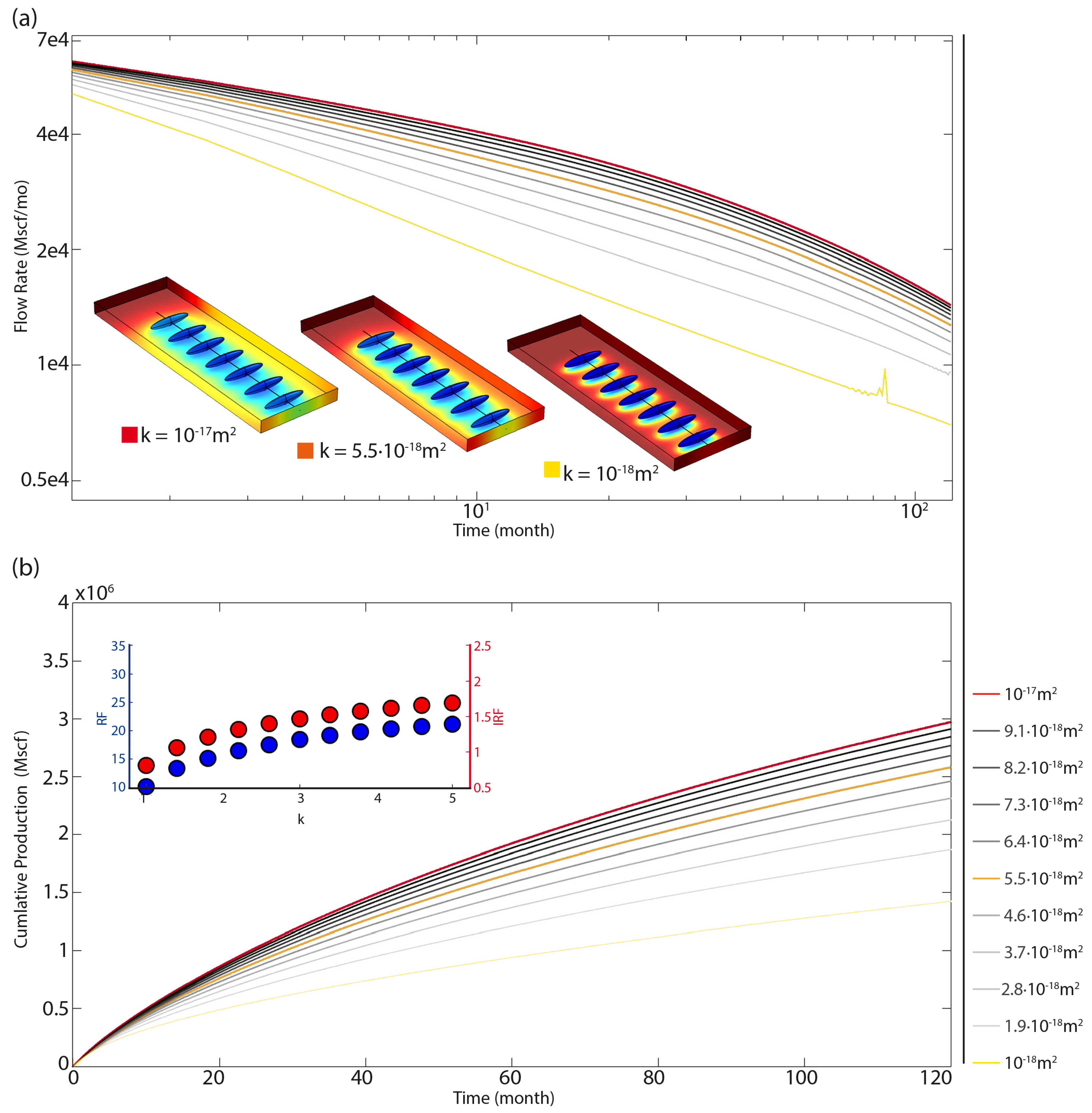
4.3.2. Permeability
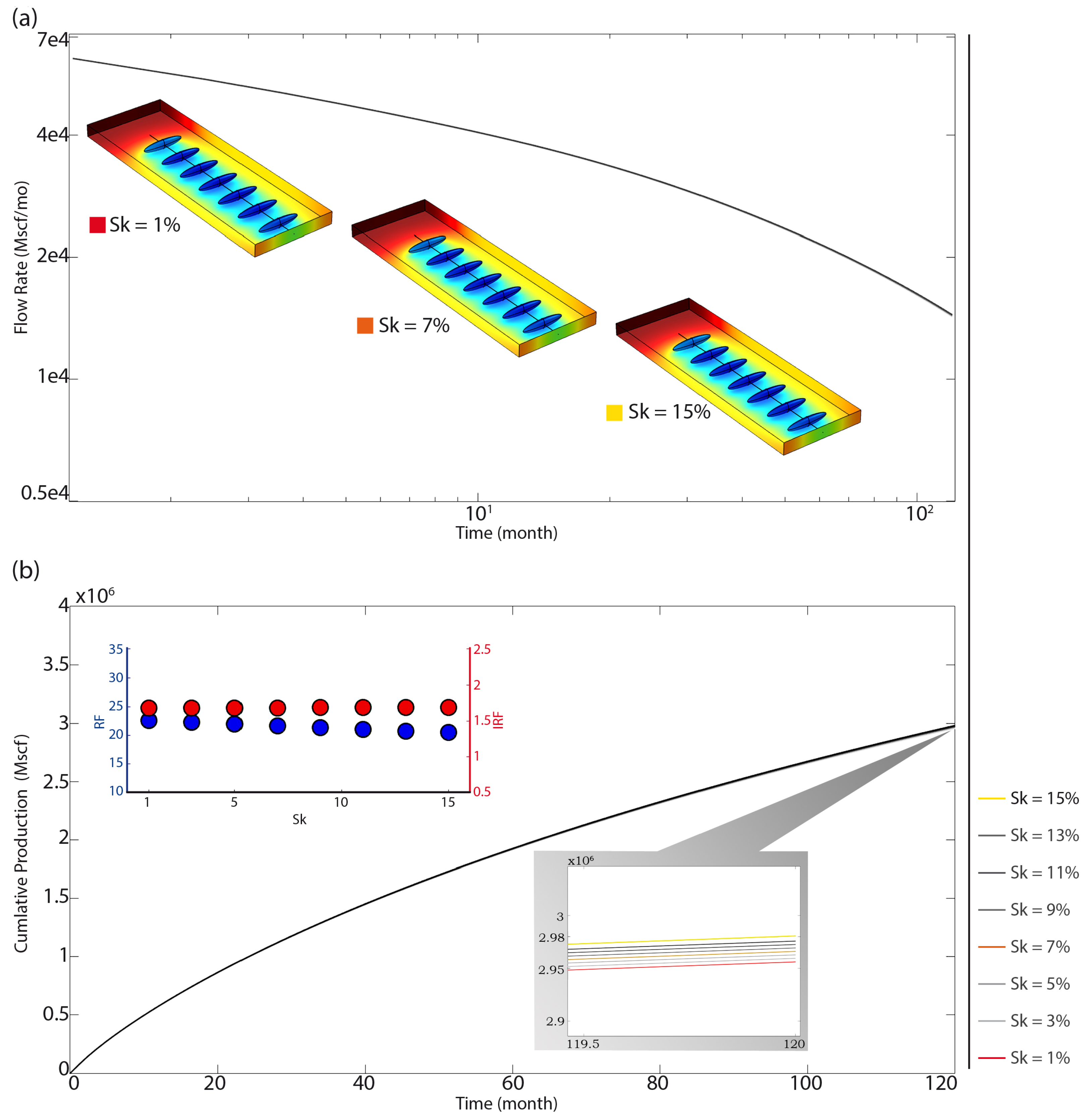
4.3.3. Kerogen Content
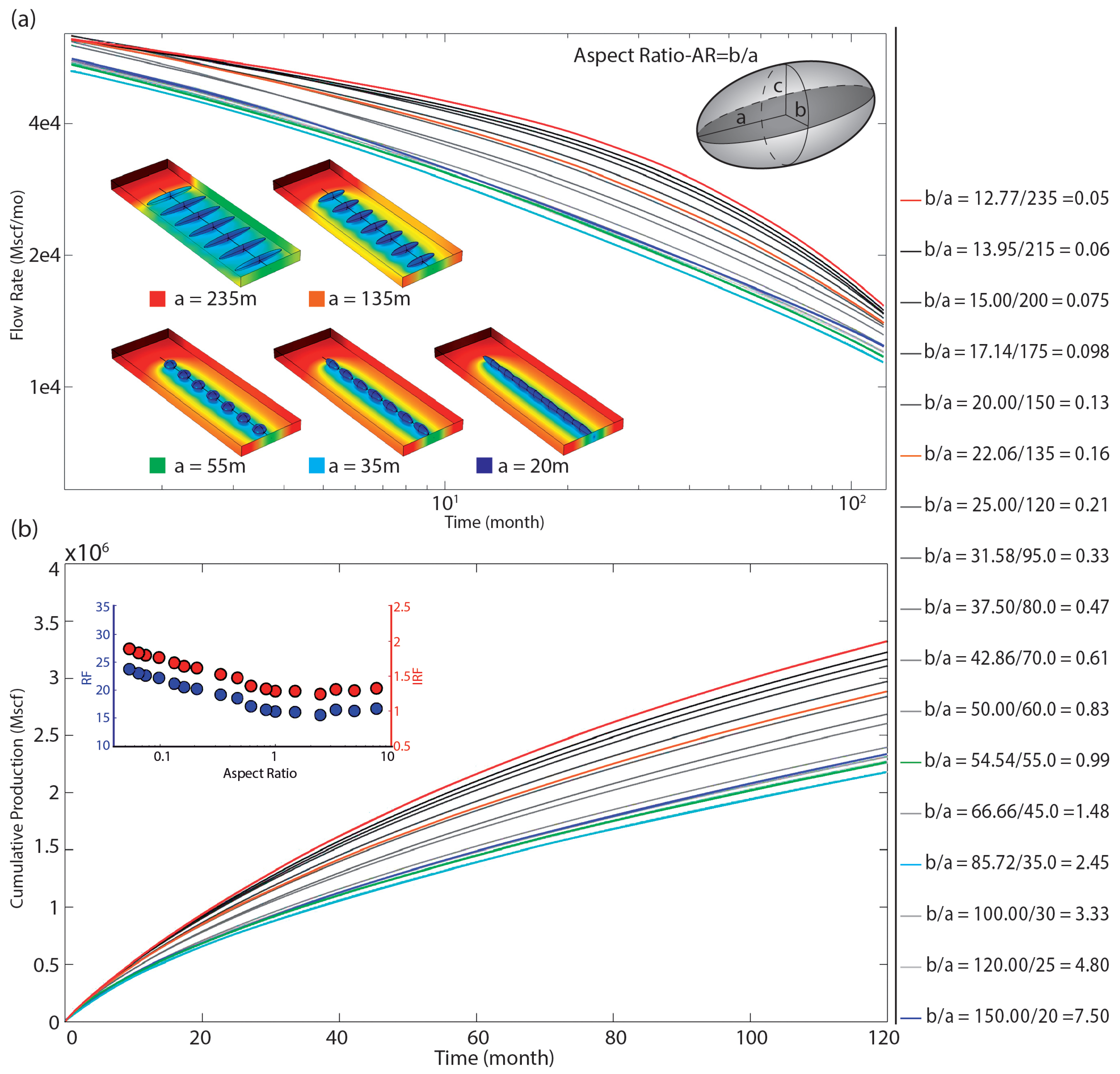
4.4. Impact of the Variation of Fracture Geometry on the Economic Performance of Shale Gas Wells
4.5. Physical Explanation for the Impact of Geometry on the Performance of Shale Gas Wells
- The surface of the fractured ellipsoids. At equal fracturing volume, which in turn is proportional to the volume of injected hydrofracturing fluid, the flatter the ellipsoid the greater its area and the closer to sphericity the ellipsoid the smaller its area. The larger the surface of the EPVs, the more methane is extracted from the formation. Equation (15) defines the surface of an ellipsoidal volume with an error estimated at
- Interference between fractures. This phenomenon occurs when the pressure drop induced by the gas leakage towards the well in each fracture, generates a change in the field pressure that propagates over the entire SRV. By the time the pressure drops in each fracture begin to overlap with each other, interference is said to have been reached. At this time, there is a change in the gas production regime going from a power-law-type regime to an exponential decline, that is, an accelerated decrease in production.
4.6. Geomechanical and Fracture Mechanics Considerations of Shale Gas Play in the EPVs Shape
- Geomechanics. The drilling direction of the well must follow a guideline as parallel as possible to the minor main compression direction. This would be an essential design criterion for achieving flat perpendicular fractures.
- Fracture mechanics. Formations must be as fragile as possible. With equal petrological parameters, the more fragile formations will explode more efficiently, generating a network of fractures that will configure a larger ellipsoidal fractured surface, in addition to generating a higher permeability.
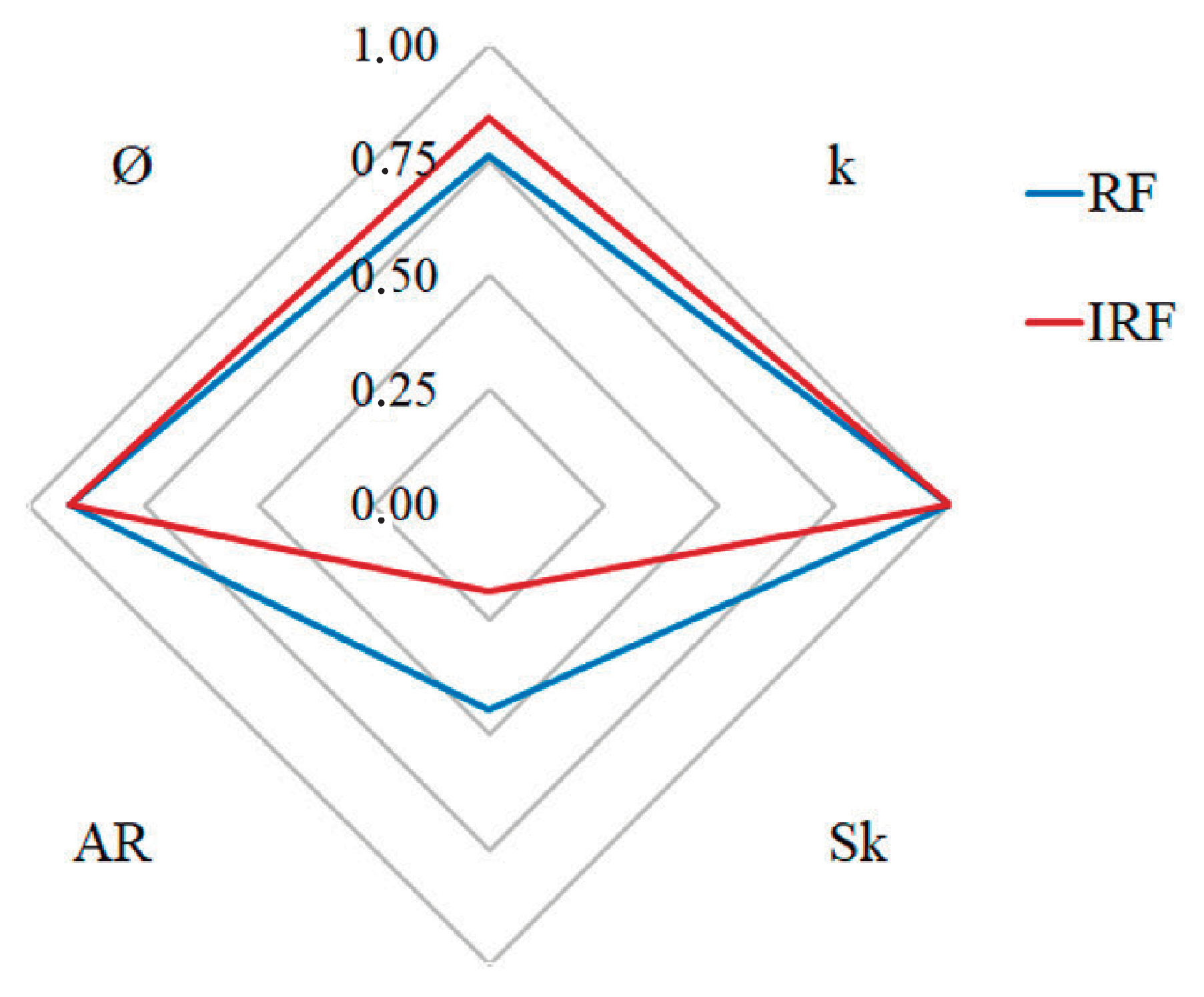
4.7. Comparative Analysis of Results
- ◊ refers to either RF or IRF.
- □ refers to any of the four production parameters: , k, or AR.
- Equation (16) establishes a metric that allows a sensitivity analysis of RF and IRF with respect to the four parameters studied.
- The subscript “f” refers to final and “i” to initial. Thus, the final and initial data of the simulations carried out in each parametric sweep are referenced.
- We adopt linearity hypothesis in the evolution of RF and IRF.
- In Equation (16) the analysis performed is dimensionless. The fundamental idea of this metric is to establish a way to measure how many units RF or IRF vary for each unit that porosity, permeability, kerogen content or Aspect Ratio vary.
- A feature of the equation that may seem unique is the multiplication of the dimensionless coefficients by . The reason for doing this is to have mean sensitivity values that are always equal to or greater than 1.
- The aim of the decimal logarithm is to reduce the size of the magnitudes that would be obtained.
- As a final step, the mean sensitivity metric is normalized to values between 0 and 1.
5. Conclusions
- The geometry of the EPSv has a determining importance in the economic performance of shale gas wells.
- Gas production efficiency and economic performance take different trends depending on whether petrological or production parameters are varied.
- Geomechanics and fracture mechanics emerge as two disciplines of more relevance than expected in the economic performance of shale gas well production.
- We show that improving porosity the RF decreases considerably, while the IRF increases. Economically, a good investment result is achieved, but a lot of GIP is wasted. In shale gas industry a good economic performance is not synonymous with a good use of available resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EPV | Effective Propped Volume |
| EPVs | Effective Propped Volume (plural) |
| SRV | Stimulated Recovery Volume |
| EUR | Estimated Ultimate Recovery |
| O&G | Oil and Gas |
| BCa | Base Case |
| GIP | Gas in Place |
| RF | Recovery Factor |
| IRF | Investment Recovery Factor |
| MMBTU | Million of British Thermal Units |
| Mscf | Thousand standard cubic feet |
| MM | Millions |
| ROI | Return on Investment |
| CAPEX | Capital Expenditure |
| OPEX | Operational Expenditures |
| IP | Initial Production |
| AR | Aspect Ratio |
| DC | Decline Curves |
| Sn | Dimensionless Ellipsoidal Surface |
| RFn | Dimensionless Recovery Factor |
References
- Brockway, P.E.; Owen, A.; Brand-Correa, L.I.; Hardt, L. Estimation of global final-stage energy-return- on-investment for fossil fuels with comparison to renewable energy sources. Nat. Energy 2019, 4, 616–621. [Google Scholar] [CrossRef] [Green Version]
- Wigley, T.M.L. Coal to gas: The influence of methane leakage. Clim. Chang. 2011, 108, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Rodhe, H. A Comparison of the Contribution of Various Gases to the Greenhouse Effect. Science 1990, 248, 1217–1219. [Google Scholar] [CrossRef] [PubMed]
- Weijermars, R. US shale gas production outlook based on well roll-out rate scenarios. Appl. Energy 2014, 124, 283–297. [Google Scholar] [CrossRef]
- Stephenson, M. Shale Gas and Fracking. The Science Behind the Controversy; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Lis, A.; Stankiewicz, P. Framing Shale Gas for Policy-Making in Poland. J. Environ. Pol. Plan. 2016, 19, 53–71. [Google Scholar] [CrossRef]
- Sher, C.; Wu, C. Fracking in China: Community Impacts and Public Support of Shale Gas Development. J. Contemp. China 2018, 27, 626–641. [Google Scholar] [CrossRef]
- Wang, K.; Vredenburg, H.; Wang, T. Liangyong, F. Financial return and energy return on investment analysis of oil sands, shale oil and shale gas operations. J. Clean. Prod. 2019, 223, 826–836. [Google Scholar] [CrossRef]
- Kinnaman, T.C. The economic impact of shale gas extraction: A review of existing studies. Ecol. Econ. 2011, 70, 1243–1249. [Google Scholar] [CrossRef] [Green Version]
- Bowker, K.A. Barnett Shale gas production, Fort Worth Basin: Issues and discussion. AAPG Bull. 2007, 91, 523–533. [Google Scholar] [CrossRef]
- Middleton, R.S.; Gupta, R.; Hyman, J.D.; Viswanathan, H.S. The shale gas revolution: Barriers, sustainability, and emerging opportunities. Appl. Energy 2017, 199, 88–95. [Google Scholar] [CrossRef]
- Shah, M.; Shah, S.; Sircar, A. A comprehensive overview on recent developments in refracturing technique for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 46, 350–364. [Google Scholar] [CrossRef]
- Li, C.; Chau, V.T.; Xie, H.; Bažant, Z.P. Recent advances in mechanics of fracking and new results on 2D simulation of crack branching in anisotropic gas or oil shale. Acta Mech. 2018, 229, 975–992. [Google Scholar] [CrossRef]
- Hattori, G.; Trevelyan, J.; Augarde, C.E. Coombs, W.M.; Aplin, A.C. Numerical Simulation of Fracking in Shale Rocks: Current Stateand Future Approaches. Arch. Comput. Methods Eng. 2017, 24, 281–317. [Google Scholar] [CrossRef]
- Scotchman, I.C. Shale gas and fracking: Exploration for unconventional hydrocarbons. Proc. Geol. Assoc. 2016, 127, 535–551. [Google Scholar] [CrossRef]
- Chau, V.T.; Bažant, Z.P.; Su, Y. Growth model for large branched three-dimensional hydraulic crack system in gas or oil shale. Philos. Trans. R. Soc. A 2016, 374. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, S. Microseismic hydraulic fracture imaging: The path toward optimizing shale gas production. Lead. Edge 2011, 30, 340–346. [Google Scholar] [CrossRef]
- Tafti, T.A. Characterizing Fracture Network in Shale Reservoir Using Microseismic Data. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 21–23 March 2012; pp. 1–16. [Google Scholar] [CrossRef]
- Hou, B.; Chen, M.; Li, Z.; Wang, Y.; Diao, C. Propagation area evaluation of hydraulic fracture networks in shale gas reservoirs. Pet. Explor. Dev. 2014, 41, 833–838. [Google Scholar] [CrossRef]
- Gong, B.; Qin, G.; Towler, B.F. Discrete Modelling of Natural and Hydraulic Fractures in shale-gas reservoir. Presented at the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar] [CrossRef]
- Lai, C.; Rallabandia, B.; Perazzoa, A.; Zhengb, Z.; Smiddyc, S.E.; Stonea, H.A. Foam-driven fracture. Proc. Natl. Acad. Sci. USA 2018, 115, 8082–8086. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Ding, Y.; Cai, B. Modeling Method for Multi-Fractured Horizontal Well in Tight Oil Reservoirs. Proc. Int. Field Explor. Dev. Conf. 2019, 80, 873–883. [Google Scholar]
- Cipolla, C.L.; Lolon, E.P.; Erdle, J.C.; Tathed, V. Modeling Well Performance in Shale-Gas Reservoirs. In Proceedings of the SPE, EAGE Annual Conference, Amsterdam, The Netherlands, 18–21 October 2009; pp. 873–883. [Google Scholar] [CrossRef]
- Satishchandra, D.; Ostebo, P.; Rune, J. Controling Parameters for Shale Gas Production Into a Well-Induced Fracture: A Fracture-Matrix Modelling Aproach. In Proceedings of the SPE, EAGE Annual Conference, Copenhagen, Denmark, 11–14 June 2018. [Google Scholar] [CrossRef]
- Lai, C.-Y.; Zheng, Z.; Dressaire, E.; Wexler, J.; Stone, H.A. Experimental study on penny-shaped fluid-driven cracks in an elastic matrix. Proc. R. Soc. A 2018, 471. [Google Scholar] [CrossRef]
- Silin, D.; Kneafsey, T. Shale Gas: Nanometer-Scale Observations and Well Modelling. J. Can. Pet. Technol. 2012, 464–475. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Lolon, E.P.; Erdle, J.C.; Rubin, B. Reservoir Modeling in Shale-Gas Reservoirs. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 23–25 September 2009; pp. 464–475. [Google Scholar] [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl. Acad. Sci. USA 2013, 110, 304–315. [Google Scholar] [CrossRef] [Green Version]
- Swami, A.S.V.; Javadpour, F. A Numerical Model for Multi-Mechanism Flow in Shale Gas Reservoirs with Application to Laboratory Scale Testing. In Proceedings of the EAGE Annual Conference & Exhibition incorporating SPE Europec, London, UK, 10–13 June 2013. [Google Scholar] [CrossRef]
- Swami, A.S.V. A Pore Scale Gas Flow Model for Shale Gas Reservoir. In Proceedings of the SPE-Americas Unconventional Resources Conference, Pittsburgh, PA, USA, 5–7 June 2012. [Google Scholar] [CrossRef]
- Xu, W. Modelling Gas Transport in Shale Gas Reservoir—Conservation Laws. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar] [CrossRef]
- Cho, Y.; Apaydin, O.G.; Ozkan, E. Pressure-Depent Natural Fracture Permeability in Shales and its Effect on Shale-Gas Well Production. SPE Res. Eval. Eng. 2013, 16, 216–228. [Google Scholar] [CrossRef]
- Singh, H.; Javadpour, F.; Ettehadtavakkol, A.; Darabi, H. Nonempirical Apparent Permeability of Shale. SPE Res. Eval. Eng. 2014, 17, 414–424. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Shale-Gas Permeability and Diffusivity Inferred by Improved Formulation of Relevant Retention and Transport Mechanisms. Transp. Porous Med. 2011, 86, 925–944. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, D.; Li, X. A radial differential pressure decay method with micro-plug samples for determining the apparent permeability of shale matrix. J. Nat. Gas Sci. Eng. 2020, 74. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Bryant, S.L. Gas Permeability of Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar] [CrossRef]
- Davarpanah, A.; Mirshekari, B. Experimental Investigation and Mathematical Modeling of Gas Diffusivity by Carbon Dioxide and Methane Kinetic Adsorption. Ind. Eng. Chem. Res. 2019, 58, 12392–12400. [Google Scholar] [CrossRef]
- Hu, X.; Xie, J.; Cai, W.; Wang, R.; Davarpanah, A. Thermodynamic effects of cycling carbon dioxide injectivity in shale reservoirs. J. Pet. Sci. Eng. 2020, 195, 1–7. [Google Scholar] [CrossRef]
- Soage, M.A. A Numerical Modelling Framework for the Optimization and Economic Analysis of Unconventional Gas Production. Ph.D. Thesis, University of A Coruna, Coruna, Spain, 2021. [Google Scholar]
- Wilson, K.C.; Durlofsky, L.J. Optimization of shale gas field development using direct search tecniques and reduce-physics models. J. Pet. Sci. Eng. 2013, 108, 304–315. [Google Scholar] [CrossRef]
- Wilson, K.C. Optimization of Shale Gas Resource Develoment Usign Reduce-Physics Surrogate Model. Master’s Thesis, Stanford University, Stanford, CA, USA, 2012. [Google Scholar]
- Seales, M.B.; Ertekin, T.; Yilin Wang, J. Recovery Efficiency in Hydraulically Fractured Shale Gas Reservoirs. ASME J. Energy Resour. Technol. 2017, 139, 042901-1–042901-8. [Google Scholar] [CrossRef]
- Han, B.; Bian, X. A hybrid PSO-SVM-based model for determination of oil recovery factor in the low-permeability reservoir. Petroleum 2018, 4, 43–49. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Chen, W.; Abdulraheem, A. Estimation of Oil Recovery Factor for Water Drive Sandy Reservoirs through Applications of Artificial Intelligence. Energies 2019, 12, 3671. [Google Scholar] [CrossRef] [Green Version]
- Clark, A.J. Determination of Recovery Factor in the Bakken Formation, Mountrail County, ND. Presented at the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar] [CrossRef]
- McGlade, C.; Speirs, J.; Sorrell, S. Methods of estimating shale gas resources—Comparison, evaluation and implications. Energy 2013, 59, 116–125. [Google Scholar] [CrossRef] [Green Version]
- COMSOL Multiphysics. Introduction to COMSOL Multiphysics; COMSOL Inc., 2018; Available online: http://www.math.chalmers.se/~torbjrn/M3/IntroductionToCOMSOLMultiphysics.pdf (accessed on 9 March 2021).
- Freeman, C.M.; Moridis, G.; IIk, D.; Blasingame, T.A. A Numerical Study of Performance for Tight Gas and Shale Gas Reservoir Systems. J. Pet. Sci. Eng. 2013, 108, 22–39. [Google Scholar] [CrossRef]
- Song, H.; Yu, M.; Zhu, W.; Wu, P.; Lou, Y.; Wang, Y.; Killough, J. Numerical investigation of gas flow rate in shale gas reservoirs with nanoporous media. Int. J. Heat Mass Transf. 2015, 80, 626–635. [Google Scholar] [CrossRef]
- Ikewun, P.; Ahmadi, M. Production Optimization and Forecasting of Shale Gas Wells Using Simulation Methods and Decline Curve Analysis. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 21–23 March 2012. [Google Scholar] [CrossRef] [Green Version]
- Shabro, V.; Torres-Verdin, C.; Javadpour, F. Numerical Simulation of Shale-Gas Production: From Pore-Scale Modeling of Slip-Flow, Knudsen Diffusion, and Langmuir Desorption to Reservoir Modeling of Compressible Fluid. Presented at the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. [Google Scholar] [CrossRef] [Green Version]
- Stueck, H.; Houseknecht, D.; Franke, D.; Gautier, D.; Bahr, A.; Ladage, S. Shale-Gas Assessment: Comparison of Gas-In-Place Versus Performance-Based Approaches. Nat. Resour. Res. 2016, 25, 315–329. [Google Scholar] [CrossRef]
- Lee, D.S.; Herman, J.D.; Elsworth, D.; Kim, H.T. A Critical Evaluation of Unconventional Gas Recovery from the Marcellus Shale, Northeastern United States. KSCE J. Civ. Eng. 2011, 15, 679–687. [Google Scholar] [CrossRef]
- Askenazi, A.; Biscayart, P.; Cáneva, M. Analogía entre la Formación Vaca Muerta y Shale Gas/Oil Plays de EEUU. SPE Argent. Sect. Young Prof. Commit. 2013. [Google Scholar]
- Vandenbroucke, M.; Largeau, C. Kerogen origin, evolution and structure. Org. Geochem. 2007, 38, 719–833. [Google Scholar] [CrossRef]
- Cheng, Y.; Jiang, S.; Zhang, D.; Liu, C. An adsorbed gas estimation model for shale gas reservoirs via statistical learning. Appl. Energy 2017, 197, 327–341. [Google Scholar] [CrossRef] [Green Version]


| Variable | Meaning | Value |
|---|---|---|
| SRV | Stimulated Reservoir Vol. | 1.800 m × 600 m × 90 m |
| EPV | Effective Propped Volume | 300 m × 40 m × 70 m |
| well length | - | 1.500 m |
| pressure gas | (30–5 MPa) | |
| initial reservoir pressure | 30 MPa | |
| bottom hole pressure | 5 MPa | |
| gas compressibility | ||
| Langmuir isotherm slope | - | |
| porosity | 3% | |
| methane density at normal conditions | ||
| kerogen density | 1250 | |
| kerogen relative volume | ||
| Langmuir isotherm | - | |
| Langmuir volume | ||
| Langmuir pressure | 3 MPa | |
| main fracture permeability | ||
| SRV permeability | ||
| methane viscosity | ||
| M | molar gas of methane | |
| Z | compresibility factor | |
| R | universal gas constant | |
| T | absolute temperature | 373 K |
| q | methane flux | Mscf/month |
| total simulation time | 10 year (s) | |
| initial time simulation | 0 s | |
| volume of the SRV | - | |
| normal vector to contour | - | |
| n.c. | normal conditions | - |
| k | AR | |||
|---|---|---|---|---|
| 0.76 | 1.00 | 0.44 | 0.91 | |
| 0.84 | 1.00 | 0.19 | 0.91 |
| Abbreviation | Meaning | Units |
|---|---|---|
| EPV | Effective Propped Volume | m3 |
| SRV | Stimulated Recovery Volume | m3 |
| Mscf | Thousand of standard cubic feet | - |
| MMscf | Million of standard cubic feet | - |
| Bscf | Billion standard cubic feet | - |
| EUR | Estimated Ultimate Recovery | Mscf (Thousand of standard cubic feet) |
| O&G | Oil and Gas | - |
| BCa | Base Case | - |
| GIP | Gas in Place | Mscf (Thousand of standard cubic feet) |
| RF | Recovery Factor | Dimensionless |
| IRF | Investment Recovery Factor | Dimensionless |
| MMBTU | Million of British Thermal Units | - |
| ROI | Return on Investment | Dimensionless |
| CAPEX | Capital Expenditure | USD ($) |
| OPEX | Operational Expenditures | USD ($) |
| IP | Initial Production | Mscf/mo (Thousand of standard cubic feet per month) |
| Aspect Ratio | AR | Dimensionless |
| Sn | Dimensionless Ellipsoidal Surface | Dimensionless |
| RFn | Dimensionless Recovery Factor | Dimensionless |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soage, A.; Juanes, R.; Colominas, I.; Cueto-Felgueroso, L. The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production. Energies 2021, 14, 2475. https://doi.org/10.3390/en14092475
Soage A, Juanes R, Colominas I, Cueto-Felgueroso L. The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production. Energies. 2021; 14(9):2475. https://doi.org/10.3390/en14092475
Chicago/Turabian StyleSoage, Andres, Ruben Juanes, Ignasi Colominas, and Luis Cueto-Felgueroso. 2021. "The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production" Energies 14, no. 9: 2475. https://doi.org/10.3390/en14092475
APA StyleSoage, A., Juanes, R., Colominas, I., & Cueto-Felgueroso, L. (2021). The Impact of the Geometry of the Effective Propped Volume on the Economic Performance of Shale Gas Well Production. Energies, 14(9), 2475. https://doi.org/10.3390/en14092475







