Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues
Abstract
:1. Introduction
2. The Voltage Control Problem
2.1. Objectives and Means for Voltage Control
- Generation curtailment during low demand: voltage along the distribution feeder is limited by reducing the injection of active power; however, if the electric power is generated from renewable energy sources, this method causes a reduced exploitation of the available source and, then, is neither efficient nor environmentally desirable;
- Energy storage: by controlling the charging and discharging of the distributed Energy Storage system (ESS), the voltage fluctuation along the DN can be reduced;
- Power electronic converters at DER sites: the converters that interface DERs to the network can be used to control the active and reactive power absorption/injection so as to regulate the voltage;
- Load management: shifting or curtailing/increasing the energy demand by customers can help to support the voltage.
- minimizing the total reactive power exchange;
- optimizing, from the economical point of view, the reactive power exchange with the transmission network through the substation;
- minimizing the active power curtailment for renewable energy generators;
- minimizing active power losses of the distribution system;
- maximizing the DER active power output;
- minimizing the voltage deviations from their rated values.
2.2. Centralized and Decentralized Control Architectures
2.3. Hierarchical Decomposition
3. Decentralized Primary Voltage Control
3.1. System Model
3.2. Controller Design
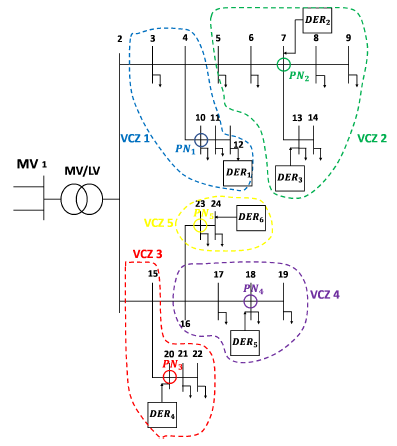
3.3. Case Study
4. Decentralized Secondary Voltage Control
4.1. Decentralized Coordinated Control Techniques
4.2. Classification of the Optimization Methods
- Stochastic methods,
- deterministic or classical methods,
- artificial intelligence or heuristic methods.
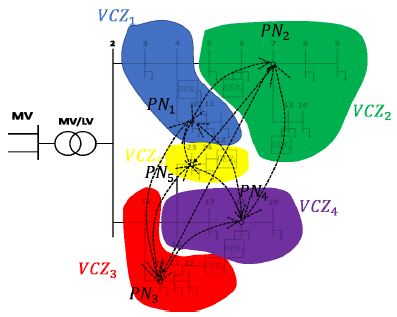
4.3. Decomposition-Based Techniques
- The sensitivity analysis is performed, and the voltage change of each node caused by single DER output is obtained;
- The values of the sensitivity coefficients are used to calculate the electrical distances of each node with all the other nodes of the network;
- Initially, each node is considered to form a single VCZ and is ordered in a matrix of N x N dimensions, where N is the total number of nodes present in the network;
- After having established the final number of clusters, let us say h, the hierarchical clustering algorithm is run over the matrix of electrical distances, to group the nodes in h VCZs;
- Within each VCZ, the corresponding PN is identified as the node with the overall minimum distance, that is obtained as the sum of this node distances to all other nodes present in that VCZ: indicates the set of PNs, .
- -
- ADMM: it is a popular algorithm for its remarkable effectiveness in minimizing objectives with linearly separable structures. It guarantees global convergence for linearly constrained quadratic problems to the optimal solution [119];
- -
- -
- The linear modeling is applied to the nonlinear power flow equations;
- -
- the OPF is rewritten for a grid partitioned into h VCZs;
- -
- additional variables are introduced;
- -
- the MMs is applied to solve the dual problem working on the Augmented Lagrangian function;
- -
- the decomposition method is applied to achieve the decentralized solution.
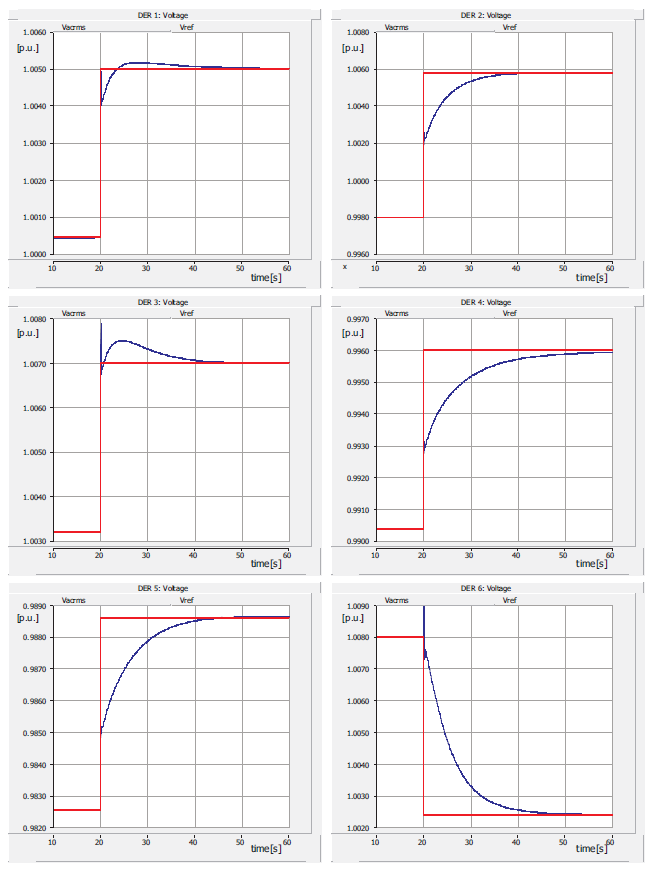
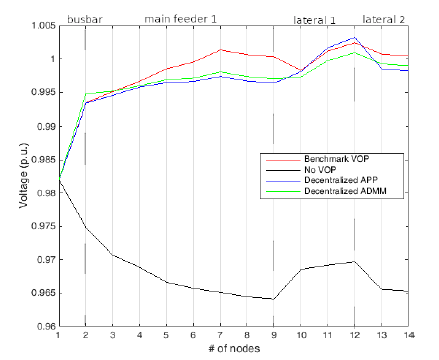
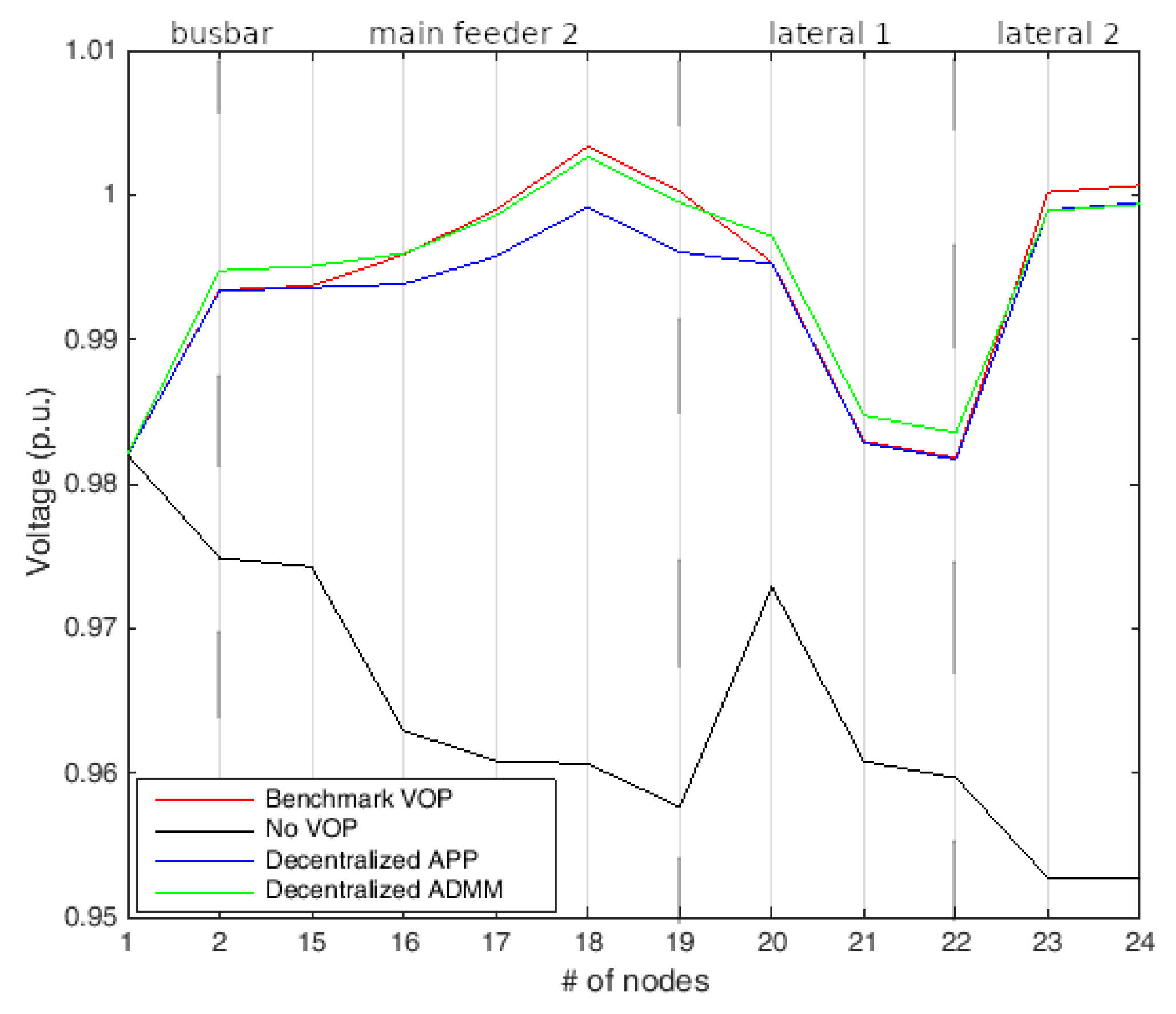
4.4. Case Study
5. Open Issues and Future Challenges
- Robust stability conditions, that have been recalled in the paper, guarantee system stability in spite of the changes of the operating conditions of DN and DERs. These conditions provided by MIMO control system theory are sufficient conditions, that can result to be too stringent so as to limit the performance of the control system in terms of dynamic response. Moreover, the larger the number of DERs, the more stringent the robust stability conditions usually become. Eventually, the presence of an integral action in the local voltage controllers is usually required because it guarantees a null regulation error at steady-state; on the other hand, some sufficient robust stability conditions cannot be fulfilled in the case of a voltage regulator with integral action.
- Alternative to the MIMO frequency-domain approach, the state-space modeling can be adopted. In this way, the robust stability can be verified directly on the closed-loop system representation, and consequently, it is not over-stringent. Moreover, the adoption of state-observers and state-feedback control laws can significantly improve the performance of the control system in terms of dynamic response. The main drawback of the state-space approach is that the design problem is more complex and its dimension is very large, especially in the presence of a large number of DERs.
- Many DERs can contribute to voltage support by varying both active and reactive power injections. Generally speaking, reactive power variations are obtained by acting on the only VSC interfacing the DER to the DN, whereas active power variations impact on the DER system, including loads, generation, and storage, and are economically valuable. Consequently, the priority action of the local voltage controller must be on reactive power; in the case that reactive power is not enough, the controller should also act on active power, accounting for its economical value. This issue has been tackled by switching the control action but this approach introduces non-linearities in the control system and can cause limit cycles or instability.
- The data exchange can be asynchronous, whereas the decomposition based techniques assume a synchronous data exchange among VCZs. Asynchronous data exchange may result in reduced communication overhead and simplified protocols, but introduces convergence problems in the algorithms.
- The communication system should be included in the performance analysis of the decentralized secondary voltage control, also accounting for communication delay and failures, as well as for corrupt data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| ADMM | Alternating Direction Method of Multipliers |
| APP | Auxiliary Problem Principle |
| C.C. | Central Control |
| CCM | Current Control Mode |
| DER | Distributed Energy Resource |
| DG | Distributed Generation |
| DN | Distribution Network |
| DSO | Distribution System Operator |
| ESS | Energy Storage System |
| EU | European Union |
| LP | Linear Programming |
| LV | Low Voltage |
| MAS | Multi-Agent System |
| MG | Micro Grid |
| MIMO | Multiple Input Multiple Output |
| MM | Method of Multipliers |
| MV | Medium Voltage |
| OLTC | ON-Load Tal Changer |
| PC | Primary Control |
| PCC | Point of Common Coupling |
| PCPM | Predictor-Corrector Proximal Multiplier method |
| PF | Power Flow |
| PI | Proportional Integral |
| PLL | Phase-Locked Loop |
| PN | Pilot Node |
| SC | Switched Capacitor |
| SGA | Smart Grid Area |
| SVR | Step Voltage Regulator |
| SVS | Static VAR System |
| TSO | Transmission System Operator |
| VCZ | Voltage Control Zone |
| VSC | Voltage Source Converter |
| Symbols | |
| The variation of the squared voltage at the i-th node | |
| Matrix infinity norm | |
| Reference current component along the d axis | |
| Reference current component along the q axis | |
| The matrix composed of vectors | |
| The sensitivity matrix of the nodal voltages at the PNs to the active powers injected by DERs | |
| The sensitivity matrix of the nodal voltages at the PNs to the reactive powers injected by DERs | |
| The matrix of transfer functions representing the DER k | |
| Block diagonal matrix composed of | |
| h | Number of VCZs |
| K | number of DERs connected to the DN |
| N | numbero of nodes in the DN |
| The active power injected by the DER connected at the k-th node of the grid | |
| Plant matrix transfer function | |
| Diagonal matrix obtained as | |
| The reactive power injected by the DER connected at the k-th node of the grid | |
| Spectral radius of a matrix | |
| Vector of the two sensitivity coefficients relating the variations of the squared voltage amplitude at node i to the variations of the active and reactive powers injected by the DER k | |
| The vector of inputs composed of the current reference signals and | |
| V | The K vector of the squared voltages at the network nodes to which DERs are connected |
| The value of V in the initial operating point | |
| The squared voltage of the ith network node | |
| The reference value of the nodal voltage amplitude | |
| The initial squared voltage amplitude for the h-th PN | |
| The diagonal matrix of the closed-loop transfer functions | |
| The set of pilot nodes |
References
- Quezada, V.H.M.; Abbad, J.R.; Roman, T.G.S. Assessment of energy distribution losses for increasing penetration of distributed generation. IEEE Trans. Power Syst. 2006, 21, 533–540. [Google Scholar] [CrossRef]
- Lopes, J.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef] [Green Version]
- Chiradeja, P.; Ramakumar, R. An approach to quantify the technical benefits of distributed generation. IEEE Trans. Energy Convers. 2004, 19, 764–773. [Google Scholar] [CrossRef]
- Tsikalakis, A.; Hatziargyriou, N. Environmental benefits of distributed generation with and without emissions trading. Energy Policy 2007, 35, 3395–3409. [Google Scholar] [CrossRef]
- Gil, H.A.; Joos, G. Models for Quantifying the Economic Benefits of Distributed Generation. IEEE Trans. Power Syst. 2008, 23, 327–335. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Hossain, M.J.; Pota, H.R. Voltage Variation on Distribution Networks With Distributed Generation: Worst Case Scenario. IEEE Syst. J. 2014, 8, 1096–1103. [Google Scholar] [CrossRef]
- Zahedi, A. Maximizing solar PV energy penetration using energy storage technology. Renew. Sustain. Energy Rev. 2011, 15, 866–870. [Google Scholar] [CrossRef]
- Zahedi, A. A review on feed-in tariff in Australia, what it is now and what it should be. Renew. Sustain. Energy Rev. 2010, 14, 3252–3255. [Google Scholar] [CrossRef]
- Gonzalez, C.; Ramirez, R.; Villafafila, R.; Sumper, A.; Boix, O.; Chindris, M. Assess the Impact of Photovoltaic Generation Systems on Low-Voltage Network: Software Analysis Tool Development. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar] [CrossRef]
- El-khattam, W.; Sidhu, T.S. Resolving the impact of distributed renewable generation on directional overcurrent relay coordination: A case study. IET Renew. Power Gener. 2009, 3, 415–425. [Google Scholar] [CrossRef]
- Jiayi, H.; Chuanwen, J.; Rong, X. Huang Jiayi and Jiang Chuanwen and Xu Rong A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Eltigani, D.; Masri, S. Challenges of integrating renewable energy sources to smart grids: A review. Renew. Sustain. Energy Rev. 2015, 52, 770–780. [Google Scholar] [CrossRef]
- McDermott, T.E.; Dugan, R.C. Distributed Generation Impact on Reliability and Power Quality Indices. In Proceedings of the 2002 Rural Electric Power Conference. Papers Presented at the 46th Annual Conference (Cat. No. 02CH37360), Colorado Springs, CO, USA, 5–7 May 2002; p. D3-1. [Google Scholar] [CrossRef]
- Khadem, S.K.; Basu, M.; Conlon, M. Power Quality in Grid Connected Renewable Energy Systems: Role of Custom Power Devices. Renew. Energy Power Qual. J. 2010, 1, 878–881. [Google Scholar] [CrossRef] [Green Version]
- Pathak, A.; Sharma, M.; Bundele, M. A critical review of voltage and reactive power management of wind farms. Renew. Sustain. Energy Rev. 2015, 51, 460–471. [Google Scholar] [CrossRef]
- Kow, K.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K. A review on performance of artificial intelligence and conventional method in mitigating PV grid-tied related power quality events. Renew. Sustain. Energy Rev. 2016, 56, 334–346. [Google Scholar] [CrossRef]
- Ruiz-Romero, S.; Colmenar-Santos, A.; Mur-Pérez, F.; López-Rey, Á. Integration of distributed generation in the power distribution network: The need for smart grid control systems, communication and equipment for a smart city—Use cases. Renew. Sustain. Energy Rev. 2014, 38, 223–234. [Google Scholar] [CrossRef]
- Varela, J.; Hatziargyriou, N.; Puglisi, L.J.; Bissel, G.; Abart, A.; Rossi, M.; Priewasser, R. The Best of IGREENGrid Practices: A Distribution Network’s Contribution to Resiliency. IEEE Power Energy Mag. 2015, 13, 81–89. [Google Scholar] [CrossRef]
- Antoniadu-Plytaria, K.; Kouveliotis-Lysikatos, I.; Georgilakis, P.; Hatziargyriou, N. Distributed and Decentralized Voltage Control of smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Mahmud, N.; Zahedi, A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation. Renew. Sustain. Energy Rev. 2016, 64, 582–595. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Adaptive power flow method for distribution systems with dispersed generation. IEEE Trans. Power Deliv. 2002, 17, 822–827. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; De Santis, M. Zoning evaluation for voltage optimization in distribution networks with distributed energy resources. Energies 2019, 12, 390. [Google Scholar] [CrossRef] [Green Version]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef] [Green Version]
- Echavarria, R.; Claudio, A.; Cotorogea, M. Analysis, Design, and Implementation of a Fast On-Load Tap Changing Regulator. IEEE Trans. Power Electron. 2007, 22, 527–534. [Google Scholar] [CrossRef]
- Liu, Y.; Bebic, J.; Kroposki, B.; de Bedout, J.; Ren, W. Distribution System Voltage Performance Analysis for High-Penetration PV. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, Georgia, 17–18 November 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N. Reactive Power Control of DGs for Distribution Network Voltage Regulation Using Multi-Agent System. IFAC-PapersOnLine 2018, 51, 528–533. [Google Scholar] [CrossRef]
- Degefa, M.; Lehtonen, M.; Millar, R.; Alahäivälä, A.; Saarijärvi, E. Optimal voltage control strategies for day-ahead active distribution network operation. Electr. Power Syst. Res. 2015, 127, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Kryonidis, G.; Kontis, E. A Coordinated Droop Control Strategy for Overvoltage Mitigation in Active Distribution Networks. IEEE Trans. Smart Grid 2018, 9, 5260–5270. [Google Scholar] [CrossRef]
- Fallahzadeh-Abarghouei, H.; Hasanvand, S.; Nikoobakht, A.; Doostizadeh, M. Decentralized and hierarchical voltage management of renewable energy resources in distribution smart grid. Int. J. Electr. Power Energy Syst. 2018, 100, 117–128. [Google Scholar] [CrossRef]
- Ruan, H.; Gao, H.; Liu, Y.; Wang, L.; Liu, J. Distributed Voltage Control in Active Distribution Network Considering Renewable Energy: A Novel Network Partitioning Method. IEEE Trans. Power Syst. 2020, 35, 4220–4231. [Google Scholar] [CrossRef]
- England, B.S.; Alouani, A.T. Real time voltage stability prediction of smart grid areas using smart meters data and improved Thevenin estimates. Int. J. Electr. Power Energy Syst. 2020, 122, 106189. [Google Scholar] [CrossRef]
- Khayat, Y.; Shafiee, Q.; Heydari, R.; Naderi, M.; Dragičević, T.; Simpson-Porco, J.W.; Dörfler, F.; Fathi, M.; Blaabjerg, F.; Guerrero, J.M.; et al. On the Secondary Control Architectures of AC Microgrids: An Overview. IEEE Trans. Power Electron. 2020, 35, 6482–6500. [Google Scholar] [CrossRef]
- Hassan, B.; Bruno, F.; Toshifumi, I. Hierarchical Microgrid Control. In Microgrid Dynamics and Control; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2017; Chapter 5; pp. 221–265. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781119263739.ch5 (accessed on 5 December 2020).
- Naderi, M.; Khayat, Y.; Batmani, Y.; Bevrani, H. Robust Multivariable Microgrid Control Synthesis and Analysis. Energy Procedia 2016, 100, 375–387. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Jackson, R.; Zulkifli, S.A.; Benbouzid, M.; Salimin, S.; Khan, M.H.; Elhassan, G.; Pathan, E. A Comprehensive Motivation of Multilayer Control Levels for Microgrids: Synchronization, Voltage and Frequency Restoration Perspective. Appl. Sci. 2020, 10, 8355. [Google Scholar] [CrossRef]
- Heydari, R.; Dragicevic, T.; Blaabjerg, F. High-Bandwidth Secondary Voltage and Frequency Control of VSC-Based AC Microgrid. IEEE Trans. Power Electron. 2019, 34, 11320–11331. [Google Scholar] [CrossRef] [Green Version]
- Sathiyanarayanan, T.; Mishra, S. Synchronous Reference Frame Theory based Model Predictive Control for Grid Connected Photovoltaic Systems. IFAC-PapersOnLine 2016, 49, 766–771. [Google Scholar] [CrossRef]
- Aguilar, A.; Tapia, R.; Valderrabano, A.; Minor, H. Design and Performance Comparison of PI and Adaptive Current Controllers for a WECS. IEEE Lat. Am. Trans. 2015, 13, 1361–1368. [Google Scholar] [CrossRef]
- Khorramabadi, S.; Bakhshai, A. Critic-Based Self-Tuning PI Structure for Active and Reactive Power Control of VSCs in Microgrid Systems. IEEE Trans. Smart Grid 2015, 6, 92–103. [Google Scholar] [CrossRef]
- Papageorgiou, P.; Krommydas, K.; Alexandridis, A. Validation of Novel PLL-driven PI Control Schemes on Supporting VSIs in Weak AC-Connections. Energies 2020, 13, 1373. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, A.; Di Fazio, A.R.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J. Modeling Guidelines and a Benchmark for Power System Simulation Studies of Three-Phase Single-Stage PhotoVoltaic Systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed Control Techniques in Microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Ferreira, P.; Carvalho, P.; Ferreira, L.; Ilic, M. Distributed Energy Resources Integration Challenges in Low-Voltage Networks: Voltage Control Limitations and Risk of Cascading. IEEE Trans. Sustain. Energy 2013, 4, 82–88. [Google Scholar] [CrossRef]
- Juamperez, M.; Yang, G.; Kjaer, S. Voltage regulation in LV grids by coordinated volt-var control strategies. J. Mod. Power Syst. Clean Energy 2014, 2, 319–328. [Google Scholar] [CrossRef] [Green Version]
- IEEE Standard Association. IEEE Std 1547-2018 Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- International Electrotechnical Commission (IEC). IEC TS 62786 Distributed Energy Resources Connection with the Grid; IEC: Geneva, Switzerland, 2017. [Google Scholar]
- Chalise, S.; Atia, H.; Poudel, B.; Tonkoski, R. Impact of active power curtailment of wind turbines connected to residential feeders for overvoltage prevention. IEEE Trans. Sustain. Energy 2016, 7, 471–479. [Google Scholar] [CrossRef]
- Mahmud, M.; Hossain, M.; Pota, H.; Oo, A. Robust Nonlinear Distributed Controller Design for Active and Reactive Power Sharing in Islanded Microgrids. IEEE Trans. Energy Convers. 2014, 29, 893–903. [Google Scholar] [CrossRef]
- Zhou, J.; Cheng, P. A Modified Q − V˙ Droop Control for Accurate Reactive Power Sharing in Distributed Generation Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 4100–4109. [Google Scholar] [CrossRef]
- Directive (EU) 2019/944 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32019L0944 (accessed on 3 February 2021).
- Shan, Y.; Hu, J.; Guerrero, J.M. A Model Predictive Power Control Method for PV and Energy Storage Systems With Voltage Support Capability. IEEE Trans. Smart Grid 2020, 11, 1018–1029. [Google Scholar] [CrossRef]
- Siratarnsophon, P.; Lao, K.W.; Rosewater, D.; Santoso, S. A Voltage Smoothing Algorithm Using Energy Storage PQ Control in PV-Integrated Power Grid. IEEE Trans. Power Deliv. 2019, 34, 2248–2250. [Google Scholar] [CrossRef]
- Jahangiri, P.; Aliprantis, D. Distributed Volt/Var control by PV inverters. IEEE Trans. Power Syst. 2013, 28, 3429–3439. [Google Scholar] [CrossRef]
- Braslavsky, J.H.; Collins, L.; Ward, J.K. Voltage Stability in a Grid-Connected Inverter With Automatic Volt-Watt and Volt-VAR Functions. IEEE Trans. Smart Grid 2019, 10, 84–94. [Google Scholar] [CrossRef]
- Majumder, R. Aspect of voltage stability and reactive power support in active distribution. IET Gener. Transm. Distrib. 2014, 8, 442–450. [Google Scholar] [CrossRef]
- Ranamuka, D.; Agalgaonkar, A.; Muttaqu, K. Online Voltage Control in Distribution Systems With Multiple Voltage Regulating Devices. IEEE Trans. Sustain. Energy 2014, 5, 617–628. [Google Scholar] [CrossRef]
- Baran, M.; El-Markabi, I. A mulitagent-based dispatching scheme for distributed generators for voltage support on distribution feeders. IEEE Trans. Power Syst. 2007, 22, 52–59. [Google Scholar] [CrossRef]
- Farag, H.E.; El-Saadany, E.F.; Seethapathy, R. A Two Ways Communication-Based Distributed Control for Voltage Regulation in Smart Distribution Feeders. IEEE Trans. Smart Grid 2012, 3, 271–281. [Google Scholar] [CrossRef]
- Tanaka, K.; Oshiro, M.; Toma, S.; Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C.H. Decentralised control of voltage in distribution systems by distributed generators. IET Proc. Gener. Transm. Distrib. 2010, 4, 1251–1260. [Google Scholar] [CrossRef]
- Yu, L.; Czarkowski, D.; de Leòn, F. Optimal Distributed Voltage Regulation for Secondary Networks With DGs. IEEE Trans. Smart Grid 2012, 3, 959–960. [Google Scholar] [CrossRef]
- Delghavi, M.B.; Yazdani, A. A Unified Control Strategy for Electronically Interfaced Distributed Energy Resources. IEEE Trans. Power Deliv. 2012, 27, 803–812. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. Linear method for steady-state analysis of radial distribution systems. Int. J. Electr. Power Energy Syst. 2018, 99, 744–755. [Google Scholar] [CrossRef]
- Kailath, T. Linear Systems; Prentice-Hall: New York, NY, USA, 1980. [Google Scholar]
- Grosdidier, P.; Morari, M. Interaction Measures for systems Under Decentralized Control. Automatica 1986, 22, 309–319. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. A Procedure to Determine the Droop Constants of Voltage Controllers coping with Multiple DG Interactions in Active Distribution Systems. Energies 2020, 13, 1935. [Google Scholar] [CrossRef] [Green Version]
- Fusco, G.; Russo, M. Robust MIMO Design of Decentralized Voltage Controllers of PV Systems in Distribution Networks. IEEE Trans. Ind. Electron. 2017, 64, 4610–4620. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Fusco, G.; Russo, M. Decentralized voltage control of distributed generation using a distribution system structural MIMO model. Control. Eng. Pract. 2016, 46, 81–90. [Google Scholar] [CrossRef]
- Khargonekar, P.; Georgiou, T.; Pascoal, A. On the Robust Stabilizability of Linear Time-Invariant Plants with Unstructured Uncertainty. IEEE Trans. Autom. Control. 1987, AC-32, 201–207. [Google Scholar] [CrossRef]
- Fusco, G.; Russo, M. Decentralized PI controllers design for voltage regulation in distribution networks with DG. Elsevier Electr. Power Syst. Res. 2019, 172, 129–139. [Google Scholar]
- Fusco, G.; Russo, M. Tuning of multivariable PI robust controllers for the decentralized voltage regulation in grid-connected distribution networks with Distributed Generation. Int. J. Dyn. Control. 2020, 8, 278–290. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Robust Optimal Power Management System for a Hybrid AC/DC Micro-Grid. IEEE Trans. Sustain. Energy 2015, 6, 675–687. [Google Scholar] [CrossRef]
- Manitoba-HVDC Research Center. PSCAD User’s Guide; Manitoba-HVDC Research Center: Winnipeg, MB, Canada, 2005. [Google Scholar]
- Jayachandran, M.; Ravi, G. Decentralized model predictive hierarchical control strategy for islanded AC microgrids. Electr. Power Syst. Res. 2019, 170, 92–100. [Google Scholar] [CrossRef]
- Tavassoli, B.; Fereidunian, A.; Mehdi, S. Communication system effects on the secondary control performance in microgrids. IET Renew. Power Gener. 2020, 14, 2047–2057. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Cost-Prioritized Droop Schemes for Autonomous AC Microgrids. IEEE Trans. Power Electron. 2015, 30, 1109–1119. [Google Scholar] [CrossRef]
- Zaery, M.; Ahmed, E.M.; Orabi, M. Low operational cost distributed prioritised coordinated control for DC microgrids. IET Smart Grid 2019, 2, 233–241. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Z.; Zhao, C.; Chen, L. Accelerated Voltage Regulation in Multi-Phase Distribution Networks Based on Hierarchical Distributed Algorithm. IEEE Trans. Power Syst. 2020, 35, 2047–2058. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. Sensitivity-based model of low voltage distribution systems with distributed energy resources. Energies 2016, 9, 801. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; De Santis, M. Zoning Evaluation for Voltage Control in Smart Distribution Networks. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Li, Z.; Guerrero, J.M. A Model Predictive Control for Renewable Energy Based AC Microgrids Without Any PID Regulators. IEEE Trans. Power Electron. 2018, 33, 9122–9126. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Expósito, A.; de la Villa Jaén, A.; Gómez-Quiles, C.; Rousseaux, P.; Van Cutsem, T. A taxonomy of multi-area state estimation methods. Electr. Power Syst. Res. 2011, 81, 1060–1069. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Paliwal, P.; Arya, A. A Review on Challenges and Techniques for Secondary Control of Microgrid. IOP Conf. Ser. Mater. Sci. Eng. 2019, 561, 012075. [Google Scholar] [CrossRef] [Green Version]
- Andreotti, A.; Petrillo, A.; Santini, S.; Vaccaro, A.; Villacci, D. A Decentralized Architecture Based on Cooperative Dynamic Agents for Online Voltage Regulation in Smart Grids. Energies 2019, 12, 1386. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Magnago, F.; Alemany, J.M. Chapter 1—Optimization Methods Applied to Power Systems: Current Practices and Challenges. In Classical and Recent Aspects of Power System Optimization; Zobaa, A.F., Abdel Aleem, S.H., Abdelaziz, A.Y., Eds.; Academic Press: New York, NY, USA, 2018; pp. 1–18. [Google Scholar] [CrossRef]
- Ebeed, M.; Kamel, S.; Jurado, F. Chapter 7—Optimal Power Flow Using Recent Optimization Techniques. In Classical and Recent Aspects of Power System Optimization; Zobaa, A.F., Abdel Aleem, S.H., Abdelaziz, A.Y., Eds.; Academic Press: New York, NY, USA, 2018; pp. 157–183. [Google Scholar] [CrossRef]
- Mehdinejad, M.; Mohammadi-Ivatloo, B.; Dadashzadeh-Bonab, R.; Zare, K. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms. Int. J. Electr. Power Energy Syst. 2016, 83, 104–116. [Google Scholar] [CrossRef]
- Khan, I.; Li, Z.; Xu, Y.; Gu, W. Distributed control algorithm for optimal reactive power control in power grids. Int. J. Electr. Power Energy Syst. 2016, 83, 505–513. [Google Scholar] [CrossRef]
- Tümay, M.; Demirdelen, T.; Bal, S.; İlker Kayaalp, R.; Doğru, B.; Aksoy, M. A review of magnetically controlled shunt reactor for power quality improvement with renewable energy applications. Renew. Sustain. Energy Rev. 2017, 77, 215–228. [Google Scholar] [CrossRef]
- Ding, M.; Chen, H.; Lin, N.; Jing, S.; Liu, F.; Liang, X.; Liu, W. Dynamic population artificial bee colony algorithm for multi-objective optimal power flow. Saudi J. Biol. Sci. 2017, 24, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Suresh Babu, B.; Palaniswami, S. Teaching learning based algorithm for OPF with DC link placement problem. Int. J. Electr. Power Energy Syst. 2015, 73, 773–781. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Zero Duality Gap in Optimal Power Flow Problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Bukhsh, W.A.; Grothey, A.; McKinnon, K.I.M.; Trodden, P.A. Local Solutions of the Optimal Power Flow Problem. IEEE Trans. Power Syst. 2013, 28, 4780–4788. [Google Scholar] [CrossRef] [Green Version]
- Khan, I.U.; Javaid, N.; Gamage, K.A.A.; Taylor, C.J.; Baig, S.; Ma, X. Heuristic Algorithm Based Optimal Power Flow Model Incorporating Stochastic Renewable Energy Sources. IEEE Access 2020, 8, 148622–148643. [Google Scholar] [CrossRef]
- Leeton, U.; Uthitsunthorn, D.; Kwannetr, U.; Sinsuphun, N.; Kulworawanichpong, T. Power Loss Minimization Using Optimal Power Flow Based on Particle Swarm Optimization. In ECTI-CON2010: The 2010 ECTI International Confernce on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology; IEEE: Piscataway, NJ, USA, 2010; pp. 440–444. [Google Scholar]
- Brownlee, J. Clever Algorithms: Nature-Inspired Programming Recipes, 1st ed.; Lulu.com: Morrisville, NC, USA, 2011. [Google Scholar]
- Tan, W.S.; Hassan, M.Y.; Majid, M.S.; Abdul Rahman, H. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- De Jong, K.A. Genetic Algorithms Are NOT Function Optimizers. In Foundations of Genetic Algorithms; Whitley, L.D., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; Volume 2, pp. 5–17. [Google Scholar] [CrossRef] [Green Version]
- Sathish Kumar, K.; Jayabarathi, T. Power system reconfiguration and loss minimization for an distribution systems using bacterial foraging optimization algorithm. Int. J. Electr. Power Energy Syst. 2012, 36, 13–17. [Google Scholar] [CrossRef]
- Shivarudraswamy, R.; Gaonkar, D.N. Coordinated Voltage Control with Reactive Power of the Distributed Generators using Genetic Algorithm. Int. J. Sci. Eng. Res. 2012, 3, 1–7. [Google Scholar]
- Khazali, A.; Kalantar, M. Optimal power flow considering fault current level constraints and fault current limiters. Int. J. Electr. Power Energy Syst. 2014, 59, 204–213. [Google Scholar] [CrossRef]
- Zdraveski, V.; Todorovski, M.; Kocarev, L. Dynamic intelligent load balancing in power distribution networks. Int. J. Electr. Power Energy Syst. 2015, 73, 157–162. [Google Scholar] [CrossRef]
- Águila Téllez, A.; López, G.; Isaac, I.; González, J. Optimal reactive power compensation in electrical distribution systems with distributed resources. Heliyon 2018, 4, e00746. [Google Scholar] [CrossRef] [Green Version]
- Daiva, S.; Saulius, G.; Liudmila, A. Energy Distribution Planning Models Taxonomy and Methods of Distributed Generation Systems. Energy Procedia 2017, 107, 275–283. [Google Scholar] [CrossRef]
- Elhedhli, S.; Akdemir, C.; Astebro, T. Classification Models Via Tabu Search: An Application to Early Stage Venture Classification. HEC Paris Res. 2015, 3. [Google Scholar] [CrossRef]
- Saddique, M.S.; Bhatti, A.R.; Haroon, S.S.; Sattar, M.K.; Amin, S.; Sajjad, I.A.; ul Haq, S.S.; Awan, A.B.; Rasheed, N. Solution to optimal reactive power dispatch in transmission system using meta-heuristic techniques–Status and technological review. Electr. Power Syst. Res. 2020, 178, 106031. [Google Scholar] [CrossRef]
- Kim, B.H.; Baldick, R. A comparison of distributed optimal power flow algorithms. IEEE Trans. Power Syst. 2000, 15, 599–604. [Google Scholar] [CrossRef]
- Erseghe, T. Distributed Optimal Power Flow Using ADMM. IEEE Trans. Power Syst. 2014, 29, 2370–2380. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Risi, C.; Russo, M.; De Santis, M. Zone-Based Voltage Optimization in Distribution Grids with DGs. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, G.; Teboulle, M. A proximal-based decomposition method for convex minimization problems. Math. Program. 1994, 64, 81–101. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Risi, C.; Russo, M.; De Santis, M. Distributed Voltage Optimization based on the Auxiliary Problem Principle in Active Distribution Systems. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Stott, B.; Alsaç, O. Optimal power flow–basic requirements for real-life problems and their solutions. Proc. SEPOPE XII Symp. 2012, 11, 1–18. [Google Scholar]
- Gao, W.; Li, G.; Zhang, Q.; Luo, Y.; Wang, Z. Solving Nonlinear Equation Systems by a Two-Phase Evolutionary Algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–12. [Google Scholar] [CrossRef]
- Barzegar, A.; Molzahn, D.K.; Su, R. A Method for Quickly Bounding the Optimal Objective Value of an OPF Problem using a Semidefinite Relaxation and a Local Solution. Electr. Power Syst. Res. 2019, 177, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lagonotte, P.; Sabonnadiere, J.C.; Leost, J.; Paul, J. Structural analysis of the electrical system: Application to secondary voltage control in France. IEEE Trans. Power Syst. 1989, 4, 479–486. [Google Scholar] [CrossRef]
- Casolino, G.M.; Di Fazio, A.R.; Losi, A.; Russo, M.; De Santis, M. A Voltage Optimization Tool for Smart Distribution Grids with Distributed Energy Resources. In Proceedings of the 2017 AEIT International Annual Conference, Beijing, China, 20–22 September 2017; pp. 1–6. [Google Scholar]
- Mihic, K.; Zhu, M.; Ye, Y. Managing randomization in the multi-block alternating direction method of multipliers for quadratic optimization. Math. Prog. Comp. 2020. [Google Scholar] [CrossRef]
- Safdarian, F.; Ciftci, O.; Kargarian, A. A Time Decomposition and Coordination Strategy for Power System Multi-Interval Operation. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Cohen, G. Auxiliary problem principle and decomposition of optimization problems. J. Optim. Theory Appl. 1980, 32, 277–305. [Google Scholar] [CrossRef]
- Losi, A.; Russo, M. On the Application of the Auxiliary Problem Principle. J. Optim. Theory Appl. 2003, 117, 377–396. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Qu, Z.; Gan, D. An Attack-Resilient Cooperative Control Strategy of Multiple Distributed Generators in Distribution Networks. IEEE Trans. Smart Grid 2016, 7, 2923–2932. [Google Scholar] [CrossRef]
- Wang, Y.; Mondal, S.; Deng, C.; Satpathi, K.; Xu, Y.; Dasgupta, S. Cyber-Resilient Cooperative Control of Bidirectional Interlinking Converters in Networked AC/DC Microgrids. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]



| DER # | Proportional Gain [p.u.] | Integral Time Constant [s] |
| 2 | 27 | 0.06 |
| 3 | 30 | 0.05 |
| 4 | 24 | 0.06 |
| 5 | 25 | 0.05 |
| 6 | 25 | 0.06 |
| VCZ | DER Nodes | Pilot Node |
|---|---|---|
| 1 | 12 | 10 |
| 2 | 7, 13 | 7 |
| 3 | 20 | 20 |
| 4 | 18 | 18 |
| 5 | 24 | 23 |
| Power | ||||||
|---|---|---|---|---|---|---|
| Active | 0.005 | 0.005 | 0.005 | 0.0025 | 0.003 | 0.002 |
| (MW) | (0, 0.02) | (0, 0.03) | (0, 0.03) | (0, 0.02) | (0, 0.03) | (0, 0.02) |
| Reactive | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| (MVAr) | (−0.0113, +0.0113) | (−0.0150, +0.0150) | (−0.0188, +0.0188) | (−0.0113, +0.0113) | (−0.0113, +0.0113) | (−0.0075, +0.0075) |
| DER | Decentralized APP | Decentralized ADMM | ||
|---|---|---|---|---|
| 1 | 0.0049 | 0.0103 | 0.0024 | 0.0113 |
| 2 | −0.0001 | 0.0140 | 0.0000 | 0.0150 |
| 3 | −0.0001 | 0.0178 | 0.0000 | 0.0188 |
| 4 | 0.0175 | 0.0103 | 0.0200 | 0.0113 |
| 5 | 0.0099 | 0.0103 | 0.0118 | 0.0113 |
| 6 | 0.0053 | 0.0065 | 0.0044 | 0.0075 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fusco, G.; Russo, M.; De Santis, M. Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues. Energies 2021, 14, 2563. https://doi.org/10.3390/en14092563
Fusco G, Russo M, De Santis M. Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues. Energies. 2021; 14(9):2563. https://doi.org/10.3390/en14092563
Chicago/Turabian StyleFusco, Giuseppe, Mario Russo, and Michele De Santis. 2021. "Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues" Energies 14, no. 9: 2563. https://doi.org/10.3390/en14092563
APA StyleFusco, G., Russo, M., & De Santis, M. (2021). Decentralized Voltage Control in Active Distribution Systems: Features and Open Issues. Energies, 14(9), 2563. https://doi.org/10.3390/en14092563








