Critical Buckling Generation of TCA Benchmark by the B1 Theory-Augmented Monte Carlo Calculation and Estimation of Uncertainties
Abstract
:1. Introduction
2. Generation of Critical Buckling
2.1. Critical Buckling Generation Using the B1 Theory-Augmented MC Method
2.2. Critical Buckling Generation Using the Fitted Cosine Function
3. Propagation of Uncertainties in Critical Buckling Generation
3.1. Estimation of the Critical Buckling Uncertainties Using the SNU S/U Formulation
3.2. Estimation of the Critical Buckling Uncertainties using the Stochastic Sampling Method
4. TCA Benchmark Analysis
4.1. TCA Benchmark Problem
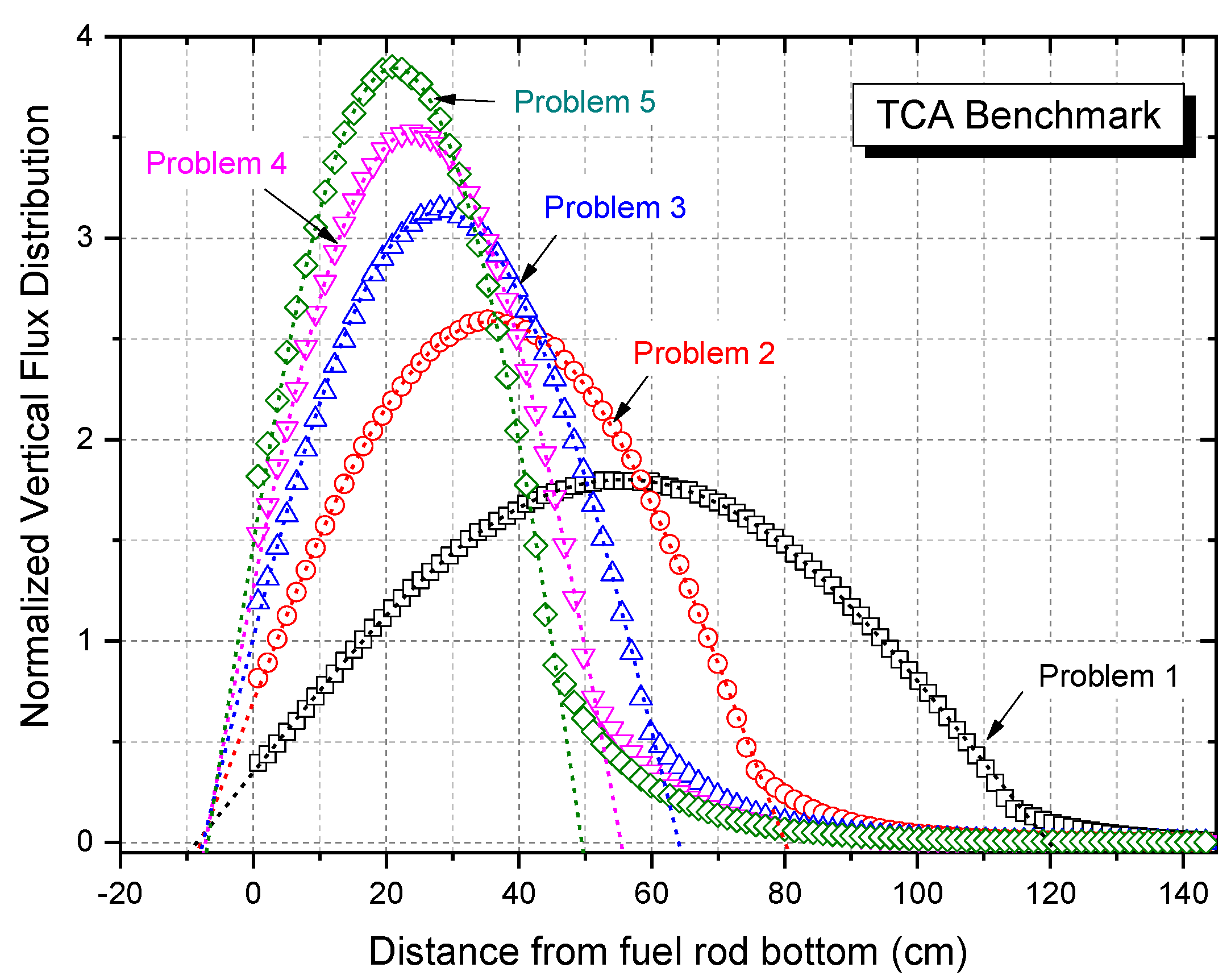
4.2. Critical Buckling Generation for TCA Benchmark Problem
4.3. Uncertainty Analysis of Critical Buckling Based on Cross Section Uncertainties
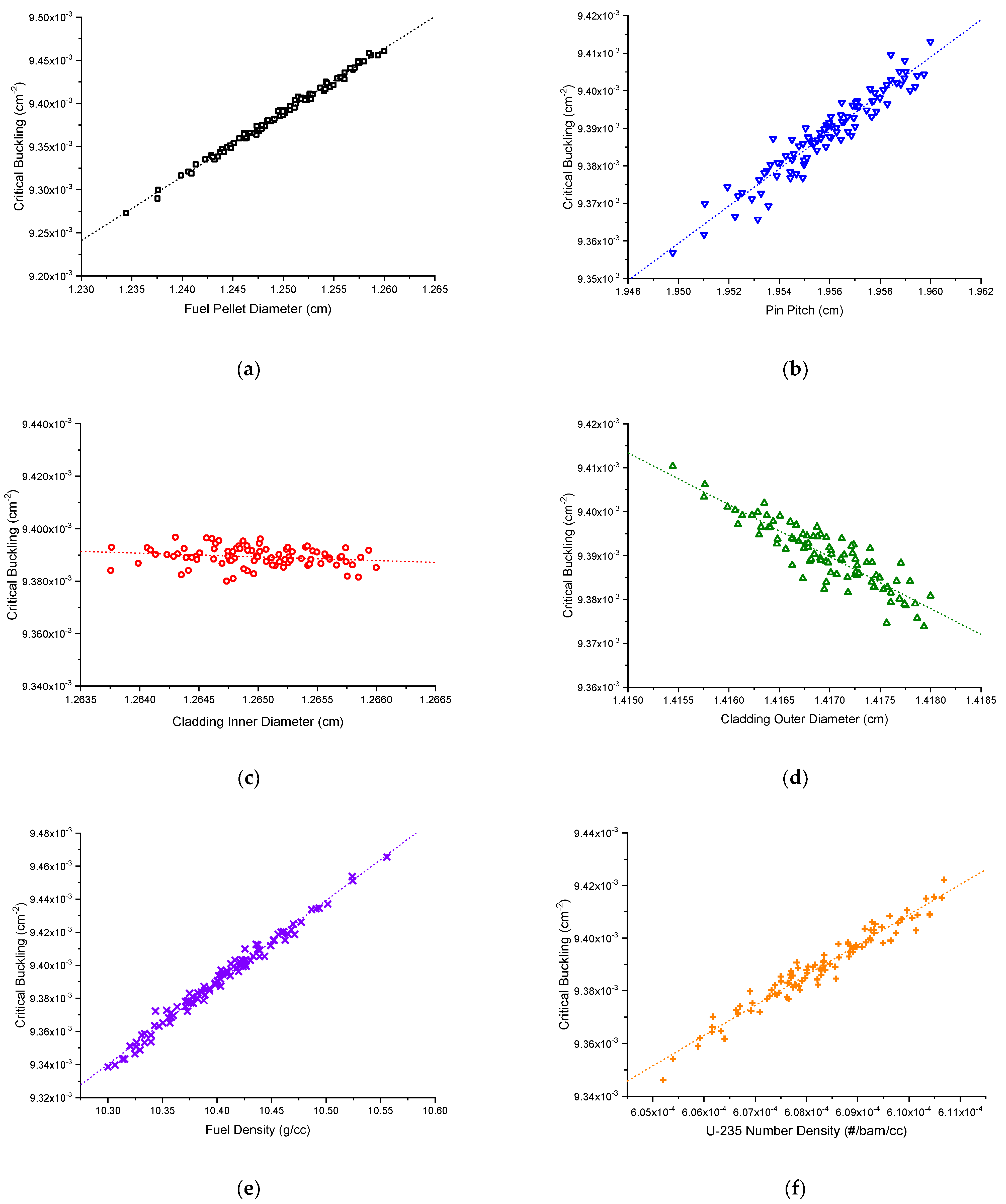
4.4. Uncertainty Analysis of Critical Buckling Based on Input Design Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MOC | Method of Characteristics |
| KAERI | Korea Atomic Energy Research Institute |
| MC | Monte Carlo |
| FGCs | Few Group Constants |
| S/U | Sensitivity and Uncertainty |
| S.S. | Stochastic Sampling |
| SNU | Seoul National University |
| IMS | Infinite Medium Spectrum |
| CS | Critical Spectrum |
| ICSBEP | International Criticality Safety Benchmark Problem |
| DRC | Design Review Criterion |
| CBC | Critical Boron Concentration |
| %RE | Percentile Relative Errors |
References
- Cho, J.Y.; Shim, C.; Han, T.Y.; Lee, K.; Lee, C.; Song, J.S.; Park, S.Y.; Park, H.J.; Jeong, H.J.; Jo, C.K.; et al. DeCART2D v1.1 User’s Manual; KAERI/UM-40/2016; Korea Atomic Energy Research Institute: Daejeon, Korea, 2016. [Google Scholar]
- Cho, J.Y.; Jeong, H.J.; Song, J.S.; Park, S.Y.; Lee, K.; Lee, C.; Shim, C.; Park, H.J.; Choi, Y.; Koo, B.S. MASTER v4.0 User’s Manual; KAERI/UM-41/2016; Korea Atomic Energy Research Institute: Daejeon, Korea, 2016. [Google Scholar]
- Shim, H.J.; Han, B.S.; Jung, J.S.; Park, H.J.; Kim, C.H. McCARD: An Monte Carlo Code for Advanced Reactor Design and Analysis. Nucl. Eng. Tech. 2012, 44, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Boyd, W.; Nelson, A.; Romano, P.K.; Shaner, S.; Forget, B.; Smith, K. Multigroup Cross-Section Generation with the OpenMC Monte Carlo Particle Transport Code. Nucl. Techonol. 2019, 205, 928–944. [Google Scholar] [CrossRef]
- Lee, H.; Kim, W.; Zhang, P.; Lemaire, M.; Khassenov, A.; Yu, J.; Jo, Y.; Park, J.; Lee, D. MCS—A Monte Carlo Particle Transport Code for Large-Scale Power Reactor Analysis. Ann. Nucl. Energy 2020, 139, 107276. [Google Scholar] [CrossRef]
- Yamamoto, T. Monte Carlo method with complex weights for neutron leakage-corrected calculations and anisotropic diffusion coefficient. Ann. Nucl. Energy 2012, 50, 141–149. [Google Scholar] [CrossRef]
- Yamamoto, T.; Sakamoto, H. Monte Carlo method for solving a B1 equation with complex-valued buckling in asymmetric geometries and generation of directional diffusion coefficients. Ann. Nucl. Energy 2018, 122, 37–46. [Google Scholar] [CrossRef]
- Shim, H.J.; Cho, J.Y.; Song, J.S.; Kim, C.H. Generation of Few Group Diffusion Theory Constants by Monte Carlo Code. Trans. Am. Nucl. Soc. 2008, 343, 343–345. [Google Scholar]
- Park, H.J.; Shim, H.J.; Kim, C.H. Generation of Few-Group Diffusion Theory Constants by Monte Carlo Code McCARD. Nucl. Sci. Eng. 2012, 172, 66–77. [Google Scholar] [CrossRef]
- Park, H.J.; Shim, H.J.; Joo, H.G.; Kim, C.H. Uncertainty Quantification of Few-group Diffusion Theory Constants Generated by the B1 Theory-Augmented Monte Carlo Method. Nucl. Sci. Eng. 2013, 175, 28–43. [Google Scholar] [CrossRef]
- Fridman, E.; Leppanen, J. On the use of the Serpent Monte Carlo code for few group cross section generation. Ann. Nucl. Energy 2011, 38, 1399–1405. [Google Scholar] [CrossRef]
- Park, H.J.; Shim, H.J.; Kim, C.H. Uncertainty Propagation in Monte Carlo Depletion Analysis. Nucl. Sci. Eng. 2011, 167, 196–208. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Arakawa, T. Critical Arrays of Low-Enriched UO2 Fuel Rods with Water-to-Fuel Volume Ratio Ranging from 1.5 to 3.0; NEA/NSC/DOC(95)03; OECD Nuclear Energy: Paris, France, 2006; Volume IV. [Google Scholar]
- Suzaki, T. Subcriticality Determination of Low-Enriched UO2 Lattices in Water by Exponential Experiment. J. Nucl. Sci. Technol. 1991, 28, 1067–1077. [Google Scholar] [CrossRef]
- Knief, R.A. Nuclear Engineering Theory and Technology of Commercial Nuclear Power, 2nd ed.; American Nuclear Society: La grange Park, IL, USA, 2008; pp. 114–119. [Google Scholar]
- Macfarlane, R.; Muir, D.W.; Boicourt, R.M.; Kahler, A.C., III; Conlin, J.L. The NJOY Nuclear Data Processing System Version; LA-UR-17-20093; Los Alamos National Laboratory: Los Alamos, NW, USA, 2016.
- Park, H.J.; Kim, K.S.; Hong, S.G.; Song, J.S. An improved DeCART Library Generation Procedure with Explicit Resonance Interference using Continuous Energy Monte Carlo Calculation. Ann. Nucl. Energy. 2017, 105, 95–105. [Google Scholar] [CrossRef]
- Park, H.J.; Kang, H.; Lee, H.C.; Cho, J.Y. Comparison of ENDF/B-VIII.0 and ENDF/B-VII.1 in criticality, depletion benchmark, and uncertainty analyses by McCARD. Ann. Nucl. Energy. 2019, 131, 443–459. [Google Scholar] [CrossRef]

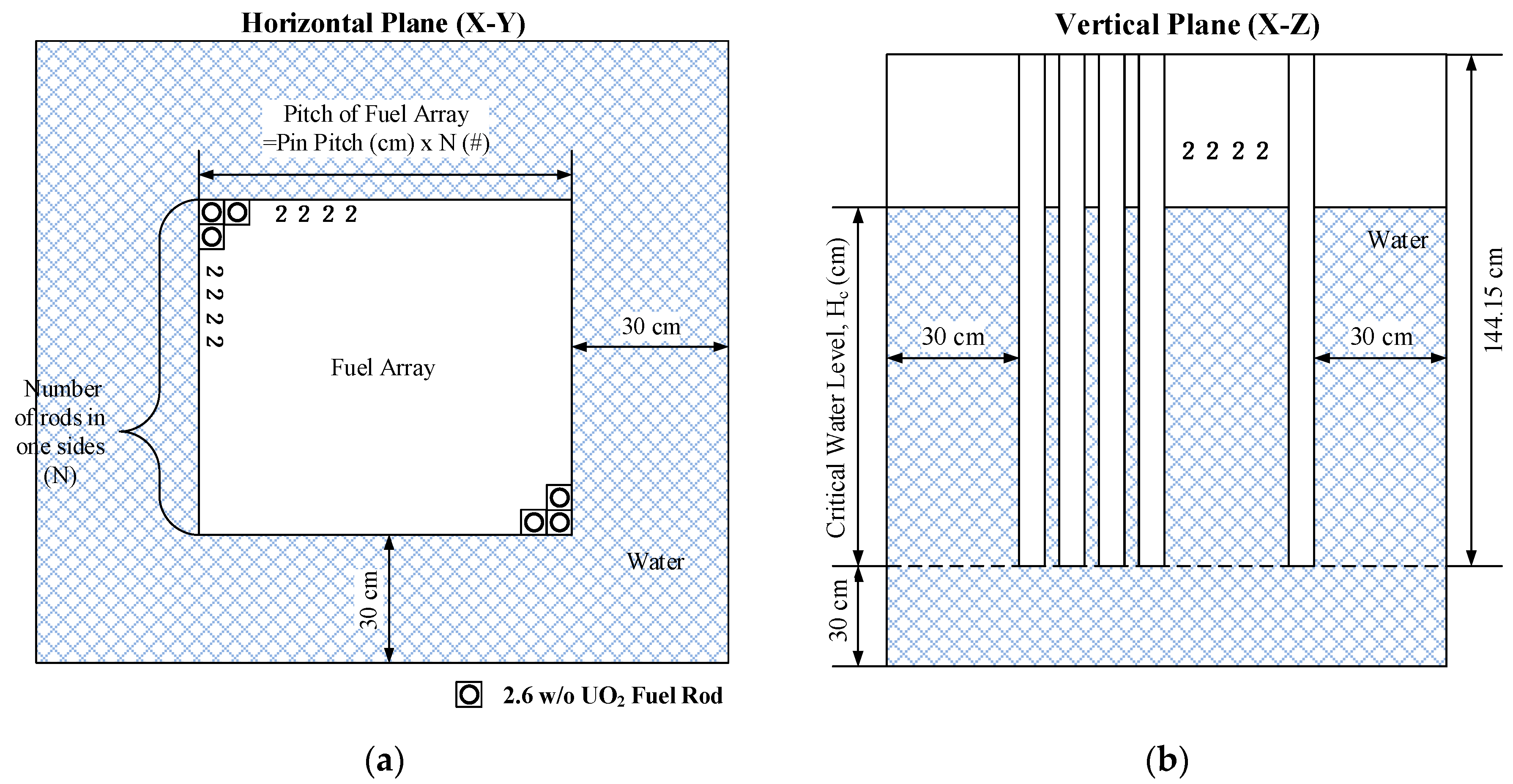
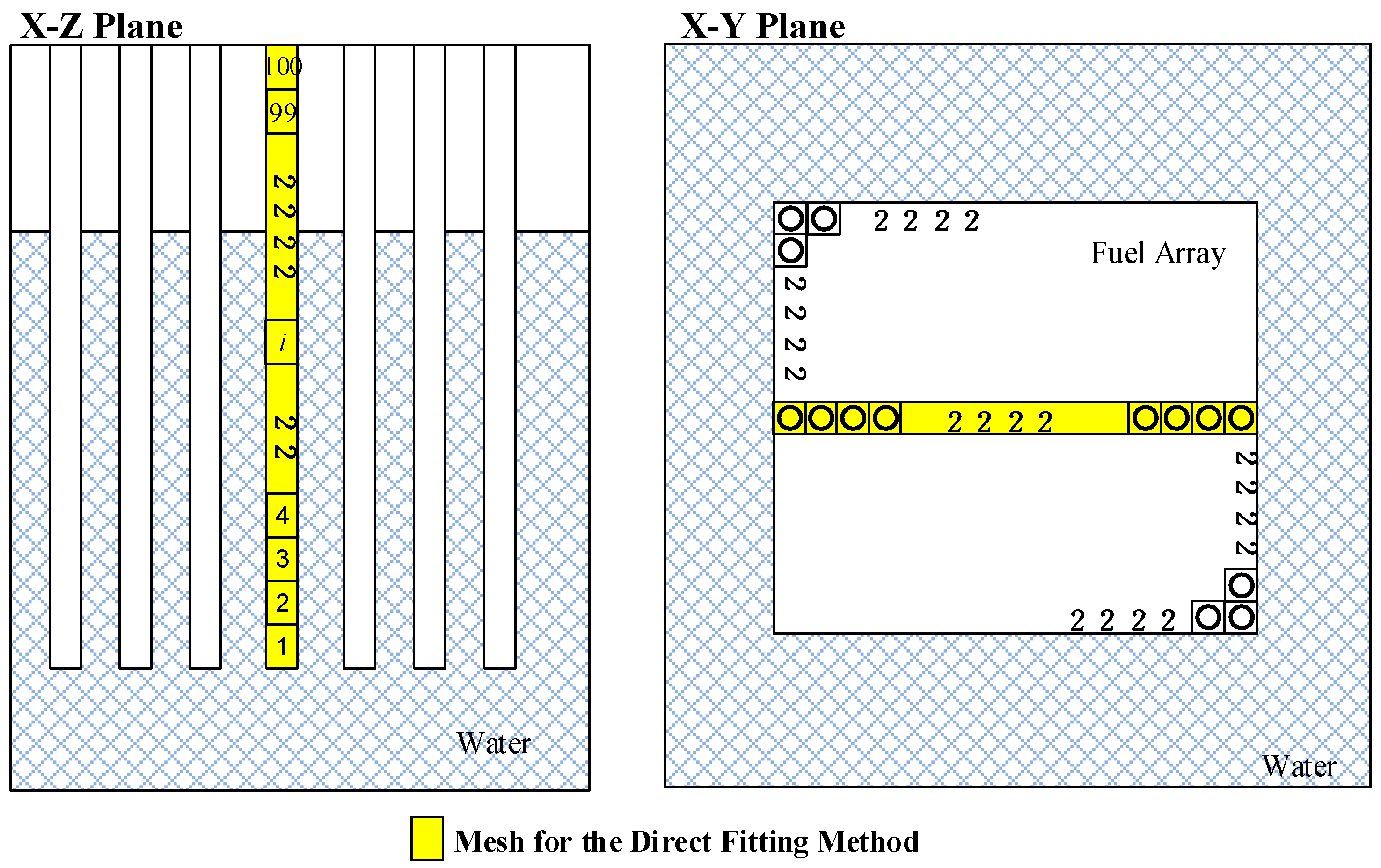

| Step | Input (I) Variables | Output(O) Variables | Functional Relation Between the I/O Variables |
|---|---|---|---|
| I | |||
| II | |||
| III |
| Problem No. | Case No. 1 | Number of Rods in One Side (N) | Critical Height Level (cm) | Extrapolation Length (cm) | Total Buckling (×10−3 cm−2) | |
|---|---|---|---|---|---|---|
| 1 | Case 4 | 17 | 114.59 ± 1.69 | 12.2 ± 0.3 | 13.9 ± 0.8 | 9.49 ± 0.21 |
| 2 | Case 5 | 18 | 75.32 ± 0.90 | 12.2 ± 0.3 | 13.9 ± 0.8 | 9.47 ± 0.19 |
| 3 | Case 6 | 19 | 60.38 ± 0.21 | 12.2 ± 0.3 | 13.9 ± 0.8 | 9.44 ± 0.17 |
| 4 | Case 7 | 20 | 51.65 ± 0.17 | 12.2 ± 0.3 | 13.9 ± 0.8 | 9.44 ± 0.15 |
| 5 | Case 8 | 21 | 46.01 ± 0.08 | 12.2 ± 0.3 | 13.9 ± 0.8 | 9.44 ± 0.14 |
| Problem No. | Vertical Extrapolation Length () by Direct Fitting Method (×10−3 cm−2) | ||
|---|---|---|---|
| Exp | McCARD | R2 | |
| 1 | 12.2 ± 0.3 | 12.5 | 0.9998 |
| 2 | 12.2 ± 0.3 | 11.7 | 0.9996 |
| 3 | 12.2 ± 0.3 | 12.6 | 0.9993 |
| 4 | 12.2 ± 0.3 | 12.0 | 0.9999 |
| 5 | 12.2 ± 0.3 | 12.8 | 0.9998 |
| Problem No. | Critical Buckling (×10−3 cm−2) | ||||
|---|---|---|---|---|---|
| Exp | B1 Method | Direct Fitting Method | |||
| Value | C/E 1 | Value | C/E 1 | ||
| 1 | 9.492 ± 0.21 | 9.388 | 0.989 | 9.490 | 0.999 |
| 2 | 9.474 ± 0.19 | 9.391 | 0.991 | 9.488 | 1.002 |
| 3 | 9.444 ± 0.17 | 9.389 | 0.994 | 9.424 | 0.998 |
| 4 | 9.443 ± 0.15 | 9.390 | 0.994 | 9.458 | 1.002 |
| 5 | 9.444 ± 0.14 | 9.388 | 0.994 | 9.379 | 0.993 |
| Problem No. | keff of DeCART2D with Critical Buckling | |||||
|---|---|---|---|---|---|---|
| Experiments | B1 Method | Direct Fitting Method | ||||
| keff | Diff 1 | keff | Diff 1 | keff | Diff 1 | |
| 1 | 0.99857 | −143 | 1.00185 | 185 | 0.99863 | −137 |
| 2 | 0.99915 | −85 | 1.00178 | 178 | 0.99868 | −132 |
| 3 | 1.00010 | 10 | 1.00184 | 184 | 1.00071 | 71 |
| 4 | 1.00012 | 12 | 1.00180 | 180 | 0.99963 | −37 |
| 5 | 1.00011 | 11 | 1.00187 | 187 | 1.00217 | 217 |
| Isotope | Reaction Type | Case | ||
|---|---|---|---|---|
| ENDF/B-VII.1 | ENDF/B-VIII.0 | |||
| 235U | 1.22% | 0.82% | ||
| 0.32% | 0.33% | |||
| 1.01% | 0.44% | |||
| 238U | 0.11% | 0.11% | ||
| 0.11% | 0.16% | |||
| 1.76% | 1.04% | |||
| 16O | 0.11% | 0.11% | ||
| Total | 3.18% | 1.49% | ||
| Item | Value | |
|---|---|---|
| 235U composition (wt.%) | 2.596 ± 0.005 | 0.15% |
| UO2 pellet density (g/cm3) | 10.4 ± 0.05 | 0.28% |
| UO2 pellet diameter (cm) | 1.25 ± 0.005 | 0.41% |
| Al alloy cladding inner diameter (cm) | 1.265 ± 0.0005 | 0.04% |
| Al alloy cladding thickness (cm) | 0.0076 ± 0.0005 | 0.07% |
| Lattice pitch (cm) | 1.956 ± 0.002 | 0.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H.J.; Cho, J.Y. Critical Buckling Generation of TCA Benchmark by the B1 Theory-Augmented Monte Carlo Calculation and Estimation of Uncertainties. Energies 2021, 14, 2578. https://doi.org/10.3390/en14092578
Park HJ, Cho JY. Critical Buckling Generation of TCA Benchmark by the B1 Theory-Augmented Monte Carlo Calculation and Estimation of Uncertainties. Energies. 2021; 14(9):2578. https://doi.org/10.3390/en14092578
Chicago/Turabian StylePark, Ho Jin, and Jin Young Cho. 2021. "Critical Buckling Generation of TCA Benchmark by the B1 Theory-Augmented Monte Carlo Calculation and Estimation of Uncertainties" Energies 14, no. 9: 2578. https://doi.org/10.3390/en14092578
APA StylePark, H. J., & Cho, J. Y. (2021). Critical Buckling Generation of TCA Benchmark by the B1 Theory-Augmented Monte Carlo Calculation and Estimation of Uncertainties. Energies, 14(9), 2578. https://doi.org/10.3390/en14092578





