A Flow Rate Dependent 1D Model for Thermally Stratified Hot-Water Energy Storage
Abstract
:1. Introduction
1.1. Literature Overview
1.2. Findings
2. Materials and Methods
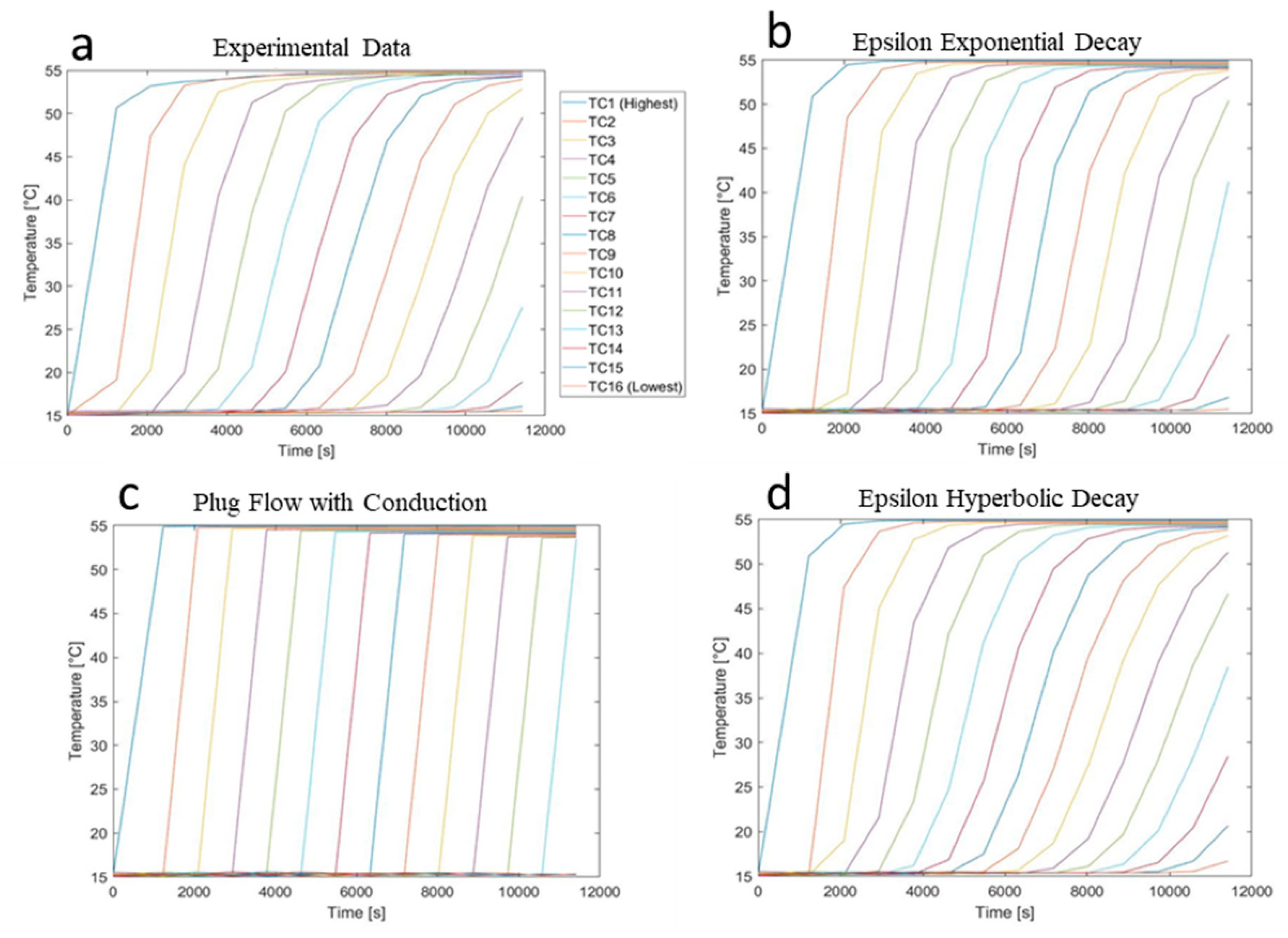
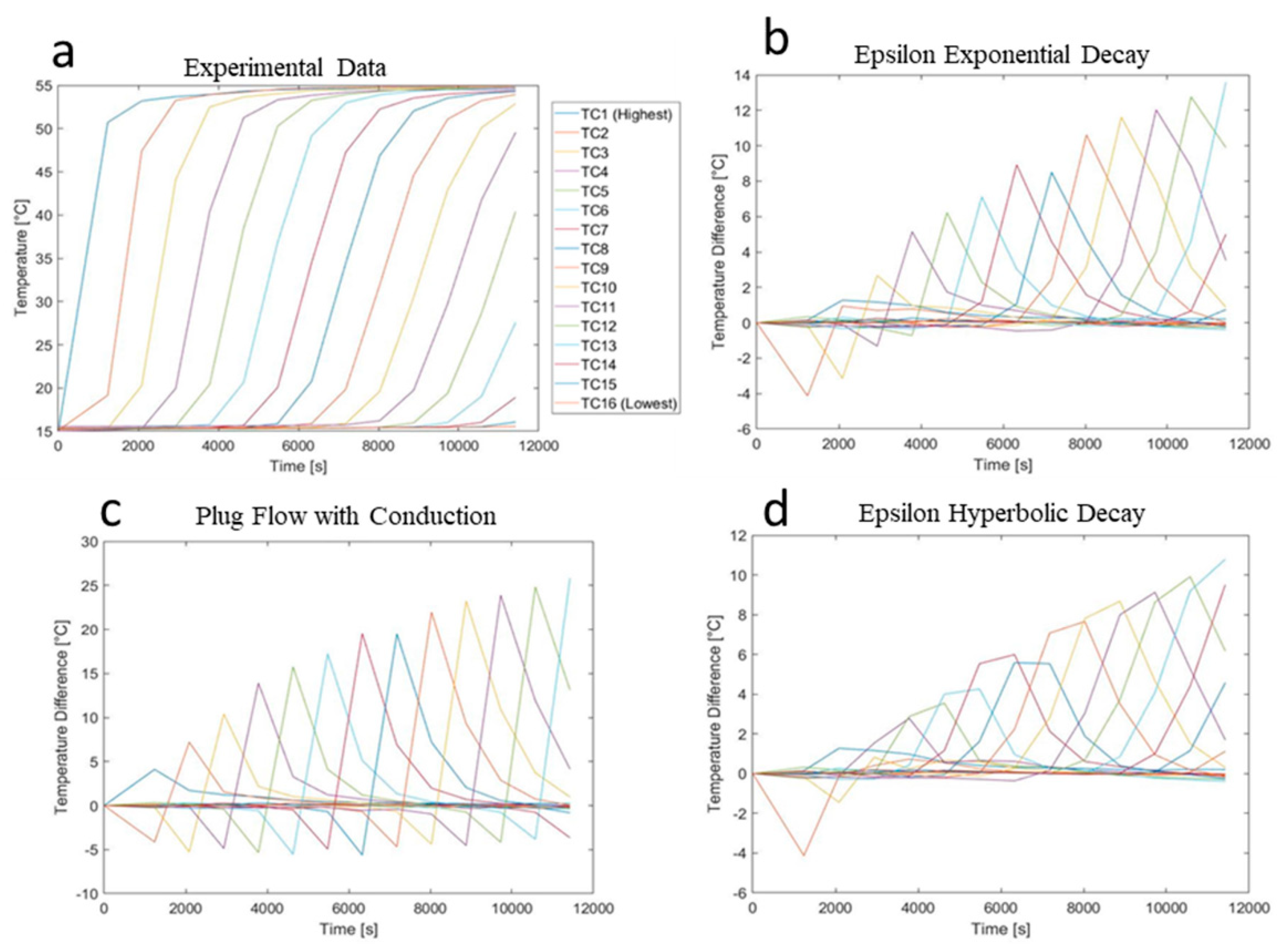
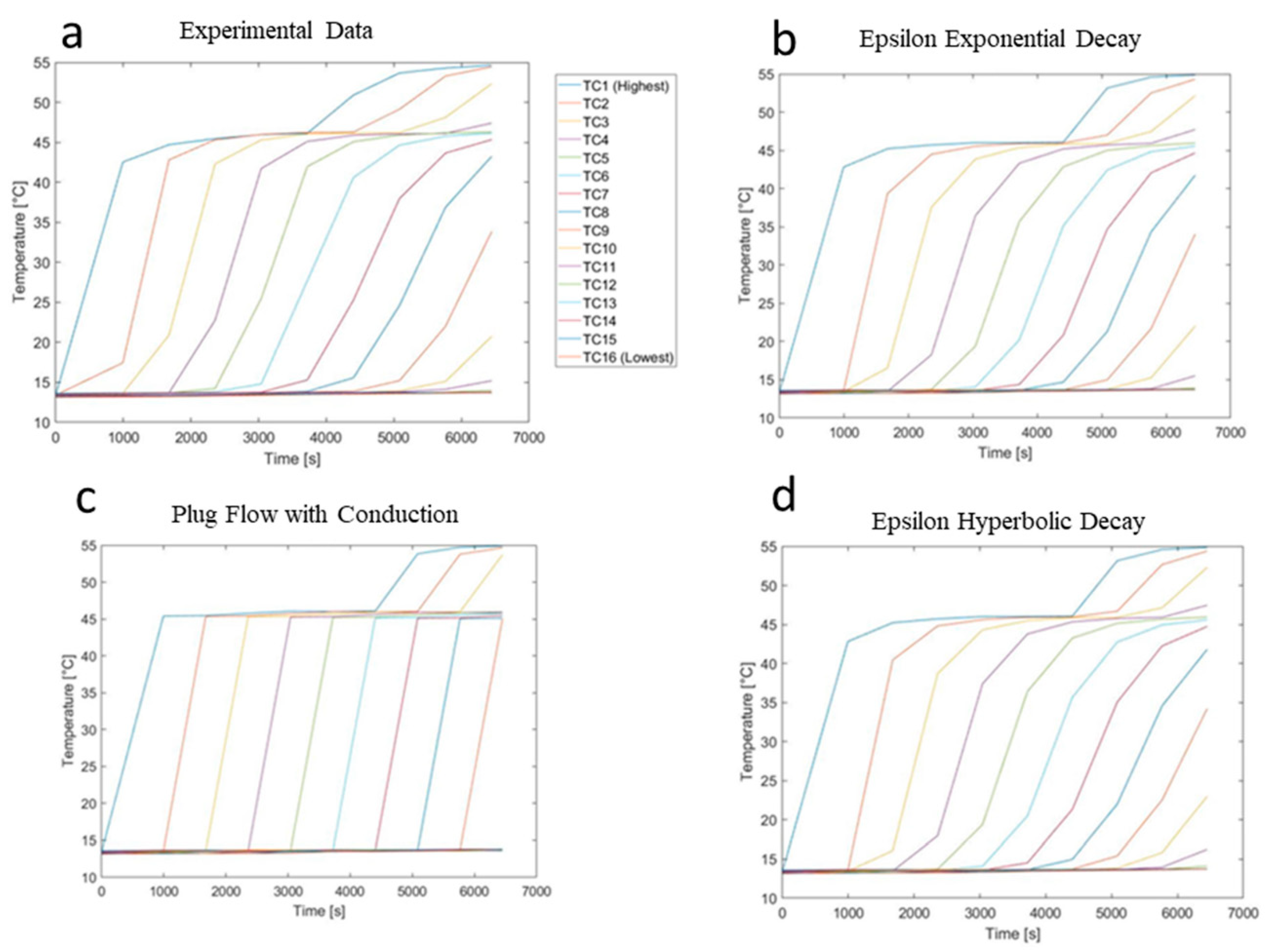
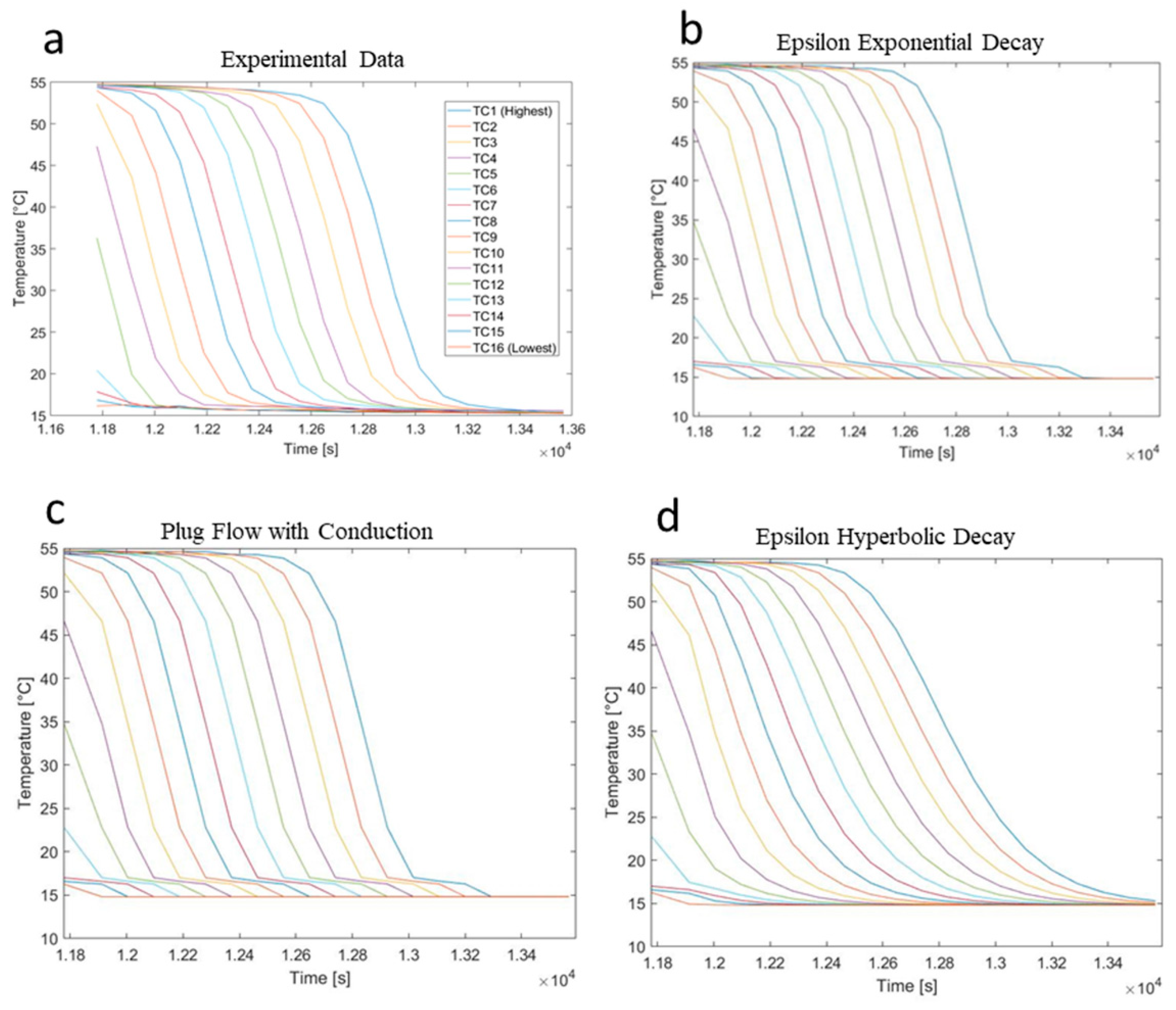
3. Results
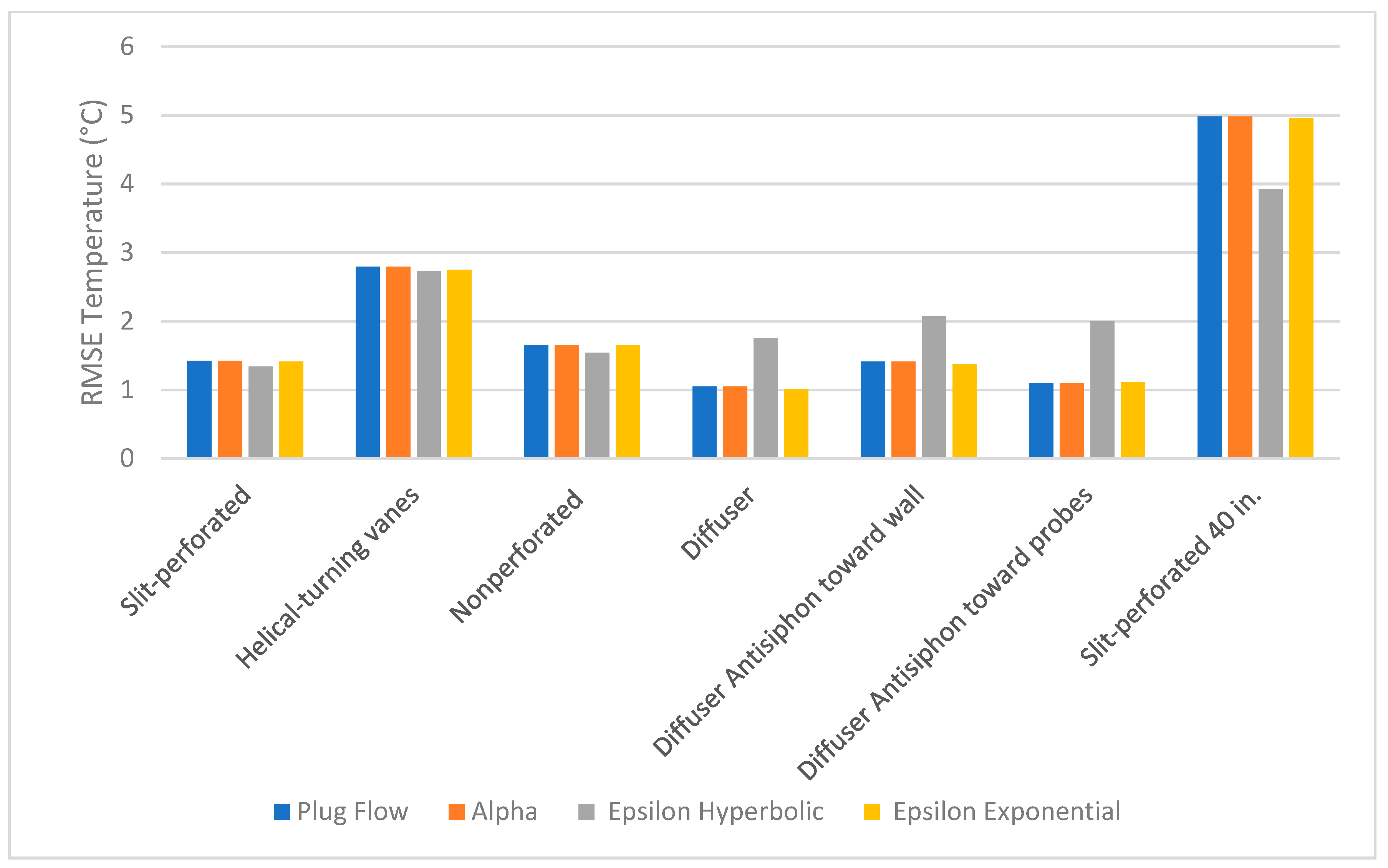
Root Mean Square Error Comparisons between Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | multiplicative fitting parameter (m2/s) |
| B | exponent fitting parameter (undefined fractional units) |
| C | volumetric Courant number |
| CED | convection-eddy diffusion |
| Cp | specific heat at constant pressure (W/kg K) |
| EDF | eddy diffusivity factor |
| n | node number |
| N | total number of nodes |
| Re | Reynolds number |
| Ri | Richardson number |
| time difference between solution steps (s) | |
| temperature a node n at the previous nondimensional time (°C) | |
| overall coefficient of heat loss times the area fraction of the tank (W/K) | |
| velocity in the vertical direction (m/s) | |
| volumetric flow rate (m3/s) | |
| volume difference between the two nodes of the solution (m3) | |
| height difference between nodes (m) | |
| y | height in vertical direction (m) |
| Greek | |
| thermal diffusivity (m2/s) | |
| inlet epsilon factor solved by empirical fits | |
| density (kg/m3) | |
| kinematic viscosity (m2/s) | |
| Subscripts | |
| amb | ambient temperature |
References
- Rendall, J. Thermal Stratification in Hot Water Tanks: A Review, an Empirical Fit, a Novel Model and a Prototype Diffuser; Texas A&M University: Kingsville, TX, USA, 2019. [Google Scholar]
- Steinert, P.; Göppert, S.; Platzer, B. Transient calculation of charge and discharge cycles in thermally stratified energy storages. Sol. Energy 2013, 97, 505–516. [Google Scholar] [CrossRef]
- Lavan, Z.; Thompson, J. Experimental study of thermally stratified hot water storage tanks. Sol. Energy 1977, 19, 519–524. [Google Scholar] [CrossRef]
- Homan, K.O. Integral Solutions for Transient Temperature Profiles in Stably-Stratified Open Enclosures. J. Heat Transf. 2003, 125, 273. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, M.; Wang, Z.; Li, X.; Chen, L. Thermal stratification in a cylindrical tank due to heat losses while in standby mode. Sol. Energy 2019, 222–234. [Google Scholar] [CrossRef]
- Njoku, H.O.; Ekechukwu, O.V.; Onyegegbu, S.O. Analysis of stratified thermal storage systems: An overview. Heat Mass Transf. 2014, 50, 1017–1030. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Huang, H.; Dou, B.; Huang, X.; Goula, M.A. The experimental investigation of the thermal stratification in a solar hot water tank. Renew. Energy 2019, 862–874. [Google Scholar] [CrossRef]
- Huang, H.; Wang, Z.; Zhang, H.; Dou, B.; Huang, X.; Liang, H.; Goula, M.A. An experimental investigation on thermal stratification characteristics with PCMs in solar water tank. Sol. Energy 2019, 177, 8–21. [Google Scholar] [CrossRef]
- Lake, A.; Rezaie, B. Energy and exergy efficiencies assessment for a stratified cold thermal energy storage. Appl. Energy 2018, 220, 605–615. [Google Scholar] [CrossRef]
- Kurşun, B. Thermal stratification enhancement in cylindrical and rectangular hot water tanks with truncated cone and pyramid shaped insulation geometry. Sol. Energy 2018, 169, 512–525. [Google Scholar] [CrossRef]
- Spall, R.E. A numerical study of transient mixed convection in cylindrical thermal storage tanks. Int. J. Heat Mass Transf. 1998, 41, 2003–2011. [Google Scholar] [CrossRef]
- Jordan, U.; Furbo, S. Thermal stratification in small solar domestic storage tanks caused by draw-offs. Sol. Energy 2005, 78, 291–300. [Google Scholar] [CrossRef]
- Bahnfleth, W.P.; Song, J.; Cimbala, J.M. Measured and modeled charging of a stratified chilled water thermal storage tank with slotted pipe diffusers. HVAC R Res. 2003, 9, 467–491. [Google Scholar] [CrossRef]
- Kaloudis, E.; Grigoriadis, D.G.E.; Papanicolaou, E.; Panidis, T. Large eddy simulations of turbulent mixed convection in the charging of a rectangular thermal storage tank. Int. J. Heat Fluid Flow 2013, 44, 776–791. [Google Scholar] [CrossRef]
- Garbrecht, O. Large Eddy Simulation of Three-Dimensional Mixed Convection on a Vertical Plate; Institute of Heat and Mass Transfer, RWTH Aachen University: Aachen, North Rhine-Westohalia, Germany, 2017. [Google Scholar]
- Matulka, A.; López, P.; Redondo, J.M.; Tarquis, A. On the entrainment coefficient in a forced plume: Quantitative effects of source parameter. Nonlinear Process. Geophys. 2014, 21, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Tinaikar, A.; Advaith, S.; Chetia, U.K.; Manu, K.V.; Basu, S. Spatio-temporal disruption of thermocline by successive laminar vortex pairs in a single tank thermal energy storage. Appl. Therm. Eng. 2016, 109, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Brown, N.M.; Lai, F.C. Enhanced thermal stratification in a liquid storage tank with a porous manifold. Sol. Energy 2011, 85, 1409–1417. [Google Scholar] [CrossRef]
- Capocelli, M.; Caputo, G.; De Falco, M.; Balog, I.; Piemonte, V. Numerical Modeling of a Novel Thermocline Thermal Storage for Concentrated Solar Power. J. Sol. Energy Eng. 2019, 141, 051001. [Google Scholar] [CrossRef]
- Nelson, J.E.B.; Balakrishnan, A.R.; Srinivasa Murthy, S. Parametric studies on thermally stratified chilled water storage systems. Appl. Therm. Eng. 1999, 19, 89–115. [Google Scholar] [CrossRef]
- Kaloudis, E.; Grigoriadis, D.G.E.; Papanicolaou, E. Numerical simulations of constant-influx gravity currents in confined spaces: Application to thermal storage tanks. Int. J. Therm. Sci. 2016, 108, 1–16. [Google Scholar] [CrossRef]
- Wildin, M.W.; Sohn, C.W. AD-A273 511 Flow and Temperature Distribution in a Naturally Stratified Thermal Storage Tank; Construction Engineering Research Lab.: Champaign, IL, USA, 1993. [Google Scholar]
- Yoo, H.; Pak, E.-T.T. Theoretical model of the charging process for stratified thermal storage tanks. Sol. Energy 1993, 51, 513–519. [Google Scholar] [CrossRef]
- Hahne, E.; Chen, Y. Numerical study of flow and heat transfer characteristics in hot water stores. Sol. Energy 1998, 64, 9–18. [Google Scholar] [CrossRef]
- Rendall, J.D.; Gluesenkamp, K.R.; Worek, W.; Abu-Heiba, A.; Nawaz, K.; Gehl, T. Empirical characterization of vertical-tube inlets in hot-water storage tanks. Int. Commun. Heat Mass Transf. 2020, 119, 104838. [Google Scholar] [CrossRef]
- Cole, R.L.; Bellinger, F.O. Thermally stratified tanks. ASHRAE Trans. 1982, 88, 1005–1007. [Google Scholar]
- Bulnes, F.K.; Gluesenkamp, K.R.; Rendall, J. Comparision of plug flow and multi-node stratified tank modeling approaches regarding computational effeciency and accuracy. In Proceedings of the ASME 2020 International Mechancial Engineering Congress and Exposition, Online, 16–19 November 2020; pp. 1–9. [Google Scholar]
- Kleinbach, E.M. Performance Study of One-Dimensional Models for Stratified Thermal Storage Tank by Master of Science University of Wisconsin-Madison. Sol. Energy 1990, 50, 155–166. [Google Scholar] [CrossRef]
- Zurigat, Y.H.; Liche, P.R.; Ghajar, A.J. Influence of inlet geometry on mixing in thermocline thermal energy storage. Int. J. Heat Mass Transf. 1991, 34, 115–125. [Google Scholar] [CrossRef]
- Han, Y.M.; Wang, R.Z.; Dai, Y.J. Thermal stratification within the water tank. Renew. Sustain. Energy Rev. 2009, 13, 1014–1026. [Google Scholar] [CrossRef]
- Gluesenkamp, K.R.; Bush, J.D. Impact on Water Heater Performance of Heating Methods that Promote Tank Temperature Stratification. In Proceedings of the ASHRAE Annual Meeting, St. Louis, MO, USA, 25–29 June 2016. [Google Scholar]
- Elatar, A.; Nawaz, K.; Shen, B.; Baxter, V.; Abdelaziz, O. Characterization of Wrapped Coil Tank Water Heater during Charging/Discharging. In Proceedings of the ASME Proceedings Paper, ASME International, Tampa, FL, USA, 3–9 November 2018; pp. 1–8. [Google Scholar]
- Shen, B.; New, J.; Baxter, V. Air source integrated heat pump simulation model for EnergyPlus. Energy Build. 2017, 156, 197–206. [Google Scholar] [CrossRef]
- Shen, B.; Nawaz, K.; Baxter, V.; Elatar, A. Development and validation of quasi-steady-state heat pump water heater model having stratified water tank and wrapped-tank condenser. Int. J. Refrig. 2018, 87, 78–90. [Google Scholar] [CrossRef]
- Shen, B.; Nawaz, K.; Elatar, A.; Baxter, V. A hardware-based heat pump water heater design model for quasi-steady-state simulation. In Proceedings of the 25th IIR International Congress of Refrigeration, Montreal, QC, Canada, 25–31 August 2019; Volume 2019, pp. 4310–4317. [Google Scholar]
- Nawaz, K.; Shen, B.; Elatar, A.; Baxter, V.; Abdelaziz, O. R1234yf and R1234ze(E) as low-GWP refrigerants for residential heat pump water heaters. Int. J. Refrig. 2017, 82, 348–365. [Google Scholar] [CrossRef]
- Nawaz, K.; Shen, B.; Elatar, A.; Baxter, V.; Abdelaziz, O. Performance optimization of CO2 heat pump water heater. Int. J. Refrig. 2018, 85, 213–228. [Google Scholar] [CrossRef]
- Rahman, A.; Smith, A.D.; Fumo, N. Performance modeling and parametric study of a stratified water thermal storage tank. Appl. Therm. Eng. 2016, 100, 668–679. [Google Scholar] [CrossRef]
- Paradis, P.L.; Rousse, D.R.; Lamarche, L.; Nesreddine, H.; Talbot, M.H. One-dimensional model of a stratified thermal storage tank with supercritical coiled heat exchanger. Appl. Therm. Eng. 2018, 134, 379–395. [Google Scholar] [CrossRef]
- Padovan, R.; Manzan, M.; De Zorzi, E.Z.; Gullì, G.; Frazzica, A. Model Development and Validation for a Tank in Tank Water Thermal Storage for Domestic Application. Energy Procedia 2015, 81, 74–81. [Google Scholar] [CrossRef] [Green Version]
- Ye, Y.; Lu, J.; Ding, J.; Wang, W.; Yan, J. Numerical simulation on the storage performance of a phase change materials based metal hydride hydrogen storage tank. Appl. Energy 2020, 278, 115682. [Google Scholar] [CrossRef]
- Neri, M.; Chiavazzo, E.; Mongibello, L. Numerical simulation and validation of commercial hot water tanks integrated with phase change material-based storage units. J. Energy Storage 2020, 32, 101938. [Google Scholar] [CrossRef]
- Ahmed, N.; Elfeky, K.E.; Qaisrani, M.A.; Wang, Q.W. Numerical characterization of thermocline behaviour of combined sensible-latent heat storage tank using brick manganese rod structure impregnated with PCM capsules. Sol. Energy 2019, 180, 243–256. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; Mazairac, W.; De Schutter, B. A 1-dimensional continuous and smooth model for thermally stratified storage tanks including mixing and buoyancy. Appl. Energy 2019, 248, 640–655. [Google Scholar] [CrossRef]
- Raccanello, J.; Rech, S.; Lazzaretto, A. Simplified dynamic modeling of single-tank thermal energy storage systems. Energy 2019, 182, 1154–1172. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991; ISBN 13 978-0-471-69867-8. [Google Scholar]
- Oppel, F.J.; Ghajar, A.J.; Moretti, P.M. Computer simulation of stratified heat storage. Appl. Energy 1986, 23, 205–224. [Google Scholar] [CrossRef]
- Zurigat, Y.H.; Liche, P.R.; Ghajar, A.J. Turbulent mixing correlations for a thermocline thermal storage tank. Appl. Energy 1986, 93, 293–309. [Google Scholar]
- Taler, D.; Sobota, T.; Jaremkiewicz, M.; Taler, J. Influence of the Thermometer Inertial on the Quality of Temperature Control in a Hot Liquid Tank Heater with Electric Energy. Energies 2020, 13, 4039. [Google Scholar] [CrossRef]
- Briggs, D.A.; Ferziger, J.H.; Koseff, J.R.; Monismith, S.G. Turbulent mixing in a shear-free stably stratified two-layer fluid. J. Fluid Mech. 1998, 354, 175–208. [Google Scholar] [CrossRef]
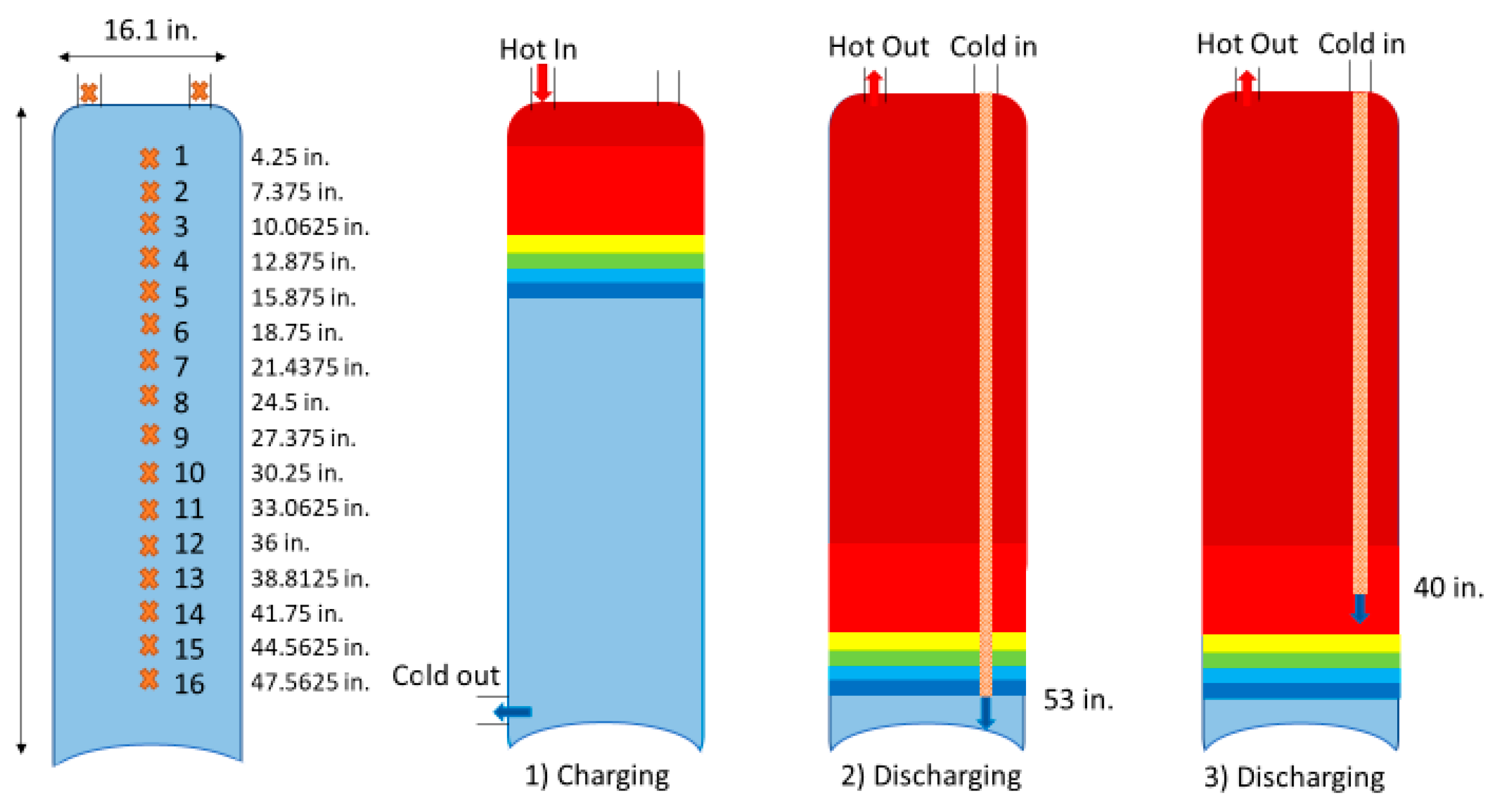
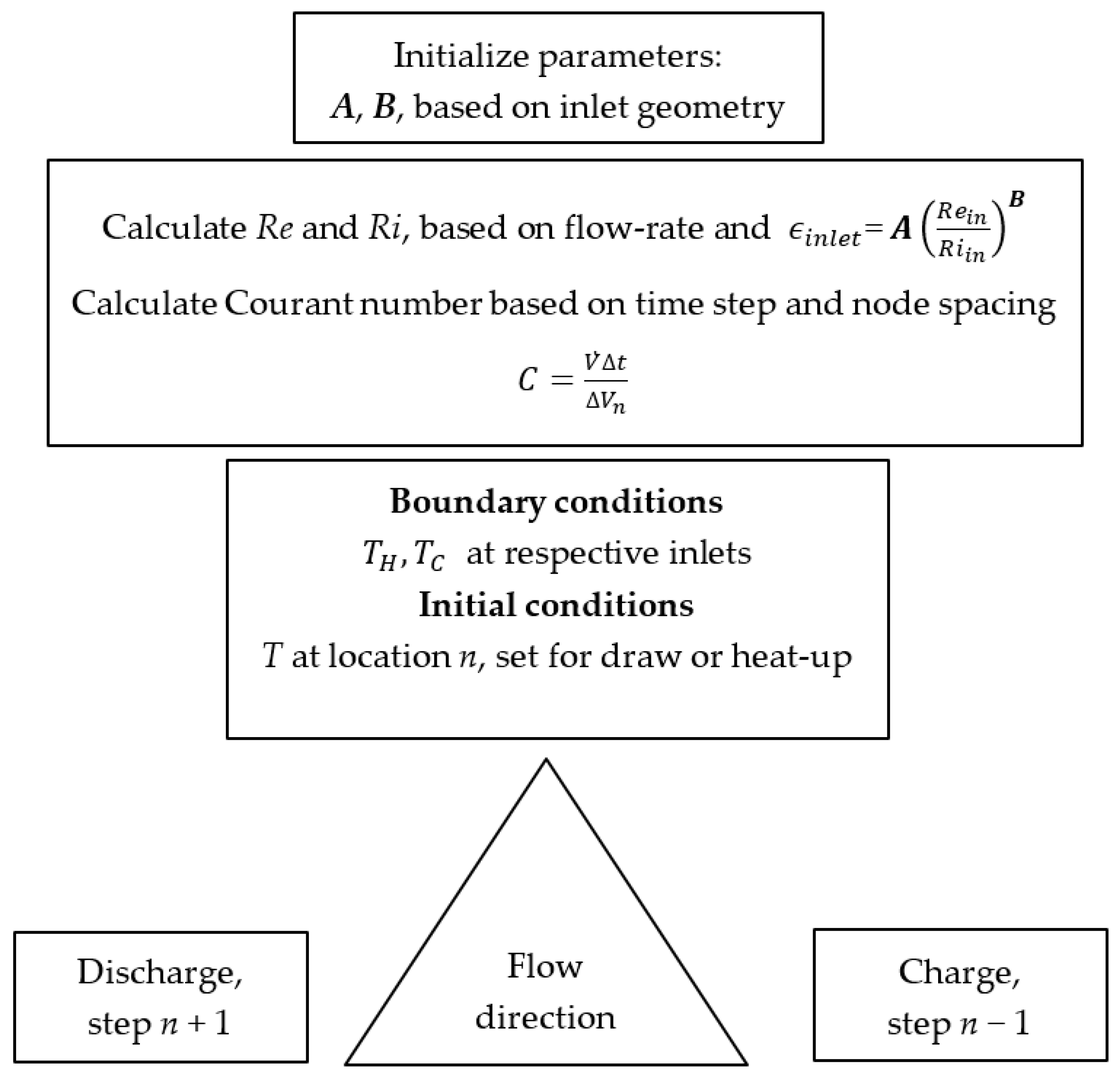



| Inlet Type | A | B | R2 | Fit Range (GPM) | Reynolds Number |
|---|---|---|---|---|---|
| Round pipe flush with top of tank | 619 | 0.3068 | 1.00 | 0.15 ≤ ≤ 0.9 | ~3200 to 16,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rendall, J.; Karg Bulnes, F.; Gluesenkamp, K.; Abu-Heiba, A.; Worek, W.; Nawaz, K. A Flow Rate Dependent 1D Model for Thermally Stratified Hot-Water Energy Storage. Energies 2021, 14, 2611. https://doi.org/10.3390/en14092611
Rendall J, Karg Bulnes F, Gluesenkamp K, Abu-Heiba A, Worek W, Nawaz K. A Flow Rate Dependent 1D Model for Thermally Stratified Hot-Water Energy Storage. Energies. 2021; 14(9):2611. https://doi.org/10.3390/en14092611
Chicago/Turabian StyleRendall, Joseph, Fernando Karg Bulnes, Kyle Gluesenkamp, Ahmad Abu-Heiba, William Worek, and Kashif Nawaz. 2021. "A Flow Rate Dependent 1D Model for Thermally Stratified Hot-Water Energy Storage" Energies 14, no. 9: 2611. https://doi.org/10.3390/en14092611
APA StyleRendall, J., Karg Bulnes, F., Gluesenkamp, K., Abu-Heiba, A., Worek, W., & Nawaz, K. (2021). A Flow Rate Dependent 1D Model for Thermally Stratified Hot-Water Energy Storage. Energies, 14(9), 2611. https://doi.org/10.3390/en14092611






