Effect of Energy Consumption Reduction on the Decrease of CO₂ Emissions during the Aircraft’s Flight

Abstract

Climate change requires the reduction of energy consumption in transport and the associated fuel consumption, and emission of pollutants into the atmosphere. This issue is particularly relevant to air transport. Referring to the current legislative actions aimed at reducing the negative impact of air transport on the environment, the paper describes the possibilities of reducing energy consumption and related emissions. The Boeing 737 aircraft equipped with Snecma CFM 56C engines was adopted for the research. The research problem focused on determining a cruising trajectory characterized by the shortest cruising time and the lowest energy consumption by the aircraft during the flight between two selected European airports in given meteorological conditions. In the analysis, the Dijsktra’s algorithm was applied and built-in MATLAB functions were used. Based on the studied case, it was shown that it was possible to reduce both energy consumption and CO₂ emissions by 10%. The novelty of the research described in the paper is the use of the energy approach and tying the energy parameters of the aircraft to the flight duration and pollutants emission in the cruise phase.

1. Introduction

With the development of transport, the problem of its adverse impact on the natural environment is associated inextricably. Air transport contributes to anthropogenic climate change, depletion of the ozone layer, and deterioration of air quality, both locally and globally.

During the main cruise of flight—the cruise phase, subsonic planes usually operate in the atmosphere that includes the upper troposphere, the tropopause, and the lower stratosphere. The incomplete combustion of fuel by turbine jet engines results in the following gaseous products: carbon dioxide (CO₂), carbon monoxide (CO), nitrogen oxides (NOx), sulfur oxides (SOx), unburned hydrocarbons (HC) and particulate matter (PM). The type of aircraft, its aerodynamic characteristics, the type of engine, the kind of fuel used, as well as the operating conditions (the flight altitude and speed, thrust or power range)—affect both the amount and type of pollutants emitted. The passenger and transport aircraft, which are equipped with engines characterized by the highest power and the highest fuel consumption relative to the generated thrust, introduce the greatest amount of pollutants into the atmosphere.

Hopefully, the trend of sustainable and responsible further development of aviation is increasingly visible, and environmental protection issues become as important as financial issues or those related to safety and security.

It is possible to minimize the adverse impact of air transport on the environment due to many already developed and constantly improved regulations and requirements in this field. The first international regulations on the reduction of fuel consumption, exhaust emissions, and noise entered into force in 1972 (Annex 16 to the ICAO Convention) [1]. In March 2018, Annex 16 of the new wording entered into force. It regulates the emission and noise limits for new aviation structures in line with CAEP (the Committee on Aviation Environmental Protection of the ICAO Council, Montreal, Canada) recommendations.

At the same time, there appear international research programs, initiatives of international organizations, local governments, and non-governmental organizations [2,3,4,5], as well as declarations of aviation companies, which aim at the sustainable and responsible development of aviation. Lots of attention is paid to the issues of reducing CO₂ emissions in the aviation sector (through so-called carbon-neutral growth) and reducing the carbon footprint of air cargo transport [6,7].

Based on the statistical data of the United Nations Framework Convention on Climate Change (UNFCCC), the CO₂ emissions associated to all flights that departed from the EU-28 and the EFTA countries in the years 1990–2016, augmented from 88 to 171 million tonnes (by +94%) [3]. And, based on the data issued by the Convention on Long-Range Transboundary Air Pollution (CLRTAP) of the United Nations Economic Commission, the NOx emissions augmented from 313 to 700 thousand tonnes (by +124%) in the same period of time. The forecasted CO₂ emissions show a steady increase of 3% to 4% annually until 2030 [3,8], and in the case of NOx emissions, they are expected to increase by at least 16% by 2040 [3,6].

Research works are also conducted in line with the above-mentioned tasks, such as research related to increasing the efficiency of air traffic, developing a new approach to flight planning, and more effective use of cargo and passenger space in the aircraft.

As previous research has shown [9,10,11,12,13], aircraft emissions could be cut down if in the process of planning the flight trajectory of the aircraft on a given route, not only the criterion of the shortest distance would be taken into account, but also the criterion of the lowest fuel consumption, which in turn results in the lowest total pollutants emissions in jet engine exhaust. Planning the flight in terms of the above mentioned criteria is complicated because of the conditions in which the aircraft travels. It is therefore essential to take into consideration the limitations coming from the organization of the airspace and the rules therein, as well as the forecast weather conditions. The duration of the flight, the amount of fuel consumed, and the cost of a given flight on a given route are determined by the weather conditions, mainly the wind direction and speed. Additionally, air density, pressure, and temperature must be known. It should be noted that temperature affects the sound speed, on the basis of which the Mach number for a plane flying with a given true air speed can be determined. The wind direction and speed, on the other hand, affect the speed of the aircraft relative to the ground (velocity over ground) and consequently the duration of its flight [9,10].

Another way to reduce pollutants emissions is to modify the structure of the aircraft or propulsion—e.g., the use of a hybrid propulsion (combination of internal combustion and electric propulsion) [14,15,16,17]. Development of new technical solutions, new aerodynamic systems, new materials, and new propulsion—these are challenges for aviation industry and scientists for the next several years [18,19,20,21].

The aim of the work presented in this paper is to show a possible method to reduce the consumption of energy stored in hydrocarbon fuel during the aircraft flight and the related exhaust emissions into the atmosphere. Previously conducted studies did not include an energy approach at all. A novelty in relation to earlier research is tying the energy consumption of the aircraft to the pollutants emissions and flight duration in the cruise phase. The presented research results from the current trends in aviation—increasing attention is paid to the possibilities of sustainable and low-emission aviation development.

2. The Research Methodology

Determining the performance of an aircraft during its flight, such as flight duration or flight time in a given phase (e.g., take-off, climb, or cruise), is possible on the basis of the energy approach. This approach enables to compare the performance of the aircraft using different propulsion configurations [14,22,23].

Four fundamental forces act on the aircraft in flight: the lift force L, the force of gravity Q, the drag force D, and the thrust $P_S$. These forces are applied at various points in the aircraft, e.g., L and D—in the center of the wing pressure, Q—in the center of gravity of the aircraft’s, and $P_S$—in the line of the power unit.

In the considerations and approximate calculations, however, it can be assumed that the forces are applied at one point—in the center of gravity of the aircraft’s [24]. In addition to the above-mentioned forces, other forces may act on the aircraft, e.g., those generated on the control surface of the aircraft’s tail. However, they are usually ignored under these conditions.

General formulas describing the resultant value of the drag and lift forces acting on the aircraft are described by the following equations:

• drag force—$D$ (N):

  $$D=\frac{1}{2}·\rho ·S·V^2·C_D,$$

  (1)
• lift force—$L$ (N):

  $$L=\frac{1}{2}·\rho ·S·V^2·C_L,$$

  (2)

  where $\rho$—air density (kg/m³); $S$—wing area (m²); $V$—speed (m/s); $C_D$—drag coefficient (-); $C_L$—lift coefficient (-).

When considering steady flight, only these four forces applied at the center of gravity of the aircraft can be considered, based on the fact that in steady flight there is the following relationship between them:

• the lift is balanced by the weight of the aircraft—$Q$ (N):

  $$L-Q=0,$$

  (3)
• the thrust of the power unit—$P_S$ (N) is equal to the drag force of the aircraft:

  $$P_S=D.$$

  (4)

This means that in steady flight, the weight of the aircraft is balanced by the lift force, and the drag force is balanced by the thrust of the engine; and these are the forces acting on the entire aircraft, not just the wing.

The Thrust Method [24] is used to determine the demand of the aircraft for thrust during flight. This method, used especially in jet aircrafts, is based on the condition of equal thrust required for flight and disposable thrust as a condition of steady flight (without acceleration) on a rectilinear path. The thrust required for flight is the force equal to drag at a given flight speed. Disposable thrust is the thrust that can be provided by the power unit at the same speed. Formula (4) shows that if the aircraft is moving in the steady flight, the required engine thrust is equal to the total drag. The required thrust is then determined by calculating the aerodynamic drag of the aircraft. The value of the required thrust is influenced by several factors; the weight of the aircraft and the wing area in a specific case are constant. If the flight occurs at a certain altitude, the air density is also constant. Therefore, in the considered conditions, the aircraft speed and the drag coefficient may change. Therefore, the thrust required for flight depends on the speed and the drag coefficient, but these quantities are closely related.

During the flight of the aircraft, the total mass of the aircraft decreases due to the fuel consumption. Along a flight path, the aircraft encounters various meteorological conditions that affect the flight parameters. As it is difficult to determine the average ambient conditions for the entire flight, it is difficult to obtain uniform aircraft performance parameters based only on the thrust method.

The problem is solved by tying the thrust required for flight to the energy required for flight of the aircraft. On the other hand, knowing the value of the energy required for the flight of an aircraft and relating it to the energy stored in the fuel on board the aircraft, it is possible to determine the range and duration of the flight, as well as tie the energy consumption to fuel consumption and the total emission of pollutants in the exhausts.

Energy approach or energy concept is not novel. In 1954, it was used by [25] to solve problems, such as determination of the optimum path for an aircraft to reach speed and altitude, where the optimum may imply either minimum time or minimum fuel. In the paper, the specific energy concept, based on computation of the total energy of an aircraft as the sum of its kinetic and potential energies, is used to solve climb problems. This approach was also used by [26] to discuss the flight path optimization issues related to missions not involving a range constraint (e.g., minimum time energy climb), as well as problems requiring a more sophisticated flight path management capability.

In the era of the development and application of different propulsions, the energy approach to flight is becoming increasingly interesting, because it allows comparing various aircraft design systems, even those that are equipped with hybrid or purely electric propulsion. Research, such as [14,21,27] is conducted to determine the energy stored on board an aircraft—coming from fuel, hydrogen cells or batteries.

Hence, it seems worthwhile to determine the aircraft performance with the energy approach due to the possibility of referring to the energy stored on board the aircraft. In this way, it is possible to avoid complicated calculations when determining the performance of the aircraft, because the value of energy stored on board is directly related to the value of energy required to perform a given maneuver during the flight.

There are studies describing flight parameters using energy indicators, e.g., [25,26], but they mainly relate to such stages of flight as climbing and descending.

The research presented in this paper considers, however, the steady flight conditions in the cruise phase. During this stage of flight, as in any other one, the basic energy balance must exist between the total energy change of the aircraft, the energy derived from the fuel, the total energy change due to a weight change in the aircraft, and the energy dissipated against the drag. However, in the steady flight, there is no energy required to lift the aircraft, there is only work the aircraft needs to do to move horizontally from one point of the airspace to another one.

Knowing that in physical terms, the work is simply the energy transferred to or from an object by applying a force along its displacement, the energy required for flight during a steady flight constitutes the thrust generated by the power unit (P_S) operating at a given displacement, or range, i.e., [14]:

• energy required for flight—$E_N$ (J):

  $$E_N=P_S·V_{flight}·t,$$

  (5)

  where: $V_{flight}$—airspeed of aircraft at given altitude (m/s); $t$—flight time in a given flight phase (s).

The research presented in this paper shows the possibility of reducing energy consumption during the cruising phase of flight—due to the fact that this phase is the main stage of the aircraft mission. Lowering the energy is beneficial both economically—reducing fuel consumption during a given flight and ecologically—reducing the total emission to the atmosphere of pollutants present in jet engine exhausts. An analysis of this issue will be performed later in the paper.

Meteorological conditions—wind speeds and direction—affect the flight duration in the cruise phase. To determine the duration of the flight, it is necessary to compute the speed of the aircraft relative to the ground, as it is always given in relation to the air flow. The speed of the aircraft relative to the ground can be computed if the angle between the direction of the flight and the direction of the wind is known.

Knowing the distance covered by the aircraft in a given i-segment of the cruise phase, it is possible to calculate the time of flight in this segment:

$$t_i=\frac{L_i}{V_{flight}\mp V_{{wind}_i}·\cos {\alpha }_{{wind}_i}},$$

(6)

where: $t_i—$duration of the flight in a given i-segment of the cruise phase (s); $L_i$—distance covered by an aircraft in a given i-segment of the cruise phase (m); $V_{flight}$—airspeed of the aircraft at a given altitude (m/s); $V_{{wind}_i}$—wind speed in a given i-segment of the cruise phase (m/s); ${\alpha }_{{wind}_i}—$angle between the flight direction and the wind direction in a given i-segment of the cruise phase (°).

Total flight time in the cruise phase, t, given in Formula (5), is the sum of the durations of the flight in all segments of this phase of flight.

The following formula is used to determine the aircraft airspeed $V_{flight}$ (m/s) at a given cruising altitude:

$$V_{flight}=Ma·a_{cr},$$

(7)

where: $Ma$—Mach number, aircraft velocity in relation to air mass; $a_{cr}$—critical speed (m/s), where:

$$a_{cr}=\sqrt{k·R·T},$$

(8)

where: $k—$adiabatic exponent, $k=1.4$; R—individual gas constant; for dry air $R=287 \frac{\mathrm{J}}{\mathrm{kg}·\mathrm{K}}$; $T$—temperature at a given cruising altitude (K).

Therefore:

$$E_N=P_S·V_{flight}·t=P_S·Ma·\sqrt{k·R·T}·t,$$

(9)

Formula (9) can be used to compute the energy consumption during a given phase of flight, e.g., a cruise phase.

3. Results

3.1. Case Study

To conduct the research, a popular medium-range passenger aircraft, equipped with bypass jet engines SNECMA CFM56-3C was selected. The basic technical data of the aircraft is summarized in

Table 1. Basic technical data of the Boeing 737-300 aircraft [28].

Model	Seating Capacity	Length (m)	Wingspan (m)	Engines Type	Take-Off Thrust (kN)	Maximum Take-Off Weight (kg)	Aircraft Range (km)	Maximum Speed (km/h)
Boeing 737-300	128–149	33.40	28.88	2x Snecma CFM56-3C	2x 140	56,742	5475	912

.

The speed and altitude characteristics of the Snecma CFM56-3C engine, presented in Figure 1, were determined based on the procedure described in detail in [12]. Based on the characteristics obtained, the operating parameters corresponding to the parameters of the aircraft flight were determined.

On the basis of earlier research conducted by the author in [12], the value of the thrust generated by the power unit, adopted for further research was $P_S=$ 56,240 N.

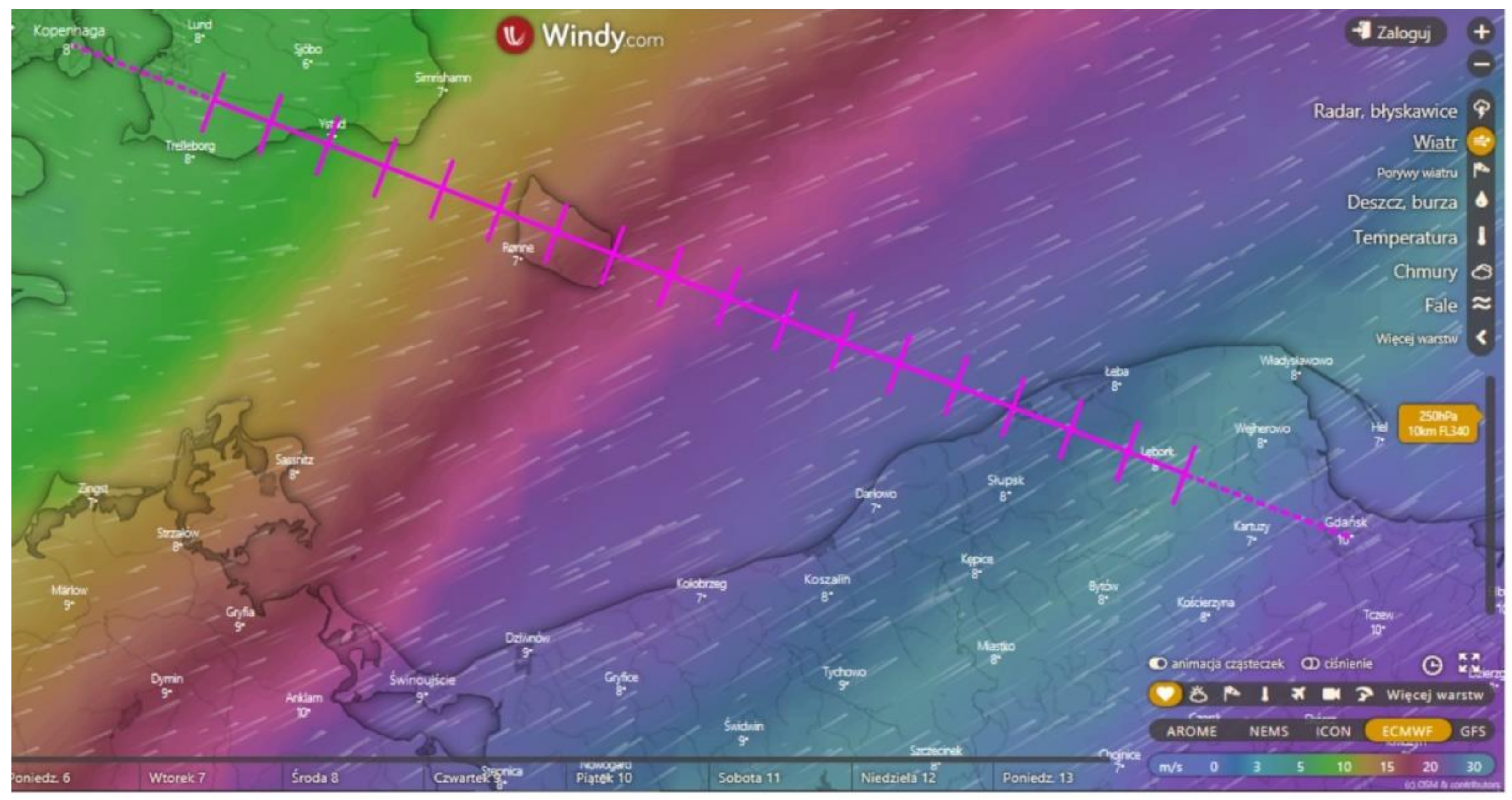
For the research an exemplary route between Copenhagen (Denmark) and Gdansk (Poland) of the length of 526 km was taken (Figure 2).

The main parameters of the exemplary flight carried out by Boeing 737-300 are shown in Figure 3.

A cruising altitude of 10,000 m was taken for the research. At this cruising altitude, the temperature T = 223.15 K. Assuming the flight speed in the cruise phase equal to 0.8 Ma, using Formula (7), the aircraft airspeed was determined: $V_{flight}$ = 239.5 m/s = 862 km/h.

Next, there was determined a trajectory, along which the aircraft will travel (purple line in Figure 4).

At 10 km, the cruise phase of the length of 408 km was assumed for further analyzes. It was next divided into 17 segments, 24 km long each (Figure 4). In each of these segments, the wind direction and speed were determined based upon meteorological data retrieved from windy.com website [30]. The research was conducted in accordance with currently used procedures of the flight trajectory tactical planning, which takes place usually about 1–2 days, and not less than two hours before the planned flight. In such a case, the weather forecast, upon which the flight is planned, is of the highest verifiability. Next, the flight plan is validated and approved.

The values of wind speeds and directions in particular segments, retrieved from [30], are presented in

Table 2. Flight conditions along the cruising trajectory at the altitude of 10 km on 6 April 2020.

Segment No.	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII	XIII	XIV	XV	XVI	XVII
Length (km)	24	24	24	24	24	24	24	24	24	24	24	24	24	24	24	24	24
$V_{win{d}_i}$ (m/s)	10	10	10	10	10	15	20	20	22	25	25	25	30	30	30	30	30
${\alpha }_{win{d}_i}$ (°)	3	20	20	43	42	40	42	43	44	45	45	45	45	45	45	45	45

. The angle between the flight direction and the wind direction, ${\alpha }_{{wind}_i}$, is given in (°).

To determine the total time of flight in cruising conditions on the route from Copenhagen to Gdansk, first the duration of flight in each segment of the cruise phase was computed, based on the wind distribution at the cruising altitude of 10 km and Formula (6). The results obtained are shown in

Table 3. Flight duration in cruising phase of the aircraft travelling with the speed of 0.8 Ma at the altitude of 10 km in meteorological conditions on 6 April 2020.

Flight Speed (Ma)	Time of Flight in a Given i-Segment of Cruise Phase ${\mathit{t}}_{\mathit{i}}$ (s)																	Total Time of Flight $\mathit{t}$ (min)
	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII	XIII	XIV	XV	XVI	XVII
0.8	96	96	96	97	97	96	94	94	94	93	93	93	92	92	92	92	92	26.70

.

Next, based on Formula (9), the energy consumption during the flight was computed, $E_N=$ 21,582 MJ.

To reduce the energy consumption on the assumed route in the cruise phase, a trajectory characterized by the lowest energy indices should be found.

3.2. Determining a Cruising Trajectory with the Lowest Energy Indices

To conduct the research, on the basis of the previous division of the airspace between Copenhagen and Gdansk in the cruise phase at the altitude of 10 km into 17 segments, it was next divided into 51 squares with a side length of 24 km. This set of squares together with their diagonals formed a grid—the edges of the graph along which the aircraft could travel from the starting point of the cruise phase to the end one. The weights were assigned to the edges of the graph. These weights were corresponding to the time required to go along a given edge. This value was determined for each edge of the graph taking into consideration both the speed and direction of wind.

To illustrate this specific case, on the map visualizing meteorological conditions at the cruising altitude of 10 km, presented in Figure 4, a layer containing the graph described above was put (Figure 5).

The flight speed in the cruise phase was assumed to be 0.8 Ma at the altitude of 10 km. Taking into account the given meteorological conditions at this altitude, as shown in the Figure 4 and Figure 5, a trajectory characterized by the lowest value of energy required for flight can be determined.

Knowing that the shorter the total flight time in the cruise phase, the lower the value of the energy required for flight, it is essential to determine the fastest path to be followed by the aircraft, i.e., the most sustainable path (trajectory) for this route, which lies on the grid presented in Figure 5. This grid is a graph made up of vertices (nodes) and edges.

Vertices of the graph store data relevant to the scenario. For example, if a graph is used to store data for a map, each vertex might represent a point defined by geographical coordinates. The connections between vertices are called edges. In a weighted graph, each edge has a weight (or cost) associated with it. In a graph representing a map, the edges could represent a connection between different points of a journey and the weight may represent the time to travel between these points. The path in such a weighted graph is an orderly sequence of successive edges to go through from the start vertex, i.e., in the analyzed case—the point defining the beginning of the cruise phase, to the end vertex, i.e., in the analyzed case—the point defining the end of the cruise phase. There may be many various paths in the graph between the two selected vertices. Paths can also be defined using a sequence of consecutively passed vertices. Each two successive vertices must be connected by an edge with the assigned weight.

Several commonly used algorithms can be used to find the most sustainable in terms of given criteria, paths between vertices in a graph, e.g., Dijkstra’s Algorithm, Floyd-Warshall Algorithm, or Bellman-Ford Algorithm. Dijkstra’s algorithm, which works on a weighted graph, stands out from the rest because of its ability to find the path with the lowest cost (e.g., the shortest path or the fastest path) between a given source vertex in the graph and every other vertex within the same structure of the graph data. It means that rather than just finding the most sustainable path from the starting vertex to another specific vertex, provided the graph does not change, the algorithm works to find such a path to every single reachable vertex. The algorithm runs until all reachable vertices have been visited.

With Dijkstra’s algorithm, it is therefore possible to solve the problem of finding the ‘most sustainable’ path, or the ‘best’ way to get from one vertex to another vertex. This is called the ‘least cost path’ or the ‘minimum cost path’. The cost of a path is calculated by adding up all individual weights for the edges that make up the path. Having a graph with the selected vertex (source), the algorithm will therefore compute the ‘cost’ from the source to all other vertices [31]. The algorithm can be easily modified to search only for the ‘least cost’ path to one fixed vertex, simply interrupting the procedure when the target vertex is reached.

The Dijkstra’s algorithm seems to be perfect to conduct the analyses on the studied case. Firstly, it will allow to find in the graph all ‘least cost’ paths between a selected vertex and all other ones and therefore determine different flight trajectories in terms of given criteria. Secondly, it will enable to compute the total value of the ‘cost’ associated with the graph edges, e.g., the total length or total transition time of each of these paths.

For the studied case of a flight from Copenhagen to Gdansk, based on the meteorological data adopted for the research, the angle of wind impact on each edge of the graph was determined and the wind speed read from the map was assigned to each edge.

Then this data was entered into a program developed in MATLAB software (ver. 2020) to perform computations and determine the paths characterized by the lowest values of cruising time and energy required for flight. By applying the MATLAB built-in function—ShortestPath, based on Dijkstra’s algorithm [32], all possible trajectories along which the Boeing 737-300 could travel in the cruise phase were determined. For all of these trajectories, the cruising time and energy required to cover the distance were computed. From among the determined trajectories, four of them (

Table 4. Cruising time and corresponding energy consumption during the flight along the four determined trajectories (D) and a reference trajectory (R) on the Copenhagen–Gdansk route.

Trajectory No.	Start Vertex No.	End Vertex No.	$$\begin{gathered} \mathbf{Cruising} \mathbf{Time} \\ \mathit{t} \left(\mathbf{min}\right) \end{gathered}$$	$$\begin{gathered} \mathbf{Total} \mathbf{Energy} \\ {\mathit{E}}_{\mathit{N}} \left(\mathbf{GJ}\right) \end{gathered}$$
No. 1 (Figure 6a)—(D)	4	65	28.02	22.649
No. 2 (Figure 6a)—(D)	1	68	27.26	22.035
No. 3 (Figure 6b)—(D)	2	67	26.38	21.324
No. 4 (Figure 6b)—(D)	1	65	25.46	20.580
No. 5 (Figure 6c)—(R)	2	66	26.70	21.582

and Figure 6a,b) were selected for further research: two of the highest values of time and energy required for flight, and two of the lowest ones. Next, these values were compared with a reference trajectory (presented in Table 4 and Figure 6c), characterized by: $t$ = 26.70 min; $E_N$ = 21,582 MJ.

The most sustainable in terms of the shortest flight time and the lowest energy required for flight would be trajectory No. 4 and the least—trajectory No. 1, which is characterized by the longest flight duration and the highest value of energy required for flight. The reference trajectory taken for the research appeared to be neither the most nor the least favorable in terms of the adopted criteria. To show to what extent the selection of a trajectory affects the amount of energy required for flight, the results obtained for different trajectories were compared. In

Table 5. The numerical and percentage difference between the flight duration and the energy consumption during the flight on the most sustainable trajectory (No. 4) in relation to the reference trajectory (No. 5) and to another determined trajectory No. 1 (trajectory No. 4. = 100%) on the Copenhagen–Gdansk route.

Relation	$\mathbf{∆}\mathit{t} \left(\mathbf{min}\right)$	$\mathbf{∆}\mathit{t} (\%)$	$\mathbf{∆}{\mathit{E}}_{\mathit{N}} \left(\mathbf{GJ}\right)$	$\mathbf{∆}{\mathit{E}}_{\mathit{N}} (\%)$
No. 4 vs. No. 5	−1.24	−4.87	−1.002	−4.87
No. 4 vs. No. 1	+2.56	+10.05	+2.069	+10.05

, the results for the reference trajectory No. 5 are compared with the results for the determined trajectories No. 1 and No. 4.

As it can be noticed, the shortening of the flight time by 1.24 min resulted in a decrease of E_N by approx. 1 GJ (nearly 5%), whereas the extension of the flight time by 2.56 min resulted in an increase of E_N by approx. 2 GJ (by 10%).

The presented results show how important is to define the appropriate starting and ending points along the route in the airspace (the points of entering and leaving the cruising phase). In real conditions, however, it is not always possible to select any starting and any end point, as these points are geographically determined (location of airports as well as the take-off and approach options). Nevertheless, theoretically, it is possible to perform such a procedure for any previously defined starting and ending point in terms of given criteria.

In the next step, the impact of the selection of the cruising trajectory on economic and ecological factors (reduction of fuel consumption and CO₂ emissions in exhausts of aircraft engines) was analyzed. To determine the CO₂ emission, the following formula was used [12]:

$$M_{C{O}_2}=M{I}_{C{O}_2}·C_H·t·l,$$

(10)

where: $M_{C{O}_2}$—emission of CO₂ in the exhaust (kg); $M{I}_{C{O}_2}$—emission index for CO₂, depending on the fuel consumption C_H, where $M{I}_{C{O}_2}=3.155$ kg/kg of fuel [33]; $t$—engine run time at a given thrust (h); $l$—number of jet engines; $C_H$—fuel consumption in given cruising conditions (kg/h), where:

$$C_H=K·SFC,$$

(11)

where: $K$—engine thrust (N); $SFC$—specific fuel consumption (kg/(N∙h)).

For the analyzed case—the reference trajectory (Figure 6c)—CO₂ emission in the exhaust can be computed, knowing that: the emission index for CO₂ is a constant value $M{I}_{C{O}_2}$ = 3.155 kg/kg fuel; fuel consumption for one Snecma CFM56-3C engine at the speed of 0.8 Ma and cruising altitude of 10 km is $C_H$ = 1700 kg/h [12]; total time of the flight in cruising phase along the reference trajectory is $t$ = 26.70 min = 0.445 h, and the number of Snecma CFM56-3C engines l = 2. Thus, the total amount of carbon dioxide emitted on this trajectory $M_{C{O}_2}$ = 4 773, 52 kg.

Knowing that for the reference trajectory, a ratio: $\frac{M_{C{O}_2} \left(\mathrm{kg}\right)}{E_N \left(\mathrm{J}\right)}=2.21176·{10}^{-7} \mathrm{kg}/\mathrm{J}$, a new coefficient, called CO₂ Emission Coefficient, $M{E}_{C{O}_2}\left(\mathrm{kg}/\mathrm{J}\right)$, was introduced, tying the value of the total energy consumed to cover the cruising distance to the value of total CO₂ emission. This coefficient corresponds to a given operating point of the engine.

Knowing that regardless of the selection of the flight trajectory on the adopted route, the engines operate at the same parameters (performance), it is possible to calculate CO₂ emissions for any other determined trajectory.

$$M_{jC{O}_2}=ME ·E_{Nj},$$

(12)

where: $M_{jC{O}_2}—$total emission of CO₂ in the exhaust (kg) emitted on a j-trajectory; $M{E}_{C{O}_2}$– CO₂ emission coefficient, $M{E}_{C{O}_2}=2.21176·{10}^{-7} \frac{\mathrm{kg}}{\mathrm{J}}$; $E_{Nj}$—total energy (J) consumption for a j-trajectory.

In this way, the total CO₂ emission values for four previously determined trajectories were calculated (

Table 6. Cruising time, and corresponding energy consumption and CO₂ emission during the flight along four determined trajectories (D) and a reference trajectory (R) on the Copenhagen–Gdansk route.

Trajectory No.	Start Vertex No.	End Vertex No.	$$\begin{gathered} \mathbf{Cruising} \mathbf{Time} \\ \mathit{t} \left(\mathbf{min}\right) \end{gathered}$$	$$\begin{gathered} \mathbf{Total} \\ \mathbf{Energy} \\ {\mathit{E}}_{\mathit{N}} \left(\mathbf{GJ}\right) \end{gathered}$$	${\mathbf{CO}}_2 \mathbf{Emission} \mathbf{Coefficient} \mathit{M}{\mathit{E}}_{\mathit{C}{\mathit{O}}_2}\left(\mathbf{k}\mathbf{g}/\mathbf{J}\right)$	$\mathbf{Total} {\mathbf{CO}}_2 \mathbf{Emission} {\mathit{M}}_{\mathit{C}{\mathit{O}}_2} \left(\mathbf{k}\mathbf{g}\right)$
No. 1 (Figure 6a)—(D)	4	65	28.02	22.649	2.21176 × 10−7	5009.51
No. 2 (Figure 6a)—(D)	1	68	27.26	22.035	2.21176 × 10−7	4873.63
No. 3 (Figure 6b)—(D)	2	67	26.38	21.324	2.21176 × 10−7	4716.30
No. 4 (Figure 6b)—(D)	1	65	25.46	20.580	2.21176 × 10−7	4551.82
No. 5 (Figure 6c)—(R)	2	66	26.70	21.582	2.21176 × 10−7	4773.52

).

To show to what extent the selection of the trajectory affects the reduction or increase of carbon dioxide emissions, the results obtained for different trajectories were compared. In

Table 7. The numerical and percentage difference between the flight duration, the energy consumption, and the total amount of CO₂ emitted on the most sustainable trajectory (No. 4). in relation to the reference trajectory (No. 5) and to another determined trajectory No. 1 (trajectory No. 4 = 100%) on the Copenhagen–Gdansk route.

Relation	$\mathbf{∆}\mathit{t} \left(\mathbf{min}\right)$	$\mathbf{∆}\mathit{t} (\%)$	$\mathbf{∆}{\mathit{E}}_{\mathit{N}} \left(\mathbf{GJ}\right)$	$\mathbf{∆}{\mathit{E}}_{\mathit{N}} (\%)$	$\mathbf{∆}{\mathit{M}}_{\mathit{C}{\mathit{O}}_2} \left(\mathbf{k}\mathbf{g}\right)$	$\mathbf{∆}{\mathit{M}}_{\mathit{C}{\mathit{O}}_2} (\%)$
No. 4 vs. No. 5	−1.24	−4.87	−1.002	−4.87	−221.70	−4.87
No. 4 vs. No. 1	+2.56	+10.05	+2.069	+10.05	+457.69	+10.05

, the results for the reference trajectory No. 5 are compared with the results for the determined trajectories No. 1 and No. 4.

As it can be noticed, the shortening of the flight time by 1.24 min resulted in a decrease of $M_{C{O}_2}$ by 221.7 kg (approx. by −5%), whereas the extension of the flight time by 2.56 min, resulted in an increase of $M_{C{O}_2}$ by 457.7 kg (by +10%).

4. Discussion

The research conducted has revealed a strong correlation between energy and emission—the lower the amount of energy consumed to cover a given distance, the lower the amount of pollutants emitted.

The research has shown that the application of the Dijkstra’s algorithm enables to determine such a trajectory of the aircraft movement in the main phase of flight—the cruise phase, which is characterized by the lowest energy consumption and the lowest emission of pollutants in the exhaust. The percentage differences between some of the indicated trajectories were significant. For example, if the aircraft moved along the trajectory No. 1, the amount of energy required for flight, as well as the total amount of emitted CO₂ would be 10% higher than in the case of trajectory No. 4. Such a result is substantial and shows that further analyses are worth conducting.

The studies on the possible methods of reduction of emissions were carried out for CO₂—the greenhouse gas. However, in further studies, the emission of other pollutants (e.g., CO, HC, NOx) will be analyzed as well, because numerous model investigations showed that these substances, emitted from aircraft engines as well as combustion and newly formed in the exhaust plume aerosols, may influence significantly the total ozone concentration, cloudiness, Earth’s radiation budget, and climate. Developing accurate calculation models for more accurate estimations of aircraft emissions, both in the Landing and Take-off cycle (LTO) and cruising phase, will enable to indicate more sustainable flight trajectories, which will contribute to more sustainable and cleaner aviation.

Reducing the pollutants emission in the exhaust of aircraft engines can be achieved not only by shaping the flight trajectory, but also by modifying the structure of the aircraft. Currently, research on the possibilities of using hybrid propulsion in aviation is conducted worldwide. For instance, Airbus company developed the E-Fan and E-Fan X aircraft concepts [34], Pipistrel company introduced the Panthera aircraft with hybrid propulsion [35], and the Boeing company developed the Phantom aircraft equipped with a fuel cell to power avionics [36,37].

If the energy consumption on board the aircraft originated from the combustion of hydrocarbon fuel is reduced, the emission of all pollutants to the atmosphere will be reduced as well.

Research on hybrid and distributed propulsion systems has been conducted recently, e.g., [14,21], where various strategies for managing the energy stored on board the aircraft are presented. Interesting is the research on a set where in an aircraft equipped with several jet engines (e.g., Boeing 747, Airbus A340, or A380) one of the internal combustion engines is replaced by an electrically driven fan. The energy required to drive the fan comes both from the batteries installed on board the aircraft and from generators coupled with internal combustion engines.

The course of further research is to analyze the possibilities of energy consumption, fuel consumption, and the amount of pollutants emitted in the exhaust after the application of the hybrid system, in which, for example, in addition to jet engines, the aircraft will be equipped with a fan driven by an electric motor. It would be interesting to investigate to what extend such a configuration would have the economic and environmental impact. However, it is a complex task as the energy generated by generators coupled with jet engines is consumed to supply the electric motor. Moreover, due to the fact that jet engines generate additional energy to power the electric motor, they work under a greater load. Therefore, to calculate correctly the actual fuel consumption and the parameters of jet engine operation, it would be necessary to calculate their thermodynamic cycle taking into account the load from the electric generator. It would also be advisable to carry out a mass balance of such an aircraft. Such research will be conducted in the future.

The results of future studies on hybrid configuration could also enable manufacturers, aircraft operators, air navigation service providers, and public authorities to identify the finest means to reduce the adverse environmental impact of air transport by implementing best practices and developing more exact aircraft operating standards. They could also be the base for founding global environmental standards grounded on an objective scientific basis.