Void Fraction Prediction Method in Gas–Liquid Flow through Channel Packed with Open-Cell Metal Foams
Abstract
:1. Introduction
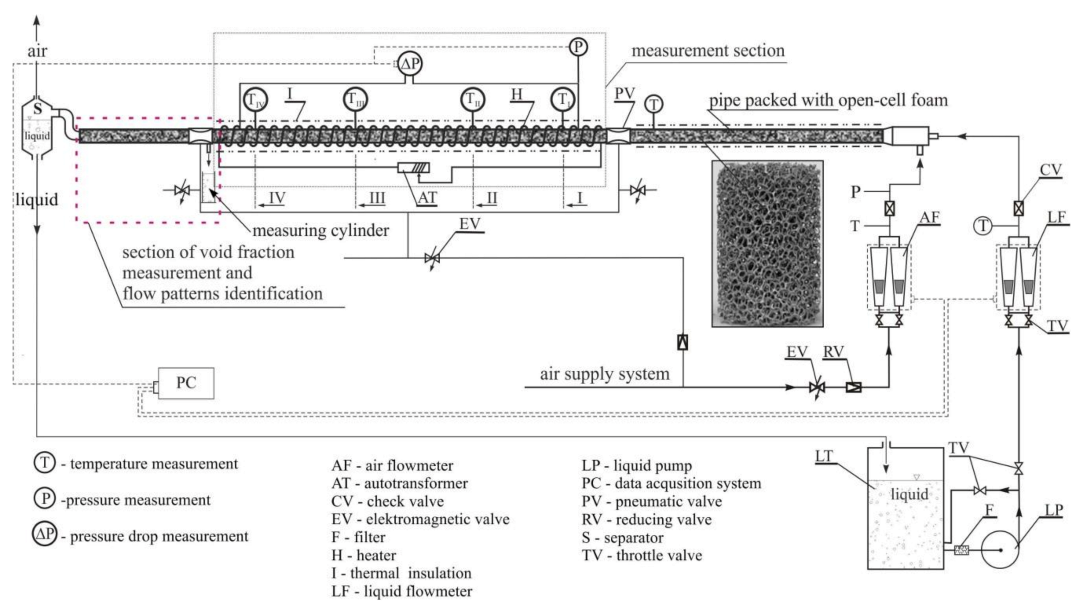
1.1. Scope of Experiment
1.2. Measurements Procedure
2. Results and Discussion
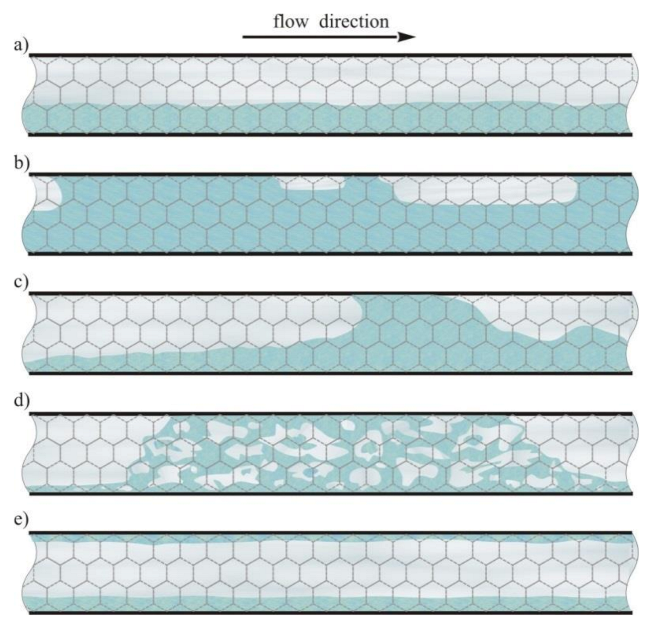
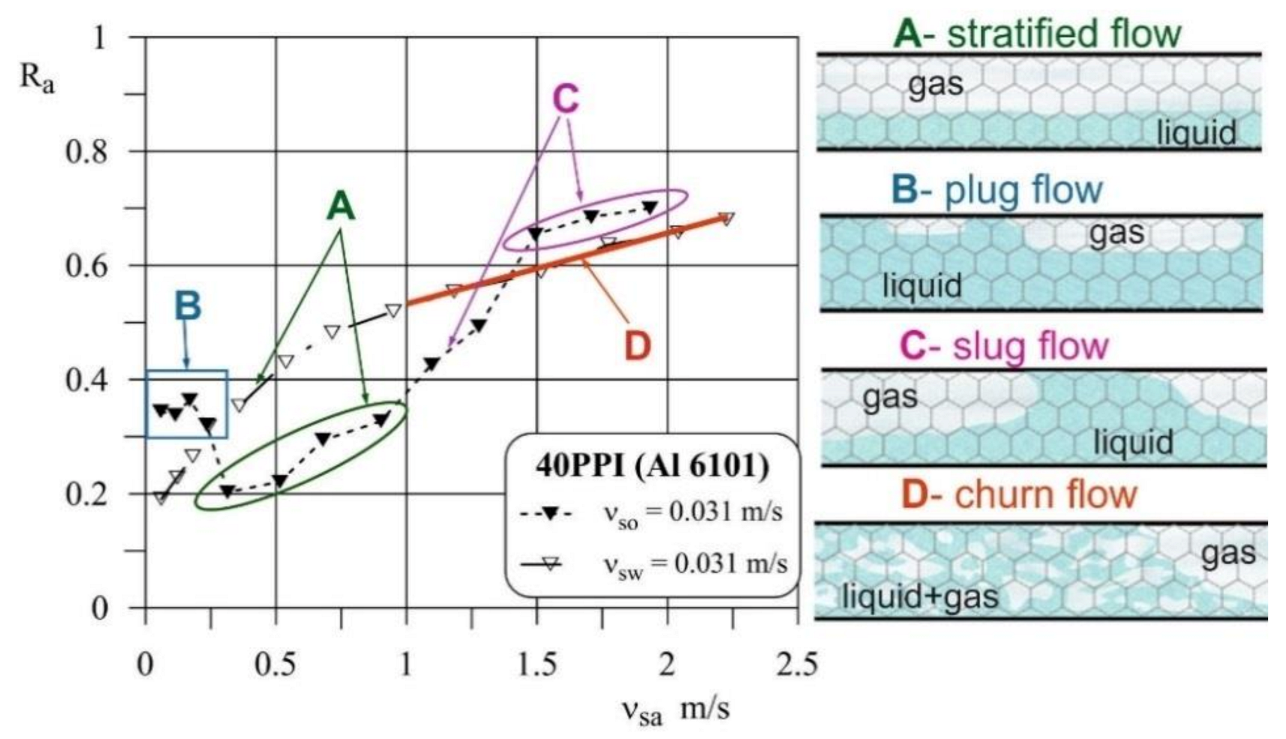
2.1. Flow Patterns
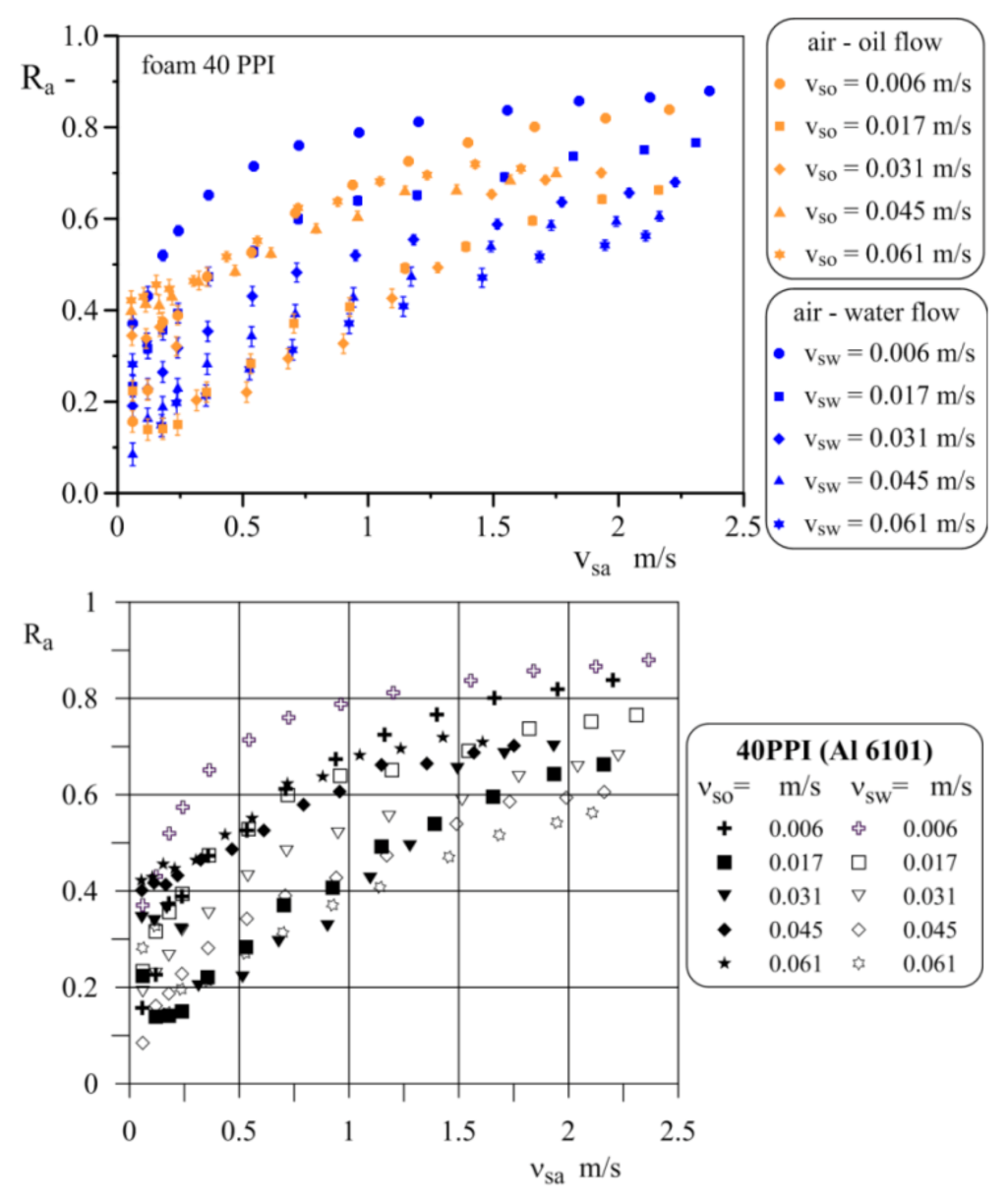
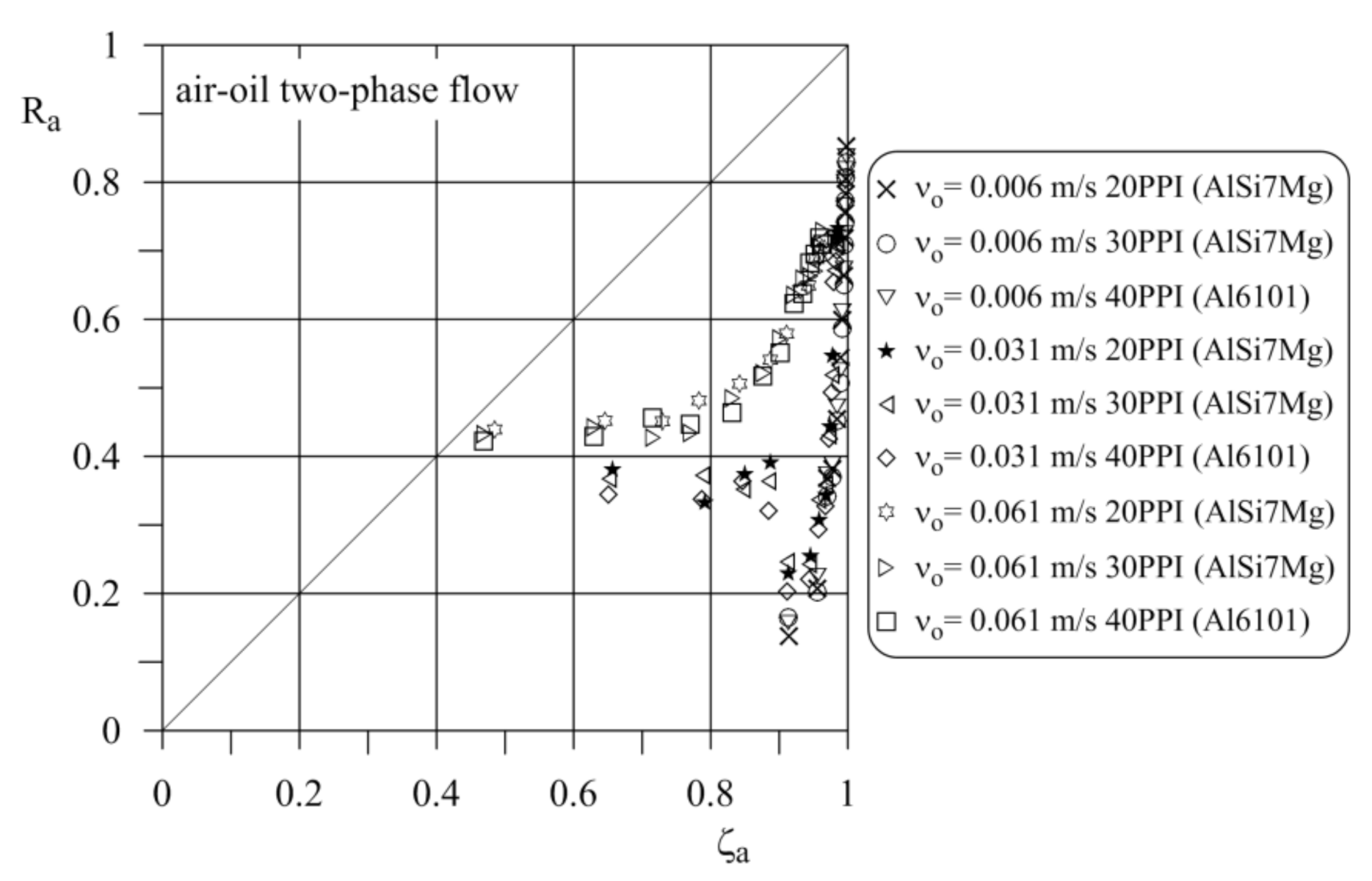
2.2. Void Fraction
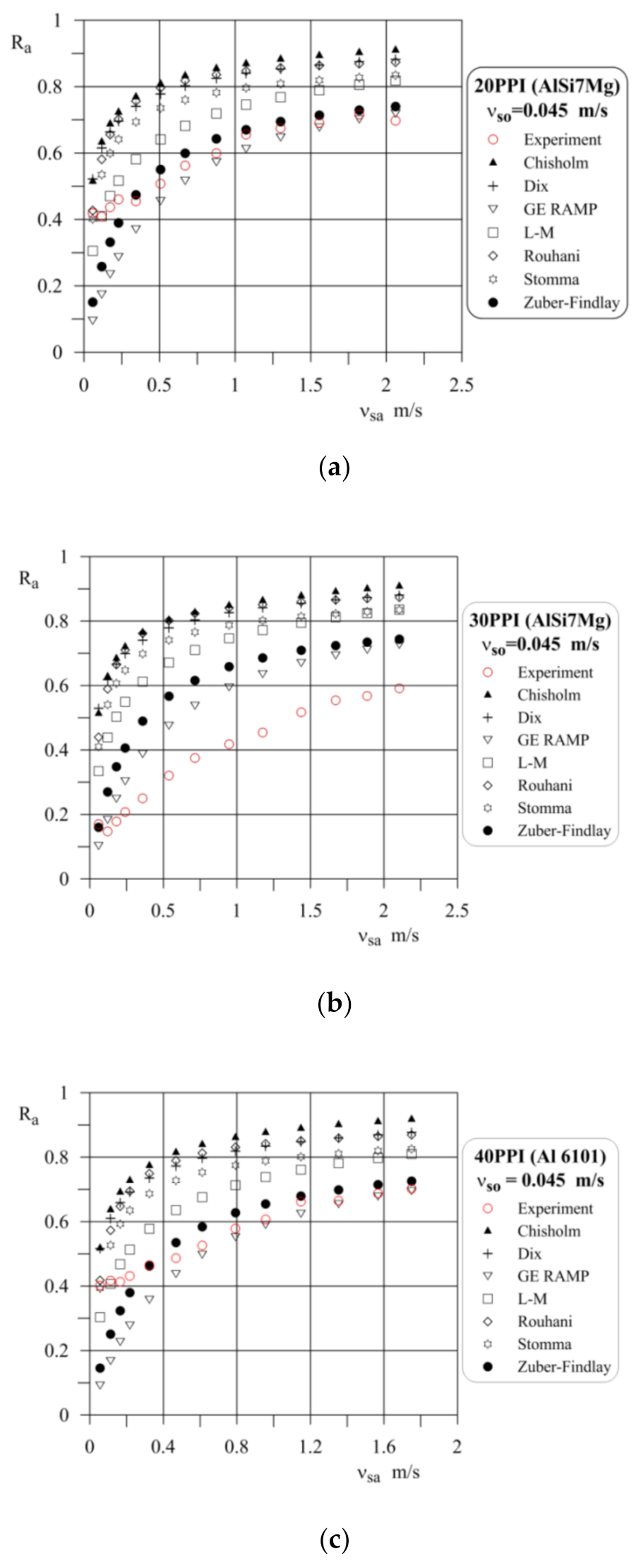
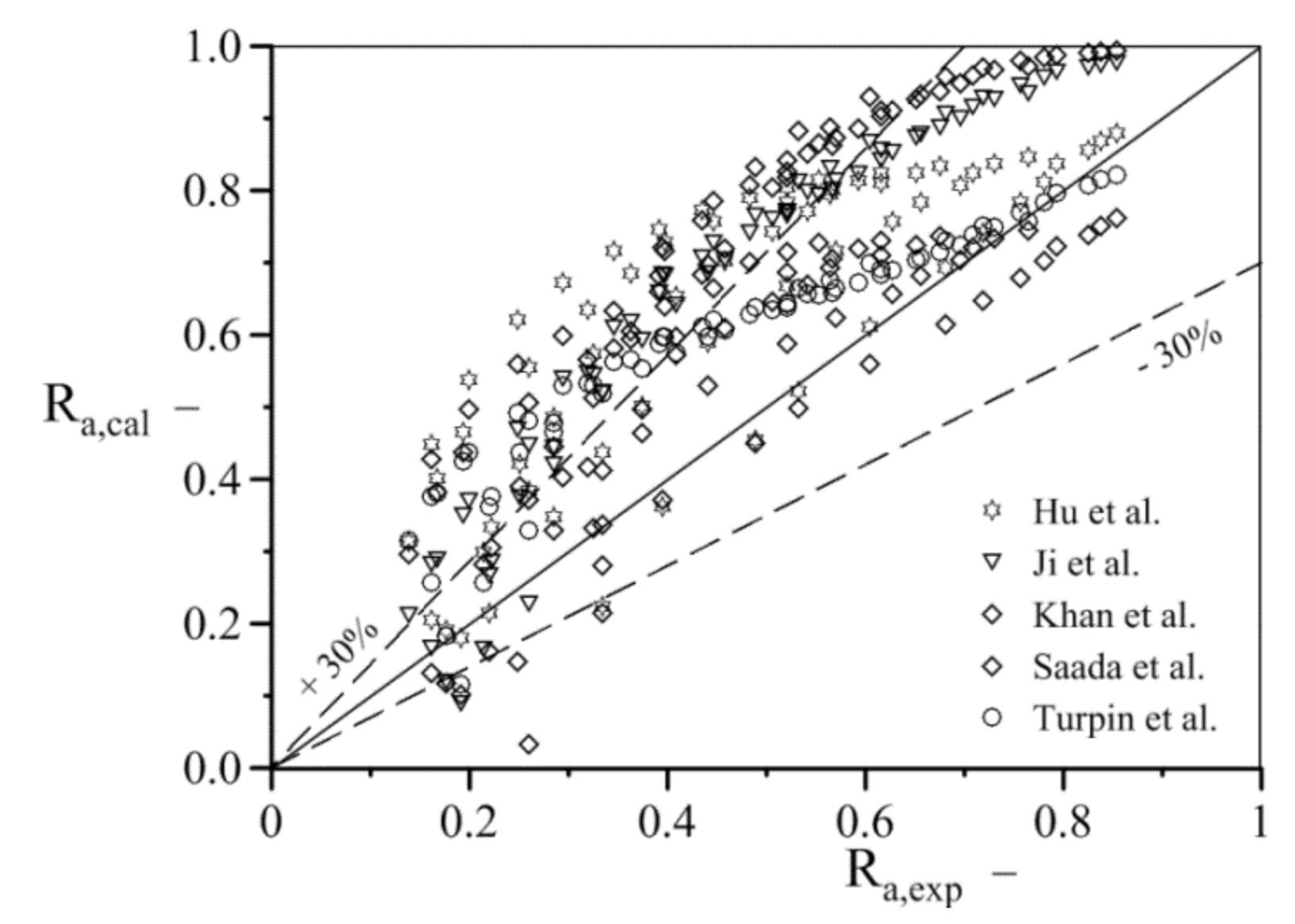
2.3. Evaluation of Model for Calculation of Void Fraction
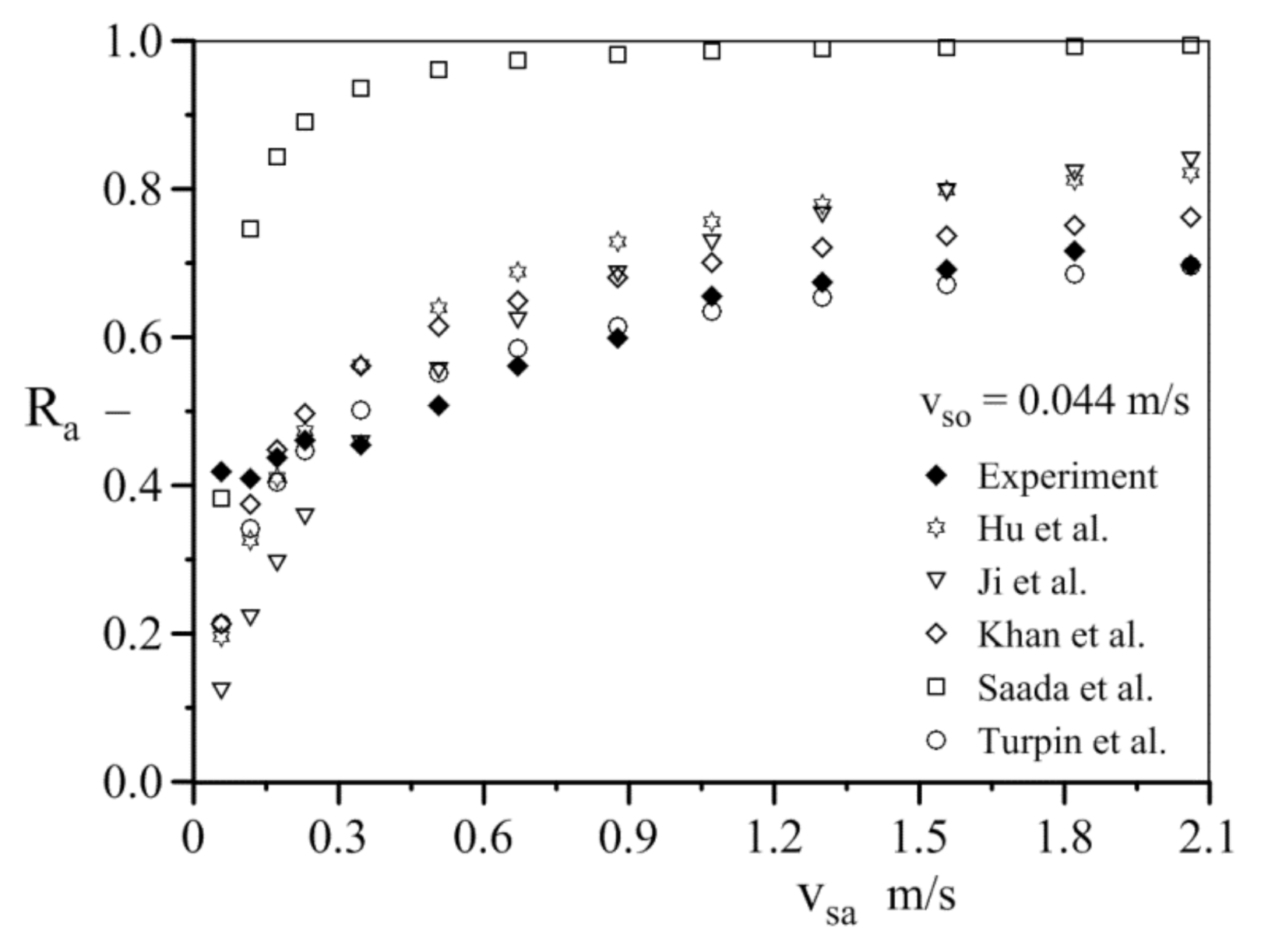
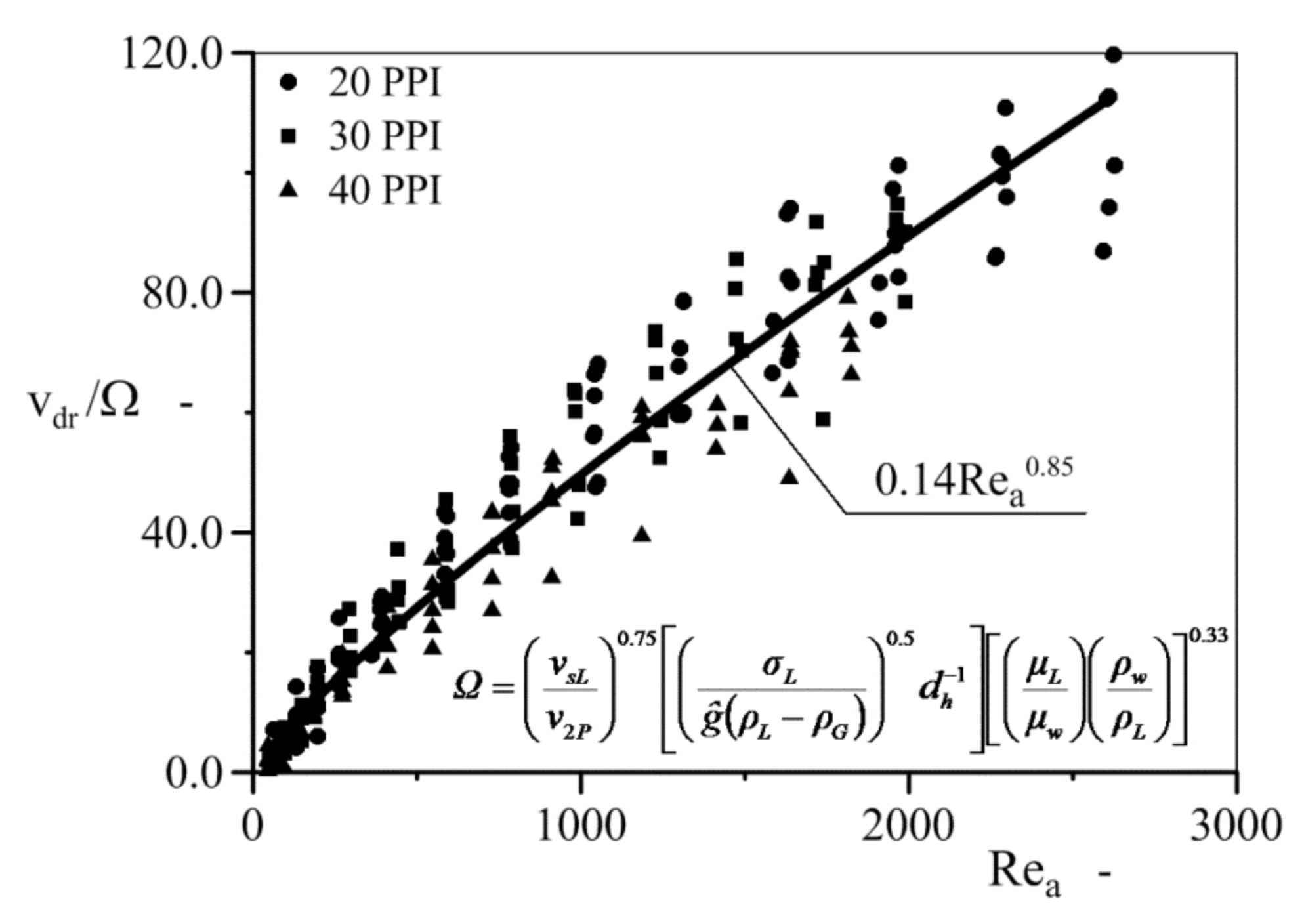
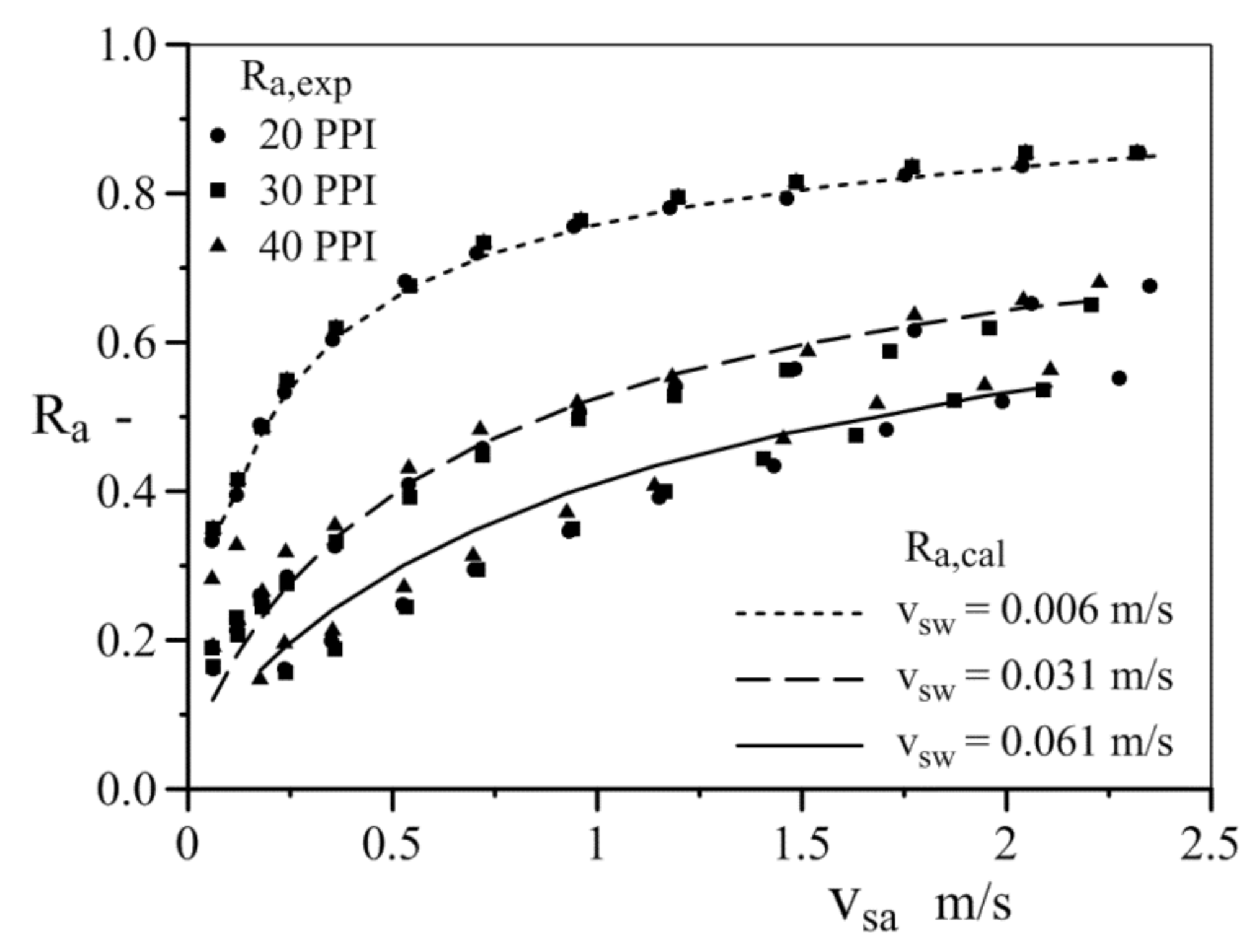
2.4. Method for Predicting the Void Fraction
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| d | internal diameter of pipe (m) |
| ğ | acceleration of gravity (m/s2) |
| mass flux (kg/(m2 s))L length, m | |
| νσ | superficial velocity (m/s) |
| R | void fraction (-) |
| Re | Reynolds number (-) |
| T | temperature (°C) |
| Q | volumetric flow rate (m3/s) |
| x | mass fraction (-) |
| Greek symbol | |
| ζ | input void fraction (-) |
| μ | viscosity (Pas) |
| ϑζ | equivalent linear dimension (m) |
| ρ | density (kg/m3) |
| σ | surface tension (N/m) |
| Subscripts | |
| a | air2P two-phase flow |
| cal | calculated value |
| c | column, channel |
| exp | measured value |
| G | gas |
| i | i-phase |
| L | liquid |
| o | oil |
| p | packing |
| w | water |
References
- Banhart, J. Manufacture, characterization and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Quadbeck, P.; Kümmel, K.; Hauser, R.; Standke, G.; Adler, J.; Stephani, G. Open Cell Metal Foams—Application-oriented Structure and Material Selection. In Proceedings of the International Conference on Cellular Materials, CellMat 2010, Dresden, Germany, 27–29 October 2010; Stephani, G., Hipke, T., Scheffler, M., Adler, J., Eds.; CELLMAT: Valladolid, Spain, 2010; pp. 279–288. [Google Scholar]
- Xu, S.; Wu, Z.; Lu, H.; Yang, L. Experimental Study of the Convective Heat Transfer and Local Thermal Equilibrium in Ceramic Foam. Processes 2020, 8, 1490. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Mahajan, R.L. Finned metal foam heatsinks for electronics cooling in forced convection. ASME J. Electron. Packag. 2002, 124, 155–163. [Google Scholar] [CrossRef]
- Vafai, K. Handbook of Porous Media, 2nd ed.; Taylor Francis: New York, NY, USA, 2005. [Google Scholar]
- Stemmet, C.P.; Jongmans, J.N.; Schaaf, J.; Kuster, B.M.F.; Schouten, J.C. Hydrodynamics of gas-liquid counter-current flow in solid foam packings. Chem. Eng. Sci. 2005, 60, 6422–6429. [Google Scholar] [CrossRef]
- Quadbeck, P.; Stephani, G.; Kümmel, K.; Adler, J.; Standke, G. Synthesis and Properties of Open-Celled Metal Foams. MSF 2007, 534–536, 1005–1008. [Google Scholar] [CrossRef]
- Gao, W.; Xu, X.; Liang, X. Flow boiling of R134a in an open–cell metal foam mini−channel evaporator. Int. J. Heat Mass Transf. 2018, 126, 103–115. [Google Scholar] [CrossRef]
- Tourvieille, J.-N.; Philippe, R.; de Bellefon, C. Milli−channel with metal foams under an applied gas–liquid periodic flow: Flow patterns, residence time distribution and pulsing properties. Chem. Eng. Sci. 2015, 126, 406–426. [Google Scholar] [CrossRef]
- Li, H.-W.; Zhang, C.-Z.; Yang, D.; Sun, B.; Hong, W.-P. Experimental investigation on flow boiling heat transfer characteristics of R141b refrigerant in parallel small channels filled with metal foam. Int. J. Heat Mass Transf. 2019, 133, 21–35. [Google Scholar] [CrossRef]
- Wan, Z.; Sun, Y.; Yang, C.; Kong, X.; Yan, H.; Chen, X.; Huang, T.; Wang, X. Experimental performance investigation on the arrangement of metal foam as flow distributors in proton exchange membrane fuel cell. Energy Convers. Manag. 2021, 231, 13846. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Du, Z.; Yu, J.; Yang, X.; Yan, J. Effect of fin-metal foam structure on thermal energy storage: An experimental study. Renew. Energy 2021, 172, 57–70. [Google Scholar] [CrossRef]
- Li, H.Y.; Leong, K.C. Experimental and numerical study on single and two-phase flow and heat transfer in aluminum foams. Int. J. Heat Mass Trans. 2011, 54, 4904–4912. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lee, K.S. Heat removal by aluminum foam heat sinks in a multi-air jet impingement. IEEE Trans. Compon. Packag. Technol. 2005, 28, 141–148. [Google Scholar]
- Liang, L.S.; Wu, X.L.; Ma, N.N.; Du, J.J.; Liu, M.B. The Sound Absorption Properties Comparison of Metal Foams and Flexible Cellular Materials. MSF 2018, 933, 357–366. [Google Scholar] [CrossRef]
- Jin, W.; Liu, J.; Wang, Z.; Wang, Y.; Cao, Z.; Liu, Y.; Zhu, X. Sound Absorption Characteristics of Aluminum Foams Treated by Plasma Electrolytic Oxidation. Materials 2015, 8, 511–7518. [Google Scholar]
- Abadi, G.B.; Moon, C.; Kim, K.C. Flow boiling visualization and heat transfer in metal−foam−filled mini tubes–Part I: Flow pattern map and experimental data. Int. J. Heat Mass Transf. 2016, 98, 857–867. [Google Scholar] [CrossRef]
- García-Moreno, F. Commercial Applications of Metal Foams: Their Properties and Production. Materials 2016, 9, 85. [Google Scholar] [CrossRef]
- Salehi, M.; Mirbagheri, S.M.H.; Ramiani, A.J. Efficient energy absorption of functionally-graded metallic foam-filled tubes under impact loading. Trans. Nonferrous Metals Soc. China 2021, 31, 92–110. [Google Scholar] [CrossRef]
- Ghidossi, R.; Bonnet, J.-P.; Rebollar-Perez, G.; Carretier, E.; Ferrasse, J.-H.; Vicente, J.; Topin, F.; Moulin, P. Separation of particles from hot gases using metallic foams. J. Mater. Process. Technol. 2009, 209, 3859–3868. [Google Scholar] [CrossRef]
- Hutter, C.; Allemann, C.; Kuhn, S.; Von Rohr, P.R. Scalar transport in a milli-scale metal foam reaktor. Chem. Eng. Sci. 2010, 65, 3169–3178. [Google Scholar] [CrossRef]
- Wenmakers, P.W.A.M.; Van der Schaaf, J.; Kuster, B.F.M.; Schouten, J.C. Enhanced liquid-solid mass transfer by carbon nanofibers on solid foam as catalyst support. Chem. Eng. Sci. 2010, 65, 247–254. [Google Scholar] [CrossRef]
- Tschentscher, R.; Nijhuis, T.A.; van der Schaaf, J.; Kuster, B.F.M.; Schouten, J.C. Gas−liquid mass transfer in rotating solid foam reactors. Chem. Eng. Sci. 2010, 65, 472–479. [Google Scholar] [CrossRef]
- Stemmet, C.P.; Schaaf, J.; Kuster, B.M.F.; Schouten, J.C. Solid foam packings for multiphase reactors: Modeling of liquid holdup and mass transfer. Chem. Eng. Res. Des. 2006, 84, 1134–1141. [Google Scholar] [CrossRef]
- Twigg, M.V.; Richardson, J.T. Fundamentals and applications of structured ceramic foam catalysts. Ind. Eng. Chem. Res. 2007, 46, 4166–4177. [Google Scholar] [CrossRef]
- Stemmet, C.P.; Meeuwse, M.; Schaaf, J.; Kuster, B.M.F.; Schouten, J.C. Gas-liquid mass transfer and axial dispersion in solid foam packings. Chem. Eng. Sci. 2007, 62, 5444–5450. [Google Scholar] [CrossRef]
- Leon, M.A.; Nijhuis, T.A.; van der Schaaf, J.; Schouten, J.C. Mass transfer modeling of a consecutive reaction in rotating foam stirrer reactors: Selective hydrogenation of a functionalized alkyne. Chem. Eng. Sci. 2012, 73, 412–420. [Google Scholar] [CrossRef]
- Zalucky, J.; Wagner, M.; Schubert, M.; Lange, R.; Hampel, U. Hydrodynamics of descending gas−liquid flows in solid foams: Liquid holdup, multiphase pressure drop and radial dispersion. Chem. Eng. Sci. 2017, 168, 480–494. [Google Scholar] [CrossRef]
- Pietrzak, M.; Płaczek, M. Void fraction predictive methods in two-phase flow across a small diameter channel. Int. J. Multiph. Flow 2019, 121, 103115. [Google Scholar] [CrossRef]
- Gardenghi, A.R.; Filho, S.E.; Chagas, D.E.; Scagnolatto, G.; Oliveira, R.M.; Tibirica, C.B. Overview of Void Fraction Measurement Techniques, Database and Correlations for Two-Phase Flow in Small Diameter Channels. Fluids 2020, 5, 216. [Google Scholar] [CrossRef]
- Hu, H.; Zhu, Y.; Ding, G.; Sun, S. Effect of oil on two-phase pressure drop of refrigerant flow boiling inside circular tubes filled with metal foam. Int. J. Refrig. 2013, 36, 516–526. [Google Scholar] [CrossRef]
- Ji, X.; Xu, J. Experimental study on the two-phase pressure drop in copper foams. Heat Mass Transf. 2012, 48, 153–164. [Google Scholar] [CrossRef]
- Madani, B.; Tadrist, L.; Topin, F. Experimental analysis of upward flow boiling heat transfer in a channel provided with copper metallic foam. Appl. Therm. Eng. 2013, 52, 336–344. [Google Scholar] [CrossRef]
- Lu, W.; Zhao, C.Y. Numerical modeling of flow boiling heat transfer in horizontal metal foam tubes. Adv. Eng. Mater. 2009, 11, 832–836. [Google Scholar] [CrossRef]
- Dyga, R.; Płaczek, M. Influence of Hydrodynamic Conditions on the Type and Area of Occurrence of Gas–Liquid Flow Patterns in the Flow through Open–Cell Foams. Materials 2020, 13, 3254. [Google Scholar] [CrossRef] [PubMed]
- Busser, T.; Serres, M.; Philippe, R.; Vidal, V. Hydrodynamics of gas-liquid co-current flow through a thin sheet of highly porous open cell solid foam. Chem. Eng. Sci. 2020, 226, 115811. [Google Scholar] [CrossRef]
- Płaczek, M.; Dyga, R.; Witczak, S. Experimental Investigation of Void Fraction in Horizontal Air-water Flow Through FeCrAlY Foam. Procedia Eng. 2012, 42, 690–703. [Google Scholar] [CrossRef] [Green Version]
- Kamath, P.M.; Balaji, C.; Venkateshan, S.P. Experimental investigation of flow assisted mixed convection in high porosity foams in vertical channels. Int. J. Heat Mass Transf. 2011, 54, 5231–5241. [Google Scholar] [CrossRef]
- Dukhan, N.; Suleiman, A.S. Simulation of Entry-Region Flow in Open-Cell Metal Foam and Experimental Validation. Transp. Porous Media 2014, 101, 229–246. [Google Scholar] [CrossRef]
- Dyga, R.; Płaczek, M.; Witczak, S.; Czernek, K. Analysis of Flow Through the Entry Region of a Channel with Metal Foam Packing. In Practical Aspects of Chemical Engineering; Ochowiak, M., Woziwodzki, S., Doligalski, M., Mitkowski, P., Eds.; Lecture Notes on Multidisciplinary Industrial, Engineering; Springer: Cham, Switzerland, 2018; pp. 101–112. [Google Scholar]
- Diani, A.; Mancin, S.; Doretti, L.; Rossetto, L. Low-GWP refrigerants flow boiling heat transfer in a 5 PPI copper foam. Int. J. Multiph. Flow. 2015, 76, 111–121. [Google Scholar] [CrossRef]
- Larkins, R.P.; White, R.R. Two-phase co-current flow in packed beds. AIChE J. 1961, 7, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Turpin, J.L.; Huntington, R.L. Prediction of pressure drop for two-phase two-component co-current flow in packed beds. AIChE J. 1967, 13, 1196–1202. [Google Scholar] [CrossRef] [Green Version]
- Weber, H.H. Untersuchungen über die Verweilzeitverteilung in Aufstromkolonnen. PhD Dissertation, TH Darmstadt, Darmstadt, Germany, 1961. [Google Scholar]
- Khan, A.; Khan, A.A.; Varma, Y.B.G. An analysis of phase holdup in concurrent gas liquid upflow through packed beds using (I) drift-flux model, and (II) slip ratio. Bioprocess Eng. 2000, 22, 165–170. [Google Scholar] [CrossRef]
- Saada, M. Fluid Mechanics of co-current two-phase flow in packed beds: Pressure drop and liquid hold-up studies. Chem. Ind. Genie Chem. 1972, 105, 1415–1421. [Google Scholar]
- Lockhart, R.C.; Martinelli, R.W. Proposed correlation of data for isothermal two-phase flow two-component flow in the pipes. Chem. Eng. Prog. 1949, 45, 39–48. [Google Scholar]
- Zuber, N.; Findlay, J.A. Average volumetric concentration in two-phase flow systems. J. Heat Trans. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Dix, G.E. Vapor Void Fraction for Forced Convection with Subcooled Boiling at Low Flow Rates. Ph.D. Thesis, University of California, Berkeley, Berkeley, CA, USA, 1971. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Trans. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
- Punches, W.C. MAYU04: A Method To Evaluate Transient Thermal Hydraulic Conditions in Rod Bundles; General Electric Co.: Boston, MA, USA, 1977. [Google Scholar]
- Stomma, Z. Two-Phase Flows—Void Fraction Values Determination; Świerk, Report INR/18187/IXD/R/A; Institute of Nuclear Research: Warsaw, Poland, 1979. [Google Scholar]
- Rouhani, Z. AB Atomenergie, Studsvik: Nyköping, Sweden, 1986. In Steady State Void Fraction and Pressure Drop in Water Cooled Reactors.; AB Atomenergie, Studsvik: Nyköping, Sweden, 1986. [Google Scholar]
- Coddington, P.; Macian, R. A study of the performance of void fraction correlations used in the context of drift-flux two-phase flow models. Nucl. Eng. Des. 2002, 3, 199–216. [Google Scholar] [CrossRef]
- Kataoka, I.; Ishii, M. Drift flux model for large diameter pipe and new correlation for pool void fraction. Int. J. Heat Mass Transf. 1987, 30, 1927–1939. [Google Scholar]




| Mixture Component | Superficial Velocity | Mass Flux Density | Reynolds Number | Inlet Void Fraction | |
|---|---|---|---|---|---|
| vsi, m/s | gi, kg·(m2s) | Rei, - | ζi, - | ||
| air, a | 0.031–8.840 0.031–2.550 * | 0.039–15.58 0.039–3.11 * | 23–13,244 | 0.207–0.999 0.319–0.998* | |
| water, w | 0.006–0.119 | 5.99–119.49 | 30–4509 | 0.001–0.793 | |
| oil, o | 0.006–0.066 | 5.40–56.71 | 3–293 | 0.002–0.681 | |
| Physical properties of fluids at 20 °C | |||||
| Fluid | Density, ρi kg/m3 | Viscosity, μi Pas | Surface tension, σi N/m | ||
| air, a | 1.164 | 1.82∙10−5 | - | ||
| water, w | 998.2 | 1.0∙10−3 | 0.070 | ||
| oil (Velol-9Q), o | 859.4 | 2.7∙10−3 | 0.046 | ||
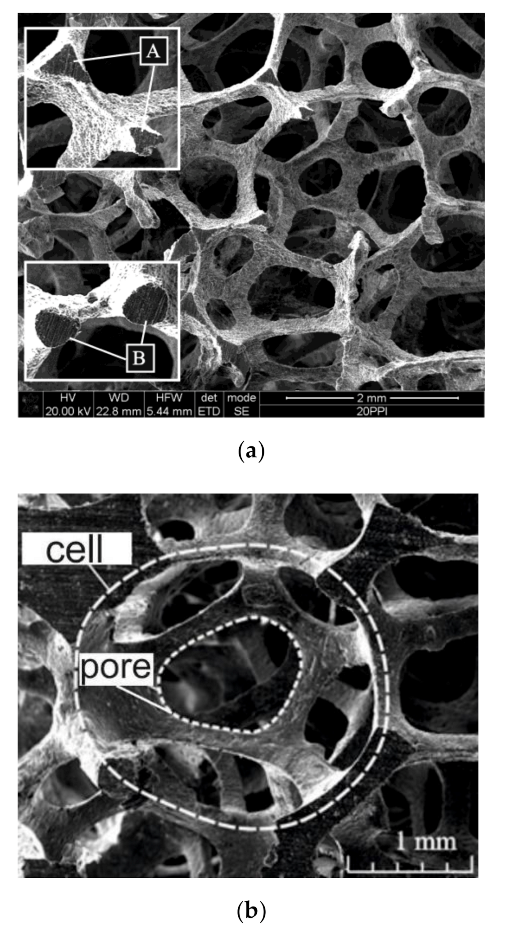
| Pore Density (PPI)/Type of Foam | Cell Diameter, dc | Pore Diameter, dp | Porosity, ε | Thermal Conductivity, kf |
|---|---|---|---|---|
| m | m | % | W/(m·K) | |
| 20 PPI (AlSi7Mg) | 3.45∙10−3 | 1.09∙10−3 | 93.4 | 150.4 |
| 30 PPI (AlSi7Mg) | 2.25∙10−3 | 0.71∙10−3 | 94.3 | 150.4 |
| 40 PPI (Al 6101) | 2.38∙10−3 | 0.82∙10−3 | 92.9 | 189.4 |
| Author | Equation |
|---|---|
| ; ; ; | |
| Stomma [52] | ; |
| Void fraction in upward flow in vertical pipe at low pressure | |
| Lockhart—Martinelli [47] | |
| Pipe diameter d = (1.49–25.8)⋅10−3m, Two-phase mixture: of Air–Water, air–Diesel Fuel Oil, Air–Kerosene, Air–Benzene, Air–S.A.E. 40 Oil, ReL = 1.1–39,000, ReG = 7–86,000 | |
| Chisholm [50] | |
| Circular tube, annular flow, correlation based on an elementary separated flow | |
| Zuber-Findlay [48] | ; ; |
| Relative movement of gas and liquid in pipe: slug, annular, churn-turbulent bubbly flow, RG > 0.8 annular flow Co = 1. | |
| GE RAMP [51] | for or for for for |
| Numerical calculations were performed by the code MAYU04 that originally analyzes one-dimensional single channel hydraulic and heat transfer transients in rod bundles. Model was used to resolve the two-phase flow equations. The equations are valid for co-current and countercurrent flow. The model is suited for Boiling Water Reactor loss-of-coolant accident analysis where pressure transients are not very severe and subcooled voids are not very important. | |
| Dix [49] | |
| Glass tube diameter d = 0.018 m | |
| Rouhani [53] | ; |
| Tube diameter: d = 21.9 mm, void fraction in flow boiling, measurement at 109 cm from the pipe, annular flow, heated perimeter O = 3.77 cm, q/A = 60–120 W/cm2 P = (19–50)·105 Pa, = 130–1450 kg/(m2s), steam quality x = 0–12%. | |
| Author | Method |
|---|---|
| Khan et al. [45] | ; ; |
| Column diameter: dc = 0.091 m, column length Lc = 1.0 m, Co-current up-flow: Air–Water flow, Air–Monoethanol amine, Type of packing: Spheres, Raschig rings, Berl saddles, Cylinders dp = (3.0–12.5)⋅10−3 m, ε = (0.3–0.69) | |
| Larkins and White [42] | log10RL = −0.774 + 0.525(log10X) − 0.109(log10 X)2 0.05 < X < 30 |
| Column diameter: dc = 50.8 mm and dc = 101.6 mm, Homogenous and heterogeneous flow regime, vertical downward flow: air–water, air–water (methyl-cellulose), air–water (0.033% soap), air–ethylene glycol, natural gas–kerosene, natural gas–lube oil, CO2-lube oil. Type of packing: Raschig rings 9.52⋅10−3 m and 3.17⋅10−3 m; Cylinders 3.17⋅10−3 m; Glass beads 3⋅10−3 m; νsG = 0–8.05 m/s, νsL = 0–0.265 m/s, ReG = 0–6200, ReL = 0–3405. | |
| Turpin and Huntington [43] | |
| Column diameter: dc = 5⋅10−2 m, dc = 10⋅10−2 m, dc = 15⋅10−2 m, Air–Water flow (Bubble flow, Pulse and Spray flow). Type of packing: tubular alumina particles: 7.62⋅10−3 m and 8.23⋅10−3 m. | |
| Saada [46] | , K = 0.48; a = 1.25 for ReG < K = 0.32; a = 0.07 for ReG > |
| Column diameter: dc = 4.52⋅10−2 m, Lc = 0.40 m, Co-current Air–Water upward flow, (Bubbly, Churn turbulent flow regimes). Type of packing: Glass ballotini spheres (dp = 5.14⋅10−4 m, dp = 9.74⋅10−4 m, dp = 20.64⋅10−4 m); ε = 34.6% | |
| Type of Foam | 20 PPI (AlSi7Mg) | 30 PPI (AlSi7Mg) | 40 PPI (Al 6101) | |||
|---|---|---|---|---|---|---|
| Model | RMS | δ (ε) | RMS | δ (ε) | RMS | δ (ε) |
| Lockhart and Martinelli [47] | 1.01 | 1.01 | 0.96 | 0.92 | 1.11 | 1.24 |
| Zuber and Findlay [48] | 0.46 | 0.20 | 0.45 | 0.19 | 0.55 | 0.30 |
| Dix [49] | 1.29 | 1.67 | 1.24 | 1.53 | 1.42 | 2.04 |
| Chisholm [50] | 1.36 | 1.86 | 1.30 | 1.71 | 1.50 | 2.27 |
| GE RAMP [51] | 0.36 | 0.13 | 0.36 | 0.13 | 0.42 | 0.17 |
| Stomma [52] | 1.20 | 1.44 | 1.14 | 1.30 | 1.32 | 1.74 |
| Rouhani [53] | 1.21 | 1.47 | 1.16 | 1.35 | 1.35 | 1.84 |
| Larkins and White [42] | 1.17 | 1.37 | 1.10 | 1.22 | 1.26 | 1.60 |
| Turpin and Huntington [43] | 0.77 | 0.60 | 0.70 | 0.49 | 0.84 | 0.69 |
| Weber (2 mm) [44] | 0.85 | 0.72 | 0.85 | 0.72 | 0.84 | 0.71 |
| Weber (5 mm) [44] | 0.86 | 0.73 | 0.86 | 0.73 | 0.85 | 0.72 |
| Type of Flow | Equation |
|---|---|
| Stratified flow | |
| Other type of flows (plug, slug, churn, annular) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Płaczek, M.; Dyga, R. Void Fraction Prediction Method in Gas–Liquid Flow through Channel Packed with Open-Cell Metal Foams. Energies 2021, 14, 2645. https://doi.org/10.3390/en14092645
Płaczek M, Dyga R. Void Fraction Prediction Method in Gas–Liquid Flow through Channel Packed with Open-Cell Metal Foams. Energies. 2021; 14(9):2645. https://doi.org/10.3390/en14092645
Chicago/Turabian StylePłaczek, Małgorzata, and Roman Dyga. 2021. "Void Fraction Prediction Method in Gas–Liquid Flow through Channel Packed with Open-Cell Metal Foams" Energies 14, no. 9: 2645. https://doi.org/10.3390/en14092645
APA StylePłaczek, M., & Dyga, R. (2021). Void Fraction Prediction Method in Gas–Liquid Flow through Channel Packed with Open-Cell Metal Foams. Energies, 14(9), 2645. https://doi.org/10.3390/en14092645






