Identification of Inter-Turn Short-Circuits in Induction Motor Stator Winding Using Simulated Annealing

Abstract

This paper presents a method of inter-turn short-circuit identification in induction motors during load current variations based on a hybrid analytic approach that combines the genetic algorithm and simulated annealing. With this approach, the essence of the method relies on determining the reference matrices and calculating the distance between the reference matric values and the test matrix. As a whole, it is a novel approach to the process of identifying faults in induction motors. Moreover, applying a discrete optimization algorithm to search for alternative solutions makes it possible to obtain the true minimal values of the matrices in the identification process. The effectiveness of the applied method in the monitoring and identification processes of the inter-turn short-circuit in the early stage of its creation was confirmed in tests carried out for several significant state variables describing physical magnitudes of the selected induction motor model. The need for identification of a particular fault is related to a gradual increase in its magnitude in the process of the induction motor’s exploitation. The occurrence of short-circuits complicates the dynamic properties of the measured diagnostic signals of the system to a great extent.

1. Introduction

The basic issue in the exploitation of different types of devices, machines, or technical systems is to provide continuous and failure-free operation. This reliability is the key requirement in the growing industry 4.0 era. Technical diagnostics is a tool to provide failure-free operation of technical objects. Diagnostics is a process in which the actual condition of an object is evaluated and, based on the result, one decides about its further exploitation or decides to subject it to a repair process. The process of technical condition assessment of electric machines in industry or in transport or other application fields includes the detection and identification unwanted operational states. The set of operational states is a series of deliberate actions performed by the machine in a specified period. It is required that the diagnostic system detects and identifies the occurrence of faults in real time or in early stages of their creation [1]. Nowadays, these requirements can only be satisfied for the systems built using high-tech technology, based on microprocessor techniques and software that implements effective methods of electric machine diagnostics. In complex electro-mechanical objects, the analysis and classification of diagnostic signals in the time–frequency domain is performed using transformation methods [2]. In recent years, it has been possible to observe an increase in neural network applications in technical diagnostics. For a wide range of neural network applications in technical diagnostics, it is worth pointing out their application in the modeling, identification, emergency state decision making and detection of faults occurring in complex processes and objects. The application of neural networks in diagnostics is reasonable, especially due to their ability to generalize the information stored in the network [1].

Among some recently published papers related to time–frequency analysis, neural networks, genetic algorithms and image processing, there are several that significantly contributed to development of fault detection during electro-mechanical energy conversion:

−

An innovative inter-turn short-circuit detection method applied in induction motors using the discrete wavelet transform approach performed on the Park vectors of current signals [3];

−

A presentation of the results of research concerning the application of axial flux in the diagnostics of an induction motor’s stator winding, supplied from a frequency converter during the motor’s operation in various conditions, registered in the LabVIEW environment [4];

−

Fault detection in an induction motor using a pattern recognition technique based on empirical wavelet transform and a convolutional neural network model used in the automatic extraction of relevant features from the image of a current signal presented in greyscale [5];

−

The application of a combination of a deep learning neural network with a complex cluster model and a classifier based on the support vector machine (SVM) in the detection of unknown electromechanical faults in industrial systems [6];

−

An analysis of stator current and vibration in the fault detection of induction motors using wavelet decomposition and the FCM data clustering method based on fuzzy logic [7];

−

The development of fault diagnosis methodology for a three-phase cage induction machine resulting from the process of training and classification using artificial neural networks applied in the processing of digital image data obtained from the calculation of power spectrum density (PSD) [8];

−

The presentation of a stator winding fault detection method in a three-phase induction motor using a discrete wavelet transform-based method and a quadrature discriminant-based method [9], and another method combining principal component analysis (PCA) with the training of selected artificial neural networks representing a multi-layer perceptron network and a network with radial base functions [10];

−

The detection of cracked bars in an induction motor using the method of stator current discrete wavelet transform coefficients, applied in the training of neural networks used in the ANFIS adaptive neural fuzzy inference system [11];

−

The design of a neutral network deep learning method and a special over-sampling technique used for the high-accuracy classification of induction motor faults [12];

−

The application of error-back-propagation-based training of a neutral network in the analysis of current and voltage components performed to detect the inter-turn short-circuit in induction motor stator winding [13];

−

A proof of the usefulness of the investigation of stator current variation in the converter drive of induction motors for the detection and classification of electrical faults using the Kohonen neural network [14];

−

The application of the genetic algorithm to the problem of the identification of parameters in the mathematical modelling of induction motors. The research was concentrated on the selection of the genetic algorithm’s stop criterion considering the convergence and accuracy of the analyzed process and the time required for numerical analysis [15];

−

The performance of tests of a control system applied to an induction machine using the genetic algorithm with many objective function used to conduct the evaluation of quality factors [16];

−

An analysis of the impact of inbreeding in the genetic algorithm on the results of parameter identification in the mathematical modelling of an induction motor [17];

−

The identification of inertia on the induction motor’s shaft from the analysis of wavelet scalograms performed using a clustering method based on the k-mean harmonics technique [18] or other methods described in the literature [19,20,21,22,23,24,25,26,27].

The paper introduces a new method for fault diagnosis based on the results of the calculated differences between the values obtained from the identification algorithm and those of the reference matrix values determined for a selected group of tests. The appropriate values were obtained by means of the simulated annealing and genetic algorithm.

The applied genetic algorithm presents a new method of determining the length of the binary chain of individuals in the population by means of calculations performed for the obtained results representing the grouping appropriately normalized measurement data.

The developed method used in identifying interturn short-circuits makes it possible to use the obtained results of computer simulations in order to carry out an accurate analysis of the values of physical quantities recorded during the laboratory measurements of an induction motor.

The use of technology based on AI supported by a discrete optimization algorithm in the analyzes of the tested signals made a large contribution in terms of the obtaining of correct results in the process of identifying interturn short-circuits.

The remaining part of this paper is organized in the following way: the second part presents the development of the connection of the system’s elements during the performance of simulation tests with various cases of inter-turn short circuits. The parameters of the examined induction motor model include the physical magnitudes investigated in the performed simulation tests and the variation of the factor of fault occurrence in the performed simulation tests. The third part contains the description of the developed fault identification algorithm, with a juxtaposition of the required parameters for the testing of the selected diagnostic method and the method of calculation of the factor required for fault assessment.

In the next section, laboratory tests and descriptions of the obtained results are presented. The conclusions are contained in the last part of this paper.

2. Materials and Theoretical Basis

Briefly, the detection of interturn-faults at an early stage is an important task in the maintenance of electrical machinery in the power industry. This problem has not been fully researched and resolved to this day. Therefore, it is still an interesting research issue.

In order to develop a more effective algorithm for the early detection of interturn short-circuits, experimental tests were carried out during which the measurement data were obtained for the development of an effective diagnostic algorithm.

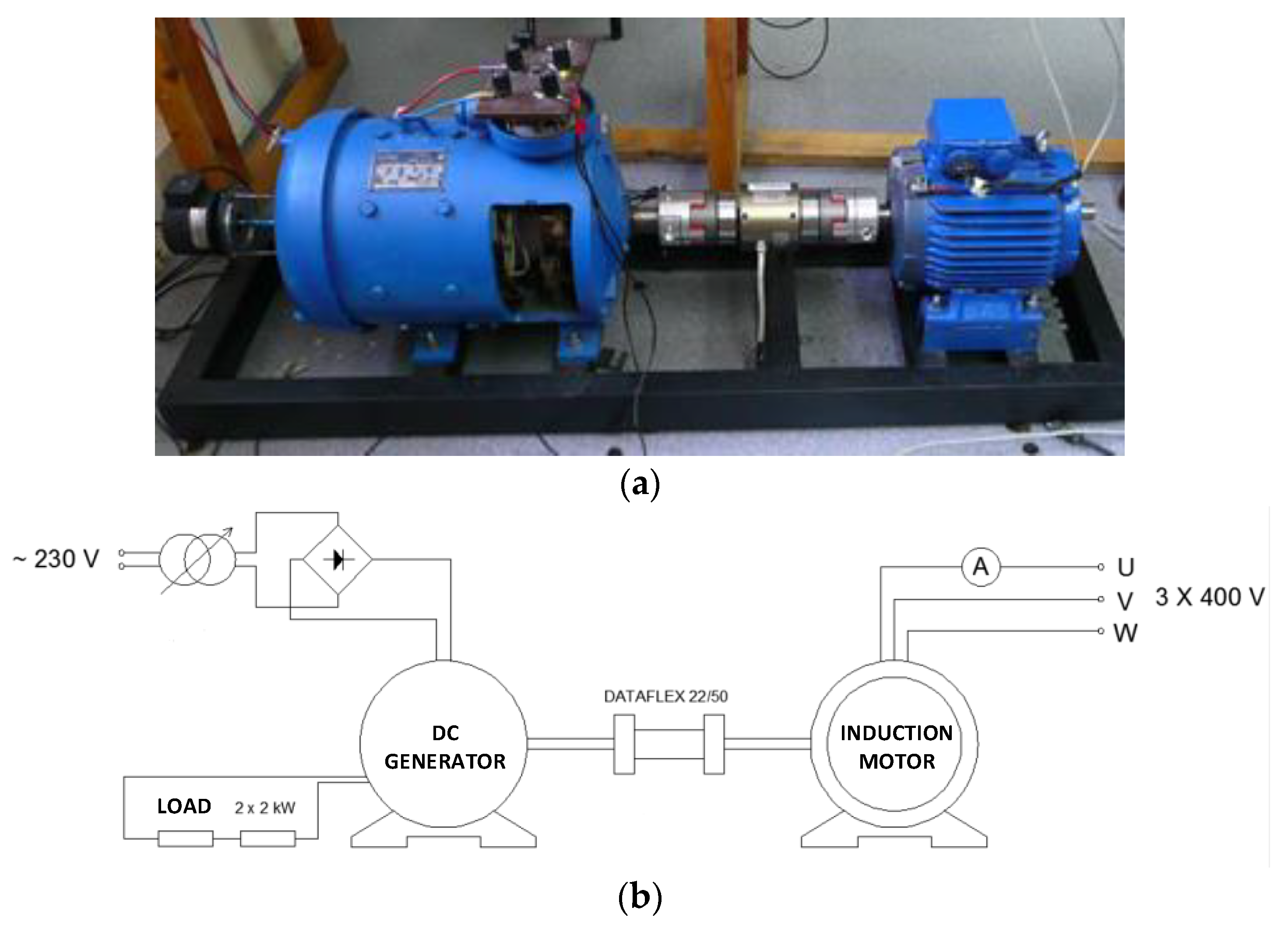
Description of the Identification Process of the Inter-Turn Short-Circuit in the Induction Motor Model

The object of interest was the Sg-112M-4 cage induction motor, with the following parameters: P_n = 4.0 kW, U_n = 380 V, I_n = 8.6 A and n_n = 1435 rpm. The motor was mechanically coupled to the PZM5545 DC generator by the clutch.

Figure 1 shows the DC generator with an autotransformer and a bridge rectifier used for the induction motor’s load changing. The load of the DC generator comprised two resistive heaters with an overall power of 4 kW. Load torque was measured with the Data FLEX 22/50 torque meter. The torque meter also outputted a voltage signal that was proportional to the measured rotational speed [19].

The DC generator, which was used as a load for the tested motor, had the following parameters: P_n = 4.5 kW, U_n = 230 V, I_n = 19.6 A, n_n = 1450 rpm and I_f = 0.86 A. Figure 2 shows a wiring diagram of the turns in one stator coil of the tested motor. The windings were connected in wye configuration and supplied from a three-phase low-voltage network. The winding number from which the turn was wired to the terminal on the terminal board on the machine’s housing is marked with a proper number in the diagram. Short circuiting of the selected turns occurred when the proper terminals were connected to a resistor and an ammeter, which was used for current control.

In order to decrease the current and provide long-term protection of the motor against overheating, an additional resistor, of resistance equal to 5 ÷ 6 Ω, was used. The additional resistor had no impact on the effects of faults that could be observed for different values of components of the measured diagnostic signals [27]. Simulation tests were carried out in five test groups with the following values of the load current I_load: 1 A, 2 A, 3 A, 4 A and 5 A. Each test group contained eight different cases of inter-turn short-circuiting. Test results for all physical magnitudes and for each case of short circuiting were stored in matrix X_1[8,500,000]. The elements of matrix X₁ were defined for each value of load current I_load.

The changes were saved in matrix K₁ in the following order: K₁ = [(short circuit between turns 1 and 2), (short circuit between turns 1 and 3), (short circuit between turns 1 and 4), (short circuit between turns 1 and 5), (short circuit between turns 1 and 10), (short circuit between turns 1 and 15), (short circuit between turns 1 and 20), (short circuit between turns 1 and 25)].

In the proposed diagnostic method, simulation tests were run for the following physical magnitudes:

(a)

Turn short-circuit current I_z;

(b)

Electromagnetic torque of the examined induction motor m_el;

(c)

Voltage signal proportional to the rotational speed of the examined induction motor’s rotor n₁;

(d)

Signal proportional to the axial flux ϕ₁;

(e)

Vibration signal—acceleration in X axis—d_x;

(f)

Vibration signal—acceleration in Y axis—d_y;

(g)

Acoustic pressure—p_s;

(h)

Phase voltage—u₁, u₂ and u₃;

(i)

Phase current—i₁, i₂ and i₃;

(j)

Neutral point voltage—u₀.

3. Proposed Method of Inter-Turn Short-Circuit Identification in Induction Motor

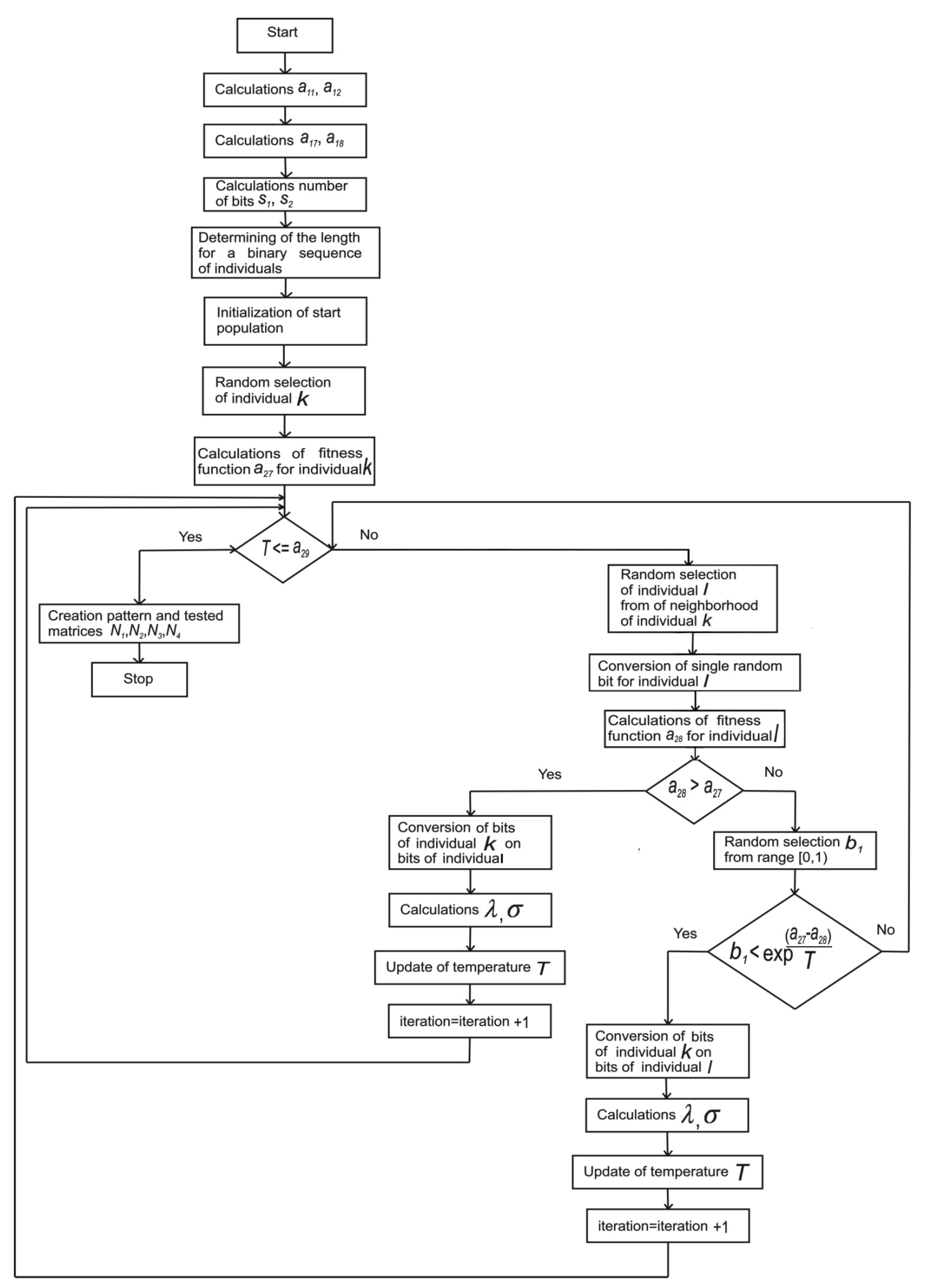
Description of Diagnostic Algorithm Used in Physical Magnitude Signal Processing Using the Genetic Algorithm of Simulated Annealing

In the identification tests performed for each case of inter-turn short-circuiting, the matrix X₃ values obtained from normalization of matrix X₁ values were used, followed by sorting of the elements of matrix X₂ into the right order.

Simulations were run with 50 kHz sampling frequency, and the simulated period was 10 s.

Elements of matrix X₃, obtained from sorting the elements of matrix X₂ in descending order for all examined physical magnitudes, were used in the diagnostic procedure.

This means that in the simulation tests, the values of matrix X₃ were defined as follows:

$$X_{3\left(i\right)(j)}=\{\begin{array}{l}\left[X_{2\left(i\right)(1)}\ge X_{2\left(i\right)(2)} \dots \ge X_{2\left(i\right)(\mathrm{500,000})}\right];\\ i\in \langle 1,8\rangle ; j=1,2\dots 500\end{array}$$

(1)

Moreover, two types of identification tests using normalization of the elements of matrix X₁ were applied:

−

Tests performed for the assumed first four cases of inter-turn short-circuiting using the parameters defined for acoustic pressure p_s;

−

Tests performed for the assumed last four cases of inter-turn short-circuiting using the parameters defined for axial flux ϕ₁.

The reference matrix elements values and the values of examined matrix calculated by the genetic algorithm of simulated annealing were used in identification tests in the diagnostic procedure.

The values of reference matrix were obtained after performing calculations in the genetic algorithm using the values of matrix X₂ defined in test group for load current I_load = 3 A.

The values of matrix X₂ elements were obtained by limiting the values of matrix X₁ to the range [a₃, a₄] for all investigated physical magnitudes according to the following formula:

$$X_{2(\left(i\right)j)}= \{\begin{array}{l}\left(\frac{(X_{1\left(i\right)(j)}-a_{1\left(i\right)})}{(a_{2\left(i\right)}-a_{1\left(i\right)})}\right) * (a_{4\left(i\right)}-a_{3\left(i\right)})+a_{3\left(i\right)};\\ i\in \langle 1,8\rangle ; j=1, 2 \dots \mathrm{500,000}\end{array}$$

(2)

where:

X₁—values of the matrix elements;

a₁—minimum value of the matrix X₁ elements defined in the test;

a₂—maximum value of the matrix X₁ elements defined in the test;

a₃—initial value of the range containing normalized values of matrix X₁ calculated in tests for acoustic pressure p_s and axial flux ϕ₁;

a₄—end value of the range containing normalized values of matrix X₁ calculated in tests for acoustic pressure p_s and axial flux ϕ₁;

i—the number of the investigated cases of inter-turn short-circuits.

The values of variables a₁, a_2, a₃ and a₄ were calculated using the following formulas:

$$a_{1\left(i\right)}=\min \left(X_{1\left(i\right)\left(j\right)}\right);$$

(3)

$$a_{2\left(i\right)}=\max \left(X_{1\left(i\right)\left(j\right)}\right);$$

(4)

$$a_{4(i)}=\min \left(a_{5(i)},a_{6(i)}\right);$$

(5)

$$a_{4(i)}=\max \left(a_{5(i)},a_{6(i)}\right);$$

(6)

The variables a₅ and a₆ were used in the calculation of matrix X₂. The values of these variables were arithmetic means and standard deviations calculated in tests for acoustic pressure p_s and axial flux ϕ₁ using the following formulas:

$$\begin{array}{l}{a}_{5(i)}=\{\begin{array}{l}\frac{{\displaystyle \sum _{j=1}^{\mathrm{500,000}}{X}_{1\left(i\right)\left(j\right)}}}{\mathrm{500,000}};\\ X_{1\left(i\right)(j)} for p_s,{\varphi }_1\end{array}\end{array}$$

(7)

$$a_{6(i)}=\{\begin{array}{l}\sqrt{\frac{{\displaystyle \sum _{j=1}^{\mathrm{500,000}}{\left(X_{1\left(i\right)(j)}-a_{3\left(i\right)}\right)}^2}}{\mathrm{499,999}}};\\ X_{1\left(i\right)(j)} for p_s,{\varphi }_1\end{array}$$

(8)

The values of tested matrix were calculated by applying the genetic algorithm, which used the matrix X₂ values obtained in the test for a given load current I_load.

Calculation of the variables a₅ and a₆ was performed after the following conditions for the selected physical magnitudes, such as acoustic pressure p_s and axial flux ϕ₁ for the load current I_load = 3 A, were met:

$$a_7>a_8; for\hspace{1em}i\in \langle 1, 4\rangle$$

(9)

$$a_9>a_{10};\hspace{1em}for\hspace{1em}i\in \langle 5, 8\rangle$$

(10)

where:

i—the number of the investigated inter-turn short-circuit case.

The variables a₇, a₈, a₉ and a₁₀ were calculated using the following formulas:

$$a_7=\max \left(X_{4\left(i\right)}\right)-a_8;\hspace{1em} i\in \langle 1, 4\rangle$$

(11)

$$a_8=\left|\min \left(X_{4\left(i\right)}\right)\right|;\hspace{1em} \hspace{1em}\hspace{1em}i\in \langle 1, 4\rangle$$

(12)

$$a_9=\max \left(X_{4\left(i\right)}\right)-a_{10};\hspace{1em} i\in \langle 5, 8\rangle$$

(13)

$$a_{10}=\left|\min \left(X_{4\left(i\right)}\right)\right|\hspace{1em} \hspace{1em} i\in \langle 5, 8\rangle$$

(14)

The values of matrix X₄ were defined according to the formula given below:

$$X_{4(i)}=\max \left(X_{1\left(i\right)(j)}\right);\hspace{1em} i\in \langle 1,8\rangle ; j=1,2\dots \mathrm{500,000}$$

(15)

The genetic algorithm with simulated annealing was used for the proposed diagnostic method.

The simulated annealing algorithm is an iterative method that searches the space of alternative solutions to a problem in order to find an optimal solution. The solution depends on the obtained difference in values between the old and the new solution and the current temperature value. The temperature value is constantly lowered and it is possible to adjust the selection of successive approximations of the solutions to the problem. The probability of choosing the best solution increases with the decreasing of the temperature value in subsequent iterations of the simulated annealing algorithm. Over time, the results stabilize and the subsequent changes are not accepted.

In the applied genetic algorithm, normalization of individuals was performed using the values of the matrix X₆ elements.

The values of the matrix X₆ elements were calculated by summing the consecutive elements of matrix X₅.

The values of matrix X₃ were used in calculations of the sequence values stored in matrix X₅.

The values of matrix X₆ were the results of calculations of five elements according to the formula:

$$X_{6\left(i\right)(j)}={\displaystyle \sum _{j=1}^k{X}_{5\left(i\right)\left(j\right)}};\hspace{1em}i\in \langle 1,8\rangle ; j=1,2 \dots 5; k=j$$

(16)

where:

X₅—the values of the matrix elements calculated in the test.

Matrix X₆ contained the successively summed arithmetic means of the respective values of the X₃ matrix. This operation increased the range of changes for the values of the matrix X₃ elements for different cases of inter-turn short-circuiting. The values of matrix X₅ can be effectively used in identification process of investigated faults.

$$X_{5(i)}=\left[m_{1\left(i\right)},m_{2\left(1\right)},m_{3\left(i\right)},m_{4\left(1\right)},m_{5\left(i\right)}\right]; i\in \langle 1,8\rangle$$

(17)

The values of the arithmetic means m₁, m₂, m₃, m₄ and m₅ were calculated as follows:

$$m_{1\left(i\right)}=\frac{{\displaystyle \sum _{j=1}^{100}{X}_{3(i)}}}{100};\hspace{1em}i\in \langle 1,8\rangle$$

(18)

$$m_{2\left(i\right)}=\frac{{\displaystyle \sum _{j=101}^{200}{X}_{3(i)}}}{1000};\hspace{1em}i\in \langle 1,8\rangle$$

(19)

$$m_{3\left(i\right)}=\frac{{\displaystyle \sum _{j=201}^{300}{X}_{3(i)}}}{100};\hspace{1em}i\in \langle 1,8\rangle$$

(20)

$$m_{4\left(i\right)}=\frac{{\displaystyle \sum _{j=301}^{400}{X}_{3(i)}}}{100};\hspace{1em}i\in \langle 1,8\rangle$$

(21)

$$m_{5\left(i\right)}=\frac{{\displaystyle \sum _{j=401}^{500}{X}_{3(i)}}}{100};\hspace{1em}i\in \langle 1,8\rangle$$

(22)

Calculation of reference matrix elements values used in identification of inter-turn short-circuits was a crucial step in the presented diagnostic method. The calculations in the presented diagnostic procedure were performed according to the genetic algorithm with simulated annealing [14]. A block diagram containing the order of the calculations run in the genetic algorithm is presented in Figure 3.

For the applied genetic algorithm, it was crucial to specify an objective function.

The choice of objective function was made using a series of simulation tests performed for various objective functions.

The correct results of the proposed diagnostic procedure were observed for F6 Schaffer’s function with two variables [14].

This function was chosen as an objective function for the applied genetic algorithm. In this way, a representation of an individual in the population, for which each of the two variables were encoded as a binary string of specified length, needed to satisfy the requirements of accuracy [14].

The operation of the genetic algorithm with simulated annealing started with the initialization of the population individuals.

The initial values of the individuals were obtained by randomizing binary strings containing values of 0 or 1.

Binary strings created in this way for the first variable used in objective function calculation were stored in matrix X₇.

In the case of the second variable used in objective function calculation, the binary strings were stored in matrix X₈.

The overall length of binary string for a population individual was obtained from summing the number of bits of each variable binary string used in objective function calculation.

Based on the results obtained for a series of simulation tests, the population size used in the identification tests performed using the genetic algorithm with simulated annealing was set to 25 or 50.

When the stop criterion of the genetic algorithm was achieved, the processing of population individuals in the next generations was stopped.

In each iteration (generation), a random selection of a binary string of one k-th individual and a new binary string l from the vicinity of the k-th individual out of all population individuals was performed. For a randomly selected binary string of the l-th individual from the vicinity of the k-th individual, one random bit was changed [14]. A block diagram of the proposed GA-SA algorithm is presented in Figure 3.

In this proposed algorithm, the value of the objective function of the l-th individual new binary string is greater than the value of objective function of the k-th individual, then the binary string of the k-th individual is changed accordingly. Otherwise, a function returning a random number in a range of [0,1] is called and one checks if the obtained value is lower than the probability distribution of the new binary string of the l-th individual.

If the random number satisfies this condition, an appropriate exchange of k-th individual binary string occurs [14].

The end condition that is used in simulated annealing checks if the probability distribution of the newly selected string for the l-th individual is similar to the Boltzmann distribution.

In this way, the so-called thermal equilibrium was defined. Temperature T is decreased in each iteration of the genetic algorithm [14].

In order to lower the temperature, logarithmic cooling scheme is used [4,20]. For varying values of the adapted parameter, this scheme improves the quality of the results of inter-turn short-circuit identification.

In order to realize the above-described steps of the simulated annealing procedure, the operations described below were performed.

For a new l-th individual, singular bits in binary strings used for objective function calculation were randomly selected and created in the following way:

$$X_{7(l,j)}=\{\begin{array}{l}1-X_{7(l,j)};\hspace{1em}\\ i\in \langle 1,8\rangle ;j=random<1,s_{1\left(i\right)}>; k\ne l; l=random\langle 1,n\rangle ;n\in <25,50>\end{array}$$

(23)

$$X_{8(l,j)}=\{\begin{array}{l}1-X_{8(l,j)};\hspace{1em}\\ i\in \langle 1,8\rangle ;j=random<1,s_{2\left(i\right)}>; k\ne l; l=random\langle 1,n\rangle ;n\in <25,50>\end{array}$$

(24)

where:

s₁—the number of bits s₁ calculated in the test;

s₂—the number of bits s₂ calculated in the test;

n—the number of population individuals.

The numbers of bits s₁ and s₂ used in the procedure were defined by two variables, a₁₇ and a₁₈. The values of these variables were obtained by increasing, with a certain accuracy, the variables a₁₁ and a₁₂.

The values of variables a₁₁ and a₁₂ create a range of variation that is used in the calculation of the length of bits for variables used in the objective function calculation.

The values of these variables were obtained by calculating the differences between the maximum and minimum values of appropriate elements of the X₆ matrix. In the calculations, the following formulas were applied:

$$a_{11(i)}=\left({a_{14(i)}}^2-{a_{13(i)}}^2\right); \hspace{1em}i\in \langle 1,8\rangle$$

(25)

$$a_{12(i)}=\left({a_{16(i)}}^2-{a_{15(i)}}^2\right);\hspace{1em}i\in \langle 1,8\rangle$$

(26)

where:

a₁₃, a₁₅—the minimum values of the matrix X₆ elements;

a₁₄, a₁₆—the maximum values of the matrix X₆ elements.

The values of variables a₁₃, a₁₄, a₁₅ and a₁₆ were defined in the following way:

$$a_{13\left(i\right)}=\min \left(X_{6\left(i\right)(1)},X_{6\left(i\right)(2)}\right);\hspace{1em}i\in \langle 1,8\rangle$$

(27)

$$a_{14\left(i\right)}=\max \left(X_{6\left(i\right)(1)},X_{6\left(i\right)(2)}\right);\hspace{1em}i\in \langle 1,8\rangle$$

(28)

$$a_{15\left(i\right)}=\min \left(X_{6\left(i\right)(4)},X_{6\left(i\right)(5)}\right);\hspace{1em}i\in \langle 1,8\rangle$$

(29)

$$a_{16\left(i\right)}=\max \left(X_{6\left(i\right)(4)},X_{6\left(i\right)(5)}\right);\hspace{1em}i\in \langle 1,8\rangle$$

(30)

The calculated values of variables a₁₁ and a₁₂ defined a range of variation of variables used in the calculation of the objective function performed in the following generations.

The first number of bits for a binary string of a population individual calculated for each generation corresponded to a variable from the range [$a_{13\left(i\right)},a_{14\left(i\right)}$]. The second number of bits for a binary string of a population individual calculated for each generation corresponded to a variable from the range [$a_{15\left(i\right)},a_{16\left(i\right)}$].

The obtained variation ranges a₁₁ and a₁₂ were used with a specified accuracy equal to 10⁵ in calculations of the variables a₁₇ and a₁₈ that are required when defining the number of bits of applied binary strings according to the following formulas:

$$a_{17(i)}= a_{11(i)}·{10}^5;\hspace{1em}i\in \langle 1,8\rangle$$

(31)

$$a_{18(i)}= a_{12(i)}·{10}^5;\hspace{1em}i\in \langle 1,8\rangle$$

(32)

Using the calculated values of variables a₁₇ and a₁₈, one can define the number of bits s₁ and s₂ using the following formulas:

$$2^{s_{1\left(i\right)}-1}<a_{17(i)}\le 2^{s_{1\left(i\right)}};\hspace{1em}i\in \langle 1,8\rangle ; s_{1\left(i\right)}\in <1,25>$$

(33)

$$2^{s_{2\left(i\right)}-1}<a_{18(i)}\le 2^{s_{2\left(i\right)}};\hspace{1em}i\in \langle 1,8\rangle ; s_{2\left(i\right)}\in <1,25>$$

(34)

The values of binary strings of one k-th individual and one new l-th individual were changed to values in the decimal system using the formulas given below:

$$a_{19(i)}=\begin{array}{l}\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{7\left(i\right)(k,j)}}·2^{\left(j-1\right)};\\ i\in \langle 1,8\rangle ; k=random\langle 1,n\rangle ; k\ne l; m=s_{1\left(i\right)}; n\in <25,50>\end{array}\right\}\end{array}$$

(35)

$$a_{20(i)}=\begin{array}{c}\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{8\left(i\right)(k,j)}·2^{\left(j-1\right)};}\\ i\in \langle 1,8\rangle ; k=random\langle 1,n\rangle ; k\ne l; m=s_{2\left(i\right)}; n\in <25,50>\end{array}\right\}\end{array}$$

(36)

$$a_{21\left(i\right)}=\begin{array}{c}\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{7\left(i\right)(l,j)}}·2^{\left(j-1\right)};\\ i\in \langle 1,8\rangle ; l=random\langle 1,n\rangle ; k\ne l; m=s_{1\left(i\right)}; n\in <25,50>\end{array}\right\}\end{array}$$

(37)

$$a_{22\left(i\right)}=\begin{array}{c}\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{8\left(i\right)(l,j)}·2^{\left(j-1\right)};}\\ i\in \langle 1,8\rangle ; l=random\langle 1,n\rangle ; k\ne l; m=s_{2\left(i\right)}; n\in <25,50>\end{array}\right\}\end{array}$$

(38)

An important step in the diagnostic procedure was the defining of the most advantageous variations of values of the k-th and l-th individuals in the population, calculated using the variables a₁₃, a₁₄, a₁₅ and a₁₆ using the formulas given below:

$$a_{23\left(i\right)}=a_{13(i)}+a_{19(i)}·\frac{\left(a_{14(i)}-a_{13(i)}\right)}{\left(s_{1(i)}-1\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(39)

$$a_{24\left(i\right)}=a_{15(i)}+a_{20(i)}·\frac{\left(a_{16(i)}-a_{15(i)}\right)}{\left(s_{2(i)}-1\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(40)

$$a_{25\left(i\right)}=a_{13(i)}+a_{21(i)}·\frac{\left(a_{14(i)}-a_{13(i)}\right)}{\left(s_{1(i)}-1\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(41)

$$a_{26\left(i\right)}=a_{15(i)}+a_{22(i)}·\frac{\left(a_{16(i)}-a_{15(i)}\right)}{\left(s_{2(i)}-1\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(42)

The obtained values of the variables a₂₃, a₂₄, a₂₅ and a₂₆ were used in the calculations of objective function values.

The values of the objective function for the k-th and l-th individuals were calculated using the formulas below:

$$a_{27(i)}=0.5+\frac{{\sin }^2\sqrt{{a_{23(i)}}^2+{a_{24(i)}}^2}-0.5}{{\left(1.0+0.001·\left(a_{23(i)}+a_{24(i)}\right)\right)}^2};\hspace{1em}i\in \langle 1,8\rangle$$

(43)

$$a_{28(i)}=0.5+\frac{{\sin }^2\sqrt{{a_{25(i)}}^2+{a_{26(i)}}^2}-0.5}{{\left(1.0+0.001·\left(a_{25(i)}+a_{26(i)}\right)\right)}^2};\hspace{1em}i\in \langle 1,8\rangle$$

(44)

where:

a₂₇—the objective function value of the k-th individual;

a₂₈—the objective function value of the l-th individual.

The binary string of the k-th individual changed when one of the two conditions presented below was satisfied:

$$a_{28\left(i\right)}> a_{27\left(i\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(45)

$$b_{1\left(i\right)\left(m\right)}< {\exp }^{\frac{\left(a_{27\left(i\right)}-a_{28\left(i\right)}\right)}{T_{\left(i\right)\left(m\right)}}};\hspace{1em}{a}_{28\left(i\right)}\le a_{27\left(i\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(46)

where:

b₁—a random value from the range [0,1] defined in the test;

T—the temperature value for the current iteration of the genetic algorithm;

m—the number of the current iteration of the genetic algorithm.

The exchange of binary strings of one k-th individual was realized in the following way:

$$X_{7\left(i\right)(k,j)}=\begin{array}{c}\{\begin{array}{l}{X}_{7\left(i\right)\left(l,j\right)};\\ i\in \langle 1,8\rangle ; j=1,2\dots s_{1\left(i\right)}; k,l=random\langle 1,n\rangle ; k\ne l; n\in <25,50>\end{array}\end{array}$$

(47)

$$X_{8\left(i\right)(k,j)}=\begin{array}{l}\{\begin{array}{l}{X}_{8\left(i\right)\left(l,j\right)};\\ i\in \langle 1,8\rangle ; j=1,2\dots s_{2\left(i\right)}; k,l=random\langle 1,n\rangle ; k\ne l; n\in <25,50>\end{array}\end{array}$$

(48)

The stop criterion of the genetic algorithm was defined as shown below:

$$T_{\left(i\right)}\le a_{29\left(i\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(49)

where:

a₂₉—the value of the variable required for the stopping of the genetic algorithm (experimentally set in the test).

The value of temperature T in the following iterations m of simulated annealing decreased according to the logarithmic cooling scheme, as shown in the formula below [4,20]:

$$T_{\left(i\right)\left(m+1\right)}=\frac{T_{\left(i\right)\left(m\right)}}{\left(1+{\lambda }_{\left(i\right)\left(m\right)}·T_{\left(i\right)\left(m\right)}\right)};\hspace{1em}i\in \langle 1,8\rangle$$

(50)

where:

λ—the value of variable adapted for the logarithmic cooling scheme calculated in the test.

In the following iterations m of simulated annealing, the value of the adapted variable λ was calculated using the formula given below [4,20]:

$${\lambda }_{\left(i\right)\left(m+1\right)}=\frac{\ln \left(1+{\delta }_{\left(i\right)}\right)}{3·{\sigma }_{\left(\mathrm{i}\right)\left(m\right)}};\hspace{1em}i\in \langle 1,8\rangle$$

(51)

where:

δ—the parameter representing the accuracy of the equilibrium state for the logarithmic cooling scheme defined in the range (0.1,10);

σ—the value of the standard deviation of the objective function for all individuals generated at a given temperature and calculated in each iteration of simulated annealing m.

The standard deviation σ of objective function in each iteration m of simulated annealing was calculated in the following manner:

$${\sigma }_{\left(i\right)\left(m\right)}=\frac{\sqrt{{\displaystyle \sum _{j=1}^{\mathrm{n}}{\left(F_{1\left(j\right)\left(m\right)}-m_{6\left(i\right)\left(m\right)}\right)}^2}}}{\mathrm{n}};\hspace{1em}i\in \langle 1,8\rangle ; n\in \langle 25,50\rangle$$

(52)

where:

F₁—the value of the objective function for a specified population individual, calculated in the test for each iteration m of the genetic algorithm;

m₆—the arithmetic mean of the objective function of all individuals calculated for each iteration m of the genetic algorithm.

The values of objective function F₁ of all population individuals were calculated using the formula presented below:

$$F_{1(i)}=0.5+\frac{{\sin }^2\sqrt{{F_{2(i)}}^2+{F_{3(i)}}^2}-0.5}{{\left(1.0+0.001·\left(F_{2(i)}+F_{3(i)}\right)\right)}^2};\hspace{1em}i\in \langle 1,8\rangle$$

(53)

where:

F₂—the values of the matrix elements being the values of the first variable for the applied objective function,

F₃—the values of the matrix elements being the values of the second variable for the applied objective function.

Calculations of the elements’ values of matrices F₂ and F₃ were performed using the following formulas:

$$F_{2\left(i\right)\left(j\right)}=\{\begin{array}{l}{a}_{13(i)}+X_{9(i)\left(j\right)}·\frac{\left(a_{14(i)}-a_{13(i)}\right)}{\left(s_{1(i)}-1\right)};\hspace{1em}\\ i\in \langle 1,8\rangle ; j=1,2\dots n; n\in \langle 25,50\rangle \end{array}$$

(54)

$$F_{3\left(i\right)\left(j\right)}=\{\begin{array}{l}{a}_{15(i)}+X_{10(i)\left(j\right)}·\frac{\left(a_{16(i)}-a_{15(i)}\right)}{\left(s_{2(i)}-1\right)};\hspace{1em}\\ i\in \langle 1,8\rangle ; j=1,2\dots n; n\in <25,50>\end{array}$$

(55)

where:

a₁₃, a₁₅—the minimum values of the matrix X₆ elements defined by formulas (27) and (29);

a₁₄, a₁₆—the maximum values of the matrix X₆ elements defined by formulas (28) and (30);

X₉—the values of the matrix containing binary strings of population individuals in a decimal system;

X₁₀—the values of the matrix containing binary strings of population individuals in a decimal system.

The values of the X₉ and X₁₀ matrices were calculated using the formulas shown below:

$$X_{9(i)\left(a\right)}=\begin{array}{l}\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{7\left(i\right)(a,j)}}·2^{\left(j-1\right)};\\ a=1,2\dots n; i\in \langle 1,8\rangle ; m=s_{1\left(i\right)}; n\in \langle 25,50\rangle \end{array}\end{array}$$

(56)

$$X_{10(i)\left(a\right)}=\begin{array}{c}\{\begin{array}{l}{\displaystyle \sum _{j=1}^m{X}_{8\left(i\right)(a,j)}·2^{\left(j-1\right)};}\\ a=1,2\dots n; i\in \langle 1,8\rangle ; m=s_{2\left(i\right)}; n\in \langle 25,50\rangle \end{array}\end{array}$$

(57)

Identification of different cases of inter-turn short-circuiting was performed using the genetic algorithm according to the order defined in matrix K₁.

For all examined physical magnitudes in the applied diagnostic procedure, reference matrix calculation was performed for eight assumed cases of inter-turn short-circuiting.

In a test group for the load current I_load = 3 A, the values of the reference matrix were calculated and stored in matrices N₁ and N₂ of size 8 × 3. Tested values were stored in matrices N₃ and N₄ of size 1 × 3.

Reference and tested matrices were derived from matrix X₁₂ after the genetic algorithm had finished its operation. This matrix contained the values obtained by sorting the elements of matrix X₁₁ in descending order.

The values of matrix X₁₁ were obtained by changing the entire binary string of a population individual that was transforming the binary strings X₇ and X₈ to the decimal system. The calculations were performed according to the formula:

$$X_{11(i)\left(a\right)}=\begin{array}{l}\{\begin{array}{l}{\displaystyle \sum _{j=1}^k{X}_{7\left(i\right)(a,j)}}·2^{\left(j-1\right)}+{\displaystyle \sum _{j=k+1}^m{X}_{8\left(i\right)(a,j)}}·2^{\left(j-1\right)};\hspace{1em}\\ a=1,2\dots n; i\in \langle 1,8\rangle ; k=s_{1\left(i\right)}; m=s_{2\left(i\right)}; n\in \langle 25,50\rangle \end{array}\end{array}$$

(58)

The values of X₁₂ were defined as:

$$X_{12\left(i\right)(a)}=\begin{array}{c}\left\{\begin{array}{l}\left[X_{11\left(i\right)(1)}\ge X_{11\left(i\right)(2)} \dots .\ge X_{11\left(i\right)(n)}\right];\\ a=1,2\dots n; i\in \langle 1,8\rangle ; n\in \langle 25,50\rangle \end{array}\right\}\end{array}$$

(59)

The values of the matrix X₁₂ elements were stored in matrices containing the reference values N₁ and N₂ and in matrices containing the test values N₃ and N₄ after the genetic algorithm finished its operation. The values of matrices N₁, N₂, N₃ and N₄ were calculated using the formulas below:

$$N_{1\left(i,j\right)}=X_{12\left(i,j\right)}; \hspace{1em} i=1 , 2\dots 8; j=1 , 2\dots 3$$

(60)

$$N_{2\left(i,j\right)}=X_{12\left(i,j\right)}; \hspace{1em} i=1 , 2\dots 4; j=1 , 2\dots 3$$

(61)

$$N_{3\left(j\right)}=X_{12\left(j\right)}; \hspace{1em} j=1 , 2\dots 3$$

(62)

$$N_{4\left(j\right)}=X_{12\left(j\right)}; \hspace{1em} j=1 , 2\dots 3$$

(63)

The results obtained from identification tests:

−

Were stored in the reference matrix N₁ and in the tested matrix N₃ for the normalization of matrix X₁, which was performed using the parameters calculated for axial flux.

−

Were stored in the reference matrix N₂ and in the tested matrix N₄ for the normalization of matrix X₁, which was performed using the parameters calculated for acoustic pressure p_s.

The calculation of the values of matrices H₁ and H₂ made it possible to perform the correct identification of cases of inter-turn short circuiting for the calculated diagnostic signals of the examined physical magnitudes at the specified load current I_load.

The calculations of the values of matrices H₁ and H₂ were performed using the Manhattan metric as shown below:

$$H_{1(i)}={\displaystyle \sum _{j=1}^3\left|N_{1(i,j)}-N_{3(j)}\right| ; i=1,2\dots 8}$$

(64)

$$H_{2(i)}={\displaystyle \sum _{j=1}^3\left|N_{2(i,j)}-N_{4(j)}\right| ; i=1,2\dots 8}$$

(65)

In general, the calculations of matrix H₁ are performed directly after the genetic algorithm stops. After calculating the index nr₃, it may be necessary to calculate the values of matrix X₂. The aim is to obtain the index $n{r}_3\in <1,4>$; the calculated values of matrix H₁ might point to an incorrect number of inter-turn short-circuit case. Otherwise, the index nr₃ (for $n{r}_3\in <5,8>$) defined in matrix H₁ makes it possible to calculate the column number in matrix K₁ containing the right case of inter-turn short-circuiting for the examined induction motor model.

In this study, the index nr₃ was defined using the minimum value of the matrix H₁ as shown below:

$$H_{1(n{r}_3)}=\min \left(H_{1(i)}\right);\hspace{1em}i\in <5,8>$$

(66)

This means that column number i in matrix K₁ corresponded to calculated index nr₃ (i = nr₃).

Generally, when obtaining index $n{r}_3\in <1,4>$, the calculation of index nr₄ in matrix H₂ is performed. This allows for the examined induction motor model to define the correct case of inter-turn short circuiting out of four first assumed cases. The calculated index nr₄ (i = nr₄) corresponds to the column number of matrix K₁.

Here, by defining the minimum value of matrix H₂, index nr₄ was defined.

$$H_{2(n{r}_4)}=\min \left(H_{2(i)}\right);\hspace{1em}i=1,2\dots 4$$

(67)

4. Results of Research on Diagnostic Algorithm Application in the Identification of Inter-Turn Short-Circuiting in Induction Motor Models

In

Table 1. Example results of H₁ matrix for electromagnetic torque m_el.

Test Parameters	Results * 1011	Test Parameters	Results * 1011
inter-turn short-circuit 1_20, load current Iobc = 1 A, population size = 25, a29 = 9 * 10−5, δ = 1.5, iteration = 35	1.5165 1.5435 1.5238 1.5451 1.5096 1.4747 0.6304 2.4499	inter-turn short-circuit 1_20, load current Iobc = 1 A, population size = 50, a29 = 9 * 10−5, δ = 5.0, iteration = 15	1.8195 1.8429 1.8197 1.8370 1.8056 1.6356 0.8436 2.1941
inter-turn short-circuit 1_10, load current Iobc = 4 A, population size = 25, a29 = 9 * 10−5, δ = 1.5, iteration = 104	0.0085 0.0355 0.0157 0.0370 0.0016 0.0334 0.8777 3.9579	inter-turn short-circuit 1_10, load current Iobc = 4 A, population size = 50, a29 = 9 * 10−5, δ = 5.0, iteration = 58	0.0141 0.0375 0.0144 0.0317 0.0003 0.1698 0.9617 3.9995

,

Table 2. Example results of H₁ matrix tests for rotational speed n_l.

Test Parameters	Results * 1011	Test Parameters	Results * 1011
inter-turn short-circuit 1_15, load current Iobc = 2 A, population size = 25, condition = 9 * 10−5, δ = 1.5, iteration = 38	0.4331 0.4192 0.4339 0.4217 0.3756 0.0739 0.8653 6.1794	inter-turn short-circuit 1_15, load current Iobc = 2 A, population size = 50, condition = 9 * 10−5, δ = 5.0, iteration = 17	0.4494 0.4454 0.4507 0.4426 0.4054 0.0029 1.5368 7.0391
inter-turn short-circuit 1_25, load current Iobc = 5 A, population size = 25, condition = 9 * 10−5, δ = 1.5, iteration = 34	7.3506 7.3494 7.3400 7.3432 7.2915 6.9687 5.7263 0.5185	inter-turn short-circuit 1_25, load current Iobc = 5 A, population size = 50, condition = 9 * 10−5, δ = 5.0, iteration = 18	7.8657 7.8617 7.8670 7.8589 7.8217 7.4134 5.8795 0.4429

,

Table 3. Example results of H₂ matrix tests for the signal proportional to axial flux ϕ₁.

Test Parameters	Results	Test Parameters	Results
inter-turn short-circuit 1_3, load current Iobc = 1 A, population size = 25, a29 = 9 * 10−6, δ = 1.5, iteration = 31	24,522 2309 12,972 20,211	inter-turn short-circuit 1_3, load current Iobc = 1 A, population size = 50, a29 = 9 * 10−6, δ = 5.0, iteration = 14	24,263 206 12,830 23,643
inter-turn short-circuit 1_5, load current Iobc = 4 A, population size = 25, a29 = 9 * 10−6, δ = 1.5, iteration = 27	36,991 20,738 16,198 5219	inter-turn short-circuit 1_5, load current Iobc = 4 A, population size = 50, a29 = 9 * 10−6, δ = 5.0, iteration = 15	45,858 23,825 21,433 902

and

Table 4. Example results of H₂ tests for acceleration in d axis X—d_x.

Test Parameters	Results	Test Parameters	Results
inter-turn short-circuit 1_4, load current Iobc = 2 A, population size = 25, a29 =9 * 10−6, δ = 1.5, iteration = 22	23,325 11,396 699 22,413	inter-turn short-circuit 1_4, load current Iobc = 2 A, population size = 50, a29 =9 * 10−6, δ = 5.0, iteration = 12	23,947 12,261 235 24,266
inter-turn short-circuit 1_2, load current Iobc = 5 A, population size = 25, a29 = 9 * 10−6, δ = 1.5, iteration = 20	0 11,929 23,588 45,738	inter-turn short-circuit 1_2, load current Iobc = 5 A, population size = 50, a29 = 9 * 10−6, δ = 5.0, iteration = 10	0 11,686 23,964 48,213

, several cases of the inter-turn short-circuits that were investigated in the identification process are contained in the column labelled Test parameters and also the correct results of the calculation of the matrices H₁ and H₂ obtained during the identification process of inter-turn short-circuiting are marked in bold. In the performed identification tests, the initial temperature of the genetic algorithm with simulated annealing was equal to T = 100.

Based on the simulation results in Table 1, Table 2, Table 3 and Table 4, one can see that for all investigated physical magnitudes, it is possible to obtain correct results in the identification of short-circuit cases when using appropriate values of the variable a₂₉ and the accuracy parameter δ.

Using the variations of test parameters in inter-turn short-circuit identification process allows for the obtaining of improvements in the calculation results for matrices H₁ and H₂.

In addition, it can be concluded on the basis of the results presented in Table 1, Table 2, Table 3 and Table 4 that increasing the population size and the precision parameter δ increases the scope of both the search for solutions for the variable neighborhood of the individual k and the random selection of binary chains of individuals from the neighborhood of the individual k. Thus, the occurrence of the stochastic process during the operation of the simulated annealing algorithm increases intensively, thus enabling the reduction in the number of iterations as well as the calculated minimum value in the matrices H₁ and H₂, respectively.

In addition to this and based on the results in Table 1, Table 2, Table 3 and Table 4, it can be stated that increasing the population size and the accuracy parameter value leads to an augmenting of the solution search range within a varied neighborhood as well as a random selection of binary chains of individuals from within the neighborhood of the individual k. As a result, the probability of a stochastic process occurring increases dramatically, thus decreasing the number of iterations and the computed minimal values in the matrices H₁ i H₂, respectively.

Next, Figure 4 shows the impact of changes in the population size and the accuracy parameter δ on the convergence of the proposed genetic algorithm.

Figure 4 shows the calculated minimum values of the H₁ matrix (see Table 1 and Table 2) and the calculated minimum values of the H₂ matrix (see Table 3 and Table 4).

Note that there were significant decreases in the minimum values calculated in the matrices H₁ and H₂, respectively, for the same investigated cases of the interturn short circuits, as well as in the obtained number of iterations occurring when there were large increases in the population size and the accuracy parameter value δ.

5. Conclusions

Based on the results of this research, one can see that in the proposed diagnostic method, the extraction of information from obtained time series for the investigated physical magnitudes of induction motors leads to increased fault detection and identification capabilities.

All variables used in the genetic algorithm provide information about fault occurrence symptoms. The assumed order of simulated annealing operations for each examined induction motor model makes it possible to efficiently solve the problem of inter-turn short-circuit identification in the system using binary strings of population individuals. The correct calculation of these values is achieved through the use of the genetic algorithm with simulated annealing.

Proper functioning of diagnostic systems with effective selectivity of dynamic state identification requires the use of reference matrices derived from repetitive analyses of the examined induction motor models.

In the presented diagnostic algorithm, an effective identification of the dynamic states of the examined induction motor model is possible when using the created reference matrices.

In addition, one may state that an effective solution by means of the proposed diagnostic method involves the determination of the length of the binary chain/sequence of individuals in the population using math operations carried out based on the values of the arithmetic means calculated for the elements of the appropriate matrices and obtained as a result of the applied grouping and normalization of the values of the tested physical quantities recorded during the performed measurements.

In comparison to the GA-based methods used in the early-stage diagnostics of short-circuit faults in the stators of induction motors [5,9], the method that uses a hybrid GA-PSO algorithm to determine the parameters of an induction motor (HGAPSO) [21], the DE methods used for the estimation of the electrical and mechanical parameters of three-phase induction motors [1] or the hybrid method based on the simulated annealing algorithm and the evaporation rate of the water cycle (SA-ERWCA) used to estimate the parameters of the reduced-order circuit of an induction machine [10], the presented algorithm, designed for the identification of interturn short-circuits, makes it possible to:

−

Obtain correct results when searching for a local optimal solution by calculating the length of the binary sequence of individuals with the parameters obtained by means of clustering in a fixed order and normalization of the data recorded via laboratory measurements and the adopted Schaffer F6 objective function;

−

Ensure the optimization of performance in terms of the quality of the results obtained via the identification process upon applying changes within the appropriate range of parameters of the genetic algorithm (population size, initial temperature value, accuracy parameter and convergence criterion);

−

Solve continuous and discrete optimization problems by ensuring a stochastic process during the GA operation.