Dynamic Modelling and Advanced Process Control of Power Block for a Parabolic Trough Solar Power Plant
Abstract
1. Introduction
- Survey the research papers focusing on the description of the control loops of PB of the parabolic trough power plant (PTPP). To the best of our knowledge, there are few studies in the relevant literature that deal with some major control loops of PB in PTPP.
- This paper describes each control loop of PB in detail using actual specifications from the Andasol II power plant.
- A detailed description of the control loops of PB using APROS software is the first study performed in this field.
- The principle purpose of this design is to provide researchers a useful tool that can be used as a reference for advanced PTPP control loops.
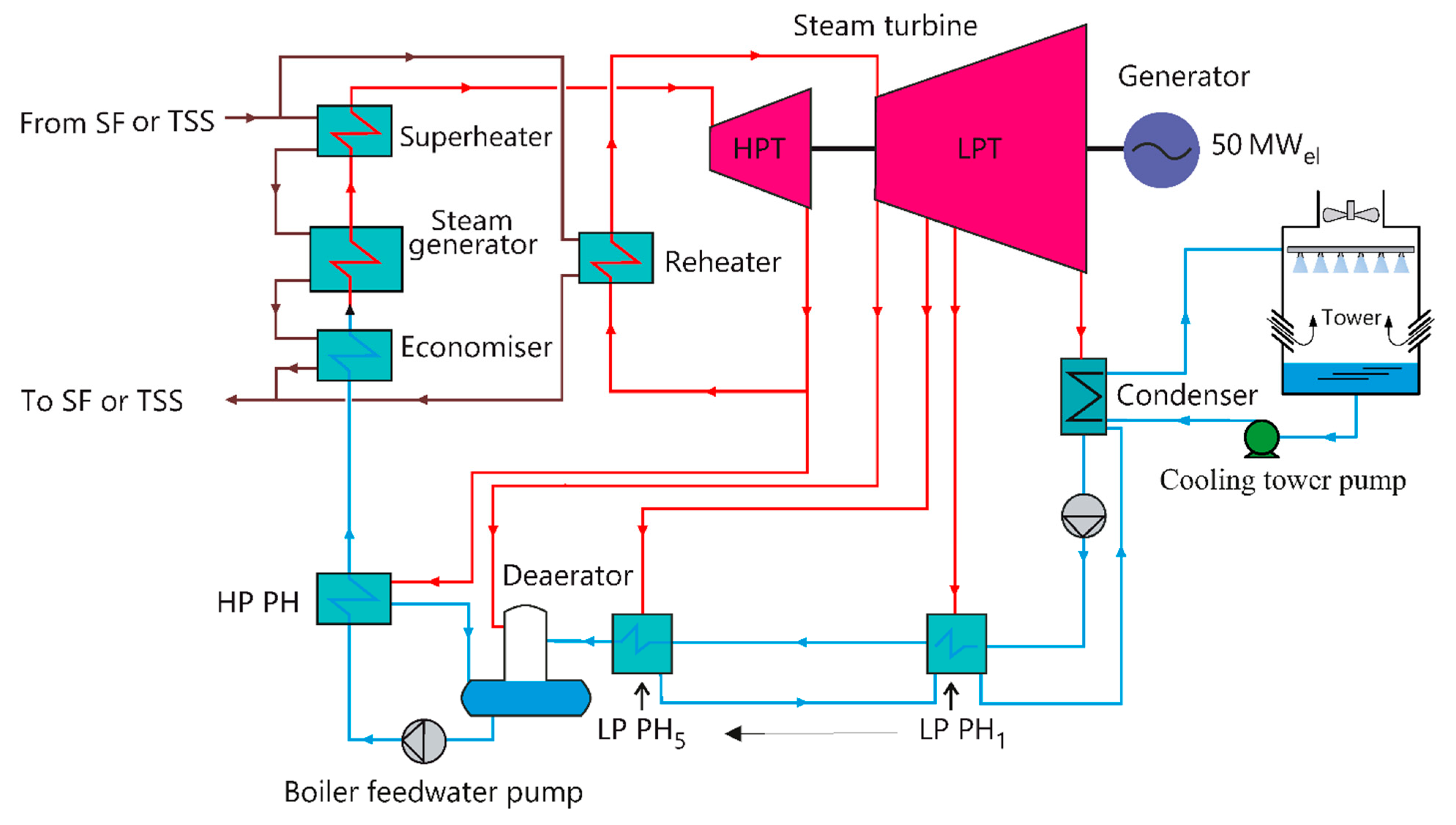
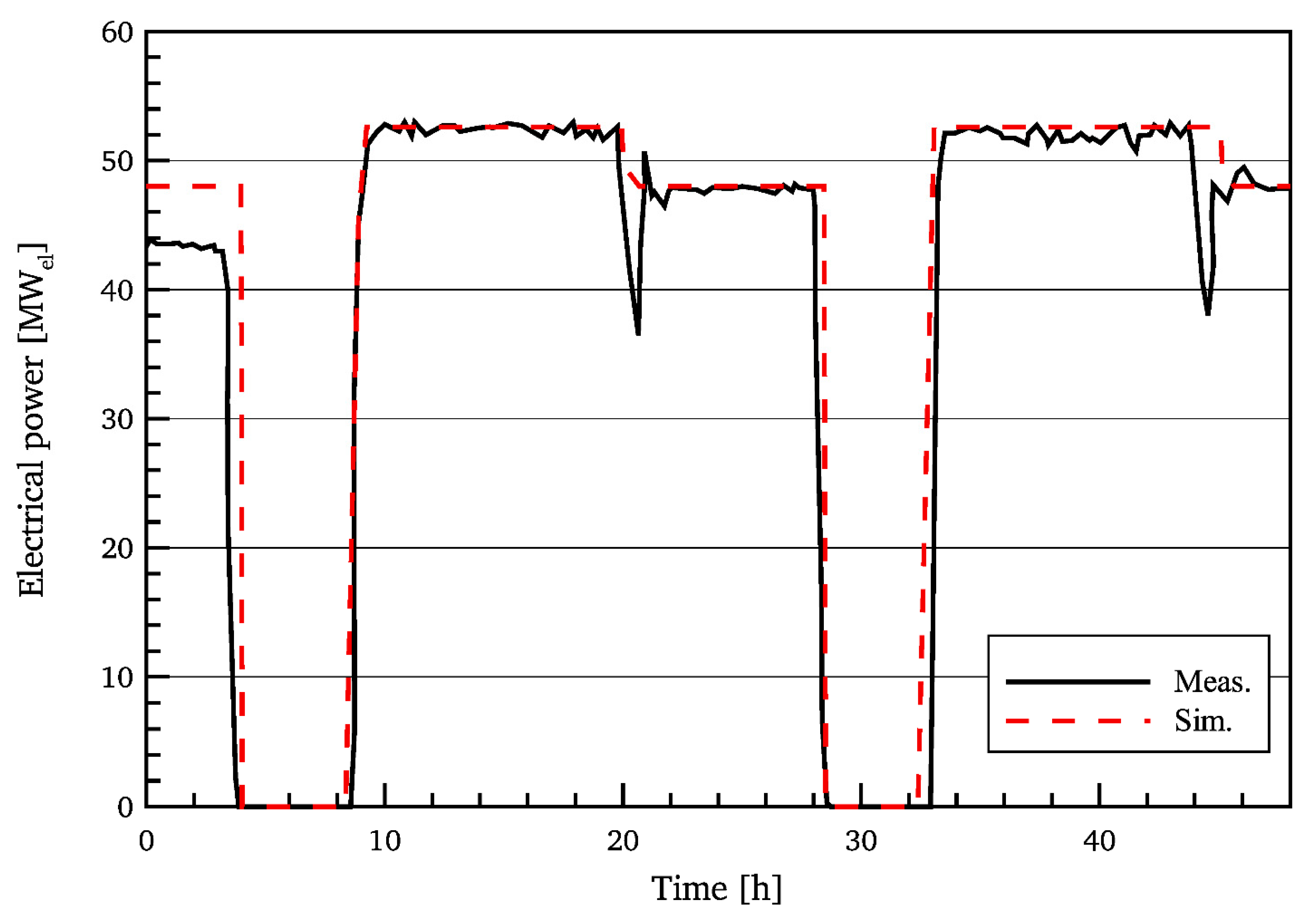
2. Modelling and Solution Method
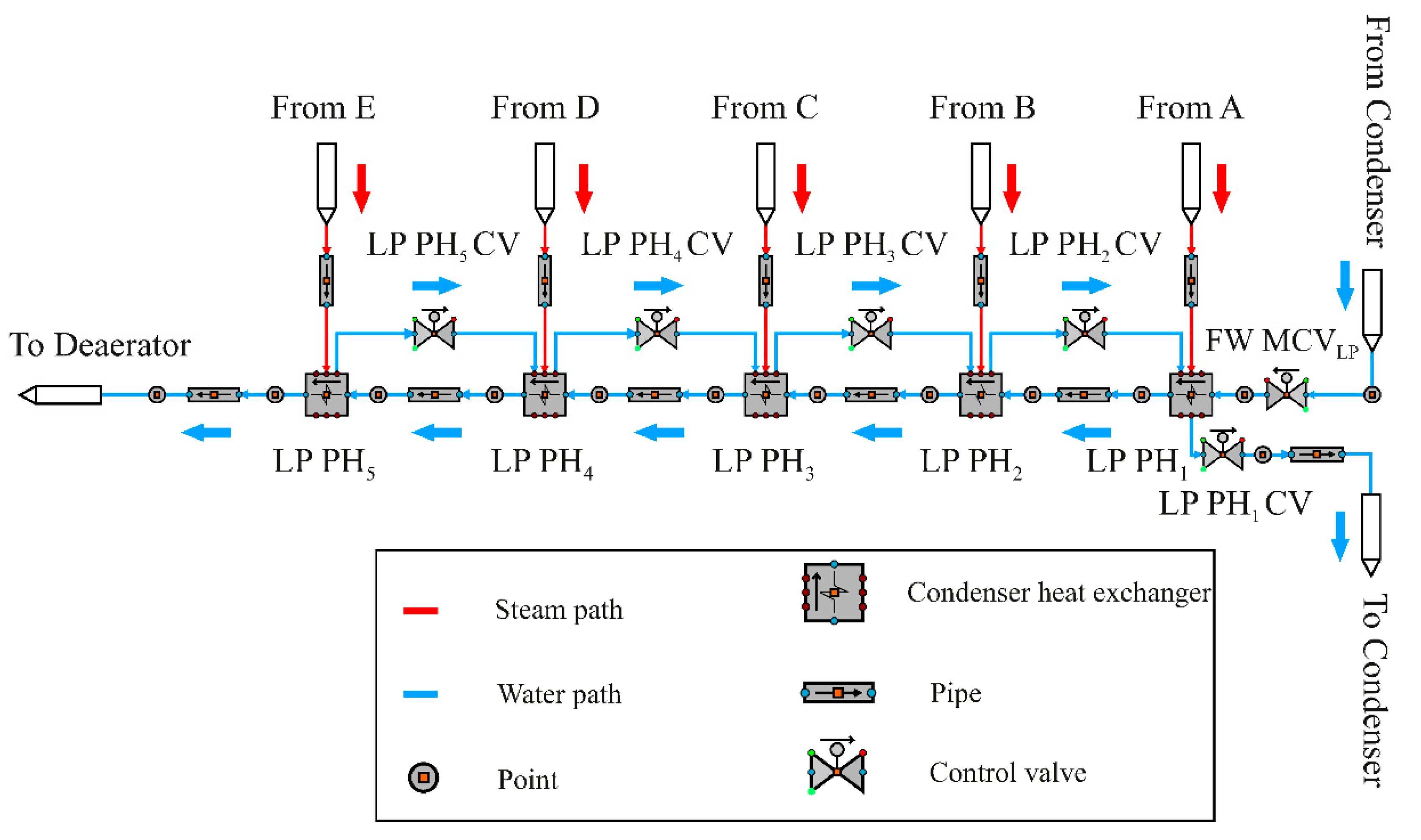
3. LP Feedwater Circuit Model
3.1. Feedwater Control Structures
3.1.1. Feedwater Main Control Valve in the LP Feedwater Circuit (FW MCVLP)
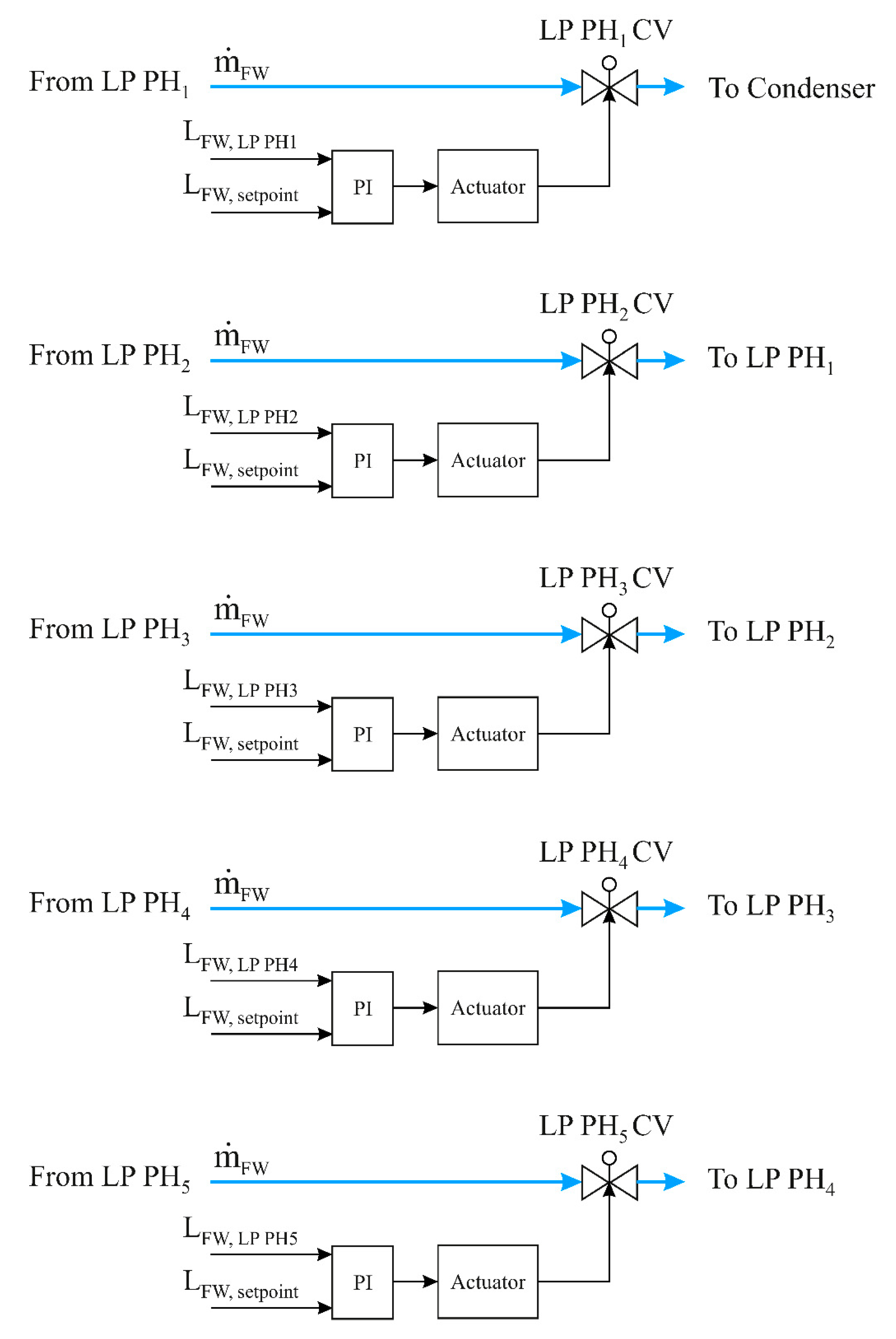
3.1.2. LP Preheater Level Controllers
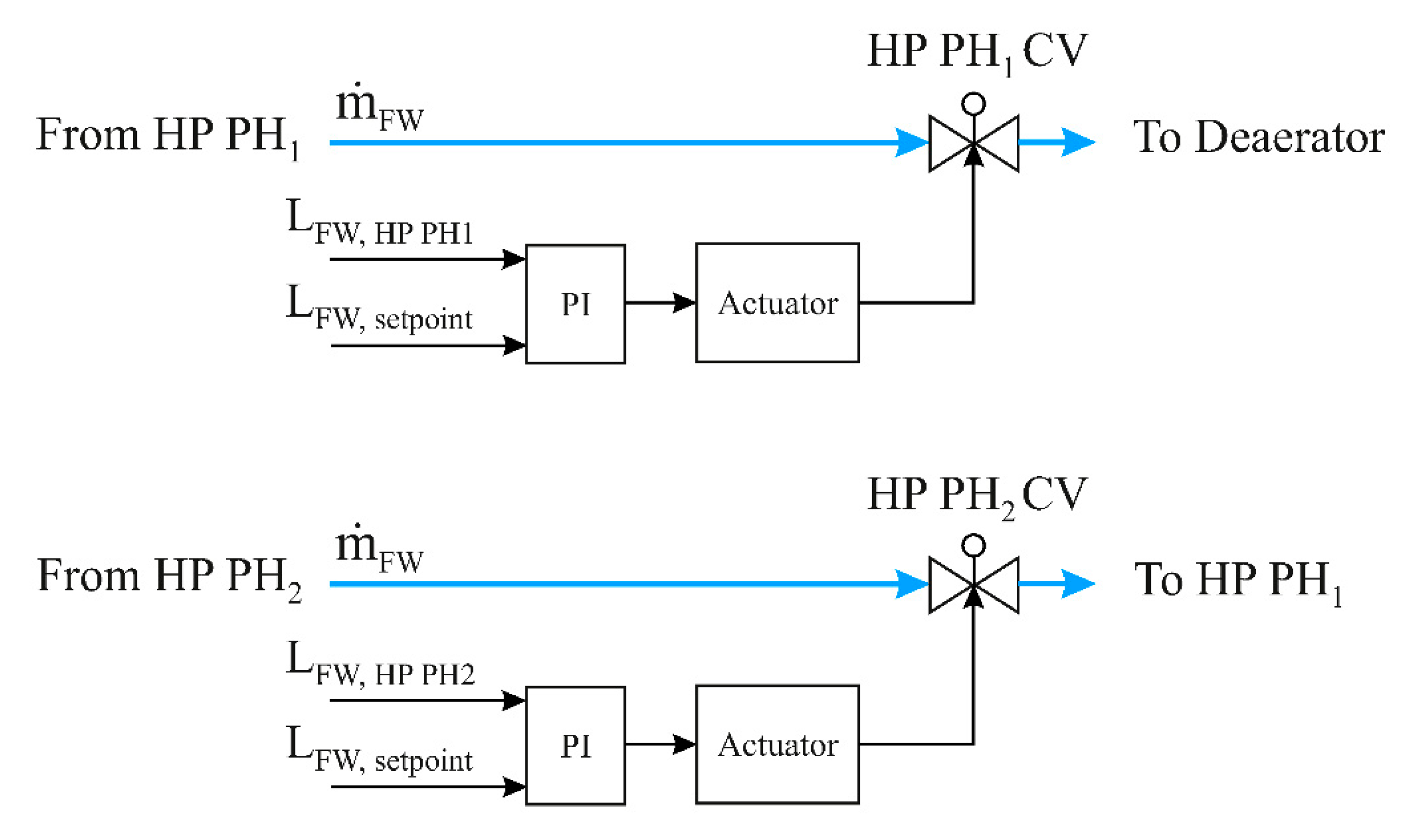
- The disparity between the real level and level setpoint of water in the shell side is measured.
- PI controller commands the actuator.
- The actuator operates the LP PH control valve in order to achieve the setpoint value.
4. Boiler Model
4.1. Boiler Control Structures
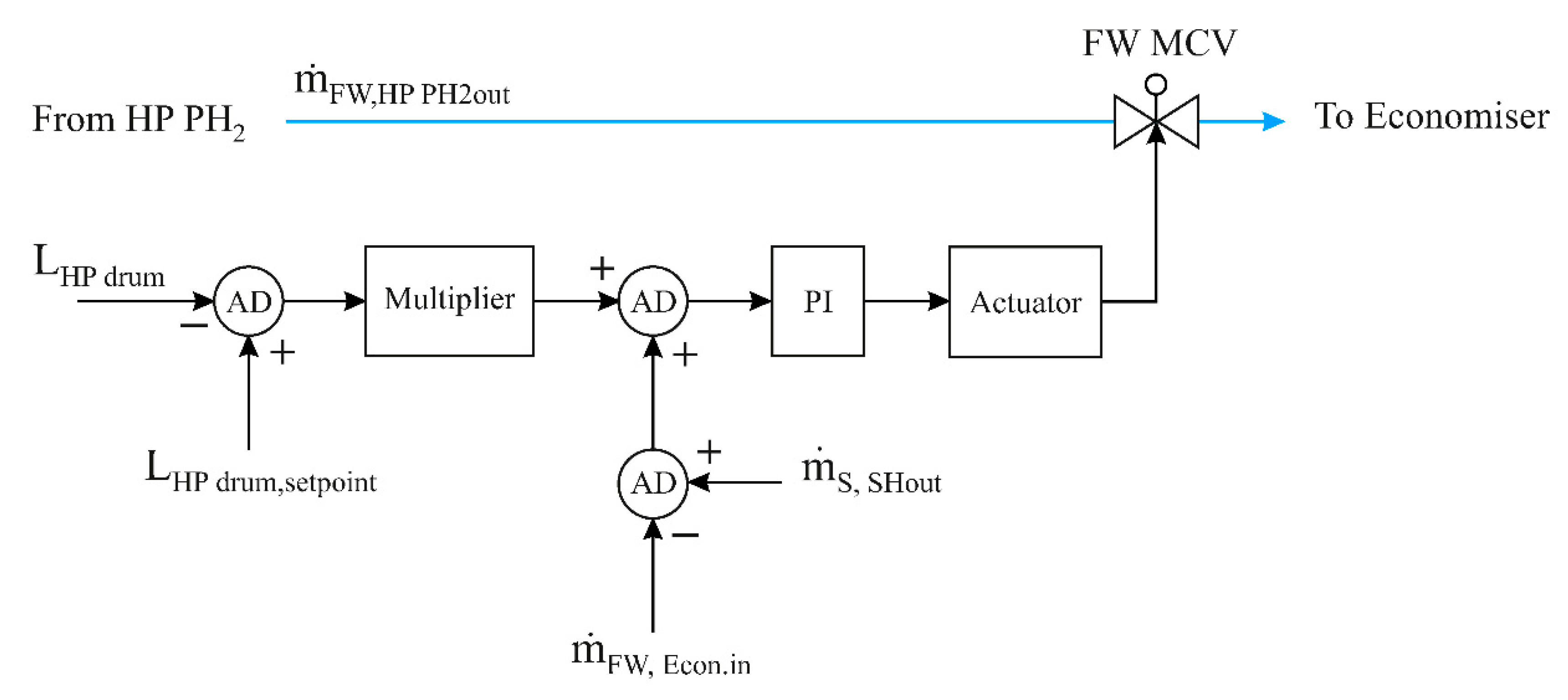
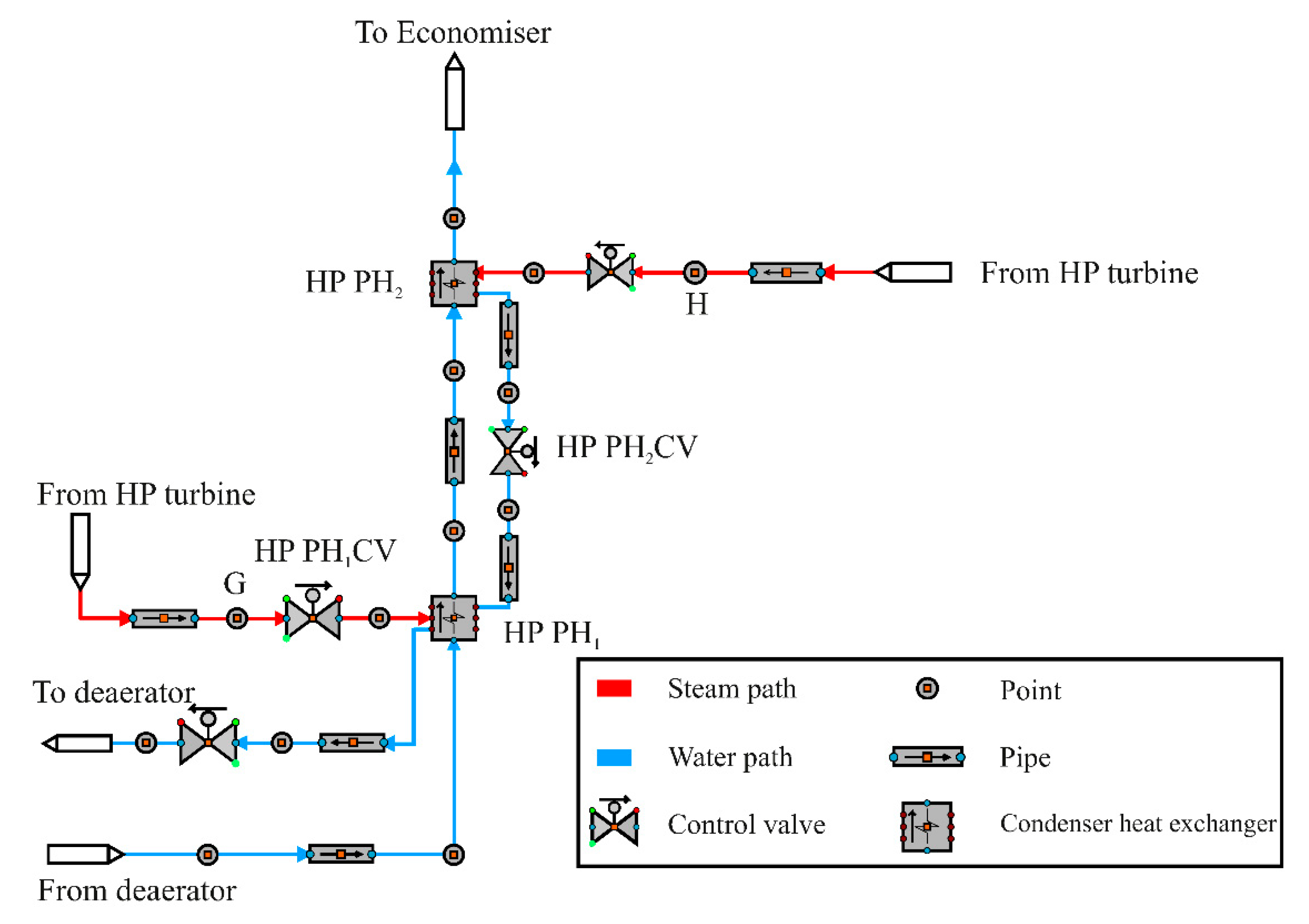
4.1.1. HP Preheater Level Control Circuits
4.1.2. HP Drum Level Controller
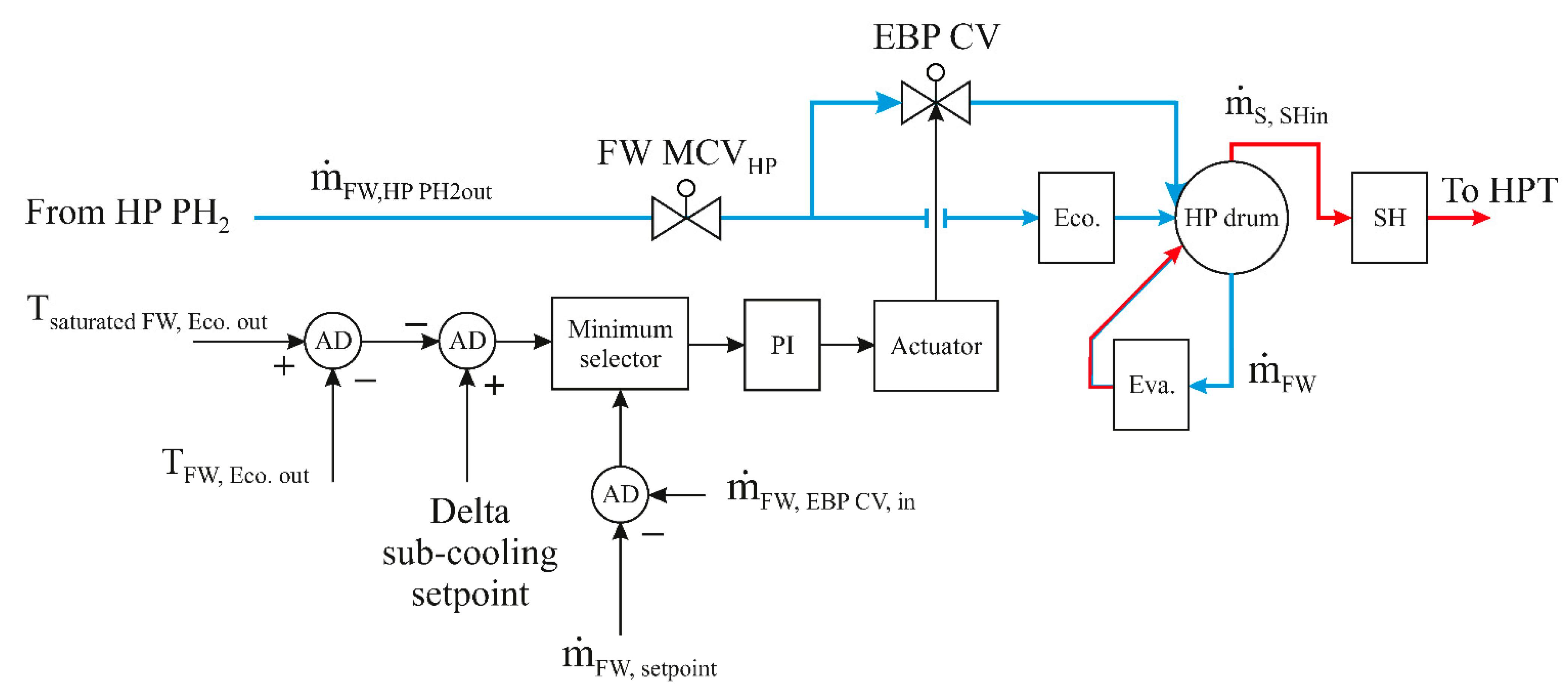
4.1.3. Economiser’s Bypass Controller (EBP CV)
- The saturated temperature of feedwater at the HP economiser outlet is measured and compared with the real temperature at the HP economiser outlet.
- Deviation between both temperatures is compared with the HP delta sub-cooling (5 °C). However, the user can easily define any other needed value depending on the demand.
- The output signal from the second comparator (AD) enters a minimum selector and then sends a PI controller.
- The PI controller sends the commands to the actuator, which regulates the feedwater temperature through the economiser’s bypass control valve (EBP CV).
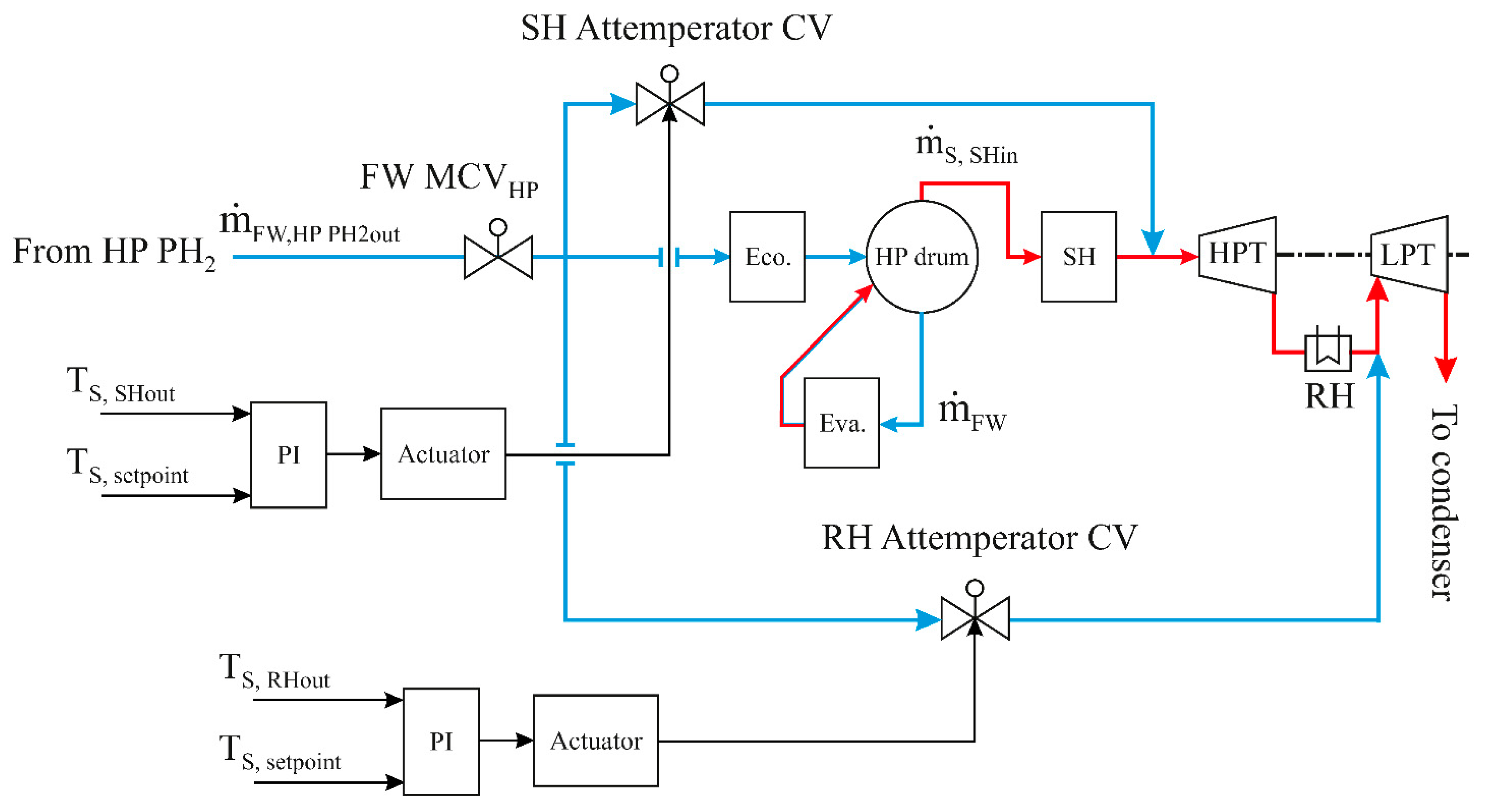
4.1.4. SH and RH Attemperator Controllers
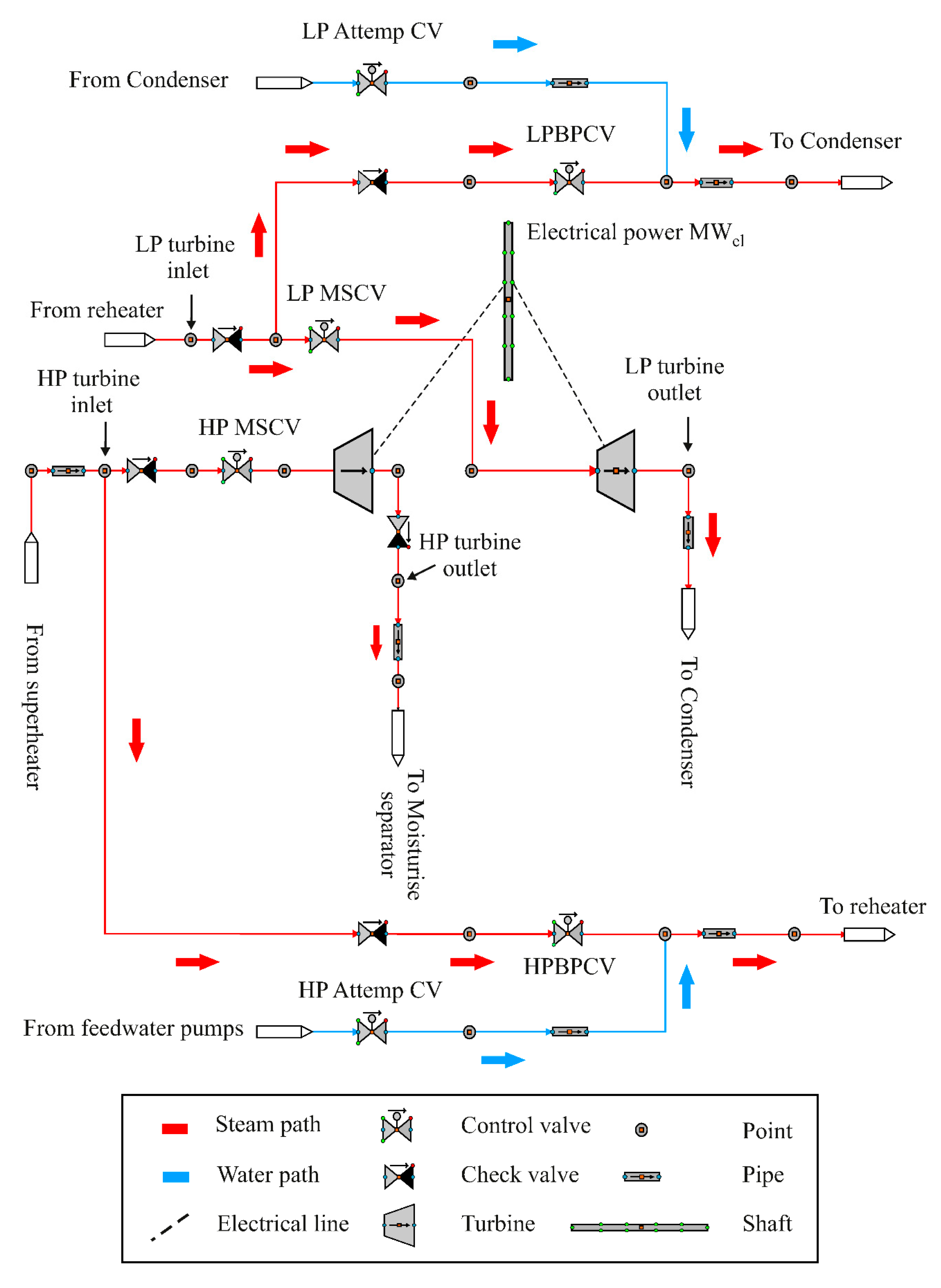
5. Steam Turbine Model
5.1. Steam Turbine Control Structures
5.1.1. LP Bypass Controller and LP Main Steam Control Valve
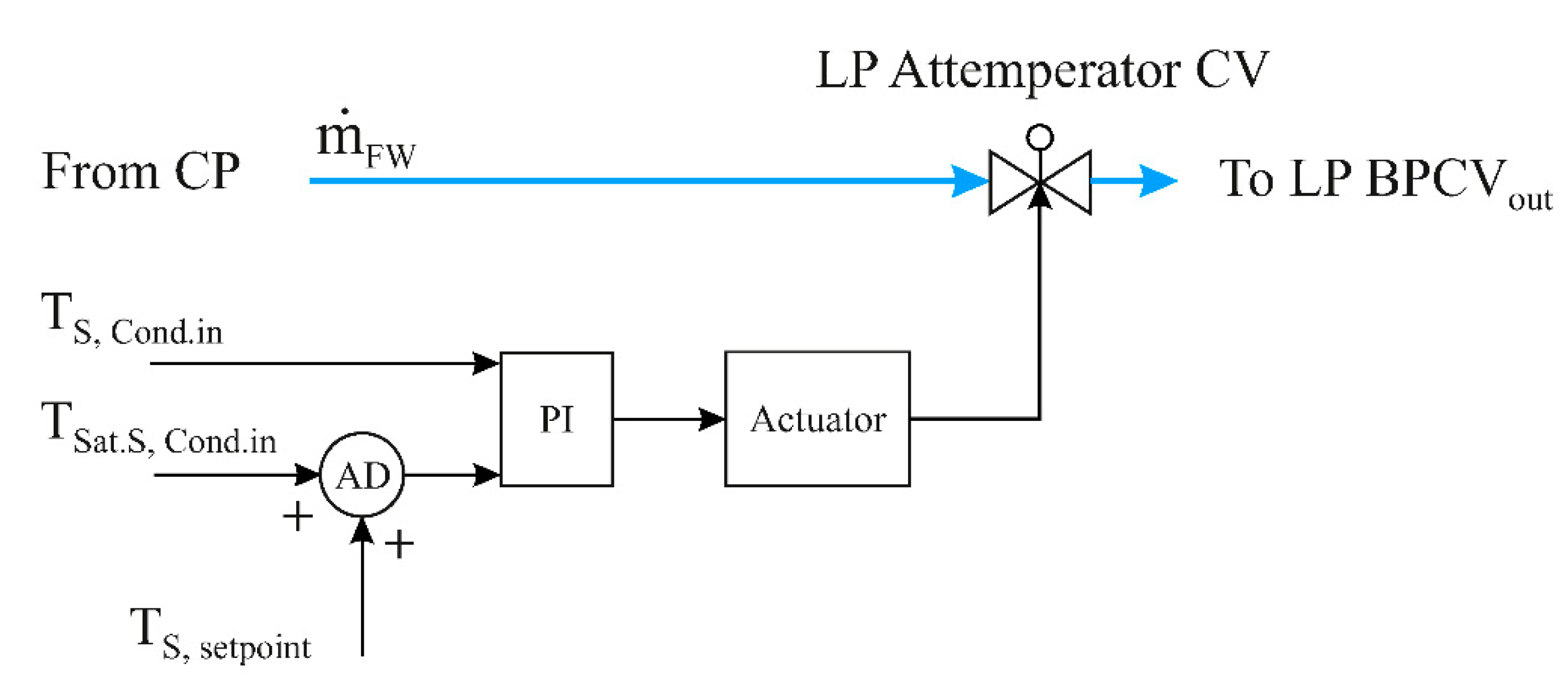
5.1.2. LP Attemperator Control Valve (LP Attemp CV)
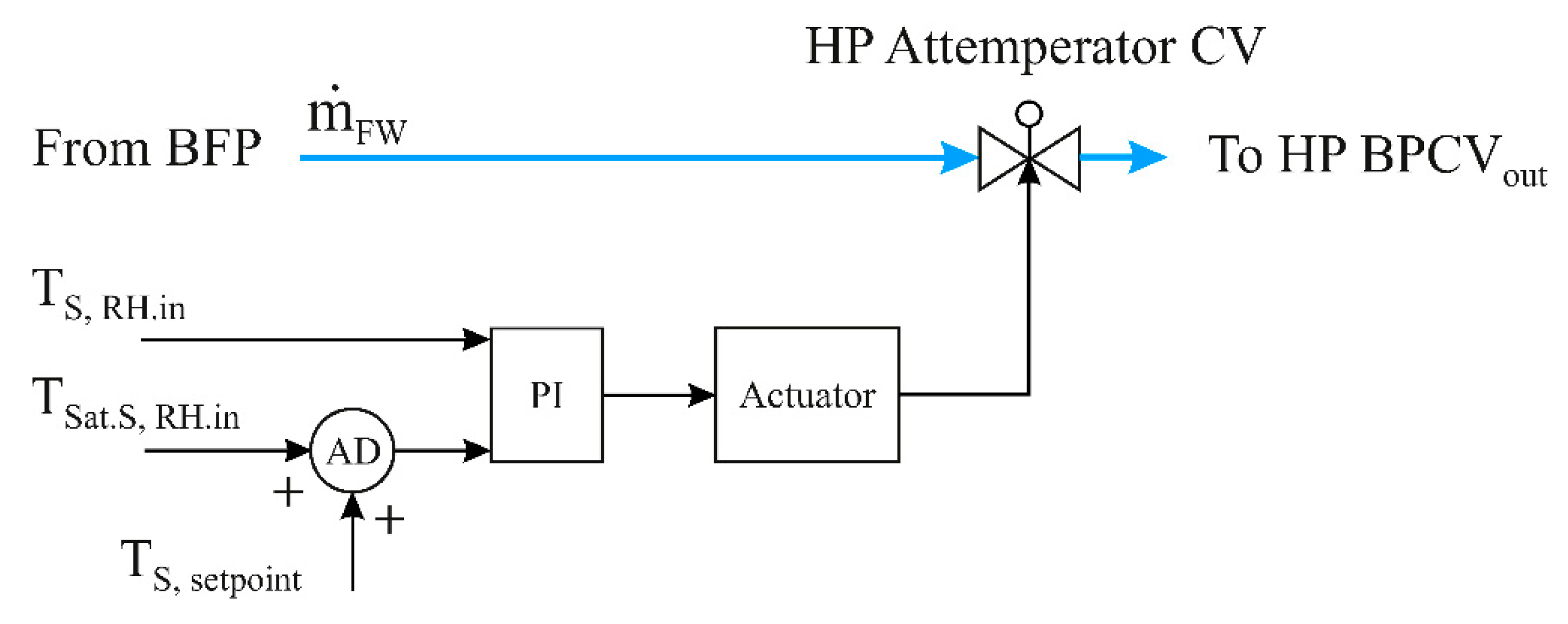
5.1.3. HP Attemperator Control Valve (HP Attemp CV)
6. Condenser Model
6.1. Condenser Control Structures
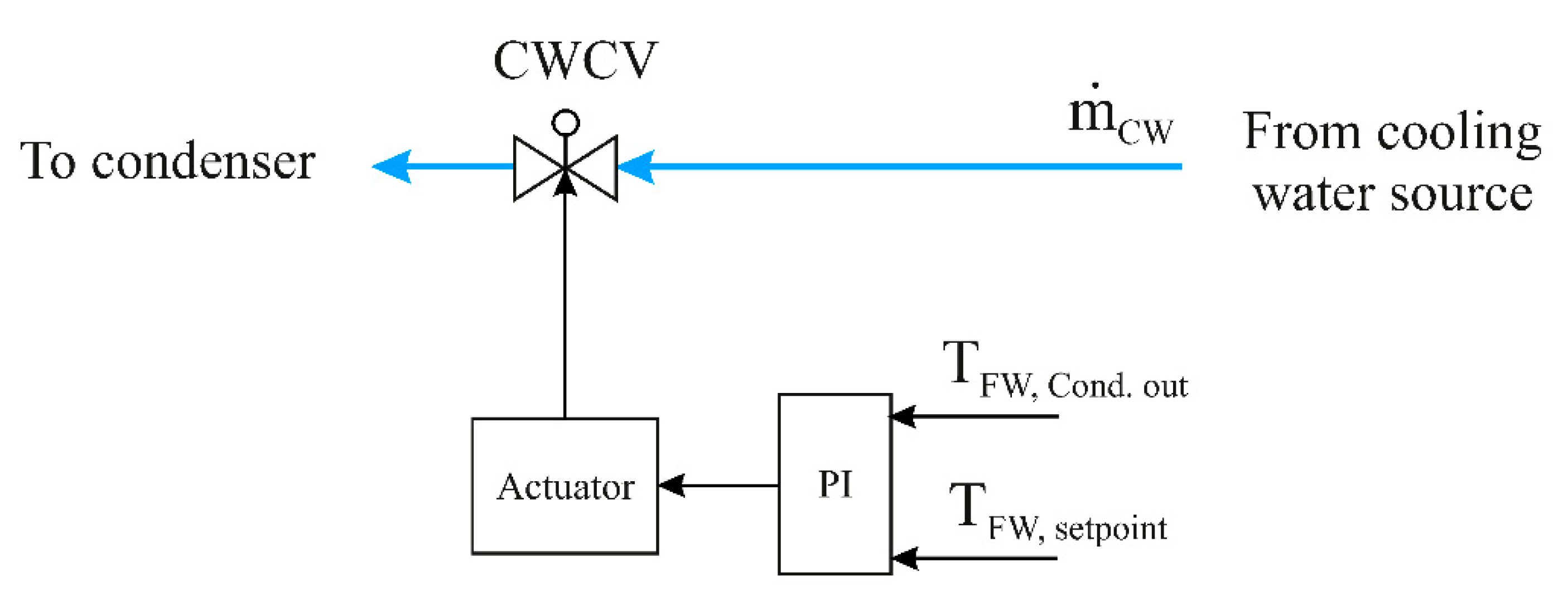
Cooling Water Control Valve (CWCV)
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| h | Enthalpy [kJ/kg] |
| ṁ | Mass flow rate [kg/s] |
| P | Pressure [bar] |
| T | Temperature [°C] |
| t | Time [sec] |
| u | Velocity [m/s] |
| ρ | Density [kg/m3] |
| DNI | Direct normal irradiation [W/m2] |
Abbreviations
| AD | Adder |
| APROS | Advanced process simulation software |
| BFP | Boiler feedwater pump |
| CP | Condenser pump |
| FW | Feedwater |
| HP | High pressure |
| HTF | Heat transfer fluid |
| LP | Low pressure |
| PB | Power block |
| PTPP | Parabolic trough power plant |
| PI | Proportional–integral controller |
| SF | Solar field |
| TSS | Thermal storage system |
| SP | Set point |
| TI | Temperature measurement component |
References
- Müller-Steinhagen, H. FaTF. Concentrating Solar Power. A Review of the Technology; Institute of Technical Thermodynamics, German Aerospace Centre: Stuttgart, Germany, 2004; p. 9. [Google Scholar]
- Kaygusuz, K. Prospect of concentrating solar power in Turkey: The sustainable future. Renew. Sustain. Energy Rev. 2011, 15, 808–814. [Google Scholar] [CrossRef]
- Bhutto, A.W.; Bazmi, A.A.; Zahedi, G.; Klemeš, J.J. A review of progress in renewable energy implementation in the Gulf Cooperation Council countries. J. Clean. Prod. 2014, 71, 168–180. [Google Scholar] [CrossRef]
- Wahhab, H.A.A.; Al-Maliki, W.A.K. Application of a Solar Chimney Power Plant to Electrical Generation in Covered Agricultural Fields. IOP Conf. Ser. Mater. Sci. Eng. 2020, 671, 012137. [Google Scholar] [CrossRef]
- Artola, V.; María, J. Performance of a 50 MW Concentrating Solar Power Plant. Master’s Thesis, Politecnico Di Bari, Bari, Italy, 2010. [Google Scholar]
- Desai, N.B.; Bandyopadhyay, S. Optimization of concentrating solar thermal power plant based on parabolic trough collector. J. Clean. Prod. 2015, 89, 262–271. [Google Scholar] [CrossRef]
- Fernández-García, A.; Rojas, E.; Pérez, M.; Silva, R.; Hernández-Escobedo, Q.; Manzano-Agugliaro, F. A parabolic-trough collector for cleaner industrial process heat. J. Clean. Prod. 2015, 89, 272–285. [Google Scholar] [CrossRef]
- Sharan, P.; Bandyopadhyay, S. Solar assisted multiple-effect evaporator. J. Clean. Prod. 2016, 142, 2340–2351. [Google Scholar] [CrossRef]
- Teske, S.L.J.; Crespo, L.; Bial, M.; Dufour, E.; Richter, C. Solar Thermal Electricity, Global Outlook 2016; Greenpeace International: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Reddy, K.; Kumar, K.R. Solar collector field design and viability analysis of stand-alone parabolic trough power plants for Indian conditions. Energy Sustain. Dev. 2012, 16, 456–470. [Google Scholar] [CrossRef]
- Chacartegui, R.; Vigna, L.; Becerra, J.; Verda, V. Analysis of two heat storage integrations for an Organic Rankine Cycle Parabolic trough solar power plant. Energy Convers. Manag. 2016, 125, 353–367. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Degrève, J.; Cacères, G. Concentrated solar power plants: Review and design methodology. Renew. Sustain. Energy Rev. 2013, 22, 466–481. [Google Scholar] [CrossRef]
- Lovegrove, K.; Stein, W. Concentrating Solar Power Technology: Principles, Developments and Applications; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Wagner, P.H.; Wittmann, M. Influence of different operation strategies on transient solar thermal power plant simulation models with molten salt as heat transfer fluid. Energy Procedia 2014, 49, 1652–1663. [Google Scholar] [CrossRef][Green Version]
- Weber, G.; Di Giuliano, A.; Rauch, R.; Hofbauer, H. Developing a simulation model for a mixed alcohol synthesis reactor and validation of experimental data in IPSEpro. Fuel Processing Technol. 2016, 141, 167–176. [Google Scholar] [CrossRef]
- Zamarreño, J.M.; Mazaeda, R.; Caminero, J.A.; Rivero, A.J.; Arroyo, J.C. A new plug-in for the creation of OPC servers based on EcosimPro© simulation software. Simul. Model. Pract. Theory 2014, 40, 86–94. [Google Scholar] [CrossRef]
- Malinowski, L.; Lewandowska, M.; Giannetti, F. Design and analysis of a new configuration of secondary circuit of the EU-DEMO fusion power plant using GateCycle. Fusion Eng. Des. 2018, 136, 1149–1152. [Google Scholar] [CrossRef]
- Bordignon, S.; Emmi, G.; Zarrella, A.; De Carli, M. Energy analysis of different configurations for a reversible ground source heat pump using a new flexible TRNSYS Type. Appl. Therm. Eng. 2021, 197, 117413. [Google Scholar] [CrossRef]
- Eck, M.; Hirsch, T. Dynamics and control of parabolic trough collector loops with direct steam generation. Sol. Energy 2007, 81, 268–279. [Google Scholar] [CrossRef]
- Greenhut, A.D.; Tester, J.W.; DiPippo, R.; Field, R.; Love, C.; Nichols, K.; Augustine, C.; Batini, F.; Price, B.; Gigliucci, G. Solar–geothermal hybrid cycle analysis for low enthalpy solar and geothermal resources. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- García, I.L.; Álvarez, J.L.; Blanco, D. Performance model for parabolic trough solar thermal power plants with thermal storage: Comparison to operating plant data. Sol. Energy 2011, 85, 2443–2460. [Google Scholar] [CrossRef]
- Ehrhart, B.; Gill, D. Evaluation of annual efficiencies of high temperature central receiver concentrated solar power plants with thermal energy storage. Energy Procedia 2014, 49, 752–761. [Google Scholar] [CrossRef]
- Chennaif, M.; Maaouane, M.; Zahboune, H.; Elhafyani, M.; Zouggar, S. Tri-objective techno-economic sizing optimization of Off-grid and On-grid renewable energy systems using Electric system Cascade Extended analysis and system Advisor Model. Appl. Energy 2022, 305, 117844. [Google Scholar] [CrossRef]
- Al-Maliki, W.A.K.; Al-Hasnawi, A.G.T.; Abdul Wahhab, H.A.; Alobaid, F.; Epple, B. A Comparison Study on the Improved Operation Strategy for a Parabolic trough Solar Power Plant in Spain. Appl. Sci. 2021, 11, 9576. [Google Scholar] [CrossRef]
- Al-Maliki, W.A.K.; Mahmoud, N.S.; Al-Khafaji, H.M.; Alobaid, F.; Epple, B. Design and Implementation of the Solar Field and Thermal Storage System Controllers for a Parabolic Trough Solar Power Plant. Appl. Sci. 2021, 11, 6155. [Google Scholar] [CrossRef]
- Ho, C.K. Software and Codes for Analysis of Concentrating Solar Power Technologies; Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2008. [Google Scholar]
- Liu, S.; Faille, D.; Fouquet, M.; El-Hefni, B.; Wang, Y.; Zhang, J.; Wang, Z.; Chen, G.; Soler, R. Dynamic simulation of a 1MWe CSP tower plant with two-level thermal storage implemented with control system. Energy Procedia 2015, 69, 1335–1343. [Google Scholar] [CrossRef]
- Mitterhofer, M.; Orosz, M. Dynamic Simulation and Optimization of an Experimental Micro-CSP Power Plant. In Proceedings of the Energy Sustainability, Bangkok, Thailand, 25–26 October 2015; p. V001T005A007. [Google Scholar]
- Ma, L.; Zhang, T.; Zhang, X.; Wang, B.; Mei, S.; Wang, Z.; Xue, X. Optimization of parabolic trough solar power plant operations with nonuniform and degraded collectors. Sol. Energy 2021, 214, 551–564. [Google Scholar] [CrossRef]
- Al-Maliki, W.A.K.; Alobaid, F.; Keil, A.; Epple, B. Dynamic Process Simulation of a Molten-Salt Energy Storage System. Appl. Sci. 2021, 11, 11308. [Google Scholar] [CrossRef]
- Ferruzza, D.; Topel, M.; Laumert, B.; Haglind, F. Optimal start-up operating strategies for gas-boosted parabolic trough solar power plants. Sol. Energy 2018, 176, 589–603. [Google Scholar] [CrossRef]
- El Hefni, B. Dynamic modeling of concentrated solar power plants with the ThermoSysPro library (Parabolic Trough collectors, Fresnel reflector and Solar-Hybrid). Energy Procedia 2014, 49, 1127–1137. [Google Scholar] [CrossRef]
- Al-Maliki, W.A.K.; Alobaid, F.; Kez, V.; Epple, B. Modelling and dynamic simulation of a parabolic trough power plant. J. Process Control 2016, 39, 123–138. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, M.; Zhao, Y.; Liu, J.; Yan, J. Dynamic simulation and performance analysis of a parabolic trough concentrated solar power plant using molten salt during the start-up process. Renew. Energy 2021, 179, 1458–1471. [Google Scholar] [CrossRef]
- Yazdi, M.; Manesh, M.H.K. Dynamic 6E analysis of direct steam generator solar parabolic trough collector power plant with thermal energy storage. Sustain. Energy Technol. Assess. 2022, 49, 101759. [Google Scholar] [CrossRef]
- Yuanjing, W.; Cheng, Z.; Yanping, Z.; Xiaohong, H. Performance analysis of an improved 30 MW parabolic trough solar thermal power plant. Energy 2020, 213, 118862. [Google Scholar] [CrossRef]
- Montañés, R.M.; Windahl, J.; Pålsson, J.; Thern, M. Dynamic modeling of a parabolic trough solar thermal power plant with thermal storage using modelica. Heat Transf. Eng. 2018, 39, 277–292. [Google Scholar] [CrossRef]
- Silva, R.; Pérez, M.; Fernández-Garcia, A. Modeling and co-simulation of a parabolic trough solar plant for industrial process heat. Appl. Energy 2013, 106, 287–300. [Google Scholar] [CrossRef]
- Alobaid, F. Start-up improvement of a supplementary-fired large combined-cycle power plant. J. Process Control 2018, 64, 71–88. [Google Scholar] [CrossRef]
- Alobaid, F.; Mertens, N.; Starkloff, R.; Lanz, T.; Heinze, C.; Epple, B. Progress in dynamic simulation of thermal power plants. Prog. Energy Combust. Sci. 2017, 59, 79–162. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Hänninen, M. Phenomenological Extensions to APROS Six-Equation Model. Non-Condensable Gas, Supercritical Pressure, Improved CCFL and Reduced Numerical Diffusion for Scalar Transport Calculation; VTT Publications 720; KULKAISIJA-UTGIVARE-PUBLISHER: Espoo, Finland, 2009. [Google Scholar]
- Siikonen, T. Numerical method for one-dimensional two-phase flow. Numer. Heat Transf. Part A Appl. 1987, 12, 1–18. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Maliki, W.A.K.; Hadi, A.S.; Al-Khafaji, H.M.H.; Alobaid, F.; Epple, B. Dynamic Modelling and Advanced Process Control of Power Block for a Parabolic Trough Solar Power Plant. Energies 2022, 15, 129. https://doi.org/10.3390/en15010129
Al-Maliki WAK, Hadi AS, Al-Khafaji HMH, Alobaid F, Epple B. Dynamic Modelling and Advanced Process Control of Power Block for a Parabolic Trough Solar Power Plant. Energies. 2022; 15(1):129. https://doi.org/10.3390/en15010129
Chicago/Turabian StyleAl-Maliki, Wisam Abed Kattea, Auday Shaker Hadi, Hussein M. H. Al-Khafaji, Falah Alobaid, and Bernd Epple. 2022. "Dynamic Modelling and Advanced Process Control of Power Block for a Parabolic Trough Solar Power Plant" Energies 15, no. 1: 129. https://doi.org/10.3390/en15010129
APA StyleAl-Maliki, W. A. K., Hadi, A. S., Al-Khafaji, H. M. H., Alobaid, F., & Epple, B. (2022). Dynamic Modelling and Advanced Process Control of Power Block for a Parabolic Trough Solar Power Plant. Energies, 15(1), 129. https://doi.org/10.3390/en15010129






