Performance Evaluation of a Full-Scale Fused Magnesia Furnace for MgO Production Based on Energy and Exergy Analysis

Abstract

A three-electrode alternating current fused magnesia furnace (AFMF) with advanced control technology was evaluated by combined energy and exergy analysis. To gain insight into the mass flow, energy flow and exergy efficiency of the present fused magnesia furnace, the exergy destruction was analysed to study the energy irreversibility of the furnace. Two different production processes, the magnesite ore smelting process (MOP) and light-calcined magnesia process (LMP), are discussed separately. Two methods were carried out to improve LMP and MOP; one of which has been applied in factories. The equipment consists of an electric power supply system, a light-calcined system and a three-electrode fused magnesia furnace. All parameters were tested or calculated based on the data investigated in industrial factories. The calculation results showed that for LMP and MOP, the mass transport efficiencies were 16.6% and 38.3%, the energy efficiencies were 62.2% and 65.5%, and the exergy destructions were 70.5% and 48.4%, respectively. Additionally, the energy efficiency and exergy efficiency of the preparation process of LMP were 39.4% and 35.6%, respectively. After the production system was improved, the mass transport efficiency, energy efficiency and exergy destruction were determined.

1. Introduction

Refractory materials are widely used in high-temperature industrial environments, such as the aerospace, steel and construction industries. Magnesia oxide plays an irreplaceable role in refractory material production because of its resistance to oxidation, deoxidation and thermal decomposition. An electric arc furnace (EAF) was first used to produce fused magnesia in 1991 to facilitate high-quality magnesia oxide production in China [1]. In the industrial process of MgO production, the main equipment used to produce fused magnesia oxide is a fused magnesia furnace, and the heat resource of the furnace consists of arc heat generation (40%) and resistance heat generation (60%) [2]. With a rapid increase in MgO requirement in several industries, over 90% of electrically fused magnesia oxide has been produced in a low energy efficiency EAF, which is a serious waste of electrical energy [3,4,5,6]. There are two common electric fused systems that are used to produce electrically fused magnesia oxide: the two-electrode direct current magnesia furnace (DFMF) and three-electrode alternating current fused magnesia furnace (AFMF). The researchers’ research focuses mainly on power supply systems and automation control. Wang et al. estimated the electrical system losses of electric arc furnaces, and Fu et al. studied the common blow-out phenomenon in electric magnesia furnaces and gave a predictive model that can predict the occurrence of the phenomenon of blasting furnaces in magnesia fusion furnaces [7,8]. Compared with the DFMF system, the AFMF system is a widely used method because of its mature technology and good production ability; however, the DFMF system is also used in some plants due to its higher energy efficiency and low equipment cost. Qin improved the basic structural parameters and operation methods of the two-electrode DC electric arc furnace and described the energy-saving characteristics of the two-electrode DC electric arc furnace. In addition, Kong et al. improved the control method of a three-electrode AC electric arc furnace and summarised the advantages of a three-phase electric arc furnace [9,10]. Furthermore, it is also clear that substantial energy consumption and large numbers of byproducts exist in both the AFMF system and DFMF system. As the requirement of high-quality MgO increases, AFMF systems play an important role in high-quality MgO production, and the improvement in the energy efficiency of AFMF systems has received much attention in the past decade. Li et al. conducted a series of studies on the cleaner production of magnesium oxide in Liaoning Province, analysed the production process from the perspective of the urban environment and production environment and gave the best production process for refractory materials using magnesium oxide [5,11]. Based on the metallurgical system, Chai et al. carried out a comparative modelling of the fused magnesia production process, applied the CPS system to the fused magnesia production process and gave the basic realisation route of the fused magnesia CPS system [12]. The AFMF system can also be divided into two processes, namely, the magnesite ore smelting process (MOP) and light-burned magnesia process (LMP), due to different raw material preparation methods.

The raw materials of the MOP process are produced in an ore-crushing plant, and magnesite ores are mined from the magnesite mines and are transported to be crushed. The main raw material of the LMP process is light calcinated magnesia. Light calcinated magnesia powder is generally produced in a light-burning plant, where the raw material ore is sent to the light-calcinating equipment for calcination at a temperature of 900–1000 K [13]. Inside, the ore decomposes and generates light calcinated magnesia. During the light calcination process, the main heat source is the combustion of the gas by the gas producer. After the light calcinated magnesia powder is produced, it is placed for cooling to room temperature.

After cooling, light-calcined magnesia powder can be pressed to pellets and sent to an electric-fused plant. In addition to the equipment used in light-calcined plants, the basic equipment of MOPs and LMPs are almost the same in electric fused plants.

The light-calcined system is the main equipment in the LMP. Unlike in the MOP, a light-calcined system is used to pretreat the raw materials by heating them at a temperature between 800 K and 1000 K. In the temperature range from 800–1000 K, the MgCO₃ in magnesite ores decompose into CO₂ and MgO. Longo et al. provided several chemical reaction equations for MgCO₃ decomposition production at different temperature ranges, and studies have shown that the production of MgO presents different states at different temperature ranges [14]. Jie Y. et al. summarised the research directions in the field of fused magnesia as optimisation, control, modelling and experimental constraints and also summarised the main problems in the field of fused magnesia and the intelligent technologies that can be applied [15].

The three-electrode alternating current fused magnesia furnace (AFMF) system plays the most important role in both MOPs and LMPs, and the system in electric fused plants mainly consists of a high-voltage transformer (HVT), material transport equipment (MTE) and an AFMF. High-voltage electrical power is translated into standard electricity with a regime of 2800 kVA through a multistage coil in the HVT. A mathematical model used to calculate the electric loss of HVTs was developed by Gutiérrez et al. considering multistage coil loss (copper loss), wire loss (iron loss) and reactive power [16]. The electrical loss assessment of an HVT was discussed by Zhou’s group with respect to source-load power uncertainty and electricity price fluctuations [17]. An MTE system consists of material feeders and material setters; a complex control system was designed by Chai based on a cyber-physical system (CPS) system, and an integrated optimal operation control algorithm was proposed [18]. Liu designed and modelled all of the equipment to lay magnesite ores, and the structural strength and stability were studied based on ANSYS workbench 17.0. At the same time, a control program compiled by a ladder diagram was also developed [19]. The AFMF is the most important equipment in both MOPs and LMPs; raw materials are preheated at the upper part of the furnace, and a smelting process occurs in the lower part of the furnace [7]. Shan explained the mechanism of ore preheating and surface heat transfer and discussed the influencing factors of the resultant heat transfer. The equipment used to heat water, which is needed for use in industrial parks, was designed and applied in Don-xing refractory company to avoid wasting heat [20]. Fu. et al. performed some research on the prediction of eruptions occurring in the AFMF, and a software and hardware set that can accurately identify the vibration frequency of raw material eruptions was developed together [21]. Li established a mathematical model to describe phenomena that occurs in furnaces, i.e., the magnetic field, fluid flow field and heat transfer; at the same time, the combustion enthalpy change was also considered in the model [22]. Although researchers have performed many studies on the control system of AFMF systems and affiliated equipment to achieve better energy efficiency, few studies have provided a clear comparison of MOPs and LMPs with respect to energy performance.

Exergy analysis has been widely used to evaluate the energy efficiency of industrial processes, and the efficiency and rationality of the exergy concept has been proven in metallurgical systems. Rong et al. applied exergy analysis to the rotary kiln-electric furnace (RKEF) system, investigated the potential for energy savings, and used waste heat to preheat the raw materials [23]. Yu et al. presented comprehensive exergy and energy analyses to compare the energy performance of RKEF systems and sintering-preheating-submerge arc furnace (SPSF) systems and concluded that SPSF systems are more environmentally friendly than RKEF systems and that waste gas could be recycled and show a better energy saving effect [24]. Zhang et al. studied the exergy loss of each component of electric vehicles, and an exergy analysis was carried out on the heat pump air conditioning system (HPACS) of electric vehicles with a battery thermal management system. The results show that under all operating conditions, the compressor is the main source of system exergy losses [25,26,27,28,29]. Harmed K. also carried out corresponding research in the field of seawater desalination. This article focuses on the recovery of sewage as the research object and uses electric energy as the energy supply for evaporation treatment to provide good environmental protection. Energy-exergy loss was evaluated. In addition, the researchers also conducted corresponding evaluations and studies on the reverse osmosis seawater desalination process based on geothermal energy [30,31,32]. Mahmoudan A. proposed a new type of integrated energy system based on a geothermal heat source and LNG radiator and carried out energy, exergy and exergy economic evaluations of the system. At the same time, parameter research was carried out on different decision variables, and finally, the TOPSIS method specified the optimal control scheme [31]. Although many exergy analyses have been applied in several industrial systems, exergy analyses of MOP and LMP in AFMF systems have not been discussed in previous studies. The preparation process of MgO requires large amounts of electricity, and the energy saving potential urgently needs to be evaluated.

In the present work, energy, exergy, and environmental analyses of a real-scale magnesite smelting process were applied to evaluate the energy efficiency, exergy efficiency and performance with respect to environmental protection of MOP and LMP. In the circumstances of a reduction in carbon emissions, the importance of evaluating the energy and exergy efficiency and eco-friendliness of energy-intensive enterprises is obvious. This study provides a series of key parameter analyses in magnesite smelting process systems and shows the tremendous potential of environmental protection, energy savings and exergy savings

2. System Description

Figure 1 shows the main equipment of the MOP and LMP systems. The two parts in the picture were taken on the top and side of the mould, showing the electrode, the mould and the finished product of fused magnesia waiting to be broken after the production process. The three-phase magnesia smelting furnace is located at No. 1 Magnesite Plant of Hai-cheng Magnesite Group Corporation. The furnace provides experimental data used in the text. The equipment mainly consists of three carbon electrodes, servo motors and crystallisers.

Figure 2 shows the total process of MOP and LMP. The arrows in the map show the translation of materials and directions of energy and mass flow. LMP and MOP utilise different pretreatments of materials of different purities. Ores were first mined from a magnesite mine and transported to a sorting centre in which the mass fraction of different batch ores can be tested and divided into three ranges. The raw materials with mass fraction of MgCO₃ between 0.7 and 0.8 are referred to as inferior ores; these raw materials must be floated in a flotation kiln first to filter out the materials with a mass fraction lower than 0.75 based on the standards summarised from production experience. Materials with a mass fraction lower than 0.75 were used to treat pollution gas. Other materials were sent to a light-calcined warehouse and were mixed with raw materials with a mass fraction between 0.8 and 0.9 (named premium ores). The materials were sent to a light-calcined bed, and after the light-calcined process, the pre-production materials were transported to the electric fused furnace. This total process is referred to as LMP. In addition to the materials mentioned above, ores with mass fractions higher than 0.9 are named excellent ores. These ores are only crushed in crushing plants first and then are transported to electric fused furnaces. This process is named MOP.

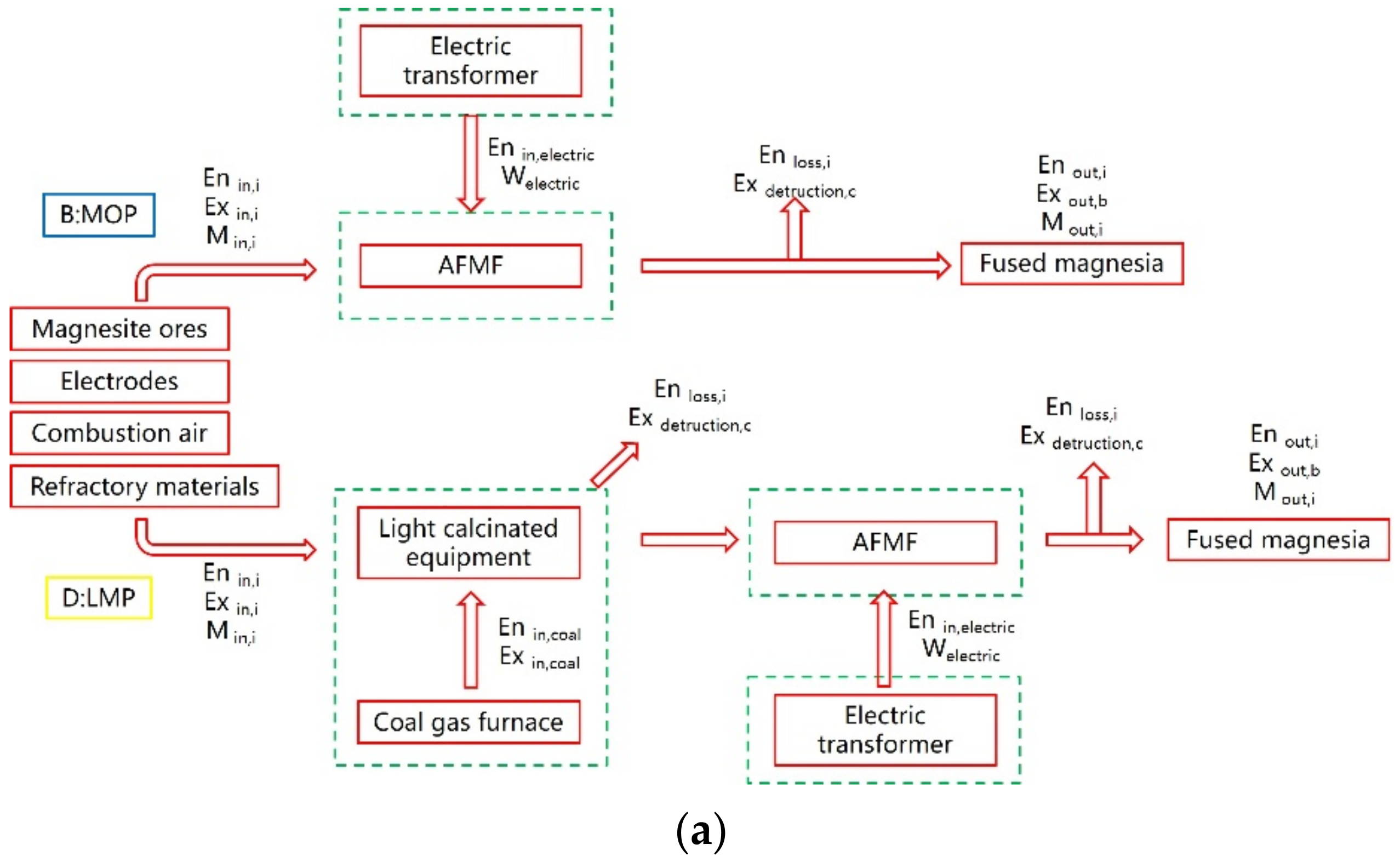
Figure 3a shows the specific production process under the two different processes of LMP and MOP, as well as the boundary division when calculating the mass–energy–exergy balance. First, regarding the mass balance, in the MOP route, ore, electrodes, combustion air and refractory materials are considered input items of the process flow. After the smelting is completed, the fused magnesia, flue gas, remaining ore and byproducts are considered outputs. In the LMP route, the ore is processed in the light calciner and then sent to AFMF to complete smelting. The decomposition process of the ore is completed in the light calciner. The mass input and output items are the same as in the MOP route. In the light calciner, less attention has been given to the flue gas emission of the calcination process because the preparation process of the raw materials is not the focus of this article. The article only calculates the mass output of its light calcinated magnesia powder. Second, regarding the energy balance, in the MOP route, Figure 3a cannot explain the preheating of the ore or the incomplete solidification of molten magnesium oxide. As a supplement, the detailed flow of internal energy is given in Figure 3b. Combining the two figures, the information on the energy balance, input items, output items, and loss items of the energy balance are all marked. Unlike the MOP process, the LMP process involves the light calcination process. To make the calculation more detailed, the electrical system, the light calcinating system and the AFMF are divided into several calculation domains. The sum of the results of each calculation domain can obtain the energy balance of the overall LMP process, and the production unit consumption of the two process routes are calculated. Finally, regarding the analysis of exergy balance, the exergy input of the MOP process mainly includes ore, electrodes, reaction air, etc., and the output items mainly include fused magnesia, auxiliary products, etc., unlike MOP, exergy loss also exists in the light calcination process, and the exergy loss is also calculated separately. Figure 3c shows the distribution of refractory materials, byproducts and fused magnesia after smelting and cooling. The main component of the byproducts is heavy calcinated magnesia. Although its market value is lower than that of fused magnesia, it is also a useful product, so some attention should be given to the output of byproducts.

3. System Modelling

3.1. Reactions Mechanism

Several different reactions occurred in both the LMP and MOP, and details of the reactions are tabulated in

Table 1. Reactions occurred in MOP.

Reactions	Equations	Abbreviations of Reactions
Combustion of carbon electrodes	C + O2 = CO2	MOP-ELET-1
	2C + O2 = 2CO	MOP-ELET-2
Decomposition of raw materials	MgCO3 = MgO + CO2	MOP-RM-1
	CaCO3 = CaO + CO2	MOP-RM-2
Reduction reaction	C + CO2 = 2CO	MOP-SAF-1
Reduction reaction	C + MgO = Mg + CO	MOP-SAF-2
Slagging reaction	SiO2 + CaO = CaO·SiO2	MOP-SAF-3
Slagging reaction	SiO2 + MgO = MgO·SiO2	MOP-SAF-4

and

Table 2. Reactions occurred in LMP.

Reactions	Equations	Abbreviations of Reactions
Combustion of carbon electrodes	C + O2 = CO2	LMP-ELET-1
	2C + O2 = 2CO	LMP-ELET-2
Decomposition of raw materials	MgCO3 = MgO + CO2	LMP-RM-1
	CaCO3 = CaO + CO2	LMP-RM-2
Reduction reaction	C + CO2 = 2CO	LMP-SAF-1
Reduction reaction	C + MgO = Mg + CO	LMP-SAF-2
Reduction reaction	C + SiO2 = Si + CO	LMP-SAF-3
Reduction reaction	C + Fe2O3 = 2FeO + CO	LMP-SAF-4
Reduction reaction	C + FeO = Fe + CO	LMP-SAF-5
Slagging reaction	SiO2 + CaO = CaO·SiO2	LMP-SAF-6
Slagging reaction	SiO2 + MgO = MgO·SiO2	LMP-SAF-7

.

3.2. Mass Balance Analysis

According to the combustion equations of the production process, the input mass flows consist of carbon electrode mass loss, preheated raw ores, combustion air and prefilled refractory materials. Fused magnesite oxide ingots, byproducts, remaining ores, flue gas and dust mixed in high-temperature gas are considered output mass flows. The mass balance equation can be written as follows:

$$\begin{array}{l}{M}_{in,}{}_{ce}+M_{in,}{}_{ho}+M_{in,}{}_{ca}+M_{in,}{}_{fm}=\\ M_{out,}{}_{mi}+M_{out,fg}+M_{out,bp}+M_{out,}{}_{ro}+M_{out,fm}\end{array}$$

(1)

The symbols in the above equation represent the mass of carbon electrodes (ce), heated raw ores (ho), combustion air (ca), filled refractory materials (fm), magnesite oxide ingot (mi), byproducts (bp), flue gas loss (fg), and remaining ores (ro).

In the process, the mass flow transfer efficiency is calculated by [27]:

$${\eta }_{mt}=\frac{M_{out,mi}}{M_{in,ce}+M_{in,ho}+M_{in,ca}+M_{in,fm}}\times 100\%$$

(2)

$M_{ce}$, $M_{ho}$, $M_{fm}$, $M_{mi}$, $M_{bp}$ and $M_{ro}$ can be obtained through experiments in a factory.

$M_{ca}$ can be calculated as:

$$M_{ca}=10.5\times M_{ce}$$

(3)

$M_{fg}$ can be calculated as:

$$M_{fg}=\frac{44}{40}\times M_{mi}+M_{ca}+M_{ce}$$

(4)

3.3. Energy Analysis

According to the actual production, the energy analysis is different from the traditional calculation of energy balance. First, at the end of the smelting process, part of the magnesia oxide is not completely solidified, and the latent heat of fusion during the smelting process is not completely released in the form of solidification heat. Because the process is submerged arc smelting, part of the heat in the high-temperature flue gas from the furnace is used to preheat the ore. To study the heat solidification heat release and flue gas preheating in more detail, they are regarded as heat income items. The energy analysis of the paper mainly consists of equations on all energy sources, energy expenditures and energy efficiency of the process. The energy balance equation is as follows:

$${\displaystyle \sum _i{E}_{in,i}=}{\displaystyle \sum _i{E}_{out,i}+{\displaystyle \sum _i{E}_{loss,i}}}$$

(5)

$${\displaystyle \sum _i{E}_{in,i}=}{E}_{in,electrode}+E_{in,electic}+E_{in,solid}+E_{in,fluegas}$$

(6)

$${\displaystyle \sum _i{E}_{out,i}=E_{out,oresheat}+E_{out,mgoheat}+}{E}_{out,oresdecom}$$

(7)

$$\begin{array}{l}{\displaystyle \sum _i{E}_{loss,i}=}{E}_{loss,elecwall}+E_{loss,furnacewall}+E_{loss,gas}+E_{loss,melting}+E_{loss,byproducts}\\ +E_{loss,electricity}+E_{loss,refractory}+E_{loss,remain}+E_{loss,elecheat}+E_{loss,other}\end{array}$$

(8)

$${\eta }_{et}=\frac{{\displaystyle \sum _i{E}_{out,i}}}{{\displaystyle \sum _i{E}_{in,i}}}$$

(9)

where $E_{in,i}$, $E_{out,i}$ and $E_{loss,i}$ are the input, output and loss energy flows, respectively. The subscripts show the different input, output and loss energy flows.

The energy calculation equations are listed in

Table 3. Basic energy equations of energy balance.

	Item	Calculation Equation
Energy balance	Heat	E = Cp × (T − T0)
	Combustion	E = m × LHV
	Wall loss	E = λ × (T − T0)
	Solid/melt potential	E = m × ΔHf

.

3.4. Exergy Analysis

Exergy analysis means calculating the exact exergy value of every part in the MOP and LMP systems based on the reasonable assumptions mentioned above, every items of exergy were shown in

Table 4. The exergy process of every part.

Inlet Exergy	Outlet Exergy	Destruction Exergy
Ores	Flue gas	Combustion
Combustion electrode	Fused magnesium	Dissociation reaction
Reaction air	Potential heat of byproducts	Heat transfer
-	Potential heat of soot	-

.

According to the Szargut study in 1988 [30], the exergy balance equations are as follows:

$${\displaystyle \sum _{a}E{x}_{in,a}+W_{electric}={\displaystyle \sum _{b}E{x}_{out,b}}+{\displaystyle \sum _{c}E{x}_{destruction,c}}}$$

(10)

$${\displaystyle \sum _{a}E{x}_{in,a}=E{x}_{in,ores}+E{x}_{in,air}+E{x}_{in,electrode}}$$

(11)

$${\displaystyle \sum _{b}E{x}_{out,b}}=E{x}_{out,gas}+E{x}_{out,fused}+E{x}_{out,byproducts}+E{x}_{out,soot}$$

(12)

$${\displaystyle \sum _{c}E{x}_{destruction,c}}=E{x}_{destruction,combustion}+E{x}_{destruction,dissociation}+E{x}_{destruction,heat}$$

(13)

$$W_{electric}=4800\times N_{num}$$

(14)

where every variable in Equations (11)–(14) is shown in Table 3, and W_electric and N_num are the electric energy input through the grid and the electricity indicator number change, respectively.

The exergy flow consists of physical exergy and chemical exergy, and the exergy balance equation can be written as:

$$Ex=E{x}_{ph}+E{x}_{ch}$$

(15)

where Ex is the total exergy in the process, Ex_ph is the physical exergy and Ex_ch is the chemical exergy.

$$E{x}_{ph}=(H-H_0)+T_0(S_0-S)+E{x}_{ch}$$

(16)

where (H − H₀) and (S₀ − S) represent the enthalpy and entropy change, respectively. T₀ refers to the reference temperature in the reference environment. In Equation (18), (H − H₀) can be calculated as follows:

$$H-H_0=m\cdot c_p(T)\cdot (T-T_0)$$

(17)

(S₀ − S) can be calculated by Equations (19) and (20), and Equation (19) can be used to calculate the entropy change in materials whose properties cannot be influenced by pressure.

$$S_0-S=m{\displaystyle \underset{T}{\overset{T_0}{\int }}\frac{c_p(T)}{T}}dT$$

(18)

Equation (20) calculates the entropy change in materials whose properties can be influenced by pressure through the addition of an amendment [19,29].

$$S_0-S=m\left({\displaystyle \underset{T}{\overset{T_0}{\int }}\frac{c_p(T)}{T}}dT-R\ln \frac{P_0}{P}\right)$$

(19)

where R is the ideal gas constant and $c_p(T)$ is the specific heat of materials at different temperatures. The equations to calculate R and $c_p(T)$ are as follows [29]:

$$c_p(T)=A_0+A_{1}T+A_2{T}^2+A_3{T}^3$$

(20)

$$R=\frac{PV}{nT}$$

(21)

$$n=\frac{m}{M}$$

(22)

where n is the mole number of the gas, T is the temperature of the gas, M is the relative molecular mass, m is the mass of the gas, and V is the volume of the gas.

Chemical exergy is another important part of the total exergy; in this paper, solid fuels should be calculated as follows:

$$E{x}_{ch}=m\cdot \mu \cdot q_{LHV}$$

(23)

where $\mu$ is the chemical exergy coefficient and $q_{LHV}$ is the low caloric value. The chemical exergy of gas generated in MOP and LMP can be calculated as:

$$E{x}_{ch}=m\cdot ({\displaystyle \sum _i{f}_i}\cdot E{x}_{ch,i}+R{T}_0{\displaystyle \sum _i{f}_i}\cdot \ln f_i)$$

(24)

In Equation (25), f_i is the mole fraction of i, and Ex_ch,i is the normal chemical exergy of i. The chemical exergy of the fused magnesia ingot and byproducts can be calculated as:

$$E{x}_{ch}=m\cdot {\displaystyle \sum _j{f}_j}\cdot E{x}_{ch,j}$$

(25)

The exergy of heat loss is given by [24,29]:

$$E{x}_{loss}=(1-\frac{T_0}{T})Q$$

(26)

$$Q=\frac{{\lambda }_{\mathrm{trans}}(T_{w,in}-T_{w,out})S}{l}$$

(27)

where ${\lambda }_{\mathrm{trans}}$ is the coefficient of heat transfer, T_w,in and T_w,out represent the temperature of the steel wall inside and outside, respectively, l is the equivalent length of heat transfer and S is the heat transfer area of heat transfer.

In MOP and LMP systems, the processes are irreversible, and several researchers have defined the exergy efficiency to evaluate the minimum energy value required for the production process of fused magnesia; thus, the exergy efficiency can be calculated as the ratio of total exergy and demanded exergy in the production process:

$$\delta =\frac{E{x}_{demand}}{E{x}_{total}}\times 100\%$$

(28)

where $\delta$ is the efficiency of exergy and Ex_demand is the exergy demanded in MOP and LMP.

To explore ways to improve the efficiency of exergy more conveniently, chemical exergy and physical exergy can be divided into avoidable exergy and inevitable exergy:

$$E{x}_{destruction}=E{x}_{destruction,avoidable}+E{x}_{destruction,inevitable}$$

(29)

Corner mark has explained the implication of terms.

4. Results Analysis

The data in the following calculation results were tested on the 4th AFMF at Hai-cheng Magnesia Group Corporation during 20 July 2021 and 31 July 2021.

4.1. Mass Balance Results

4.1.1. Mass Conservations

The mass fraction of the MOP and LMP can be calculated as follows. First, the total mass balance is shown in Figure 3a. The mass input includes the flow of ores, carbon electrodes and combustion air; similarly, the output flows were fused magnesia ingot, flue gas soot, byproducts, remaining ores and additional materials. The mass balance equation is shown in Equation (1). The weights of ores, carbon electrodes, fused magnesia, byproducts, remaining ores and additional materials were tested in a factory. These amounts are weighed by a floor scale, where the raw material part is measured before being added into the furnace, and the product part is measured after the product is cooled and sorted. The total mass balance results are shown in

Table 5. MOP system mass flow balance.

Input Flows	Amount (kg/h)	per (%)	Output Flows	Amount (kg/h)	per (%)
Mho	3800	13.1	Mmi	907.6	16.3
Mce	65.3	1.2	Mfg	2909.7	13.2
Mca	714.3	71.5	Mbp	720.5	1.6
Mfm	776.1	14.2	Mro	100	2.5
			Mfm	776.1	14.2
Total	5455.7	100	Total	5455.7	100

and

Table 6. LMP system mass flow balance.

Input Flows	Amount (kg/h)	per (%)	Output Flows	Amount (kg/h)	per (%)
Mho	3800	71.6	Mmi	2031	38.3
Mce	62.7	1.2	Mfg	730.7	13.7
Mca	668	12.6	Mbp	1669	31.5
Mfm	776.1	14.6	Mro	100	1.9
			Mfm	776.1	14.6
Total	5306.8		Total	5306.8	100

.

4.1.2. The Properties of the Flue Gas

Due to a government policy, CO₂ emission is an important limitation, and monitoring carbon dioxide emission is very important, but in normal operation, it is impractical to obtain the emission of CO₂ exactly. In the present study, it is assumed that the sources of CO₂ emission were the combustion of carbon electrodes and the decomposition of ores. The main composition of ores was MgCO₃ (85–90%) and CaCO₃ (5–8%), the composition of combustion air was assumed to consist of O₂ (21%), N₂ (78.7%) and CO₂ (0.3%), and the composition of carbon electrodes was mainly graphite. The results were calculated based on Equations (1)–(4) and are shown in Table 5 and Table 6. In addition, in the LMP route, due to the few mass loss during the light burning process is, the mass transfer efficiency can generally reach more than 95% in actual production. In this section, the mass flow of the light burning process is not analysed separately.

4.1.3. Mass Conversion Rate

The magnesia carbonate content in the ores was significant in comparison to the calcium carbonate content; the lowest temperature in the furnace reached at least 900 K, and the magnesia carbonate and calcium carbonate were totally decomposed in fused magnesia and byproducts range which can be seen in Figure 3c. The mass conversion rate was calculated as follows:

$${\eta }_{mc}=\frac{M_{mi}}{M_{ho}+M_{ce}+M_{ca}+M_{fm}}$$

(30)

${\eta }_{mc}$ is the mass conversion rate of the process. The maximum theoretical mass conversion rates of MOP and LMP were 34% and 71.6%, the actual mass conversion rates of MOP and LMP were 16.6% and 38.3% and the difference between the actual results and theoretical results was 17.4% and 33.3%, respectively. The quality conversion rate has considerable room for improvement.

In addition, in order to better analyse the output of magnesia per ton of raw materials, the different qualities of fused magnesia produced per ton of ore have also been counted.

In

Table 7. Proportion of products.

	Raw Materials	Fused Magnesia (97.5%)	Fused Magnesia (97%)	Fused Magnesia (96%)	Fused Magnesia (95%)	Byproducts
MOP	3900 kg/h	175 kg/h	236 kg/h	341 kg/h	155 kg/h	720.5 kg/h
		(0.046)	(0.062)	(0.089)	(0.041)	(0.180)
LMP	8400 kg/h	465 kg/h	621 kg/h	533 kg/h	412 kg/h	1669 kg/h
		(0.055)	(0.074)	(0.063)	(0.049)	(0.199)

, the output mass and output ratio of fused magnesia with different purity under the two routes are shown respectively. The output ratio is the ratio of different purity fused magnesia and raw materials. It is obvious that under the LMP route, the ratio of raw materials converted into magnesia with 97.5% purity is 0.055, and the ratio of raw materials converted into magnesia 97% is 0.074, which are 0.009 and 0.012 higher than those under the MOP route, respectively. The results show that the LMP route has more advantages in preparing high-quality fused magnesia than MOP. In addition, under the LMP route, the output ratio of byproducts is 0.199, which still has great potential for fused magnesia quality improvement.

4.2. Energy Balance Results

In MOP systems, the input energy flow mainly consists of the combustion of carbon electrodes, electricity power, preheating power of flue gas and solidification exotherm energy. The output energy flow consists of the following: the potential energy of carbon electrodes, the decomposition energy of ores, the melting potential energy of MgO at 3073 K, the potential energy of byproducts when the temperature increased from 973 K–1673 K, the heat loss of the flue gas and refractory materials, the potential energy of byproducts when the temperature increased from 973 K–3073 K and the energy loss of electric system. Therefore, the energy balance can be expressed as Equations (6)–(8). In addition, since the raw materials of the LMP must be light calcined, and the reason for the energy balance calculation in different regions has been explained in the previous section, in this section, the energy balance of the electrical system, the preparation process of raw materials and AFMF involved in the LMP and MOP are separately evaluated for energy, and the unit consumption of the product is comprehensively analysed at the end.

4.2.1. Energy Balance of Electric System

The structure of the electric system of the fused magnesia furnace is shown in Figure 4. It generally includes electric blockers, electric reactors, electric transformers, carbon electrodes and arc zones. Generally, the factory voltmeter is connected after the reactor and before the transformer, which is equivalent to the circuit shown in the figure above. In the electrical system of this article, the impedance loss caused by the blocker and the reactor is not calculated because the single furnace meter cannot accurately reflect the corresponding power consumption. At the same time, due to the special structure of the three-phase EAF, the three electrodes forming the three-phase electric arc need to be connected in a star shape.

Figure 5 shows the load equivalent circuit from the primary side of the transformer to the secondary side of the transformer and finally to the arc zone. In this process, the circuit on the left represents the primary side, and the circuit on the right represents the secondary side. Each component area has a corresponding reactance and impedance. Due to the extremely high voltage on the primary side, the circuit impedance and inductance loss are small, so they are omitted in the equivalent change process. On the secondary side, the impedance and inductive reactance of the transformer’s secondary coil (corner mark 2) and the impedance and inductance of the short network part (corner mark b) are mainly considered. In addition, RA is the arc resistance. Therefore, the reactance in the simplified circuit is recorded as the total reactance X, and the total impedance in the circuit is recorded as the impedance R.

The energy loss of the electric system can be calculated based on GB/T 19212.3-2012, and the equation follows:

$$E_{elecloss}=\sqrt{(R^2+X^2)}·I^2+E_{transloss}$$

(31)

where E_elecloss is the total energy loss of the electric system, R = 0.00056 Ω is the resistance of the electric short net, X = 0.0042 Ω is the reactance of the electric short net, I = 8151 A is the current of the electric short net, and E_transloss = 25.5 kW, which was demanded based on the industry standard in China “GB/T 19212.3-2012”.

4.2.2. Raw Materials Preparation Energy Balance of LMP

As the raw material of the LMP system was light-calcined magnesia oxide, the preparation process of this material was also analysed in this section. The basic equations of the process were almost the same as the equations above. The calculation results were listed in

Table 8. Energy calculation results of the preparation process.

Input Energy	per	Amount (kWh/t)	Output Energy	per	Amount (kWh/t)
Coal chemistry	100	1929.1	Gas loss		109.1
			Cooling air loss		124.8
			MgO heat		14.7
			Ores decomposition		634.4
			Vaporisation		161.5
			Wall loss		148.1
			Other loss		736.5
total	100	1929.1	total		1929.1

.

The preparation process was divided into two processes, gas preparation and light-calcined magnesia oxide preparation. All calculation results are listed in Table 8, and the total efficiency of gas preparation was 81.6%. During the light-calcined magnesia oxide preparation process, gas combustion was the main energy source of the process, accounting for approximately 80.8%, the preheated ores brought a 16.4% energy input, and the energy consumption per ton was 6,944,000 kJ (1929.1 kWh). In the output energies, the physical heat of flue gas and magnesia oxide was 43,027,875 kJ (1195.2 kWh) per ton. The calculation in this section provides a basis for the following analysis. The coefficients specific heat capacity equations are shown in

Table 9. The coefficients specific heat capacity equation.

Materials	A0	A1	A2	A3	Range
CO	28.16	0.168 × 10−2	0.537 × 10−5	−2.222 × 10−9	273 K–1800 K
CO2	22.26	5.981 × 10−2	−3.501 × 10−5	7.469 × 10−9	273 K–1800 K
O2	25.48	1.520 × 10−2	−0.716 × 10−5	1.312 × 10−9	273 K–1800 K
H2O	32.24	0.192 × 10−2	1.055 × 10−5	−3.595 × 10−9	273 K–1800 K
N2	28.90	−0.157 × 10−2	0.808 × 10−5	−2.873 × 10−9	273 K–1800 K

.

4.2.3. Energy Balance of MOP and LMP

In Equation (21), the constants A0–A3 are listed in Table 6. The specific heat capacity of flue gas was the average of all components, and the calculation equation was as follows [31]:

$$C_{p,average}=\frac{1}{n}{\displaystyle \sum _1^n{C}_{p,i}}$$

(32)

where C_p,i is the specific heat of i and C_p,average is the average specific heat of all components.

The basic equations applied to the calculation of

Table 10. Energy calculation results of MOP.

Input Energy	per	Amount (kWh/t)	Output Energy	per	Amount (kWh/t)
Electrode comb	9.1	421.3	Electrodes wall loss	0.1	4.3
Electricity	60.9	2826	Potential heat of electrodes	1	45.6
Solidification	10.3	479	Decomposition ores	17.5	811.9
Flue gas preheat	19.7	909.6	Ores heating	15.6	721.2
-			Magnesium oxide heating	17.5	813.4
-			Byproducts heating	4.4	205.4
-			Melting potential heat	11.6	538.3
			Wall loss	4.4	202.2
			Flue gas	16.3	757
			Remained ores	0.3	11.7
			Electricity loss	7.3	341.1
			Refractory materials	3.5	161.9
			Other loss	0.5	21.9
Total	100	4635.9	Total	100	4635.9

and

Table 11. Energy calculation results of LMP.

Input Energy	per	Amount (kWh/t)	Output Energy	per	Amount (kWh/t)
Electrode comb	7.6	179.4	Electrodes wall loss	0.1	1.9
Electricity	50.2	1182.3	Potential heat of electrodes	0.9	20.2
Solidification	39.1	920.3	Magnesium oxide heating	42.8	1008.8
Flue gas preheat	3.1	74	Byproducts heating	17.3	406.9
			Melting potential heat	22.7	534
			Wall loss	3.8	89.7
			Flue gas	2.7	63.4
			Remained ores	0.2	4.9
			Electricity loss	6.4	151.2
			Refractory materials	3	71.8
			Other loss	0.1	3.2
Total	100	2356	Total	100	2356

are given in the initial part of Section 4. All the calculation results are given in Table 10 and Table 11 and are summarised in Figure 6 and Figure 7. It is not difficult to see that in MOP, similar to the LMP system (Figure 8), the main energy source is electric energy, which accounts for 61% and 50% of the total energy input, i.e., 2826 kWh/t and 1182.3 kWh/t, respectively. At the same time, there are considerable byproducts as a result of the two processes. The economic value of byproducts is much lower than that of fused magnesia, and the product quality has substantial room for improvement. The difference is that there is a large amount of preheating of flue gas during the MOP process. This part of the energy accounts for 19.7% of the total energy input. Compared with an open EAF, the energy efficiency is improved. In addition, when the molten magnesia oxide solidifies, a large amount of heat will be released, accounting for 10.1% of the energy input. The actual product unit consumption is 2803 kWh/t, and the theoretical product unit consumption is 1600 kWh/t. In addition, in the LMP, since the raw material was light burnt magnesia powder, the amount of flue gas generated during the reaction process was not large, which led to a poor preheating effect of the ore, but the output of fused magnesia was much higher than that in the MOP. This situation led to 39.1% of the total energy of the solidification exotherm in the LMP. This calculation result clearly shows that the MOP process is affected by the lower output, the LMP is affected by the lack of a preheating process, and both have great potential for product quality improvement and energy efficiency improvement.

To more scientifically reflect the effects of the two process routes, the comprehensive energy consumption of the two process routes is calculated and compared. In the MOP route, the energy consumption per ton of magnesium oxide is 2826 kWh/t. In the LMP route, the energy consumption per ton is 2826 kWh/t. The energy consumption per ton of magnesium oxide is 3111.4 kWh/t, of which the energy consumption of the light burning part is 1929.1 kWh/t, and the energy consumption of the AFMF part is 1182.3 kWh/t. In general, the unit consumption of the LMP process is slightly higher than that of the MOP process. However, from another point of view, in the LMP process, the residual energy of the fused magnesia is 1415.7 kWh/t, and the energy of the residual fused magnesia in the MOP process is 1018.8 kWh/t, which shows that the LMP process has greater energy-saving potential.

4.3. Exergy Balance Results

4.3.1. Exergy Balance

Through the energy analysis in the previous section, the input and output channels of the energy flow and their values are determined. The energy quality and rationality can be discussed through exergy analysis. The exergy input items of MOP and LMP include carbon electrodes, combustion air, ores, electric energy and the exergy output items include magnesia ingot, byproducts, flue gas and heat loss through walls. The main exergy loss methods were as follows: decomposition exergy loss, wall heat transfer exergy loss, exergy loss of refractory materials and gas heat transfer (see also in Table 3 and Figure 3c).

The main exergy balance equation is shown in Equation (11). Ex_electric was determined to be 2544 kW based on Equation (15). Ex_ores, Ex_fused and Ex_byproducts can be calculated based on Equation (26). As the main element of the byproducts was MgO, Ex_MgO consisted of Ex_fused and Ex_byproducts, and the value was 573.7 kW. During the combustion process of electrodes, compressible gas was generated and can be calculated based on Equations (16)–(25). The exergy output of flue gas was 279.4 kW, and the thermal exergy caused by heat loss through the walls was determined by Equations (27) and (28). Standard chemical exergy values are listed in

Table 12. Standard chemical exergy values of ores, fused magnesium ingot, and byproducts.

Species	Standard Chemical Exergy (kJ/kmol)
CaCO3	1000
MgCO3	37,900
MgO	66,800
C	410,534
O2	3933
CO2	20,125
CaO	110,200
SiO2	1900
Fe2O3	16,500
MgO·SiO2	198,960
CaO·SiO2	275,400
Fe2O3·SiO2	18,400

. All calculation results can be seen in

Table 13. Exergy calculation results of preparation.

Input Exergy	kWh/t	Output Exergy	kWh/t	Exergy Destruction	kWh/t
Gas preparation
Excoals	1937.1	Exgas,	1461.3	Heat and mass transfer	475.8
Total	1937.1	Total	1461.3	Total	475.8
Light calcined magnesium oxide preparation 0.11
Gas chemistry	1450.5	MgO physical	146.4	Heat and mass transfer	371.6
gas physical	128.7	Flue gas	544.1	Combustion	390.8
Ores physical	10.9			Ores dissociation	137.2
Total	1590.1	Total	690.5	Total	899.6

,

Table 14. Exergy calculation results of MOP.

Input Exergy	kWh/t	Output Exergy	kWh/t	Exergy Destruction	kWh/t
Ores	522.1	Magnesia chemical	355.3	Combustion	46.2
Electrodes	688.8	Magnesia physical	504.2	Dissociation	1385
Combustion air	10.6	Flue gas chemical	335.7	Heat and mass transfer	576.8
Leaking air	1.1			Byproduct chemical	282.1
Electric	2826.7			Byproduct physical	177.9
				Prefilled materials	47.9
				Wall loss	339.1
Total	4050.2	Total	1195.2	Total	2855

and

Table 15. Exergy calculation results of LMP.

Input Exergy	kWh/t	Output Exergy	kWh/t	Exergy Destruction	kWh/t
Ores	583.9	Magnesia chemical	352.6	Combustion	23.8
Electrodes	293.3	Flue gas chemical	16.1	Heat and mass transfer	248.5
Combustion air	4.5	Magnesia physical	733.7	Byproducts chemical	289.8
Leaking air	0.5			Byproducts physical	331.6
Electric	1253.2			Prefilled materials	21.0
				Wall loss	122.8
Total	2139.9	Total	1102.4	Total	1037.5

.

The calculation results of preparation process were shown in Figure 9 and Table 13. During the gas preparation process, the exergy input was coal chemistry exergy, with a value of 1937.1kWh/t, the exergy destruction was 475.8kWh/t and the exergy efficiency of gas preparation was 75.4%.

In the LMP process, the exergy calculation results were determined in the same manner as above. In addition, as the main raw material was light-calcined magnesia, the exergy flow of the preparation of the LMP process was determined as follows:

In the light-calcined magnesia oxide preparation process, the main exergy input was gas exergy, with a value of 1450.5kWh/t. The exergy output consisted of the physical exergy of magnesia oxide and flue gas, i.e., 146.4kWh/t and 544.1kWh/t, respectively. The exergy destruction methods were heat and mass transfer, combustion and ore dissociation, and the total exergy destruction was 899.6kWh/t.

Table 14 and Table 15, Figure 10 and Figure 11 show the exergy balance calculation results of MOP and LMP. In MOP, the exergy input items are electric energy exergy, electrode chemical exergy, and ore chemical exergy, the values of which are 2826.7 kWh/t, 688.8 kWh/t, 522.1 kWh/t. The main exergy output item is the chemical exergy and physical exergy of fused magnesia the values of which are respectively 355.3 kWh/t and 335.7 kWh/t, the exergy efficiency is 29.5%. In LMP, the exergy input items are also electric energy exergy, electrode chemical exergy, the values are 583.9 kWh/t, 293.3 kWh/t, 1253.2 kWh/t. The exergy output items are the chemical exergy and physical exergy of fused magnesia. The values are respectively 352.6 kWh/t, 733.7 kWh/t, the exergy efficiency is 51.5%. Exergy loss and other calculations are shown later.

4.3.2. Exergy Destruction

Generally, an exergy reduction process is always accompanied by an entropy increase process which was shown in

Table 16. Entropy of reactions.

	T (K)	Mass (kg/s)	N (kmol/s)	S (kj/kmol*k)	xi
Combustion of electrodes
C	315	0.018	0.0014	5.694	0.097
O2	315	0.047	0.0014	205.138	0.254
N2	315	0.12	0.0043	191.598	0.649
CO2	973	0.065	0.0014	213.76	0.351
N2	973	0.12	0.0043	191.598	0.649
Dissociation of ores
MgCO3	973	1.04	0.0122	147.32	0.934
CaCO3	1173	0.073	0.00073	214.76	0.066
MgO	973	0.45	0.012	64.315	0.436
CO2	973	0.512	0.012	250.635	0.497
CaO	1173	0.041	0.00073	102.67	0.040
CO2	1173	0.032	0.00073	278.03	0.031

. Entropy production is always an irreversible process, such as friction heat generation, electrothermal effects, chemical reactions, and limited temperature difference heat transfer. For MOP and LMP processes, the irreversible process is roughly divided into three types: electrode combustion, ore decomposition and heat and component transfer in the overall process. In Equations (17)–(20), the basic entropy change calculation formula is given. In the MOP process, according to Equations (17)–(20), in order to evaluate the exergy destruction, the following series of equations are proposed to calculate the entropy production value:

$$S_0-S=(\Delta S_{combustion}-S_{combustion})+(\Delta S_{discomp}-S_{discomp})$$

(33)

where $\Delta S$ is the entropy change, $S_{combustion}$ is the entropy transfer during the electrode combustion process and $S_{dissociate}$ is the entropy transfer during the ore dissociation process. The entropy changes of the combustion process and dissociation process are named $\Delta S_{combustion}$ and $\Delta S_{combustion}$, respectively, for the electrode combustion process:

$$\Delta S_{combustion}=S_{prod}-S_{react}$$

(34)

where subscripts prod and react stand for production and reactants. The entropy values used to calculate the entropy change are listed in Table 13. The entropy change in electrode combustion was determined to be 40.7 kW.

The entropy transfer caused by heat transfer can be calculated as follows [32]:

$$S_{combustion}=\frac{m_{elec}·q_{carbon}-m_{elec}·c_{pelec}·T_{elec}}{T_{elec}}$$

(35)

where T_elec is the combustion temperature of the electrodes and combustion air. In this study, because the actual combustion temperature cannot be tested directly, the value was assumed to be 700 °C. During the electrode combustion process, the entropy transfer equals 3.75 kW, and the total entropy generation through the combustion process is 36.9 kW.

The exergy destruction of the decomposition of ores consists of two parts: the exergy destruction of the decomposition of ores and the mass transfer of CO₂. Similar to the calculation process above, the exergy destruction of the decomposition of ores can also be calculated, and the results are shown in Table 13. The reactions considered in the decomposition process were endothermic reactions, and the entropy transfer can be calculated as:

$$S_{discomp}=-\frac{Q_{discomp}}{T_{ediscomp}}$$

(36)

According to the energy balance results, the entropy transfers of MgCO₃ and CaCO₃ dissociation are −60.56 kJ/kmol·K and −116 kJ/kmol·K, respectively, and the exergy destruction of this part is 707 kW; thus, the total exergy destruction of the ore decomposition process is 1246.5 kW.

Another part of the exergy destruction of ores decomposition process was the generation of CO₂, according to the Equation (20), the exergy destruction caused by the mass transfer of the system is equal to 183.1 kW, during the MOP process, the mass and heat transfer exergy destruction of prefilled refractory materials are determined as follows:

$$Ex{d}_{heat and mass transfer}^{others}=E{x}_{input}-E{x}_{output}-Ex{d}_{combustion}-Ex{d}_{decomposition}-Ex{d}_{heat \mathrm{and} \mathrm{mass} \mathrm{transfer}}^{C{O}_2}$$

(37)

Because the mass and heat transfer boundary of prefilled refractory materials and other materials can hardly be defined, the value of exergy destruction was determined by the difference among the results of exergy input, exergy output and other exergy destruction methods.

4.3.3. Analysis of Exergy Balance

Four processes were discussed above: LMP, MOP, light-calcined preparation and gas preparation. The calculation results were shown in Figure 9, Figure 10 and Figure 11 and Table 13, Table 14 and Table 15. Large amounts of exergy were wasted during the processes; thus, the exergy recycling potential will be discussed.

For the MOP process, the exergy destruction of ore dissociation was light-calcined magnesia, which is a pretreated raw material. Therefore, its preparation process is also considered in this article, including the preparation of fuel gas and light-calcined magnesia in the raw material preparation process. In the gas preparation process, the coal-gas conversion process is realised. In this process, coal and water vapour undergo an oxidation-reduction reaction, and part of the exergy is lost in the heat and mass transfer process. The overall transfer efficiency of the process is 75.4%. In the preparation process of light-calcined magnesia, a large amount of carbon dioxide is generated, which leads to complicated air flow in the equipment. The mixing of high-temperature carbon dioxide and room temperature air produces a large amount of exergy loss. This part of the loss is 3378.5 kW. At the same time, during the fuel combustion process, a large amount of chemical reaction exergy losses (43.4%) are produced. In theory, improving the quality of fuel can effectively reduce this part of the loss. In the LMP system, the products of the above preparation process are used as raw materials for production. The main inevitable exergy loss in the production process is heat and mass transfer loss, which accounts for 35.9% of the total exergy loss. The physical exergies of the byproducts and magnesia product are 673.2 kW and 1489.4 kW, respectively, and these two parts can be used for ore preheating or other recovery methods. The total exergy efficiency of the process was 12.7%, and the value was at a low level.

According to the exergy and energy balance calculation above, the reasons for the low efficiencies of MOP and LMP are summarised as follows. First, the MOP production equipment is not completely closed, causing a large amount of gas generated during the smelting process to overflow and carry a large amount of energy. Relying only on the accumulation of materials in the furnace body cannot fully recover this part of the energy. Second, in the products of MOP and LMP, the output of byproducts due to the low furnace temperature is close to 50%. Excessively high byproducts reduce the production efficiency of the furnace, indicating that the energy input of the furnace body is not enough to completely decompose and melt the raw materials in the furnace. Finally, in the LMP raw material preparation process, the high-temperature light-calcined magnesia powder is not directly used in LMP. A large amount of physical heat of the light-calcined magnesia powder is wasted in the storage and transport process, and the light-calcined magnesia needs to be reheated in LMP. For the above reasons, the improvement methods are proposed in the next section.

4.4. Analysis of Improving Methods

The analysis of the improved methods is mainly aimed at the MOP and LMP processes. Optimisation research on the gas preparation process and the preparation process of light burnt magnesia will continue in future research. This section divides the improvement measures into three parts in response to the problems summarised above. The first is to seal the furnace body to reduce the flue gas emissions and recover the heat taken away by the high-temperature magnesia ingot at the same time. The second is to increase smelting power, improve product quality and reduce energy loss caused by byproducts.

4.4.1. The Energy Saving Potential of Energy Saving Recycling

Preheat treatment of decomposed ore is often proposed in production processes such as submerged arc furnaces. Therefore, this article refers to the existing waste heat recovery research content and the energy balance calculation results and proposes a closed furnace body and heat recovery equipment. Based on this method, the heat carried by the flue gas in the LMP process and the heat of the high-temperature magnesia oxide lumps in the MOP process can be recovered for material production, where the energy conversion rate is set to 1 to determine the potential for energy-saving recycling.

The energy recycling potential and efficiency are shown in Figure 12. The avoidable energy loss of preparation was the most of three processes due to the energy loss of a large amount of flue gas during the preparation process. The avoidable energy loss of the LMP process was the second of the processes. Due to the physical energy of the magnesia ingot and flue gas, the energy loss of wall heat transfer and the electric system cannot be avoided. The energy loss recycling potential of LMP was the least of the processes as a result of the energy loss of ore dissociation that occurred in the preparation process. The proportions of avoidable energy loss of the LMP, MOP and preparation were 20.7%, 19.8% and 53.2%, respectively; only the recovery potential was estimated in this section. The actual recovery path and equipment design were not studied, but will be investigated in future research.

4.4.2. The Replacement of Different Electric Transformer

According to the previous calculation results, it is not difficult to see that the high proportion of byproducts in the product due to an insufficient furnace temperature is an important cause of low energy efficiency. Therefore, under the premise that other factors do not change, transformers with ratings of 3500 kVA and 4200 kVA are used. Using the factory production data, the calculation evaluation of the energy efficiency and exergy efficiency were carried out.

According to the calculation results in Figure 13, the high output of byproducts has led to a large amount of energy loss and exergy loss. At the same time, the production of byproducts is due to the small volume of the high-temperature zone of the molten pool. The energy loss of byproducts accounts for 4.4% and 17.3%. The maximum temperature of the molten pool and the volume of the molten pool can be increased by increasing the power of the transformer. The calculation results are shown in Figure 13. The energy and exergy efficiency of the LMP was higher than that of the MOP. After increasing the transformer power, the energy efficiency of MOP and LMP increased to 52.5% and 71.2%, and the exergy efficiency increased to 32.5% and 53.7%, respectively.

5. Conclusions

Based on the energy and exergy analysis of the LMP, MOP, and preparation process, the main conclusions are described as follows:

• The energy efficiencies of LMP, MOP, and the preparation process were 65.5%, 46.7%, and 39.4%, respectively, and the calculation consisted of all processes in the fused magnesia production process. The results show that the fused magnesia production process has great potential for energy savings in electric systems, raw material preparation and AFMFs.
• The exergy efficiencies of the LMP, MOP, and the preparation process were 51.6% 29.5% and 35.6%, respectively, and the exergy destruction mainly consisted of heat and mass transfer, byproduct physical and chemical exergy and decomposition of ores.
• The energy recycling potential of the three processes was calculated to ensure the value of avoidable energy loss, and the proportions of avoidable energy loss of the LMP, MOP and preparation process were 20.7%, 19.8% and 53.2%, respectively. Another energy saving method was carried out to improve the energy efficiency of LMP and MOP. As the electrical transformer power increased, the energy efficiency of LMP and MOP increased to 52.5% and 71.2%, respectively, and the exergy efficiency of LMP and MOP slightly increased to 32.5% and 53.7%, respectively.