Design and Implementation of an Intelligent Blade Pitch Control System and Stability Analysis for a Small Darrieus Vertical-Axis Wind Turbine
Abstract
:1. Introduction
2. An H-Type Vawt Modeling
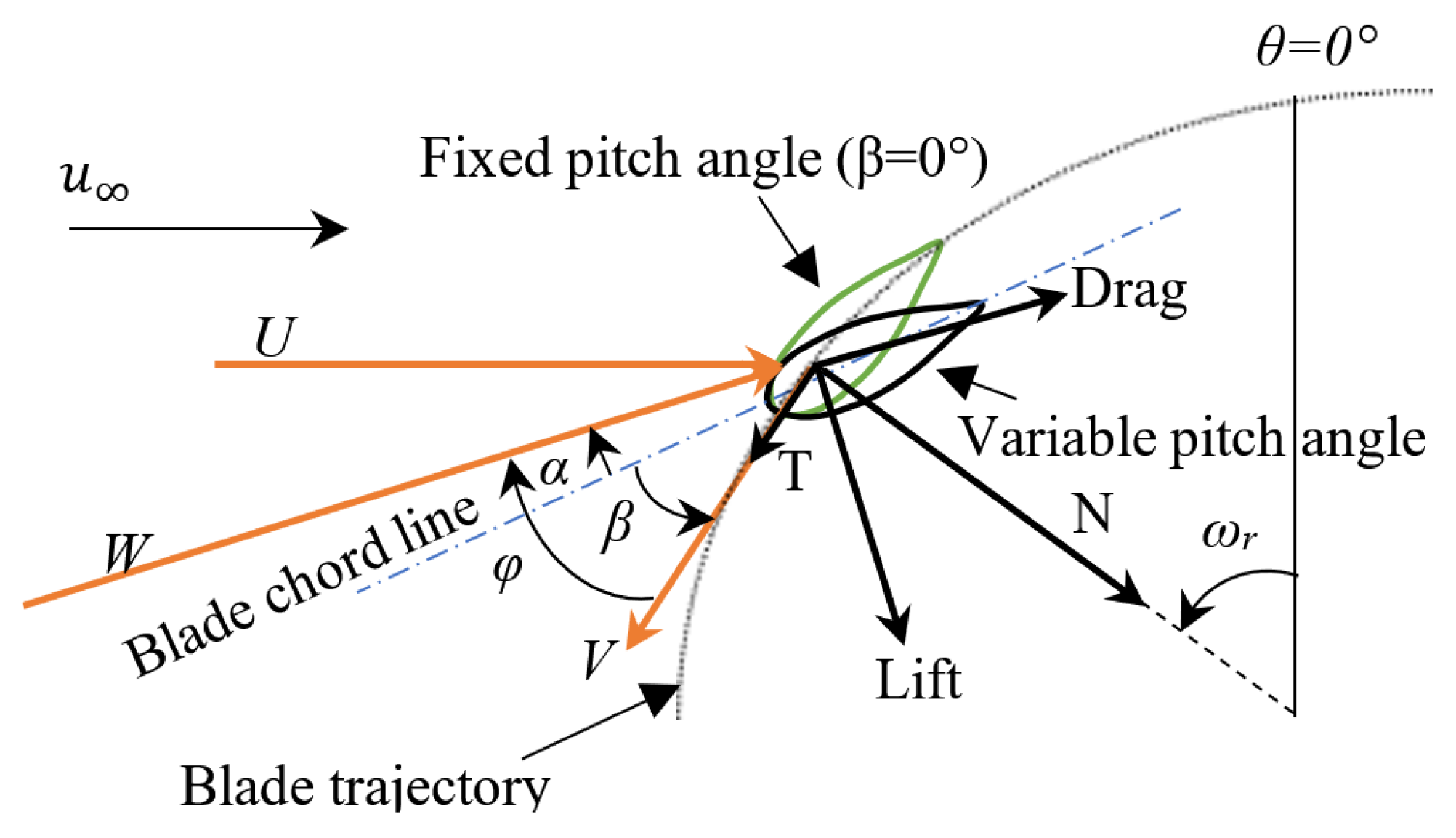
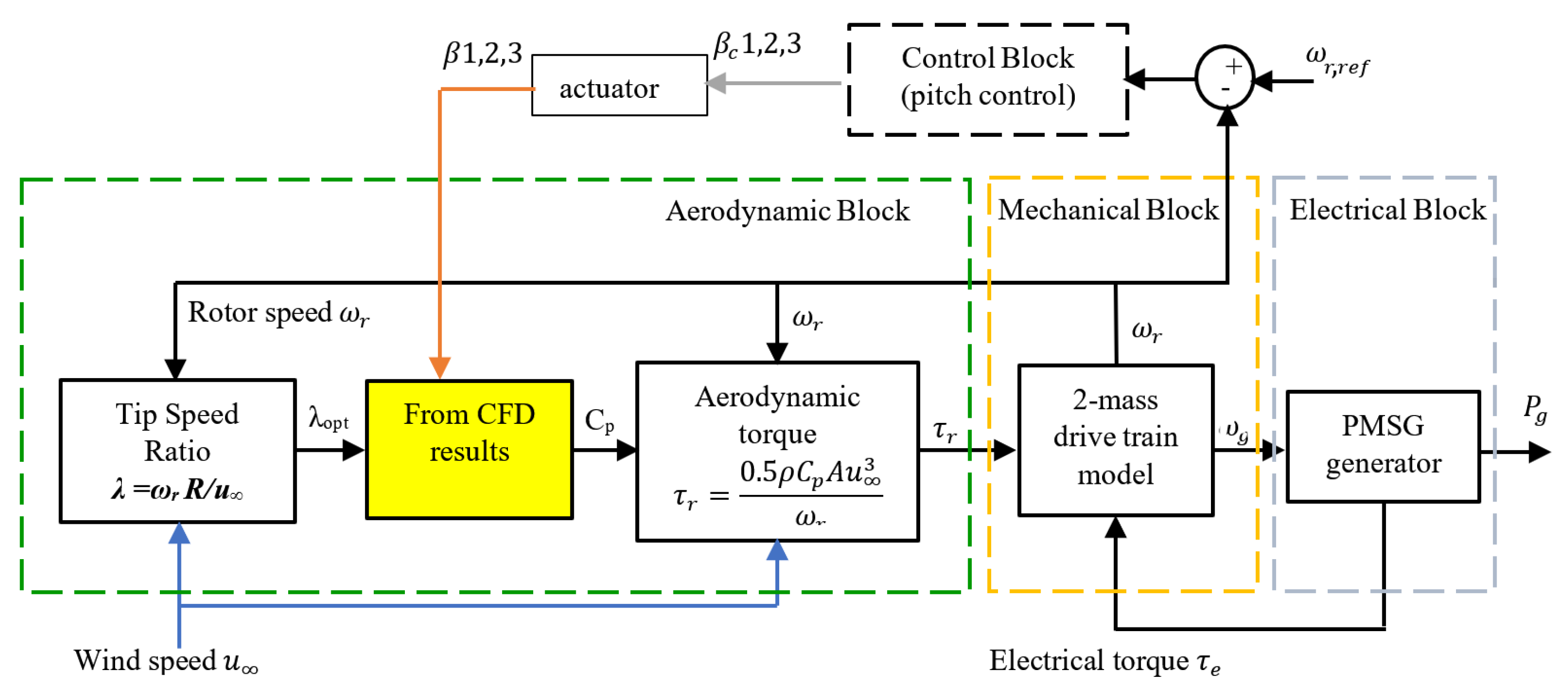
2.1. Aerodynamic Block
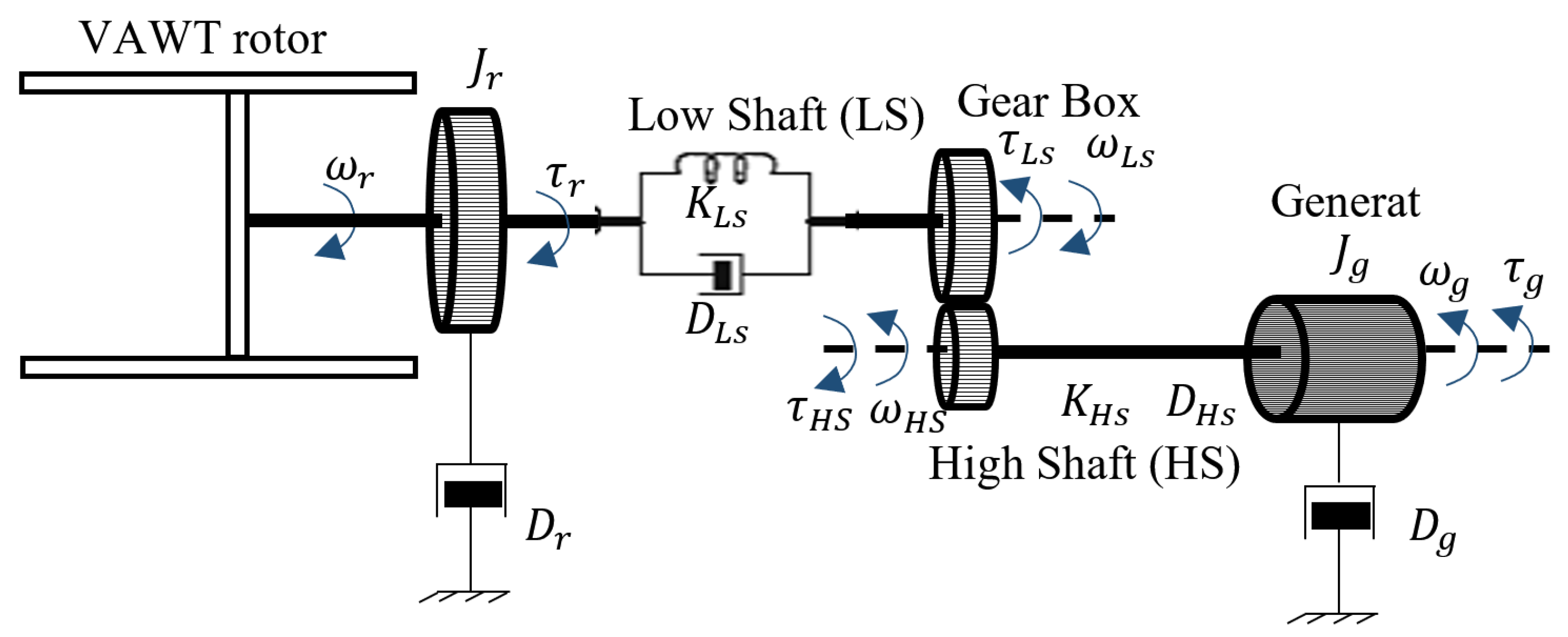
2.2. Mechanical Block
- The and terms are equal to zero because of their direct coupling inside the gear box;
- The rotor and generator self-damping and are neglected.
2.3. Pitch Actuators
2.4. Nonlinear State-Space Representation of the System
3. Stability Analysis of an H-Type VAWT
3.1. Lyapunov Stability
3.2. Lyapunov’s Direct Method
- is positive definite locally in ;
- is negative semidefinite locally in .
- is positive definite;
- is negative definite;
- →∞ as →∞.
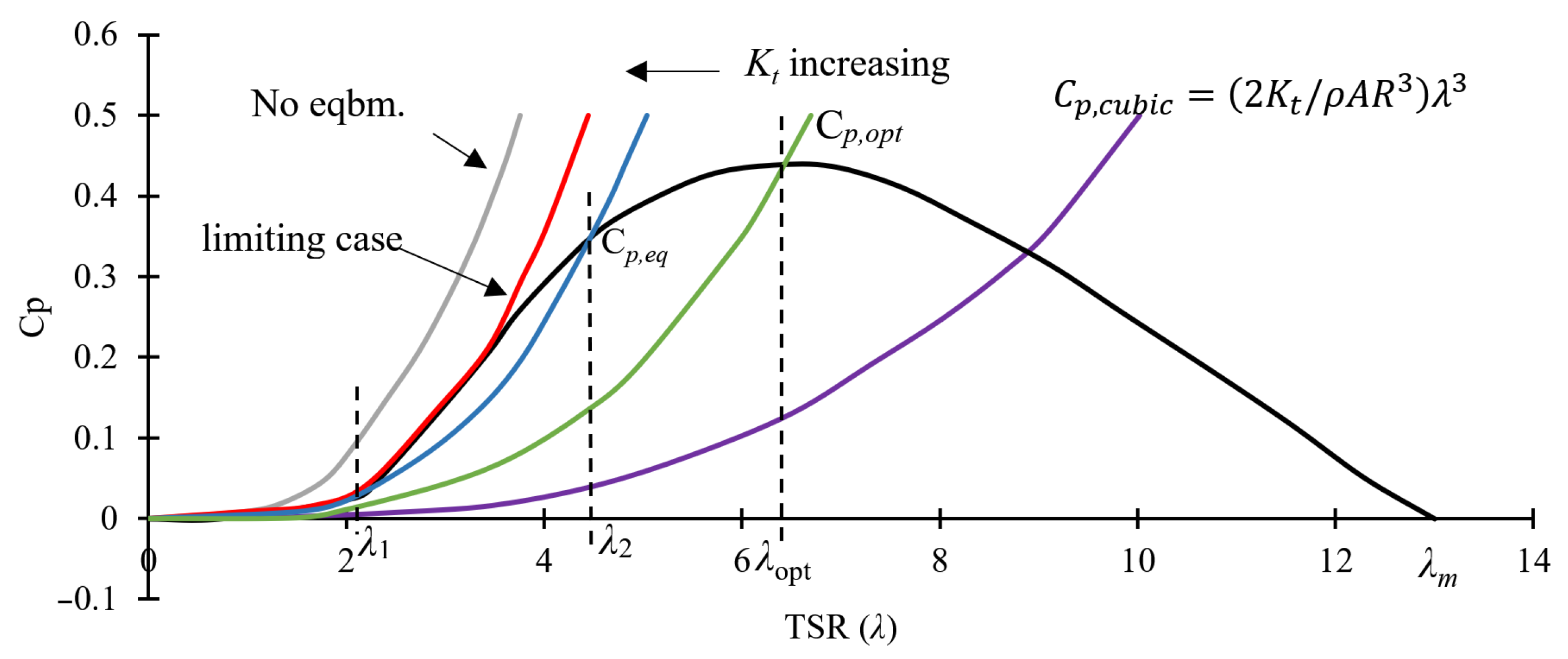
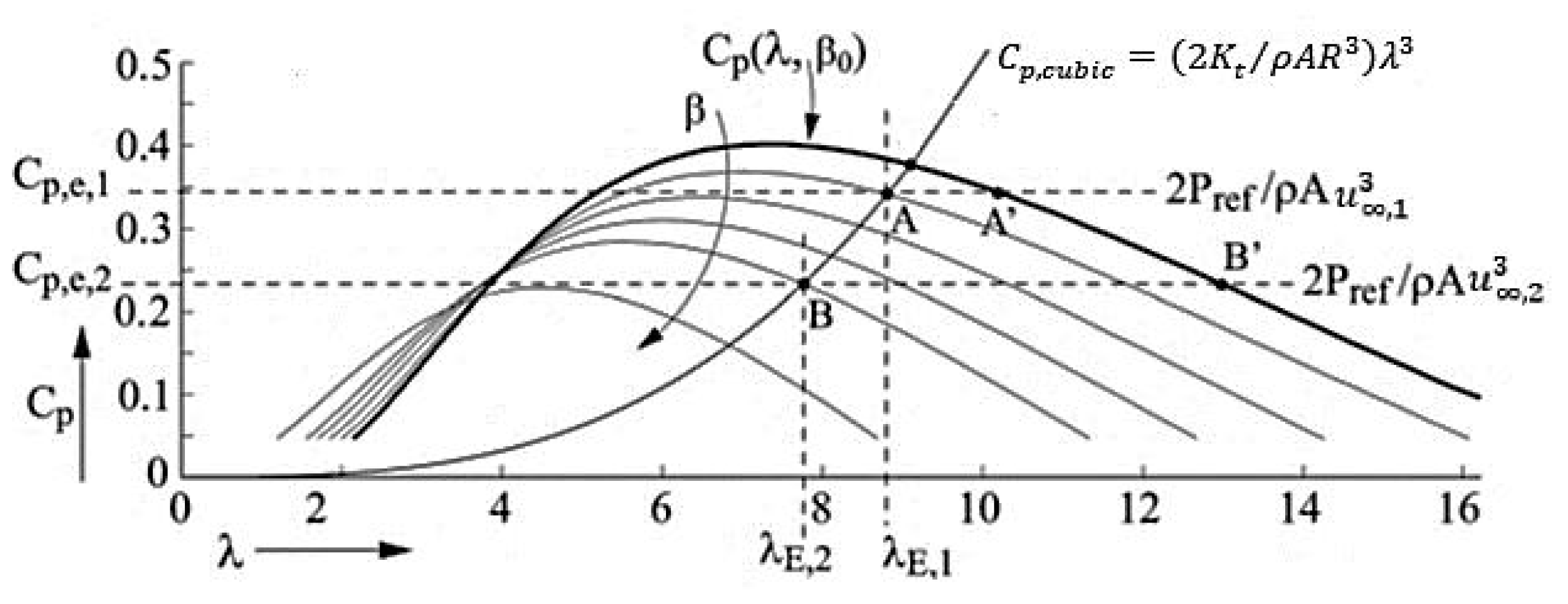
3.3. Constant Pitch Angle Model
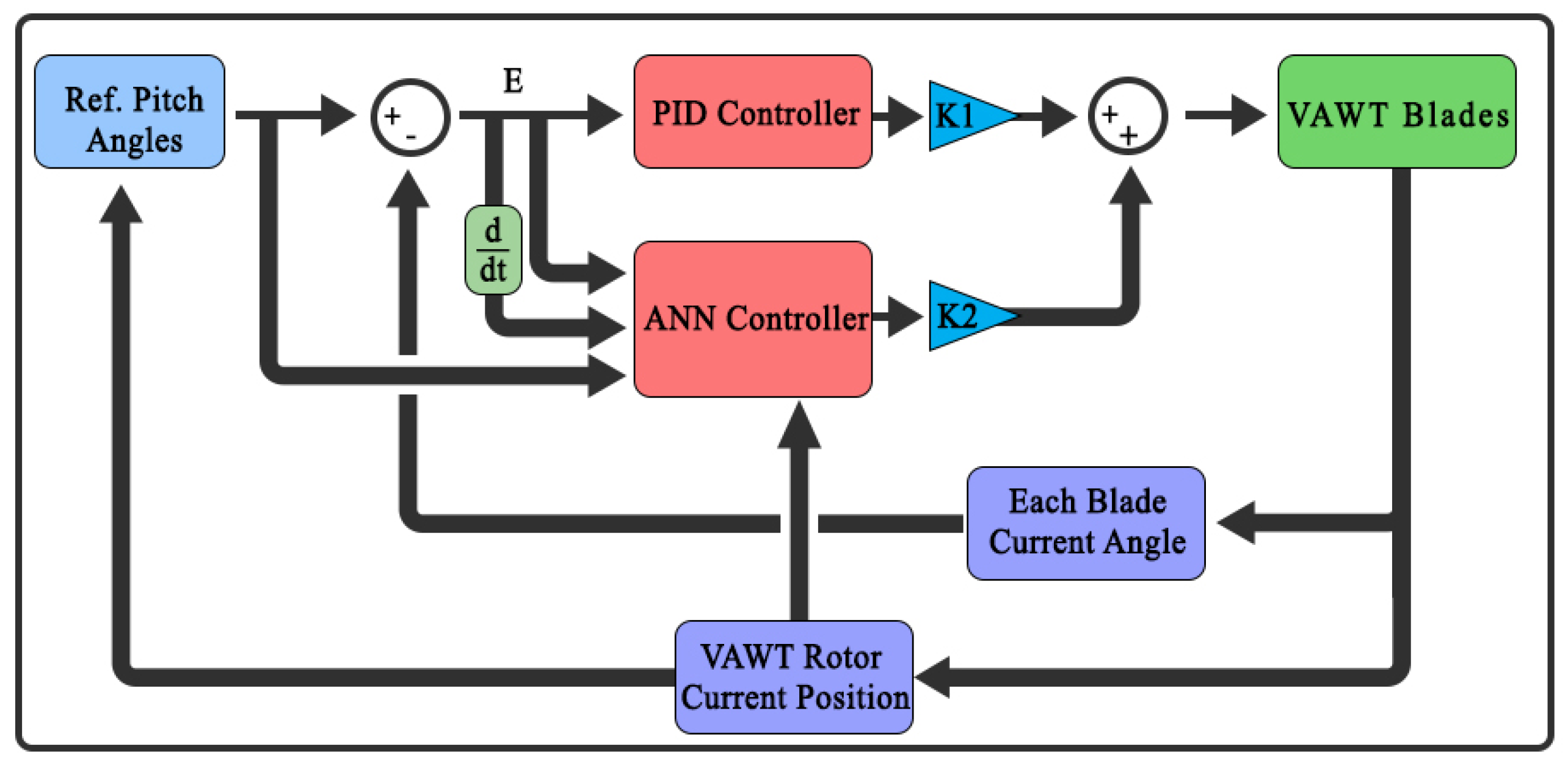
3.4. Variable Pitch Angle Model
- The error e for both the PID and MLP-ANN controllers are similar with
- A single-input single-output (SISO) MLP-ANN with one hidden layer is proposed for the stability analysis of an H-type VAWT. The control law for the MLP-ANN controller is given bywhere is the nonlinear transformation of the error (signal) e (input of the SISO MLP-ANN) provided by the neural network.
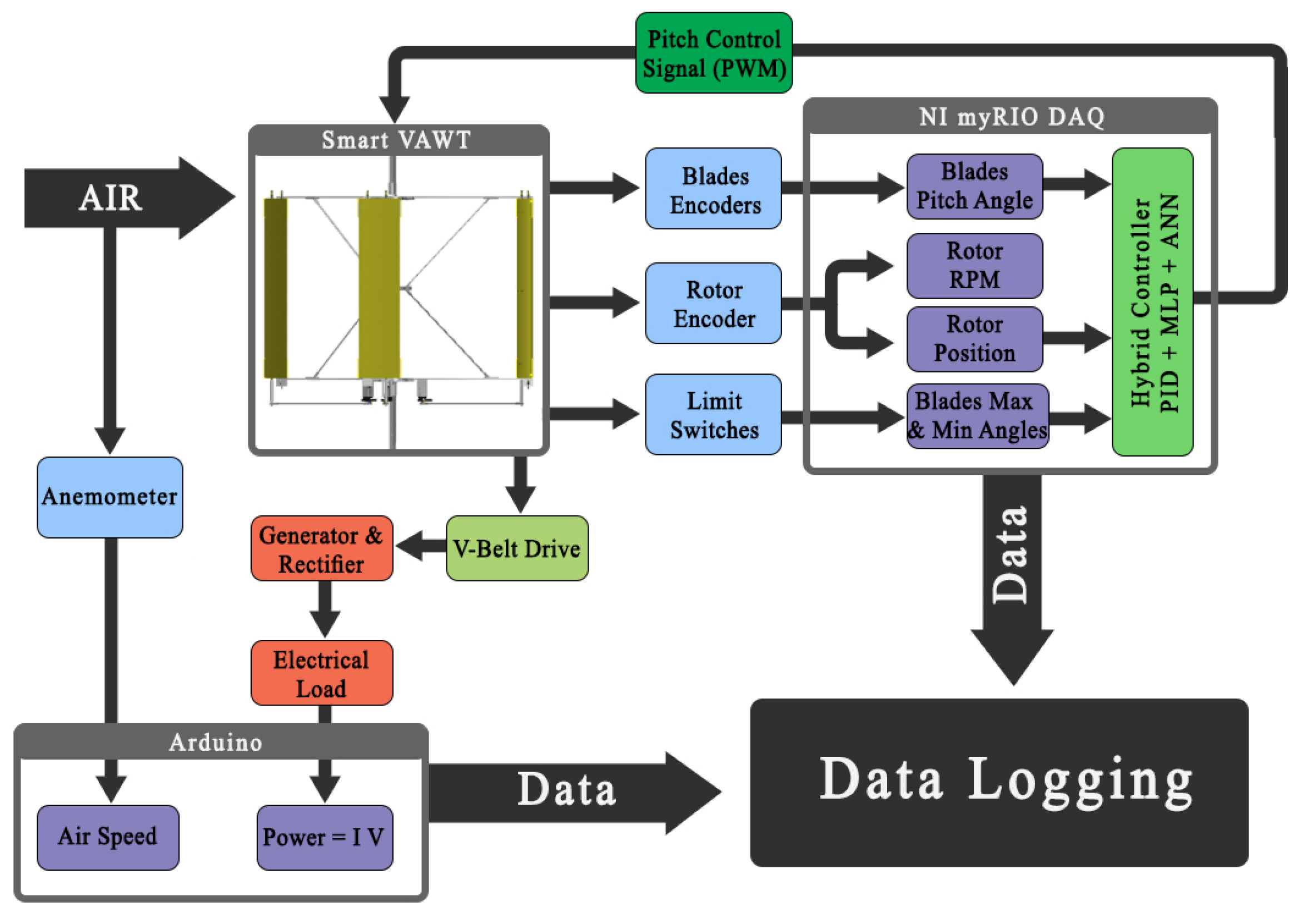
4. Experimental Validation
Design and Implementation of the Proposed Blade Pitch Control System
5. Experimental Results
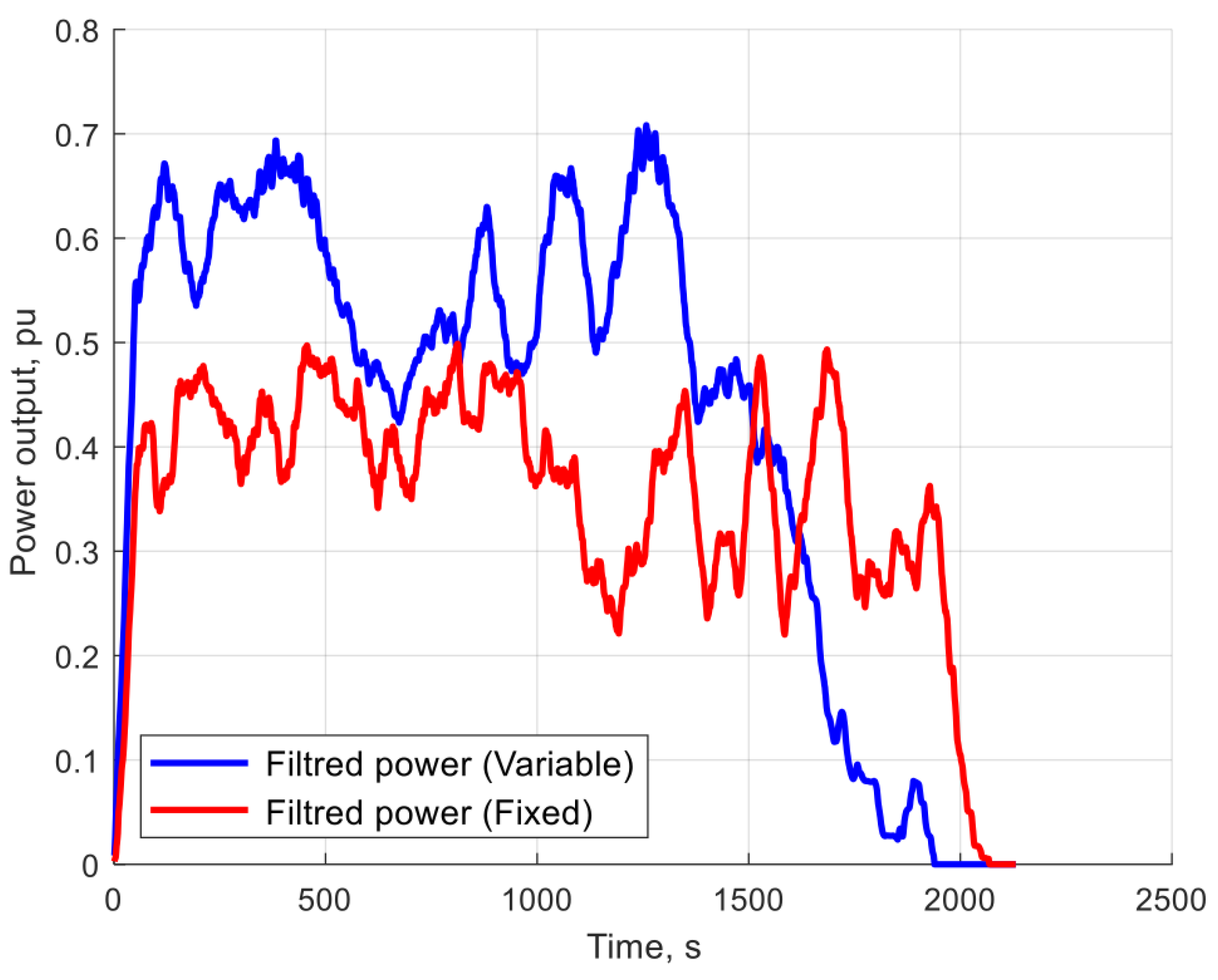
5.1. Power Curve
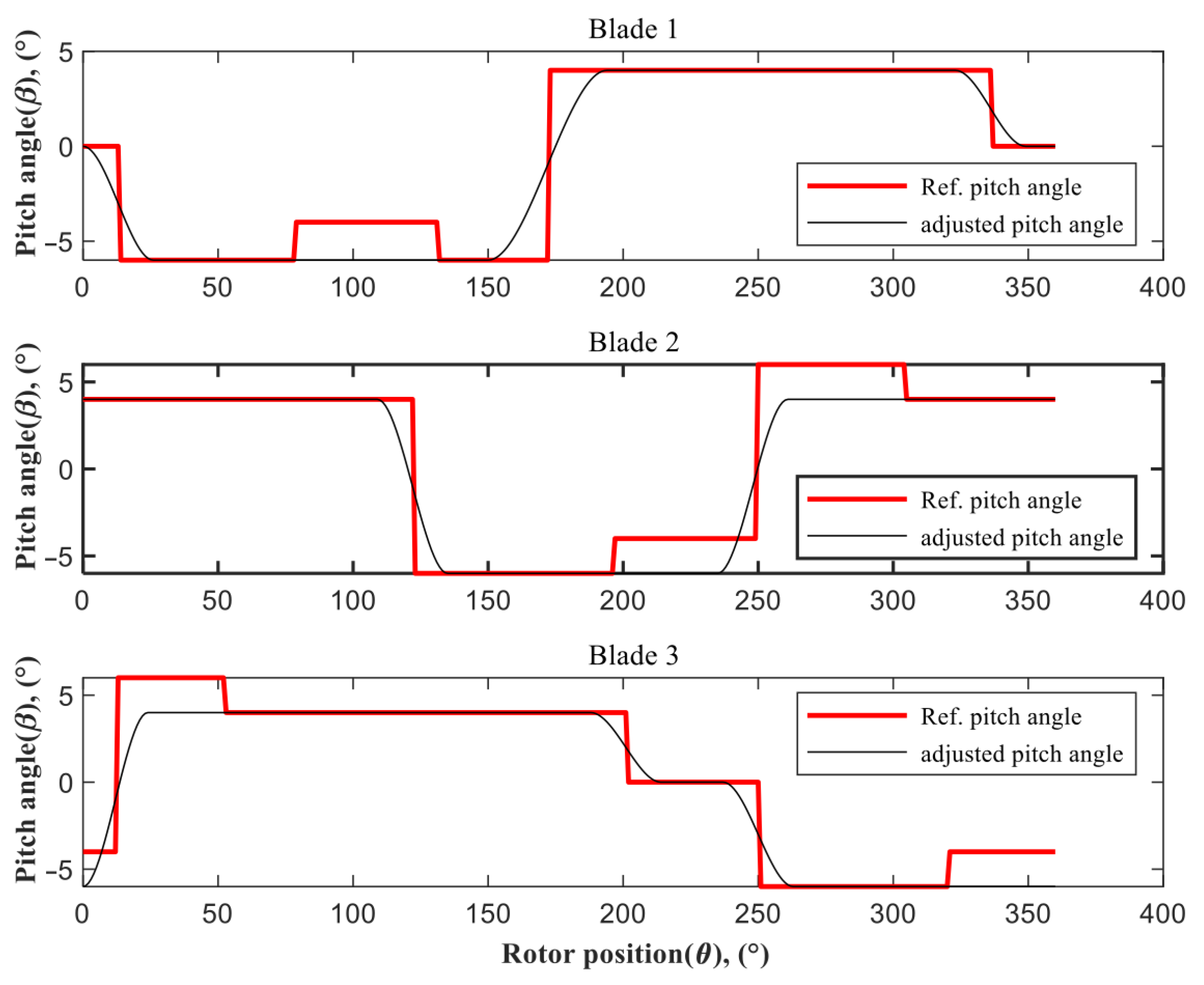
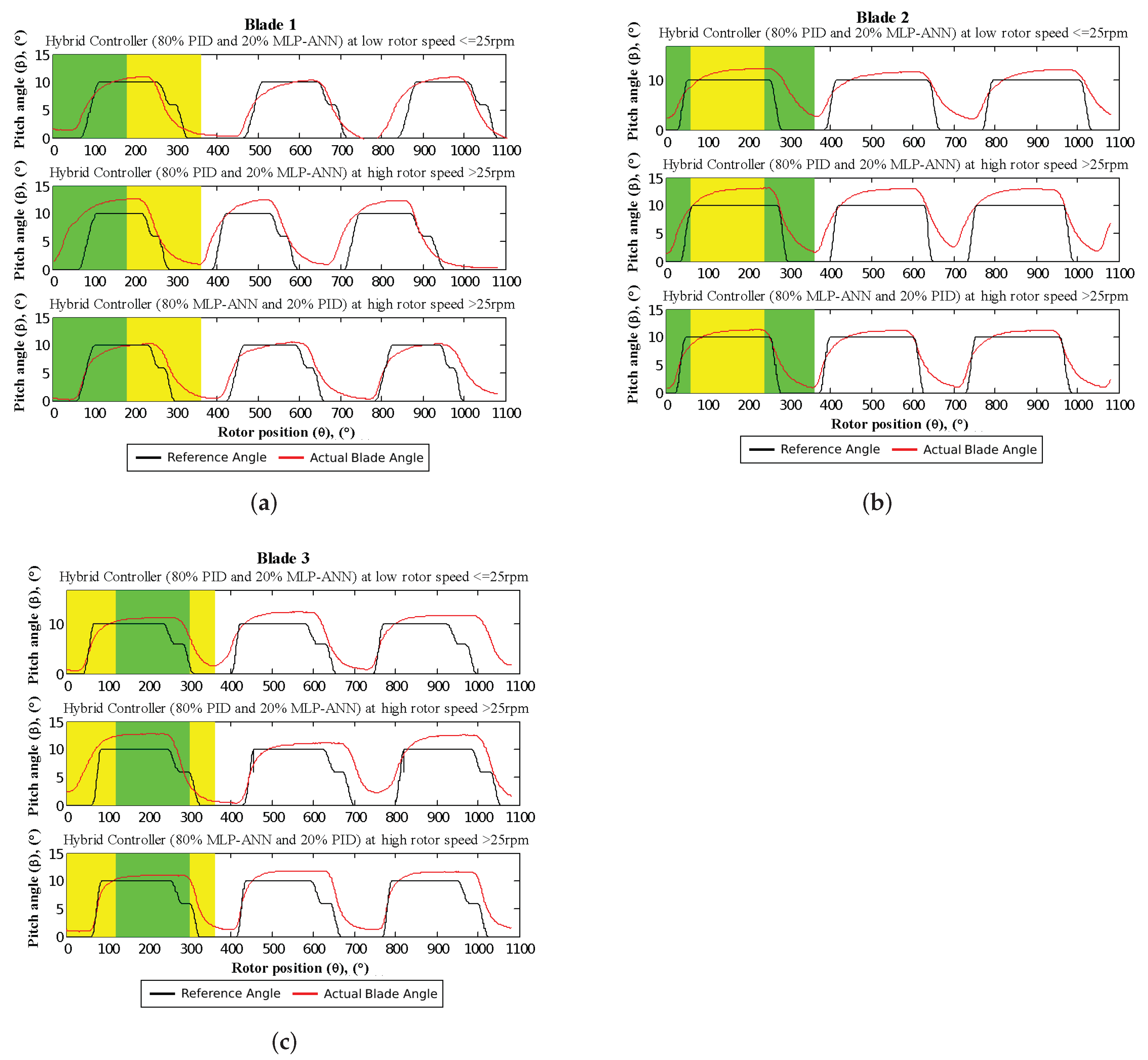
5.2. Pitch Angle Control System Effectiveness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Würfel, P.; Würfel, U. Physics of Solar Cells: From Basic Principles to Advanced Concepts; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2010, 35, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y. Numerical Simulation of the Aerodynamic Performance of an H-Rotor. Master’s Thesis, University of Louisville, Louisville, KY, USA, 2011. [Google Scholar]
- Carrigan, T.J.; Dennis, B.H.; Han, Z.X.; Wang, B.P. Aerodynamic shape optimization of a vertical-axis wind turbine using differential evolution. ISRN Renew. Energy 2012, 2012, 528418. [Google Scholar] [CrossRef] [Green Version]
- Dyachuk, E.; Rossander, M.; Goude, A.; Bernhoff, H. Measurements of the aerodynamic normal forces on a 12-kW straight-bladed vertical axis wind turbine. Energies 2015, 8, 8482–8496. [Google Scholar] [CrossRef] [Green Version]
- Bos, R. Self-Starting of a Small Urban Darrieus Rotor—Strategies to Boost Performance in Low-Reynolds-Number Flows. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Khalid, S.S.; Liang, Z.; Qi-Hu, S.; Xue-Wei, Z. Difference between fixed and variable pitch vertical axis tidal turbine-using CFD analysis in CFX. Res. J. Appl. Sci. Eng. Technol. 2013, 1, 319–325. [Google Scholar]
- Jain, P.; Abhishek, A. Performance prediction and fundamental understanding of small scale vertical axis wind turbine with variable amplitude blade pitching. Renew. Energy 2016, 97, 97–113. [Google Scholar] [CrossRef]
- Lazauskas, L. Three pitch control systems for vertical axis wind turbines compared. Wind. Eng. 1992, 16, 269–282. [Google Scholar]
- Kirke, B.K. Evaluation of Self-Starting Vertical Axis Wind Turbines for Stand-Alone Applications. Ph.D. Thesis, Griffith University Gold Coast, Meadowbrook, QLD, Australia, 1998. [Google Scholar]
- Baker, J. Features to aid or enable self starting of fixed pitch low solidity vertical axis wind turbines. J. Wind. Eng. Ind. Aerodyn. 1983, 15, 369–380. [Google Scholar] [CrossRef]
- Hill, N.; Dominy, R.; Ingram, G.; Dominy, J. Darrieus turbines: The physics of self-starting. Proc. Inst. Mech. Eng. Part J. Power Energy 2009, 223, 21–29. [Google Scholar] [CrossRef]
- Ebert, P.; Wood, D. Observations of the starting behaviour of a small horizontalaxis wind turbine. Renew. Energy 1997, 12, 245–257. [Google Scholar] [CrossRef]
- Li, C.; Zhu, S.; Xu, Y.l.; Xiao, Y. 2.5 D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef] [Green Version]
- Van, T.L.; Nguyen, T.H.; Lee, D.C. Advanced pitch angle control based on fuzzy logic for variable-speed wind turbine systems. IEEE Trans. Energy Convers. 2015, 30, 578–587. [Google Scholar] [CrossRef]
- Lee, S.H.; Joo, Y.J.; Back, J.; Seo, J.H. Sliding mode controller for torque and pitch control of wind power system based on PMSG. In Proceedings of the ICCAS 2010, Gyeonggi-do, Korea, 27–30 October 2010; pp. 1079–1084. [Google Scholar]
- Kasabov, N.K. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Tiwari, R.; Babu, N.R. Comparative Analysis of Pitch Angle Controller Strategies for PMSG Based Wind Energy Conversion System. Int. J. Intell. Syst. Appl. 2017, 9, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Sargolzaei, J. Prediction of the power ratio and torque in wind turbine Savonius rotors using artificial neural networks. In Proceedings of the WSEAS International Conference on Renewable Energy Sources, Arcachon, France, 14–16 October 2007; pp. 14–16. [Google Scholar]
- Hossain, A.; Rahman, A.; Rahman, M.; Hasan, S.; Hossen, J. Prediction of power generation of small scale vertical axis wind turbine using fuzzy logic. J. Urban Environ. Eng. 2009, 3, 43–51. [Google Scholar] [CrossRef]
- Lee, M.J.; Hwang, G.H.; Jang, W.T.; Cha, K.H. Robotic agent control based on adaptive intelligent algorithm in ubiquitous networks. In KES International Symposium on Agent and Multi-Agent Systems: Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 539–548. [Google Scholar]
- Pezeshki, S.; Badalkhani, S.; Javadi, A. Performance Analysis of a Neuro-PID Controller Applied to a Robot Manipulator. Int. J. Adv. Robot. Syst. 2012, 9, 163. [Google Scholar] [CrossRef]
- Abdalrahman, G.; Melek, W.; Lien, F.S. Pitch angle control for a small-scale Darrieus vertical axis wind turbine with straight blades (H-Type VAWT). Renew. Energy 2017, 114, 1353–1362. [Google Scholar] [CrossRef] [Green Version]
- Semrau, G. Dynamic Modeling and Characterization of a Wind Turbine System Leading to Controls Development. Master’s Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2010. [Google Scholar]
- Thomsen, S.C. Nonlinear Control of a Wind Turbine. Master’s Thesis, Technical University of Denmark, Lyngby, Denmark, 2006. [Google Scholar]
- Semrau, G.; Rimkus, S.; Das, T. Nonlinear systems analysis and control of variable speed wind turbines for multiregime operation. J. Dyn. Syst. Meas. Control 2015, 137, 041007. [Google Scholar] [CrossRef]
- Johnson, K.E.; Pao, L.Y.; Balas, M.J.; Fingersh, L.J. Control of variable-speed wind turbines: Standard and adaptive techniques for maximizing energy capture. IEEE Control Syst. Mag. 2006, 26, 70–81. [Google Scholar]
- Khan, S.A.; Rajkumar, R.K.; Rajkumar, R.K.; Aravind, C.V. Performance analysis of 20 pole 1.5 kW three phase permanent magnet synchronous generator for low speed vertical axis wind turbine. Energy Power Eng. 2013, 5, 423–428. [Google Scholar] [CrossRef]
- Muhando, E.B.; Senjyu, T.; Uehara, A.; Funabashi, T.; Kim, C.H. LQG design for megawatt-class WECS with DFIG based on functional models’ fidelity prerequisites. IEEE Trans. Energy Convers. 2009, 24, 893–904. [Google Scholar] [CrossRef]
- Jiao, X.; Meng, W.; Yang, Q.; Fu, L.; Chen, Q. Adaptive Continuous Neural Pitch Angle Control for Variable-Speed Wind Turbines. Asian J. Control. 2019, 21, 1–14. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear System; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Nikravesh, S.K.Y. Nonlinear Systems Stability Analysis: Lyapunov-Based Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Murray, R.M. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Sapna, S.; Tamilarasi, A.; Kumar, M.P. Backpropagation learning algorithm based on Levenberg Marquardt algorithm. Comp. Sci. Inform. Technol. 2012, 2, 393–398. [Google Scholar]



| Blade 1 | 0.12 | 100 | 0.043 |
| Blade 2 | 0.088 | 100 | 0.009 |
| Blade 3 | 0.1 | 100 | 0.01 |
| RMSE | 80% PID and 20% MLP-ANN at Low RPM | 80% PID and 20% MLP-ANN at High RPM | 80% MLP-ANN and 20% PID at High RPM |
|---|---|---|---|
| Blade 1 | 3.2181 | 3.2741 | 1.7961 |
| Blade 2 | 1.6629 | 2.8732 | 1.8962 |
| Blade 3 | 2.6248 | 3.0238 | 2.4718 |
| PO (Ref.) Pitch = | 80% PID and 20% MLP-ANN at Low RPM, (%) | 80% PID and 20% MLP-ANN at High RPM, (%) | 80% MLP-ANN and 20% PID at High RPM, (%) |
|---|---|---|---|
| Blade 1 | 10.4 | 27 | 1.7 |
| Blade 2 | 25 | 31.5 | 11.7 |
| Blade 3 | 13.3 | 28 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdalrahman, G.; Daoud, M.A.; Melek, W.W.; Lien, F.-S.; Yee, E. Design and Implementation of an Intelligent Blade Pitch Control System and Stability Analysis for a Small Darrieus Vertical-Axis Wind Turbine. Energies 2022, 15, 235. https://doi.org/10.3390/en15010235
Abdalrahman G, Daoud MA, Melek WW, Lien F-S, Yee E. Design and Implementation of an Intelligent Blade Pitch Control System and Stability Analysis for a Small Darrieus Vertical-Axis Wind Turbine. Energies. 2022; 15(1):235. https://doi.org/10.3390/en15010235
Chicago/Turabian StyleAbdalrahman, Gebreel, Mohamed A. Daoud, William W. Melek, Fue-Sang Lien, and Eugene Yee. 2022. "Design and Implementation of an Intelligent Blade Pitch Control System and Stability Analysis for a Small Darrieus Vertical-Axis Wind Turbine" Energies 15, no. 1: 235. https://doi.org/10.3390/en15010235
APA StyleAbdalrahman, G., Daoud, M. A., Melek, W. W., Lien, F.-S., & Yee, E. (2022). Design and Implementation of an Intelligent Blade Pitch Control System and Stability Analysis for a Small Darrieus Vertical-Axis Wind Turbine. Energies, 15(1), 235. https://doi.org/10.3390/en15010235







