Weighted Bandwidth Method for Stability Assessment of Complex DC Power Systems on Ships
Abstract
:1. Introduction
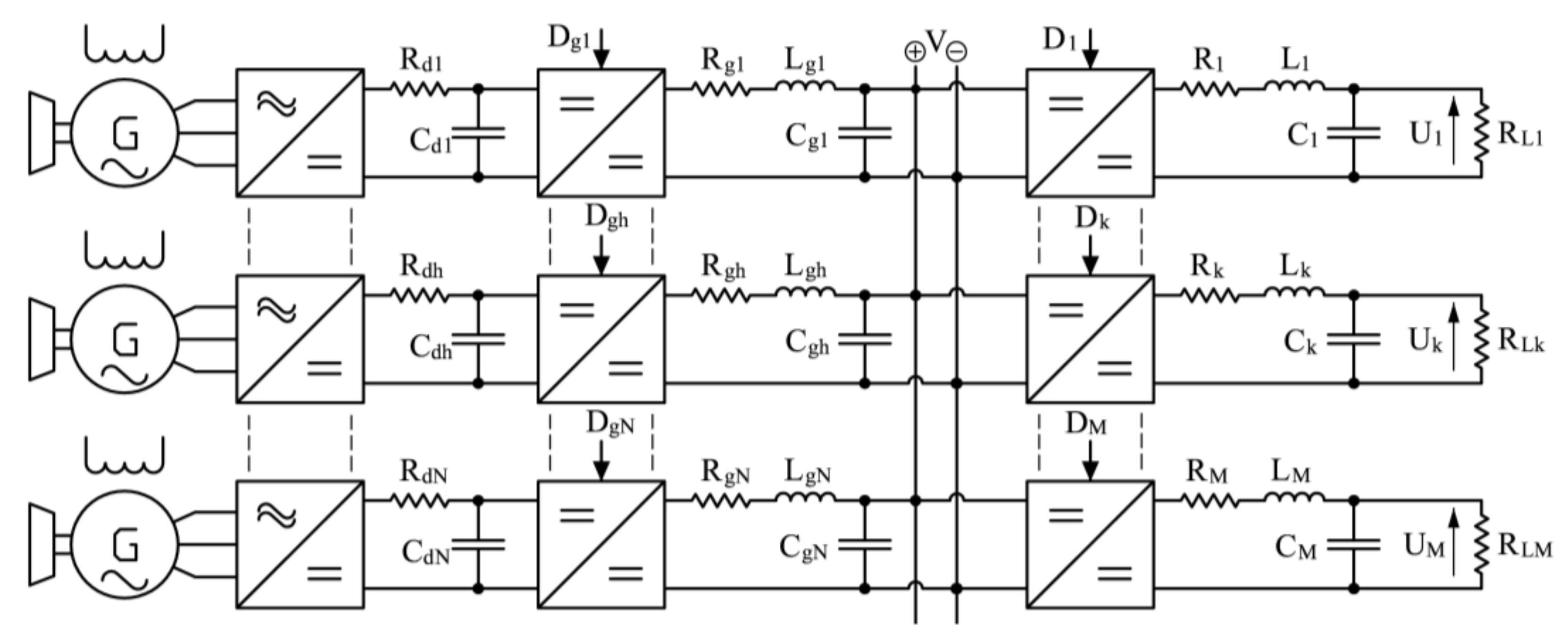
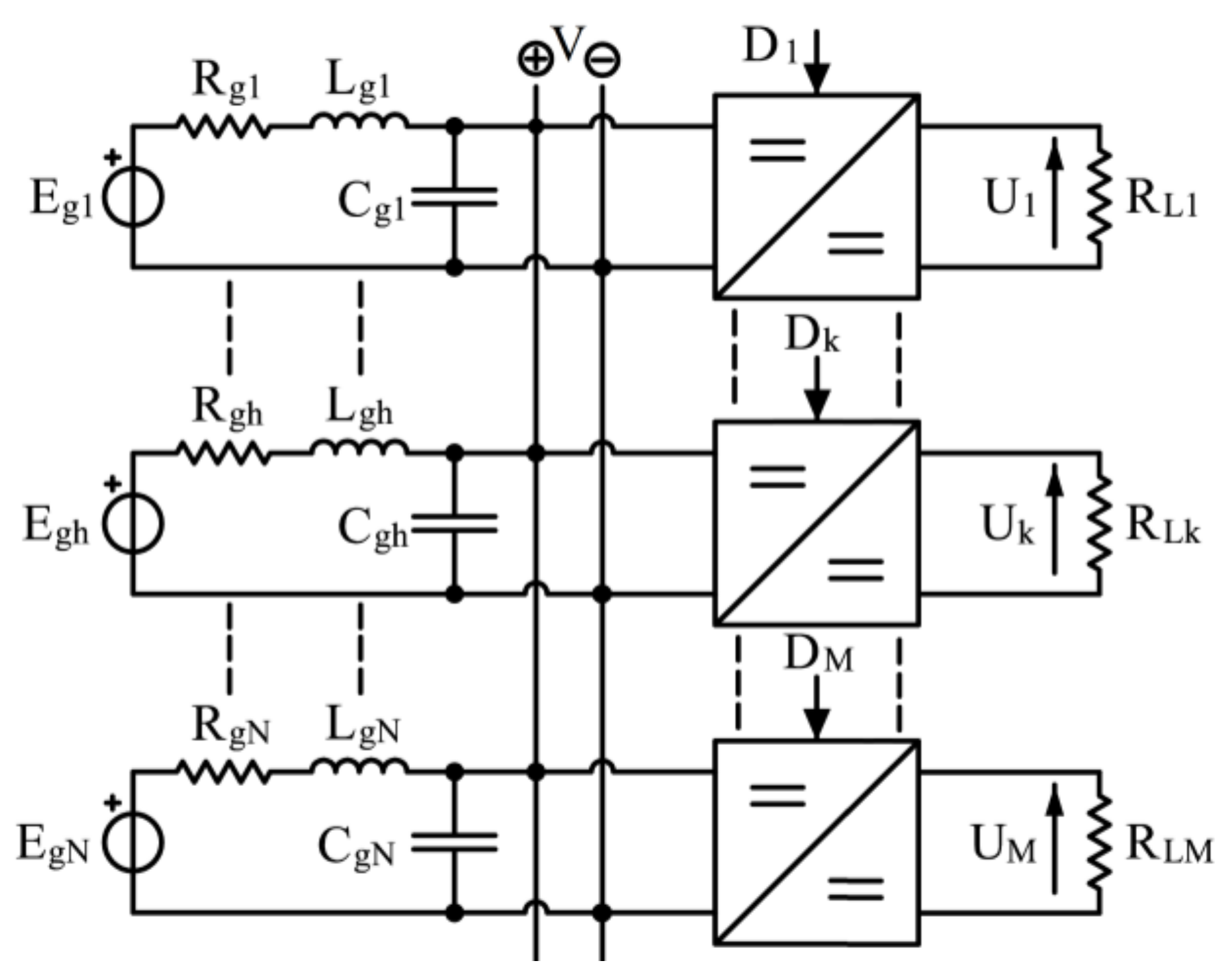
2. DC Microgrid Modeling
2.1. Power System Topology
2.2. Modeling Assumptions and Range of Validity
2.3. Analytical Model
3. Weighted Bandwidth Method
3.1. Set Membership
3.2. Loads Order and Power Equivalence
3.3. Linear Combinations of Control Bandwidths
3.4. WBM Less Conservativeness
4. DC Stability Analysis
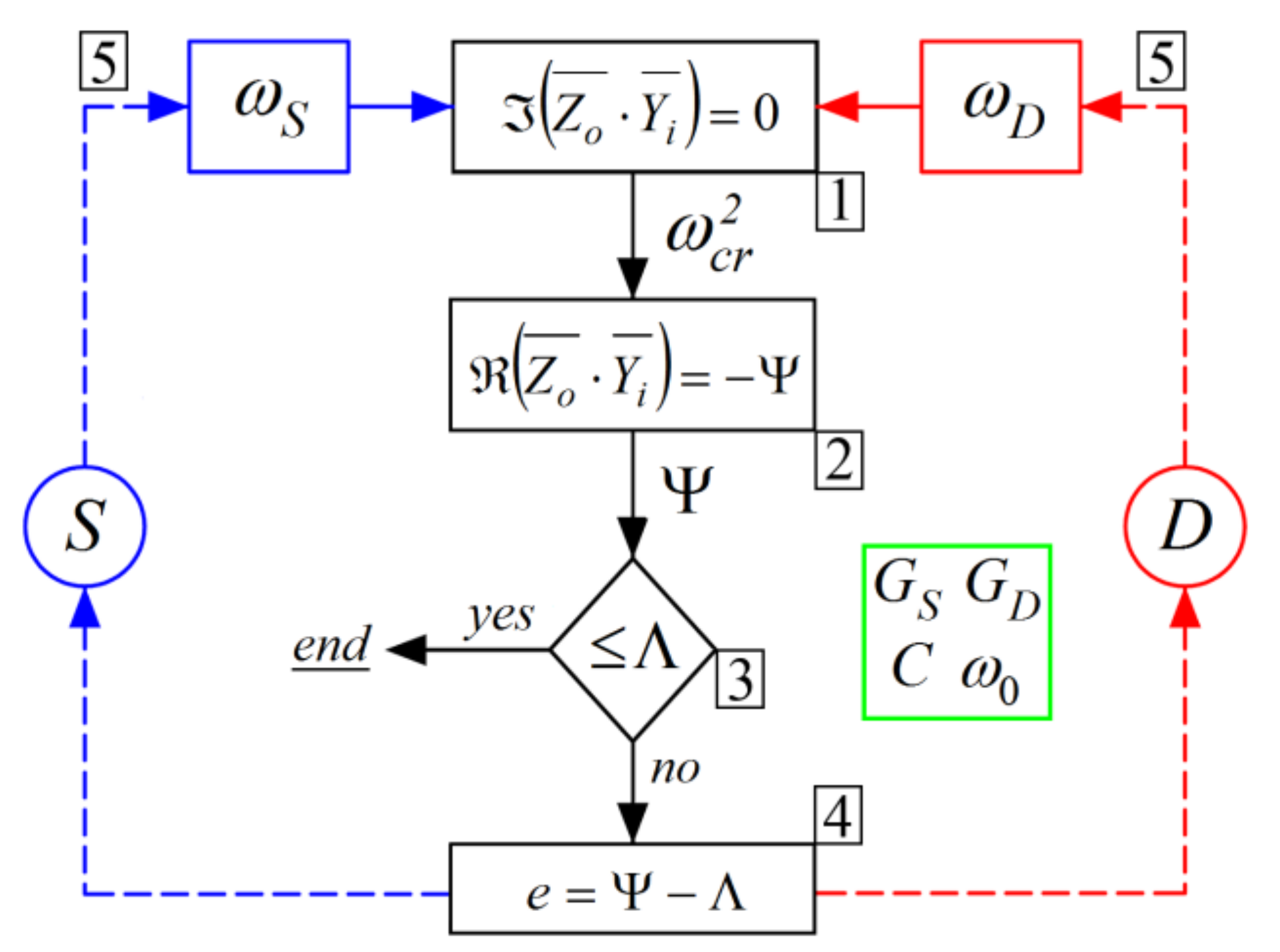
4.1. Stability Criterion
4.2. Iterative Process for WBM Stability Assessment
5. Validation of WBM Stability Assessment
5.1. Power System Data
5.2. Test Setup
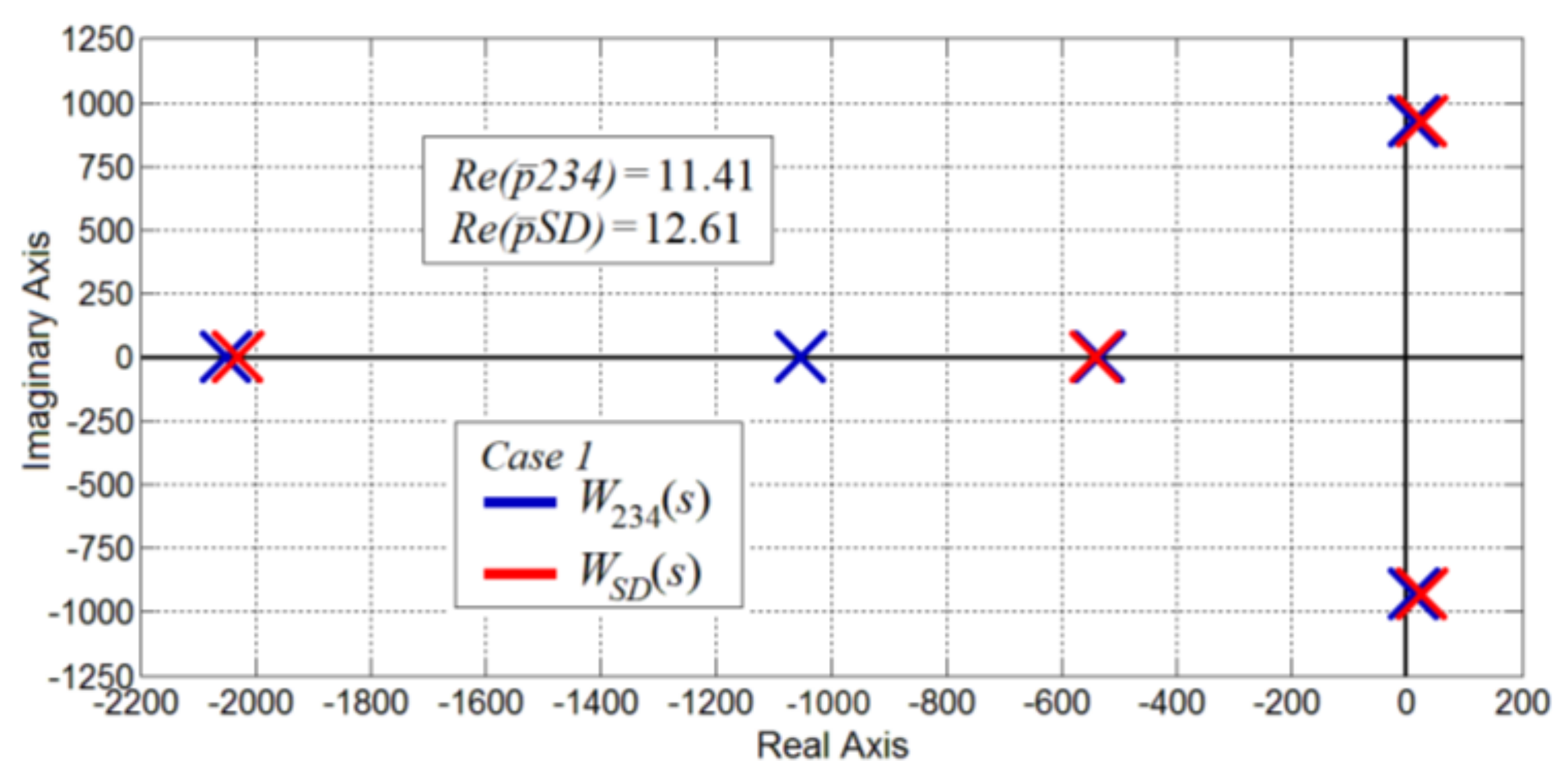
5.3. Stability Assessment
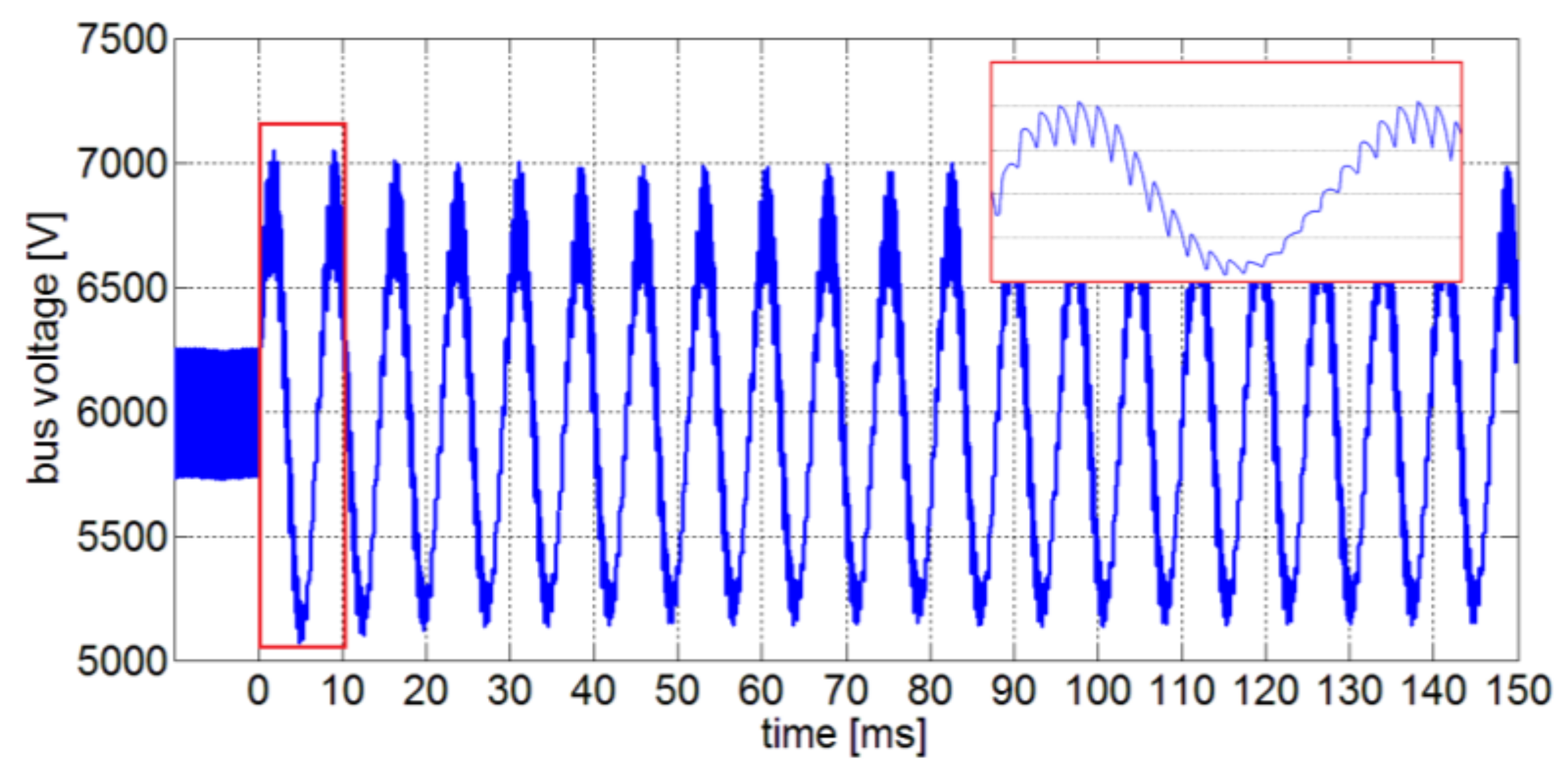
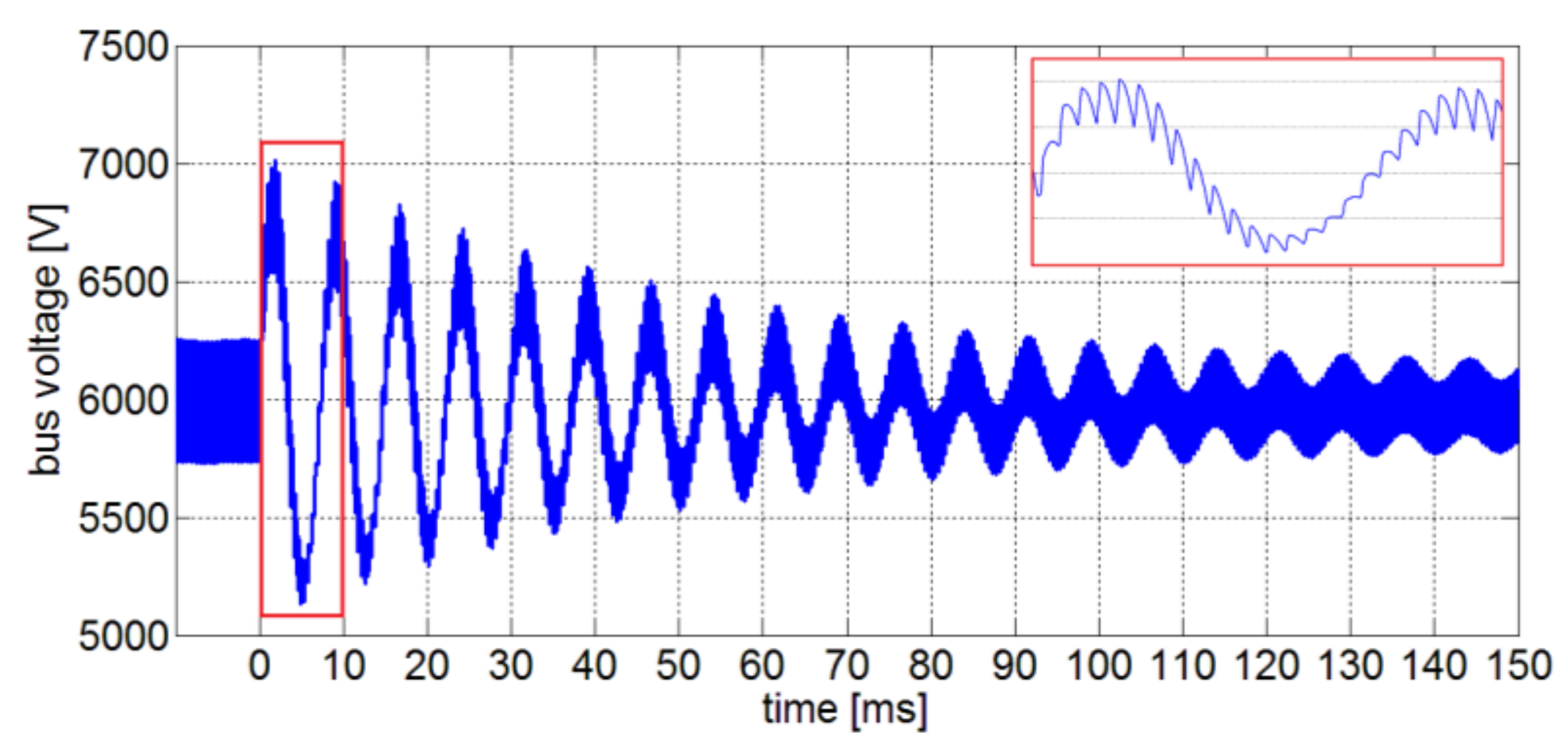
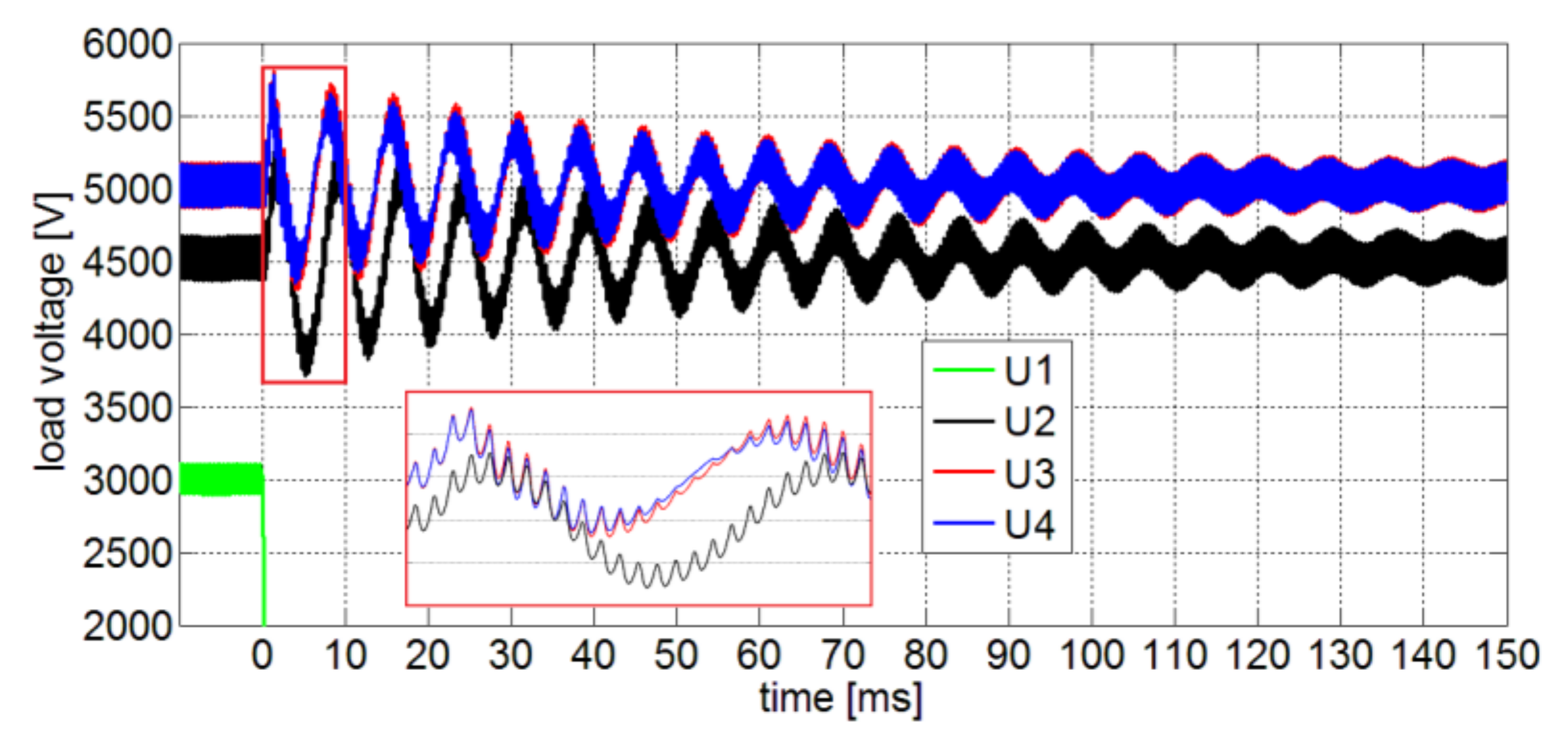
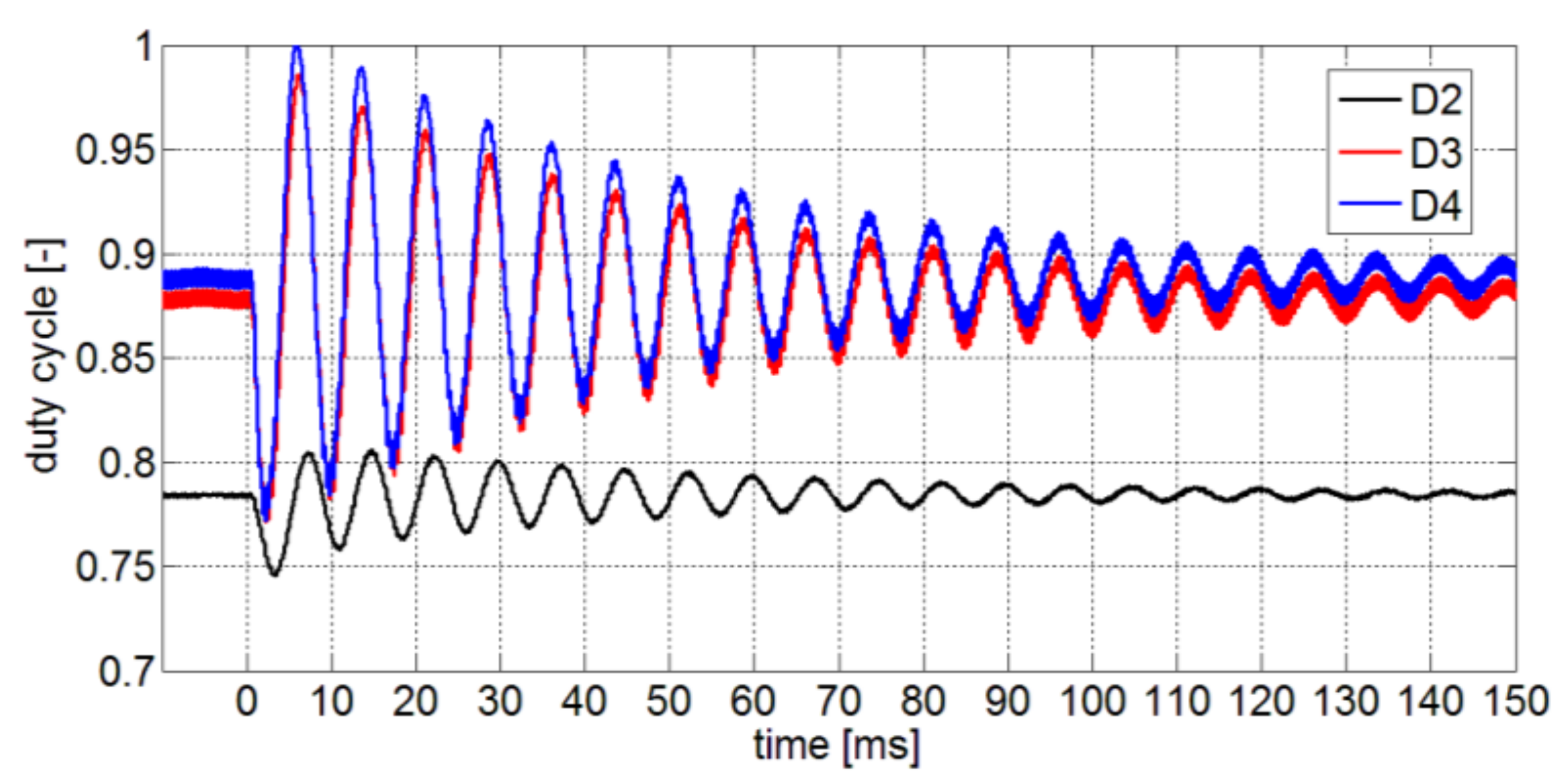
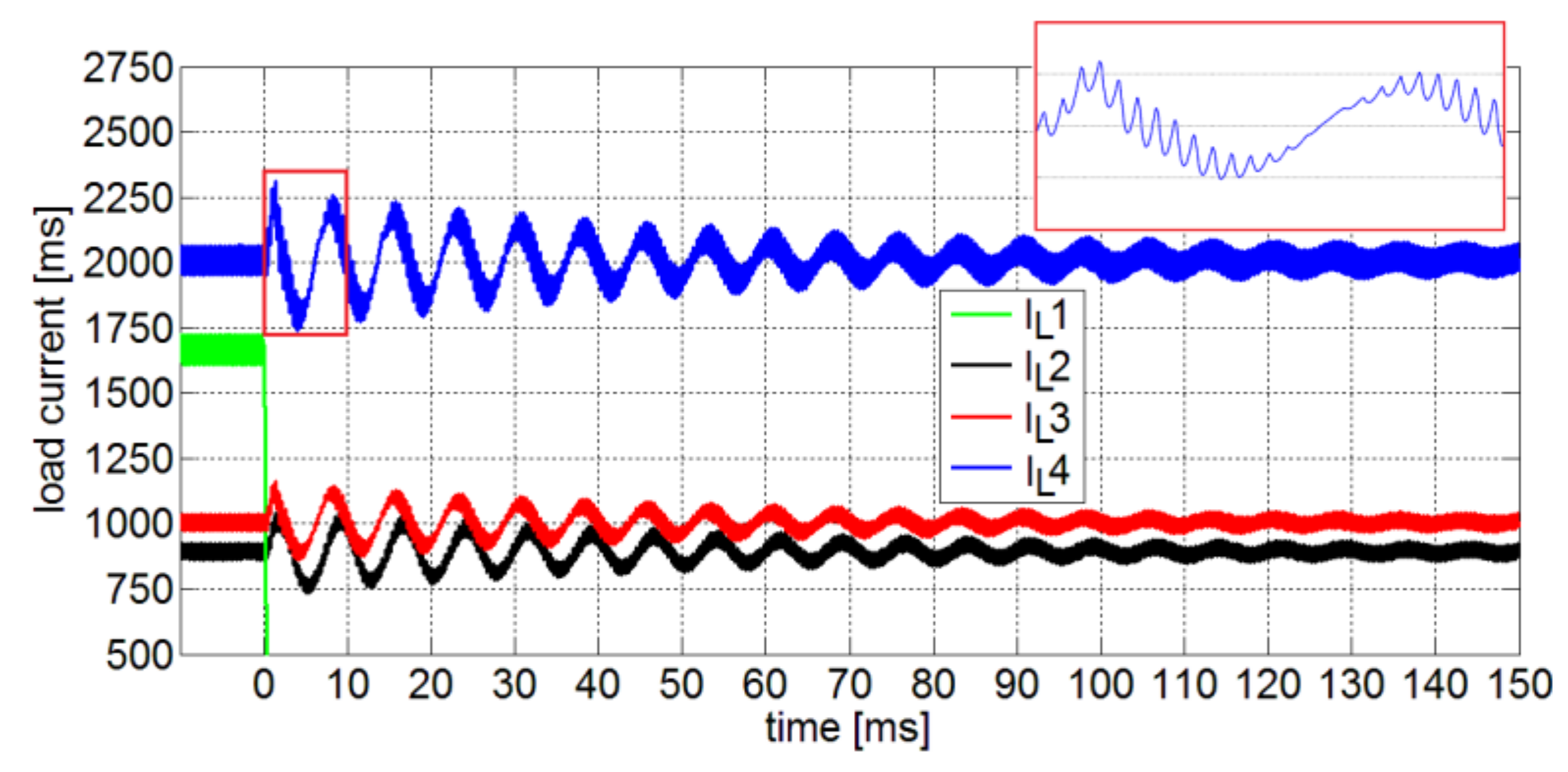
5.4. Hardware in the Loop Validation
5.5. Considerations on Stability Assessment and HIL Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dragicevic, T.; Vasquez, J.C.; Guerrero, J.; Škrlec, D. Advanced LVDC Electrical Power Architectures and Microgrids: A step toward a new generation of power distribution networks. IEEE Electrif. Mag. 2014, 2, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Zubieta, L.E. Are Microgrids the Future of Energy? DC Microgrids from Concept to Demonstration to Deployment. IEEE Electrif. Mag. 2016, 4, 37–44. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Ericsen, T.; Raju, R.; Burgos, R.; Boroyevich, D. Advances in Power Conversion and Drives for Shipboard Systems. Proc. IEEE 2015, 103, 2285–2311. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Zhao, S.; Wei, X.; Kang, Y. Design and Implementation of a Modular Multilevel Converter with Hierarchical Redundancy Ability for Electric Ship MVDC System. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 189–202. [Google Scholar] [CrossRef]
- Lemmon, A.N.; Graves, R.C.; Kini, R.L.; Hontz, M.R.; Khanna, R. Characterization and Modeling of 10-kV Silicon Carbide Modules for Naval Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 309–322. [Google Scholar] [CrossRef]
- Javaid, U.; Freijedo, F.D.; Dujic, D.; van der Merwe, W. MVDC supply technologies for marine electrical distribution systems. CPSS Trans. Power Electron. Appl. 2018, 3, 65–76. [Google Scholar] [CrossRef]
- Islam, M.M. Shipboard Power System with LVDC and MVDC for AC and DC Application. In VFD Challenges for Shipboard Electrical Power System Design; IEEE: Piscataway, NJ, USA, 2019; pp. 35–37. [Google Scholar]
- Moore, T.J.; Richardson, J.M.; Markle, S.P. NPES Technology Development Roadmap. Naval Sea Systems Command. 2019. Available online: https://news.usni.org/2019/06/26/u-s-naval-power-and-energy-systems-technology-development-roadmap (accessed on 22 November 2021).
- IEEE Standards Association. IEEE Recommended Practice for 1 kV to 35 kV Medium-Voltage DC Power Systems on Ships; IEEE Std 1709-2018 (Revision of IEEE Std 1709–2010); IEEE: Piscataway, NJ, USA, 2018; pp. 1–54. [Google Scholar]
- Cuzner, R.M.; Soman, R.; Steurer, M.M.; Toshon, T.A.; Faruque, M.O. Approach to Scalable Model Development for Navy Shipboard Compatible Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 28–39. [Google Scholar] [CrossRef]
- Soman, R.; Steurer, M.M.; Toshon, T.A.; Faruque, M.O.; Cuzner, R.M. Size and Weight Computation of MVDC Power Equipment in Architectures Developed Using the Smart Ship Systems Design Environment. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 40–50. [Google Scholar] [CrossRef]
- Sudhoff, S.; Corzine, K.; Glover, S.; Hegner, H.; Robey, H. DC link stabilized field oriented control of electric propulsion systems. IEEE Trans. Energy Convers. 1998, 13, 27–33. [Google Scholar] [CrossRef]
- Sudhoff, S.D.; Glover, S.F.; Lamm, P.T.; Schmucker, D.H.; Delisle, D.E. Admittance space stability analysis of power electronic systems. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 965–973. [Google Scholar] [CrossRef]
- Wang, C.; Duan, J.; Fan, B.; Yang, Q.; Liu, W. Decentralized High-Performance Control of DC Microgrids. IEEE Trans. Smart Grid 2019, 10, 3355–3363. [Google Scholar] [CrossRef]
- Rivetta, C.H.; Emadi, A.; Williamson, G.A.; Jayabalan, R.; Fahimi, B. Analysis and control of a buck DC-DC converter operating with constant power load in sea and undersea vehicles. IEEE Trans. Ind. Appl. 2006, 42, 559–572. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Cupelli, M.; Ponci, F.; Sulligoi, G.; Vicenzutti, A.; Edrington, C.S.; El-Mezyani, T.; Monti, A. Power Flow Control and Network Stability in an All-Electric Ship. Proc. IEEE 2015, 103, 2355–2380. [Google Scholar] [CrossRef] [Green Version]
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef] [Green Version]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 881–888. [Google Scholar]
- Huangfu, Y.; Pang, S.; Nahid-Mobarakeh, B.; Guo, L.; Rathore, A.K.; Gao, F. Stability Analysis and Active Stabilization of On-board DC Power Converter System with Input Filter. IEEE Trans. Ind. Electron. 2018, 65, 790–799. [Google Scholar] [CrossRef]
- Potty, K.A.; Bauer, E.; Li, H.; Wang, J. Smart Resistor: Stabilization of DC Microgrids Containing Constant Power Loads Using High-Bandwidth Power Converters and Energy Storage. IEEE Trans. Power Electron. 2020, 35, 957–967. [Google Scholar] [CrossRef]
- Pakdeeto, J.; Areerak, K.; Bozhko, S.; Areerak, K. Stabilization of DC MicroGrid Systems by Using the Loop-Cancellation Technique. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2652–2663. [Google Scholar] [CrossRef]
- Sulligoi, G.; Bosich, D.; Giadrossi, G.; Zhu, L.; Cupelli, M.; Monti, A. Multiconverter Medium Voltage DC Power Systems on Ships: Constant-Power Loads Instability Solution Using Linearization via State Feedback Control. IEEE Trans. Smart Grid 2014, 5, 2543–2552. [Google Scholar] [CrossRef]
- Bosich, D.; Sulligoi, G.; Mocanu, E.; Gibescu, M.M. Medium Voltage DC Power Systems on Ships: An Offline Parameter Estimation for Tuning the Controllers’ Linearizing Function. IEEE Trans. Energy Convers. 2017, 32, 748–758. [Google Scholar] [CrossRef]
- Cupelli, M.; Zhu, L.; Monti, A. Why Ideal Constant Power Loads Are Not the Worst Case Condition From a Control Standpoint. IEEE Trans. Smart Grid 2015, 6, 2596–2606. [Google Scholar] [CrossRef] [Green Version]
- Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S. Dynamic Consideration of DC Microgrids with Constant Power Loads and Active Damping System—A Design Method for Fault-Tolerant Stabilizing System. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 562–570. [Google Scholar] [CrossRef]
- Alacano, A.; Valera, J.J.; Abad, G.; Izurza, P. Power-Electronic-Based DC Distribution Systems for Electrically Propelled Vessels: A Multivariable Modeling Approach for Design and Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1604–1620. [Google Scholar] [CrossRef]
- Javaid, U.; Freijedo, F.D.; Dujic, D.; Van Der Merwe, W. Dynamic Assessment of Source—Load Interactions in Marine MVDC Distribution. IEEE Trans. Ind. Electron. 2017, 64, 4372–4381. [Google Scholar] [CrossRef]
- Javaid, U.; Freijedo, F.D.; Van Der Merwe, W.; Dujic, D. Stability Analysis of Multi-Port MVDC Distribution Networks for All-Electric Ships. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1164–1177. [Google Scholar] [CrossRef]
- Pastore, S.; Bosich, D.; Sulligoi, G. Analysis of small-signal voltage stability for a reduced-order cascade-connected MVDC power system. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 6771–6776. [Google Scholar]
- Pastore, S.; Bosich, D.; Sulligoi, G. A frequency analysis of the small-signal voltage model of a MVDC power system with two cascade DC-DC converters. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Chalfant, J. Early-Stage Design for Electric Ship. Proc. IEEE 2015, 103, 2252–2266. [Google Scholar] [CrossRef]
- Ericsen, T. The Second Electronic Revolution (It’s All about Control). In Proceedings of the 2009 Record of Conference Papers-Industry Applications Society 56th Annual Petroleum and Chemical Industry Conference, Anaheim, CA, USA, 14–16 September 2009; Volume 46, pp. 1778–1786. [Google Scholar]
- Sulligoi, G.; Bosich, D.; Vicenzutti, A.; Khersonsky, Y. Design of Zonal Electrical Distribution Systems for Ships and Oil Platforms: Control Systems and Protections. IEEE Trans. Ind. Appl. 2020, 56, 5656–5669. [Google Scholar] [CrossRef]
- Du, W.; Fu, Q.; Wang, H.F. Small-Signal Stability of a DC Network Planned for Electric Vehicle Charging. IEEE Trans. Smart Grid 2020, 11, 3748–3762. [Google Scholar] [CrossRef]
- Feng, X.; Ye, Z.; Xing, K.; Lee, F.; Borojevic, D. Individual load impedance specification for a stable DC distributed power system. In Proceedings of the APEC’99. Fourteenth Annual Applied Power Electronics Conference and Exposition. 1999 Conference Proceedings (Cat. No. 99CH36285), Dallas, TX, USA, 14–18 March 1999; Volume 2, pp. 923–929. [Google Scholar]
- Riccobono, A.; Santi, E. Comprehensive Review of Stability Criteria for DC Power Distribution Systems. IEEE Trans. Ind. Appl. 2014, 50, 3525–3535. [Google Scholar] [CrossRef]
- Siegers, J.; Arrua, S.; Santi, E. Stabilizing Controller Design for Multibus MVdc Distribution Systems Using a Passivity-Based Stability Criterion and Positive Feedforward Control. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 14–27. [Google Scholar] [CrossRef]
- Riccobono, A.; Cupelli, M.; Monti, A.; Santi, E.; Roinila, T.; Abdollahi, H.; Arrua, S.; Dougal, R.A. Stability of Shipboard DC Power Distribution: Online Impedance-Based Systems Methods. IEEE Electrif. Mag. 2017, 5, 55–67. [Google Scholar] [CrossRef]
- Rygg, A.; Molinas, M. Apparent Impedance Analysis: A Small-Signal Method for Stability Analysis of Power Electronic-Based Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1474–1486. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ruan, X.; Tse, C. Impedance-Based Local Stability Criterion for DC Distributed Power Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 916–925. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance- and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Su, M.; Liu, Z.; Sun, Y.; Han, H.; Hou, X. Stability Analysis and Stabilization Methods of DC Microgrid With Multiple Parallel-Connected DC–DC Converters Loaded by CPLs. IEEE Trans. Smart Grid 2018, 9, 132–142. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE Std 141--1993; IEEE Recommended Practice for Electric Power Distribution for Industrial Plants. IEEE: Piscataway, NJ, USA, 1994; pp. 1–768.
- Oh, C.-H.; Go, S.-I.; Choi, J.-H.; Ahn, S.-J.; Yun, S.-Y. Voltage Estimation Method for Power Distribution Networks Using High-Precision Measurements. Energies 2020, 13, 2385. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.Y.; Park, P. A Less Conservative Stability Criterion for Discrete-Time Lur’e Systems with Sector and Slope Restrictions. IEEE Trans. Autom. Control 2019, 64, 4391–4395. [Google Scholar] [CrossRef]
- Lin, C.; Wang, Q.C.; Lee, T.H. A less conservative robust stability test for linear uncertain time-delay systems. IEEE Trans. Autom. Control 2006, 51, 87–91. [Google Scholar] [CrossRef]





| k = 1 | k = 2 | k = 3 | k = 4 | |
|---|---|---|---|---|
| Pnk [MW] | 5 | 4 | 5 | 10 |
| Vn [V] | 6000 | 6000 | 6000 | 6000 |
| Unk [V] | 3000 | 4500 | 5000 | 5000 |
| Dnk | 0.5 | 0.75 | 0.83 | 0.83 |
| Ink [A] | 1600 | 862 | 960 | 1900 |
| fsk [Hz] | 2500 | 2500 | 2500 | 2500 |
| ΔP%k | 4 | 3 | 4 | 5 |
| ΔV%k | 7 | 7 | 7 | 7 |
| ΔI%k | 30 | 30 | 30 | 30 |
| Rfk [mΩ] | 78.1 | 161.4 | 217.0 | 138.5 |
| Lfk [mH] | 1.2 | 1.7 | 1.2 | 0.6 |
| Cfk [µF] | 114.3 | 41.0 | 41.1 | 81.4 |
| ωfk [rad/s] | 2646 | 3742 | 4583 | 4583 |
| RLk [Ω] | 1.80 | 5.06 | 5.00 | 2.50 |
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| ω1 [rad/s] | 200 | 200 | 200 |
| ω2 [rad/s] | 500 | 200 | 200 |
| ω3 [rad/s] | 1000 | 1000 | 914 |
| ω4 [rad/s] | 1200 | 1200 | 1097 |
| Before | After | |
|---|---|---|
| ωB [rad/s] | 832 | 907 |
| PS [MW] | 9 | 4 |
| PD [MW] | 15 | 15 |
| m1 [·] | 0.56 | 0.00 |
| m2 [·] | 0.44 | 1.00 |
| m3 [·] | 0.33 | 0.33 |
| m4 [·] | 0.67 | 0.67 |
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| ωS [rad/s] before/after | 333/500 | 200/200 | 200/200 |
| ωD [rad/s] | 1133 | 1133 | 1036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosich, D.; Giadrossi, G.; Pastore, S.; Sulligoi, G. Weighted Bandwidth Method for Stability Assessment of Complex DC Power Systems on Ships. Energies 2022, 15, 258. https://doi.org/10.3390/en15010258
Bosich D, Giadrossi G, Pastore S, Sulligoi G. Weighted Bandwidth Method for Stability Assessment of Complex DC Power Systems on Ships. Energies. 2022; 15(1):258. https://doi.org/10.3390/en15010258
Chicago/Turabian StyleBosich, Daniele, Giovanni Giadrossi, Stefano Pastore, and Giorgio Sulligoi. 2022. "Weighted Bandwidth Method for Stability Assessment of Complex DC Power Systems on Ships" Energies 15, no. 1: 258. https://doi.org/10.3390/en15010258
APA StyleBosich, D., Giadrossi, G., Pastore, S., & Sulligoi, G. (2022). Weighted Bandwidth Method for Stability Assessment of Complex DC Power Systems on Ships. Energies, 15(1), 258. https://doi.org/10.3390/en15010258






