Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives
Abstract
:1. Introduction
- (1).
- An advanced modulation method for an H8 inverter is proposed to minimize the CMV variations between +Vdc/6 and −Vdc/6;
- (2).
- Proper switching operation of the series-connected switch in the H8 inverter is considered during the modulation sequence to completely eliminate the highest CMV of +Vdc/2 or −Vdc/2 even at the dead time interval;
- (3).
- At a high modulation range, a novel vector synthesis method is proposed, which is based on two sampling periods but in the same modulation manner;
- (4).
- As a result, both the CMCs and current THDs can be improved over the entire modulation range, compared with the conventional methods.
2. Review of Conventional Strategies
2.1. RSPWM, MRSPWM, and HMSPWM
2.2. Basic Operation of H8 Inverter
3. Proposed SVM-Based CMC Reduction Method
3.1. Low Modulation Range (MI ≤ 0.604)
3.1.1. Selection of Voltage Vector
3.1.2. Modulation Sequence
3.2. High Modulation Range (0.604 < MI ≤ 1)
3.2.1. Modulation Method Depending on Sub-Sectors
Sub-Sector 1: RSPWM Area
Sub-Sector 2: VA Area
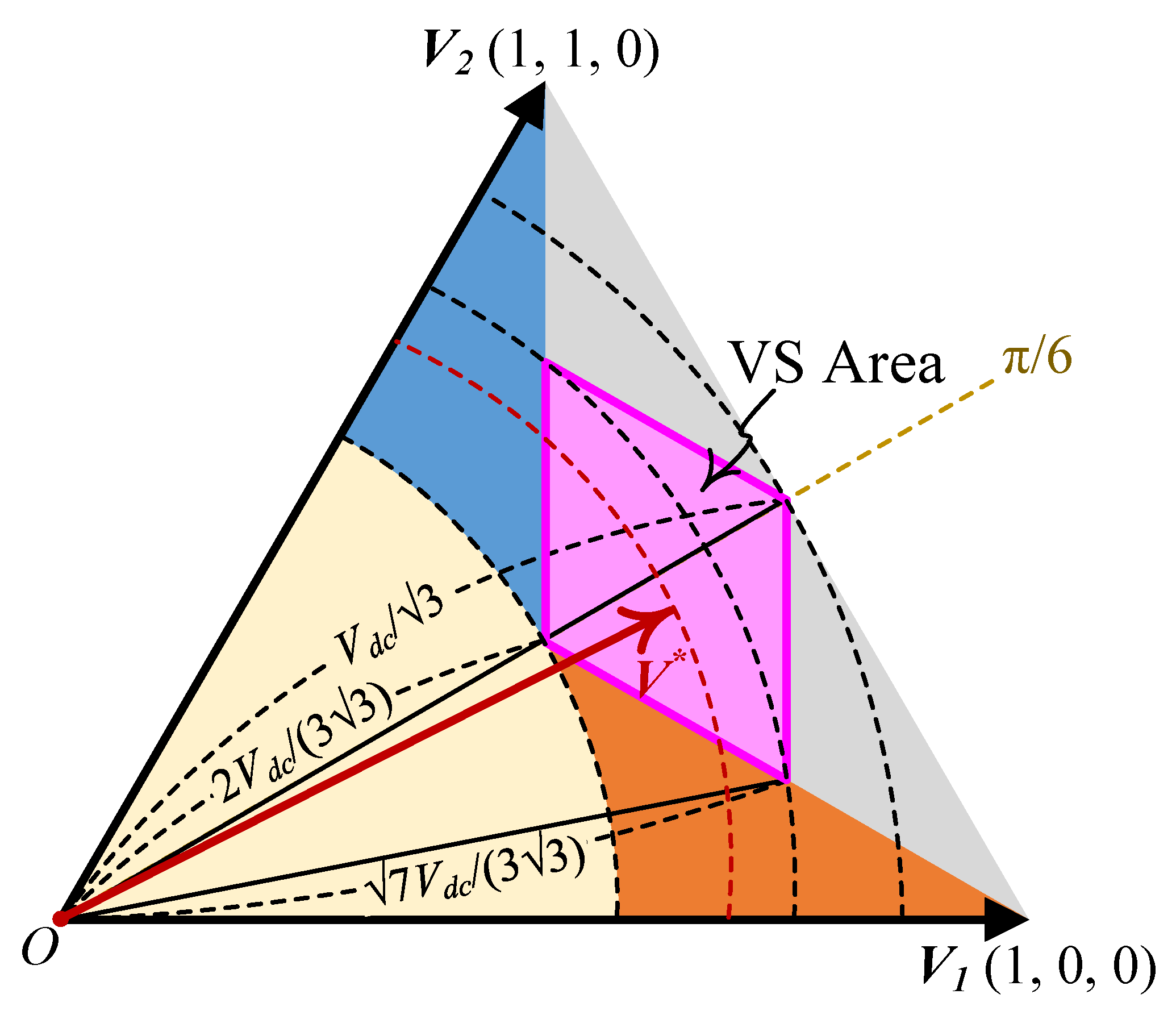
Sub-Sector 3: Vs. Area
3.2.2. Six-Step Operation
4. Simulation Results
4.1. Low Modulation Range (MI ≤ 0.604)
4.2. High Modulation Range (MI > 0.604)
5. Experimental Results
5.1. Low Modulation Range (MI ≤ 0.604)
5.2. High Modulation Range (MI > 0.604)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, D.; Li, S.; Wu, Y.; Choi, W.; Sarlioglu, B. Comparative Analysis on Conducted CM EMI Emission of Motor Drives: WBG Versus Si Devices. IEEE Trans. Ind. Electron. 2017, 64, 8353–8363. [Google Scholar] [CrossRef]
- Robles, E.; Fernandez, M.; Andreu, J.; Ibarra, E.; Ugalde, U. Advanced power inverter topologies and modulation techniques for common-mode voltage elimination in electric motor drive systems. Renew. Sustain. Energy Rev. 2021, 140, 110746. [Google Scholar] [CrossRef]
- Robles, E.; Fernandez, M.; Ibarra, E.; Andreu, J.; Kortabarria, I. Mitigation of Common Mode Voltage Issues in Electric Vehicle Drive Systems by Means of an Alternative AC-Decoupling Power Converter Topology. Energies 2019, 12, 3349. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhao, H. Review on pulse-width modulation strategies for common-mode voltage reduction in three-phase voltage-source inverters. IET Power Electron. 2016, 9, 2611–2620. [Google Scholar] [CrossRef]
- Chen, X.; Xu, D.; Liu, F.; Zhang, J. A Novel Inverter-Output Passive Filter for Reducing Both Differential- and Common-Mode dv/dt at the Motor Terminals in PWM Drive Systems. IEEE Trans. Ind. Electron. 2007, 54, 419–426. [Google Scholar] [CrossRef]
- Muetze, A.; Sullivan, C.R. Simplified Design of Common-Mode Chokes for Reduction of Motor Ground Currents in Inverter Drives. IEEE Trans. Ind. Appl. 2011, 47, 2570–2577. [Google Scholar] [CrossRef]
- Han, D.; Morris, C.T.; Lee, W.; Sarlioglu, B. Comparison Between Output CM Chokes for SiC Drive Operating at 20- and 200-kHz Switching Frequencies. IEEE Trans. Ind. Appl. 2017, 53, 2178–2188. [Google Scholar] [CrossRef]
- Lai, Y.-S. Investigations into the effects of PWM techniques on common mode voltage for inverter-controlled induction motor drives. In Proceedings of the 1999 Winter Meeting (Cat. No.99CH36233), New York, NY, USA, 31 January–4 February 1999; Volume 1, pp. 35–40. [Google Scholar] [CrossRef]
- Hava, A.M.; Ün, E. Performance Analysis of Reduced Common-Mode Voltage PWM Methods and Comparison with Standard PWM Methods for Three-Phase Voltage-Source Inverters. IEEE Trans. Power Electron. 2009, 24, 241–252. [Google Scholar] [CrossRef]
- Un, E.; Hava, A.M. A Near-State PWM Method with Reduced Switching Losses and Reduced Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Appl. 2009, 45, 782–793. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Testa, A. Reduction of common-mode currents in PWM inverter motor drives. IEEE Trans. Ind. Appl. 1999, 35, 469–476. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Scelba, G.; Testa, A. A novel space-vector modulation technique for common mode emissions reduction. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics, Bodrum, Turkey, 10–12 September 2007; pp. 199–204. [Google Scholar] [CrossRef]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Testa, A. Continuous PWM to square wave inverter control with low common mode emissions. In Proceedings of the PESC 98 Record. 29th Annual IEEE Power Electronics Specialists Conference (Cat. No.98CH36196), Fukuoka, Japan, 22 May 1998; Volume 1, pp. 871–877. [Google Scholar] [CrossRef]
- Cacciato, M.; De Caro, S.; Scarcella, G.; Scelba, G.; Testa, A. Improved space-vector modulation technique for common mode currents reduction. IET Power Electron. 2013, 6, 1248–1256. [Google Scholar] [CrossRef]
- Freddy, T.K.S.; Rahim, N.A.; Hew, W.-P.; Che, H.S. Modulation Techniques to Reduce Leakage Current in Three-Phase Transformerless H7 Photovoltaic Inverter. IEEE Trans. Ind. Electron. 2014, 62, 322–331. [Google Scholar] [CrossRef]
- Jung, W.-S.; Choo, K.-M.; Kim, J.-C.; Kim, W.-J.; Won, C.-Y. H7 Inverter Using Zener Diode with Model Predictive Current Control for Common-Mode Voltage Reduction in PMSM Drive System. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Morris, C.T.; Han, D.; Sarlioglu, B. Reduction of Common Mode Voltage and Conducted EMI Through Three-Phase Inverter Topology. IEEE Trans. Power Electron. 2017, 32, 1720–1724. [Google Scholar] [CrossRef]
- Xiang, Y.; Pei, X.; Wang, M.; Shi, P.; Kang, Y. An Improved H8 Topology for Common-Mode Voltage Reduction. IEEE Trans. Power Electron. 2018, 34, 5352–5361. [Google Scholar] [CrossRef]
- Concari, L.; Barater, D.; Buticchi, G.; Concari, C.; Liserre, M. H8 Inverter for Common-Mode Voltage Reduction in Electric Drives. IEEE Trans. Ind. Appl. 2016, 52, 4010–4019. [Google Scholar] [CrossRef] [Green Version]
- Concari, L.; Barater, D.; Toscani, A.; Concari, C.; Franceschini, G.; Buticchi, G.; Liserre, M.; Zhang, H. Assessment of Efficiency and Reliability of Wide Band-Gap Based H8 Inverter in Electric Vehicle Applications. Energies 2019, 12, 1922. [Google Scholar] [CrossRef] [Green Version]
- Jeong, W.-S.; Choo, K.-M.; Lee, J.-H.; Won, C.-Y. Space Vector-Based Common-Mode Currents Reduction Method for H8 Inverter Topology in Low-Voltage DC Microgrid. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–7. [Google Scholar] [CrossRef]


























| Voltage Vector | Switching State (Sa, Sb, Sc) 1 | CMV Level 2 |
|---|---|---|
| V0 | (0, 0, 0) | −Vdc/2 |
| V1 | (1, 0, 0) | −Vdc/6 |
| V2 | (1, 1, 0) | +Vdc/6 |
| V3 | (0, 1, 0) | −Vdc/6 |
| V4 | (0, 1, 1) | +Vdc/6 |
| V5 | (0, 0, 1) | −Vdc/6 |
| V6 | (1, 0, 1) | +Vdc/6 |
| V7 | (1, 1, 1) | +Vdc/2 |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Vdc | DC-Link Voltage | 70 | V |
| Ts | Sampling Period | 250 | μs |
| fs | Sampling Frequency | 8 | kHz |
| Td | Dead-Time Interval | 4 | μs |
| Prate | Rated Power of SPMSM | 750 | W |
| Vdc_rate | Rated DC-Link Voltage | 200 | V |
| ωrate | Rated Speed | 3000 | rpm |
| Irate | Rated Current | 4.4 | A |
| Trate | Rated Torque | 2.39 | Nm |
| p | Number of Poles | 10 | - |
| Rs | Stator Resistance | 0.6333 | Ω |
| Ls | Stator Inductance | 2.08 | mH |
| Vpk/krpm | Peak Line-to-Line Back EMF Constant | 45 | V/krpm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, W.-S.; Lee, Y.-S.; Lee, J.-H.; Lee, C.-H.; Won, C.-Y. Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives. Energies 2022, 15, 266. https://doi.org/10.3390/en15010266
Jeong W-S, Lee Y-S, Lee J-H, Lee C-H, Won C-Y. Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives. Energies. 2022; 15(1):266. https://doi.org/10.3390/en15010266
Chicago/Turabian StyleJeong, Won-Sang, Yoon-Seong Lee, Jung-Hyo Lee, Chang-Hee Lee, and Chung-Yuen Won. 2022. "Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives" Energies 15, no. 1: 266. https://doi.org/10.3390/en15010266
APA StyleJeong, W.-S., Lee, Y.-S., Lee, J.-H., Lee, C.-H., & Won, C.-Y. (2022). Space Vector Modulation (SVM)-Based Common-Mode Current (CMC) Reduction Method of H8 Inverter for Permanent Magnet Synchronous Motor (PMSM) Drives. Energies, 15(1), 266. https://doi.org/10.3390/en15010266






