Nonlinear Modeling of Dynamic Characteristics of Pump-Turbine
Abstract
:1. Introduction
2. Constructing the Mathematical Model for Pump-Turbine Governing System
2.1. Pump-Turbine Model
2.1.1. Research Method of Mathematical Model of Hydraulic Turbine
2.1.2. Derivation of Nonlinear Model of Pump-Turbine
2.2. Generator Model
2.3. Diversion Pipeline Model
2.4. Governor Equation
3. Obtaining the Transfer Coefficient for Pump-Turbine in Generating Mode
3.1. Calculation Method of Transfer Coefficient for Pump-Turbine
3.2. Acquisition of Transfer Coefficient for Pump-Turbine
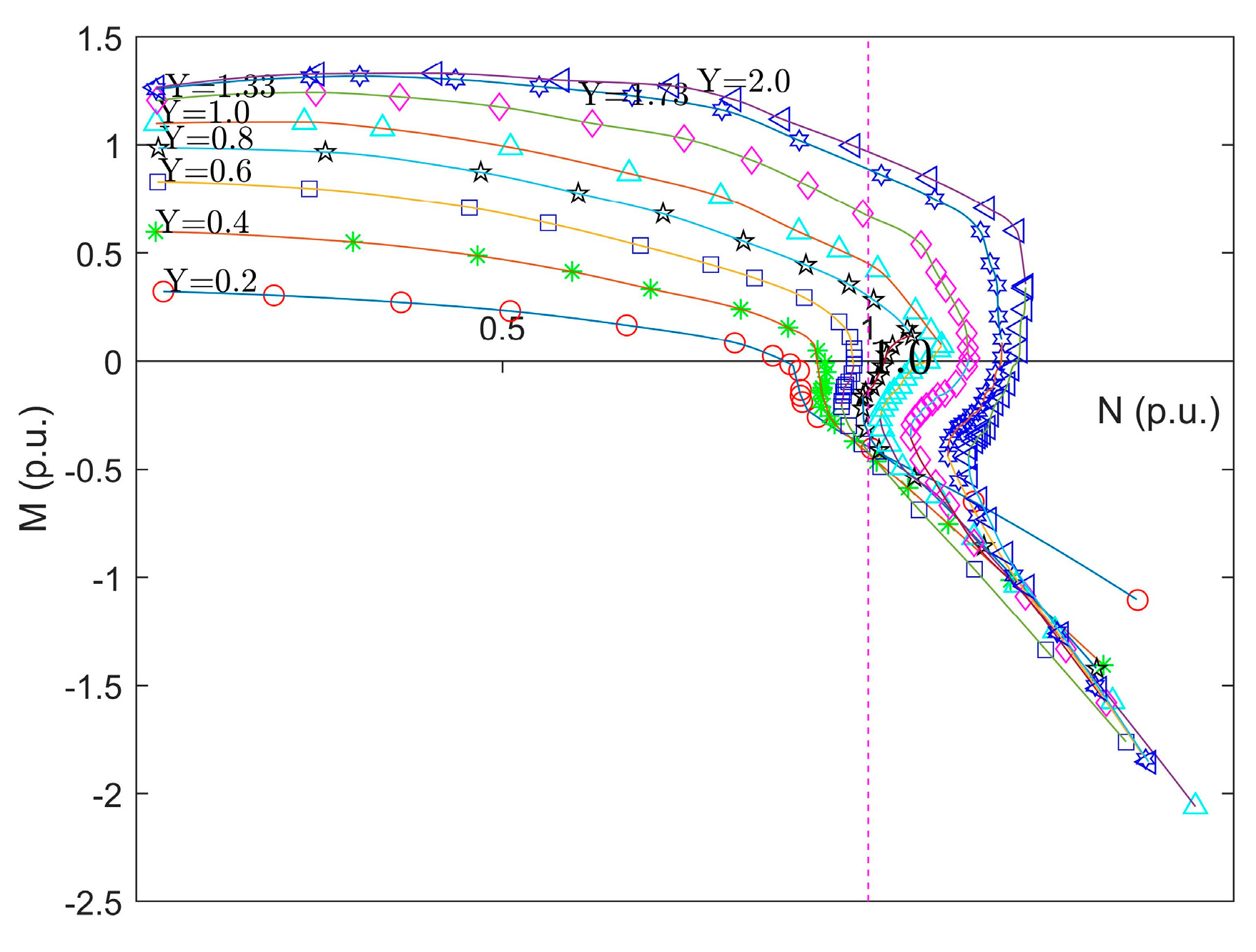
3.2.1. Drawing of Complete Characteristic Curve for Pump-Turbine
3.2.2. Acquisition of Transfer Coefficients
4. Nonlinear Dynamics Analysis of the System
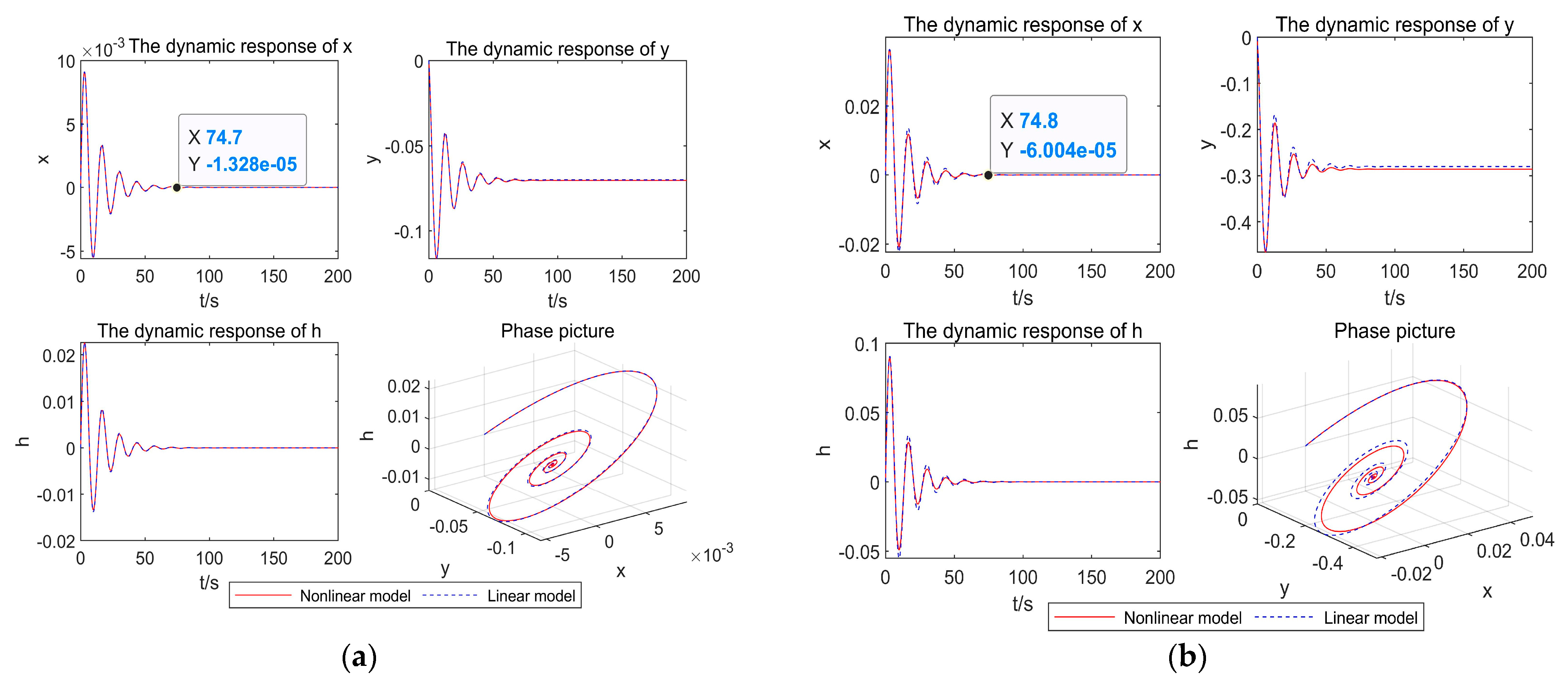
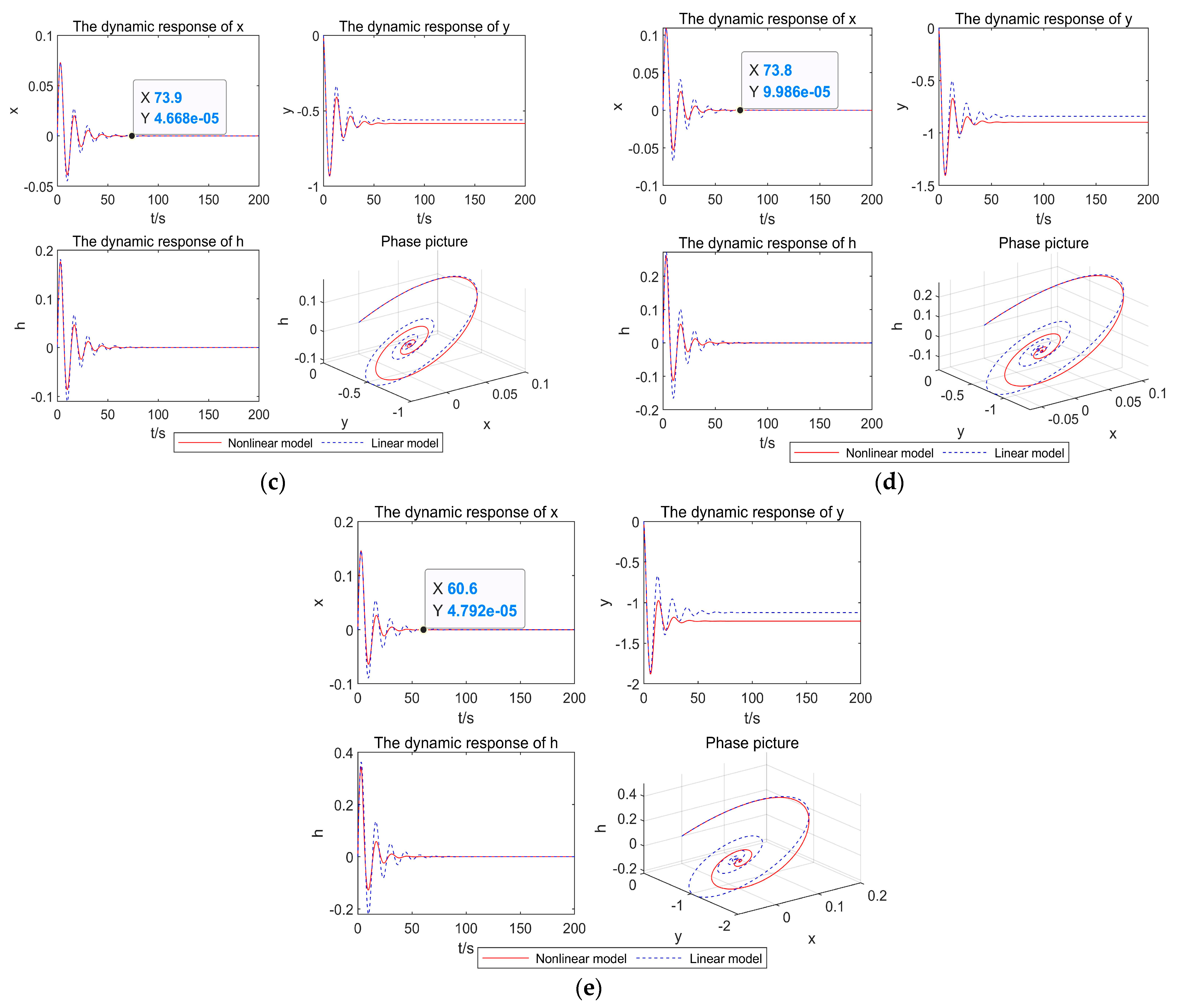
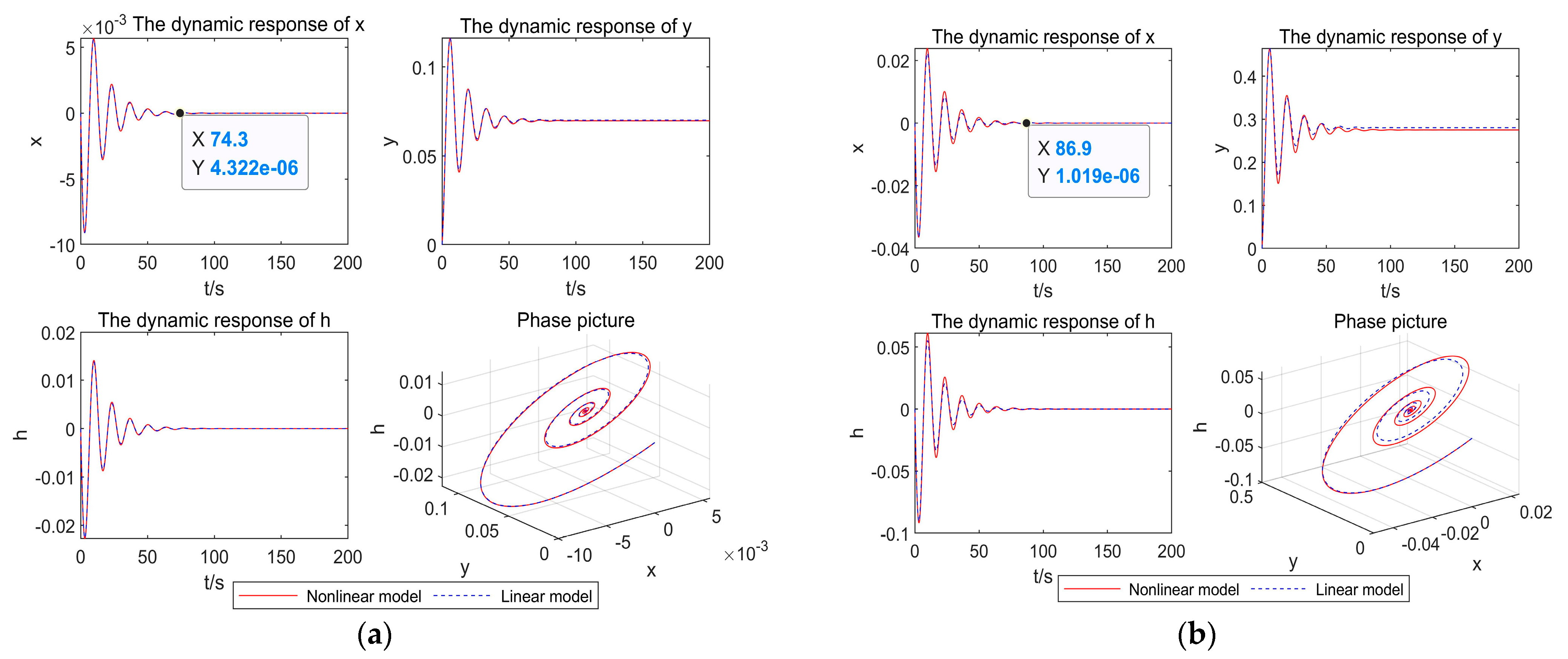
4.1. Nonlinear Dynamics Analysis of the System under Load Rejection Conditions
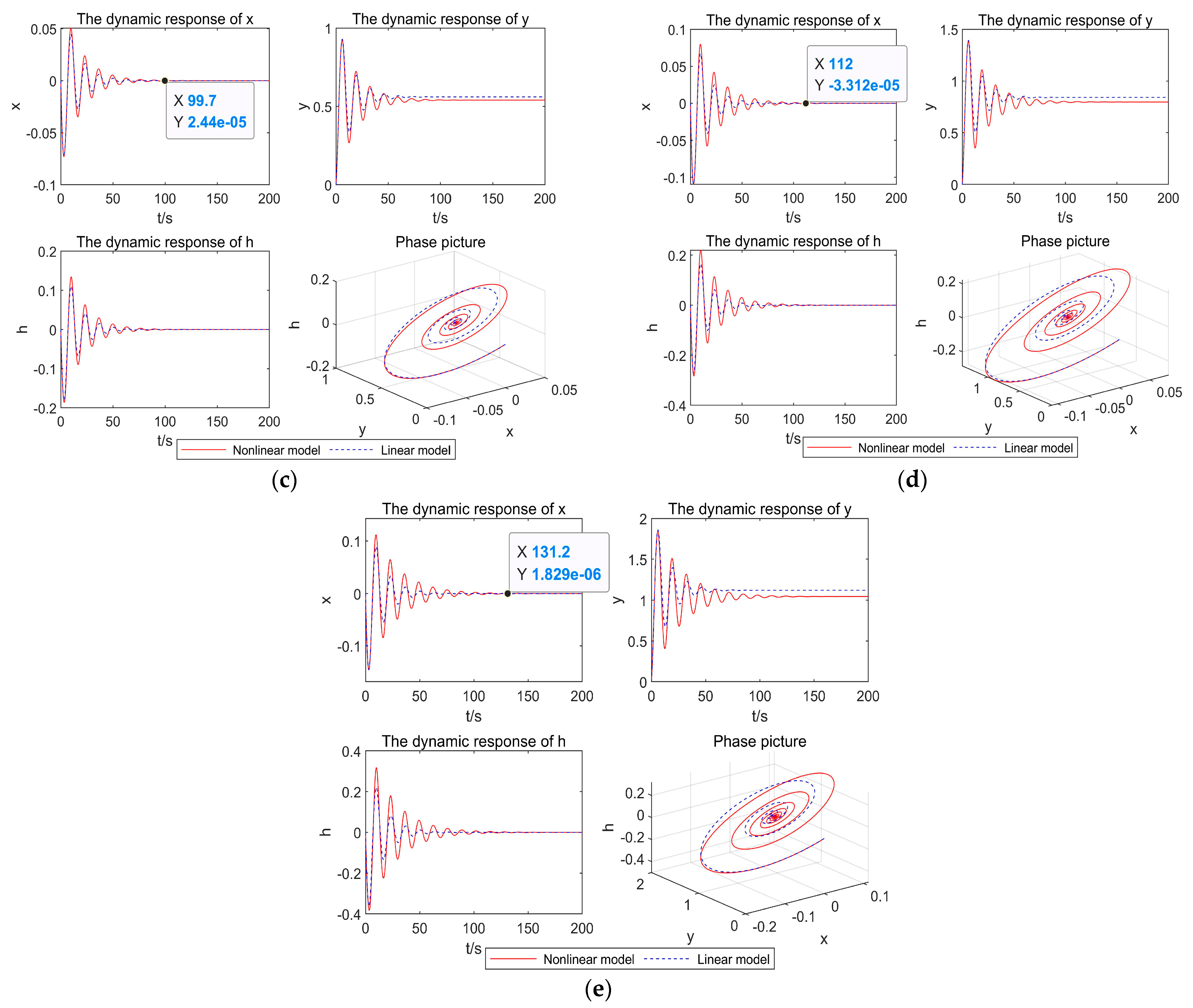
4.2. Nonlinear Dynamics Analysis of the System under Load Increasing Conditions
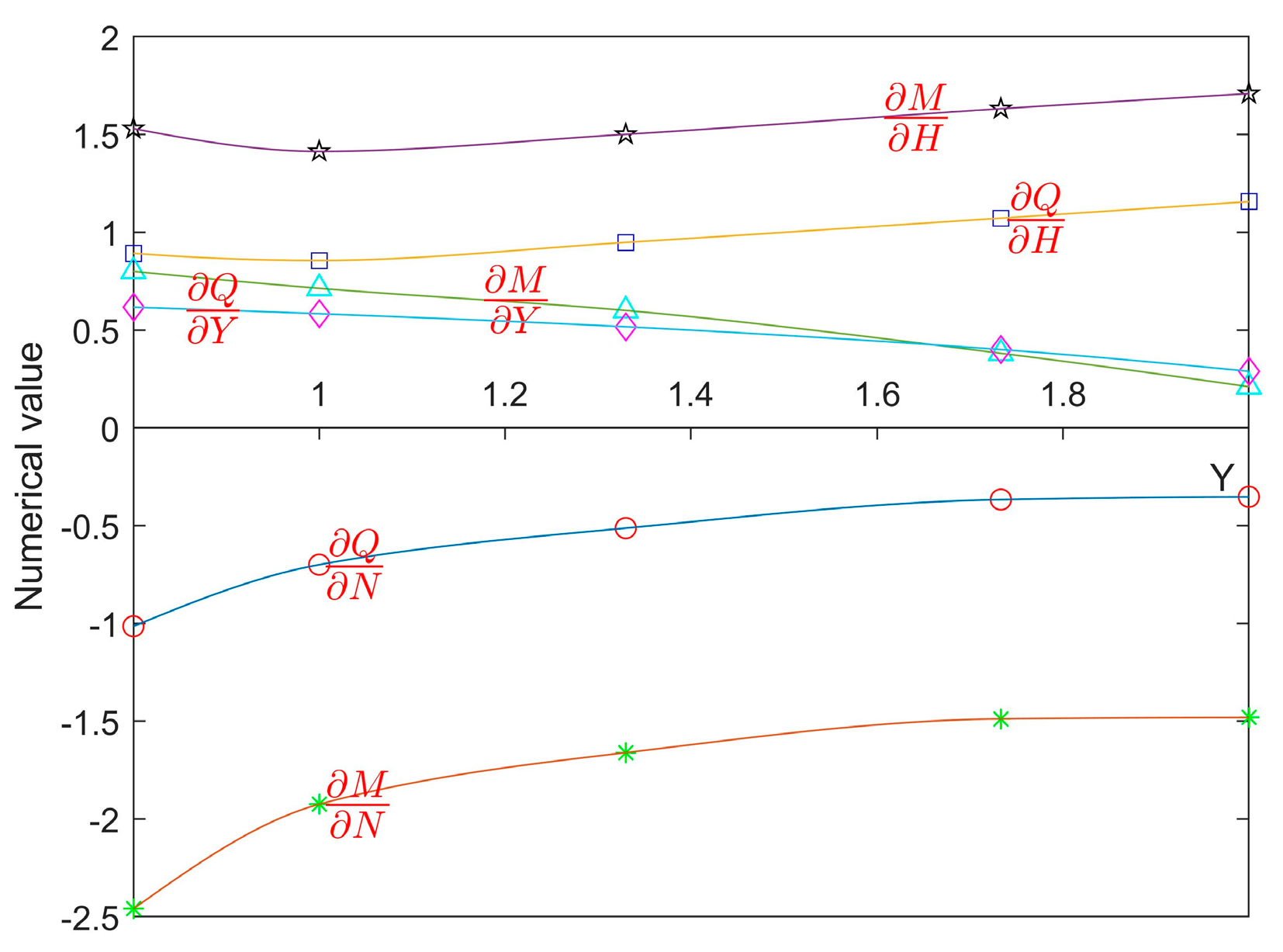
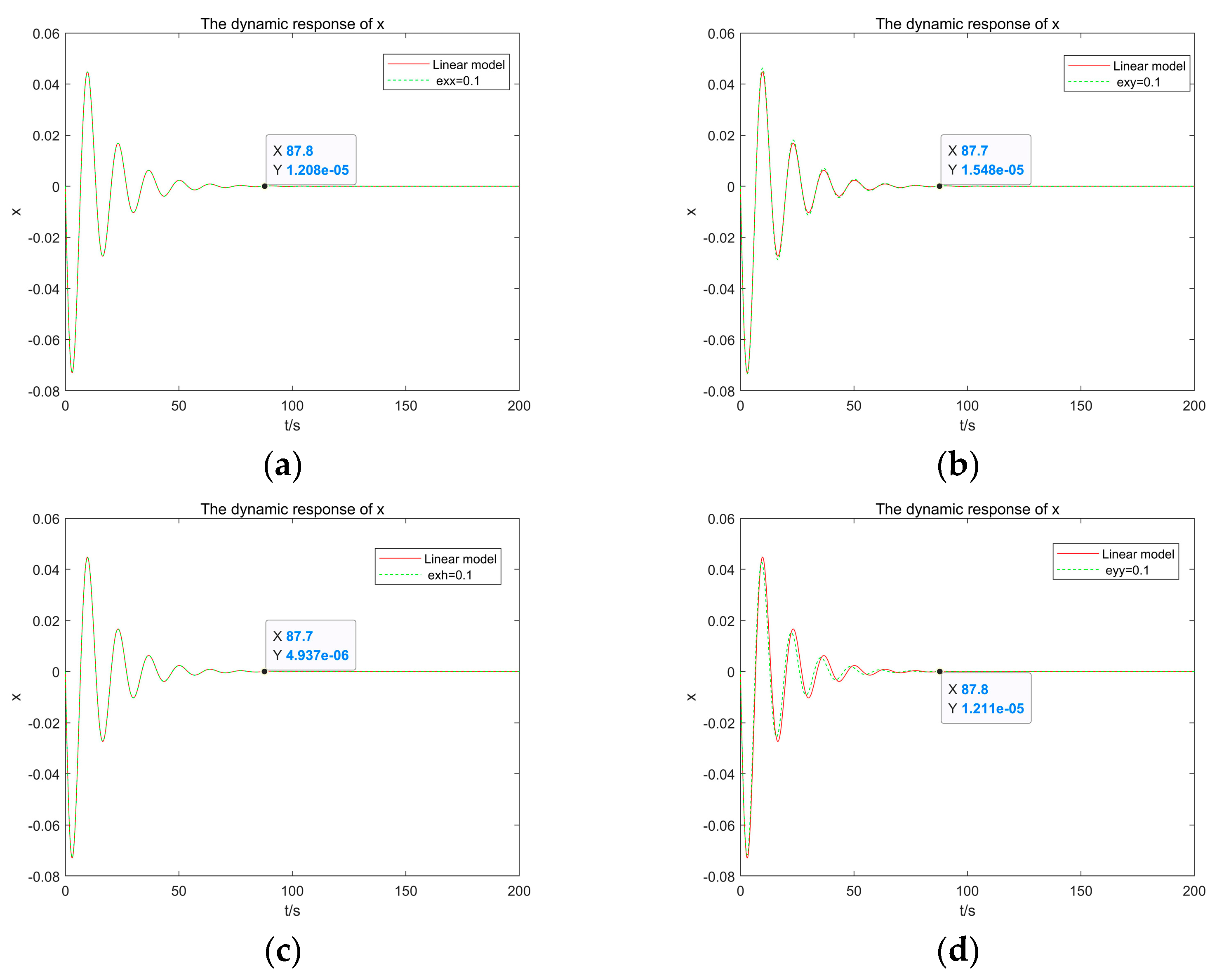
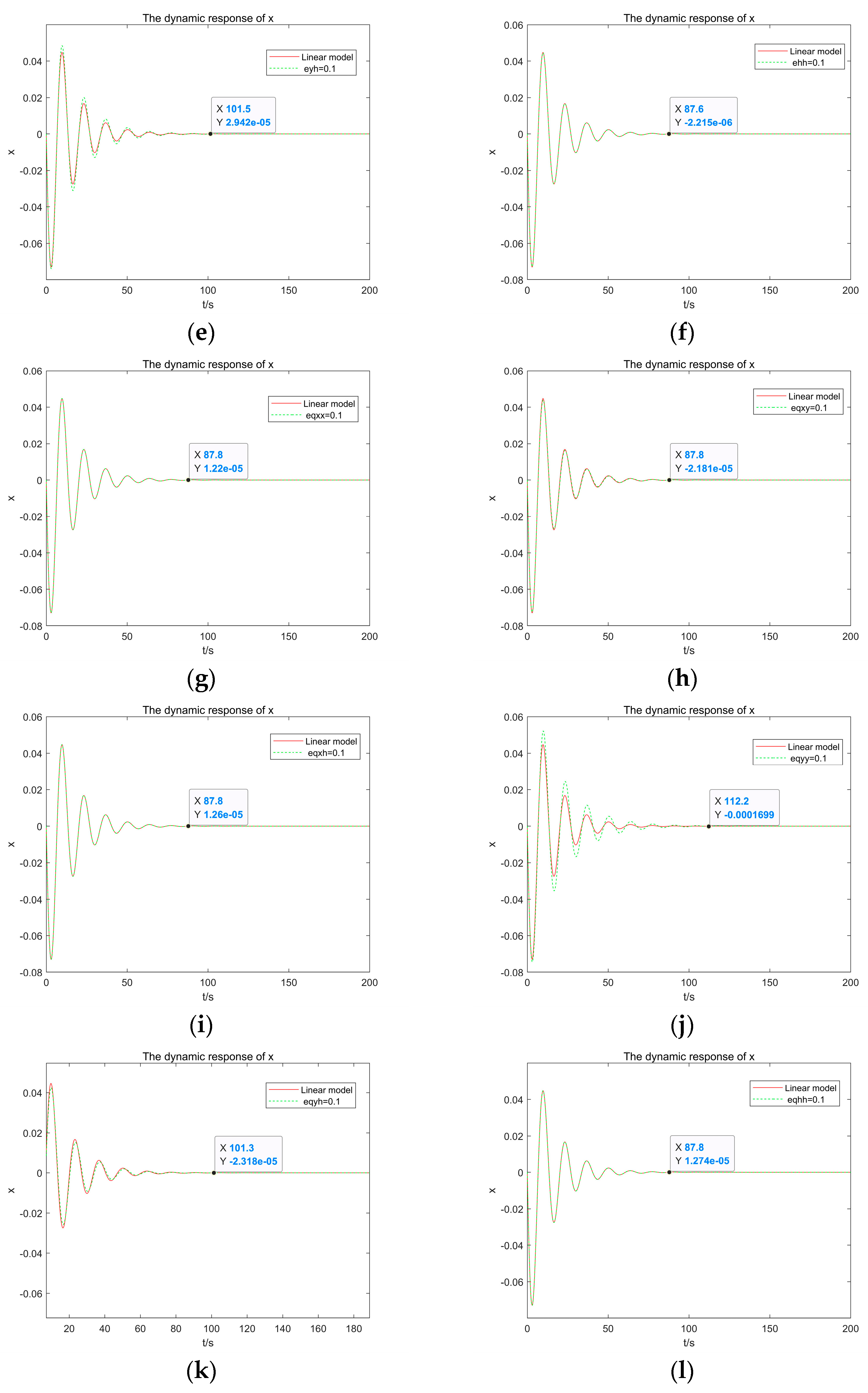
4.3. Sensitivity Analysis of Second Derivative Terms
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bitew, G.T.; Han, M.; Mekonnen, S.A.; Patrobers, S.; Khan, Z.W.; Tuan, L.K. Pumped energy storage system technology and its AC–DC interface topology, modelling and control analysis: A review. J. Eng. 2019, 2019, 705–710. [Google Scholar] [CrossRef]
- Xiong, Y. Analysis on Model Test of Pump Turbine for Fujian Zhouning Pumped-Storage Power Station. Hydropower Pumped Storage 2020, 6, 65–69. [Google Scholar]
- Cai, W.J.; Wang, Y.T.; Shi, H.D.; Zhang, M.J.; Xu, Q. Study on Optimization Strategy of Speed and Opening of Variable Speed Pumped Storage Unit. Large Electr. Mach. Hydraul. Turbine 2020, 4, 58–63. [Google Scholar]
- Liu, D.M.; Xu, W.L.; Zhao, Y.Z. Study on Cavitation and Operation Characteristics of Variable Speed Pumped Storage Units. Hydropower Pumped Storage 2020, 6, 36–45. [Google Scholar]
- Wang, L.K.; Lu, J.L.; Liao, W.L.; Zhao, Y.P.; Ji, Q.F. Numerical Analysis of the Hydraulic Force of a Pump Turbine under Partial Load Conditions in Turbine Mode; IOP Publishing: Bristol, UK, 2019; Volume 240, p. 72041. [Google Scholar]
- Lv, C.; Xu, Y.; Wu, X.; Zhang, Q. Characteristic Analysis and Optimal Regulation of Primary Frequency Regulation Condition in Low Water Head Area Based on Hydraulic-Mechanical-Electrical Coupling Model of Pumped Storage Unit. Complexity 2020, 2020, 6161784. [Google Scholar] [CrossRef] [Green Version]
- Men, C.S. Study on Dynamic Characteristics of Regulating System Based on Hydro-Turbine Compound Model Tocom-binedinternal Model and External Model. Ph.D. Thesis, Xi’an University of Technology, Xian, China, 2018. [Google Scholar]
- Zhao, W.; Shi, T.; Wang, L.; Cao, Q.; Zhang, H. An adaptive hybrid atom search optimization with particle swarm optimization and its application to optimal no-load PID design of hydro-turbine governor. J. Comput. Des. Eng. 2021, 8, 1204–1233. [Google Scholar] [CrossRef]
- Xu, Y.H. Study on Parameter Identification and Control Optimization of Governing System for Pumped Storage Unit. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2017. [Google Scholar]
- Zhang, C. Study on Nonlinear Identification and Control Optimization of Pumped Turbine Governing System. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Xu, X.Y.; Guo, W.C. Stability of Speed Regulating System of Hydropower Station under Effect of Nonlinear Turbine Charac-teristics. Hydropower Energy Sci. 2020, 38, 121–125. [Google Scholar]
- Liu, J.Y. Characteristic Analysis of Typical Transient of Pumped Storage Power Station Based on Characteristic Curve. Master’s Thesis, Northwest Agriculture and Forestry University, Shanxi, China, 2017. [Google Scholar]
- Zhou, J.; Zhao, Z.; Zhang, C.; Li, C.; Xu, Y. A Real-Time Accurate Model and Its Predictive Fuzzy PID Controller for Pumped Storage Unit via Error Compensation. Energies 2017, 11, 35. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. Transient Dynamical Modeling and Stability Analysis of Hydroelectric Powersystems. Ph.D. Thesis, Northwest Agriculture and Forestry University, Shanxi, China, 2019. [Google Scholar]
- Zhao, Z.; Yang, J.; Yang, W.; Hu, J.; Chen, M. A coordinated optimization framework for flexible operation of pumped storage hydropower system: Nonlinear modeling, strategy optimization and decision making. Energy Convers. Manag. 2019, 194, 75–93. [Google Scholar] [CrossRef]
- Fang, Z. Research on intelligent control of hydraulic turbine governing system. Intell. City 2021, 7, 49–50. [Google Scholar]
- Xia, X.; Ji, J.; Li, C.-S.; Xue, X.; Wang, X.; Zhang, C. Multiobjective Optimal Control for Hydraulic Turbine Governing System Based on an Improved MOGWO Algorithm. Complexity 2019, 2019, 3745924. [Google Scholar] [CrossRef]
- Piraisoodi, T.; Siluvairaj, W.I.M.; Kappuva, M.A.K. Multi-objective robust fuzzy fractional order proportional–integral–derivative controller design for nonlinear hydraulic turbine governing system using evolutionary computation techniques. Expert Syst. 2019, 36, e12366. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, W.; Wang, G.H.; Xia, C.; Li, Z.Q.; Yu, D.H.; Ma, C.Y. Source-grid Coordination of Hydraulic Turbine Governing System. Power Syst. Technol. 2021, 45, 1852–1861. [Google Scholar]
- Chang, Y.; Su, H.C.; Li, X.Q.; Yang, Y.Q.; Hou, Y.Z. Analysis of Transient Stability Methods of Power System. Yunnan Electr. Power Technol. 2007, 2, 1–4. [Google Scholar]
- Zhang, J.L.; Ou, J.P.; Yu, D.R. Rule self-adjusting fuzzy control method based on phase plane trajectory characteris-tics. Control. Theory Appl. 2003, 4, 607–611. [Google Scholar]
- Zhang, H.; Su, D.; Guo, P.; Zhang, B.; Mao, Z. Stochastic dynamic modeling and simulation of a pump-turbine in load-rejection process. J. Energy Storage 2021, 35, 102196. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.; Zhang, H.; Wang, F. Modeling and stability analysis of a fractional-order Francis hydro-turbine governing system. Chaos Solitons Fractals 2015, 75, 50–61. [Google Scholar] [CrossRef]
- Chen, D.; Ding, C.; Do, Y.; Ma, X.; Zhao, H.; Wang, Y. Nonlinear dynamic analysis for a Francis hydro-turbine governing system and its control. J. Frankl. Inst. 2014, 351, 4596–4618. [Google Scholar] [CrossRef]
- Nagode, K.; Škrjanc, I. Modelling and Internal Fuzzy Model Power Control of a Francis Water Turbine. Energies 2014, 7, 874–889. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Yuan, X.; Yuan, Y.; Chen, Z.; Li, Y. Nonlinear dynamic analysis and robust controller design for Francis hydraulic turbine regulating system with a straight-tube surge tank. Mech. Syst. Signal Process. 2017, 85, 927–946. [Google Scholar] [CrossRef]
- Li, G.; Wu, X.; Cui, W.; Qiu, W.; Zhou, T. Study of Hydraulic Disturbance of Pumped Storage Unit. IOP Conf. Ser. Earth Environ. Sci. 2021, 768, 12010. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Xu, B.; Wang, F. Nonlinear modeling and dynamic analysis of hydro-turbine governing system in the process of load rejection transient. Energy Convers. Manag. 2015, 90, 128–137. [Google Scholar] [CrossRef]
- Guo, W.; Yang, J.; Wang, M.; Lai, X. Nonlinear modeling and stability analysis of hydro-turbine governing system with slopin-g ceiling tailrace tunnel under load disturbance. Energy Convers. Manag. 2015, 106, 127–138. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Wang, Z.; Zhang, N.; Peng, B. Load Frequency Control of a Novel Renewable Energy Integrated Micro-Grid Containing Pumped Hydropower Energy Storage. IEEE Access 2018, 6, 29067–29077. [Google Scholar] [CrossRef]
- Zhang, N. Study on Nonlinear Model Parameter Identification and Control Optimization of Pumped Storage Unit Governing System. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Li, H.; Chen, D.; Zhang, H.; Wu, C.; Wang, X. Hamiltonian analysis of a hydro-energy generation system in the transient of sudden load increasing. Appl. Energy 2017, 185, 244–253. [Google Scholar] [CrossRef] [Green Version]
- IEEE Working Gourp. Hydraulic turbine and turbine control models for system dynamic studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar] [CrossRef]
- Chen, D.; Ding, C.; Ma, X.; Yuan, P.; Ba, D. Nonlinear dynamical analysis of hydro-turbine governing system with a surge tank. Appl. Math. Model. 2013, 37, 7611–7623. [Google Scholar] [CrossRef]
- Wang, L.; Han, Q.; Chen, D.; Wu, C.; Wang, X. Non-linear modelling and stability analysis of the PTGS at pump mode. IET Renew. Power Gener. 2017, 11, 827–836. [Google Scholar] [CrossRef]
- Li, H.; Chen, D.; Zhang, H.; Wang, F.; Ba, D. Nonlinear modeling and dynamic analysis of a hydro-turbine governing system in the process of sudden load increase transient. Mech. Syst. Signal Process. 2016, 80, 414–428. [Google Scholar] [CrossRef] [Green Version]
- Ling, D.J.; Shen, Z.Y. Bifurcation analysis of hydro-turbine governing system with saturation nonlinearity. J. Hydro Electr. Eng. 2007, 26, 126–131. [Google Scholar]
- Wei, S.P. Turbine Regulation; Huazhong University of Science and Technology Press: Wuhan, China, 2009. [Google Scholar]
- Wu, R.Q.; Chen, J.Z. Hydraulic Transition Process of Hydropower Station; China Water Conservancy and Hydropower Press: Beijing, China, 1996. [Google Scholar]
- Wu, Q.Q. A Dynamic Model Establishment and Numerical Simulation of Hydraulic-Mechanical-Electric-Structural System for Hydropower Station. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2017. [Google Scholar]
- Zhou, X.J.; Ni, J.B.; Han, W.F.; Yang, J.; Ding, J.H. Influence of pump-turbine complete characteristic curve on transient process trajectory. Water Resour. Hydropower Eng. 2021, 52, 85–93. [Google Scholar]
- Chen, Y.; Wang, Y.; Dai, L.Q. Numerical treatment of synthetic characteristic curves in turbine modeling. J. Water Resour. Water Eng. 2020, 31, 155–161. [Google Scholar]
- Zheng, Y.; Chen, Q.; Liu, W.; Yan, D. A predictive governing control method of the pumped-storage unit based on lumped-parameter model equivalence. IOP Conf. Series Earth Environ. Sci. 2021, 774, 012141. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, J. Transition Process of Hydraulic Units; Peking University Press: Beijing, China, 2008. [Google Scholar]
- Izena, A.; Kihara, H.; Shimojo, T.; Hirayama, K.; Furukawa, N.; Kageyama, T.; Goto, T.; Okamura, C. Practical hydraulic turbine model. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Quebec, QC, Canada, 18–22 June 2006; p. 7. [Google Scholar]
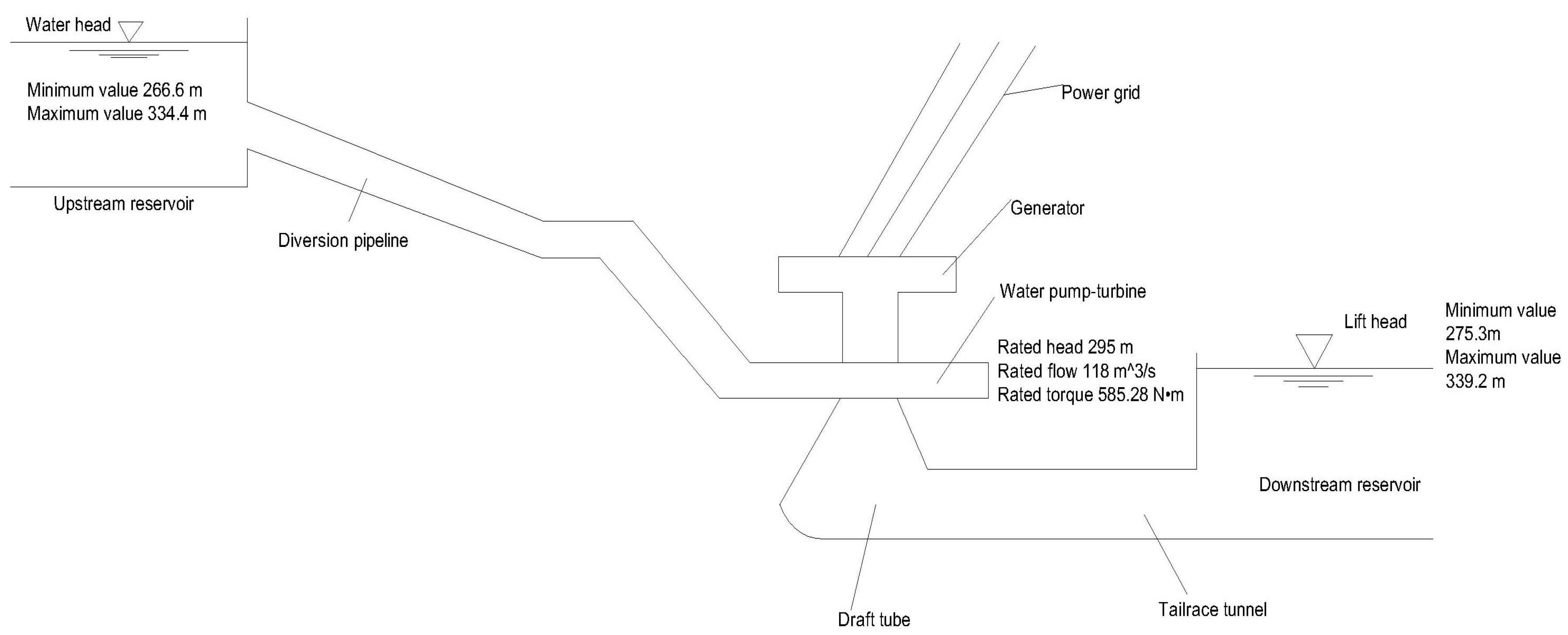


| Parameter | Value | |
|---|---|---|
| Category | Maximum value | Minimum value |
| Water head | 334.4 m | 266.6 m |
| Lift head | 339.2 m | 275.3 m |
| Rated head | 295 m | |
| Rated flow | 118 m3·s−1 | |
| Rated torque | 585.28 N·m | |
| Operating Point | Time/s | |
|---|---|---|
| Category | Linear model | Nonlinear model |
| 5% | 74.8 | 74.7 |
| 20% | 75.1 | 74.8 |
| 40% | 74.5 | 73.9 |
| 60% | 74.4 | 73.8 |
| 80% | 73.9 | 60.6 |
| Operating Point | Time/s | |
|---|---|---|
| Category | Linear Model | Nonlinear Model |
| 5% | 67.4 | 74.3 |
| 20% | 76.9 | 86.9 |
| 40% | 87.8 | 99.7 |
| 60% | 80.8 | 112 |
| 80% | 67.4 | 131.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, K.; Zhao, W. Nonlinear Modeling of Dynamic Characteristics of Pump-Turbine. Energies 2022, 15, 297. https://doi.org/10.3390/en15010297
Wang L, Zhang K, Zhao W. Nonlinear Modeling of Dynamic Characteristics of Pump-Turbine. Energies. 2022; 15(1):297. https://doi.org/10.3390/en15010297
Chicago/Turabian StyleWang, Liying, Kaidi Zhang, and Weiguo Zhao. 2022. "Nonlinear Modeling of Dynamic Characteristics of Pump-Turbine" Energies 15, no. 1: 297. https://doi.org/10.3390/en15010297
APA StyleWang, L., Zhang, K., & Zhao, W. (2022). Nonlinear Modeling of Dynamic Characteristics of Pump-Turbine. Energies, 15(1), 297. https://doi.org/10.3390/en15010297






