Modeling of Internal Combustion Engine Ignition Systems with a Circuit Containing Fractional-Order Elements †
Abstract
:1. Introduction
2. Selected Elements of Fractional Order Calculus
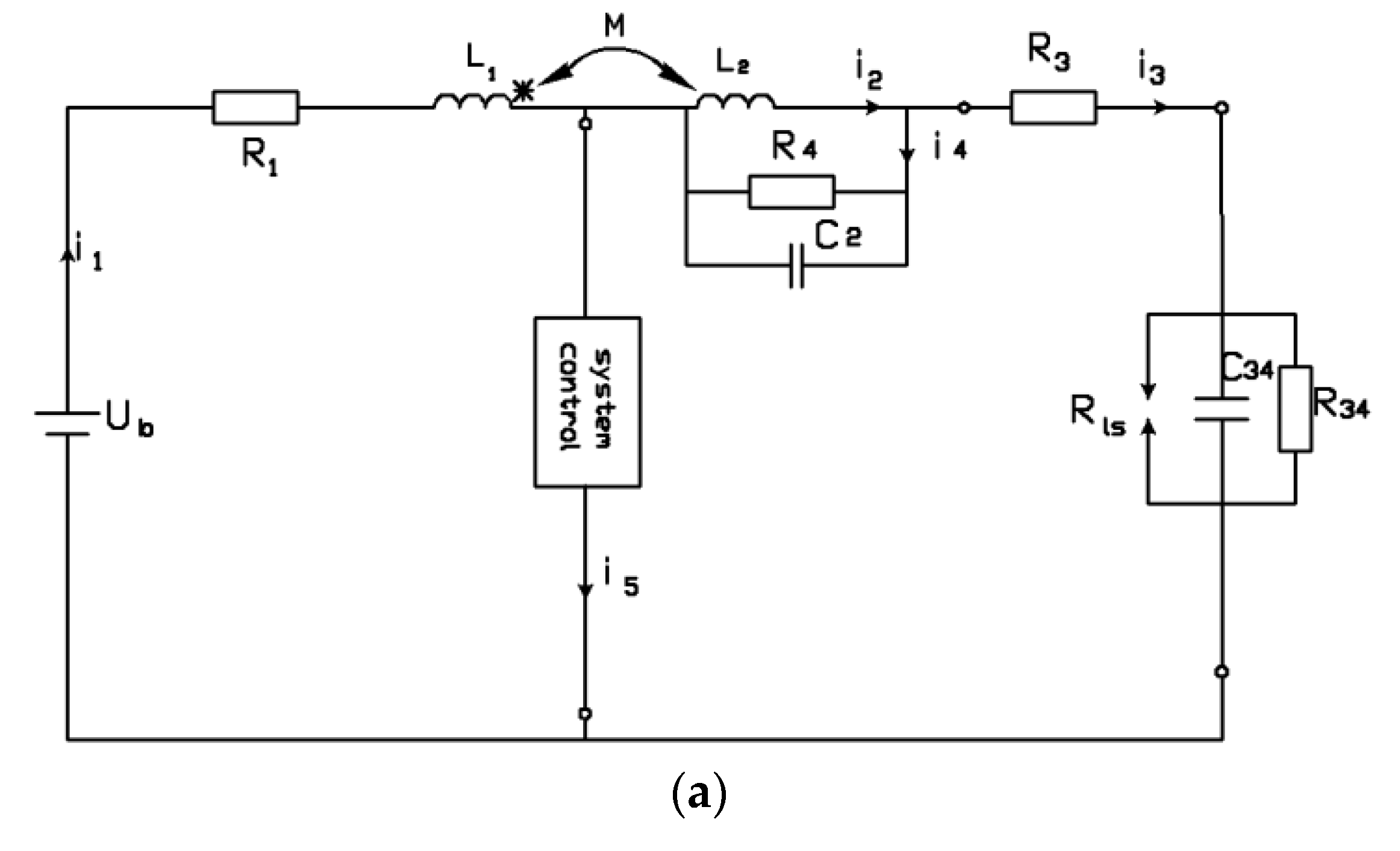
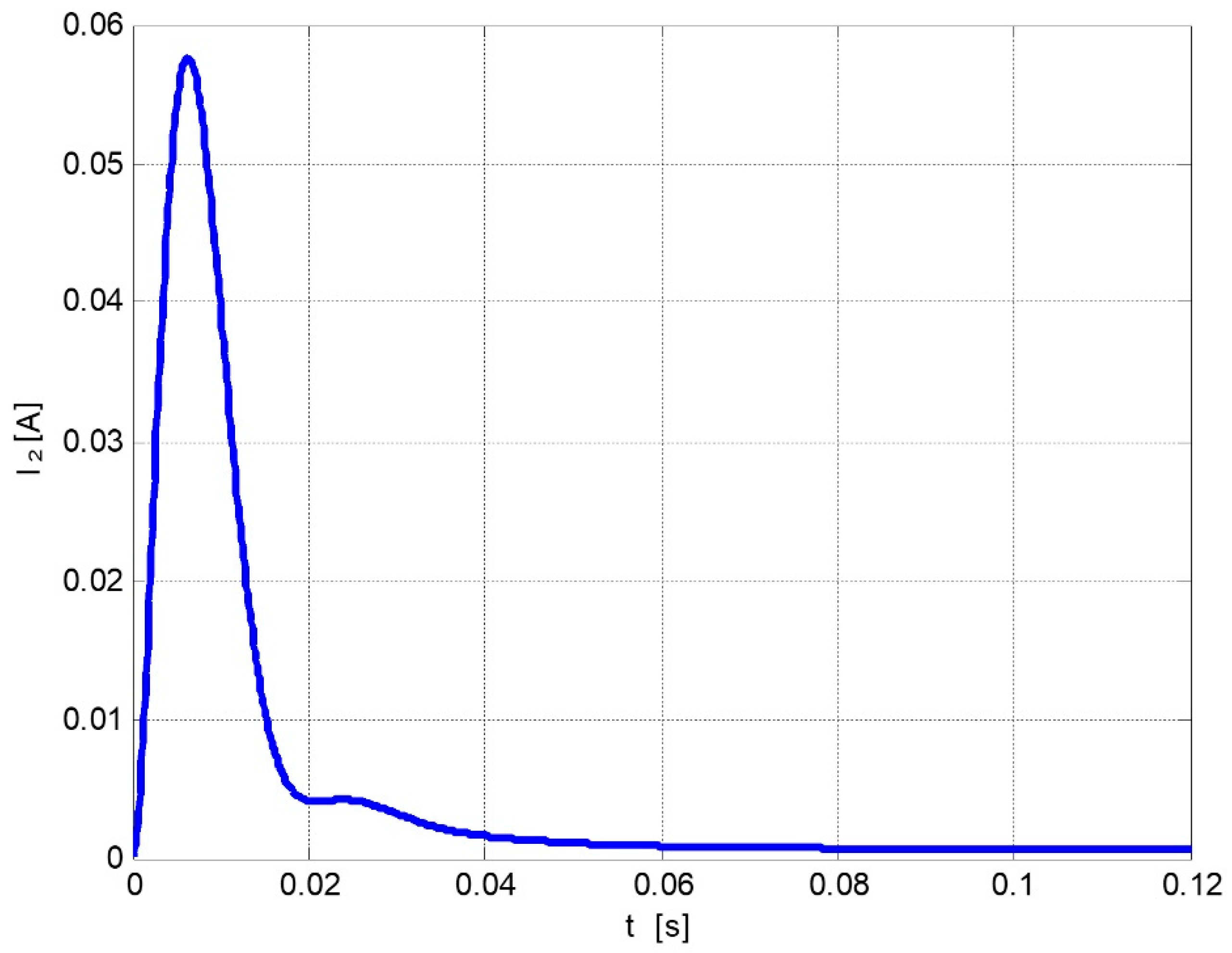
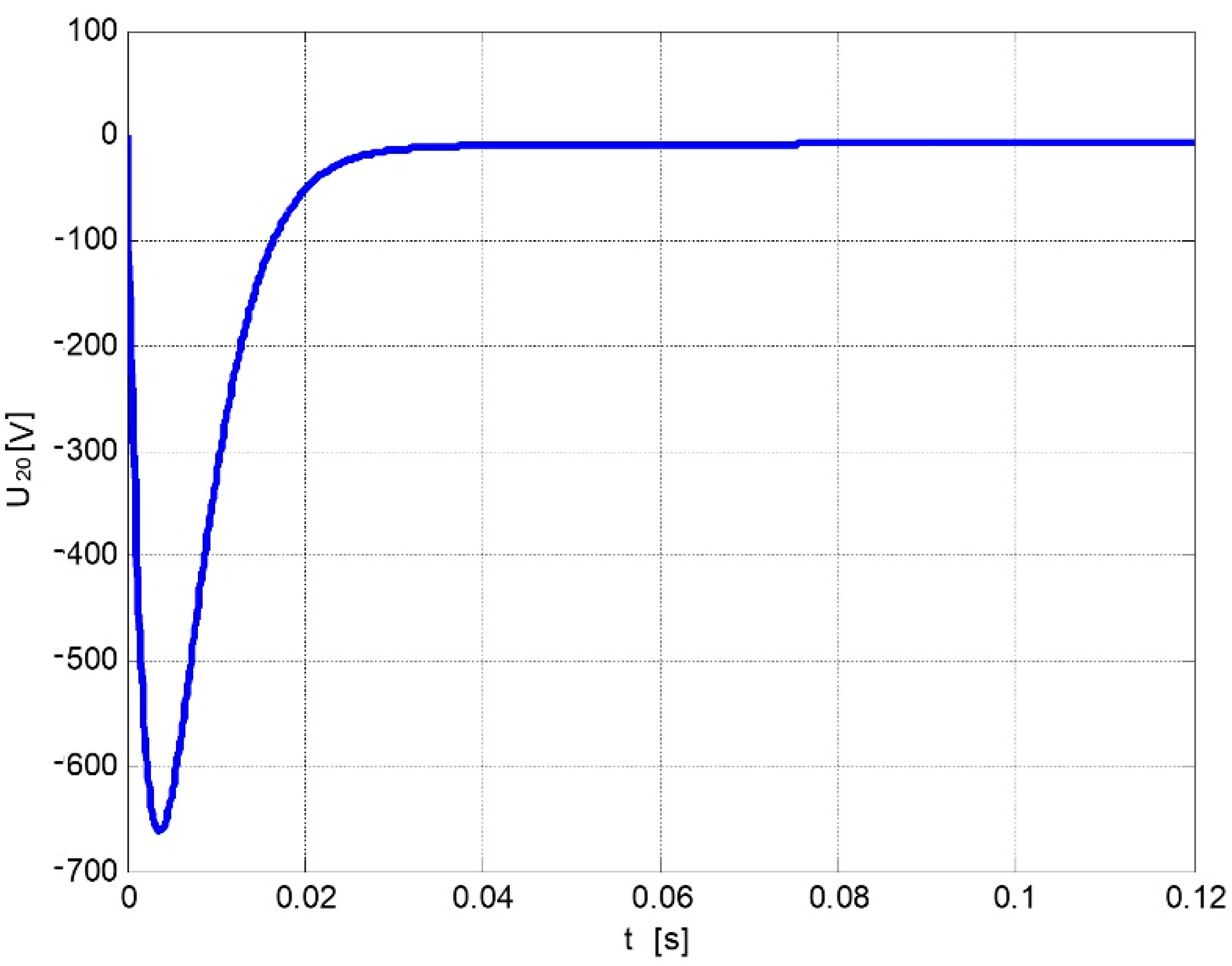
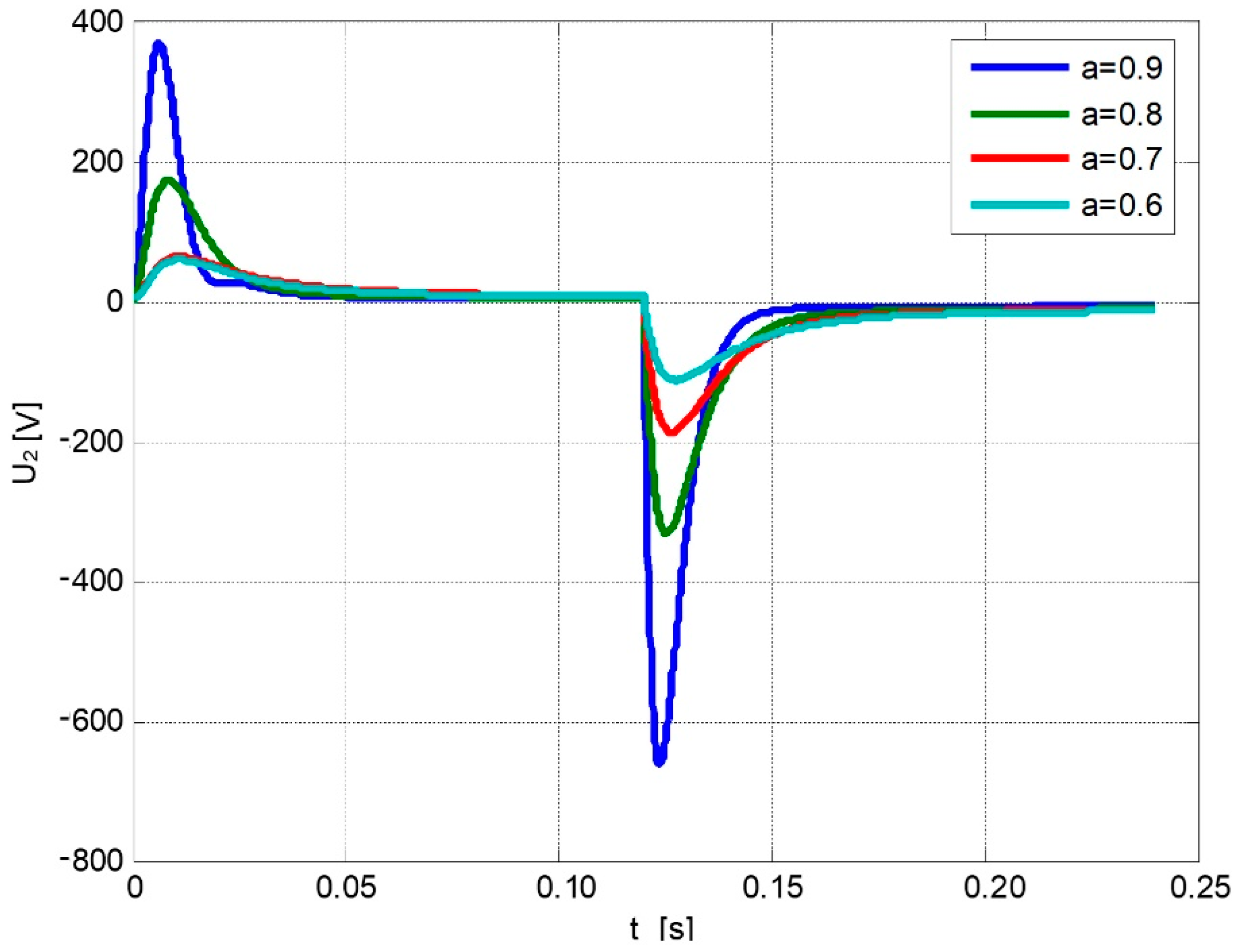
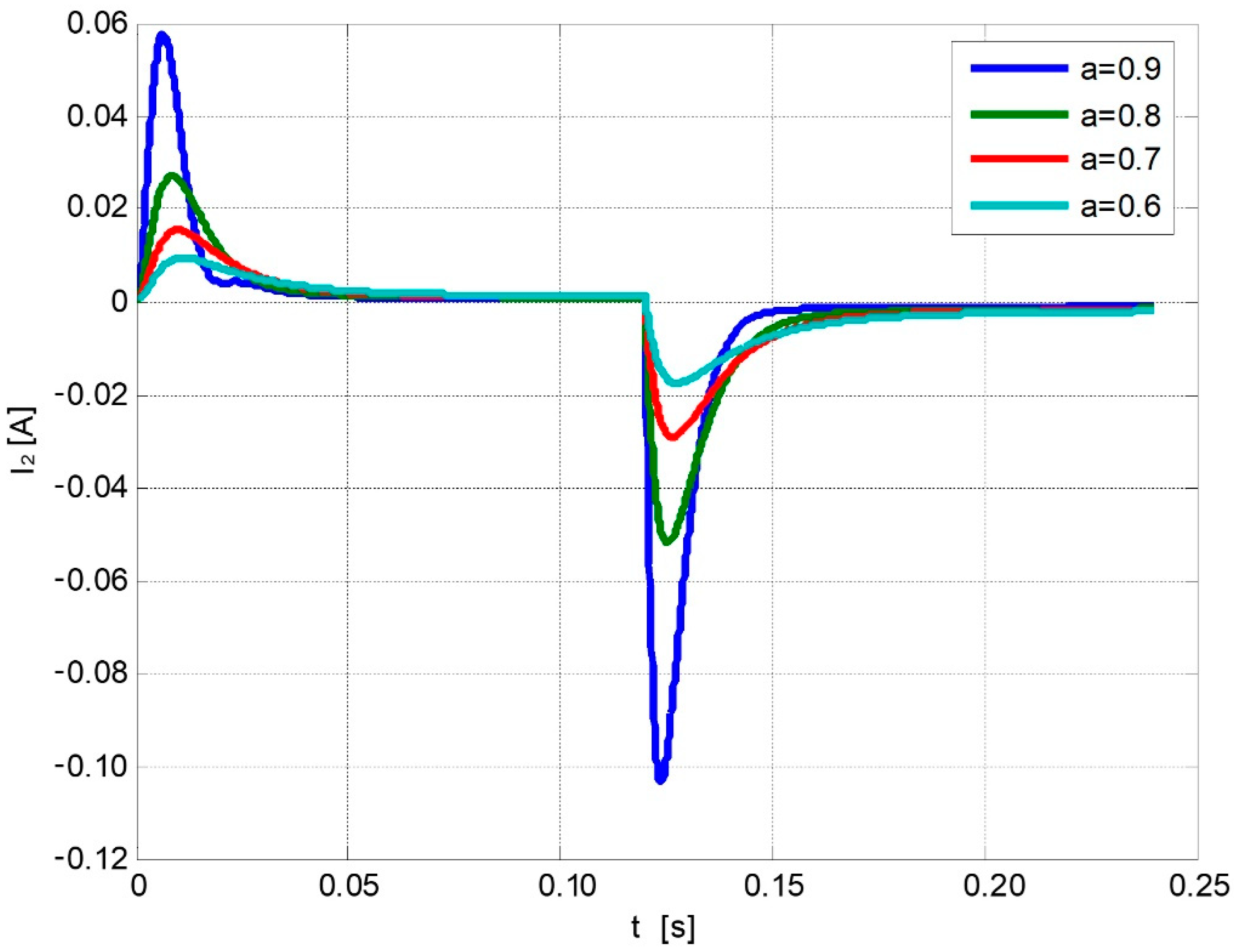
3. Distributorless Ignition System Model and Numerical Simulation Results
- the inductance, capacitance, and resistance of wires on the low-voltage side was omitted;
- the initial discharge voltage was assumed to be equal to the spark plug voltage; and
- the spark plug, at this stage of the analysis, was assumed to be a break in the circuit.
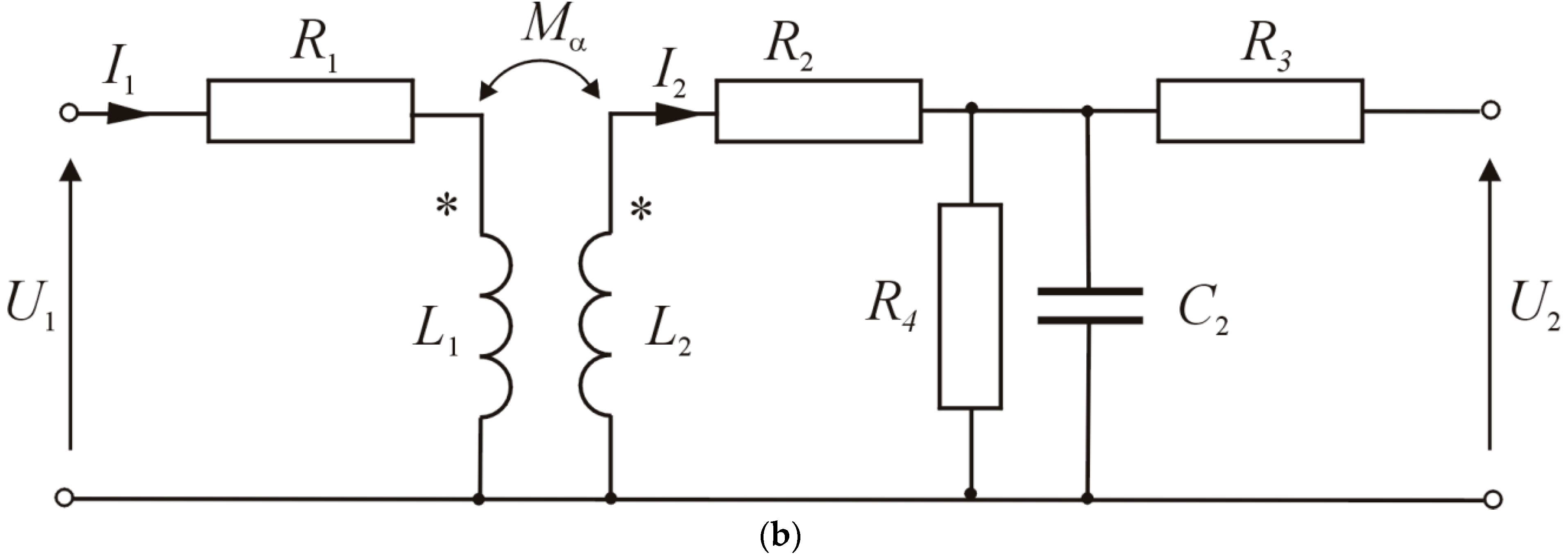
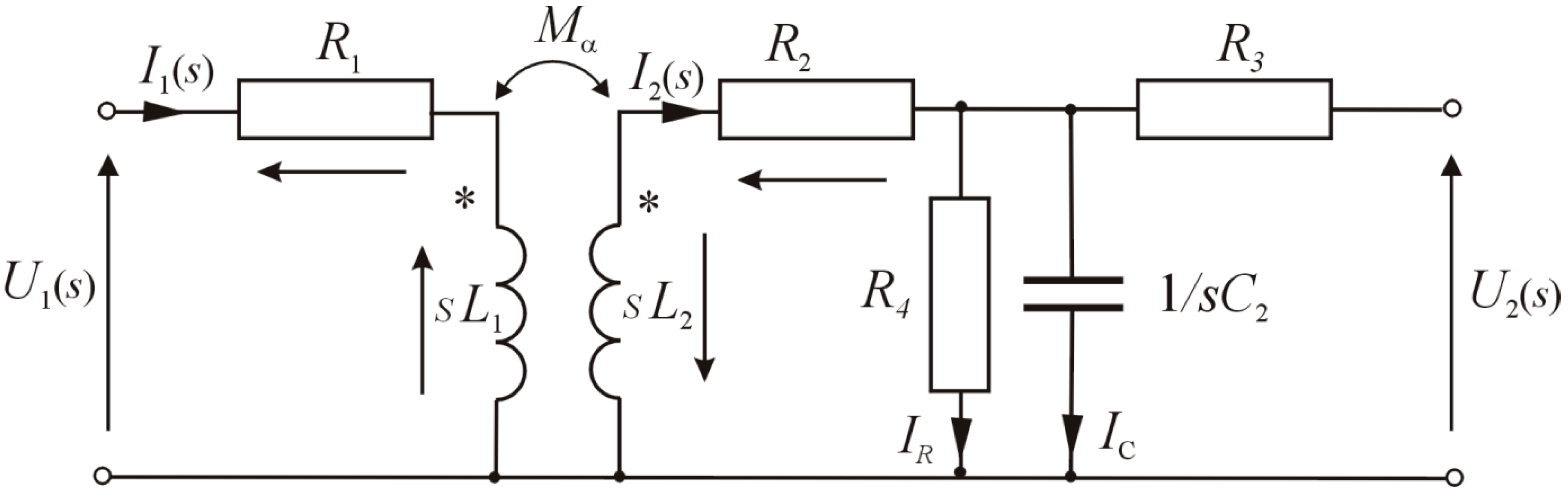
- U1 = 13 V—battery voltage;
- R1 = 0.9 Ω—coil primary winding resistance;
- L1 = 0.0025 H—coil primary winding inductance;
- L2 = 40 H—coil secondary winding inductance;
- R2 = 6400 Ω—ignition coil secondary winding resistance;
- R4= 50 MΩ—resistance representing losses in the coil core;
- R3 = 5 kΩ—radio interference reduction;
- C2 = 170 pF—coil self-capacitance.
- -
- a current break in the ignition coil;
- -
- a transformation of the impulse from the primary to the secondary side (magnetic coupling);
- -
- conduction of a high-voltage impulse through high-voltage wires—treated as a long line;
- -
- an arc discharge on the spark plug.
- -
- a capacitive phase—a very short high-current impulse;
- -
- an inductive phase—a long arc discharge time (compared to the capacitive phase) with low current value.
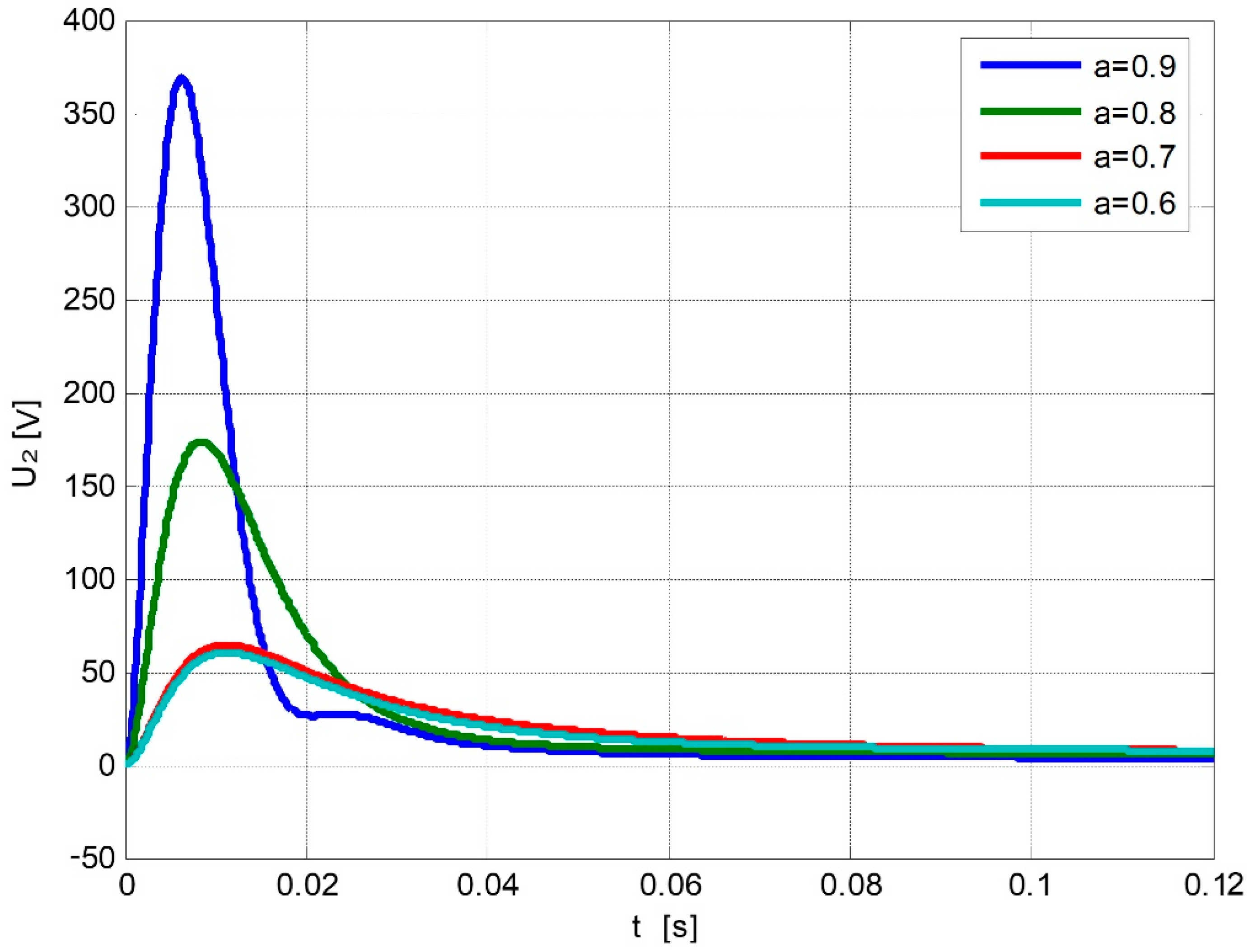
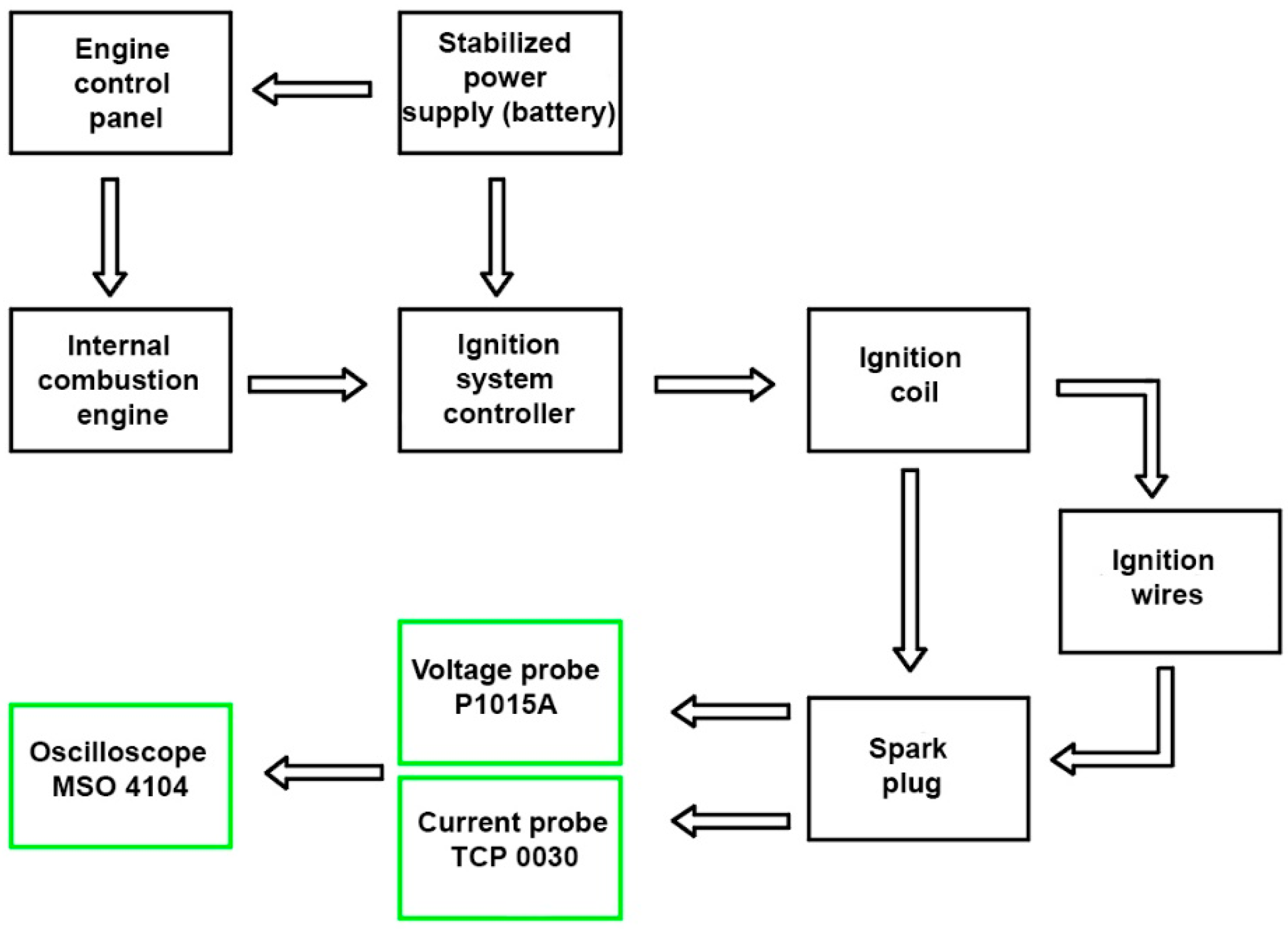
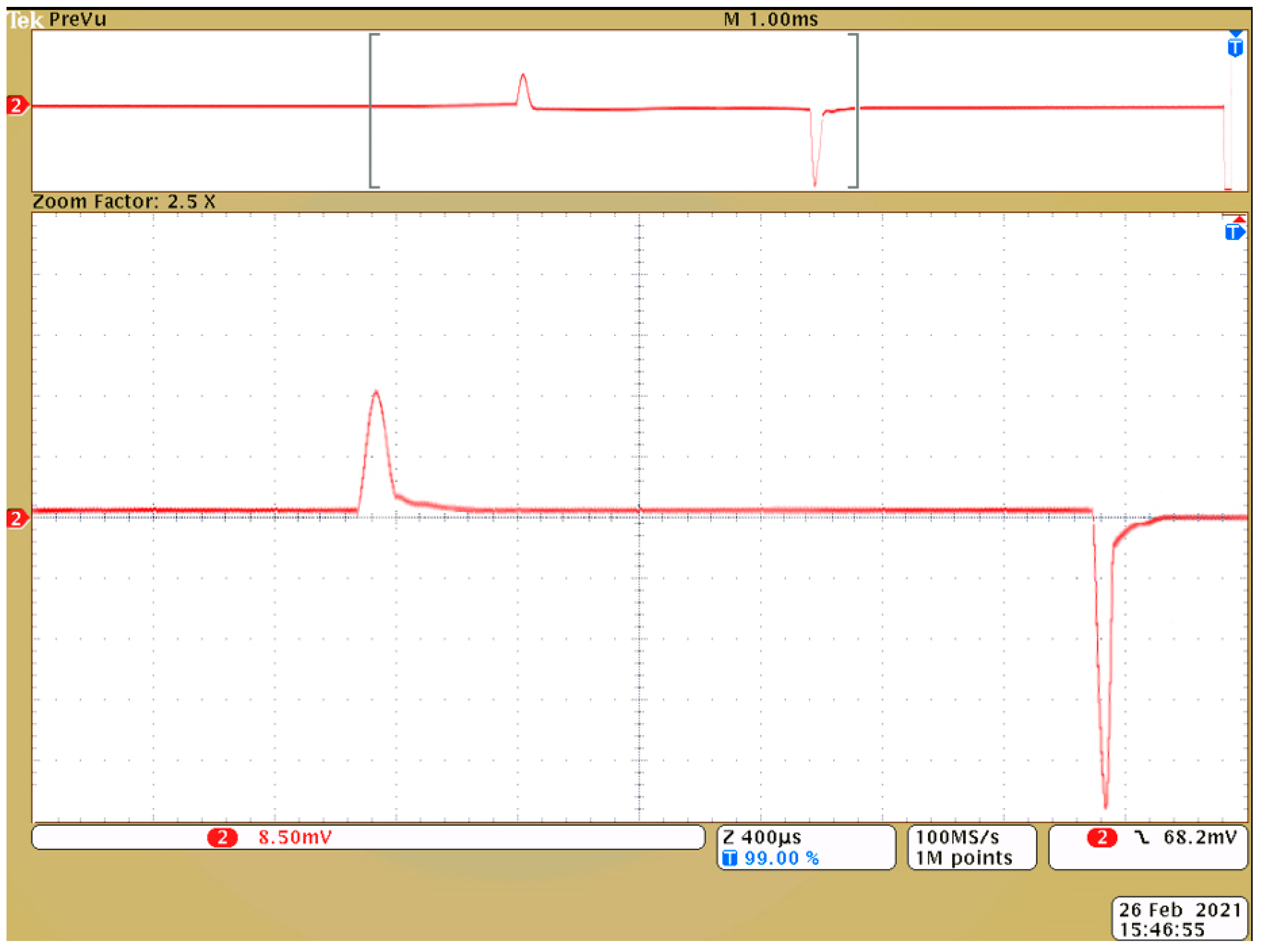
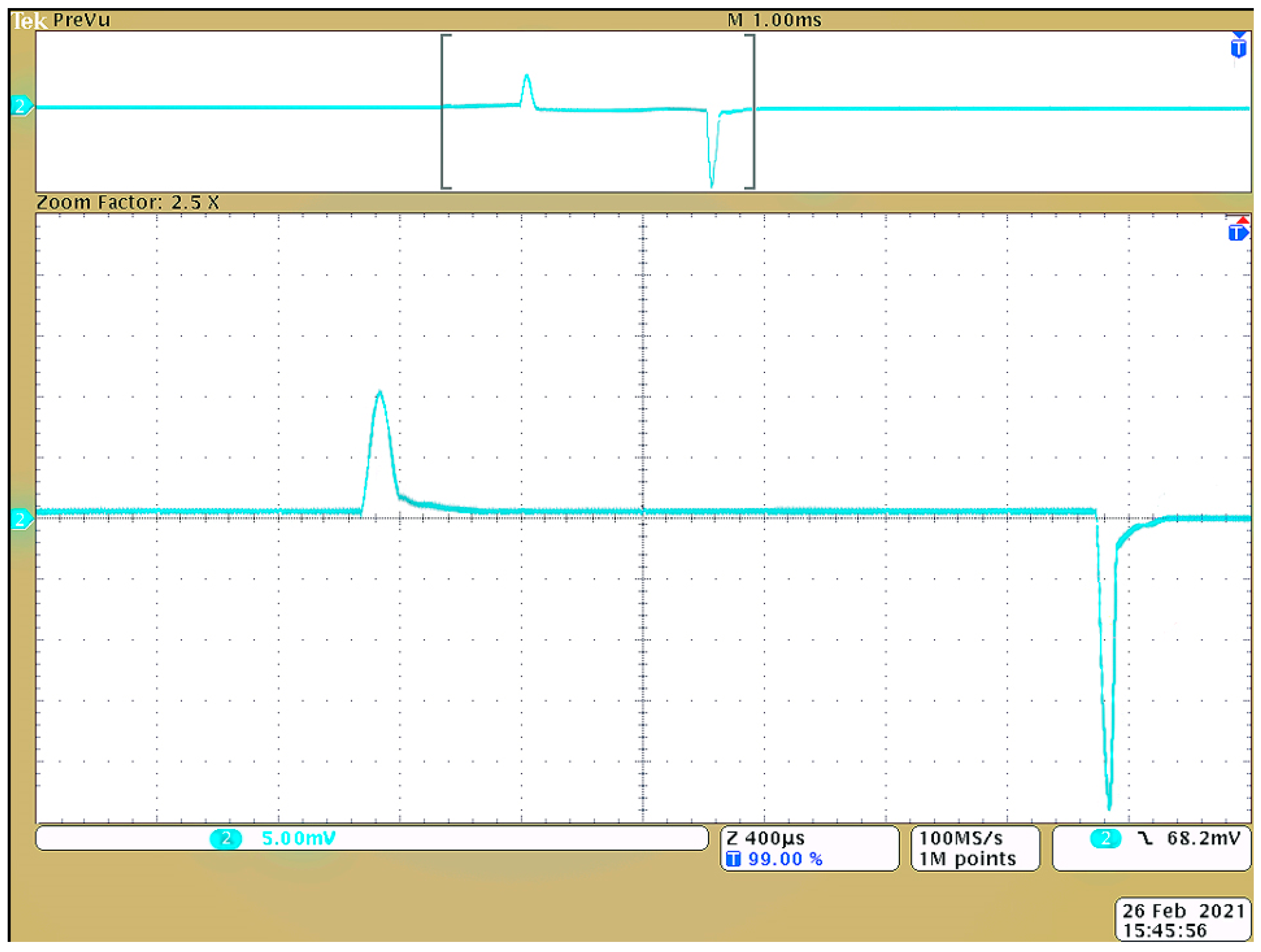
4. Experimental Studies of Spark Discharge
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nowakowski, W. Układy Impulsowe; WKiŁ: Warszawa, Poland, 1982. [Google Scholar]
- Hosseini, S.M. The Operation and Model of UPQC in Voltage Sag Mitigation Using EMTP by Direct Method. Emerg. Sci. J. 2018, 2, 148–156. [Google Scholar] [CrossRef]
- Parsa, N.; Khajouei, G.; Masigol, M.; Hasheminejad, H.; Moheb, A. Application of electrodialysis process for reduction of electrical conductivity and COD of water contaminated by composting leachate. Civ. Eng. J. 2018, 4, 1034. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Tan, Q.; Ives, M.; Liu, M.; Li, L.; Chen, X.; Zheng, M. Parametric Analysis of Ignition Circuit Components on Spark Discharge Characteristics; SAE Technical Paper 2016-01-1011; SAE International: Warrendale, PE, USA, 2016. [Google Scholar] [CrossRef]
- Stevenson, R.C.; Palma, R.; Yang, C.S.; Park, S.K.; Mi, C. Comprehensive Modeling of Automotive Ignition Systems; SAE Technical Paper 2007-01-1589; Visteon/ACH-LLC, CAE, University of Michigan: Dearborn, MI, USA, 2007. [Google Scholar] [CrossRef] [Green Version]
- Qisong, W.; Yongping, Z.; Song, L.; Zhiwei, Z. Research on Energy Simulation Model for Vehicle Ignition System. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Harbin, China, 3–5 September 2008. [Google Scholar]
- Altronic Inc. Advanced Digital Ignition System for Industrial Engines; Altronic CPU-95: Girard, OH, USA, 1996. [Google Scholar]
- Wang, Q.; Zheng, Y.; Yu, J.; Jia, J. Circuit model and parasitic parameter extraction of the spark plug in the ignition system. Turk. J. Electr. Eng. Comput. Sci. 2012, 20, 2012. [Google Scholar]
- Sosnowski, M. Modelowanie i Analiza Przebiegu Wyładowania Iskrowego w Silniku z Zapłonem Wymuszonym. Ph.D. Thesis, Akademia Jana Dlugosza w Czestochowie, January 2008. [Google Scholar]
- Coopmans, C.; Petras, I. Analogue fractional-order generalized memristive devices. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar] [CrossRef]
- Fouda, M.E.; Radwan, A.G. Fractional-order memristor Response under DC and Periodic Signals. Circuits Syst. Signal Processing 2015, 34, 961–970. [Google Scholar] [CrossRef]
- Jalloul, A.; Jelassi, K.; Melchior, R.; Trigeassou, J.-C. Fractional modelling of rotor skin effect in induction machines. In Proceedings of the 4th IFAC Workshop Fractional Differentiation and its Applications, Badajoz, Spain, 18–20 July 2013. [Google Scholar]
- Soltan, A.; Radwan, A.G.; Soliman, A.M. Fractional-order mutual inductance: Analysis and design. Int. J. Circuit Appl. 2016, 44, 85–97. [Google Scholar] [CrossRef]
- Różowicz, S.; Zawadzki, A.; Włodarczyk, M.; Wachta, H.; Baran, K. Properties of fractional-order magnetic coupling. Energies 2020, 13, 1539. [Google Scholar] [CrossRef] [Green Version]
- Jesus, I.S.; Machado, J.T.M. Application of Integer and Fractional Models in Electrochemical Systems. In Mathematical Problems in Engineering; Hindawi Publishing Corporation: London, UK, 2012. [Google Scholar] [CrossRef]
- Martin, R.; Quintana, J.J.; Ramos, A.; de la Nuez, I. Modeling electrochemical double layer capacitor, from classical to fractional impedance. Conf. Pap. J. Comput. Nonlinear Dyn. 2008, 3, 61–66. [Google Scholar]
- Radwan, A.G.; Fouda, M.E. On the Mathematical Modeling of Memristor, Memcapacitor, and Meminductor; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Petras, I.; Chen, Y.Q. Fractional-Order Circuit Elements with Memory. In Proceedings of the 13th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 28–31 May 2012. [Google Scholar] [CrossRef]
- Włodarczyk, M.; Zawadzki, A. Connecting a Capacitor to Direct Voltage in Aspect of Fractional Degree Derivatives. Przegląd Elektrotechniczny 2009, 85, 120–122. (In Polish) [Google Scholar]
- Podlubny, I. Fractional Calculus: Methods for Applications; XXXVII Summer School on Mathematical Physics: Ravello, Italy, 2012. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and applications of differentiation and integration to arbitrary order. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Caputo, M. Linear Models of Dissipation Whose Q Is Almost Frequency Independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Carlson, G.; Halijak, C. Approximation of fractional capacitors (1/s)ˆ(1/n) by a regular newton process. IEEE Trans. Circuit Theory 1964, 11, 210–213. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Krishna, B.T. Studies on fractional order differentiators and integrators: A survey. Signal Processing 2011, 91, 386–426. [Google Scholar] [CrossRef]
- Różowicz, S.; Tofil, S.Z. The influence of impurities on the operation of selected fuel ignition systems in combustion engines. Archives of Electrical Engineering. 2016, 65, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.N.; Chandler, P.; Schumacher, C.; Banda, S.; Pachter, M. Adaptive feedback linearizing nonlinear close formation control of UAVs. Proceeding of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; pp. 854–858. [Google Scholar]
- Zawadzki, A.; Włodarczyk, M. CFE Method—Quality Analysis of The Approximation of Reverse Laplace Transform Of Fractional Order. Prace Naukowe Politechniki Śląskiej. (in Polish). Elektryka 2017, 3–4, 243–244. (In Polish) [Google Scholar]
- Różowicz, S. The effect of different ignition cables on spark plug durability. In Przegląd Elektrotechniczny; Wydawnictwo SIGMA: Warszawa, Poland, 2018; Volume 94, pp. 191–195. (In Polish) [Google Scholar]
- Różowicz, S. Use of the mathematical model of the ignition system to analyze the spark discharge, including the destruction of spark plug electrodes. In Proceedings of the 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Lodz, Poland, 14–16 September 2017. [Google Scholar]
- Różowicz, S.; Zawadzki, A. Experimental verification of signal propagation in automotive ignition cables modelled with distributed parameter circuit. Arch. Electr. Eng. 2019, 68, 667–675. [Google Scholar]
- Różowicz, S. Voltage modelling in ignition coil using magnetic coupling of fractional order. Arch. Electr. Eng. 2019, 68, 227–235. [Google Scholar]
- Zawadzki, A.; Różowicz, S. Application of input-state of the system transformation for linearization of selected electrical circuits. J. Electr. Eng.-Elektrotechnicky Casopism 2016, 67, 199–205. [Google Scholar] [CrossRef] [Green Version]
- Zawadzki, A.; Różowicz, S. Application of input—State of the system transformation for linearization of some nonlinear generators. Int. J. Control. Autom. Syst. 2015, 13, 1–8. [Google Scholar] [CrossRef]
- Szcześniak, A.; Myczuda, Z. A method of charge accumulation in the logarithmic analog-to-digital converter with a successive approximation. Przegląd Elektrotechniczny 2010, 86, 336–340. (In Polish) [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Różowicz, S.; Zawadzki, A.; Włodarczyk, M.; Różowicz, A. Modeling of Internal Combustion Engine Ignition Systems with a Circuit Containing Fractional-Order Elements. Energies 2022, 15, 337. https://doi.org/10.3390/en15010337
Różowicz S, Zawadzki A, Włodarczyk M, Różowicz A. Modeling of Internal Combustion Engine Ignition Systems with a Circuit Containing Fractional-Order Elements. Energies. 2022; 15(1):337. https://doi.org/10.3390/en15010337
Chicago/Turabian StyleRóżowicz, Sebastian, Andrzej Zawadzki, Maciej Włodarczyk, and Antoni Różowicz. 2022. "Modeling of Internal Combustion Engine Ignition Systems with a Circuit Containing Fractional-Order Elements" Energies 15, no. 1: 337. https://doi.org/10.3390/en15010337
APA StyleRóżowicz, S., Zawadzki, A., Włodarczyk, M., & Różowicz, A. (2022). Modeling of Internal Combustion Engine Ignition Systems with a Circuit Containing Fractional-Order Elements. Energies, 15(1), 337. https://doi.org/10.3390/en15010337







