New Ways for the Advanced Quality Control of Liquefied Natural Gas
Abstract
:1. Introduction
2. Materials and Methods
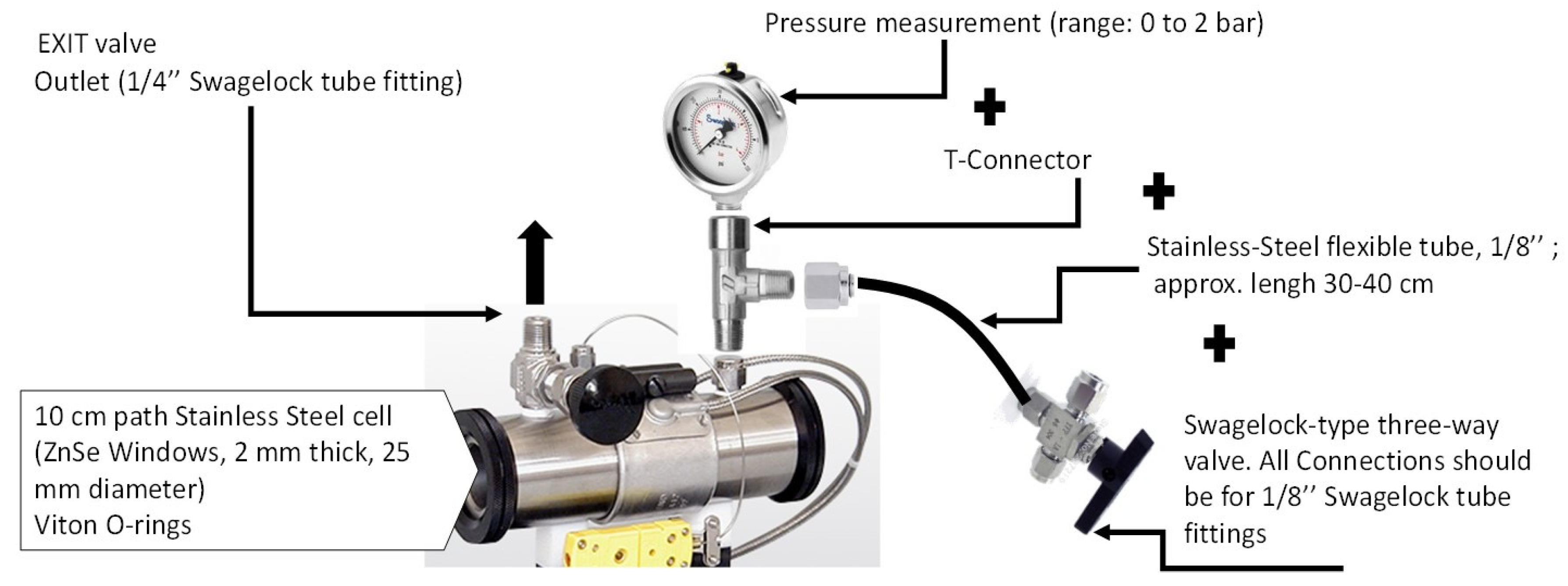
2.1. Instrumentation
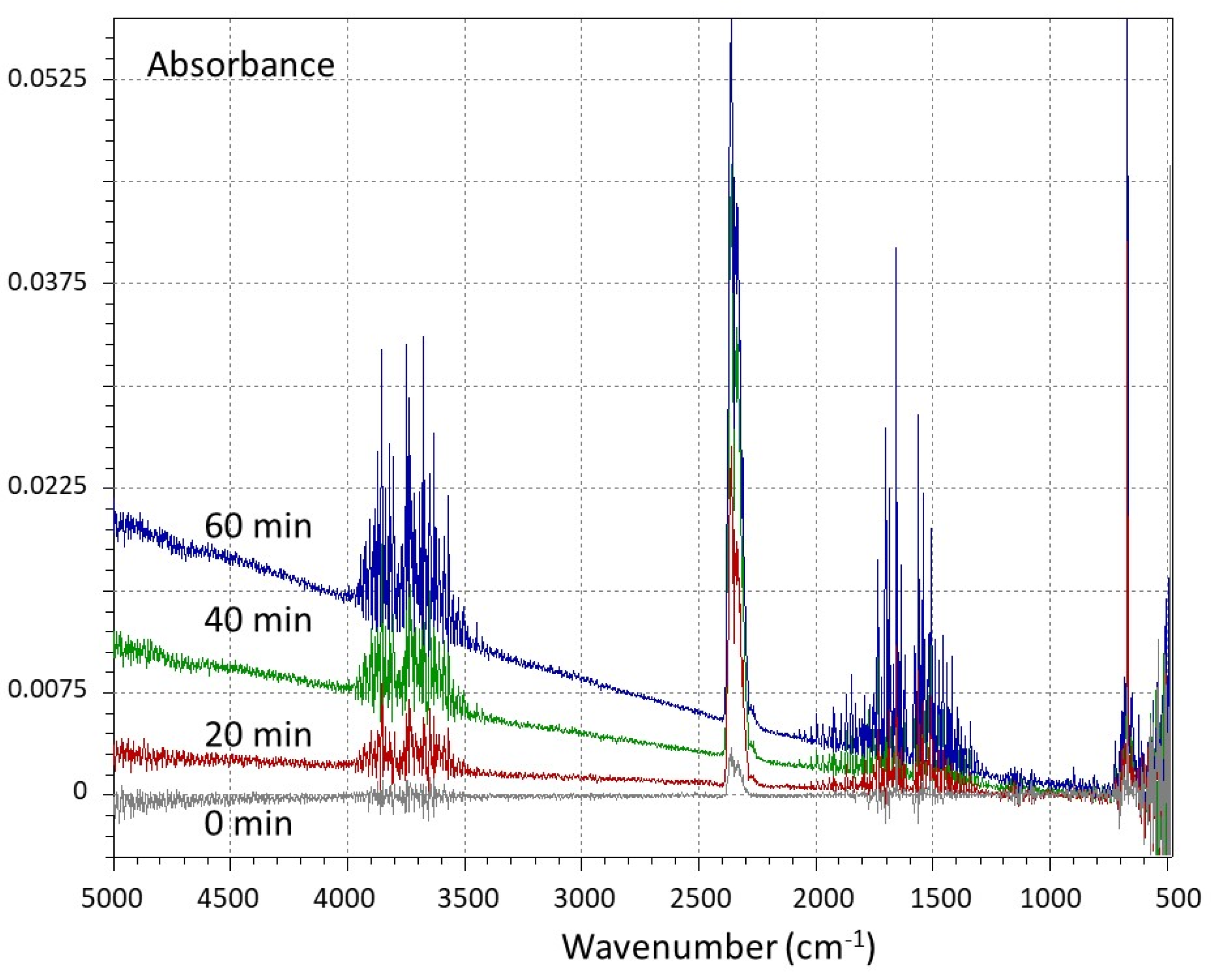
2.2. Gas Broadening
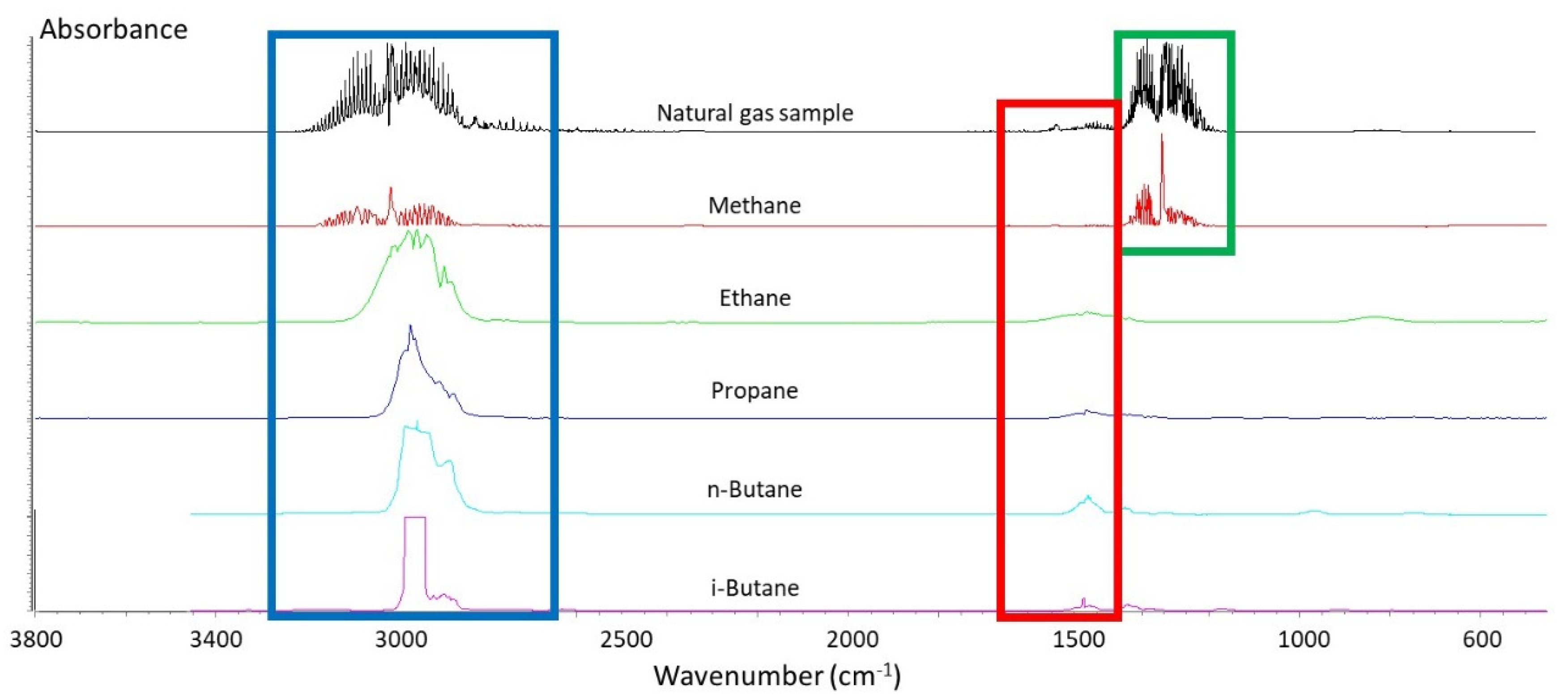
2.3. Peak Identification
2.4. Chemometric Predictive Models
2.4.1. Samples
2.4.2. Simplified Workflow for Model Development
- Stage 1: Preliminary assays: it is always important to visualize the spectra in order to evaluate gross differences among them, unusual signals, potential range of variables to be considered, presence of outlying samples, etc. A preliminary model can also be done to feel what its results look like and whether the samples spread through the working range of interest.
- Stage 2: spectra usually need what is called data pre-processing. This step attempts to get rid of useless information or undesired characteristics that may be detrimental for the predictions. For instance, baseline correction or noise filtering are typical steps before developing models. Very common pre-processings are the first derivative [16,64] (sometimes the 2nd derivative is also used) and mean centering [2]. Combinations of pre-processings are also common. Several options used for LNG modeling are shown in Table 3. This stage of model development is in general recommended, although some applications argued that no pre-processing was needed [4]. There is not a definitive answer to this issue, and the unique ‘true’ advice is to try different pre-processings and see which one improves the models.
- Stage 3: A critical point to develop a satisfactory PLS model (also critical for many other techniques that use abstract factors) is to ascertain the number of factors that must be included in the model (this is called model dimensionality). Although including many factors to take account of the majority of the variance (consider variance and information as synonymous for this purpose) contained into the spectra might seem to be a good idea, it is worth considering that those factors might be unrelated to the property of interest. They might be related to baseline effects or some spurious behavior of a peak, contributing to bad predictions. Of course, we also assume that too few factors will not be sufficient to extract enough relevant information to get a sound model. So, we need to equilibrate overfitting (too many factors) with underfitting (too few factors). One of the best options for this, though not perfect, consists of performing cross-validation. This empirically evaluates a cost function so that a minimum in the error is searched for [65]. Cross-validation is iterative and sometimes takes some computer time. Its conceptual idea can be resumed in a pseudo-code as follows:
- Fix a number of factors, let us say 1.
- Develop a model, and test how well it predicts those samples left out of it. The error can be stored in the computer memory.
- Reintegrate those spectra to the calibration set and extract another small subset of samples.
- Develop a model, test it with the second set of left-out spectra, and sum the error to the previous one.
- Continue the process until all samples (or possible subsets of samples) are excluded from the calibration stage and predicted afterwards. The summed errors yield the overall prediction error (=RMSECV).
- Return to 1 and increase the number of factors by one, and repeat the process again.
- Stage 4: A reason why developing a model is an iterative process is because we have to check for the existence of outlying samples. If they are present, all the previous stage is biased, and the model is not reliable. The problem is how to detect them. Likely, in the same way as you detect wrong points in a traditional calibration plot: by calculating statistics to evaluate the behavior of the samples into the model. Two of the most important and useful ones are the ‘Q residuals’ and the ‘Hotelling’s T2′ statistics [70] (another usual statistic is the leverage, although it is closely related to the T2 one). The former detects whether a spectrum has some new or different spectral characteristic(s) that could not be modeled with the present model (note: ‘different’ refers to its comparison with the residuals of the other calibration spectra in the model), whereas the second evaluates how close the spectrum is to the average spectrum of the calibration set. Clearly, we would like samples with spectra close to the average and without new spectral characteristics.
- Stage 5: The external validation set of samples is of use not only to assess that the model yields no overfitting but to evaluate how good the predictions of new samples are. A typical plot, such as that in Figure 12, is of most information as it yields insight on the closeness of the individual predictions to the true values, and samples predicted badly (possible outliers?), in addition to the overall average error.
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ISO 6974-1: 2013 Natural Gas—Determination of Composition and Associated Uncertainty by Gas Chromatography—Part 1: General Guidelines and Calculation of Composition; ISO: Geneva, Switzerland, 2013.
- Ferreiro, B.; Andrade, J.; López-Mahía, P.; Muniategui, S.; Vázquez, C.; Pérez, A.; Rey, M.; Vales, C. Fast quality control of natural gas for commercial supply and transport utilities. Fuel 2021, 305, 121500. [Google Scholar] [CrossRef]
- Kiefer, J. Recent advances in the characterization of gaseous and liquid fuels by vibrational spectroscopy. Energies 2015, 8, 3165–3197. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, M.F.; Santos, J.R.B.; Silva, A.N.; Soares, S.F.C.; Araujo, M.C.U. A cheap handheld NIR spectrometric system for automatic determination of methane, ethane, and propane in natural gas and biogas. Microchem. J. 2021, 170, 106752. [Google Scholar] [CrossRef]
- Koturbash, T.; Karpash, M.; Darvai, I.; Rybitskyi, I.; Kutcherov, V. Development of new instant technology of natural gas quality determination. In Proceedings of the ASME 2013 Power Conference, Boston, MA, USA, 29 July–1 August 2013; Volume 1. [Google Scholar] [CrossRef] [Green Version]
- Looney, B. Statistical Review of World Energy 2021. Rev. World Energy Data 2021, 70, 8–20. [Google Scholar]
- Hosseini, M.; Dincer, I.; Ozbilen, A. Expert Opinions on Natural Gas Vehicles Research Needs for Energy Policy Development; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128137352. [Google Scholar]
- BP, P.L.C. Natural Gas Demand. Available online: https://www.bp.com/en/global/corporate/energy-economics/energy-outlook/demand-by-fuel/natural-gas.html (accessed on 20 October 2021).
- Rahmouni, C.; Tazeroutb, M.; Le-Corre, O. Determination of the combustion properties of natural gases by pseudo-constituents. Fuel 2003, 82, 1399–1409. [Google Scholar] [CrossRef]
- Roy, P.S.; Ryu, C.; Park, C.S. Predicting Wobbe Index and methane number of a renewable natural gas by the measurement of simple physical properties. Fuel 2018, 224, 121–127. [Google Scholar] [CrossRef]
- Karpash, O.; Darvay, I.; Karpash, M. New approach to natural gas quality determination. J. Pet. Sci. Eng. 2010, 71, 133–137. [Google Scholar] [CrossRef]
- Sweelssen, J.; Blokland, H.; Rajamäki, T.; Boersma, A. Capacitive and Infrared Gas Sensors for the Assessment of the Methane Number of LNG Fuels. Sensors 2020, 20, 3345. [Google Scholar] [CrossRef]
- Sweelssen, J.; Blokland, H.; Rajamäki, T.; Sarjonen, R.; Boersma, A. A versatile capacitive sensing platform for the assessment of the composition in gas mixtures. Micromachines 2020, 11, 116. [Google Scholar] [CrossRef] [Green Version]
- Boersma, A.; Sweelsen, J.; Blokland, H. Gas Composition Sensor for Natural Gas and Biogas. Procedia Eng. 2016, 168, 197–200. [Google Scholar] [CrossRef]
- Makhoukhi, N.; Péré, E.; Creff, R.; Pouchan, C. Determination of the composition of a mixture of gases by infrared analysis and chemometric methods. J. Mol. Struct. 2005, 744–747, 855–859. [Google Scholar] [CrossRef]
- Haghi, R.K.; Yang, J.; Tohidi, B. Fourier Transform Near-Infrared (FTNIR) Spectroscopy and Partial Least-Squares (PLS) Algorithm for Monitoring Compositional Changes in Hydrocarbon Gases under In Situ Pressure. Energy Fuels 2017, 31, 10245–10259. [Google Scholar] [CrossRef]
- Ribessi, R.L.; Neves, T.D.A.; Rohwedder, J.J.R.; Pasquini, C.; Raimundo, I.M.; Wilk, A.; Kokoric, V.; Mizaikoff, B. IHEART: A miniaturized near-infrared in-line gas sensor using heart-shaped substrate-integrated hollow waveguides. Analyst 2016, 141, 5298–5303. [Google Scholar] [CrossRef] [Green Version]
- Dąbrowski, K.M.; Kuczyński, S.; Barbacki, J.; Włodek, T.; Smulski, R.; Nagy, S. Downhole measurements and determination of natural gas composition using Raman spectroscopy. J. Nat. Gas Sci. Eng. 2019, 65, 25–31. [Google Scholar] [CrossRef]
- Eichmann, S.C.; Kiefer, J.; Benz, J.; Kempf, T.; Leipertz, A.; Seeger, T. Determination of gas composition in a biogas plant using a Raman-based sensorsystem. Meas. Sci. Technol. 2014, 25, 075503. [Google Scholar] [CrossRef]
- Sieburg, A.; Knebl, A.; Jacob, J.M.; Frosch, T. Characterization of fuel gases with fiber-enhanced Raman spectroscopy. Anal. Bioanal. Chem. 2019, 411, 7399–7408. [Google Scholar] [CrossRef]
- Specac Product Catalogue. Available online: https://www.specac.com/en/documents/catalogues (accessed on 25 November 2021).
- Microptik Gas Sampling. Available online: https://www.microptik.eu/product/gas-sampling (accessed on 25 November 2021).
- Jasco Gas Cells. Available online: https://jascoinc.com/products/spectroscopy/ftir-spectrometers/ftir-accessories/gas-cells/ (accessed on 25 November 2021).
- Guiding Photonics Gas Cells. Available online: https://guidingphotonics.com/gas-cells/ (accessed on 21 September 2021).
- Kriesel, J.M.; Gat, N.; Bernacki, B.E.; Erikson, R.L.; Cannon, B.D.; Myers, T.L.; Bledt, C.M.; Harrington, J.A. Hollow core fiber optics for mid-wave and long-wave infrared spectroscopy. In Proceedings of the International Society for Optics and Photonics, Orlando, FL, USA, 26–28 April 2011; Volume 8018, p. 80180V. [Google Scholar]
- Li, N.; Tao, L.; Yi, H.; Kim, C.S.; Kim, M.; Canedy, C.L.; Merritt, C.D.; Bewley, W.W.; Vurgaftman, I.; Meyer, J.R. Methane detection using an interband-cascade LED coupled to a hollow-core fiber. Opt. Express 2021, 29, 7221–7231. [Google Scholar] [CrossRef]
- Pike Technologies. Choice of Window Materials for Transmission Sampling of Liquids in the Mid-IR Spectral Region. Available online: https://www.piketech.com/skin/fashion_mosaic_blue/application-pdfs/CrystalChoiceForTransmission.pdf (accessed on 25 November 2021).
- Shimadzu Corporation Safety of Windows and Prisms Used in FTIR. Available online: https://www.shimadzu.com/an/service-support/technical-support/analysis-basics/tips-ftir/safety.html (accessed on 20 September 2021).
- Spectra-Tech. How to Select an Infrared Transmission Window 2012. Available online: https://kinecat.pl/wp-content/uploads/2012/11/crystal_ref.pdf (accessed on 25 November 2021).
- Smith, B.C. Fundamentals of Fourier Transform Infrared Spectroscopy, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 1420069306. [Google Scholar]
- Griffiths, P.R.; De Haseth, J.A. Fourier Transform Infrared Spectrometry; John Wiley & Sons: Chichester, UK, 2007; Volume 171, ISBN 0470106298. [Google Scholar]
- Harris, D.C. Análisis Químico Cuantitativo; Reverté: Barcelona, Spain, 2007; ISBN 8429172246. [Google Scholar]
- Skoog, D.A.; Holler, F.J.; Nieman, T.A. Principios de Análisis Instrumental, 7th ed.; Cengage Learning: Boston, MA, USA, 2018; ISBN 978-607-481-390-6. [Google Scholar]
- Stuart, B. Infrared Spectroscopy. In Kirk-Othmer Encyclopedia of Chemical Technology, 1st ed.; John Wiley & Sons: Chichester, UK, 2015; pp. 73–101. ISBN 0471238961. [Google Scholar]
- Anderson, P.W. Pressure Broadening in the Microwave and Infra-Red Regions. Phys. Rev. 1949, 76, 647–661. [Google Scholar] [CrossRef]
- Jabloński, A. General Theory of Pressure Broadening of Spectral Lines. Phys. Rev. 1945, 68, 78–93. [Google Scholar] [CrossRef]
- Margenau, H.; Watson, W.W. Pressure effects of foreign gases on the sodium D-lines. Phys. Rev. 1933, 44, 92–98. [Google Scholar] [CrossRef]
- Ferreiro, B.; Andrade, J.M.; Paz-Quintáns, C.; López-Mahía, P.; Muniategui-Lorenzo, S.; Rey-Garrote, M.; Vázquez-Padín, C.; Vales, C. Improved Sensitivity of Natural Gas Infrared Measurements Using a Filling Gas. Energy Fuels 2019, 33, 6929–6933. [Google Scholar] [CrossRef]
- NIST Public. IR Spectra Database. Available online: https://webbook.nist.gov/chemistry/name-ser/ (accessed on 25 November 2021).
- Es-Sebar, E.; Farooq, A. Intensities, broadening and narrowing parameters in the ν3 band of methane. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Shimanouchi, T. Tables of Molecular Vibrational Frequencies: Part 6. J. Phys. Chem. Ref. Data 1973, 2, 121–162. [Google Scholar] [CrossRef]
- Gough, K.M.; Murphy, W.F.; Raghavachari, K. The harmonic force field of propane. J. Chem. Phys. 1987, 87, 3332–3340. [Google Scholar] [CrossRef]
- Hudson, R.L.; Gerakines, P.A.; Yarnall, Y.Y.; Coones, R.T. Infrared spectra and optical constants of astronomical ices: III. Propane, propylene, and propyne. Icarus 2021, 354, 114033. [Google Scholar] [CrossRef]
- Evans, J.C.; Bernstein, H.J. The vibrational spectra of isobutane and isobutane-d1. Can. J. Chem. 1956, 34, 1037–1045. [Google Scholar] [CrossRef]
- Brereton, R.G. Chemometrics: Data Analysis for the Laboratory and Chemical Plant; John Wiley & Sons: Chichester, UK, 2003; ISBN 0470845740. [Google Scholar]
- Otto, M. Chemometrics: Statistics and Computer Application in Analytical Chemistry; John Wiley & Sons: Chichester, UK, 2016; ISBN 3527340971. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Martens, H. Reliable and relevant modelling of real world data: A personal account of the development of PLS Regression. Chemom. Intell. Lab. Syst. 2001, 58, 85–95. [Google Scholar] [CrossRef]
- Gupta, S.K.; Mittal, M. Predicting the methane number of gaseous fuels using an artificial neural network. Biofuels 2019, 12, 1191–1198. [Google Scholar] [CrossRef]
- Bai, P.; Duan, X.; He, C.; Li, Y. Natural gas infrared spectrum analysis based on multi-level and SVM-subset. In Proceedings of the 2009 IEEE International Conference on Virtual Environments, Human-Computer Interfaces and Measurements Systems, Hong Kong, 11–13 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 336–339. [Google Scholar]
- Udina, S.; Carmona, M.; Pardo, A.; Calaza, C.; Santander, J.; Fonseca, L.; Marco, S. A micromachined thermoelectric sensor for natural gas analysis: Multivariate calibration results. Sens. Actuators B Chem. 2012, 166–167, 338–348. [Google Scholar] [CrossRef]
- Nurida, M.Y.; Norfadilah, D.; Aishah, M.R.S.; Phak, C.Z.; Saleh, S.M. Monitoring of CO2 Absorption Solvent in Natural Gas Process Using Fourier Transform Near-Infrared Spectrometry. Int. J. Anal. Chem. 2020, 2020, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ponte, S.; Andrade, J.M.; Vázquez, C.; Ferreiro, B.; Cobas, C.; Pérez, A.; Rey, M.; Vales, C.; Pellitero, J.; Santacruz, B.; et al. Prediction of the methane number of commercial liquefied natural gas samples using mid-IR gas spectrometry and PLS regression. J. Nat. Gas Sci. Eng. 2021, 90, 103944. [Google Scholar] [CrossRef]
- Wise, B.M.; Gallagher, N.B.; Bro, R.; Shaver, J.; Windig, W.; Koch, J. PLS_Toolbox; Eigenvector Research Inc.: Manson, WA, USA, 2006. [Google Scholar]
- ThermoFisher Scientific. Available online: https://www.thermofisher.com/order/catalog/product/INF-15004 (accessed on 25 November 2021).
- Aspen Technology Inc. Unscrambler. Available online: https://www.aspentech.com/en/products/msc/aspen-unscrambler (accessed on 24 November 2021).
- MultiD Analyses, B.D. Genex. Available online: https://multid.se/genex/ (accessed on 24 November 2021).
- IBM Co. IBM SPSS Software. Available online: https://www.ibm.com/es-es/analytics/spss-statistics-software (accessed on 24 November 2021).
- Statgraphics Technologies, Inc. Available online: https://www.statgraphics.com/ (accessed on 24 November 2021).
- Leardi, R.; Melzi, C.; Polotti, G. CAT (Chemometric Agile Tool), Freely. Available online: http://gruppochemiometria.it/index.php/software (accessed on 4 November 2021).
- Broad, N.; Graham, P.; Hailey, P.; Hardy, A.; Holland, S.; Hughes, S.; Lee, D.; Prebble, K.; Salton, N.; Warren, P. Guidelines for the Development and Validation of Near-Infrared Spectroscopic Methods in the Pharmaceutical Industry. In Handbook of Vibrational Spectroscopy; John Wiley & Sons: Chichester, UK, 2002; Volume 5, pp. 3590–3610. [Google Scholar]
- Validation of Analytical Procedures: Text and Methodology. In ICH Harmonised Tripartite Guideline; Somatek Inc.: San Diego, CA, USA, 2014.
- European Medicines Agency Guideline on the Use of Near Infrared Spectroscopy (NIRS) by the Pharmaceutical Industry and the Data Requirements for New Submissions and Variations. 2012. Available online: https://www.ema.europa.eu/en/use-near-infrared-spectroscopy-nirs-pharmaceutical-industry-data-requirements-new-submissions (accessed on 25 November 2021).
- Rohwedder, J.J.R.; Pasquini, C.; Fortes, P.R.; Raimundo, I.M.; Wilk, A.; Mizaikoff, B. iHWG-μNIR: A miniaturised near-infrared gas sensor based on substrate-integrated hollow waveguides coupled to a micro-NIR-spectrophotometer. Analyst 2014, 139, 3572. [Google Scholar] [CrossRef] [Green Version]
- Andrade-Garda, J.M.; Carlosena-Zubieta, A.; Boqué-Martí, R.; Ferré-Baldrich, J. Partial Least Squares Regression. In Basic Chemometric Techniques in Atomic Spectroscopy; Andrade-Garda, J.M., Ed.; Royal Society of Chemistry: Cambridge, UK, 2013; pp. 280–347. ISBN 1849737967. [Google Scholar]
- Malinowski, E.R.; Howery, D.G. Factor Analysis in Chemistry; Wiley: Hoboken, NJ, USA, 1980; ISBN 0471058815. [Google Scholar]
- Eigenvector Research Eigenvector Wiki. Available online: https://www.wiki.eigenvector.com/index.php?title=Confusionmatrix (accessed on 14 May 2021).
- Faber, N.M.; Rajkó, R. How to avoid over-fitting in multivariate calibration-The conventional validation approach and an alternative. Anal. Chim. Acta 2007, 595, 98–106. [Google Scholar] [CrossRef]
- Wiklund, S.; Nilsson, D.; Eriksson, L.; Sjöström, M.; Wold, S.; Faber, K. A randomization test for PLS component selection. J. Chemom. 2007, 21, 427–439. [Google Scholar] [CrossRef]
- Vinzi, V.E.; Chin, W.W.; Henseler, J.; Wang, H. Handbook of Partial Least Squares; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-540-32825-4. [Google Scholar]
- Sanz, M.B.; Sarabia, L.A.; Herrero, A.; Ortiz, M.C. Multivariate analytical sensitivity in the determination of selenium, copper, lead and cadmium by stripping voltammetry when using soft calibration. Anal. Chim. Acta 2003, 489, 85–94. [Google Scholar] [CrossRef]
- Ortiz, M.C.; Sarabia, L.A.; Sánchez, M.S. Tutorial on evaluation of type I and type II errors in chemical analyses: From the analytical detection to authentication of products and process control. Anal. Chim. Acta 2010, 674, 123–142. [Google Scholar] [CrossRef]
- Ortiz, M.C.; Sarabia, L.A.; Herrero, A.; Sánchez, M.S.; Sanz, M.B.; Rueda, M.E.; Giménez, D.; Meléndez, M.E. Capability of detection of an analytical method evaluating false positive and false negative (ISO 11843) with partial least squares. Chemom. Intell. Lab. Syst. 2003, 69, 21–33. [Google Scholar] [CrossRef]
- ISO 11843. Capability of Detection–Part 2: Methodology in the Linear Calibration Case; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- SANCO/2004/2726 Guidelines for the Implementation of Decision 2002/657/EC. Rev 4-December 2008. Available online: https://ec.europa.eu/food/system/files/2016-10/cs_vet-med-residues_cons_2004-2726rev4_en.pdf (accessed on 25 November 2021).
- European Commission. Commission Decision 2002/657/EC of 12 August 2002 implementing Council Directive 96/23/EC concerning the performance of analytical methods and the interpretation of results. Off. J. Eur. Communities 2002, 50, 8–36. [Google Scholar]
- Faber, K.; Kowalski, B.R. Prediction error in least squares regression: Further critique on the deviation used in The Unscrambler. Chemom. Intell. Lab. Syst. 1996, 34, 283–292. [Google Scholar] [CrossRef]
- Faber, N.M.; Schreutelkamp, F.H.; Vedder, H.W. Estimation of prediction uncertainty for a multivariate calibration model. Spectrosc. Eur. 2004, 16, 17–21. [Google Scholar]
- Faber, K.; Kowalski, B.R. Improved prediction error estimates for multivariate calibration by correcting for the measurement error in the reference values. Appl. Spectrosc. 1997, 51, 660–665. [Google Scholar] [CrossRef]









| Window Material | Effective Range (cm−1) | Window Material | Effective Range (cm−1) |
|---|---|---|---|
| AgCl | 25,000–360 | KBr | 40,000–340 |
| AMTIR (GeAsSe) | 11,000–625 | KRS-5 (TlBr + TlI) | 16,600–250 |
| BaF2 | 50,000–740 | NaCl | 40,000–625 |
| CaF2 | 50,000–1025 | Sapphire (Al2O3) | 50,000–1525 |
| Chalcogenide (AsSeTe) | 4000–900 | Si | 8000–660 |
| CsI | 33,000–200 | SiO2 | 50,000–2500 |
| Diamond | 40,000–12.5 | ZnS | 17,000–690 |
| Ge | 5500–475 | ZnSe | 10,000–550 |
| Methane [40] | Ethane [41] | Propane [42,43] | |||||
| Description | ῦ (cm−1) | Description | ῦ (cm−1) | Description | ῦ (cm−1) | Description | ῦ (cm−1) |
| CH asymmetric stretch | 3019 | CH3 asymmetric stretch | 2985 | CH stretch | 2957 | CH3 & CH2 rocking | 1186 |
| CH symmetric stretch | 2917 | CH3 symmetric stretch | 2895 | CH stretch | 2870 | CH3 wagging, deformation | 1155 |
| CH symmetric bend | 1543 | CH3 Asymmetric deformation | 1469 | CH3 & CH2 scissoring | 1466 | C-C asymmetric stretch | 1051 |
| CH asymmetric bend | 1311 | CH Symmetric deformation | 1379 | CH3 & CH wagging (in phase) | 1384 | CH3 & CCH deformation | 919 |
| CH3 rocking | 821 | CH3 & CH wagging (out of phase) | 1368 | C-C symmetric stretching | 869 | ||
| CH2 & CH wagging | 1331 | CH2 & CH3 twisting & rocking | 746 | ||||
| n-Butane [41] | i-Butane [44] | ||||||
| Description | ῦ (cm−1) | Description | ῦ (cm−1) | ||||
| CH3 asymmetric stretch | 2968 | CH3 asymmetric stretch | 2968 | ||||
| CH3 asymmetric stretch | 2965 | CH3 symmetric stretch | 2956 | ||||
| CH3 asymmetric stretch | 2912 | CH3 symmetric stretch | 2894 | ||||
| CH3 symmetric stretch | 2872 | CH asymmetric stretch | 2872 | ||||
| CH2 symmetric stretch | 2853 | CH3 asymmetric stretch | 2748 | ||||
| CH3 asymmetric deformation | 1460 | CH3 symmetric stretch | 2629 | ||||
| CH3 scissoring | 1442 | CH3 asymmetric stretch | 1477 | ||||
| CH3 twisting | 1300 | CH3 asymmetric bend | 1379 | ||||
| CH3 rocking | 1151 | CH asymmetric bend | 1334 | ||||
| CC stretching | 1059 | CCH3 bend | 1177 | ||||
| CC stretching | 837 | CC stretch | 925 | ||||
| CC bend | 797 | ||||||
| Author | Pre-Processing |
|---|---|
| Haghi et al. [16] | 1st derivative (Savitzky–Golay algorithm), smoothing over five points plus orthogonal signal correction (OSC). |
| Ferreiro et al. [2] | Iterative baseline correction (automatic weighted least squares, using a polynomial of order 2), spectral normalization (total area = 1), and mean centring. |
| Barbosa et al. [4] | 2nd derivative with Savitzky-Golay smoothing using 21-point windows and a 2nd order polynomial. |
| Rohwedder et al. [64] | 1st derivative (Savitzky–Golay algorithm) employing a 7-points window, 2nd order polynomial for baseline correction and smoothing. |
| Nurida et al. [52] | Baseline correction and mean center (for CO2 absorption). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreiro, B.; Andrade, J.; Paz-Quintáns, C.; López-Mahía, P.; Muniategui-Lorenzo, S. New Ways for the Advanced Quality Control of Liquefied Natural Gas. Energies 2022, 15, 359. https://doi.org/10.3390/en15010359
Ferreiro B, Andrade J, Paz-Quintáns C, López-Mahía P, Muniategui-Lorenzo S. New Ways for the Advanced Quality Control of Liquefied Natural Gas. Energies. 2022; 15(1):359. https://doi.org/10.3390/en15010359
Chicago/Turabian StyleFerreiro, Borja, Jose Andrade, Carlota Paz-Quintáns, Purificación López-Mahía, and Soledad Muniategui-Lorenzo. 2022. "New Ways for the Advanced Quality Control of Liquefied Natural Gas" Energies 15, no. 1: 359. https://doi.org/10.3390/en15010359
APA StyleFerreiro, B., Andrade, J., Paz-Quintáns, C., López-Mahía, P., & Muniategui-Lorenzo, S. (2022). New Ways for the Advanced Quality Control of Liquefied Natural Gas. Energies, 15(1), 359. https://doi.org/10.3390/en15010359







