Modelling the Transition towards a Carbon-Neutral Electricity System—Investment Decisions and Heterogeneity
Abstract
:1. Introduction
2. Methodology
2.1. Model Description
2.1.1. Overall Structure
2.1.2. Technologies
2.1.3. Time Slices
2.1.4. The Electricity Market
2.1.5. The Investment Decision Process
2.2. Carbon Tax
3. Case Design: Homogeneous and Heterogeneous Agents
3.1. Homogeneous Case
3.2. Heterogeneous Hurdle Rates (HHR) Case
3.3. Heterogeneous Foresight (HF) Case
4. Results and Discussion
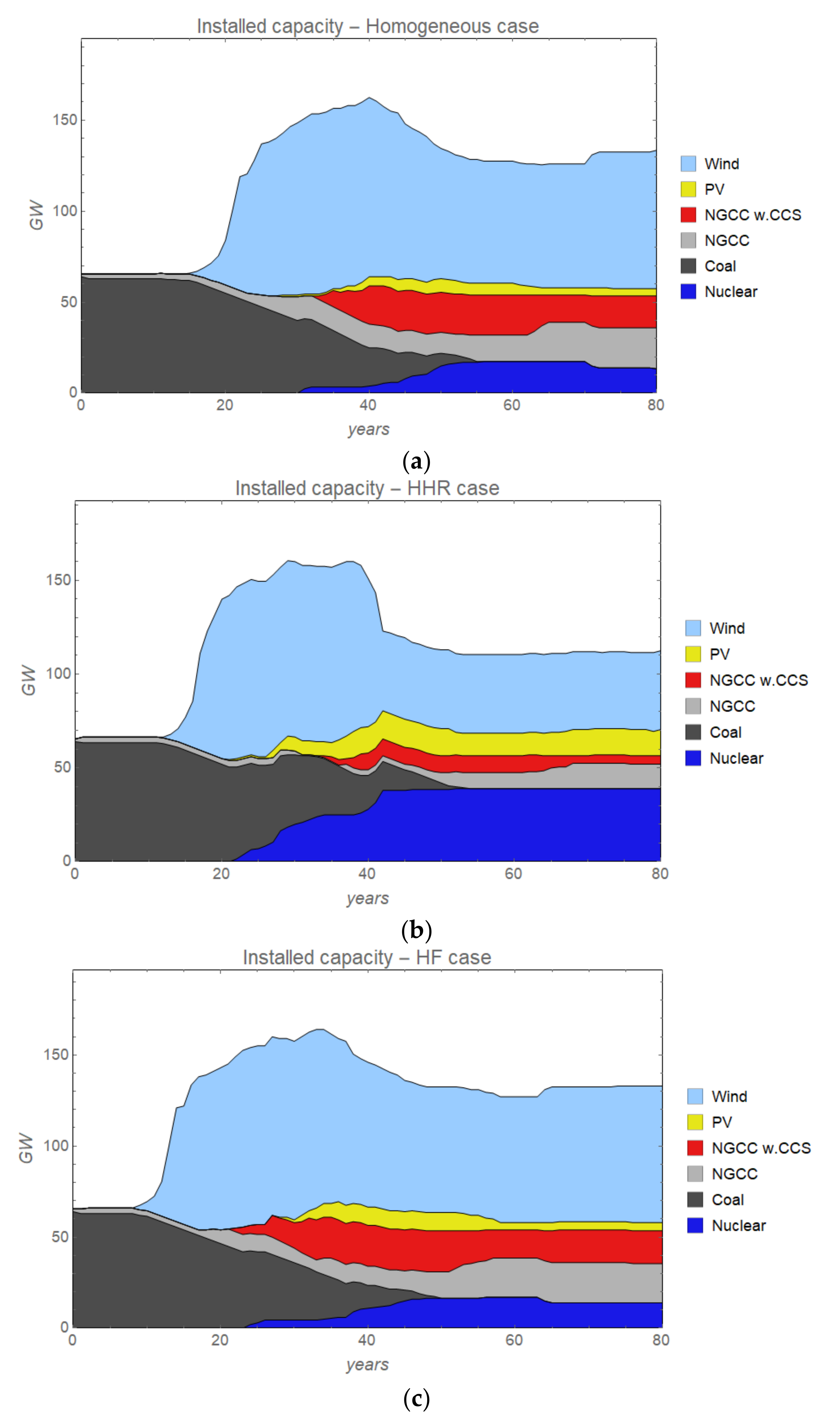
4.1. Installed Capacity
4.1.1. Homogeneous Case
4.1.2. Heterogeneous Hurdle Rate (HHR) Case
4.1.3. Heterogeneous Foresight (HF) Case
4.2. Electricity Price and Production
4.2.1. Average Electricity Price
4.2.2. Average Revenues per kWh Received by Wind—The So-Called “Cannibalisation Effect”
4.2.3. Electricity Price Variations
4.3. CO2 Emissions
4.4. Economic Performances—Ex-Post Analysis of the Investments
4.4.1. Internal Rate of Return of Investments
4.4.2. Economic Performance of Individual Agents
5. Impacts of Assumptions and Simplifications
5.1. Type of Agents
5.2. Electricity Demand
5.3. Size of the Plant
6. Conclusions
- The first phase takes place when wind starts to increase rapidly in response to the increasing carbon tax. This tax makes the electricity price grow, which makes investment in wind profitable. However, as the tax continues to grow, the price of electricity tends to increase most during those time periods of the year when wind output is low (because during those time periods dispatchable coal-based power generation is still used in combination with natural gas fired power plants).
- This takes us into the second phase (around the years 30–40) when changes of the profitability of future investment start to occur. During this phase it becomes more profitable to invest in technologies that can generate electricity also during time periods when wind output is low (and the electricity price is high). Thus, in this phase we see investments in nuclear, gas-fired power plants with biogas and natural gas with CCS, but also solar PV, and during this period wind capacity actually drops.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations. Paris Agreement; United Nations: Paris, France, 2015; pp. 1–27. [Google Scholar]
- Rogelj, J.; Shindell, D.; Jiang, K.; Fifita, S.; Forster, P.; Ginzburg, V.; Handa, C.; Kheshgi, H.; Kobayashi, S.; Kriegler, E.; et al. Mitigation Pathways Compatible with 1.5 °C in the Context of Sustainable Development; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018. [Google Scholar]
- Johansson, D.J.A.; Azar, C.; Lehtveer, M.; Peters, G.P. The role of negative carbon emissions in reaching the Paris climate targets: The impact of target formulation in integrated assessment models. Environ. Res. Lett. 2020, 15, 124024. [Google Scholar] [CrossRef]
- Azar, C.; Lindgren, K.; Larson, E.; Möllersten, K. Carbon Capture and Storage from Fossil Fuels and Biomass—Costs and Potential Role in Stabilizing the Atmosphere. Clim. Chang. 2006, 74, 47–79. [Google Scholar] [CrossRef]
- Braff, W.A.; Mueller, J.M.; Trancik, J.M.M.J.E. Value of storage technologies for wind and solar energy. Nat. Clim. Chang. 2016, 6, 964–969. [Google Scholar] [CrossRef]
- Capros, P.; Paroussos, L.; Fragkos, P.; Tsani, S.; Boitier, B.; Wagner, F.; Busch, S.; Resch, G.; Blesl, M.; Bollen, J. EURpean decarbonisation pathways under alternative technological and policy choices: A multi-model analysis. Energy Strat. Rev. 2014, 2, 231–245. [Google Scholar] [CrossRef]
- Capros, P.; Paroussos, L.; Fragkos, P.; Tsani, S.; Boitier, B.; Wagner, F.; Busch, S.; Resch, G.; Blesl, M.; Bollen, J. Description of models and scenarios used to assess EURpean decarbonisation pathways. Energy Strat. Rev. 2014, 2, 220–230. [Google Scholar] [CrossRef]
- Reichenberg, L.; Hedenus, F.; Odenberger, M.; Johnsson, F. The marginal system LCOE of variable renewables—Evaluating high penetration levels of wind and solar in EURpe. Energy 2018, 152, 914–924. [Google Scholar] [CrossRef]
- Hansen, P.; Liu, X.; Morrison, G.M. Agent-based modelling and socio-technical energy transitions: A systematic literature review. Energy Res. Soc. Sci. 2019, 49, 41–52. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chappin, E.J.; de Vries, L.J.; Richstein, J.C.; Bhagwat, P.; Iychettira, K.; Khan, S. Simulating climate and energy policy with agent-based modelling: The Energy Modelling Laboratory (EMLab). Environ. Model. Softw. 2017, 96, 421–431. [Google Scholar] [CrossRef] [Green Version]
- Jonson, E.; Azar, C.; Lindgren, K.; Lundberg, L. Exploring the competition between variable renewable electricity and a carbon-neutral baseload technology. Energy Syst. 2018, 11, 21–44. [Google Scholar] [CrossRef] [Green Version]
- Kraan, O.; Kramer, G.; Nikolic, I. Investment in the future electricity system—An agent-based modelling approach. Energy 2018, 151, 569–580. [Google Scholar] [CrossRef]
- Barazza, E.; Strachan, N. The impact of heterogeneous market players with bounded-rationality on the electricity sector low-carbon transition. Energy Policy 2020, 138, 111274. [Google Scholar] [CrossRef]
- Egli, F.; Steffen, B.; Schmidt, T.S. Bias in energy system models with uniform cost of capital assumption. Nat. Commun. 2019, 10, 4588. [Google Scholar] [CrossRef]
- Hirth, L.; Steckel, J.C. The role of capital costs in decarbonizing the electricity sector. Environ. Res. Lett. 2016, 11, 114010. [Google Scholar] [CrossRef]
- Bartlet, N.; Coleman, T.; Schmid, S. Putting a Price on Carbon—The State of Internal Carbon Pricing by Corporates Globally; CDP: Brussels, Belgium, 2021; 24p, Available online: https://cdn.cdp.net/cdp-production/cms/reports/documents/000/005/651/original/CDP_Global_Carbon_Price_report_2021.pdf?1618938446 (accessed on 21 October 2021).
- Trading Economics. EU Carbon Permits. 2021. Available online: https://tradingeconomics.com/commodity/carbon (accessed on 20 May 2021).
- EURpean Commission. EU Emissions Trading System (EU ETS). 2021. Available online: https://ec.EURpa.eu/clima/eu-action/eu-emissions-trading-system-eu-ets_en (accessed on 17 November 2021).
- Kruger, J. Hedging an Uncertain Future: Internal Carbon Prices in the Electric Power Sector. 2017. Available online: https://media.rff.org/documents/RFF-Rpt-Kruger-Internal20Carbon20Pricing.pdf (accessed on 17 November 2021).
- Barradale, M.J. Investment under uncertain climate policy: A practitioners׳ perspective on carbon risk. Energy Policy 2014, 69, 520–535. [Google Scholar] [CrossRef]
- Fuss, S.; Johansson, D.J.; Szolgayova, J.; Obersteiner, M. Impact of climate policy uncertainty on the adoption of electricity generating technologies. Energy Policy 2009, 37, 733–743. [Google Scholar] [CrossRef]
- Yang, M.; Blyth, W.; Bradley, R.; Bunn, D.; Clarke, C.; Wilson, T. Evaluating the power investment options with uncertainty in climate policy. Energy Econ. 2008, 30, 1933–1950. [Google Scholar] [CrossRef]
- Brealey, R.A.; Myers, S.C.; Allen, F. Principles of Corporate Finance, 11th ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Konstantin, P.; Konstantin, M. Investment Appraisal Methods. In Power and Energy Systems Engineering Economics: Best Practice Manual; Springer International Publishing: Cham, Switzerland, 2018; pp. 39–64. [Google Scholar]
- IEA. World Energy Investment 2019; IEA: Paris, France, 2019. [Google Scholar]
- IRENA. Renewable Power Generation Costs in 2017; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- EIA. The Electricity Market Module of the National Energy Modeling System: Model Documentation 2018; U.S. Energy Information Administration: Washington, DC, USA, 2018. [Google Scholar]
- Noothout, P.; de Jager, D.; Tesnière, L.; van Rooijen, S.; Karypidis, N.; Brückmann, R.; Jirouš, F.; Breitschop, B.; Angelopoulos, D.; Doukas, H.; et al. The Impact of Risks in Renewable Energy Investments and the Role of Smart Policies; Fraunhofer ISI: Brussels, Belgium, 2016. [Google Scholar]
- BP, P.L.C. Statistical Review of World Energy; BP: London, UK, 2021; Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 11 October 2021).
- Capion, K. Guest Post: Why German Coal Power is Falling Fast in 2019. 2019. Available online: https://www.carbonbrief.org/guest-post-why-german-coal-power-is-falling-fast-in-2019 (accessed on 20 May 2021).
- Joskow, P.L. Comparing the Costs of Intermittent and Dispatchable Electricity Generating Technologies. Am. Econ. Rev. 2011, 101, 238–241. [Google Scholar] [CrossRef] [Green Version]
- Sepulveda, N.A.; Jenkins, J.D.; de Sisternes, F.J.; Lester, R.K. The Role of Firm Low-Carbon Electricity Resources in Deep Decarbonization of Power Generation. Joule 2018, 2, 2403–2420. [Google Scholar] [CrossRef] [Green Version]
- Anwar, M.B.; Stephen, G.; Dalvi, S.; Frew, B.; Ericson, S.; Brown, M.; O′Malley, M. Modeling investment decisions from heterogeneous firms under imperfect information and risk in wholesale electricity markets. Appl. Energy 2022, 306, 117908. [Google Scholar] [CrossRef]
- Royal Dutch Shell P.L.C. CDP Climate Change 2021 Information Request; Royal Dutch Shell, P.L.C.: The Hague, The Netherlands, 2021; Available online: https://www.shell.com/sustainability/transparency-and-sustainability-reporting/performance-data/greenhouse-gas-emissions.html#vanity-aHR0cHM6Ly93d3cuc2hlbGwuY29tL2doZy5odG1s (accessed on 8 November 2021).
- Sensfuß, F.; Ragwitz, M.; Genoese, M. The merit-order effect: A detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy 2008, 36, 3086–3094. [Google Scholar] [CrossRef] [Green Version]
- Hirth, L. The market value of variable renewables: The effect of solar wind power variability on their relative price. Energy Econ. 2013, 38, 218–236. [Google Scholar] [CrossRef] [Green Version]
- López Prol, J.; Steininger, K.W.; Zilberman, D. The cannibalization effect of wind and solar in the California wholesale electricity market. Energy Eco. 2020, 85, 104552. [Google Scholar] [CrossRef]
- Brown, T.; Reichenberg, L. Decreasing market value of variable renewables is a result of policy. Energy Econ. 2021, 100, 105354. [Google Scholar] [CrossRef]
- Ballester, C.; Furió, D. Effects of renewables on the stylized facts of electricity prices. Renew. Sustain. Energy Rev. 2015, 52, 1596–1609. [Google Scholar] [CrossRef]
- Ketterer, J.C. The impact of wind power generation on the electricity price in Germany. Energy Econ. 2014, 44, 270–280. [Google Scholar] [CrossRef] [Green Version]
- Woo, C.K.; Moore, J.; Schneiderman, B.; Ho, T.; Olson, A.; Alagappan, L.; Chawla, K.; Toyama, N.; Zarnikau, J. Merit-order effects of renewable energy and price divergence in California’s day-ahead and real-time electricity markets. Energy Policy 2016, 92, 299–312. [Google Scholar] [CrossRef]
- Auer, H.; Haas, R. On integrating large shares of variable renewables into the electricity system. Energy 2016, 115, 1592–1601. [Google Scholar] [CrossRef]
- Brown, S. German State Awards EUR 317 Million To Loss-Making Coal Plants; Ember: London, UK, 2021; Available online: https://ember-climate.org/commentary/2020/12/08/german-hard-coal/ (accessed on 11 October 2021).
- Carbon Tracker Initiative. Four in Five EU Coal Plants Unprofitable as Renewables and Gas Power Ahead; Carbon Tracker Initiative: London, UK, 2019; Available online: https://carbontracker.org/four-in-five-eu-coal-plants-unprofitable-as-renewables-and-gas-power-ahead/ (accessed on 2 November 2021).
- Gils, H.C. Economic potential for future demand response in Germany—Modeling approach and case study. Appl. Energy 2016, 162, 401–415. [Google Scholar] [CrossRef] [Green Version]
- Göransson, L.; Johnsson, F. A comparison of variation management strategies for wind power integration in different electricity system contexts. Wind. Energy 2018, 21, 837–854. [Google Scholar] [CrossRef]
- Schill, W.-P. Electricity Storage and the Renewable Energy Transition. Joule 2020, 4, 2059–2064. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Azar, C.; Lindgren, K. Modelling the Transition towards a Carbon-Neutral Electricity System—Investment Decisions and Heterogeneity. Energies 2022, 15, 84. https://doi.org/10.3390/en15010084
Yang J, Azar C, Lindgren K. Modelling the Transition towards a Carbon-Neutral Electricity System—Investment Decisions and Heterogeneity. Energies. 2022; 15(1):84. https://doi.org/10.3390/en15010084
Chicago/Turabian StyleYang, Jinxi, Christian Azar, and Kristian Lindgren. 2022. "Modelling the Transition towards a Carbon-Neutral Electricity System—Investment Decisions and Heterogeneity" Energies 15, no. 1: 84. https://doi.org/10.3390/en15010084
APA StyleYang, J., Azar, C., & Lindgren, K. (2022). Modelling the Transition towards a Carbon-Neutral Electricity System—Investment Decisions and Heterogeneity. Energies, 15(1), 84. https://doi.org/10.3390/en15010084





