Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis
Abstract
:1. Introduction
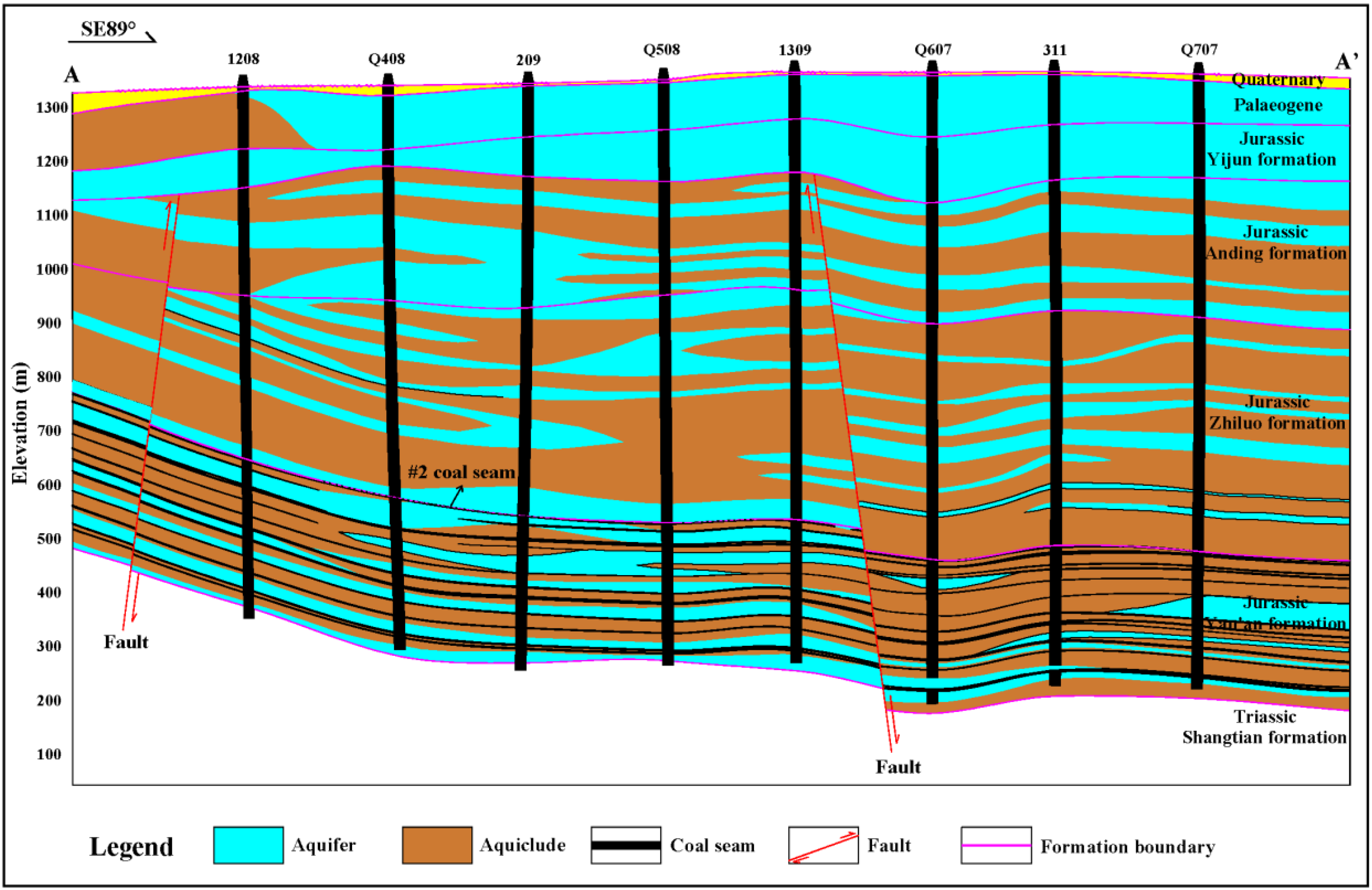
2. Height Measurement of WCFZ in Western Ordos Basin
3. Univariate Regression Analysis
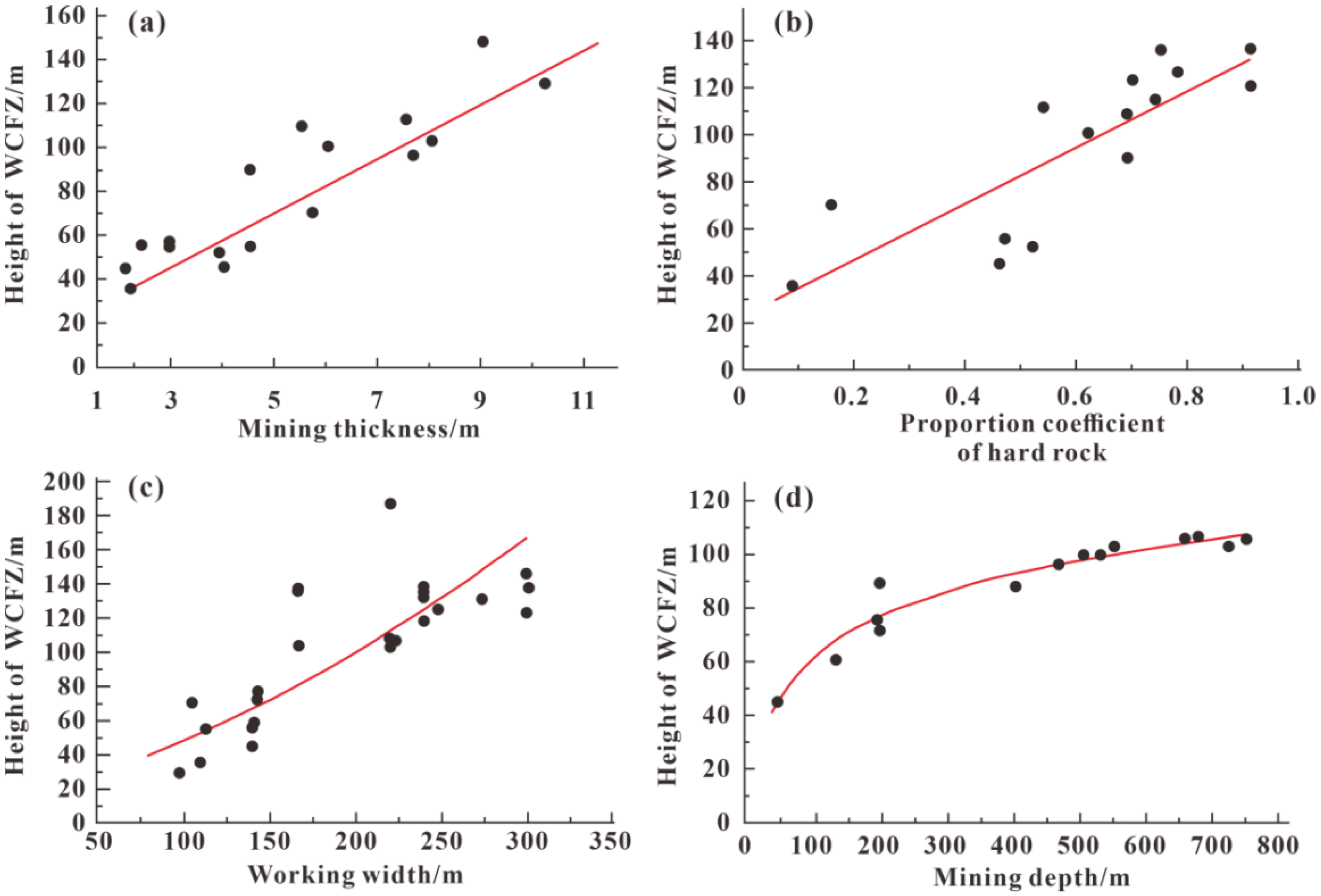
3.1. Mining Thickness (M)
3.2. Proportion Coefficient of Hard Rock (b)
3.3. Working Width (L)
3.4. Mining Depth (S)
4. Multiple Regression Analysis to Predict the Height of WCFZ
4.1. Grey Correlation Method
4.1.1. Construction of Comparative Sequence
4.1.2. Determination of Optimal Reference Sequence
4.1.3. Calculation of Correlation Degree
4.1.4. Calculation of Weight of Each Factor
4.2. Fuzzy Ordered Binary Comparison Method
4.2.1. Consistency Sequencing
4.2.2. Mood Operators and Relative Weights
4.2.3. Ordered Binary Comparison and Quantization
4.3. Comprehensive Weight Calculation
4.4. Model Determination
5. Error Contrast Analysis
6. Study Case
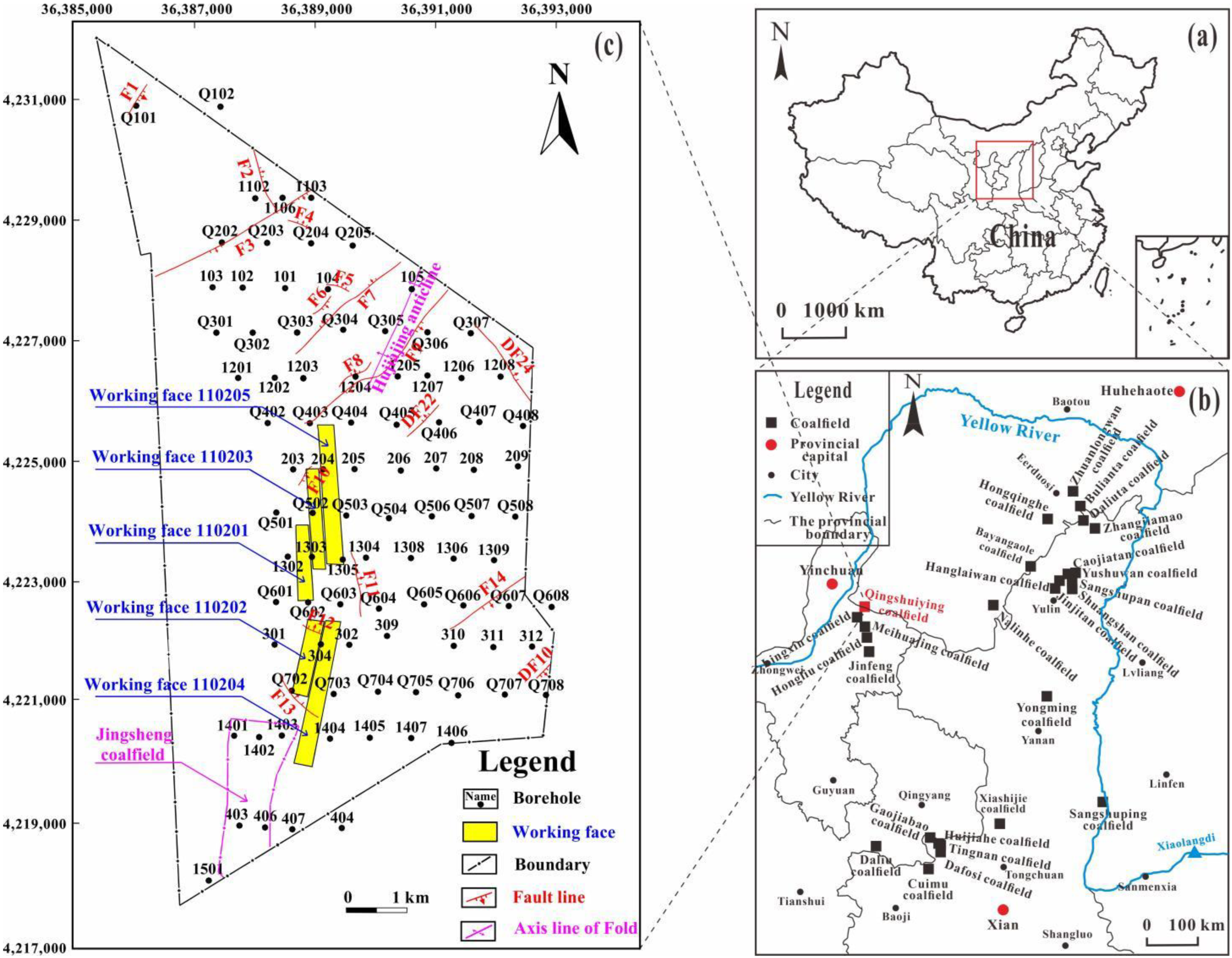
6.1. Overview of the Study Area
6.2. Calculation of the Height of WCFZ Based on Borehole
- (1)
- Index factor acquisition
- (2)
- Calculation of the height of WCFZ
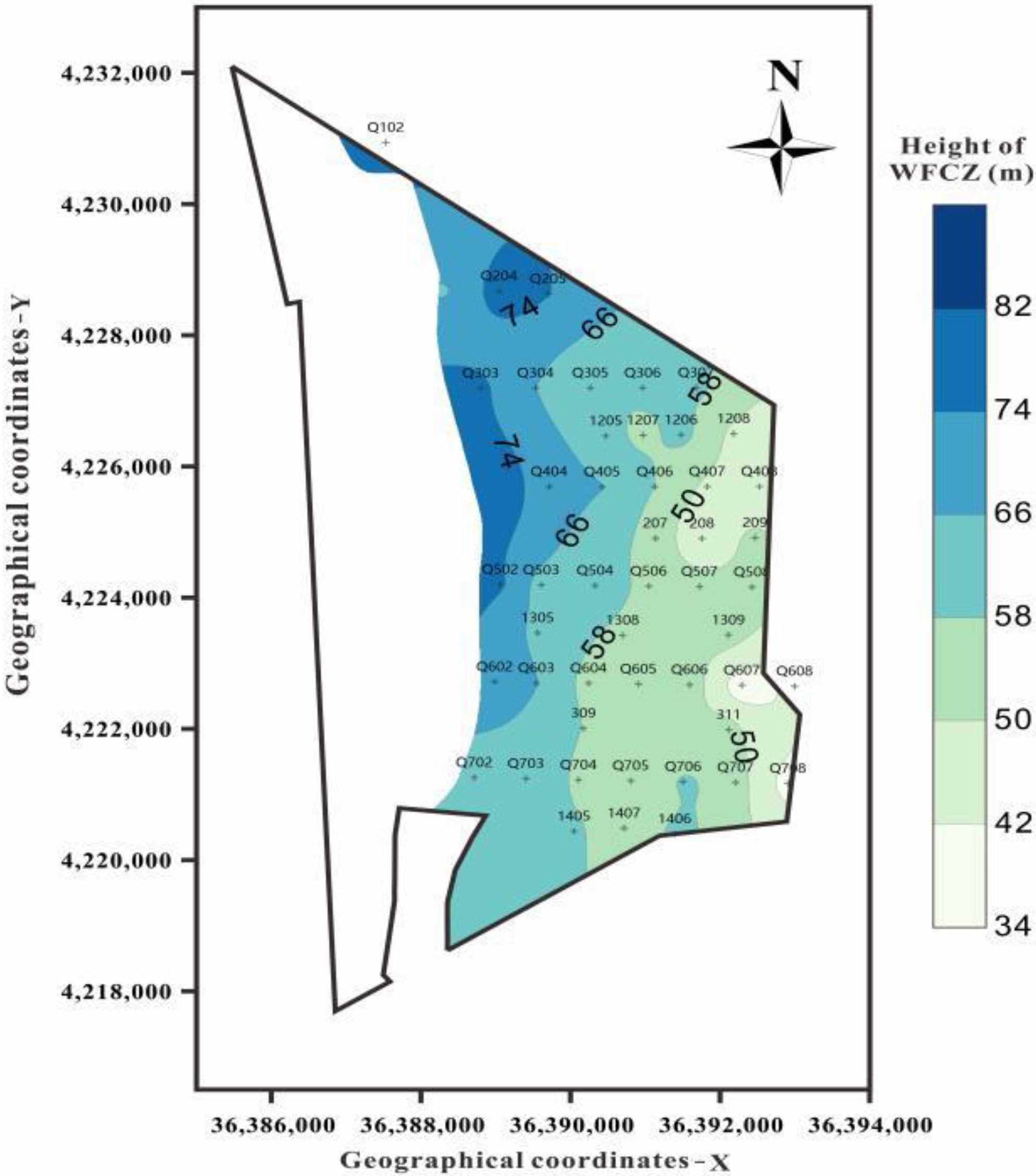
6.3. Safety Zoning of Risk Cracking
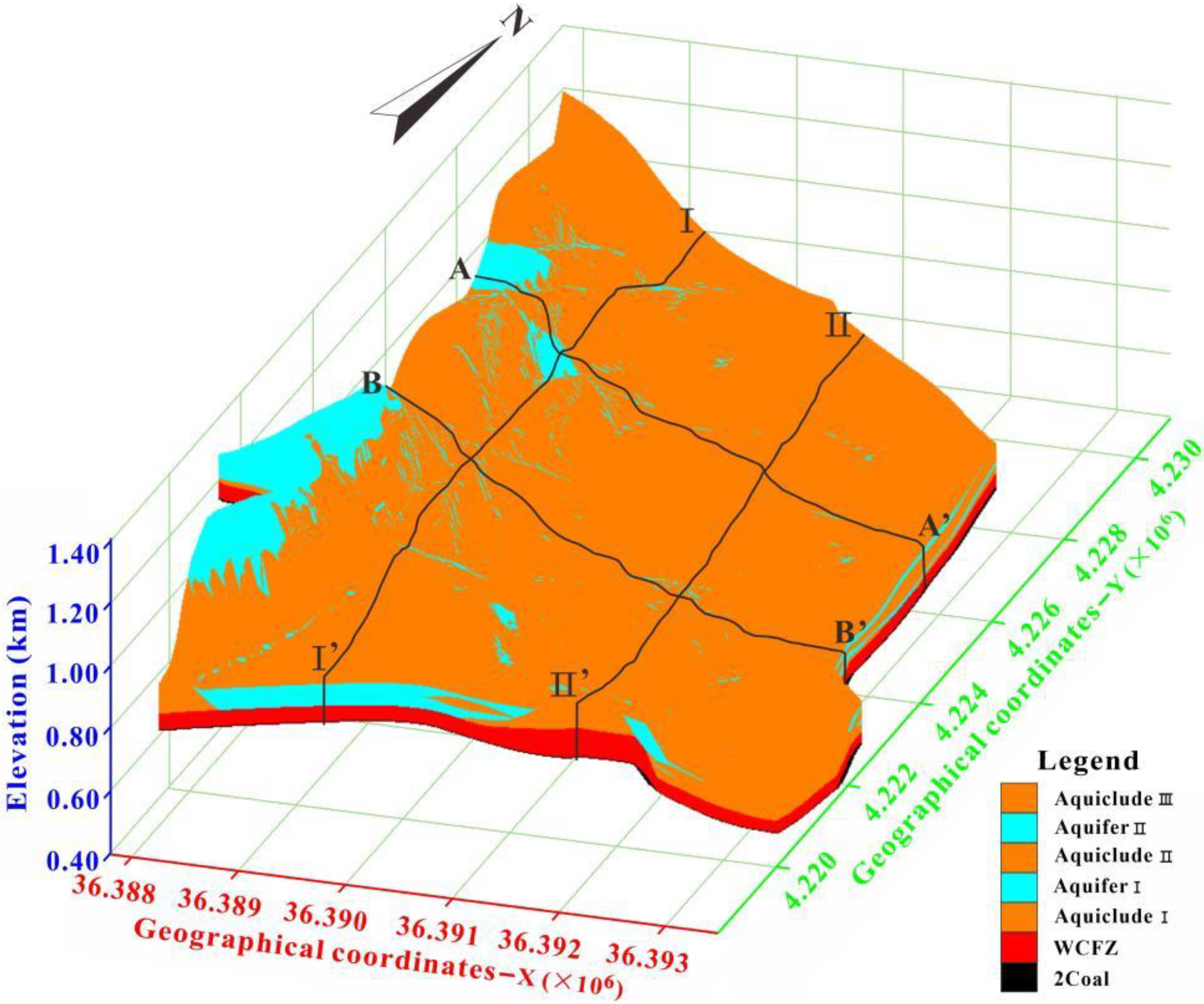
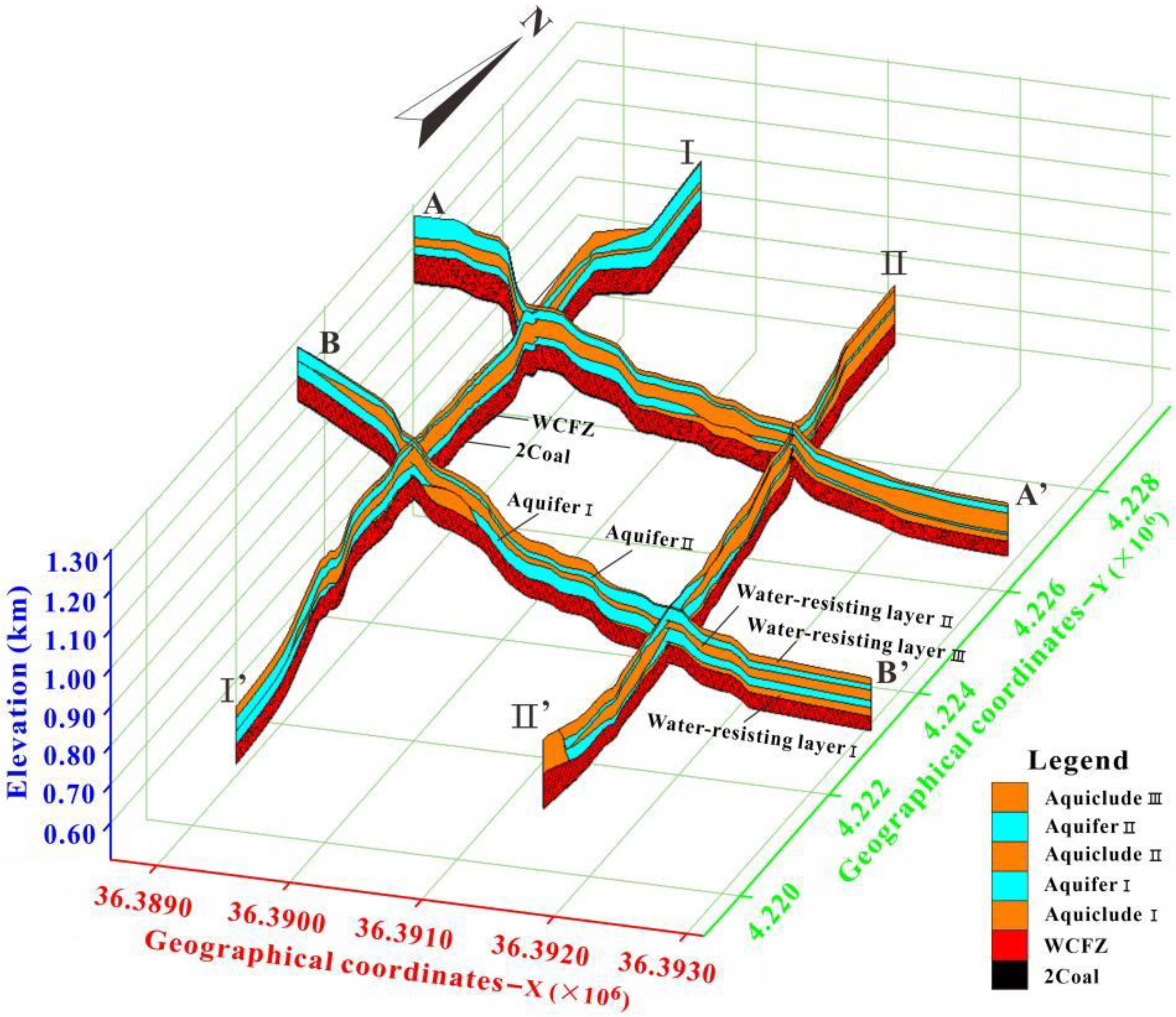
6.4. 3D Structure Model of WCFZ
7. Conclusions
- 1.
- The optimal unitary function models of mining thickness and proportion coefficient of hard rock were unitary linear equations, with R2 of 0.863 and 0.674, respectively. The optimal unitary function models of the working width were S-shaped curves with R2 of 0.725. The optimal unitary function models of mining depth were logarithmic curves with R2 of 0.939. The sensitivity of each factor to the height of the WCFZ was in this order: mining thickness > proportion coefficient of hard rock > working width > mining depth.
- 2.
- Based on the comprehensive consideration of five influencing factors: mining method, mining thickness, proportion coefficient of hard rock, working width, and mining depth, a multiple regression prediction model for the height of the WCFZ under fully mechanized caving in the western Ordos Basin area was established. The error of this model was basically controlled within 10%, which is much smaller than the traditional empirical equations.
- 3.
- The prediction model was applied to Qingshuiying Coalfield, and the height of the WCFZ was predicted based on borehole data. The distribution characteristics of the WCFZ height showed an increased trend from southeast to northwest in the study area, and the prediction zone of cracking safety was obtained by reference to the water-rich condition of the strata.
- 4.
- A 3D visualization model of the WCFZ was established in the study area to clearly show the spatial distribution law of the WCFZ and the spatial relationship between the WCFZ and the overlying aquifer (aquiclude). The visualization model has achieved the desired application effect and provided an advanced technology for the prevention and control of Coal Mine water.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, T.; Shao, L.Y.; Xia, Y.C.; Fu, X.H.; Sun, Y.Z.; Sun, Y.J.; Ju, Y.W.; Bi, Y.L.; Yu, J.C.; Xie, Z.Q.; et al. Major achievements and future research directions of the coal geology in China. Geol. China 2017, 44, 242–262. [Google Scholar] [CrossRef]
- Guo, X.; Hu, Z.; Fu, S.; Dong, Y.; Jiang, G.; Li, Y. Experimental study of the remediation of acid mine drainage by Maifan stones combined with SRB. PLoS ONE 2022, 7, e0261823. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.Q.; Wang, S.M.; Fan, L.M.; Wu, L.Q.; Rong, H.; Zhang, F. Key elements and framework model of groundwater system in Jurassic coal measures of Ordos Basin. J. China Coal Soc. 2020, 45, 2411–2422. [Google Scholar] [CrossRef]
- Gu, J.Y.; Zhang, X.Y. Sedimentary characteristics and sequence framework of intracontinental foreland Basin in the western China. Acta Sedimentol. Sin. 2005, 23, 187–193. [Google Scholar]
- Li, P.Y. Mine water problems and solutions in China. Mine Water Environ. 2018, 37, 217–221. [Google Scholar] [CrossRef]
- Liu, S.L.; Li, W.P.; Wang, Q.Q. Height of the Water-flowing fractured zone of the Jurassic coal seam in northwestern China. Mine Water Environ. 2018, 37, 312–321. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, Y.X.; Gan, Q.; Nie, X.D.; Zhu, G.P.; Hu, Y. Investigations into mining-induced stress-fracture- seepage field coupling in a complex hydrogeology environment: A case study in the bulianta colliery. Mine Water Environ. 2019, 38, 632–642. [Google Scholar] [CrossRef]
- Light, D.D.M.; Donovan, J.J. Mine-water flow between contigu-ous flooded underground coal mines with hydraulically compro-mised barriers. Environ. Eng. Geosci. 2015, 21, 147–164. [Google Scholar] [CrossRef]
- Adams, R.; Younger, P.L. A strategy for modeling groundwater rebound in abandoned deep mine systems. Groundwater 2001, 39, 249–261. [Google Scholar] [CrossRef]
- Booth, C.J. Strata-movement concepts and the hydrogeological impact of underground coal mining. Groundwater 1986, 24, 507–515. [Google Scholar] [CrossRef]
- Miao, X.X.; Cui, X.M.; Wang, J.A.; Xu, J.L. The height of fractured water-conducting zone in undermined rock strata. Eng. Geol. 2011, 120, 32–39. [Google Scholar] [CrossRef]
- Wang, H.L.; Jia, C.Y.; Yao, Z.K.; Zhang, G.B. Height measurement of the water-conducting fracture zone based on stress monitoring. Arab. J. Geosci. 2021, 14, 1392. [Google Scholar] [CrossRef]
- Zhai, W.; Li, W.; Huang, Y.L.; Ouyang, S.Y.; Ma, K.; Li, J.M.; Gao, H.D.; Zhang, P. A Case Study of the Water Abundance Evaluation of Roof Aquifer Based on the Development Height of Water-Conducting Fracture Zone. Energies 2020, 13, 4095. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, S.Y. Determination of caved and water-conducting fractured zones of “two soft and one hard” unstable coal seam. Acta Geod. Geophys. 2020, 55, 451–475. [Google Scholar] [CrossRef]
- Guo, C.F.; Yang, Z.; Li, S.; Lou, J.F. Predicting the water-conducting fracture zone (WCFZ) height using an MPGA-SVR approach. Sustainability 2020, 12, 1809. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.K.; Wu, Q. An approach to predict the height of fractured water-conducting zone of coal roof strata using random forest regression. Sci. Rep. 2018, 8, 10986. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Zhao, Y.X.; Zhang, C.; Han, P.H. A model to estimate the height of the water-conducting fracture zone for longwall panels in western China. Mine Water Environ. 2020, 39, 823–838. [Google Scholar] [CrossRef]
- Xie, X.S.; Hou, E.K.; Wang, S.M.; Sun, X.Y.; Hou, P.F.; Wang, S.B.; Xie, Y.L.; Huang, Y.A. Formation mechanism and the height of the water-conducting fractured zone induced by middle deep coal seam mining in a sandy region: A case study from the Xiaobaodang coal mine. Adv. Civ. Eng. 2021, 2021, 6684202. [Google Scholar] [CrossRef]
- Gusev, V.N.; Ilyukhin, D.A. Determination of water conducting fracture zone for mining and geological conditions of the Verkhnekamsk salt deposit. In Innovation-Based Development of the Mineral Resources Sector: Challenges and Prospects: Proceedings of the 11th Russian-German Raw Materials Conference, Potsdam, Germany, 7–8 November 2018; CRC Press: Boca Raton, FL, USA, 2018; pp. 195–204. [Google Scholar]
- Li, X.B.; Li, Q.S.; Xu, X.H.; Zhao, Y.Q.; Li, P. Multiple influence factor sensitivity analysis and height prediction of water-conducting fracture zone. Geofluids 2021, 2021, 8825906. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Q.M.; Li, W.P.; Li, T.; He, J.H. Height of water-conducting fractured zone in coal mining in the soil-rock composite structure overburdens. Environ. Earth Sci. 2019, 78, 242. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, S.G.; Guo, S.; Wan, T.; Wang, J. Mechanisms of the development of water-conducting fracture zone in overlying strata during shortwall block backfill mining: A case study in Northwestern China. Environ. Earth Sci. 2018, 77, 543. [Google Scholar] [CrossRef]
- Zhu, T.E.; Li, W.P.; Wang, Q.Q.; Hu, Y.B.; Fan, K.F.; Du, J.F. Study on the height of the mining-induced water-conducting fracture zone under the Q(2l) loess cover of the Jurassic coal seam in Northern Shaanxi, China. Mine Water Environ. 2020, 39, 57–67. [Google Scholar] [CrossRef]
- Du, F.; Gao, R. Development patterns of fractured water-conducting zones in Longwall mining of thick coal seams-a case study on safe mining under the Zhuozhang River. Energies 2017, 10, 1856. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Wang, L.G.; Lu, Y.L.; Li, Z.L.; Li, W.S.; Wang, K. Height of water-conducting fractured zone in a coal seam overlain by thin bedrock and thick clay layer: A case study from the Sanyuan Coal Mine in North China. Environ. Earth Sci. 2020, 79, 125. [Google Scholar] [CrossRef]
- Shi, L.Q.; Wu, H.B.; Li, Y.L.; Lv, W.K. Optimization model of PCA-GA-Elman for development height prediction of water-conducting fissure zone. J. Henan Polytech. Univ. 2021, 40, 10–18. [Google Scholar] [CrossRef]
- Hu, X.J.; Li, W.P.; Cao, D.T.; Liu, M.C. Index of multiple factors and expected height of fully mechanized water flowing fractured zone. J. China Coal Soc. 2012, 37, 613–620. [Google Scholar] [CrossRef]
- Aydin, H.; Bayram, A.; Esme, U.; Kazancoglu, Y.; Guven, O. Application of grey relation analysis (GRA) and taguchi method for the parametric optimization of friction stir welding (FSW) process. Mater. Tehnol. 2010, 44, 205–211. [Google Scholar]
- Kim, G.Y.; Jong, Y.; Liu, S.F. Generalized hybrid grey relation method for multiple attribute mixed type decision making. J. Grey Syst. 2014, 26, 142–153. [Google Scholar]
- Wakchaure, K.N.; Thakur, A.G.; Gadakh, V.; Kumar, A. Multi-Objective optimization of friction stir welding of aluminium alloy 6082-T6 using hybrid taguchi-grey relation analysis-ANN method. Mater. Today Proc. 2018, 5, 7150–7159. [Google Scholar] [CrossRef]
- Xia, X.T.; Meng, F.N.A.; Lv, T.M. Grey relation method for calculation of embedding dimension and delay time in phase space reconstruction. J. Grey Syst. 2010, 22, 105–116. [Google Scholar]
- Cui, Z.C.; Yang, Y.Z.; Gao, X.L.; Xiao, H.; Liu, H.C. Research and application of ecological river courses restoration technology. In Proceedings of the International Conference on Water Resource and Environment, Shanghai, China, 23–26 July 2016. [Google Scholar] [CrossRef] [Green Version]
- Scannapieco, D.; Naddeo, V.; Zarra, T.; Belgiorno, V. River water quality assessment: A comparison of binary and fuzzy logic-based approaches. Ecol. Eng. 2012, 47, 132–140. [Google Scholar] [CrossRef]
- Wang, W.C.; Xu, D.M.; Chau, K.W.; Lei, G.J. Assessment of river water quality based on theory of variable fuzzy sets and fuzzy binary comparison method. Water Resour. Manag. 2014, 28, 4183–4200. [Google Scholar] [CrossRef]
- Liu, H. Research on Determination method of Index Weight in Comprehensive Evaluation. J. Hebei Univ. Technol. 1996, 4, 75–80. [Google Scholar]
- State Bureau of Coal Industry. Rules for Coal Pillar Reservation and Coal Pressure Mining in Buildings, Water Bodies, Railways and Main Shafts; Coal Industry Press: Beijing, China, 2017. [Google Scholar]
- Alessandro, S.; Paola, M.; Giuseppe, P.; Paolo, C.; Francesco, P.; Valentina, C.; Michele, S. The Integration of 3D Modeling and Simulation to Determine the Energy Potential of Low-Temperature Geothermal Systems in the Pisa (Italy) Sedimentary Plain. Energies 2018, 11, 1591. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.Q.; Dong, D.L.; Zhang, F.; Xu, Z.C. A novel three-dimensional mine area hydrogeological model based on groundwater modeling systems. J. Coast. Res. 2020, 105, 141–146. [Google Scholar] [CrossRef]
- Du, B. Model investigation for groundwater aquifer structure in a mining area based on groundwater modeling system (GMS). Coal Geol. China 2020, 32, 27–32. [Google Scholar] [CrossRef]

| Coalfield | Working Face/Borehole | Mining Method | Mining Depth (S)/m | Working Width (L)/m | Mining Thickness (M)/m | Proportion Coefficient of Hard Rock (b)/m | Measured Height of WCFZ (Hf)/m |
|---|---|---|---|---|---|---|---|
| Bayangaole | 311,101 | ZF | 620.00 | 260.00 | 5.27 | 0.78 | 126.00 |
| Bulianta | 12,406 | ZF | 200.00 | 310.00 | 4.50 | 0.69 | 89.50 |
| Caojiatan | 122,106 | ZF | 279.99 | 350.00 | 6.00 | 0.91 | 136.10 |
| Cuimu | 210,303 | ZF | 552.19 | 200.00 | 6.50 | 190.51 | |
| Dafosi | 41,104 | ZF | 400.00 | 180.00 | 3.90 | 110.00 | |
| Daliu | 1203 | ZF | 49.00 | 135.00 | 4.00 | 0.52 | 45.00 |
| Daliuta | 52,306 | ZF | 180.00 | 301.00 | 7.00 | 0.90 | 137.32 |
| Gaojiabao | 41,101 | ZF | 400.00 | 120.00 | 4.36 | 88.03 | |
| Hanglaiwan | 30,101 | ZF | 300.00 | 248.00 | 7.50 | 0.67 | 112.60 |
| H3 | ZF | 241.30 | 300.00 | 4.50 | 0.69 | 108.32 | |
| H4 | ZF | 244.00 | 300.00 | 4.50 | 0.74 | 114.38 | |
| Hongliulin | 25,202 | ZF | 135.00 | 350.00 | 5.80 | 60.70 | |
| Hongqinghe | 3−1101 | ZF | 669.00 | 240.00 | 6.10 | 107.00 | |
| 3−1401 | ZF | 740.00 | 241.00 | 6.00 | 106.10 | ||
| Hujiahe | 401,101 | ZF | 525.00 | 180.00 | 6.00 | 0.62 | 100.00 |
| 401,102 | ZF | 650.00 | 180.00 | 10.00 | 0.62 | 133.00 | |
| 401,103 | ZF | 650.00 | 180.00 | 8.00 | 0.62 | 106.40 | |
| Jinjitan | 101 | ZF | 260.00 | 300.00 | 5.50 | 108.59 | |
| 102 | ZF | 264.98 | 300.00 | 5.50 | 0.54 | 111.32 | |
| 12−2101 | ZF | 260.00 | 300.00 | 5.50 | 0.90 | 109.72 | |
| JT6 | ZF | 270.20 | 300.00 | 5.00 | 0.912 | 120.25 | |
| JKY2 | ZF | 260.00 | 300.00 | 5.50 | 0.70 | 122.64 | |
| JSD2 | ZF | 247.60 | 300.00 | 5.50 | 0.44 | 115.00 | |
| JSD4 | ZF | 232.38 | 300.00 | 5.50 | 0.79 | 146.18 | |
| Longde | 205 | ZF | 195.90 | 182.00 | 3.96 | 75.78 | |
| 206 | ZF | 199.90 | 182.00 | 3.96 | 71.66 | ||
| Namuhe | ZF | 544.00 | 240.00 | 6.00 | 103.23 | ||
| Sangshuping | 3303 | ZF | 370.00 | 153.00 | 5.70 | 0.16 | 70.00 |
| Shenshupan | No. 3 | ZF | 673.00 | 200.00 | 10.00 | 0.95 | 120.00 |
| Shuangshan | No. 3 | ZF | 713.00 | 200.00 | 8.00 | 0.93 | 103.09 |
| Tingnan | 106 | ZF | 463.07 | 116.05 | 7.65 | 0.63 | 96.45 |
| 107 | ZF | 453.00 | 116.00 | 7.60 | 0.62 | 86.40 | |
| 104 | ZF | 550.02 | 200.00 | 6.00 | 0.60 | 136.20 | |
| 105 | ZF | 575.00 | 200.00 | 6.00 | 135.23 | ||
| Y3 | ZF | 702.00 | 200.00 | 9.00 | 0.39 | 148.30 | |
| Y1-1 | ZF | 533.20 | 200.00 | 7.50 | 0.35 | 140.20 | |
| 303 | ZF | 500.00 | 180.00 | 3.50 | 100.00 | ||
| Xibu | ZF | 568.40 | 180.40 | 2.94 | 0.85 | 57.00 | |
| ZF | 550.00 | 180.00 | 2.40 | 0.81 | 55.32 | ||
| ZF | 489.00 | 160.00 | 4.50 | 0.47 | 54.79 | ||
| ZF | 516.00 | 206.10 | 2.95 | 0.74 | 54.50 | ||
| ZF | 420.50 | 209.00 | 3.90 | 0.52 | 52.01 | ||
| ZF | 679.00 | 180.00 | 2.10 | 0.46 | 44.54 | ||
| ZF | 412.00 | 157.00 | 2.20 | 0.09 | 35.40 | ||
| Xiashijie | 223 | ZF | 620.00 | 240.00 | 7.00 | 187.40 | |
| Yongming | 5103 | ZF | 275.00 | 148.00 | 1.40 | 29.58 | |
| Yushuwan | 20,104 | ZF | 280.00 | 255.00 | 5.00 | 0.75 | 135.40 |
| Y3 | ZF | 276.00 | 255.00 | 5.00 | 0.54 | 130.50 | |
| Y4 | ZF | 279.30 | 255.00 | 5.00 | 0.62 | 137.30 | |
| Y6 | ZF | 275.80 | 255.00 | 5.00 | 0.57 | 117.80 | |
| Zhangjiamao | 3201 | ZF | 500.00 | 104.00 | 11.10 | 0.83 | 152.34 |
| Zhuanlongwan | 23,103 | ZF | 210.00 | 260.00 | 4.50 | 92.10 |
| Linear Equation | Conic | Cubic Curve | Logistic Curve | S-Shape Curve | Exponential Curve | Power Function Curve | |
|---|---|---|---|---|---|---|---|
| Mining thickness | 0.863 | 0.852 | \ | \ | \ | 0.825 | 0.829 |
| Proportion coefficient of hard rock | 0.674 | \ | \ | 0.539 | 0.549 | \ | 0.587 |
| Working width | 0.620 | \ | 0.712 | 0.660 | 0.725 | 0.636 | \ |
| Mining depth | 0.834 | 0.923 | \ | 0.939 | 0.859 | 0.764 | 0.934 |
| Mining Thickness | Proportion Coefficient of Hard Rock | Working Width | Mining Depth | |
|---|---|---|---|---|
| Weight determined by grey correlation analysis (wi) | 0.2995 | 0.2956 | 0.2398 | 0.1651 |
| Weight determined by fuzzy ordered binary comparison (wj) | 0.449 | 0.316 | 0.164 | 0.071 |
| Comprehensive weight (wz) | 0.39 | 0.31 | 0.2 | 0.1 |
| Mining Thickness | Mining Depth | Working Width | Proportion Coefficient of Hard Rock | ti | |
|---|---|---|---|---|---|
| Mining thickness | 0.5 | 1 | 1 | 1 | 3.5 |
| Mining depth | 0 | 0.5 | 0 | 0 | 0.5 |
| Working width | 0 | 1 | 0.5 | 0 | 1.5 |
| Proportion coefficient of hard rock | 0 | 1 | 1 | 0.5 | 2.5 |
| Number | Working Face Name | Mining Thickness (M)/m | Proportion Coefficient of Hard Rock (b)/m | Mining Depth (S)/m | Working Width (L)/m | Measured Height of WCFZ/m | Empirical Formula (19) | Empirical Formula (20) | Prediction Model of This Paper | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Predictive Value/m | Relative Error % | Predictive Value/m | Relative Error % | Predictive Value/m | Relative Error % | |||||||
| 1 | Qingshuiying Coalfield 11201 | 5.43 | 0.75 | 210 | 280 | 62.84 | 49.79 | 20.77 | 56.60 | 9.92 | 60.39 | 3.90 |
| 2 | Meihuajing Coalfield 11201 | 2.7 | 0.65 | 220 | 256 | 46.45 | 39.69 | 14.55 | 42.86 | 7.72 | 46.18 | 0.59 |
| 3 | Jinfeng Coalfield 011802 | 4.6 | 0.72 | 500 | 280 | 63.12 | 47.57 | 24.63 | 52.90 | 16.20 | 57.40 | 9.06 |
| 4 | Lingxin Coalfield 051503 | 3.5 | 0.72 | 250 | 280 | 59.24 | 43.64 | 26.33 | 47.42 | 19.96 | 52.17 | 11.94 |
| 5 | Hongliu Coalfield 1221 | 5.3 | 0.7 | 330 | 302 | 62.59 | 49.47 | 20.96 | 56.04 | 10.46 | 60.11 | 3.97 |
| 6 | Hongliu Coalfield 1010206 | 5.28 | 0.68 | 280 | 300 | 56.02 | 49.42 | 11.77 | 55.96 | 0.11 | 59.28 | −5.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Dong, F.; Zhang, Y.; Cheng, W.; Zhai, P.; Ren, X.; Liu, Z.; Zhai, Y.; Li, X. Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis. Energies 2022, 15, 3850. https://doi.org/10.3390/en15113850
Yin H, Dong F, Zhang Y, Cheng W, Zhai P, Ren X, Liu Z, Zhai Y, Li X. Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis. Energies. 2022; 15(11):3850. https://doi.org/10.3390/en15113850
Chicago/Turabian StyleYin, Huiyong, Fangying Dong, Yiwen Zhang, Wenju Cheng, Peihe Zhai, Xuyan Ren, Ziang Liu, Yutao Zhai, and Xin Li. 2022. "Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis" Energies 15, no. 11: 3850. https://doi.org/10.3390/en15113850
APA StyleYin, H., Dong, F., Zhang, Y., Cheng, W., Zhai, P., Ren, X., Liu, Z., Zhai, Y., & Li, X. (2022). Height Prediction and 3D Visualization of Mining-Induced Water-Conducting Fracture Zone in Western Ordos Basin Based on a Multi-Factor Regression Analysis. Energies, 15(11), 3850. https://doi.org/10.3390/en15113850





