Pulse-Amplitude-Modulation Full-Bridge Diode-Clamped Multilevel LLC Resonant Converter Using Multi-Neighboring Reference Vector Discontinuous PWM

Abstract

A full-bridge diode-clamped multilevel LLC resonant converter suitable for power conversion systems that use high input voltage, such as railway vehicles, is proposed in this paper. In order to eliminate the voltage deviations of the capacitors connected in series to the high voltage input DC link, a novel modulation strategy referred to as multi-neighboring reference vector discontinuous pulse-width modulation (MNRV DPWM) is proposed. Unlike the existing two-level resonant converter that varies the operating frequency to hold the output voltage constant, the proposed multilevel resonant converter modulates the amplitude of the fundamental wave input to a resonance tank while fixing the operating frequency at the resonance point. Therefore, the design of passive elements becomes easier, and stable operation is possible over a wide operating range with only one power conversion stage. In this paper, the control algorithm and operation characteristics of the newly proposed full-bridge diode-clamped four-level LLC resonant converter are analyzed in detail and design guidelines are presented. The feasibility of the proposed converter is verified through a simulation and an experiment with a prototype converter.

1. Introduction

Due to excellent soft switching characteristics such as primary-side zero-voltage switching (ZVS) and secondary-side zero-current switching (ZCS), LLC resonant converters are widely used in many areas such as electric vehicles, servers, uninterruptible power supplies, and TV power adapters. Furthermore, with regard to an LLC resonant converter operating at a high switching frequency, the power density can be greatly improved due to the reduction in the size of the passive element [1,2]. However, because the output voltage is controlled through frequency variations, a wide range of frequency sweeps is required in a wide input/load variation system, making it difficult to design optimal passive devices [3]. In addition, because most resonant converters developed thus far are based on a frequency-controlled two-level topology, they are not widely used in high-power systems with very high input voltages, such as railroad vehicles, due to the limited endurance voltage of the switching devices. Currently, as part of the effort to replace the existing low-frequency transformers, resonance topology-based power converters are widely applied to the auxiliary power systems of railway vehicles, with most being composed of two stages. One type is an LLC resonant converter controlled in an open loop with a fixed operating frequency, and the other is a constant-voltage regulator connected before or after the LLC converter, which also serves to provide proper voltage for the normal operation of the LLC resonant converter. This complicates the overall system configuration [4,5].

Meanwhile, multilevel converters have been studied extensively in an effort to overcome the limitations of the two-level topology [6,7,8,9,10]. The multilevel converter, as exemplified by the diode-clamped method, the flying capacitor method, and the cascaded H-bridge, can be applied to a high-voltage, high-power system with devices with low withstand voltages. It also has the advantage of a low harmonic content and low dv/dt generation. Among these three, in a system that receives power from a single external power supply line such as a railroad vehicle, the diode-clamped topology with a simple power stage configuration is suitable. However, with diode-clamped topologies, it is not easy to balance the DC link capacitor voltages to ensure equal voltage sharing and good performance, especially for level four and higher. Over the past three decades, numerous researchers have attempted to find appropriate modulation strategies to solve the voltage balance problem in a three-phase diode-clamped multilevel converter [11,12,13,14]. The addition of an external circuit to compensate for voltage deviations and a hybrid method that utilizes a diode-clamped circuit and a flying capacitor together both complicate the system and are not cost effective [15,16,17]. Recently, the voltage imbalance problem of a three-phase diode-clamped DC/AC inverter with three or more levels was resolved using a virtual vector scheme [18,19,20]. The voltage imbalance was eliminated by combining reference vectors whose associated current sum is zero with the aid of a virtual reference vector. However, in a three-phase system, the amount of calculation is increased because the phase angle as well as the magnitude of the reference voltage must be considered. In addition, it is not easy to find an optimal switching pattern due to the considerable redundancy of the switching pairs. The increased switching loss compared to the general space vector pulse-width modulation (SVPWM) scheme is another issue. Recently, carrier-overlapped PWM (COPWM) applicable to diode-clamped multilevel inverters was proposed [21]. With multiple carrier-based modulation, it can control capacitor voltage deviation while maintaining volt-second balance in a diode-clamped multilevel inverter with four or more levels. However, this method is effective under ideal conditions and requires a little complex closed-loop control under non-ideal conditions and increases switching losses compared to the conventional single-carrier method [22]. As previously discussed, most of the multilevel topologies known to date have been applied to three-phase inverter systems. Therefore, in order to apply the diode-clamped multilevel topology to the single-phase DC/DC converter, a new switching modulation technique is required that can effectively eliminate voltage deviations in series-connected DC link capacitors while simultaneously controlling the output voltage simply in a closed-loop control manner.

A multi-phase, multi-level LLC converter with a two-level topology-based modular structure has been proposed for high-voltage and high-power systems [23]. Because it is based on the existing frequency modulation method, it is difficult to optimally design passive components under wide input/load variation conditions. Additionally, a separate resonance tank is required for each sub-module, increasing the required number of passive elements. A suitable solution for voltage deviation between series-connected DC link capacitors has not been proposed. Input-series-output-parallel (ISOP) topology based on a two-level DAB converter can handle high voltage and high power [24]. However, the ISOP topology requires an additional passive element for each sub-module, which complicates the overall system. An additional control algorithm to guarantee a stable operation and an adequate input voltage distribution is also mandatory.

On the other hand, a fixed-frequency three-level full-bridge LLC resonant converter has been proposed [25]. The output voltage can be controlled by modulating the magnitude of the fundamental wave component of the voltage input to the resonance tank. However, since it does not operate as a typical diode-clamped topology, it is difficult to control because each switch must be duty-controlled separately. In addition, there is no mention of a DC link voltage deviation problem. Although various modulation techniques have been proposed for the LLC resonant converter, a suitable method for a diode-clamped multilevel converter with four levels or more has not yet been reported [26].

Meanwhile, single-phase diode-clamped multilevel AC/DC and DC/AC converters based on MNRV DPWM were proposed recently [27,28]. This MNRV DPWM is characterized by the presence of several adjacent reference vectors with different capacitor charging/discharging characteristics depending on the position of the command voltage in order to offset the voltage deviation of series-connected DC link capacitors and to match the magnitude of the command voltage on average. However, because AC/DC and DC/AC converters use a relatively low fundamental frequency to utilize a commercial grid or drive a motor, they use a relatively high frequency modulation index (m_f) to reduce capacitor voltage fluctuations due to the limited capacitance. To apply this MNRV DPWM to a DC/DC converter, some modifications of the modulation strategy are required, as in [29].

Based on [29], this paper presents a novel switching modulation scheme suitable for single-phase full-bridge diode-clamped multilevel LLC resonant converters with an addition of detailed circuit analysis, various types according to the carrier deformation, loss analysis, and experimental results. By using the linear amplitude modulation characteristics of the proposed diode-clamped multilevel converter, an LLC resonant converter based on voltage amplitude modulation with a fixed switching frequency at the resonant point is proposed, thus enabling an optimal passive device design and ensuring stable operation over a wide operating range. In addition, capacitor voltage deviation compensation is implemented using only m_f = 2 owing to the high fundamental switching frequency of the DC/DC converter. The proposed method utilizes only the clamped switching pair based on DPWM to facilitate the design of the switching pattern and reduce the switching losses. This paper briefly introduces a modified MNRV DPWM suitable for DC/DC converters, analyzes the operating characteristics of the proposed voltage-magnitude-modulation-based diode-clamped multilevel LLC resonant converter, and presents design guidelines. In addition, various types of LLC resonant converters are examined according to the deformation of the carrier. The performance and feasibility of the proposed converter are verified through simulations and experiments.

2. General Approach: Multi-Neighboring Reference Vector Discontinuous PWM (MNRV DPWM)

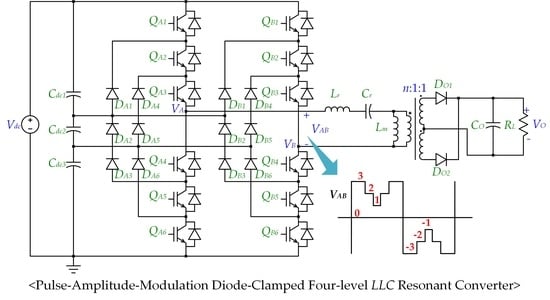
Figure 1 shows the circuit diagram of the single-phase diode-clamped four-level PWM converter. The AC voltage source V_S supplies input power to the full-bridge switching stack through boost inductor L_B with an equivalent series resistance of R_B. The full-bridge switching stage is composed of the switches Q_A1~Q_A6 and Q_B1~Q_B6 and the clamping diodes D_A1~D_A6 and D_B1~D_B6. The output DC link stage consists of three series-connected capacitors, C_dc1, C_dc2, and C_dc3. R_L implies output load resistance.

Figure 2a shows the switching pairs of A and B legs and the capacitor charging/discharging status according to the position of the command voltage V_C^* of the single-phase diode-clamped four-level PWM converter. In the full-bridge four-level topology, 0, E, 2E, and 3E imply reference vectors representing each step voltage that can be output as a leg-to-leg voltage. The numbers in parentheses refer to switching pairs (AB) that can express the reference vectors, and C and D positioned to the right of them are the charging and discharging states of the capacitor, respectively. For example, if V_C^* is located at ②, in carrier-based sinusoidal pulse-width modulation (CB-SPWM), adjacent reference vectors are E and 2E, and (AB) expressing E has redundancy via (10), (21), and (32). With regard to (10), the charging/discharging state of the three capacitors connected in series as the top capacitor (C_dc1), intermediate capacitor (C_dc2), and bottom capacitor (C_dc3) is DDC, which means that that C_dc1 and C_dc2 are discharging and C_dc3 is charging. For CB-PWM, which is widely used in single-phase AC/DC converters, two reference vectors adjacent to V_C^* are selected and their duration is adjusted to satisfy the magnitude of V_C^* and generate a symmetrical PWM pattern to minimize the ripple, as shown in Figure 2b. However, from level 4 or higher, a voltage imbalance inevitably occurs due to the limited selectable reference vectors capable of actively controlling the charging/discharging state of the capacitors. In particular, when the unity power factor is controlled as in the PWM converter, the voltage of the middle capacitor among the capacitors constituting the DC link stage is excessively charged compared to the other capacitors. This occurs because the charging/discharging behavior cannot be actively controlled with only two adjacent reference vectors.

When (AB) is (20), (30), and (31), the capacitor charging/discharging states are DCC, CCC, and CCD, respectively, and it can be confirmed that C_dc2 is always in the charged state. In particular, for a PWM converter in which the phase difference between V_C^* and the input current is small, the capacitor charging current is largest when V_C^* is located in ① (large vector region (LRV)); moreover, even if V_C^* is located in different regions such as ② and ③ (the small vector region (SVR)), this overcharged state is not overcome, and the voltage deviation intensifies. Due to the characteristics of the diode-clamped multilevel converter, if the switching state is implemented by selecting two adjacent vectors as in the conventional CB-SPWM, the voltage deviation of the capacitor cannot be eliminated. Figure 3 shows the voltage imbalance problem of the PWM converter when applying CB-SPWM. V_S is the input voltage source; I_S is the input current; and V_dc1, V_dc2, and V_dc3 are the terminal voltages of C_dc1, C_dc2, and C_dc3, respectively. V_AB is the switching leg voltage. As expected, the middle capacitor voltage V_dc2 increases continually after applying CB-SPWM.

Meanwhile, total harmonic distortion (THD) of the switching leg voltage V_AB was analyzed under the following conditions of V_S = 220V_rms(60 Hz ac), output voltage V_dc = 500 V, output power P_O = 30 kW, source frequency f_S = 60 Hz, m_f = 55, L_B = 4 mH, and R_B = 1 mΩ. THD results were 0.23 and 0.43 for the CB-SPWM and the proposed MNRV DPWM, respectively, which reveals the much-increased high-frequency harmonic components of V_AB in the proposed method. However, the CB-SPWM-based multilevel converter corresponds to an ideal case that is difficult to implement in practice due to a voltage imbalance problem. When compared with the existing two-level converter, the THD value of MNRV DPWM was reduced by 0.15. On the other hand, the multilevel topology enables the use of the low withstand voltage devices with lower switching losses than higher withstand voltage devices. Therefore, in the proposed method, switching frequency can be further increased, thereby reducing the size of filter for harmonic reduction and facilitating its design.

In order to solve the voltage deviation problem of the single-phase diode-clamped multilevel converter, MNRV DPWM was proposed [27]. Figure 2c shows the reference vectors selected according to the location of V_C^* and the switching pairs that can represent them, also showing the capacitor charging and discharging states according to the clamping mode (CM). When V_C^* is located in LVR, E, 2E, and 3E are selected as reference vectors. If E is selected, which was not chosen in CB-SPWM, (10) and (32) can be utilized, and these switching pairs can serve to discharge C₂ (DDC, CDD). Therefore, if E is used as a reference vector along with 2E and 3E, the voltage increase of C₂ can be suppressed, and if the duration times of reference vectors E, 2E, and 3E are properly adjusted, the magnitude of V_C^* can be tracked on average. In this paper, to reduce the switching redundancy and minimize the switching loss, the clamped switching states in ±180° DPWM are employed [30]. This means that only (3×), (×3), (0×), and (×0) are used among all switching pairs that can represent the reference vectors. (3×) and (×3) indicate that legs A or B, respectively, are clamped with a positive DC rail, called the upper clamping mode (UCM), where CM = 1. Similarly, (0×) and (×0) indicate the clamping of legs A or B, respectively, to the negative DC rail, called the lower clamping mode (LCM), where CM = −1. The generation of multiple references to eliminate voltage deviations among DC link capacitors in [21] is similar to the proposed method. However, MNRV DPWM is used, since V_C^* is clamped to the positive or negative DC rail during every half cycle, resulting in the advantage of reducing the switching redundancy and minimizing the switching loss. Meanwhile, in the UCM and LCM, the symmetry of the charging and discharging patterns for the same reference vector are horizontally opposite to each other. For example, (31) and (20) are switching pairs expressing reference vector 2E in the UCM and LCM, respectively, but the capacitor charging/discharging patterns are symmetric in those opposite to each other as CCD and DCC. As a symmetrical characteristic, the charging/discharging characteristics when V_C^* is negative are identical to the case when V_C^* is positive.

The procedure for calculating the duration time of the MNRV based on the reduced capacitor voltage deviation is as follows. First, V_dc1, V_dc2, and V_dc3 are input. Between V_dc1 and V_dc3, which are the top and bottom capacitor voltages, respectively, we select a voltage with a large absolute difference from the reference value, V_{dc_ref}/3, which is the target voltage of the unit capacitor. If the selected voltage is V_dc1 and V_{dc_ref}/3 − V_dc1 is greater than zero, the UCM is selected. On the other hand, if the difference is less than zero, the LCM is selected. If the selected voltage is V_dc3 and V_{dc_ref}/3 − V_dc3 is greater than zero, we select the LCM, and if the difference is less than zero, we select the UCM, because when the charging/discharging behavior of the capacitor according to CM is analyzed, for the UCM, V_dc1 tends to increase and V_dc3 decrease, and vice versa in the LCM. When CM is selected, the compensation controller calculates the duty compensation values for the reference vectors proportional to the voltage deviations among the capacitors. In a four-level converter, three capacitors and two voltage-deviation compensators are needed. There are several methods for configuring the controllers implementing the two voltage deviation compensators. Here, two controllers, one compensating for the difference between (V_dc1 + V_dc2)/2 and V_dc3 and the other compensating for that between V_dc1 and (V_dc2 + V_dc3)/2, are used. These design methods are natural charging/discharging characteristics of reference voltage vectors and easy to expand to a general high-dimensional multilevel converter.

As shown in Equation (1), the two compensation controllers output d_{comp12_3} and d_{comp1_23}, which are used to compensate for the voltage difference between (V_dc1 + V_dc2)/2 and V_dc3 and the voltage difference between V_dc1 and (V_dc2 + V_dc3)/2, respectively. In Equation (1), K_P and K_I mean the proportional and integral gains of the PI controller, respectively. According to the position of V_C^* and CM, the duties of the each MNRV are calculated as follows. If V_C^* belongs to the LVR, we select E, 2E, and 3E as the MNRV. Here, with E as a basic vector for the duty calculation, the duties of the E, 2E, and 3E vectors are calculated as Equation (2). Here, d_E, d_2E, and d_3E are the duties of E, 2E, and 3E, respectively. V_E, V_2E, and V_3E are the voltage levels of E, 2E, and 3E, respectively, meaning V_{dc_ref}/3, V_{dc_ref}∙2/3, and V_{dc_ref}. Equation (2) is applied differently depending on CM, and its meaning is as follows. The duties of the MNRVs must basically satisfy the magnitude of V_C^*. At the same time, the voltage deviations among all capacitors are reduced by applying two controller outputs (d_{comp12_3} and d_{comp1_23}) differently according to CM. For example, if (V_dc1 + V_dc2)/2 > V_dc3 in the UCM, d_{comp12_3} increases and d_2E decreases. In the UCM, d_2E is the duty of the switching pair (31), which serves to increase V_dc1 and V_dc2 and decrease V_dc3. Therefore, V_dc1 and V_dc2 decrease and V_dc3 increases due to the reduced d_2E. According to the negative feedback, d_{comp12_3} is stabilized and the capacitor voltage deviations are also reduced. The same can be explained in the LCM. Using the previously calculated duties of each reference vector, the PWM command values of each of the switches in the LRV are determined via Equation (3). Here, N_max refers to the maximum value at the period of a single carrier considering the DSP implementation. For a positive V_C^*, leg A is clamped to the positive DC rail in the UCM and leg B is clamped to the negative DC rail in the LCM.

$$\begin{array}{l}{d}_{comp12\_3}=K_P(\frac{V_{dc1}+V_{dc2}}{2}-V_{dc3})+K_I{\displaystyle {\int }_0^t(\frac{V_{dc1}+V_{dc2}}{2}-V_{dc3})dt},\\ d_{comp1\_23}=K_P(V_{dc1}-\frac{V_{dc2}+V_{dc3}}{2})+K_I{\displaystyle {\int }_0^t(V_{dc1}-\frac{V_{dc2}+V_{dc3}}{2})dt}.\end{array}$$

(1)

$$\begin{array}{ll}LVR@UCM& LVR@LCM\\ d_{2E}=d_E-d_{comp12\_3},& d_{2E}=d_E+d_{comp1\_23},\\ d_{3E}=1-d_E-d_{2E},& d_{3E}=1-d_E-d_{2E},\\ {V_C}^{\ast }=V_E{d}_E+V_{2E}{d}_{2E}+V_{3E}{d}_{3E},& {V_C}^{\ast }=V_E{d}_E+V_{2E}{d}_{2E}+V_{3E}{d}_{3E},\\ d_E=\frac{{V_C}^{\ast }+d_{comp12\_3}(V_{2E}-V_{3E})-V_{3E}}{V_E+V_{2E}-2V_{3E}},& d_E=\frac{{V_C}^{\ast }-d_{comp1\_23}(V_{2E}-V_{3E})-V_{3E}}{V_E+V_{2E}-2V_{3E}}.\end{array}$$

(2)

$$\begin{array}{l}\begin{array}{l}LVR@UCM\\ \left(\begin{array}{c}PWM\_CMD\_A1\\ PWM\_CMD\_A2\\ PWM\_CMD\_A3\end{array}\right)=N_{\max }\left(\begin{array}{l}1\\ 1\\ 1\end{array}\right), \left(\begin{array}{c}PWM\_CMD\_B1\\ PWM\_CMD\_B2\\ PWM\_CMD\_B3\end{array}\right)=N_{\max }\left(\begin{array}{l}0\\ d_E\\ d_E+d_{2E}\end{array}\right),\end{array}\\ \begin{array}{l}LVR@LCM\\ \left(\begin{array}{c}PWM\_CMD\_A1\\ PWM\_CMD\_A2\\ PWM\_CMD\_A3\end{array}\right)=N_{\max }\left(\begin{array}{l}{d}_{3E}\\ d_{2E}+d_{3E}\\ 1\end{array}\right), \left(\begin{array}{c}PWM\_CMD\_B1\\ PWM\_CMD\_B2\\ PWM\_CMD\_B3\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ 0\end{array}\right).\end{array}\end{array}$$

(3)

On the other hand, when V_C^* is located in the SVR, 0, E, 2E, and 3E are selected as reference vectors for a similar principle. To achieve a smooth transition at the moment of a region change, the range of the reference vectors in SVR must be wider than that of the LVR to increase the common reference vectors between the LVR and SVR. Each duty is calculated as in Equation (4). Here, d₀ is the duty of the 0 vector. Using the calculated duties of each reference vector, the PWM command values of each of the switches in the SRV are determined as in Equation (5).

Using the symmetric characteristic of the full-bridge topology, the duties of the MNRVs when V_C^* is negative are determined to be identical to those in the positive V_C^* case except for the interchange of legs A and B.

$$\begin{array}{ll}SVR@UCM& SVR@LCM\\ d_{2E}=d_{3E}-d_{comp12\_3},& d_{2E}=d_{3E}+d_{comp1\_23},\\ d_E=d_{3E}-d_{comp1\_23},& d_E=d_{3E}+d_{comp12\_3},\\ d_0=1-d_E-d_{2E}-d_{3E},& d_0=1-d_E-d_{2E}-d_{3E},\\ {V_C}^{\ast }=V_0{d}_0+V_E{d}_E+V_{2E}{d}_{2E}+V_{3E}{d}_{3E},& {V_C}^{\ast }=V_0{d}_0+V_E{d}_E+V_{2E}{d}_{2E}+V_{3E}{d}_{3E},\\ d_{3E}=\frac{{V_C}^{\ast }+d_{comp1\_23}{V}_E+d_{comp12\_3}{V}_{2E}}{V_E+V_{2E}+V_{3E}},& d_{3E}=\frac{{V_C}^{\ast }-d_{comp12\_3}{V}_E-d_{comp1\_23}{V}_{2E}}{V_E+V_{2E}+V_{3E}}.\end{array}$$

(4)

$$\begin{array}{l}\begin{array}{l}SVR@UCM\\ \left(\begin{array}{c}PWM\_CMD\_A1\\ PWM\_CMD\_A2\\ PWM\_CMD\_A3\end{array}\right)=N_{\max }\left(\begin{array}{l}1\\ 1\\ 1\end{array}\right), \left(\begin{array}{c}PWM\_CMD\_B1\\ PWM\_CMD\_B2\\ PWM\_CMD\_B3\end{array}\right)=N_{\max }\left(\begin{array}{l}{d}_0\\ d_0+d_E\\ d_0+d_E+d_{2E}\end{array}\right),\end{array}\\ \begin{array}{l}SVR@LCM\\ \left(\begin{array}{c}PWM\_CMD\_A1\\ PWM\_CMD\_A2\\ PWM\_CMD\_A3\end{array}\right)=N_{\max }\left(\begin{array}{l}{d}_{3E}\\ d_{2E}+d_{3E}\\ d_E+d_{2E}+d_{3E}\end{array}\right), \left(\begin{array}{c}PWM\_CMD\_B1\\ PWM\_CMD\_B2\\ PWM\_CMD\_B3\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ 0\end{array}\right).\end{array}\end{array}$$

(5)

The MNRV DPWM applied to a single-phase diode-clamped four-level converter can be expanded to a general diode-clamped N-level converter as follows. Based on the analysis of the voltage fluctuation characteristics of the DC link capacitors of the reference step voltage vectors, appropriate MNRVs are selected according to the position of V_C^* and the capacitor voltage deviation compensation parameters are designed. MNRV selections applied to the five-level, six-level, and general N-level diode-clamped topologies are shown in Figure 4.

The general rule for selecting MNRVs according to the V_C^* position is as follows. Compensation parameters for controlling the voltage deviations of capacitors are N − 2 in the N − level case. First, the charging/discharging states of the capacitors according to the reference step voltage are analyzed as follows. In the N-level case, the maximum step voltage is (N − 1)∙E, and the capacitor charging/discharging state is CC…CC regardless of CM. Because all capacitors are charged with the same amount of current, there is no voltage deviation. The step voltage one step lower is (N − 2)∙E and the capacitor charging/discharging states are CC…CD and DC…CC in the UCM and LCM, respectively. The outermost capacitor is changed to the discharge mode. In the UCM, the capacitor located at the bottom of the DC link stage, and in the LCM, the capacitor located at the top of the DC link stage, change from charging to discharging mode. The next step voltage is (N − 3)∙E, and the capacitor charging/discharging states are CC…CDD and DDC…CC in the UCM and LCM, respectively. That is, whenever the step voltage decreases by one step, it can be seen that the capacitor charging/discharging states change from charging to discharging from the lower end of the DC link stage in the UCM and from the upper end of the DC link stage in the LCM. Applying this to all step voltages, the following rule can be found. The total number of different charging/discharging states of capacitors is 2(N − 2). At this time, there are step voltage pairs in which the sum of two step voltages is (N − 1)∙E, and the capacitor charging/discharging states in the UCM and LCM of these two step voltages are related to the same capacitor voltage compensation parameters with opposite signs. The two step voltages in this case are cross oppositely coupled to each other; therefore, there are N−2 independent capacitor charging/discharging states in the overall step voltage. Thus, N−2 independent d_comp parameters can be generated, i.e., d_{comp1_2...(N−1)}, d_{comp12_3...(N−1)},..., d_{comp1...(N−2)_(N−1)}. In order to control the capacitor voltage deviation completely regardless of the position of V_C^*, the MNRV should be selected so that all independent compensation parameters are included. For every V_C^* location, it is sufficient to set the MNRV such that N−2 independent duty compensation parameters are included in order to eliminate the voltage deviations of all capacitors. However, large fluctuations in the duty compensation value may adversely affect normal operation; i.e., the duty of a particular reference vector can be negative or greater than one due to the addition of duty-compensation parameters. Accordingly, it is better to include all different charging/discharging states of the capacitors for more reliable operation by limiting the duty-compensation effort. Including all capacitor charging and discharging states is good for stable operation but increases the switching losses. However, as will be described later, by designing an appropriate carrier, a voltage-deviation-compensation operation may occur in the ZVS region, thereby minimizing an increase in the switching loss. Because the outermost vectors (0, (N − 1)∙E) do not affect the capacitor voltage deviation, the capacitor-voltage-deviation-compensation parameters are designed from independent capacitor charging/discharging states of the remaining intermediate reference vectors.

In the five-level case, for example, there are three independent charging/discharging states: CDDD(DCCC), CCDD(DDCC), and CCCD(DDDC). The capacitor charging/discharging states of the reference voltages E in the UCM and 3E in the LCM are CDDD and DCCC, respectively. They both can be used to control the voltage deviation between V_dc1 and (V_dc2 + V_dc3 + V_dc4)/3. It can be seen that the charging/discharging states of 2E in the UCM and LCM are CCDD and DDCC, respectively, and are related to the voltage deviations between (V_dc1 + V_dc2)/2 and (V_dc3 + V_dc4)/2. Similarly, the charge/discharge states of 3E in the UCM and E in the LCM are CCCD and DDDC, respectively, and they can be utilized to control the voltage deviation between (V_dc1 + V_dc2 + V_dc3)/3 and V_dc4 with opposite signs. Therefore, in the five-level case, three independent compensation parameters are required to control the capacitor voltage deviation: d_{comp1_234}, d_{comp12_34}, and d_{comp123_4}. They are related to the voltage differences between V_dc1 and (V_dc2 + V_dc3 + V_dc4)/3, (V_dc1 + V_dc2)/2 and (V_dc3 + V_dc4)/2, and (V_dc1 + V_dc2 + V_dc3)/3 and V_dc4, respectively. Therefore, if V_C^* belongs to the LVR, the range of the MNRV should be E ~ 4E in order to utilize all six different charging/discharging states of the capacitors. On the other hand, if V_C^* is located in the SVR, the MNRV range should be 0 ~ 3E for the same reason. In addition, when V_C^* moves between the LVR and SVR, the duties of the reference voltage vectors may suddenly change, which is a factor that degrades the linearity of the output voltage. Therefore, in order to minimize duty changes of the reference voltage vectors and thus ensure smooth transitions between the LRV and SRV, the minimum reference voltage in the LVR and the maximum reference voltage in the SVR should be selected as the basic vector for the MNRV.

In this way, by selecting the MNRV according to the positions of V_C^* and designing compensation parameters for the deviations of the capacitor voltages, extension to a high-dimensional N-level diode-clamped converter is possible. For a general N-level case, the LRV and SRV range from roundup{(N − 1)/2}∙E to (N − 1)∙E and from 0 to roundup{(N − 1)/2}∙E, respectively. The corresponding MNRVs are from E to (N − 1)∙E and from 0 to (N − 2)∙E, as shown in Figure 4. It should be noted that thus far MNRV DPWM has been described based on the incoming current to the switching legs, as in a PWM converter. Therefore, the charging/discharging states and CM selection should be reversed in DC/DC owing to the reversed reference current direction.

3. Proposed Full-Bridge Diode-Clamped Four-Level LLC Resonant Converter

Circuit and Control Algorithm for the Proposed Diode-Clamped 4-Level LLC Resonant Converter

Figure 5 shows the circuit of the proposed full-bridge diode-clamped four-level LLC resonant converter. The voltage source V_dc supplies input power through the DC link stage composed of three series-connected capacitors, C_dc1, C_dc2, and C_dc3. The full-bridge switching stage is composed of the switches Q_A1~Q_A6 and Q_B1~Q_B6, and the clamping diodes D_A1~D_A6 and D_B1~D_B6 that connect the unit step capacitor voltages of the DC link stage to each switching node. The resonance tank stage composed of resonant inductor L_r, resonant capacitor C_r, and magnetizing inductor L_m receives voltage amplitude modulated sag-type voltage with a fixed frequency from switching leg voltage V_leg(=V_AB = V_A − V_B). The resonant current I_Lr charges the output capacitor C_O through an n:1:1 center-tapped transformer and the output rectification stage composed of diodes D_O1 and D_O2 and supplies power to the load R_L.

AC/DC or DC/AC converters have a relatively high m_f to reduce the harmonic components and to control the fundamental component on average during one fundamental period. However, in a DC/DC converter, it is desirable to increase the frequency of the AC switching pulse until it is within an acceptable switching loss range to reduce the size of the passive element. Given that such a high fundamental frequency increases the number of compensations for capacitor voltage deviation during the unit time, MNRV DPWM for a DC/DC converter can be implemented with small m_f, i.e., m_f = 2. A DC/DC converter to which MNRV DPWM is applied can also linearly modulate the magnitude of the reference voltage akin to a multilevel inverter. Therefore, when applied to a resonant converter, the output voltage can be controlled by modulating the magnitude of V_C^* while fixing the frequency to the resonance point. This simplifies the design of the passive components compared to those in conventional frequency-swept resonant converters.

The control block diagram of the proposed MNRV DPWM-based diode-clamped four-level LLC resonant converter is shown in Figure 6. The output V_ampl of the constant-voltage controller is multiplied by a pulse that swings between 1 and −1 at a rate of 50% with switching frequency f_sw to obtain pulse-shaped command voltage V_C^*. Here, f_sw is designed as the resonance frequency (f_r = 1/[2π∙(L_rC_r)^0.5]) for maximum efficiency. CM is set to be between 1 and −1, referring to the UCM and LCM, respectively, according to V_dc1 and V_dc3. In order to remove the voltage deviations among the capacitors, V_dc1, V_dc2, and V_dc3 are input to the PI controller to calculate the duty compensation parameters (d_{comp1_23}, d_{comp12_3}). According to the position of V_C^*, appropriate MNRVs are selected and the duration times of each reference vectors are calculated, with the PWM CMDs of the A and B legs finally output. These values are compared to the triangular carrier to determine the on/off status of every upper switch in the A and B legs. According to the complementary rule of the diode-clamped topology, the on/off statuses of the lower switches are determined as opposite to the corresponding upper switches’ on/off states in the same leg. Q_A1 and Q_A4, Q_A2 and Q_A5, and Q_A3 and Q_A6 are the complementary switch pairs in leg A. The same applies to leg B.

4. Analysis

4.1. Overall Operation Characteristics of the Proposed Converter

In this section, we analyze the operation mode of the proposed diode-clamped four-level resonant LLC converter. The operation state of the circuit is largely classified according to CM. Figure 7 shows the circuit operation status in the UCM and LCM, and (AB) on the right side of each circuit represents the switching status of the A and B phases. The shaded red line in the figure represents the current path flowing through the channel or body diode of the conducting switches. Except for (30), (03), (33), and (00), the magnitude and direction of the current flowing through the series-connected capacitors C_dc1, C_dc2, and C_dc3 differ depending on the switching pattern as follows. In the switching pairs of (31) and (13), the charging/discharging state is DDC, and in (32) and (23) the charging/discharging state is DCC. In (20) and (02) the charging/discharging state is CDD, and in (10) and (01) the charging/discharging state is CCD. Therefore, it is expected that a voltage deviation will occur because the charging/discharging patterns of each capacitor differ depending on the duration of the specific switching pair. Here, the amount of charging/discharging current flowing through each capacitor is related to I_Lr. If there are two capacitors connected in series, the charging/discharging current becomes 1/3 × I_Lr, and if there is one capacitor, it becomes 2/3 × I_Lr. For example, for (32), C_dc1 is discharged with a current of 2/3 × I_Lr and C_dc2 and C_dc3 are charged with 1/3 × I_Lr. The core principle of MNRV DPWM is to set several reference vectors, including all independent charging/discharging characteristics of DC link capacitors depending on the location of V_C^*, and adjust their duration time to reduce the voltage deviations of the capacitors and to satisfy the magnitude of V_C^* on average at the same time.

Figure 8 depicts the equivalent circuit of the resonance tank at the resonance point. Regardless of CM, when V_C^* > 0, one from among V_dc, 2/3 × V_dc, and 1/3 × V_dc is applied to V_leg, and nV_O is applied to the magnetizing inductor L_m. When the voltage of V_leg − nV_O is supplied to L_r-C_r, I_Lr and I_Lm increase in the positive direction. Meanwhile, when V_C^* < 0, one from among −V_dc, −2/3 × V_dc, and −1/3 × V_dc is applied to V_leg and −nV_O is applied to L_m. I_Lr and I_Lm decrease by V_leg + nV_O supplied to L_r-C_r.

Based on this circuit operation state, Figure 9 shows the main operating waveforms of the proposed full-bridge diode-clamped four-level LLC resonant converter. CM is determined as the UCM or LCM according to the characteristics of the capacitor voltage deviation at the start of one switching period. Here, it is assumed that the converter is operated in the UCM for one cycle and operated in the LCM during the next cycle in a steady state. The operation during one cycle is a series of symmetrical half-cycle operations, and the operation during the half-cycle is divided into six modes.

4.1.1. Operation under the UCM

Mode 1 [t₀,t₁]: At t₀, CM is changed from the LCM to the UCM; the A leg upper switches Q_A1, Q_A2, and Q_A3 are all turned on with the ZVS condition owing to the negative current of I_Lr, and the B leg upper switches Q_B1, Q_B2, and Q_B3 are all turned off. V_leg with V_dc is input to the resonance tank stage, and the resonance current I_Lr formed by L_r and C_r is transferred to the secondary side of the transformer; D_O1 then conducts, and the output voltage V_O multiplied by the turn ratio of n is applied to L_m. At this time, the switching state is (30), and the currents flowing through C_dc1, C_dc2, and C_dc3 are all identical to I_dc−I_Lr; here, I_dc is the outgoing current of V_dc such that voltage deviations do not occur in the capacitor. This mode is terminated at t₁ when Q_B6 turns off (when Q_B3 turns on). In mode 1, resonant current I_Lr and resonant voltage V_Cr are determined by Equation (6). Here, V_leg is V_dc and I_Lr(0) and V_Cr(0) refer to the initial values of I_Lr and V_Cr at t₀, respectively. The characteristic impedance Z equals (L_r/C_r)^0.5, and the angular frequency ω is 2πf_r.

$$\begin{array}{l}{I}_{Lr}(t)=I_{Lr}(0)\cos \omega t+\frac{V_{leg}-n{V}_o-V_{Cr}(0)}{Z}\sin \omega t,\\ V_{Cr}(t)\hspace{0.17em}\hspace{0.17em}=Z{I}_{Lr}(0)\sin \omega t+[V_{leg}-n{V}_o-V_{Cr}(0)]\cdot (1-\cos \omega t)+V_{Cr}(0).\end{array}$$

(6)

Mode 2 [t₁,t₂]: When Q_B6 is off at t₁, the switching state becomes (31), and C_dc1 and C_dc2 are discharged with a current of 1/3 × I_Lr and C_dc3 is charged with a current of 2/3 × I_Lr. V_leg becomes 2/3 × V_dc, and the voltage applied to L_r-C_r is changed from V_dc to 2/3 × V_dc; thus, the slope of I_Lr changes. L_m is still charged with nV_O due to the conduction of D_O1. This mode continues until Q_B5 turns off at t₂. In mode 2, I_Lr and V_Cr are also determined by Equation (6), except for V_leg = 2/3 × V_dc, and I_Lr(0) and V_Cr(0) are changed to I_Lr(t₁) and V_Cr(t₁), respectively.

Mode 3 [t₂,t₃]: When Q_B5 is turned off at t₂, the switching state is (32); accordingly, C_dc1 is discharged with a current of 2/3 × I_Lr, and C_dc2 and C_dc3 are charged with a current of 1/3 × I_Lr. Because V_leg is changed from 2/3 × V_dc to 1/3 × Vdc, the slope of the I_Lr also changes. L_m is still charged with nV_O. This mode ends when Q_B5 is turned on at t₃. In mode 3, I_Lr and V_Cr are also determined by Equation (6), except for V_leg = 1/3 × V_dc, and I_Lr(0) and V_Cr(0) are changed to I_Lr(t₂) and V_Cr(t₂), respectively.

Mode 4 [t₃,t₄]: When Q_B5 is turned on at t₃, the switching state is (31) again, and operation in this mode is identical to that in mode 2. This mode ends when Q_B6 turns on at t₄.

Mode 5 [t₄,t₅]: When Q_B6 is turned on at t₄, the switching state is (30), and operation in this mode is identical to that in mode 1. This mode is terminated when I_Lr equals I_Lm at t₅. At the end of this mode, D_O1 is turned off with the ZCS condition.

Mode 6 [t₅,t₆]: At t₅, I_Lr = I_Lm, the primary and the secondary sides of the transformer are separated, and the resonance period becomes longer due to the large inductance of L_m contributing to the resonance. This mode continues until the polarity of V_C^* becomes negative. In mode 6, I_Lr and V_Cr are determined by Equation (7). Here, V_leg is V_dc and I_Lr(0) and V_Cr(0) refer to the initial values of I_Lr and V_Cr at t₅, respectively. The characteristic impedance Z’ equals [(L_r + L_m)/C_r]^0.5, and the angular frequency ω’ is 1/[(L_r + L_m)∙C_r]^0.5.

$$\begin{array}{l}{I}_{Lr}(t)=I_{Lr}(0)\cos {\omega }^{\prime }t+\frac{V_{leg}-V_{Cr}(0)}{Z^{\prime }}\sin {\omega }^{\prime }t\\ V_{Cr}(t)\hspace{0.17em}\hspace{0.17em}=Z^{\prime }{I}_{Lr}(0)\sin {\omega }^{\prime }t+[V_{leg}-V_{Cr}(0)]\cdot (1-\cos {\omega }^{\prime }t)+V_{Cr}(0)\end{array}$$

(7)

Due to the symmetry of the DC/DC converter, operation during the remaining half cycle where V_C^* is negative can easily be inferred from the previous positive half cycle of V_C^*; accordingly, a description thereof will be omitted. Regarding the capacitor charging and discharging status, in the UCM, V_dc1 continues to discharge and V_dc3 continues to charge regardless of the polarity of V_C^*. Therefore, under actual operating conditions, the UCM is selected when V_dc1 > V_dc3.

4.1.2. Operation under the LCM

When V_C^* changes from negative to positive again, one cycle of LCM operation begins. Operation in the LCM has cross-symmetric duality with that of the UCM as follows. When Q_A(m)/Q_B(m) is turned on/off in the UCM, Q_B(7-m)/Q_A(7-m) is turned on/off in the LCM at the same timing, where m = 1, 2, ..., 6. That is, the turn on/off timing of switch pairs Q_A1 and Q_B6, Q_A2 and Q_B5, Q_A3 and Q_B4, Q_A4 and Q_B3, Q_A5 and Q_B2, and Q_A6 and Q_B1, located in cross-opposite directions, are correspondingly matched. Thus, when the A/B leg is clamped to the positive DC rail in the UCM, the B/A leg is clamped to the negative DC rail in the LCM at the same timing. This duality can be confirmed by examining Figure 7 and Figure 9, and thus a detailed description of operation in the LCM is skipped here to save space.

In the LCM, V_dc3 continues to discharge and V_dc1 continues to charge regardless of the polarity of V_C^*. Therefore, under actual operating conditions, the LCM is selected when V_dc1 < V_dc3.

4.2. Voltage Transfer Gain

In this section, the input–output voltage transfer gain M is derived through a fundamental harmonic analysis (FHA) [31]. Figure 10 shows the V_leg waveform when 1/3 × V_dc ≤ |V_C^*| < 2/3 × V_dc. For convenience of the calculation, the original sag-type V_leg is divided into a square-wave swinging at ±V_dc with full duty and three square waves with the opposite phase, swinging at ±V_dc/3 during angular sections [π/2 ± α], [π/2 ± β], and [π/2 ± γ], respectively. The fundamental component is analyzed as Equation (8).

$$V_{leg}^F=\frac{4}{\pi }{V}_{dc}-\frac{4}{\pi }\cdot \frac{V_{dc}}{3}(\sin \alpha +\sin \beta +\sin \gamma )$$

(8)

Here, α, β, and γ are given by Equation (9). On the other hand, if 2/3 × V_dc ≤ |V_C^*|, γ becomes 0, as shown in Figure 9.

$$\alpha =0.5\pi (d_0+d_E+d_{2E}),\hspace{0.17em}\beta =0.5\pi (d_0+d_E),\gamma =0.5\pi d_0$$

(9)

The fundamental component is reduced compared to the full duty square wave due to the voltage sag section, as shown in Equation (10). Here, k = L_m/L_r, Q = Z/R_ac, and R_ac = 8n²R_L/π². The length of the sag section is related to the duty of the MNRV, which is also related to V_C^*. This means that even if the frequency is fixed, the output voltage can be adjusted by changing V_C^*. This is a distinguishing feature of the voltage modulation method used in MNRV DPWM compared to the conventional two-level resonant converter using the frequency modulation method.

$$|M|=\frac{n{V}_O}{V_{dc}}=\frac{1-\frac{\sin \alpha +\sin \beta +\sin \gamma }{3}}{\sqrt{{\left[1+\frac{1}{k}\{1-{\left(\frac{f_r}{f}\right)}^2\}\right]}^2+{\left[Q(\frac{f}{f_r}-\frac{f_r}{f})\right]}^2}}$$

(10)

5. Design Guideline

5.1. Design of the Resonant Tank

The proposed converter regulates the output voltage by modulating the magnitude of V_leg while fixing the operating frequency to the resonance point. Therefore, the voltage gain range can be determined from the length of the voltage sag section in the normal operating range as shown in Equation (10). If the load increases while the output voltage is fixed, the DC link capacitors’ charging/discharging current increases and the duty compensation effort must be increased. Therefore, the period of the voltage sag section may be out of the normal range and may no longer be able to undertake voltage compensation. With fixed V_dc and V_O values, d_E decreases as n increases. At this time, if the load increases, d_E may have an abnormal value due to the increased duty compensation parameters; therefore, n must be appropriately designed considering the sag section under the maximum load condition. When n is determined, a Q factor must be selected. A high Q implies a large L_r and small C_r, leading to a large reactor size and increased withstand voltage in C_r. On the other hand, if Q is decreased, the shape of the resonance current deviates from a sinusoidal wave, increasing the root mean square (RMS) value of I_Lr. Thus, an appropriate value must be selected. C_r is determined as C_r = 1/(2π∙f_r∙Q∙R_ac), and L_r is determined by L_r = 1/[(2π∙f_r)²∙C_r]. L_m is selected by determining the ratio k between L_m and L_r. Reducing L_m ensures ZVS operation while increasing circulating current and switch losses. Conversely, a large L_m reduces circulating current and switch losses, but ZVS operation may not be guaranteed. In addition, L_m affects the voltage gain in the region other than the resonance point. Therefore, an appropriate value of L_m must be selected.

5.2. Resonant Current and Voltage

In this section, the peak resonant current I_{Lr_pk} and voltage V_{Cr_pk} are calculated in order to select an appropriate device by determining the rated switch current and the withstand voltage of the resonance capacitor. When operating at the resonance point, I_Lr and I_Lm are in a steady state, as shown in Figure 11. Here, it is assumed that I_Lr and V_Cr are sinusoidal for convenience of calculation, as in Equation (11). The initial phase difference ϕ between the I_Lr and V_leg waveforms is determined as Equation (12). From the observation that the difference between I_Lr and I_Lm during a half cycle is equal to the output current divided by n, I_{Lr_pk} is determined to be Equation (13) [2]. I_{Lr_pk} is proportional to the load current and inversely proportional to L_m. This is consistent with the fact that as the L_m value decreases, the RMS value of I_Lr increases with the increased circulating current. From the energy balance principle, V_{Cr_pk} is calculated as Equation (14).

$$I_{Lr}(t)=I_{Lr\_}{}_{pk}\sin (\omega t-\varphi )$$

(11)

$$\varphi ={\sin }^{-1}\left(\frac{n{V}_{O}T}{4I_{Lr\_pk}{L}_m}\right)$$

(12)

$$I_{Lr\_pk}=\frac{I_O\sqrt{\frac{n^4{R}_L{}^2}{f_r^2{L}_m{}^2}+4{\pi }^2}}{4n}$$

(13)

$$V_{Cr\_pk}=I_{Lr\_pk}\cdot Z$$

(14)

5.3. Input and Output Capacitances

The input DC link capacitances can be calculated from the charging/discharging current of the capacitor and the duration time of the voltage sag period. MNRV DPWM determines the duration time of the reference vector to satisfy the magnitude of V_C^* on average during the unit switching period, as shown in Figure 12. Therefore, the relationship among α, β, and V_C^* can be derived as in Equation (15) (assuming γ = 0 when |V_C^*| ≥ 2/3 × V_dc).

In addition, given that the duty compensation parameters in the steady state are very small, we can assume that d_E = d_2E and α = 2β. The input–output voltage relationship of Equation (10) at the resonance point can be simplified as Equation (16) in a high V_C^* case where α and β are small, and α can be expressed as Equation (17). Thus, d_E can be derived via Equation (18).

$$V_C^{\ast }=V_{dc}-\frac{2V_{dc}}{3\pi }(\alpha +\beta )=V_{dc}(1-\frac{\alpha }{\pi })$$

(15)

$$V_{dc}=\frac{n{V}_O}{1-\frac{\sin \alpha +\sin \beta }{3}}\approx \frac{n{V}_O}{1-\frac{\alpha }{2}}$$

(16)

$$\alpha =2(1-\frac{n{V}_O}{V_{dc}})$$

(17)

$$d_E=1-\frac{V_C^{\ast }}{V_{dc}}=\frac{\alpha }{\pi }=\frac{2}{\pi }(1-\frac{n{V}_O}{V_{dc}})$$

(18)

Figure 13 describes the characteristics of the voltage change of the input DC link capacitors in the LCM. From Equation (19), the increment ΔV_dc1 during the unit half cycle, which equals decrement ΔV_dc3, is related to C_dc, f_sw, I_{Lr_pk}, α, β, and ϕ. When the target voltage fluctuation amount ΔV_dc,target is determined, the C_dc value is given as in Equation (20) using the previously obtained values of I_{Lr_pk}, α, β, and ϕ. If CM alternates between the UCM and LCM at every resonant period in a steady state, the total voltage change per unit capacitor becomes 2 × ΔV_dc.

$$\begin{array}{ll}\Delta V_{dc1}=\Delta V_{dc3}& =\frac{1}{C_{dc}}\left[\begin{array}{l}{\displaystyle {\int }_{\frac{T}{4}-0.5(d_E+d_{2E})\frac{T}{2}}^{\frac{T}{4}-0.5d_E\frac{T}{2}}\frac{2}{3}{I}_{Lr\_pk}\sin (\omega t-\varphi )dt}+{\displaystyle {\int }_{\frac{T}{4}-0.5d_E\frac{T}{2}}^{\frac{T}{4}+0.5d_E\frac{T}{2}}\frac{1}{3}{I}_{Lr\_pk}\sin (\omega t-\varphi )dt}\\ +{\displaystyle {\int }_{\frac{T}{4}+0.5d_E\frac{T}{2}}^{\frac{T}{4}+0.5(d_E+d_{2E})\frac{T}{2}}\frac{2}{3}{I}_{Lr\_pk}\sin (\omega t-\varphi )dt}\end{array}\right]\\ & =\frac{I_{Lr\_pk}}{3\pi C_{dc}{f}_{SW}}(2\sin \alpha -\sin \beta )\cos \varphi \end{array}$$

(19)

$$C_{dc}\approx \frac{I_O}{∆V_{dc,target}}\cdot \frac{\sqrt{\frac{n^4{R}_L{}^2}{f_r^2{L}_m{}^2}+4{\pi }^2}}{4n\pi f_r}\cdot \sqrt{1-\frac{n^2{V}_O{}^2{T}^2}{16I_{Lr\_pk}{}^2{L}_m{}^2}}\cdot \left(1-\frac{n{V}_O}{V_{dc}}\right)$$

(20)

The output capacitor current I_CO in the steady state, assuming a continuous current mode, is shown in Figure 14. Because I_CO equals the output diode current (I_DO1 or I_DO2) minus I_O, the net charge increment of C_O and Q_CO from t₁ and t₂, respectively, is calculated using Equation (21). Here, t₁ = sin⁻¹(2/π)/ω, t₂ = [π-sin⁻¹(2/π)]/ω. Thus, to satisfy the target output voltage fluctuation range ΔV_Co,target, C_O is determined by Equation (22).

$$Q_{CO}={\displaystyle {\int }_{t_1}^{t_2}{I}_{CO}}(t)dt={\displaystyle {\int }_{t_1}^{t_2}{I}_O(\frac{\pi }{2}\sin \omega t-1)dt}=0.105\frac{I_O}{f_{sw}}$$

(21)

$$C_O=0.105\times \frac{I_O}{∆V_{Co,target}{f}_r}$$

(22)

6. Four Representative Sag Types of V_leg According to the Carrier Deformation

For stable operation of the MNRV DPWM-based full-bridge diode-clamped multilevel resonant converter as described thus far, an appropriate carrier design is required. In DC/DC converters, it is important to maintain the symmetry of the voltage applied to the transformer. In order to maintain the symmetry of V_leg, which is the resonant tank input voltage, the carrier counting direction and initial value must be set appropriately according to CM. Figure 15 shows the representative V_leg that can be implemented according to the carrier deformation. V_leg basically takes the shape of a square wave for maximum power transfer. Additionally, at the middle, edge, or rear of the waveform, taking the form of a stepped sag, i.e., V_dc→2/3 × V_dc→1/3 × V_dc→2/3 × V_dc→V_dc, V_leg decreases and increases again. Compensation for the voltage deviations of the DC link capacitors is performed in that sag section. Depending on the location of the sag, we refer to these as the middle, edge, rear, and end sags, where sag sections occur respectively at the middle, edge, rear, and end of V_leg. In fact, the type described and interpreted thus far corresponds to the middle sag.

V_leg sag types are determined by the initial value and the counting direction of the carrier at the time the UCM and LCM start [29]. For example, when the UCM starts, if the carrier decreases from its maximum value and the carrier increases from its minimum value at the moment the LCM starts, it becomes a middle sag type with a dip in the middle. The remaining sag types can also be implemented by properly designing the initial value and the counting direction of the carrier. In addition to these four types, various V_leg waveforms can be created depending on the shape of the carrier. Each sag type has distinct characteristics. For the middle sag, the compensation ability for voltage deviation is excellent because the voltage-deviation-compensation operation occurs near the peak value of the resonance current, while the switching losses are greatest due to the large switching current. In addition, the sag occurs in the middle of the square wave, which has the greatest influence on the fundamental component of V_leg, meaning that the input C_O output voltage transfer gain is low. However, given that the period in which the output diode conducts is the longest, the RMS values of the output diode current and the resonance current are smallest, which is advantageous when conducting a large current. Regarding the edge sag, because the sag section appears at the edge, the ability to compensate for voltage deviations is somewhat lower, but the fundamental component of V_leg is larger than that in the middle sag case. In addition, unlike the middle sag, where all compensation operations for voltage deviation occur under hard switching conditions, the edge sag case can reduce the switching losses because part of the compensation operations for voltage deviation may occur in the ZVS region. The rear sag is characterized as intermediate between the middle sag and the edge sag. All three of these types utilize up and down carriers. On the other hand, the end sag shows the highest efficiency because the number of switching operations is reduced compared to other types because the sag occurs only at the end of the square wave and uses up or down carriers.

7. Simulation and Experiments

7.1. Simulation

To verify the operation of the proposed four-level LLC resonant converter, a simulation was conducted with the conditions shown in

Table 1. Simulation condition.

PO (kW)	Vdc (V)	VO (V)	Lr (mH)	Lm (mH)	Cr (nF)	Cdc (μH)	CO (μH)	n	fsw (kHz)
1	700	350	1.5	4.28	168	100	11	1.68	10

.

Figure 16 presents the simulation results in a steady state for the middle, edge, rear, and end sags. From the top are V_C^*, CM, GateA, GateB, V_dc, I_Cdc, I_Lr, I_Lm, I_DO, V_A, V_B, I_{QA_upper}, I_{QA_lower}, and I_DA. Here, I_Cdc is the current flowing through each DC link capacitor, and I_{QA_upper}, I_{QA_lower}, and I_DA are the upper and lower switch currents and the clamping diode currents for leg A, respectively. Although the currents of the switches and clamping diodes for leg B are not shown here, their characteristics are symmetric with those of leg A.

All four results are consistent with those described above. In a steady state, CM alternates between the UCM and LCM for every cycle. For every half cycle, one leg is clamped with a positive or negative DC rail, and the switch gates of the other leg that is not clamped are turned on/off in a specific pattern determined by the PWM_CMDs and pre-defined carrier according to the sag types. The resonance current generated according to the magnitude of the fundamental component of the V_leg input to the resonance tank is transferred to the secondary side for constant control of the output voltage. In the sag section, voltage deviations among input DC link capacitors are reduced, and when the load or input voltage source changes, instead of sweeping f_sw, V_ampl changes to control the fundamental component of V_leg.

The voltage transfer gain decreased in the order of the edge, end, rear, and middle sag types. Therefore, the magnitude of V_C^* required to maintain a constant output voltage under identical conditions was found to be largest at the middle sag, as expected. On the other hand, the RMS values of the output diode and the resonance currents increased in the order of the middle, rear, end, and edge sag types. Owing to the reduced switching number in the end sag case, the overall efficiency was largest for the end sag. The compensation operation for the deviation of the capacitor voltage was performed in three steps during one cycle on average, and the switching step voltage of the four-level converter was lower by one third compared to that of a two-level converter. Therefore, the switching loss of the end sag type was expected to be nearly identical to that of the conventional two-level converter.

Figure 17 shows the loss analysis result of the switching devices according to the sag types when P_O = 1000 W. Losses were calculated by means of thermal loss modeling with PLECS software, utilizing the datasheets of the actual devices mentioned in Section 7.2 [32]. Here, P_cond,Q and P_sw,Q are conduction and switching losses of the main switches, respectively. P_cond,D and P_sw,D are the conduction and switching losses of the clamping diodes, respectively. Lastly, P_Cond,DO denotes the conduction losses of the output diodes. As expected, the middle sag had largest switching losses compared to the other types while also showing the smallest conduction losses. Considering the winding losses of the magnetic material, it is predicted that the middle sag type would be more advantageous under a heavy load condition.

7.2. Experiments

A prototype circuit (Figure 18) was designed to confirm the operation of the proposed converter and to compare the performance outcomes according to the voltage sag types. The experimental conditions are identical to those in Table 1, except that here P_O varied between 500 W and 1500 W. The following devices were used in this experiment. The main switches were Fuji-Electric FGW35N60HD, the clamping diodes were ST-Microelectronic STTH15RQ06-Y, and the output diodes were Vishay VS-HFA06TB120S-M3. The center-tapped transformer had four stacked ferrite cores of the EE6565S with an air gap, and its turn ratio was 47:28:28. The resonant inductor consisted of four stacked ferrite cores of the EE4242S with an air gap. The controller was implemented using TI TMS320F28377D. Increased active switch control, voltage balancing of DC link capacitors, and CM selection increased the amount of computation in the MNRV DPWM compared to conventional two-level converters. Extra logic was also added to handle the clamped PWM CMDs every half cycle and the carrier whose phase is inverted whenever CM changes. It takes a lot of interrupt service routine (ISR) time to set and change the relevant registers of every switching pair that is different from each other. This increased ISR time limits the increase in the switching frequency. In this paper, the PWM switching part was implemented using the embedded ePWM module of the DSP due to the laboratory limitations. In order to overcome this limitation of increasing the switching frequency, it is necessary to implement a PWM switching part by using an FPGA with a parallel operation function and fast processing speed. This allows for a much higher switching frequency than in this experiment.

Figure 19 shows the V_A, V_B, V_leg, V_O, and I_Lr waveforms according to the voltage sag types when P_O = 1500 W. It can be seen that the output voltages held constant at 350 V in all four voltage sag types and that the V_leg values input to the resonance tank differed depending on the sag type, showing unique resonance current shapes. In addition, the selection of CM differed according to the magnitudes of V_dc1 and V_dc3. On the other hand, the RMS value of I_Lr was lowest in the middle sag case because the conduction time of the output diode was longest for that sag type. However, because the voltage transfer gain was lowest in the middle sag case, the length of d_3E was longest for the middle sag at a higher V_ampl, whereas for the edge and end sags, it was conversely short.

Figure 20 and Figure 21 show the waveforms when P_O = 1000 W and 500 W, respectively, showing results similar to those in the previous analysis. As the load decreased, it can be seen that conduction time of the output diode was shortened as the magnitude of the resonance current decreased. Figure 22 confirms the DC link capacitor voltage balancing capability for each voltage sag type. As described above, the voltage imbalance was eliminated by changing the CM based on the voltage deviation of the upper and lower capacitors. Meanwhile, the d_comp parameters in Equation (1) had the smallest value in the middle sag case, where the sag operation was performed at the peak point of the resonance current.

Using a Yokogawa WT333E power meter, the power conversion efficiencies for each sag type were measured and compared as shown in Figure 23. When the load was small, the middle sag type with large switching loss showed the lowest efficiency (91.1% efficiency at P_O = 500 W), but as the load increased, the middle sag type with the smallest RMS values of the resonance current and output diode current showed the highest efficiency (95.2% efficiency at P_O = 1500 W). In fact, in this experiment, because the transformer turn ratio was designed to be small considering the middle sag with a small voltage transfer gain, the period of resonance section was reduced in the edge, rear, and end sag cases. Thus, the resonance currents and the output diode currents of edge, rear, and end sag types became large, resulting in high conduction losses of switches and high copper losses of the transformer and inductor. Therefore, if optimally designed for each sag type, the efficiency rate of the edge, rear, and end sag types can be improved compared to those in this experiment. With an optimal design of the transformer turn ratio for each sag type, the V_C^* should be placed at a high level of LVR in its normal operating range.

8. Conclusions

In this paper, we proposed an amplitude-modulating full-bridge diode-clamped multilevel LLC resonant converter suitable for power conversion systems that use high input voltages. A new modulation scheme called MNRV DPWM was applied to eliminate voltage deviations in DC link capacitors connected in series. The proposed multilevel resonant converter operates by modulating the magnitude of the fundamental wave input to the resonant tank while fixing the operating frequency at the resonant point. The fixed operating point facilitates the design of passive devices and enables stable operation over a wide operating range with just one power conversion stage. In this paper, we proposed a control algorithm and analyzed the operating characteristics of the proposed diode-clamped four-level LLC resonant converter and presented design guidelines. The feasibility and effectiveness of the proposed converter were verified through a simulation and via experimentation with the prototype converter.