Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System
Abstract
:1. Introduction
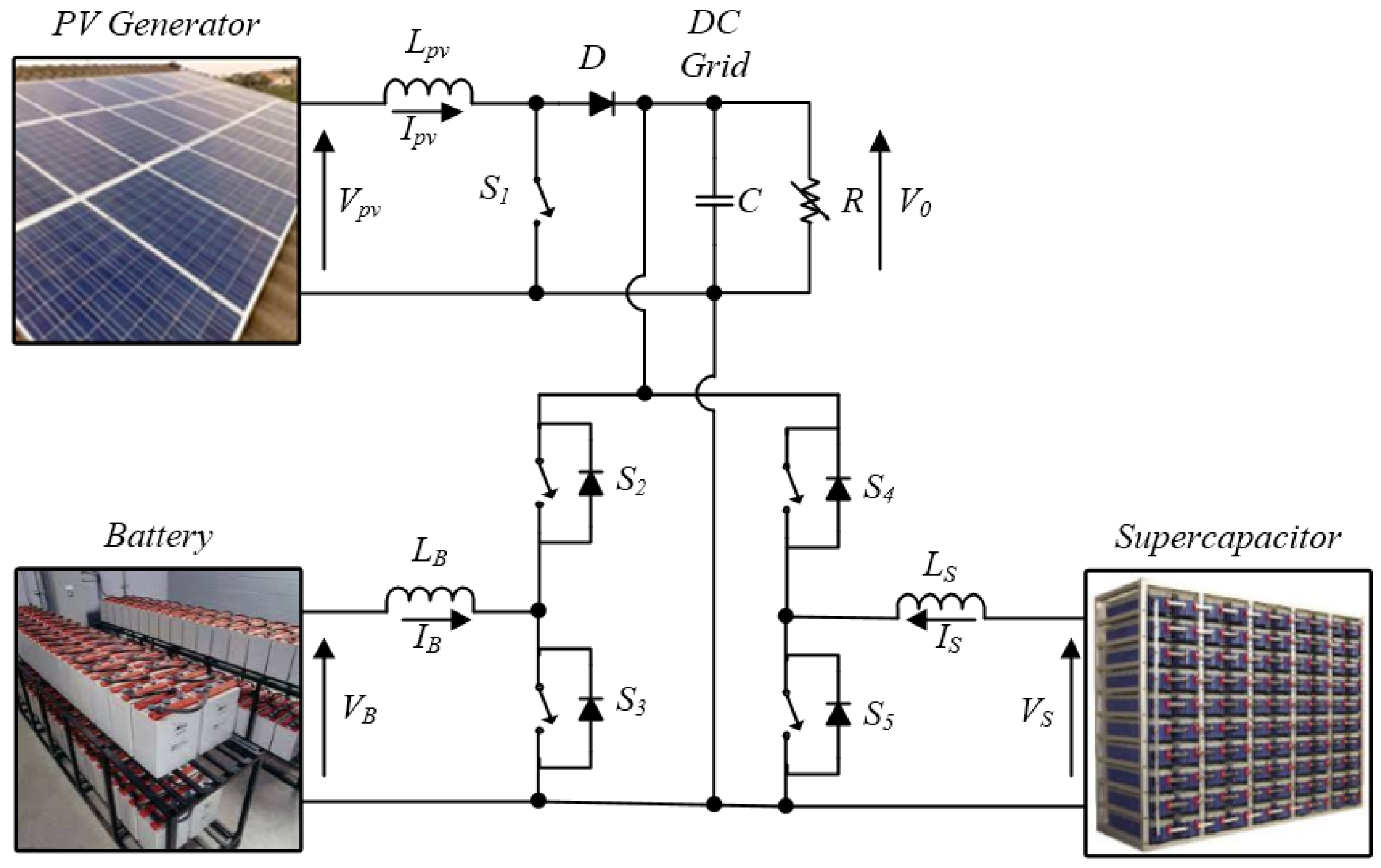
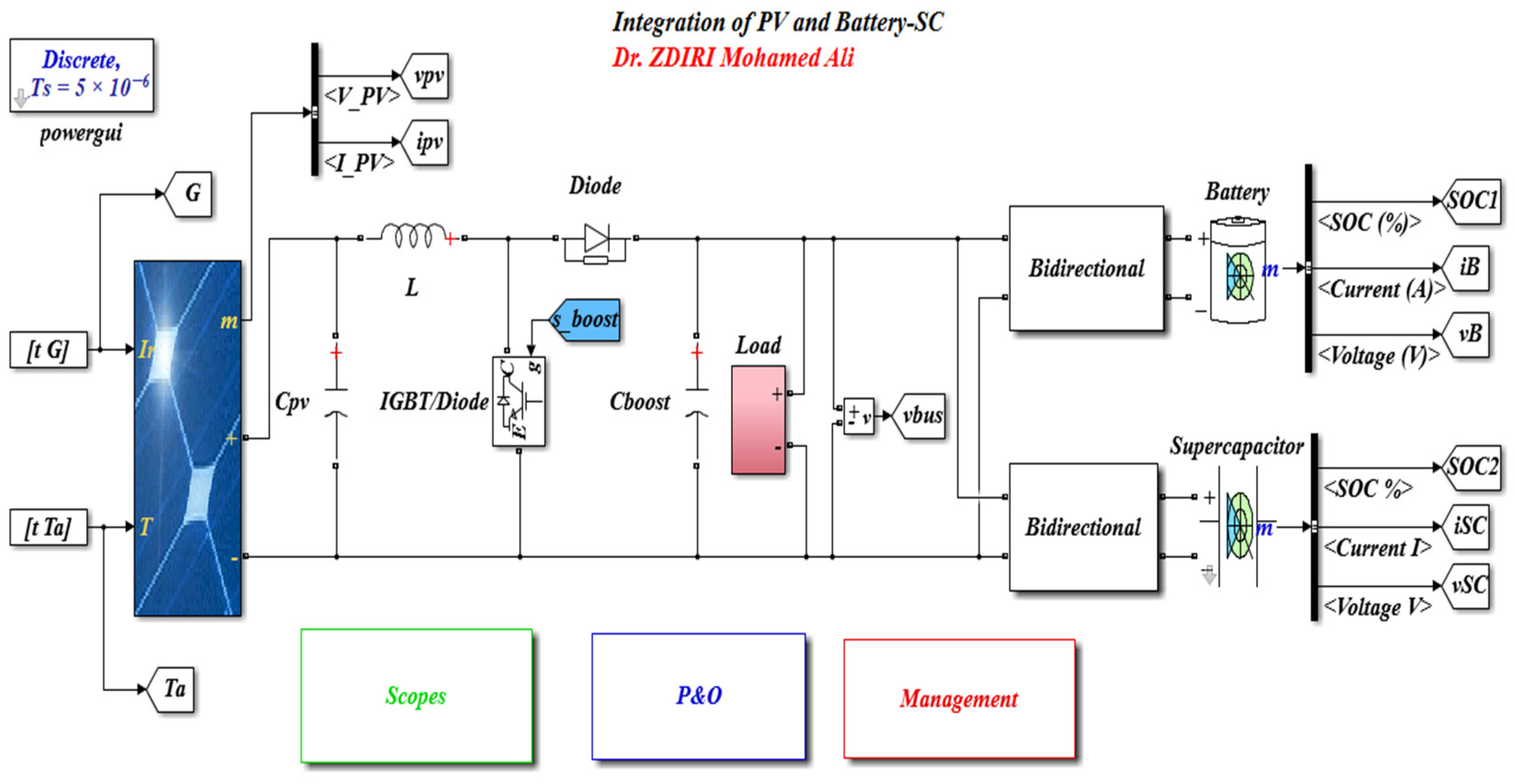
2. DC Electrical Grid Configuration
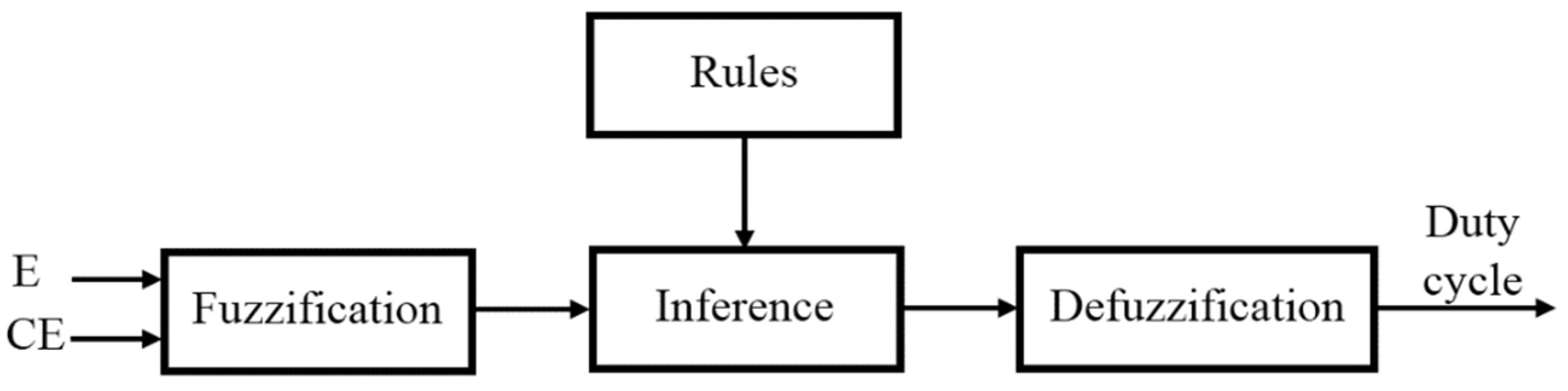
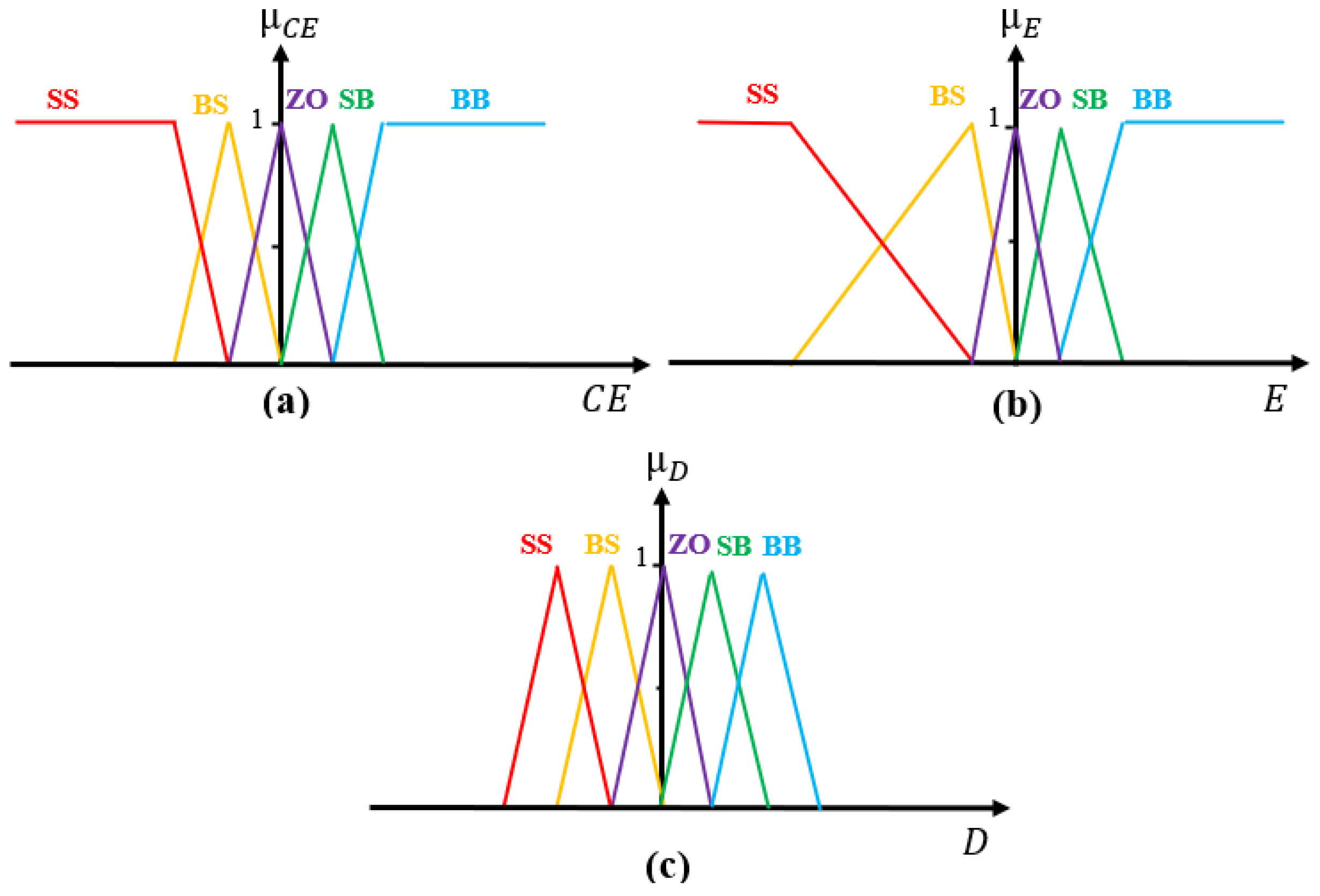
- Fuzzification: The fuzzification process entails that every variable used to define the control rules need be described by the fuzzy set notations and linguistic labels. Figure 3, below, highlights the MFs of the input and output variables. Each MF comprises five fuzzy sets: SS, BS, ZO, SB, and BB (S and B represent low and high, respectively).
- Inference: Developing the cartography applying the FLC of a given input to output is referred to as the inference technique. In this study, a Mamdani fuzzy inference is used. Table 2 depicts the relevant associated rules.
- Defuzzification: The FLC crisp output is computed throughout the defuzzification phase. In our context, a defuzzifier of gravity center type is applied.
3. HESS Control Strategy
3.1. Conventional HESS Control Strategy
3.2. Proposed HESS Control Strategy
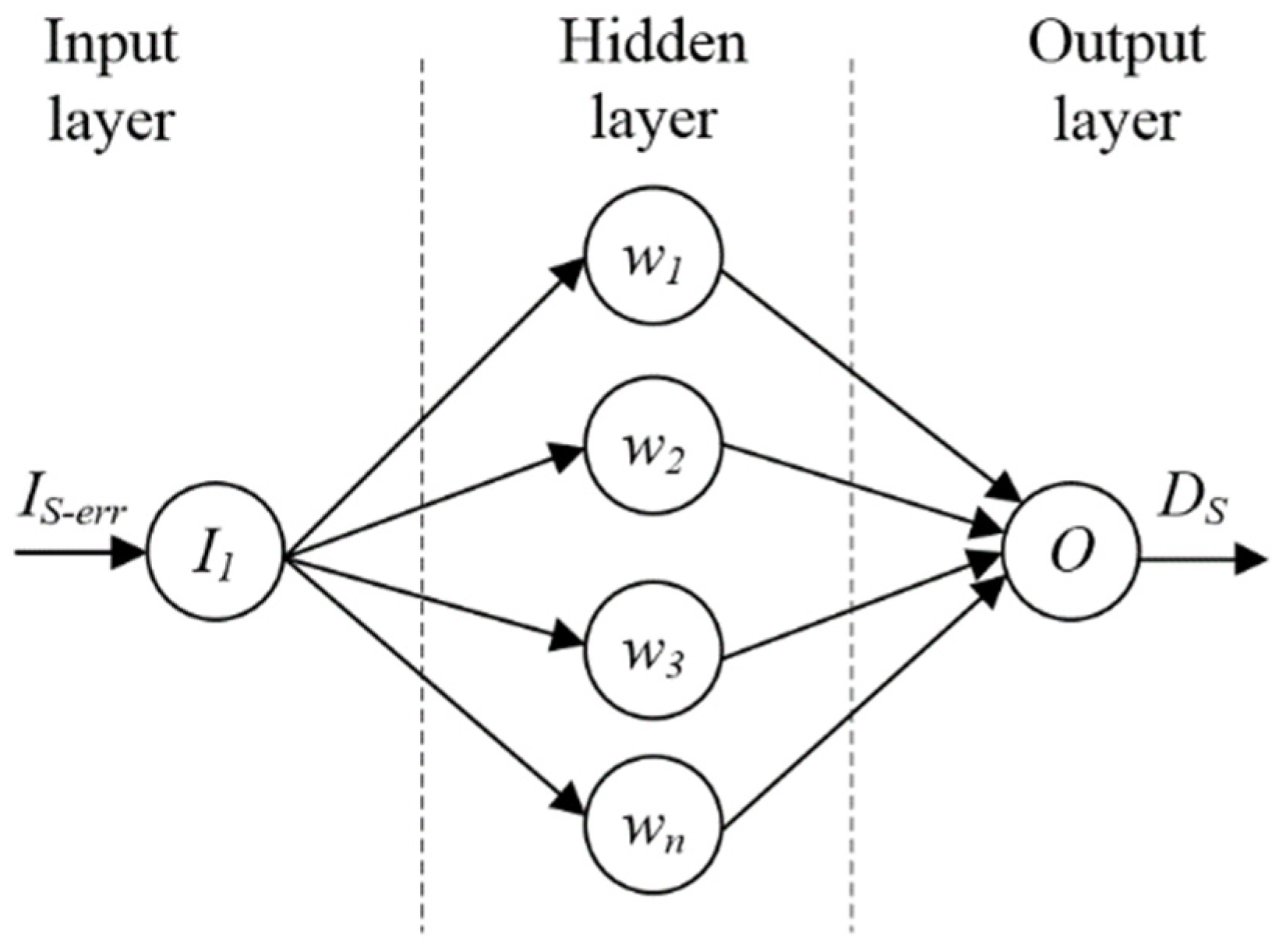
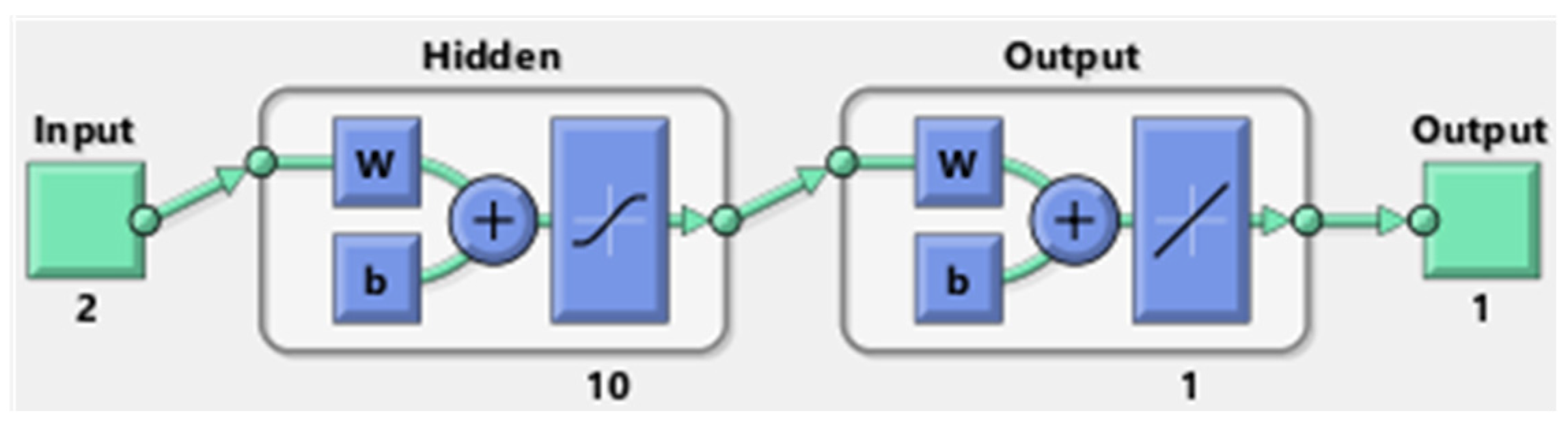
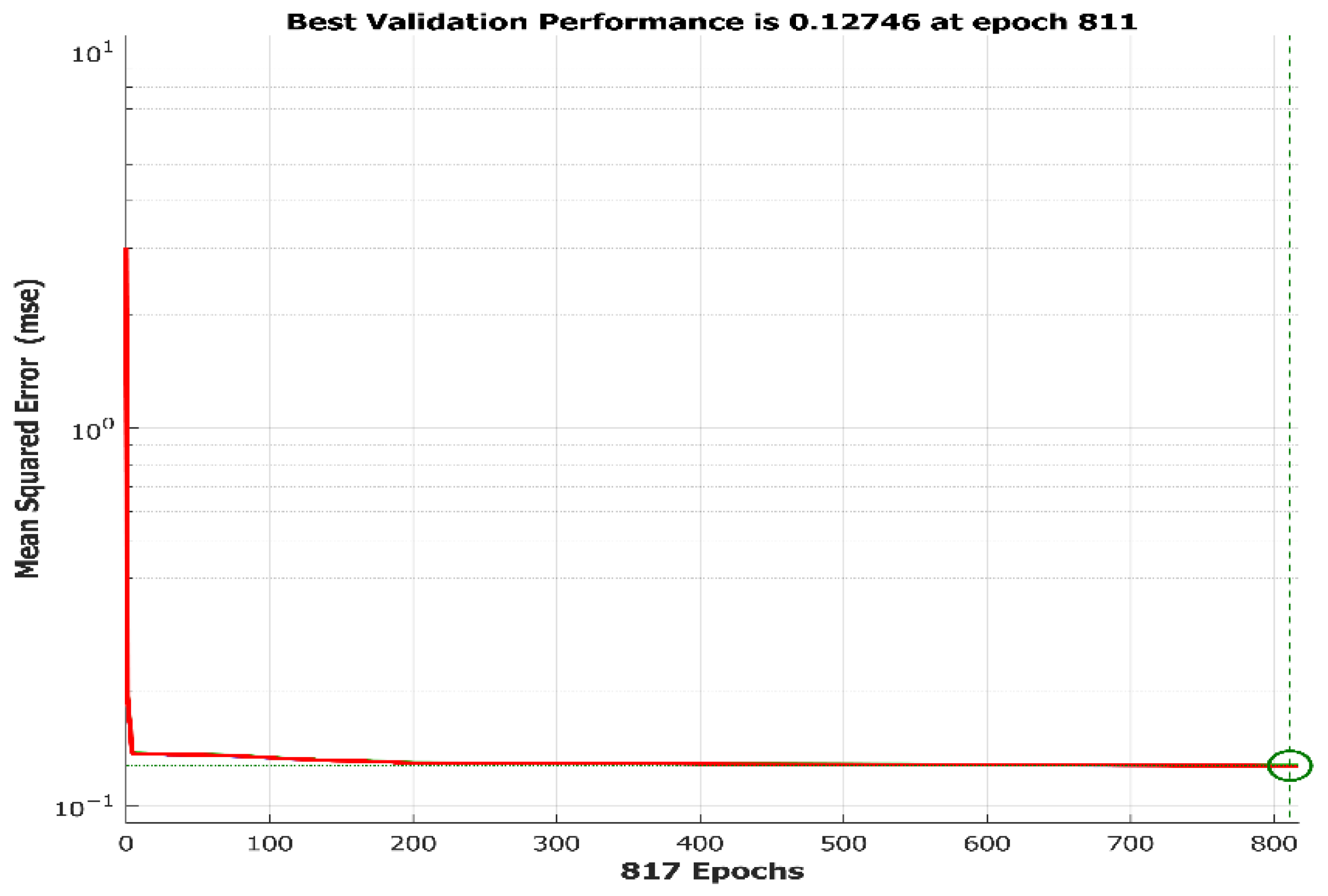
3.2.1. The ANN Controller
3.2.2. SM Controller
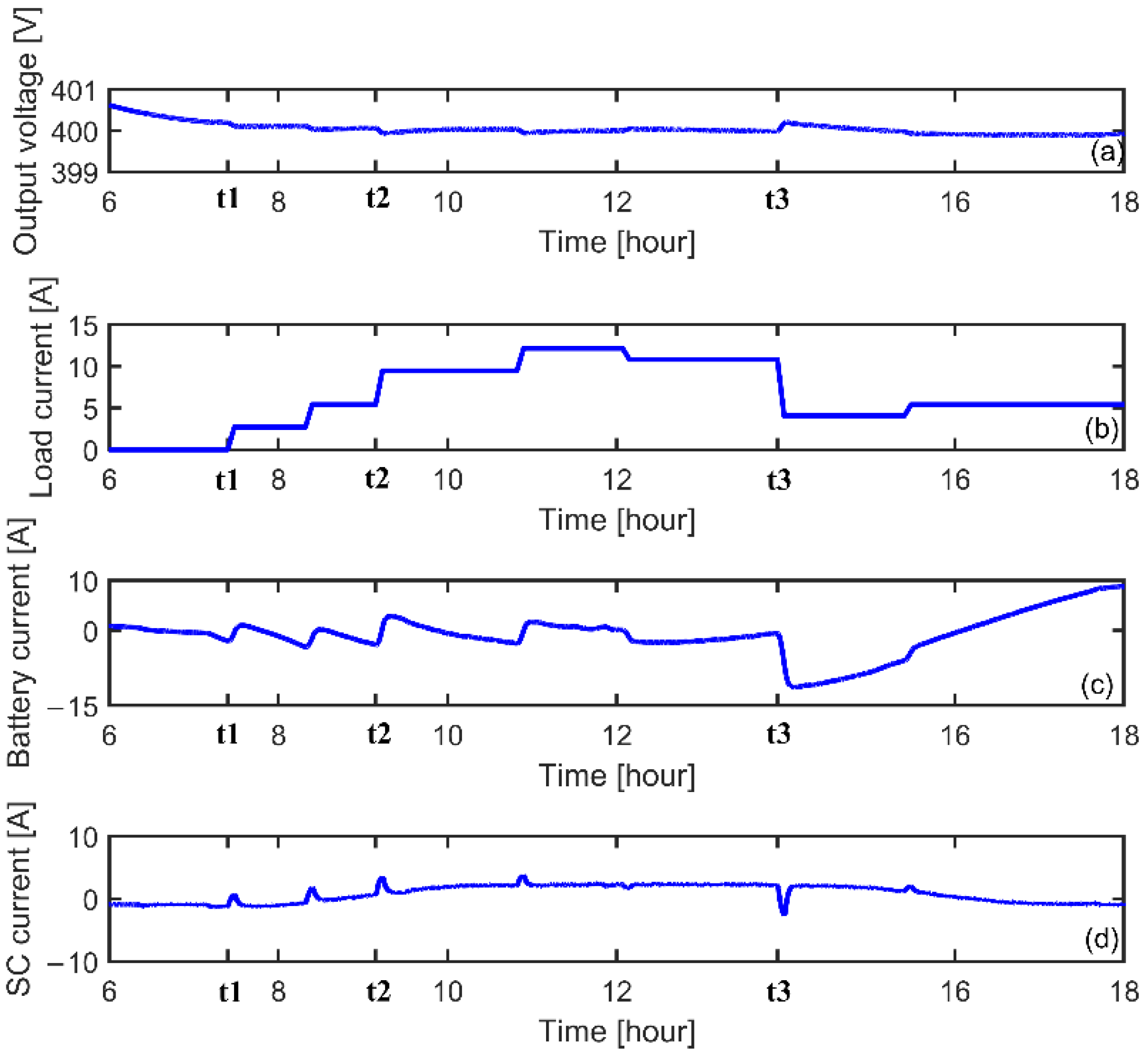
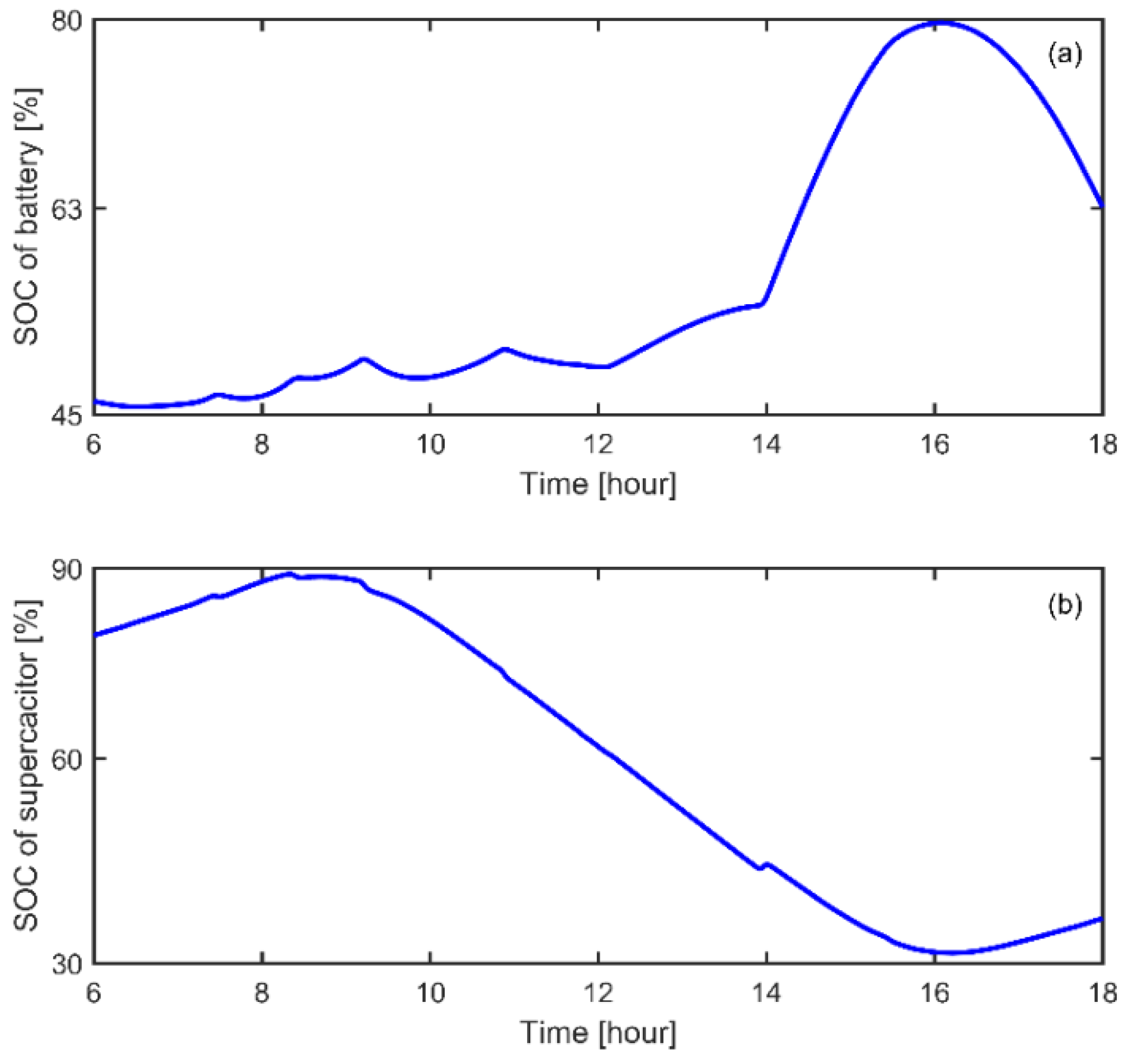
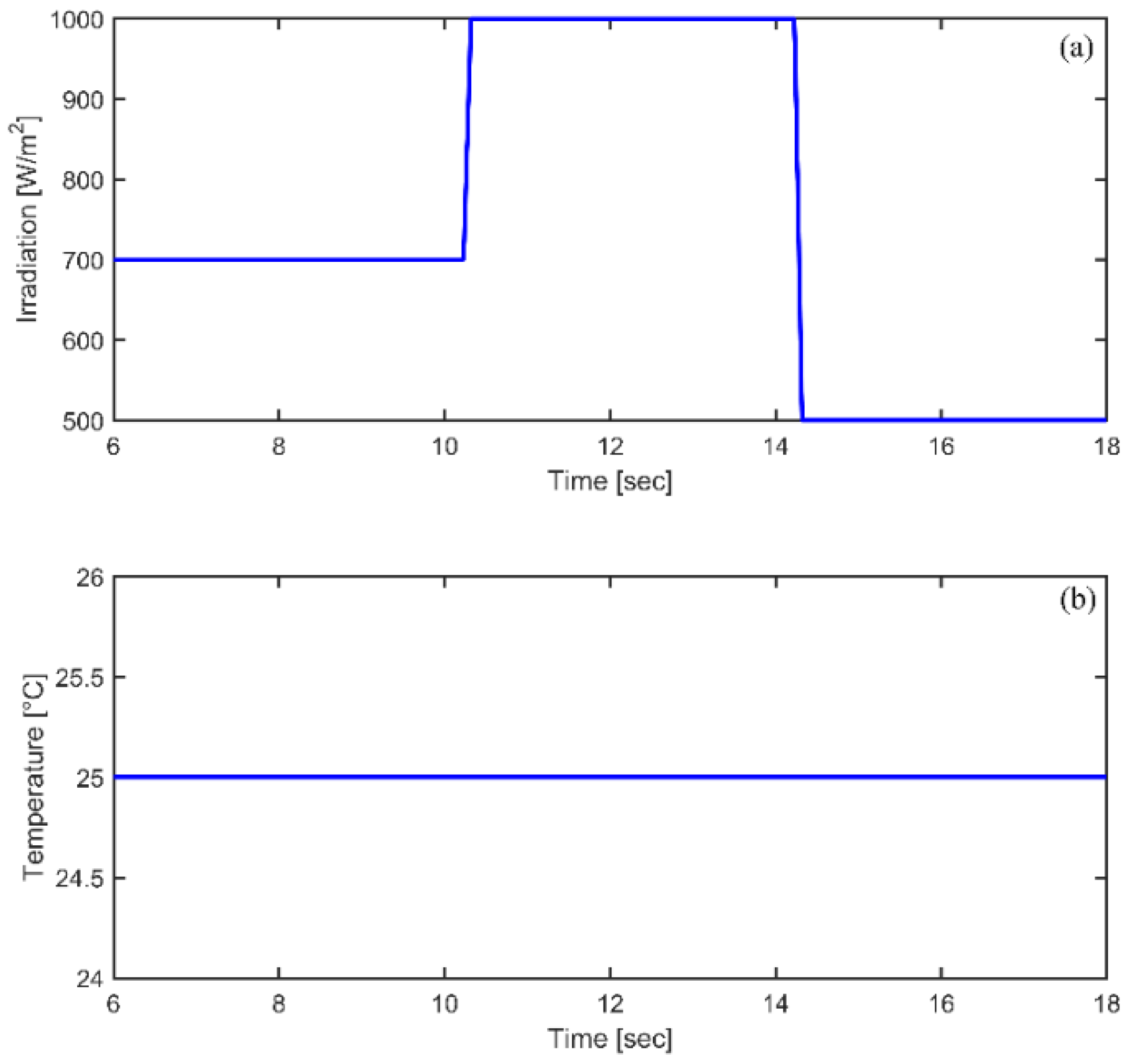
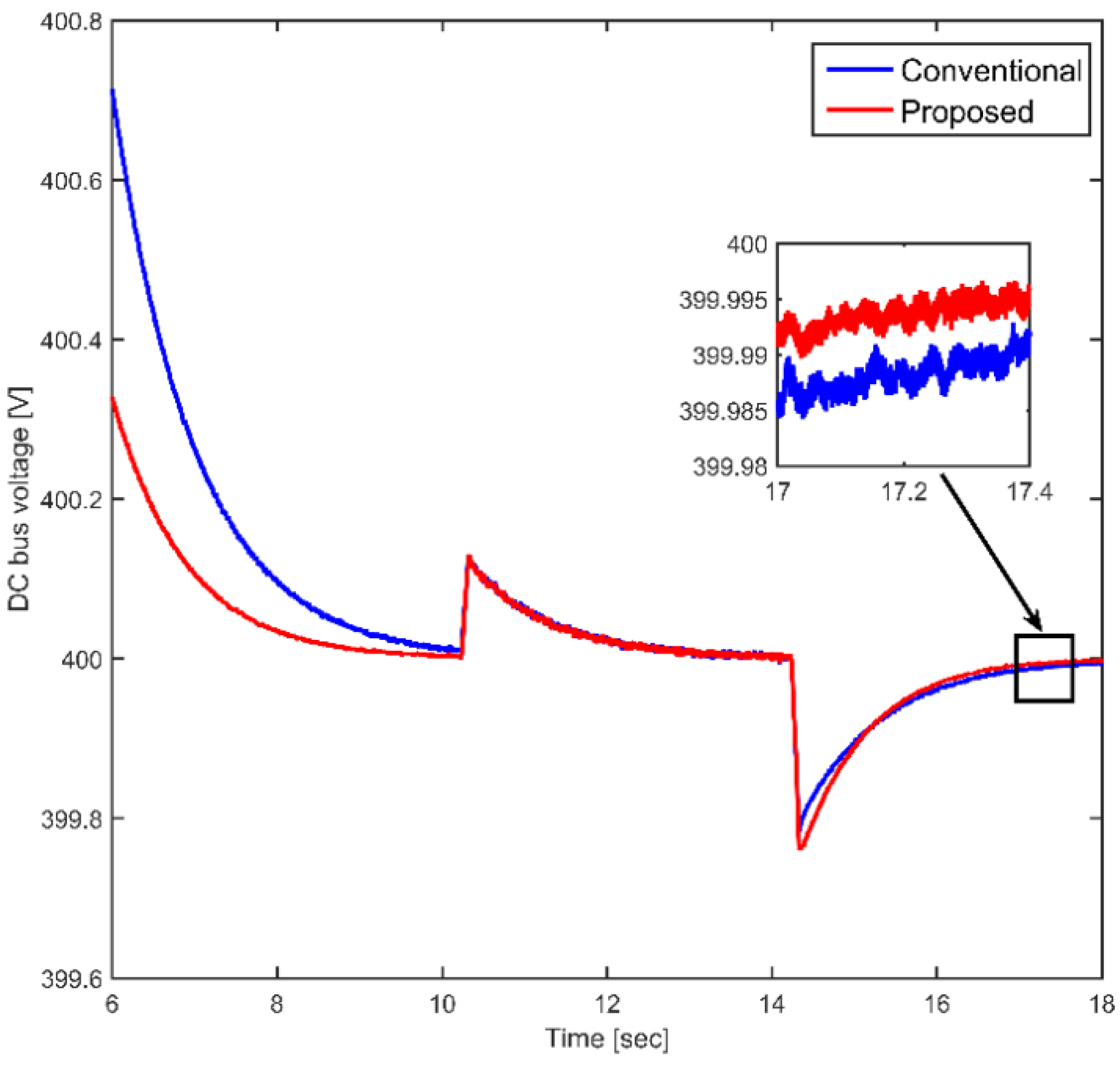
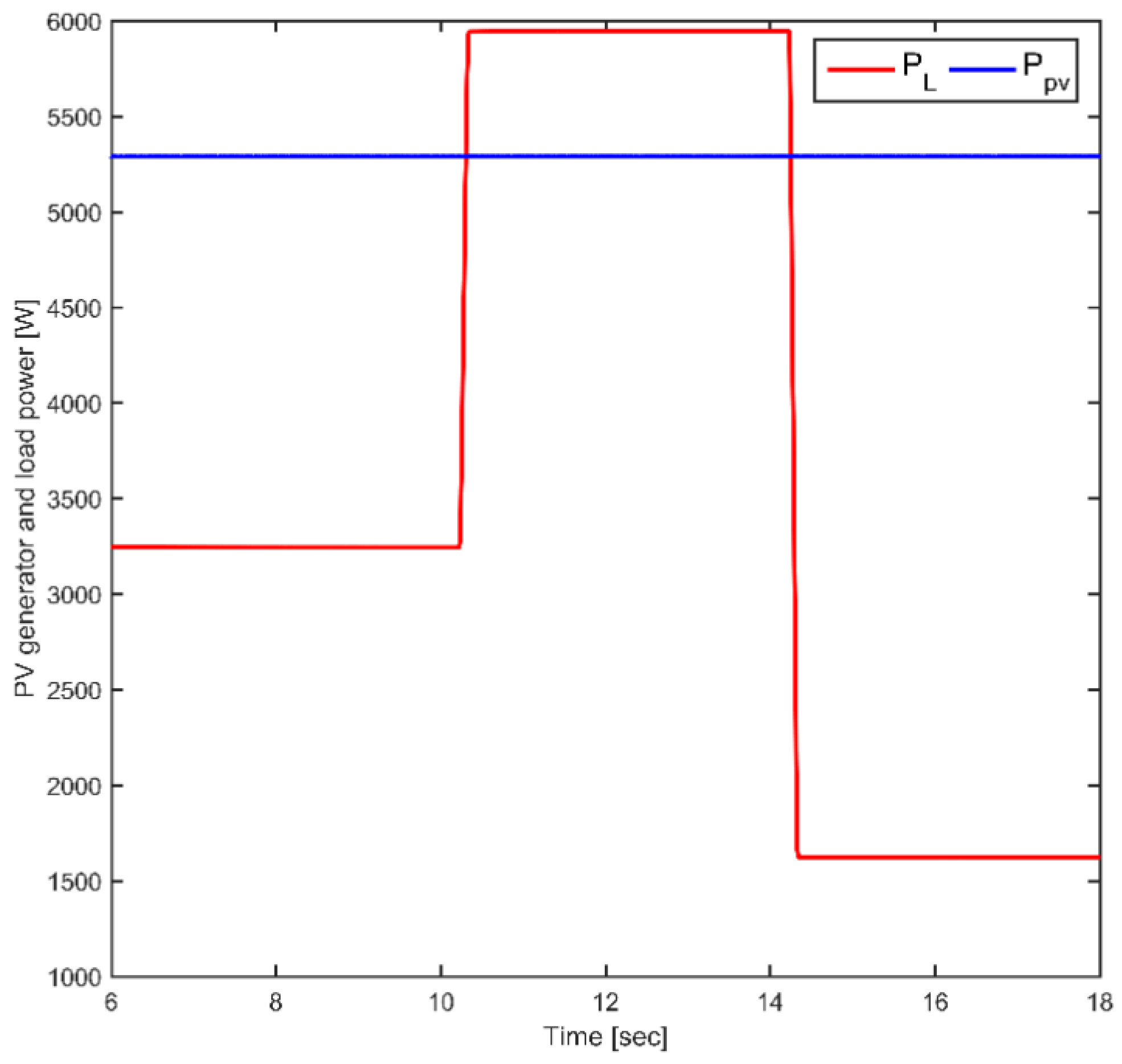
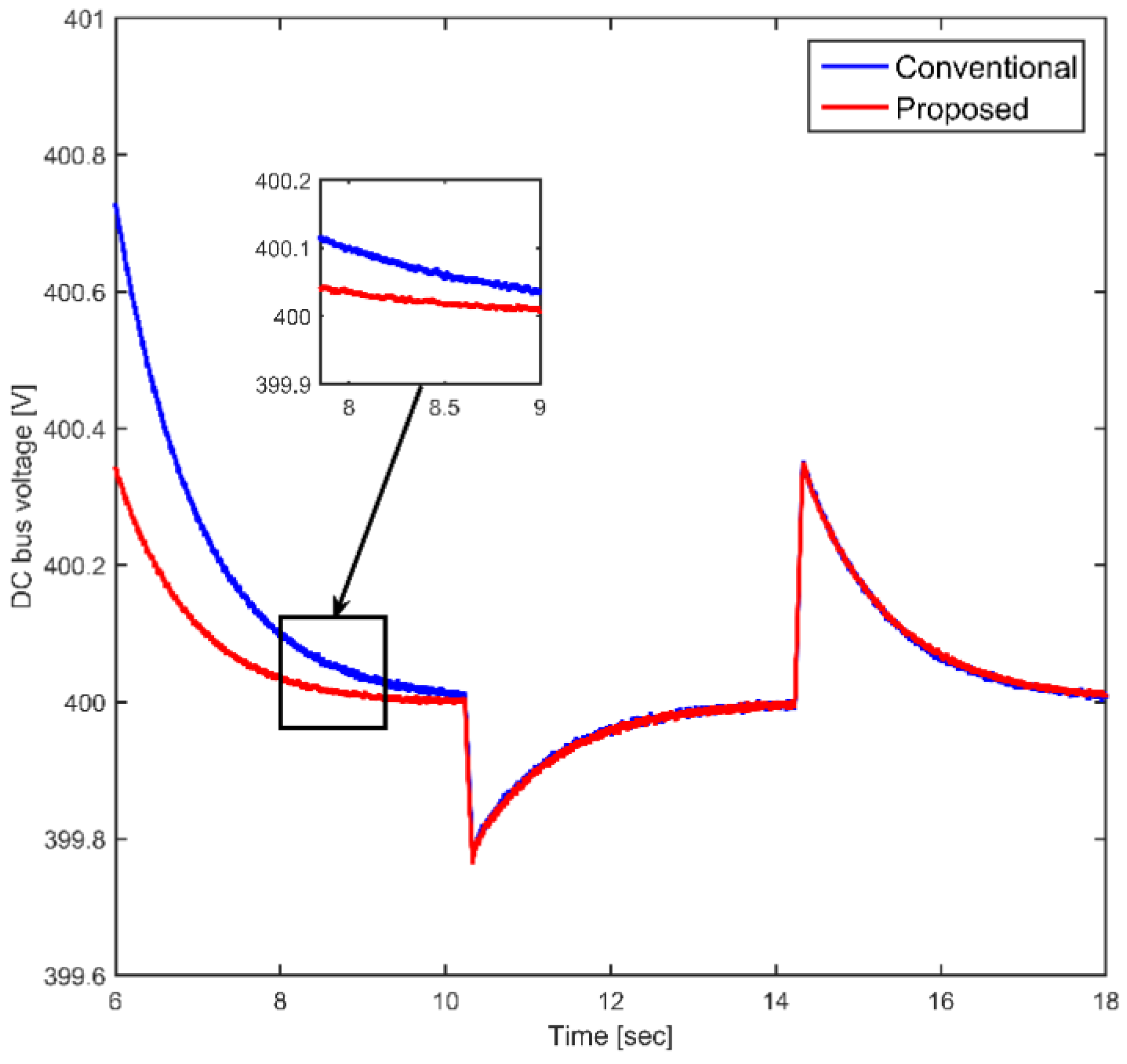
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RAPSAs | Remote area power system applications |
| HESS | Hybrid energy storage system |
| PV | Photovoltaic |
| SC | Super capacitor |
| DC | Direct current |
| MPPT | Maximum power point tracking |
| FLC | Fuzzy logic controller |
| EMA | Energy management algorithm |
| MPC | Model predictive controller |
| MF | Membership function |
| ANN | Artificial neural network |
| SM | Sliding mode |
| VSC | Variable structure control |
References
- Twidell, J.W.; Weir, A.D. Renewable Energy Resources; Taylor and Francis: Abingdon, UK, 2015. [Google Scholar]
- Benson, C.L.; Magee, C.L. On improvement rates for renewable energy technologies: Solar PV, wind turbines, capacitors, and batteries. Renew. Energy 2014, 68, 745–751. [Google Scholar] [CrossRef]
- Svazas, M.; Navickas, V.; Bilan, Y.; Vasa, L. The Features of the Shadow Economy Impact’ on Biomass Energy Sector. Energies 2022, 15, 2932. [Google Scholar] [CrossRef]
- Khodayar, M.E.; Barati, M.; Shahidehpour, M. Integration of high reliability distribution system in microgrid operation. IEEE Trans. Smart Grid 2012, 3, 1997–2006. [Google Scholar] [CrossRef]
- Brown, H.E.; Suryanarayanan, S.; Natarajan, S.A.; Rajopadhye, S. Improving reliability of islanded distribution systems with distributed renewable energy resources. IEEE Trans. Smart Grid 2012, 3, 2028–2038. [Google Scholar] [CrossRef]
- Quiggin, D.; Cornell, S.; Tierney, M.; Buswell, R.A. simulation and optimization study: Towards a decentralized microgrid, using real world fluctuation data. Energy 2012, 41, 549–559. [Google Scholar] [CrossRef] [Green Version]
- Ton, D.T.; Wang, W.T.P. A more resilient grid: The U.S. department of energy joins with stakeholders in an R&D plan. IEEE Power Energy Mag. 2015, 13, 26–34. [Google Scholar]
- Vandoorn, T.L.; Meersman, B.; De Kooning, J.D.M.; Vandevelde, L. Transition from islanded to grid-connected mode of microgrids with voltage-based droop control. IEEE Trans. Power Syst. 2013, 28, 2545–2553. [Google Scholar] [CrossRef] [Green Version]
- Giacomoni, A.M.; Goldsmith, S.Y.; Amin, S.M.; Wollenberg, B.F. Analysis, modeling, and simulation of autonomous microgrids with a high penetration of renewables. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Som, T.; Chakraborty, N. Studies on economic feasibility of an autonomous power delivery system utilizing alternative hybrid distributed energy resources. IEEE Trans. Power Syst. 2014, 29, 172–181. [Google Scholar] [CrossRef]
- Moseley, P.T. Energy storage in remote area power supply (RAPS) systems. J. Power Sources 2006, 155, 83–87. [Google Scholar] [CrossRef]
- Kellogg, W.; Nehrir, M.H.; Venkataramanan, G.; Gerez, V. Generation unit sizing and cost analysis for stand-alone wind, photovoltaic, and hybrid wind/PV systems. IEEE Trans. Energy Convers 1998, 13, 70–75. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Active power management of a supercapacitor-battery hybrid energy storage system for standalone operation of DFIG based wind turbines. In Proceedings of the 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA, 7–11 October 2012. [Google Scholar]
- Sathish Kumar, R.; Sathish Kumar, K.; Mishra, M.K. Dynamic energy management of micro grids using battery super capacitor combined storage. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, India, 7–9 December 2012; pp. 1078–1083. [Google Scholar]
- Glavin, M.; Chan, P.; Armstrong, S.; Hurley, W. A stand-alone photovoltaic supercapacitor battery hybrid energy storage system. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2018; pp. 1688–1695. [Google Scholar]
- Şahin, M.E.; Blaabjerg, F.A. Hybrid PV-battery/supercapacitor system and a basic active power control proposal in MATLAB/Simulink. Electronics 2020, 9, 129. [Google Scholar] [CrossRef] [Green Version]
- Hredzak, B.; Agelidis, V.; Jang, M. A model predictive control system for a hybrid battery-ultracapacitor power source. IEEE Trans. Power Electron. 2014, 29, 1469–1479. [Google Scholar] [CrossRef]
- Lahyani, A.; Venet, P.; Guermazi, A.; Troudi, A. Battery/supercapacitors combination in uninterruptible power supply (UPS). IEEE Trans. Power Electron. 2013, 28, 1509–1522. [Google Scholar] [CrossRef]
- Wei, L.; Joos, G.; Belanger, J. Real-time simulation of a wind turbine generator coupled with a battery supercapacitor energy storage system. IEEE Trans. Power Electron. 2010, 57, 1137–1145. [Google Scholar] [CrossRef]
- Ortuzar, M.; Moreno, J.; Dixon, J. Ultracapacitor-based auxiliary energy system for an electric vehicle: Implementation and evaluation. IEEE Trans. Ind. Electron. 2007, 54, 2147–2156. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.; Bhattacharya, S.; Huang, A. Rule-based control of battery energy storage for dispatching intermittent renewable sources. IEEE Trans. Sustain. Energy 2010, 1, 117–124. [Google Scholar] [CrossRef]
- Gee, A.M.; Robinson, F.V.P.; Dunn, R.W. Analysis of battery lifetime extension in a small-scale wind-energy system using supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K.; Isa, D. Hybrid energy storage systems and control strategies for stand-alone renewable energy power systems. Renew. Sustain. Energy Rev. 2016, 66, 174–189. [Google Scholar] [CrossRef]
- Javed, K.; Ashfaq, H.; Singh, R.; Hussain, S.M.; Ustun, T.S. Design and performance analysis of a stand-alone PV system with hybrid energy storage for rural India. Electronics 2019, 8, 952. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Lai, C.H.; Wong, S.H.W.; Wong, M.L.D. Battery-supercapacitor hybrid energy storage system in standalone DC microgrids: A review. IET Renew. Power Gener. 2017, 11, 461–469. [Google Scholar] [CrossRef]
- Muqeet, H.A.; Javed, H.; Akhter, M.N.; Shahzad, M.; Munir, H.M.; Nadeem, M.U.; Bukhari, S.S.H.; Huba, M. Sustainable Solutions for Advanced Energy Management System of Campus Microgrids: Model Opportunities and Future Challenges. Sensors 2022, 22, 2345. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V. Model predictive control of a hybrid battery-ultracapacitor power source. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 2294–2299. [Google Scholar]
- Hredzak, B.; Agelidis, V. Direct current control of a battery ultracapacitor power supply. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4024–4028. [Google Scholar]
- Zhang, J.; Huang, L.; Shu, J.; Wang, H.; Ding, J. Energy management of PV-diesel-battery hybrid power system for island stand-alone micro-grid. Energy Procedia 2017, 105, 2201–2206. [Google Scholar] [CrossRef]
- Aziz, A.S.; Tajuddin, M.F.N.; Adzman, M.R.; Ramli, M.A.; Mekhilef, S. Energy management and optimization of a PV/diesel/battery hybrid energy system using a combined dispatch strategy. Sustainability 2019, 11, 683. [Google Scholar] [CrossRef] [Green Version]
- Emara, D.; Ezzat, M.; Abdelaziz, A.Y.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Novel control strategy for enhancing microgrid operation connected to photovoltaic generation and energy storage systems. Electronics 2021, 10, 1261. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, X. Dual Heuristic Dynamic Programming Based Energy Management Control for Hybrid Electric Vehicles. Energies 2022, 15, 3235. [Google Scholar] [CrossRef]
- Dai, K.; Zhang, C.; Li, Q.; Huang, X.; Zhang, H. An Adaptive Energy Management Strategy for Simultaneous Long Life and High Wake-Up Success Rate of Wireless Sensor Network Nodes. Energy Technol. 2021, 9, 2100522. [Google Scholar] [CrossRef]
- Gharibeh, H.F.; Yazdankhah, A.S.; Azizian, M.R.; Farrokhifar, M. Online energy management strategy for fuel cell hybrid electric vehicles with installed PV on roof. IEEE Trans. Ind. Appl. 2021, 57, 2859–2869. [Google Scholar] [CrossRef]
- Ravada, B.R.; Tummuru, N.R.; Ande, B.N.L. Photovoltaic-Wind and Hybrid Energy Storage Integrated Multisource Converter Configuration-Based Grid-Interactive Microgrid. IEEE Trans. Ind. Electron. 2020, 68, 4004–4013. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, X.; Zhang, G.; Fan, J.; Jia, S. Neural network adaptive sliding mode control for omnidirectional vehicle with uncertainties. ISA Trans. 2019, 86, 201–214. [Google Scholar] [CrossRef]
- Chu, Y.; Fei, J.; Hou, S. Adaptive global sliding-mode control for dynamic systems using double hidden layer recurrent neural network structure. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1297–1309. [Google Scholar] [CrossRef]
- Ahmed, S.; Muhammad Adil, H.M.; Ahmad, I.; Azeem, M.K.; Huma, Z.; Abbas Khan, S. Supertwisting sliding mode algorithm based nonlinear MPPT control for a solar PV system with artificial neural networks based reference generation. Energies 2020, 13, 3695. [Google Scholar] [CrossRef]
- Zdiri, M.A.; Khelifi, B.; Ben Salem, F.; Hadj Abdallah, H. A Comparative Study of Distinct Advanced MPPT Algorithms for a PV Boost Converter. Int. J. Renew. Energy Res. 2021, 11, 1156–1165. [Google Scholar]
- Zdiri, M.A.; Ben Ammar, M.; Ben Salem, F.; Hadj Abdallah, H. PWM-VSI Diagnostic and Reconfiguration Method Based on Fuzzy Logic Approach for SSTPI-Fed IM Drives under IGBT OCFs. Math. Probl. Eng. 2021, 2021, 9505845. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Narasamma, N.L. Design and analysis of novel control strategy for battery and supercapacitor storage system. IEEE Trans. Sustain. Energy 2014, 5, 1137–1144. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Mode Control Design Principles and Application to Electric Drives. IEEE Trans. Ind. Appl. 1993, 40, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineers guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Divakaran, A.M.; Minakshi, M.; Bahri, P.A.; Paul, S.; Kumari, P.; Divakaran, A.M.; Manjunatha, K.N. Rational design on materials for developing next generation lithium-ion secondary battery. Prog. Solid State Chem. 2021, 62, 100298. [Google Scholar] [CrossRef]
- Divakaran, A.M.; Hamilton, D.; Manjunatha, K.N.; Minakshi, M. Design, development and thermal analysis of reusable Li-ion battery module for future mobile and stationary applications. Energies 2020, 13, 1477. [Google Scholar] [CrossRef] [Green Version]





| SC | Lead Acid Battery | Lithium-Ion Battery | |
|---|---|---|---|
| Density of specific energy (Wh/kg) | 1–10 | 10–100 | 150–200 |
| Density of specific power (W/kg) | <10,000 | <1000 | <2000 |
| Life-cycle | >500,000 | 1000 | 5000 |
| Charge–discharge efficiency (%) | 85–98 | 70–85 | 99 |
| Discharge time | 0.3–30 s | 0.3–3 h | 0.3–3 h |
| Quick charge time | 0.3–30 s | 1–5 h | 0.5–3 h |
| CE | E | ||||
|---|---|---|---|---|---|
| SS | BS | ZO | SB | BB | |
| SS | BB | BB | SB | BB | BB |
| BS | BB | SB | SB | SB | BB |
| ZO | BS | BS | ZO | SB | SB |
| SB | SS | BS | BS | BS | SS |
| BB | SS | SS | BS | SS | SS |
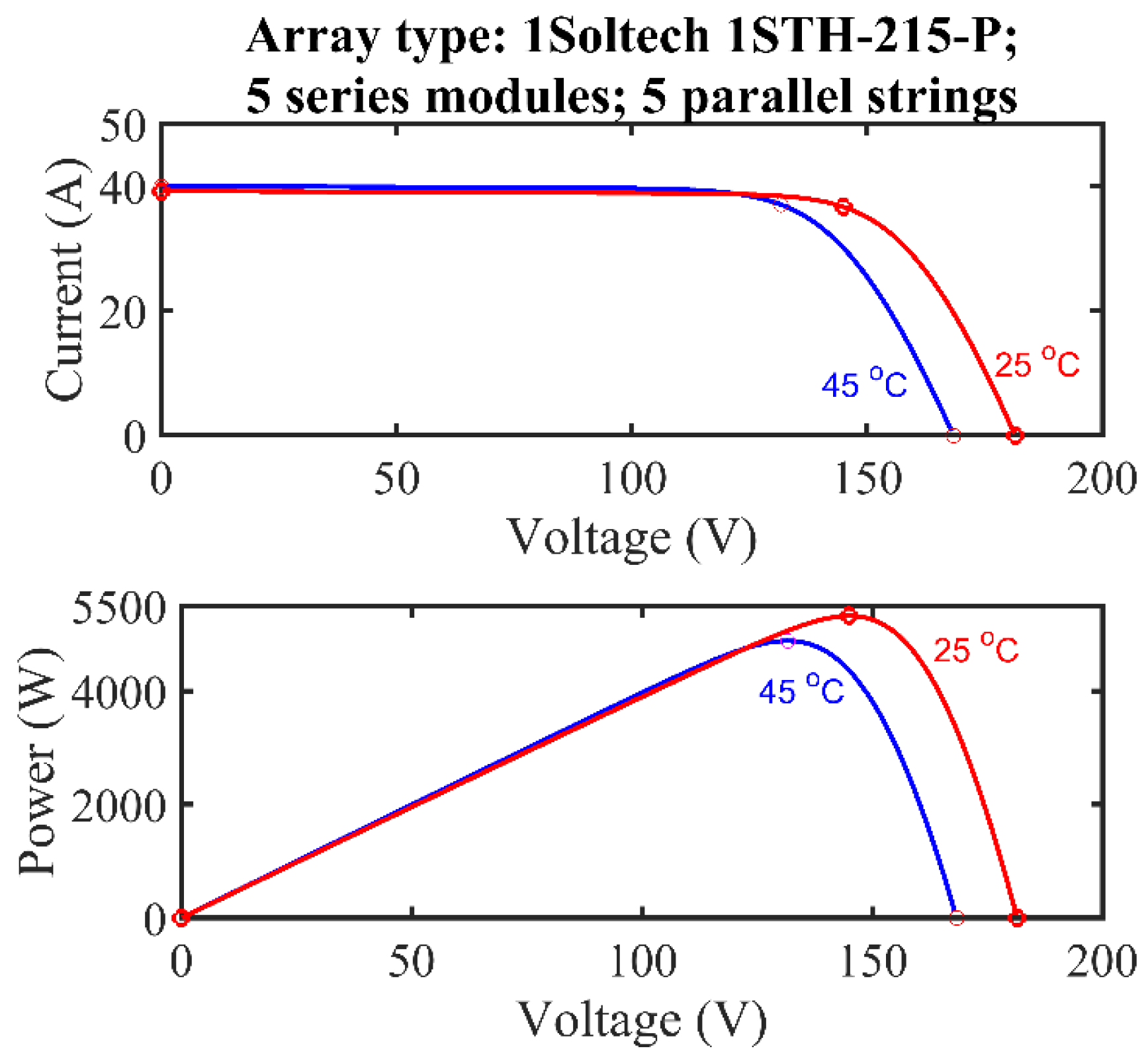
| PV Generator Parameters | |
|---|---|
| Maximum power | 5329 W |
| Voltage at MPP | 181.5 V |
| Current at MPP | 39.2 A |
| PV module series and parallel strings | Ns = 5, Np = 5 |
| DC/DC converter and line parameters | |
| DC bus voltage | 400 V |
| S1, S2, S3, S4 and S5 | IGBT/Diode |
| Switching frequency | 10 kHz |
| Capacitor (C) | 3300 µF |
| DC/DC converter inductor | Lpv = 5 mH, LB = 2 mH, LS = 1 mH |
| Super capacitor parameters | |
| Voltage and Capacity | 2.7 V, 310 F |
| Module and array | (Nsc = 5, Npc = 2) × 20 series |
| Battery parameters | |
| Battery model | Lithium-ion |
| Voltage | 220 V |
| Capacity | 50 Ah |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdiri, M.A.; Guesmi, T.; Alshammari, B.M.; Alqunun, K.; Almalaq, A.; Salem, F.B.; Hadj Abdallah, H.; Toumi, A. Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System. Energies 2022, 15, 4099. https://doi.org/10.3390/en15114099
Zdiri MA, Guesmi T, Alshammari BM, Alqunun K, Almalaq A, Salem FB, Hadj Abdallah H, Toumi A. Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System. Energies. 2022; 15(11):4099. https://doi.org/10.3390/en15114099
Chicago/Turabian StyleZdiri, Mohamed Ali, Tawfik Guesmi, Badr M. Alshammari, Khalid Alqunun, Abdulaziz Almalaq, Fatma Ben Salem, Hsan Hadj Abdallah, and Ahmed Toumi. 2022. "Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System" Energies 15, no. 11: 4099. https://doi.org/10.3390/en15114099
APA StyleZdiri, M. A., Guesmi, T., Alshammari, B. M., Alqunun, K., Almalaq, A., Salem, F. B., Hadj Abdallah, H., & Toumi, A. (2022). Design and Analysis of Sliding-Mode Artificial Neural Network Control Strategy for Hybrid PV-Battery-Supercapacitor System. Energies, 15(11), 4099. https://doi.org/10.3390/en15114099






