Model for Optimal Power Coefficient Tracking and Loss Reduction of the Wind Turbine Systems
Abstract
:1. Introduction
1.1. Background and Literature Review
1.2. Research Gap and Originality Highlights
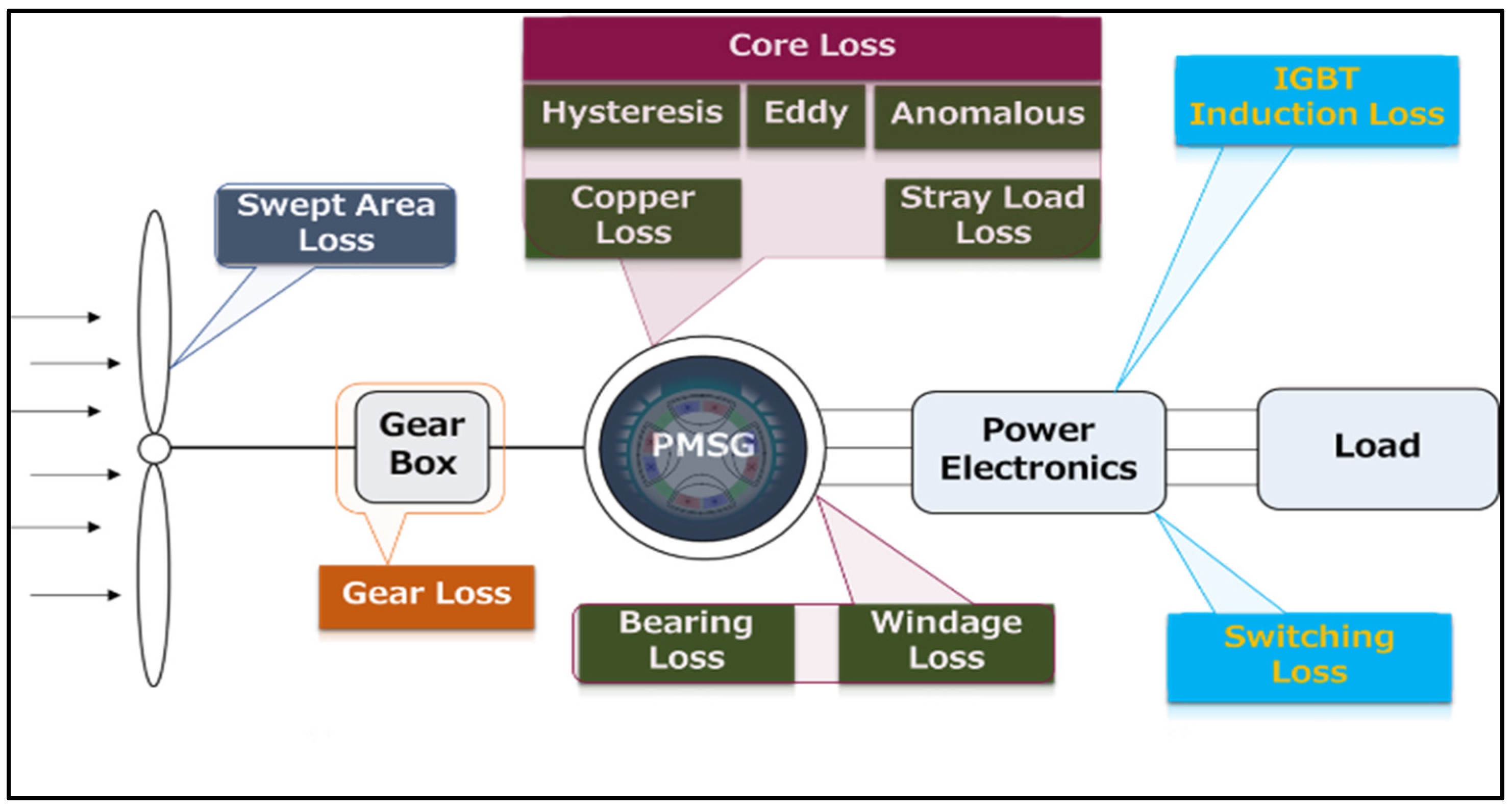
2. Model Development
3. Results and Discussion
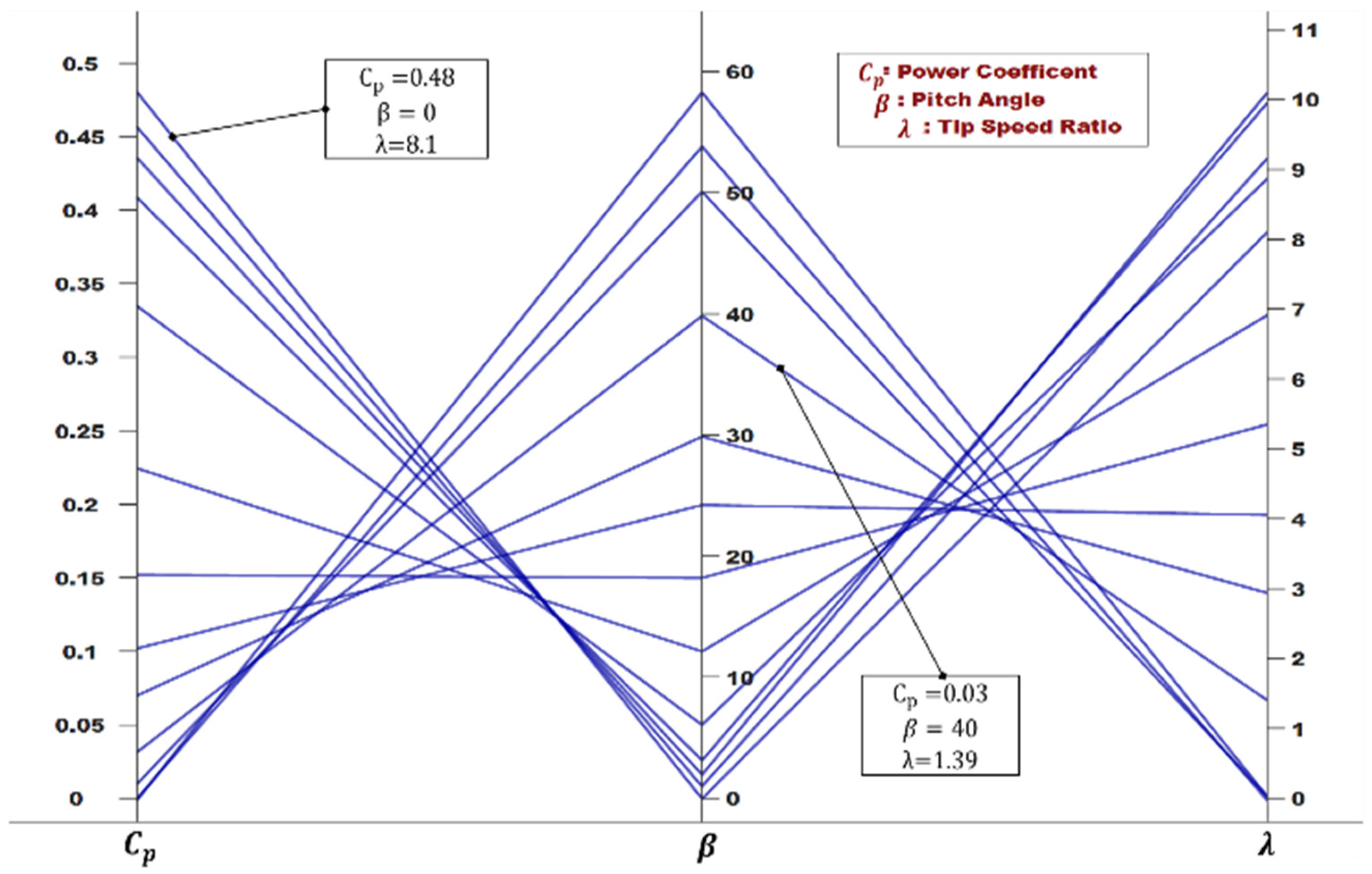
3.1. Estimation of the Optimal Value of the Power Coefficient in a Direct Drive Configuration
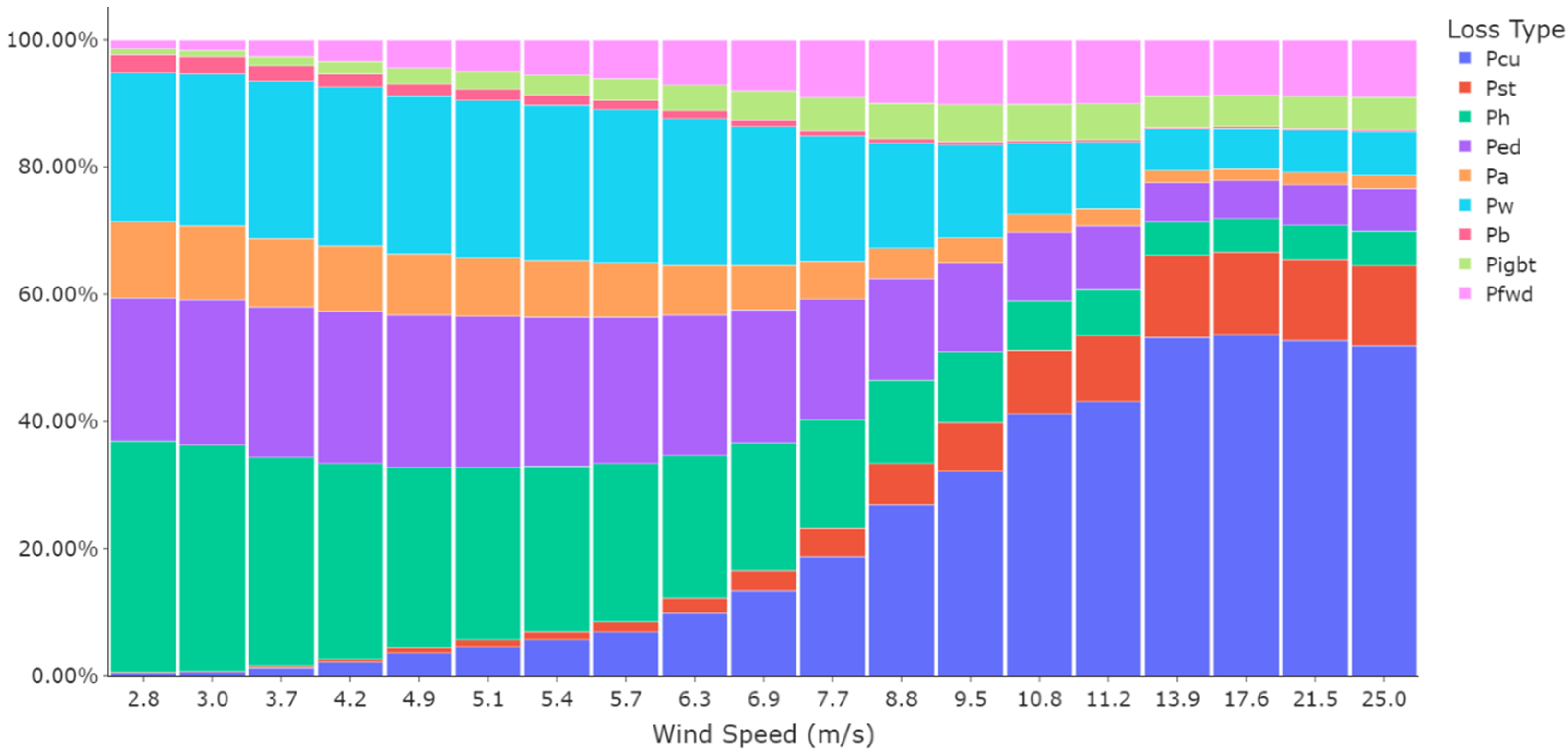
3.1.1. Power Loss Estimation Based on the Optimal Value of Cp
3.1.2. Validation of the Model Results with the Experimental System
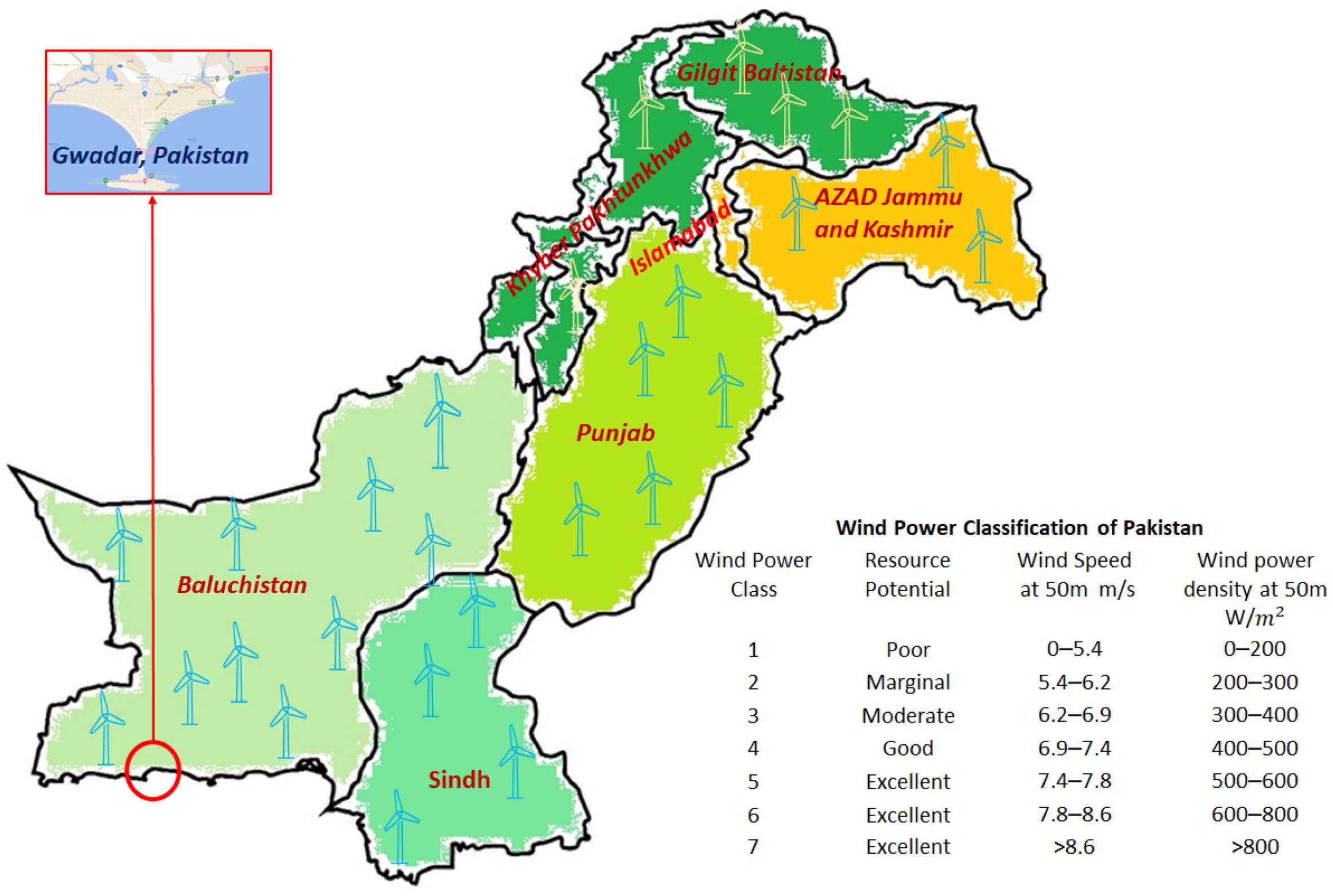
3.2. Model Application to a Real Case Study in Pakistan Considering the Indirect Drive Configuration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoshida, Y.; Farzaneh, H. Optimal design of a stand-alone residential hybrid microgrid system for enhancing renewable energy deployment in Japan. Energies 2020, 13, 1737. [Google Scholar] [CrossRef] [Green Version]
- Esteban, M.; Portugal-Pereira, J.; Mclellan, B.C.; Bricker, J.; Farzaneh, H.; Djalilova, N.; Ishihara, K.N.; Takagi, H.; Roeber, V. 100% renewable energy system in Japan: Smoothening and ancillary services. Appl. Energy 2018, 224, 698–707. [Google Scholar] [CrossRef] [Green Version]
- Hinokuma, T.; Farzaneh, H.; Shaqour, A. Techno-economic analysis of a fuzzy logic control based hybrid renewable energy system to power a university campus in Japan. Energies 2021, 14, 1960. [Google Scholar] [CrossRef]
- Ugranli, F.; Karatepe, E. Optimal wind turbine sizing to minimize energy loss. Int. J. Electr. Power Energy Syst. 2013, 53, 656–663. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R.C. Analytical strategies for renewable distributed generation integration considering energy loss minimization. Appl. Energy 2013, 105, 75–85. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Harrison, G.P. Minimizing energy losses: Optimal accommodation and smart operation of renewable distributed generation. IEEE Trans. Power Syst. 2011, 26, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.H.; Wang, J.S.; Chang, M.H.; Mutuku, J.K.; Hoang, A.T. Efficiency improvement of a vertical-axis wind turbine using a deflector optimized by Taguchi approach with modified additive method. Energy Convers. Manag. 2021, 245, 114609. [Google Scholar] [CrossRef]
- Baran, J.; Jaderko, A. A method of maximum power point tracking for a variable speed wind turbine system. In Proceedings of the 2019 Applications of Electromagnetics in Modern Engineering and Medicine (PTZE), Janow Podlaski, Poland, 9–12 June 2019; Volume 2, pp. 13–16. [Google Scholar] [CrossRef]
- Vijayalakshmi, S.; Ganapathy, V.; Vijayakumar, K.; Dash, S.S. Maximum Power Point Tracking for Wind Power Generation System at Variable Wind Speed using a Hybrid Technique. Int. J. Control Autom. 2015, 8, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Yaakoubi, A.E.; Amhaimar, L.; Attari, K.; Harrak, M.H.; Halaoui, M.E.; Asselman, A. Non-linear and intelligent maximum power point tracking strategies for small size wind turbines: Performance analysis and comparison. Energy Rep. 2019, 5, 545–554. [Google Scholar] [CrossRef]
- Pande, J.; Nasikkar, P.; Kotecha, K.; Varadarajan, V. A review of maximum power point tracking algorithms for wind energy conversion systems. J. Mar. Sci. Eng. 2021, 9, 1187. [Google Scholar] [CrossRef]
- Xia, Y.; Yin, M.; Li, R.; Liu, D.; Zou, Y. Integrated structure and maximum power point tracking control design for wind turbines based on degree of controllability. JVC J. Vib. Control 2019, 25, 397–407. [Google Scholar] [CrossRef]
- Lanzafame, R.; Messina, M. Horizontal axis wind turbine working at maximum power coefficient continuously. Renew. Energy 2010, 35, 301–306. [Google Scholar] [CrossRef]
- Wei, L.; Zhan, P.; Liu, Z.; Tao, Y.; Yue, D. Modeling and analysis of maximum power tracking of a 600 kW hydraulic energy storage wind turbine test rig. Processes 2019, 7, 706. [Google Scholar] [CrossRef] [Green Version]
- Adams, T.M.; Mertz, B.E. Horizontal Axis Wind Turbine Power Coefficient as Relative Capture Area. J. Fluid Flow Heat Mass Transf. 2021, 8, 254–261. [Google Scholar] [CrossRef]
- Sohoni, V.; Gupta, S.C.; Nema, R.K. A Critical Review on Wind Turbine Power Curve Modelling Techniques and Their Applications in Wind Based Energy Systems. J. Energy 2016, 2016, 8519785. [Google Scholar] [CrossRef] [Green Version]
- Chinamalli, P.K.S.; Naveen, T.S.; Shankar, C.B. Power Loss Minimization of Permanent Magnet Synchronous Generator Using Particle Swarm Optimization. Int. J. Mod. Eng. Res. 2021, 2, 4069–4076. Available online: http://www.ijmer.com/papers/Vol2_Issue6/AO2640694076.pdf (accessed on 1 December 2021).
- Lap-Arparat, P.; Leephakpreeda, T. Real-time maximized power generation of vertical axis wind turbines based on characteristic curves of power coefficients via fuzzy pulse width modulation load regulation. Energy 2019, 182, 975–987. [Google Scholar] [CrossRef]
- Song, D.; Liu, J.; Yang, Y.; Yang, J.; Su, M.; Wang, Y.; Gui, N.; Yang, X.; Huang, L.; Joo, Y.H. Maximum wind energy extraction of large-scale wind turbines using nonlinear model predictive control via Yin-Yang grey wolf optimization algorithm. Energy 2021, 221, 119866. [Google Scholar] [CrossRef]
- Jia, L.; Hao, J.; Hall, J.; Nejadkhaki, H.K.; Wang, G.; Yan, Y.; Sun, M. A reinforcement learning based blade twist angle distribution searching method for optimizing wind turbine energy power. Energy 2021, 215, 119148. [Google Scholar] [CrossRef]
- Santiago, J.A.E.; Danguillecourt, O.L.; Duharte, G.I.; Díaz, J.E.C.; Añorve, A.V.; Hernandez Escobedo, Q.; Enríquez, J.P.; Verea, L.; Galvez, G.H.; Portela, R.D.; et al. Dimensioning optimization of the permanent magnet synchronous generator for direct drive wind turbines. Energies 2021, 14, 7106. [Google Scholar] [CrossRef]
- Inoue, A.; Ali, M.H.; Takahashi, R.; Murata, T.; Tamura, J.; Kimura, M.; Futami, M.; Ichinose, M.; Ide, K. A calculation method of the total efficiency of wind generator. In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; Volume 2, pp. 1595–1600. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Liu, S.; Liu, J.; Liu, X. A comparative study of MPC and economic MPC of wind energy conversion systems. Energies 2018, 11, 3127. [Google Scholar] [CrossRef] [Green Version]
- Telecommunications, C.; Crawford, T.; Hill, G. A Low-Speed, High-Torque, Direct-Drive Permanent Magnet Generator for Wind Thrbines. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference. Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy, Rome, Italy, 8–12 October 2000; pp. 147–154. [Google Scholar]
- Huynh, C.; Zheng, L.; Acharya, D. Losses in high speed permanent magnet machines used in microturbine applications. J. Eng. Gas Turbines Power 2009, 131, 2–7. [Google Scholar] [CrossRef]
- Choi, J.Y.; Ko, K.J.; Jang, S.M. Experimental works and power loss calculations of surface-mounted permanent magnet machines. J. Magn. 2011, 16, 64–70. [Google Scholar] [CrossRef] [Green Version]
- Muyeen, S.M. Wind Energy Conversion Systems: Technology and Trends; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2012; p. 78. [Google Scholar] [CrossRef] [Green Version]
- Farzaneh Laboratory. Experimental Setup, Energy and Environmental Engineering Department, Kyushu University Japan. Available online: http://farzaneh-lab.kyushu-u.ac.jp/Experiment.html (accessed on 1 December 2021).
- Desmond, C.; Murphy, J.; Blonk, L.; Haans, W. Description of an 8 MW reference wind turbine. J. Phys. Conf. Ser. 2016, 753, 9. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Tao, T.; Liu, Y.; Hu, H. A field study of ice accretion and its effects on the power production of utility-scale wind turbines. Renew. Energy 2021, 167, 917–928. [Google Scholar] [CrossRef]
- Jelavić, M.; Petrović, V.; Barišić, M.; Ivanović, I. Wind turbine control beyond the cut-out wind speed. In Proceedings of the Annual Conference and Exhibition of European Wind Energy Associatio, Vienna, Austria, 4–7 February 2013; Volume 1, pp. 343–349. [Google Scholar]
- Wijewardana, S.; Shaheed, M.H.; Vepa, R. Optimum Power Output Control of a Wind Turbine Rotor. Int. J. Rotating Mach. 2016, 2016, 6935164. [Google Scholar] [CrossRef]
- Abdelqawee, I.M.; Yousef, A.Y.; Hasaneen, K.M.; Nashed, M.N.F.; Hamed, H.G. Standalone wind energy conversion system control using new maximum power point tracking technique. Int. J. Emerg. Technol. Adv. Eng. Certif. J. 2019, 9, 95–100. [Google Scholar] [CrossRef]
- Sun, H.; Han, Y.; Zhang, L. Maximum Wind Power Tracking of Doubly Fed Wind Turbine System Based on Adaptive Gain Second-Order Sliding Mode. J. Control. Sci. Eng. 2018, 2018, 5342971. [Google Scholar] [CrossRef] [Green Version]
- Al Ameri, A.; Ounissa, A.; Nichita, C.; Djamal, A. Power loss analysis for wind power grid integration based on Weibull distribution. Energies 2017, 10, 463. [Google Scholar] [CrossRef] [Green Version]
- Kjaer, A.B.; Korsgaard, S.; Nielsen, S.S.; Demsa, L.; Rasmussen, P.O. Design, Fabrication, Test, and Benchmark of a Magnetically Geared Permanent Magnet Generator for Wind Power Generation. IEEE Trans. Energy Convers. 2020, 35, 24–32. [Google Scholar] [CrossRef]
- Samraj, D.B.; Perumal, M.P. Analogy of the losses in surface and interior permanent magnet synchronous wind turbine generators. Int. J. Sci. Technol. Res. 2019, 8, 2507–2515. [Google Scholar]
- G. D. Corporation. General Algebraic Modeling System Variable Attributes about Initial, Lower, and Upper Values. Available online: https://www.gams.com/latest/docs/UG_Variables.html (accessed on 1 December 2021).
- International Rectifier. Automativ Grade. AUIRG4BC30S-S AUIRG4BC30S-S/SL Reverse Transfer Capacitance; International Rectifier: El Segungo, CA, USA, 2022; pp. 1–14. [Google Scholar]
- Pluta, W.A. Przegląd Elektrotechniczny (Electrical Review), Core Loss Models in Electrical Steel Sheets with Different Orientation. 2011, 9, pp. 37–42. Available online: http://pe.org.pl/articles/2011/9b/8.pdf (accessed on 1 December 2021).
- Mitsubishi Electric Inverter, Technical Note, No.30, Capacity Selection II [Data]. Available online: https://dl.mitsubishielectric.com/dl/fa/document/manual/inv/sh060003eng/sh060003engg.pdf (accessed on 1 December 2021).
- Shaqour, A.; Farzaneh, H.; Yoshida, Y.; Hinokuma, T. Power control and simulation of a building integrated stand-alone hybrid PV-wind-battery system in Kasuga City, Japan. Energy Rep. 2020, 6, 1528–1544. [Google Scholar] [CrossRef]
- Baloch, M.H.; Abro, S.A.; Sarwar Kaloi, G.; Mirjat, N.H.; Tahir, S.; Nadeem, M.H.; Gul, M.; Memon, Z.A.; Kumar, M. A research on electricity generation from wind corridors of Pakistan (two provinces): A technical proposal for remote zones. Sustainability 2017, 9, 1611. [Google Scholar] [CrossRef] [Green Version]
- Baloch, M.H.; Kaloi, G.S.; Memon, Z.A. Current scenario of the wind energy in Pakistan challenges and future perspectives: A case study. Energy Rep. 2016, 2, 201–210. [Google Scholar] [CrossRef] [Green Version]
- Pakistan Broadcasting Corporation (PBC), Ministry of Information and Broadcasting Government of Pakistan. Available online: http://www.moib.gov.pk/Pages/168/PBC (accessed on 1 December 2021).
- Abrar, S.; Farzaneh, H. Scenario analysis of the low emission energy system in pakistan using integrated energy demand-supply modeling approach. Energies 2021, 14, 3303. [Google Scholar] [CrossRef]
- Khlaifat, N.; Altaee, A.; Zhou, J.; Huang, Y.; Braytee, A. Optimization of a small wind turbine for a rural area: A case study of Deniliquin, New South Wales, Australia. Energies 2020, 13, 2292. [Google Scholar] [CrossRef]
- Jiao, S.; Patterson, D.; Camilleri, S. Boost Converter Design for 20KW Wind Turbine Generator. Int. J. Renew. Energy Eng. 2020, 2, 118–122. [Google Scholar]
- Mohd, M.; Shadab, A.; Mallick, M. Simulation and Control of 20 Kw Grid Connected Wind System. Int. J. 2013, 3, 275–284. Available online: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:SIMULATION+AND+CONTROL+OF+20+KW+GRID+CONNECTED+WIND+SYSTEM#0 (accessed on 1 December 2021).
- Abdel-Salam, M.; Ahmed, A.; Abdel-Sater, M. Maximum power point tracking for variable speed grid connected small wind turbine. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 600–605. [Google Scholar] [CrossRef]






| Parameter | Value | Reference |
|---|---|---|
| Wind Turbine | ||
| ) | 100 W | [28] |
| Blade length (L) | 0.58 m | [28] |
| ) | m/s | [29] |
| 2.8 m/s | [30] | |
| 25 m/s | [31] | |
| Aerodynamic Power Coefficients and Wind Regime Limits | ||
| C1 | 0.5176 | [32] |
| C2 | 116 | [33] |
| C3 | 0.4 | [34] |
| C4 | 5 | [23] |
| C5 | −21 | [33] |
| C6 | 0.0068 | [32] |
| TSR Coefficients | ||
| C7 | 1 | [34] |
| C8 | 0.08 | [23] |
| C9 | 1 | [32] |
| C10 | 0.035 | [35] |
| Copper Loss | ||
| ) | 24 V | [36] |
| ) | 3 | [37] |
| Armature resistence (Ra) | 0.195 Ω | [38] |
| Mechanical losses | ||
| 0.00005 | [22] | |
| IGBT Loss | ||
| 655 mJ | [39] | |
| 0.5 s | [39] | |
| 0.00233675 | [38] | |
| 2.19211 | [27] | |
| 0.26 mJ | [39] | |
| 3.45 mJ | [39] | |
| a | 1.09619 | [27] |
| b | 0.00112801 | [38] |
| ) | 2.2 V | [27] |
| Magnetic flux density (B) | [40] | |
| Induction Motor | |
|---|---|
| Torque type | 12:V/F control (variable) |
| Rated power | 0.4 kW |
| Number of poles | 4 |
| Rated voltage | 200 V |
| Rated current | 2.2 A |
| Frequency | 50 Hz |
| V/F control | 12A12 |
| Power factor | 75.6 |
| Rated rpm | 1410 |
| Permanent Magnet Synchronous Generator | |
| Item type | AC wind generator |
| Model | NE-100S |
| Number of phases | 3 |
| Magnetic steel material | Neodymium |
| Breaking method | Electromagnetic |
| Brand | WolfGo |
| Manufacturing country | China |
| Tachometer | TI-900 (measuring range: 2.5 to 99,999 rpm) |
| Clamp-on power meter | Hioki PW3360-20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohail, K.; Farzaneh, H. Model for Optimal Power Coefficient Tracking and Loss Reduction of the Wind Turbine Systems. Energies 2022, 15, 4159. https://doi.org/10.3390/en15114159
Sohail K, Farzaneh H. Model for Optimal Power Coefficient Tracking and Loss Reduction of the Wind Turbine Systems. Energies. 2022; 15(11):4159. https://doi.org/10.3390/en15114159
Chicago/Turabian StyleSohail, Kashif, and Hooman Farzaneh. 2022. "Model for Optimal Power Coefficient Tracking and Loss Reduction of the Wind Turbine Systems" Energies 15, no. 11: 4159. https://doi.org/10.3390/en15114159
APA StyleSohail, K., & Farzaneh, H. (2022). Model for Optimal Power Coefficient Tracking and Loss Reduction of the Wind Turbine Systems. Energies, 15(11), 4159. https://doi.org/10.3390/en15114159









