A Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter
Abstract
:1. Introduction
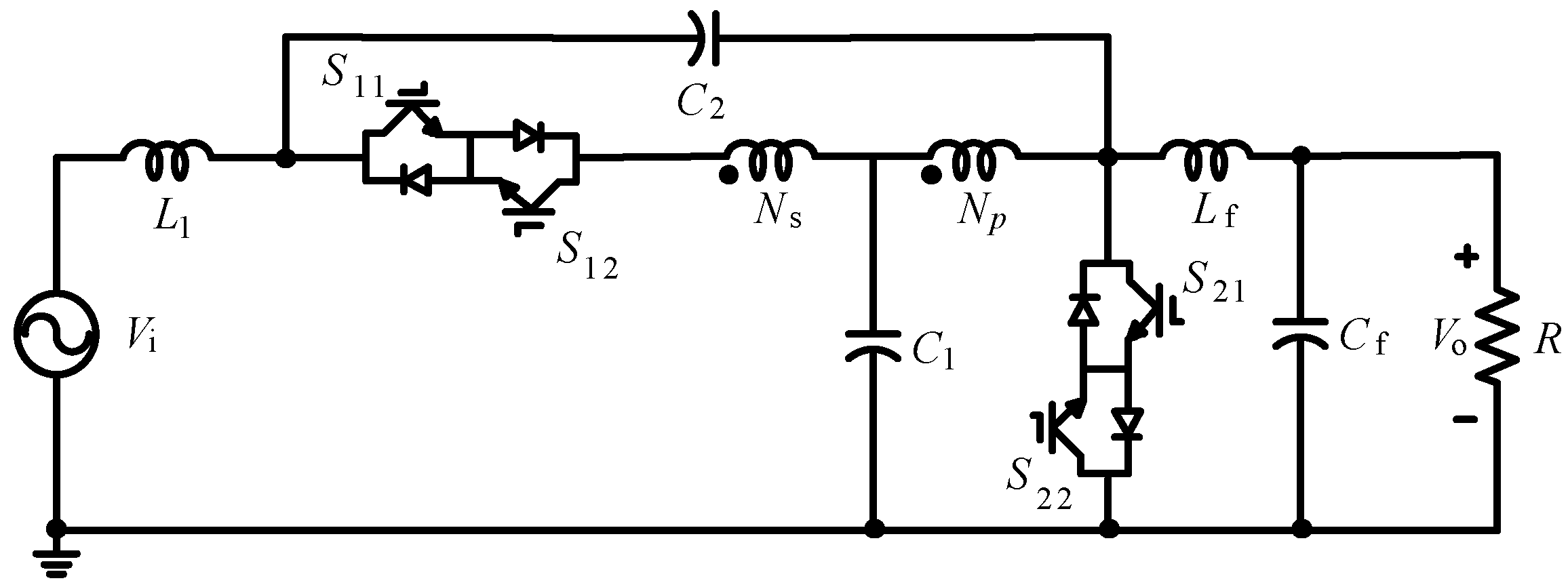
2. Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter
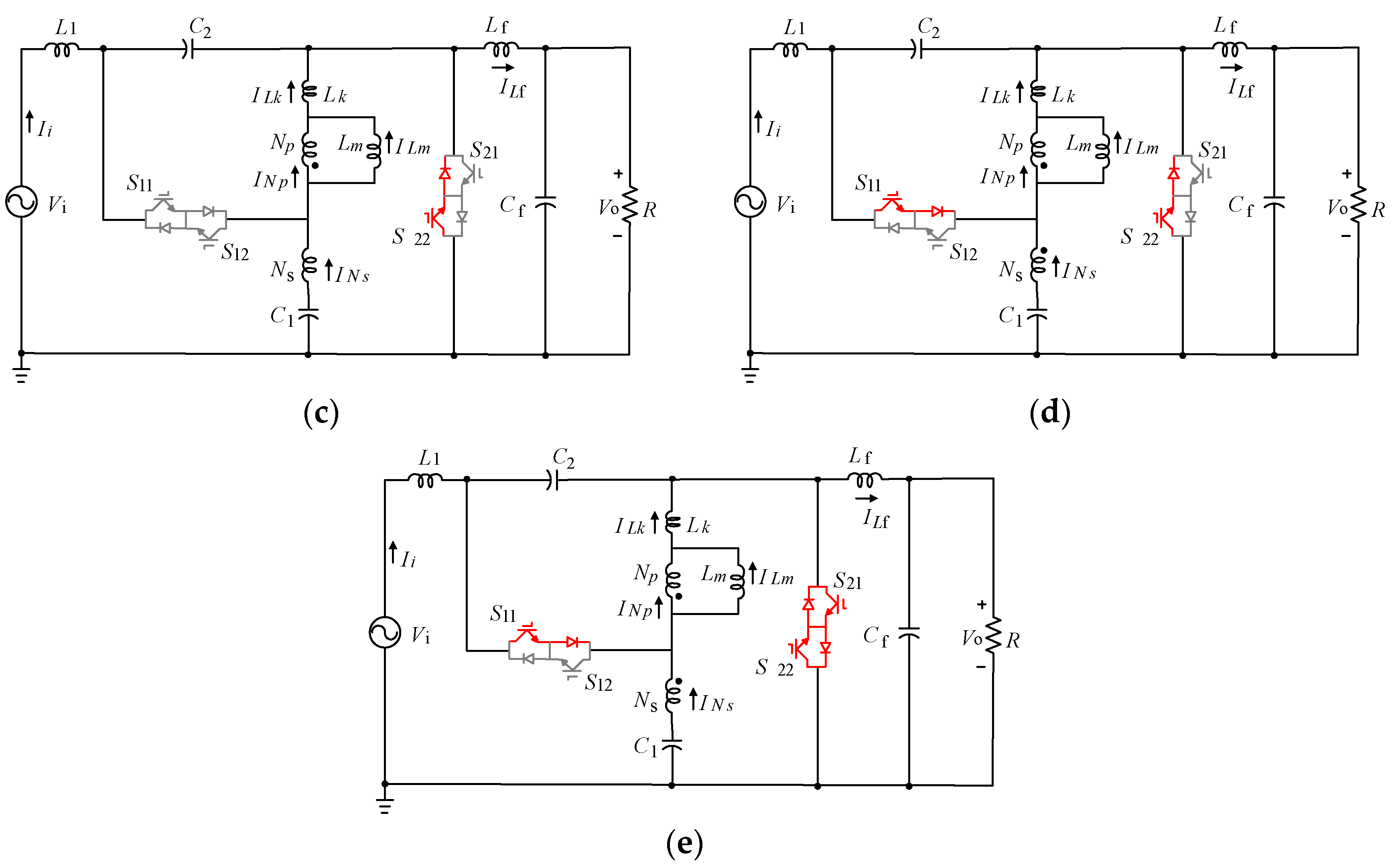
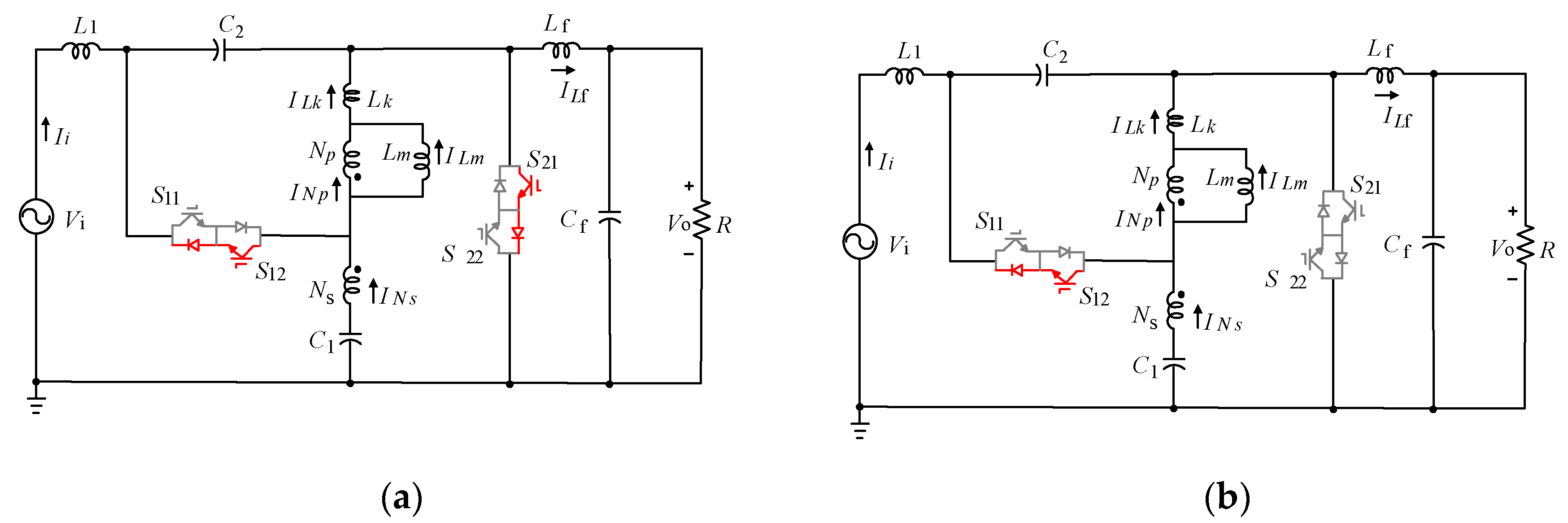
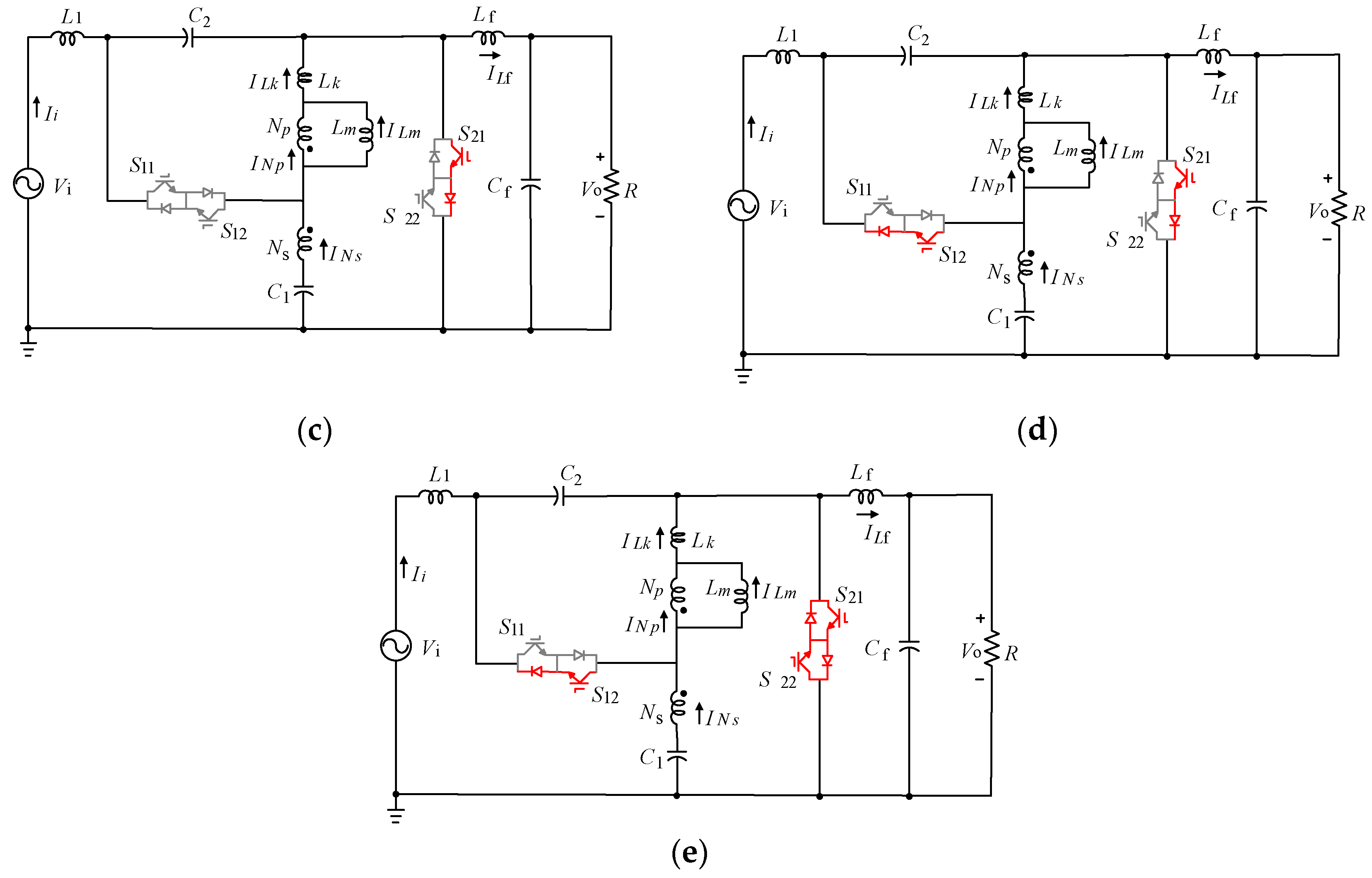
2.1. Commutation Strategy
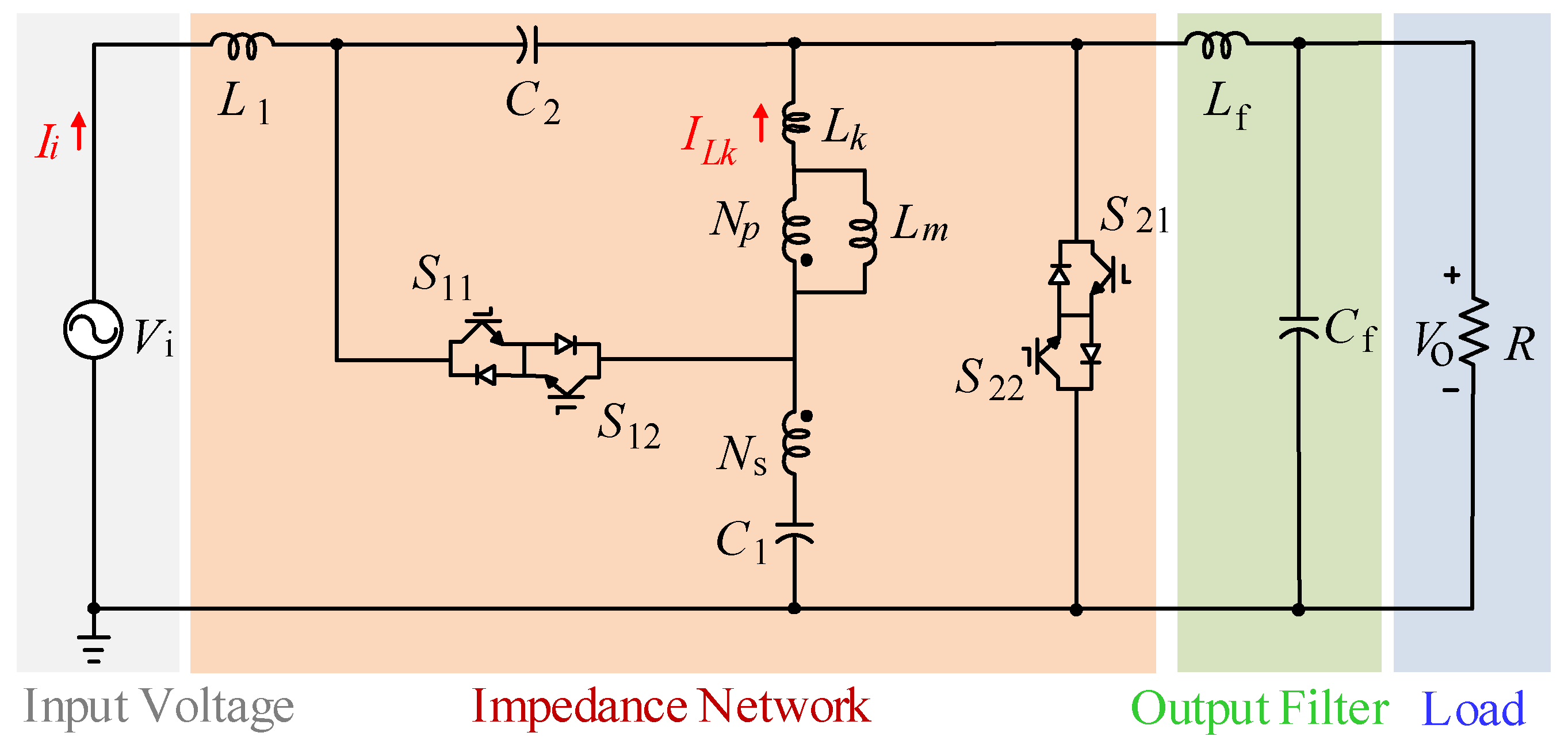
2.2. Circuit Analysis
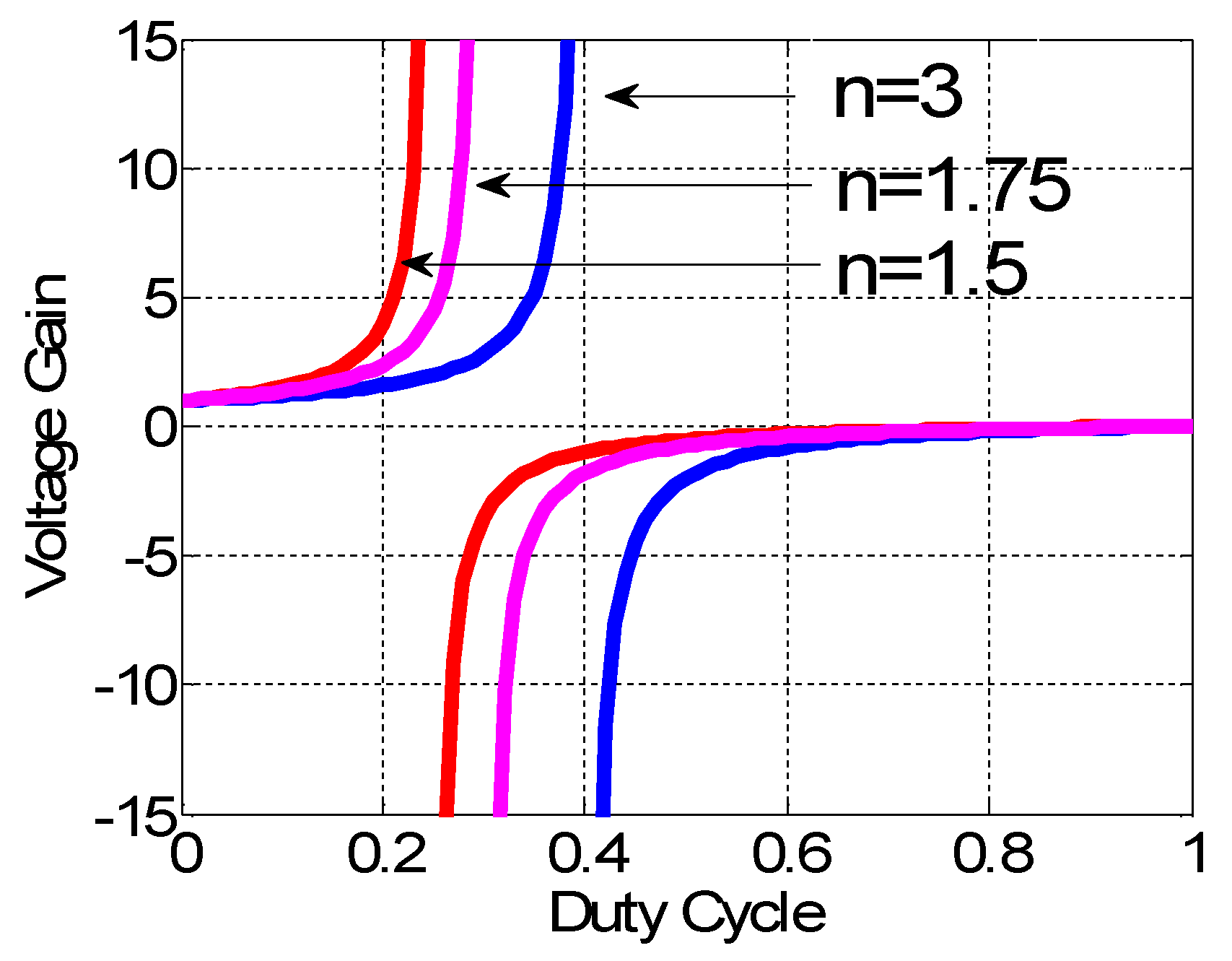
3. Parameter Design of the Proposed Converter
4. Application of the Proposed Converter
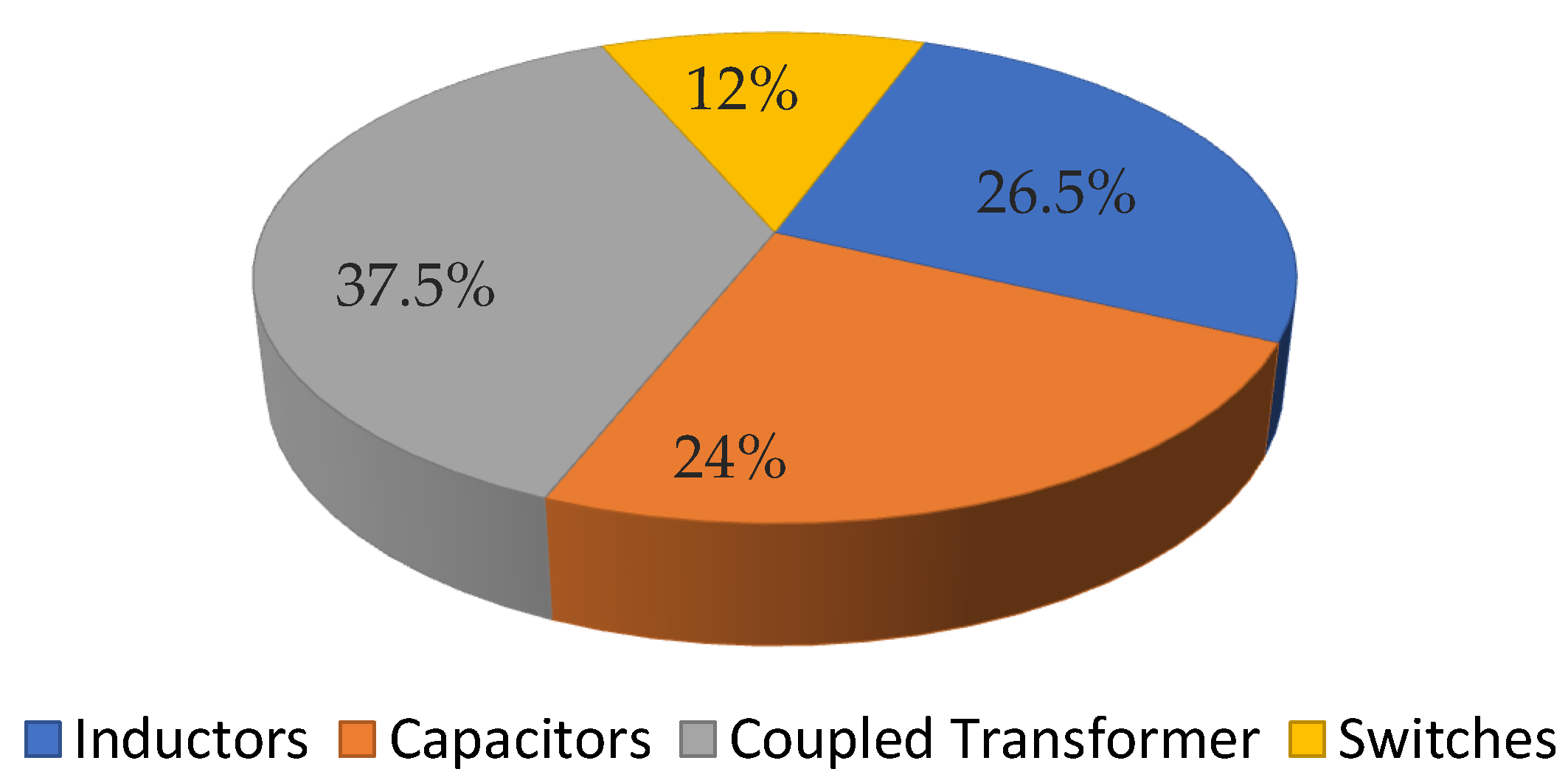
5. Comparative Analysis of the Proposed Converter
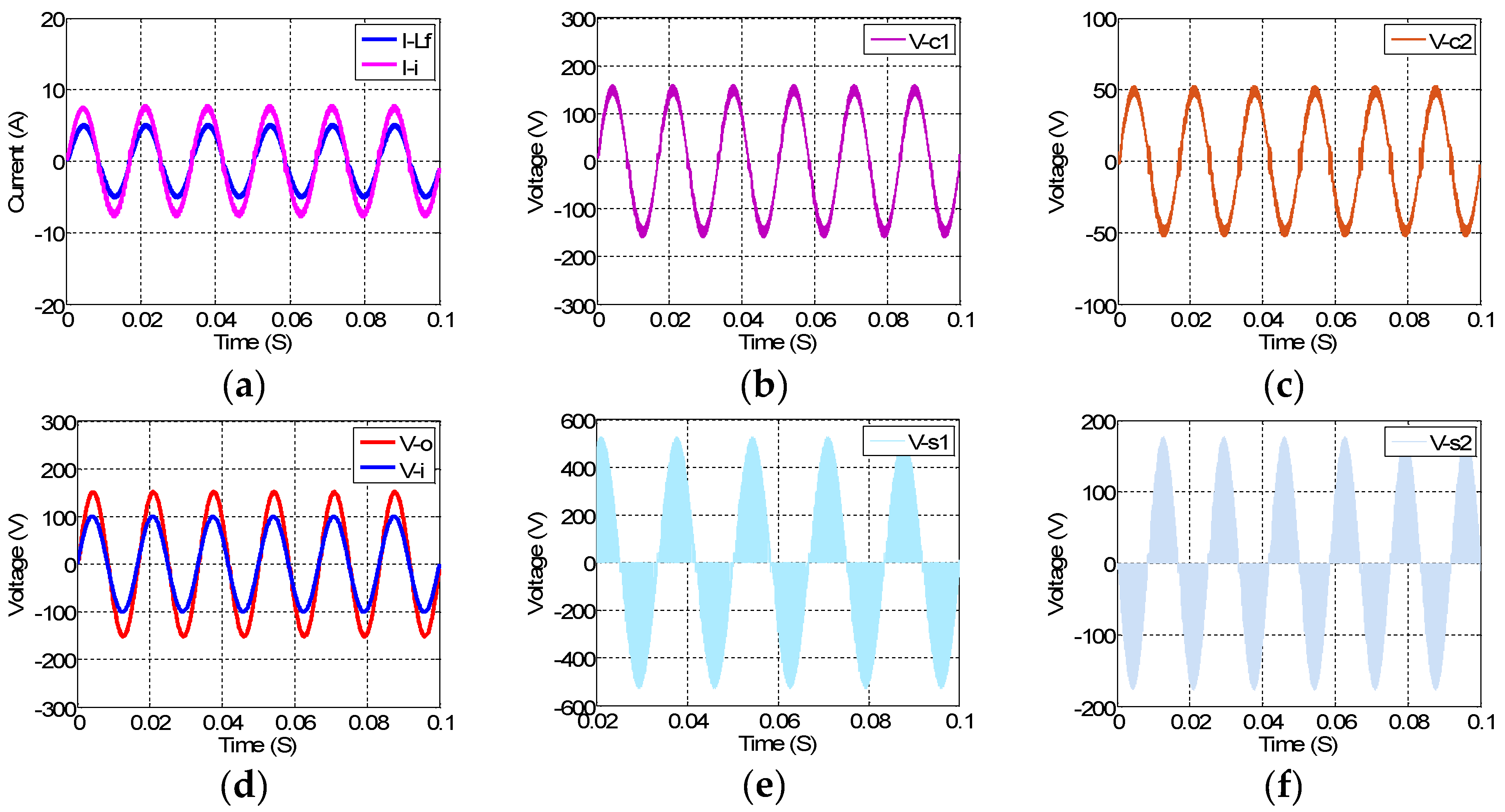
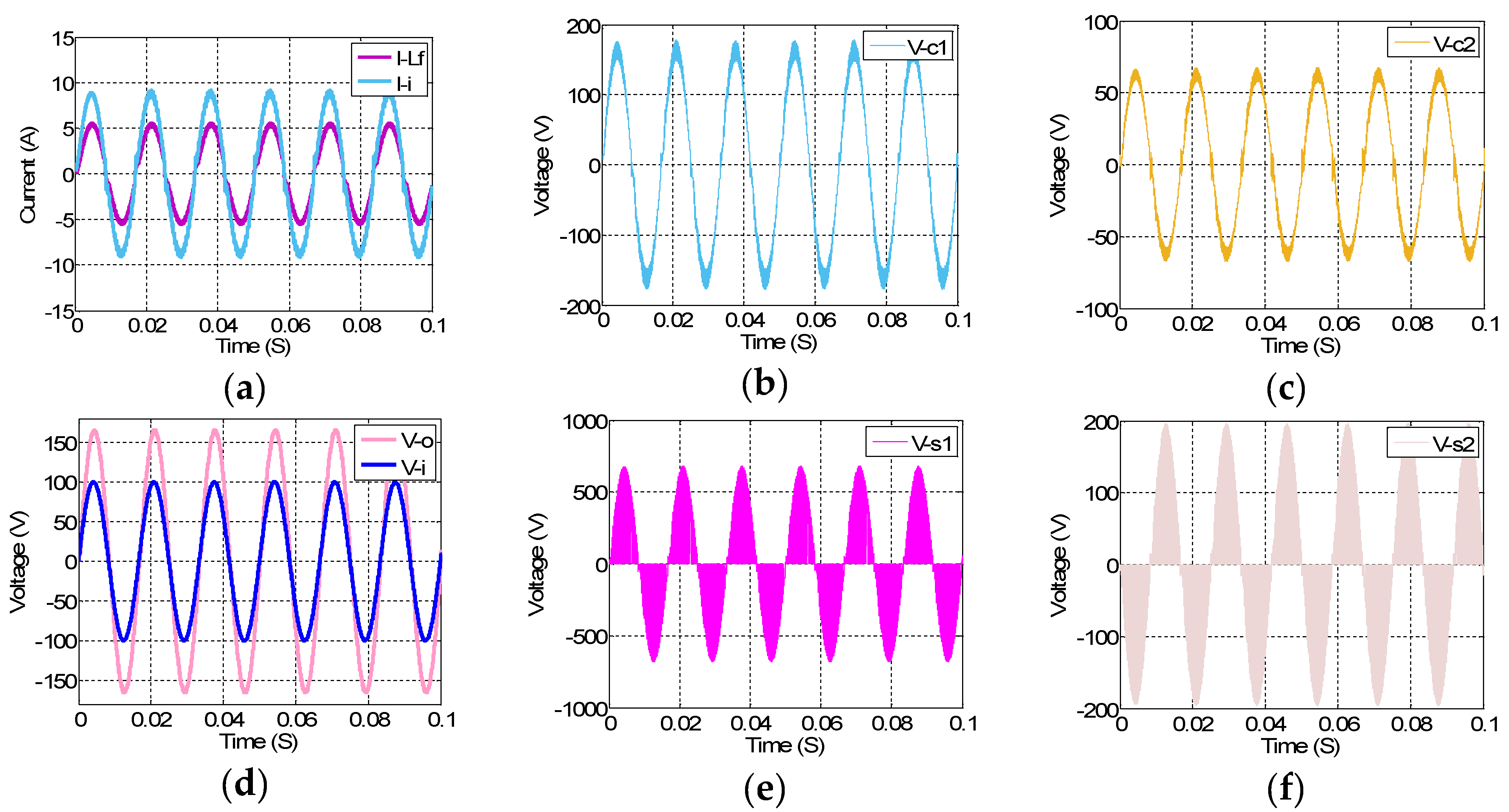
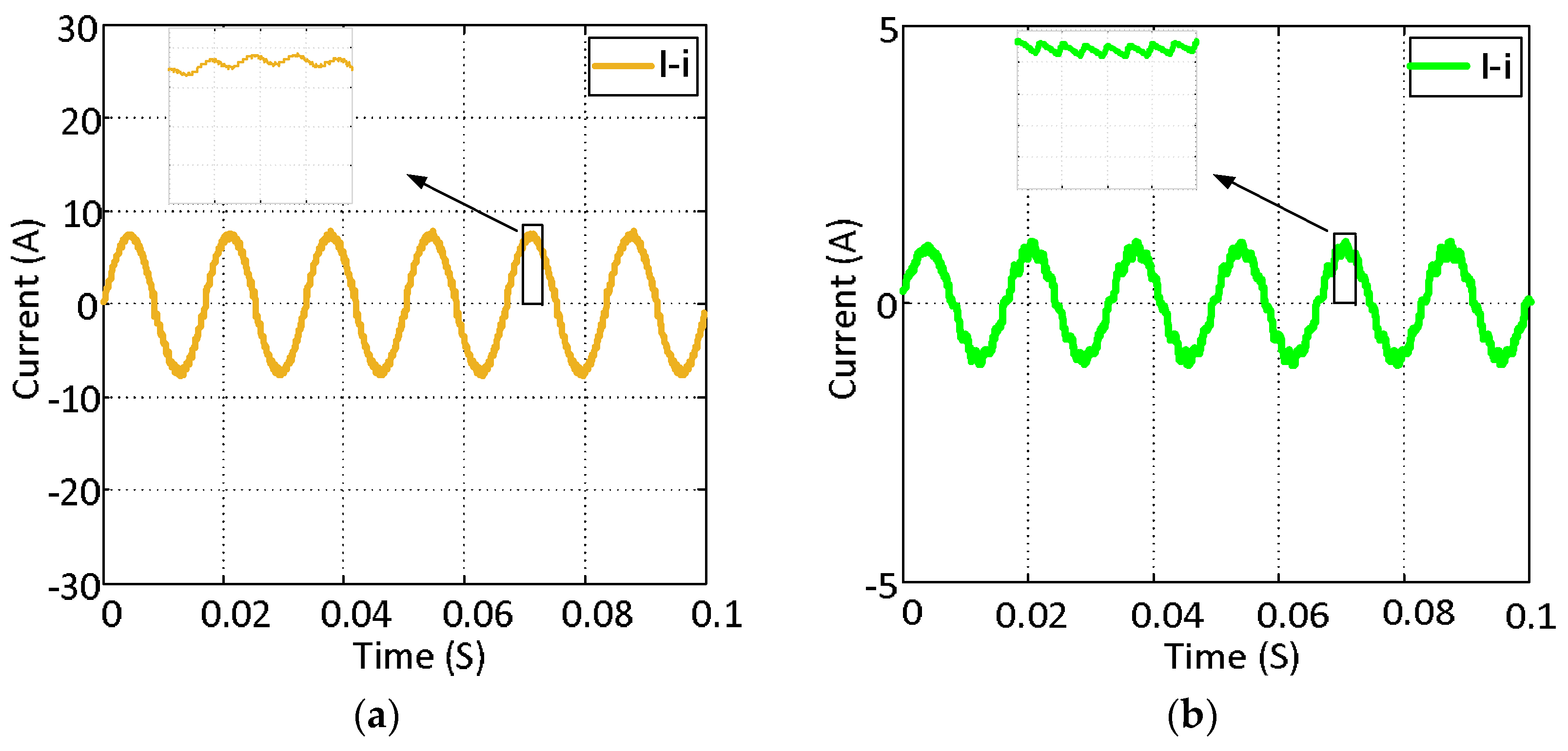
6. Simulation Results
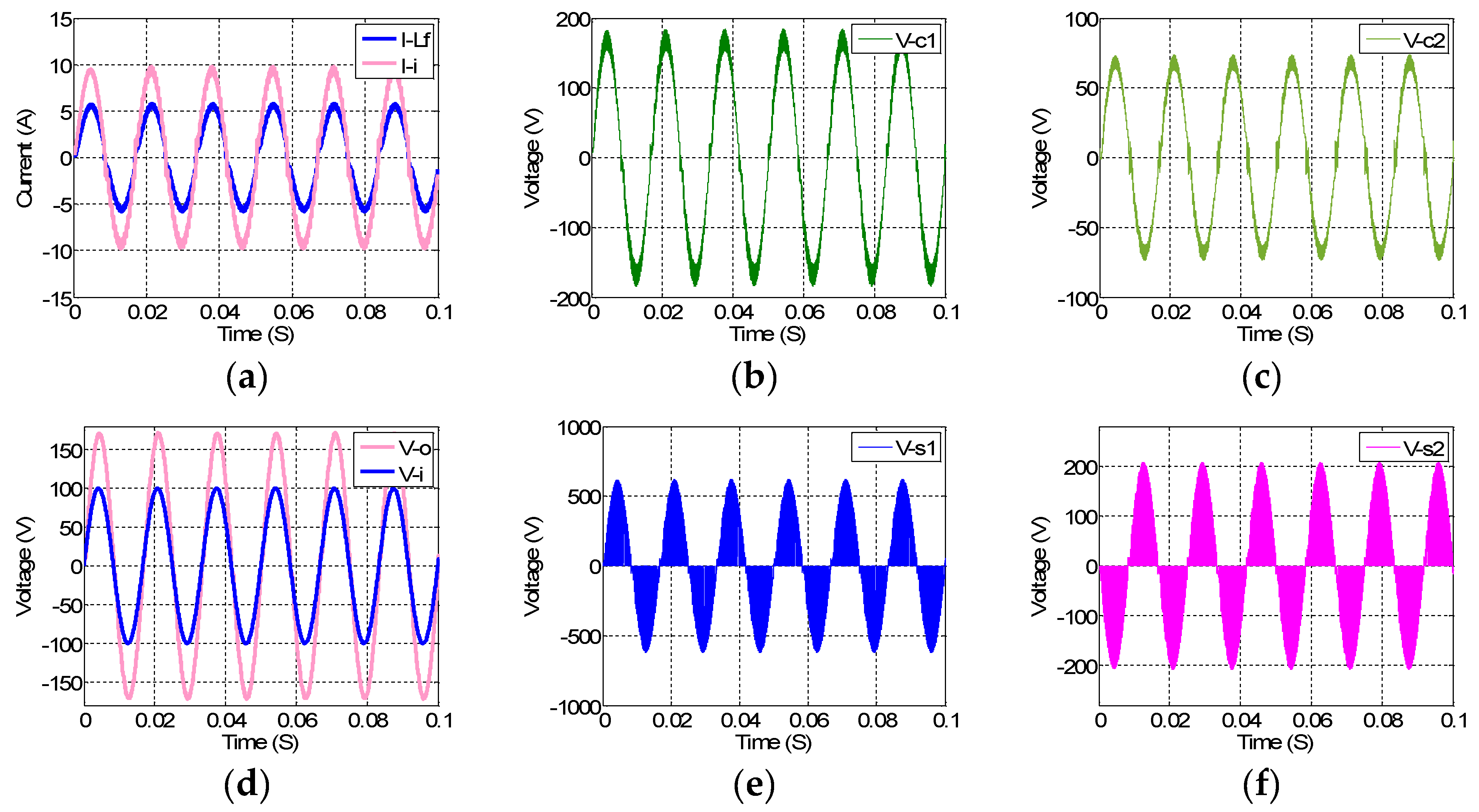
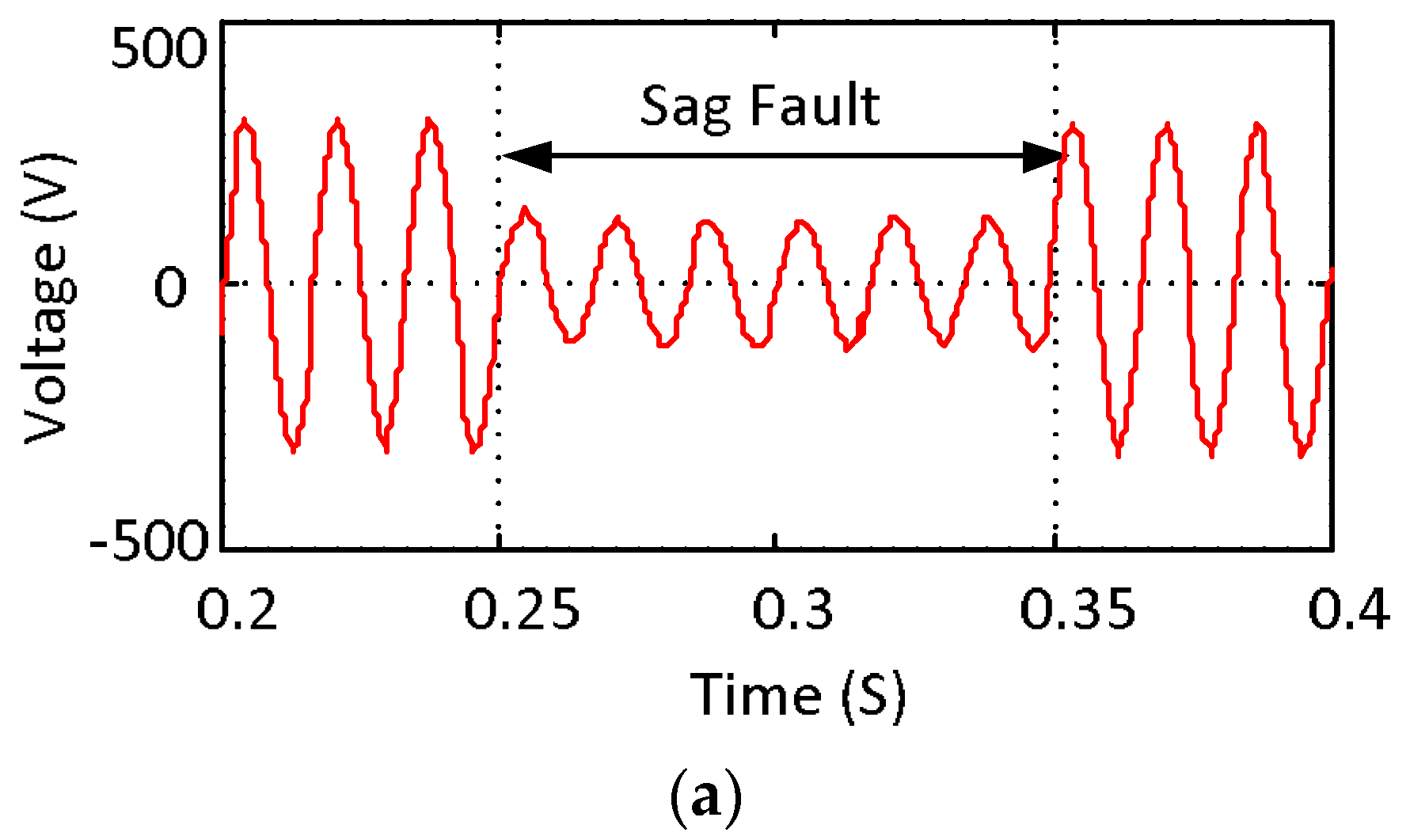
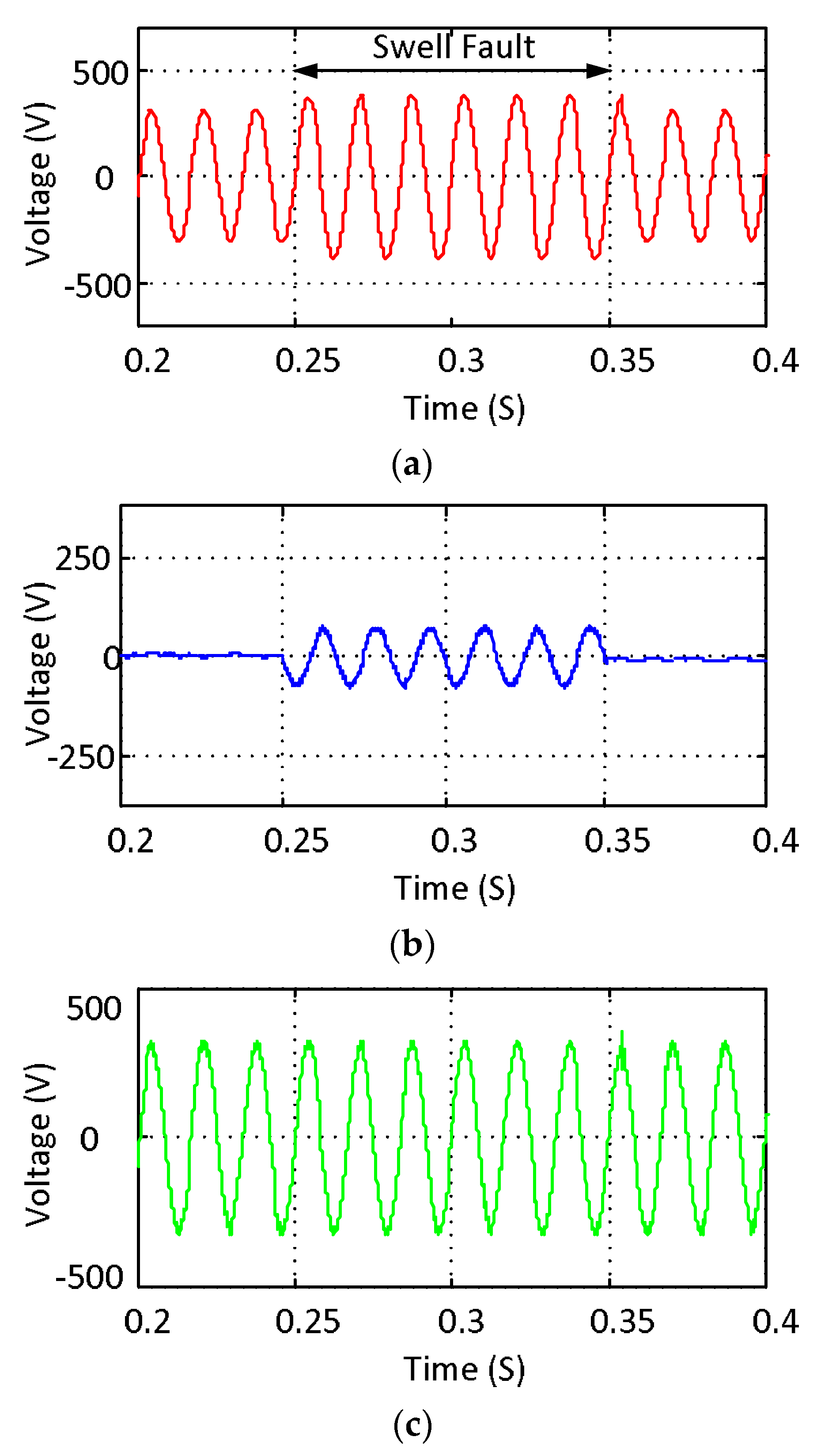
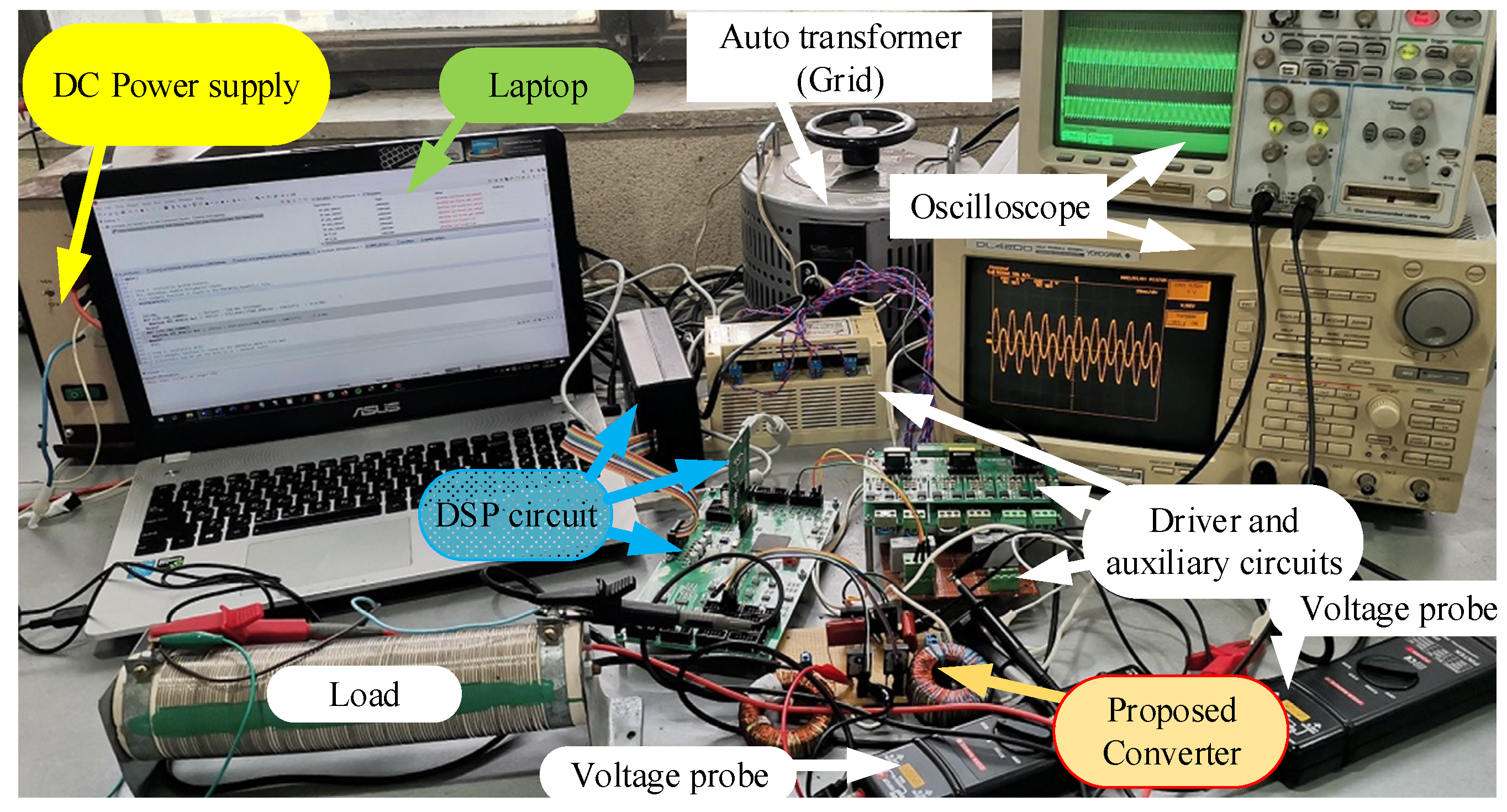
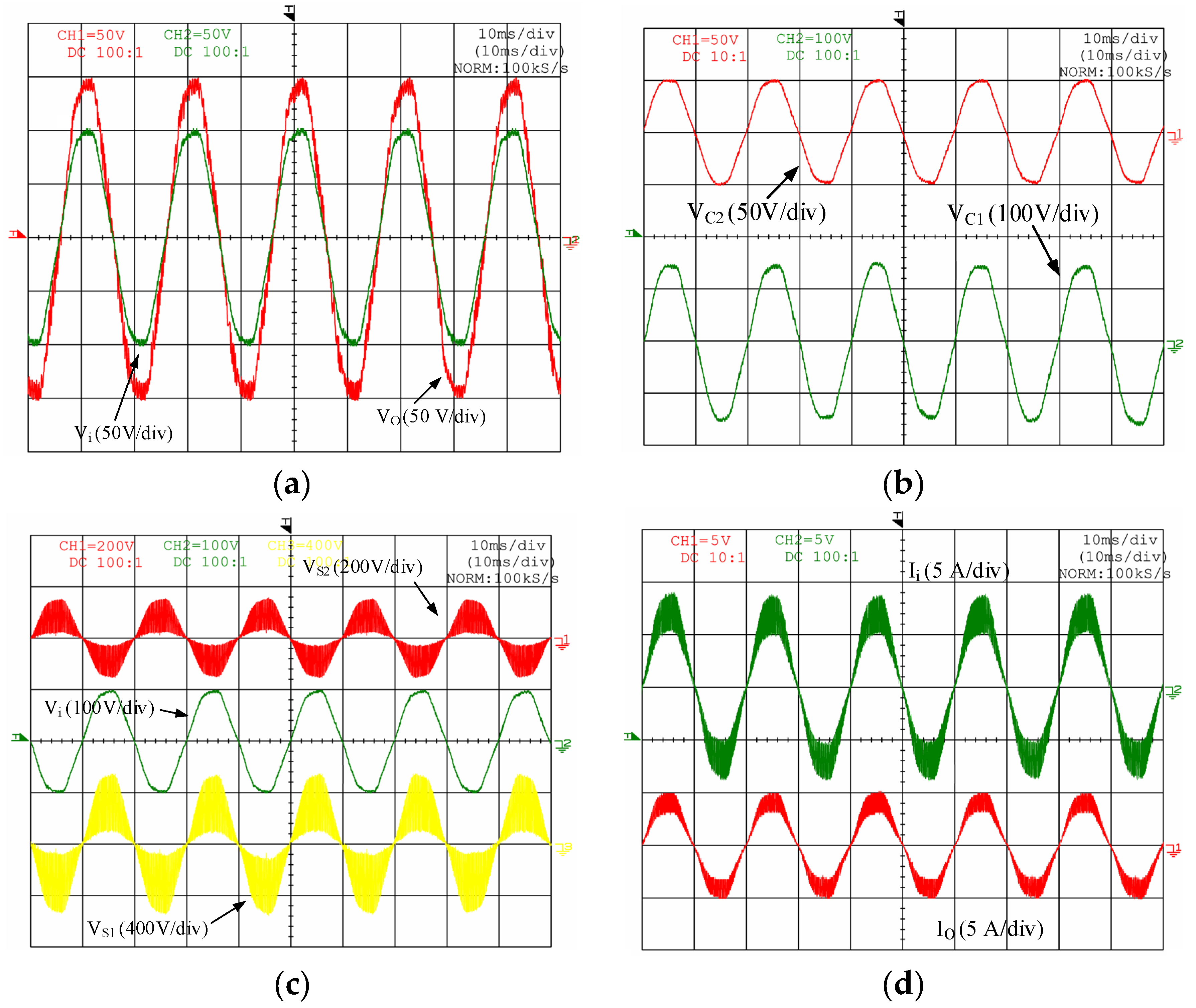
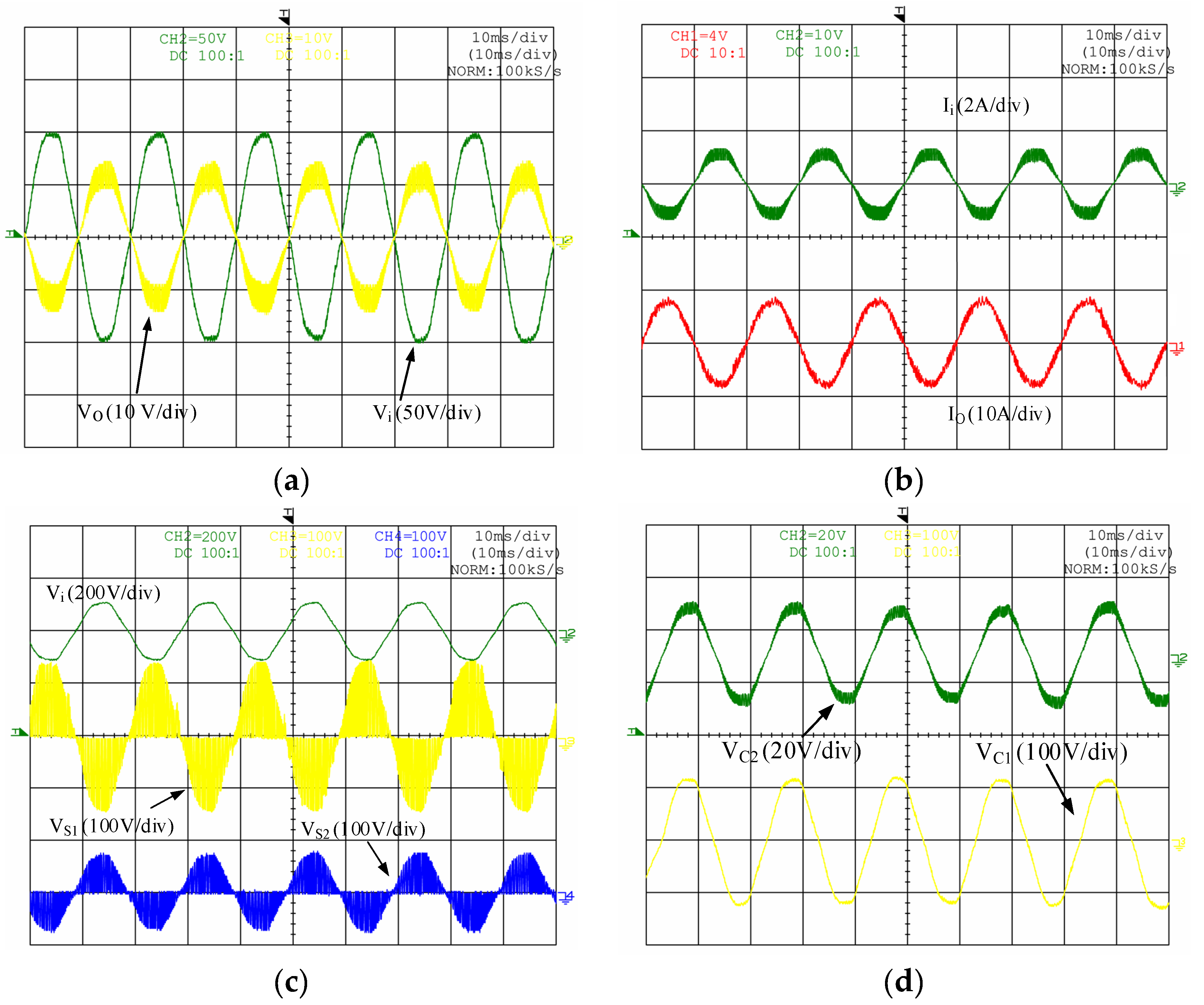
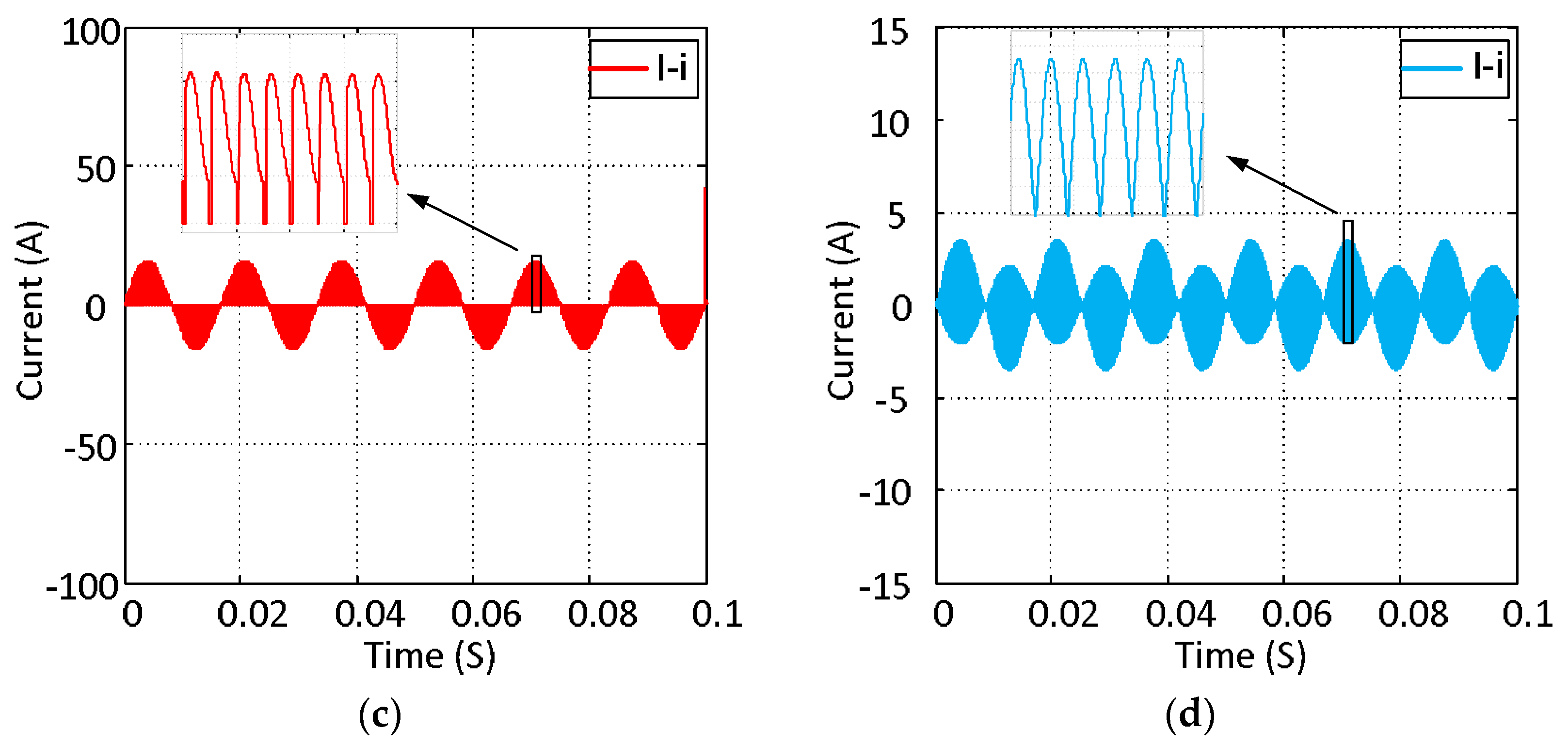
7. Experimental Results
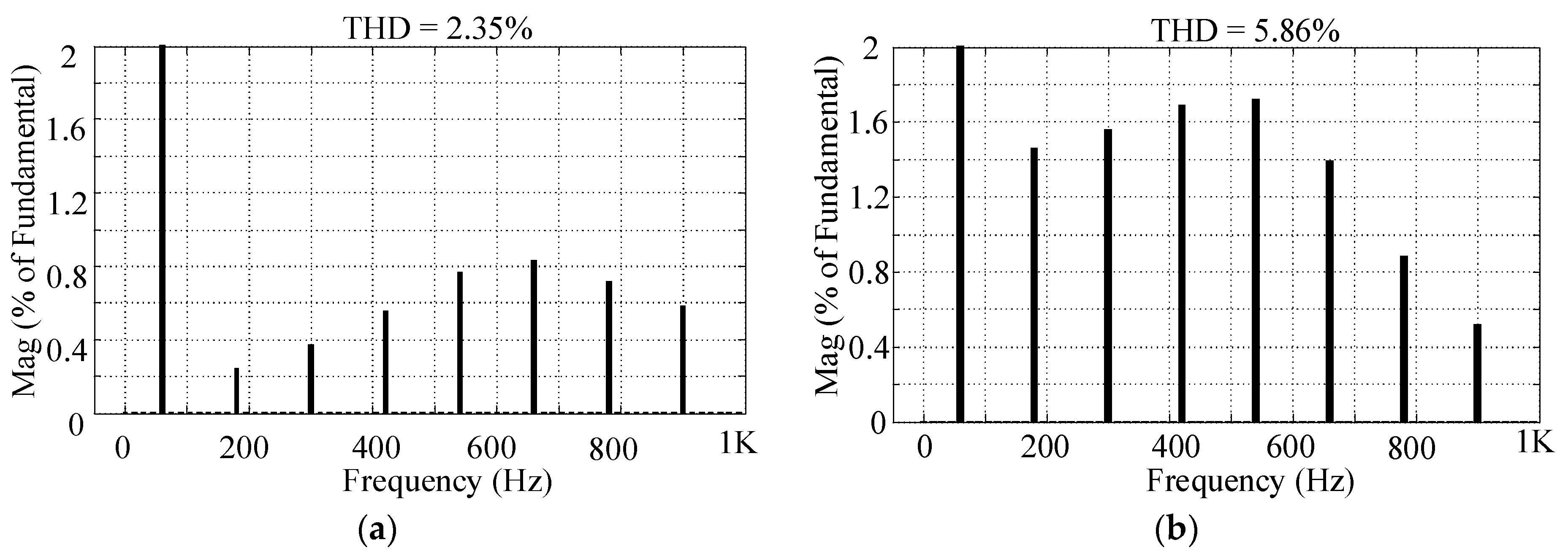
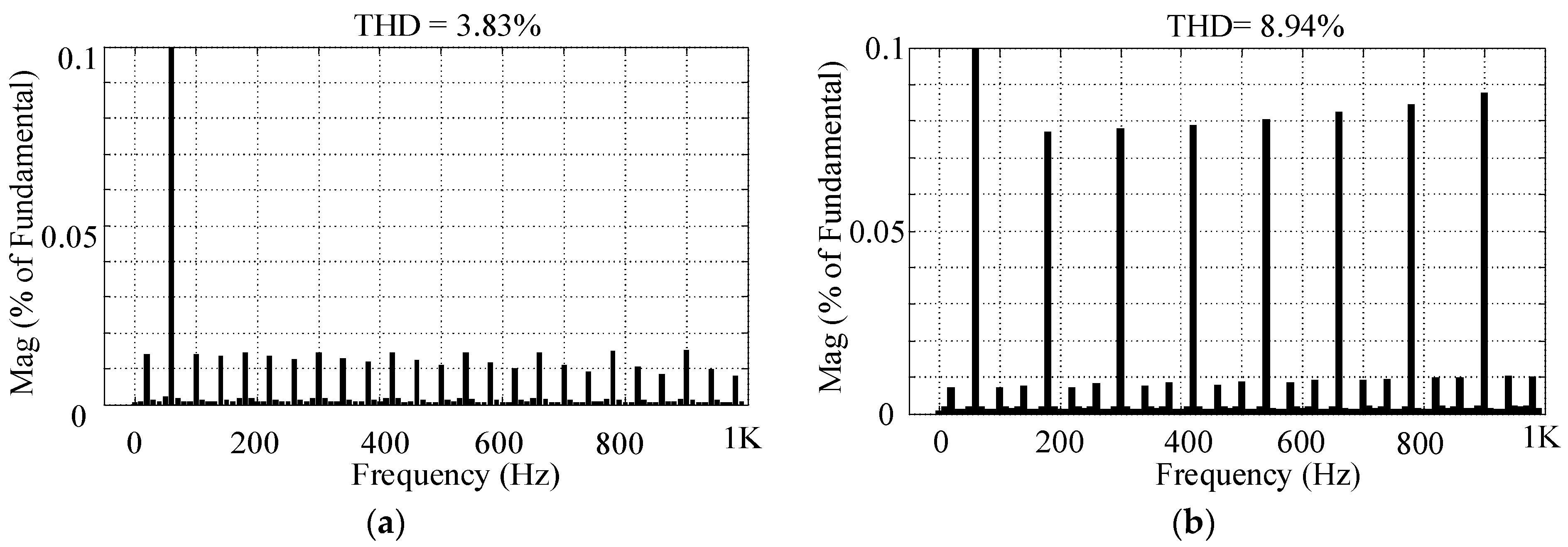
8. THD Analysis
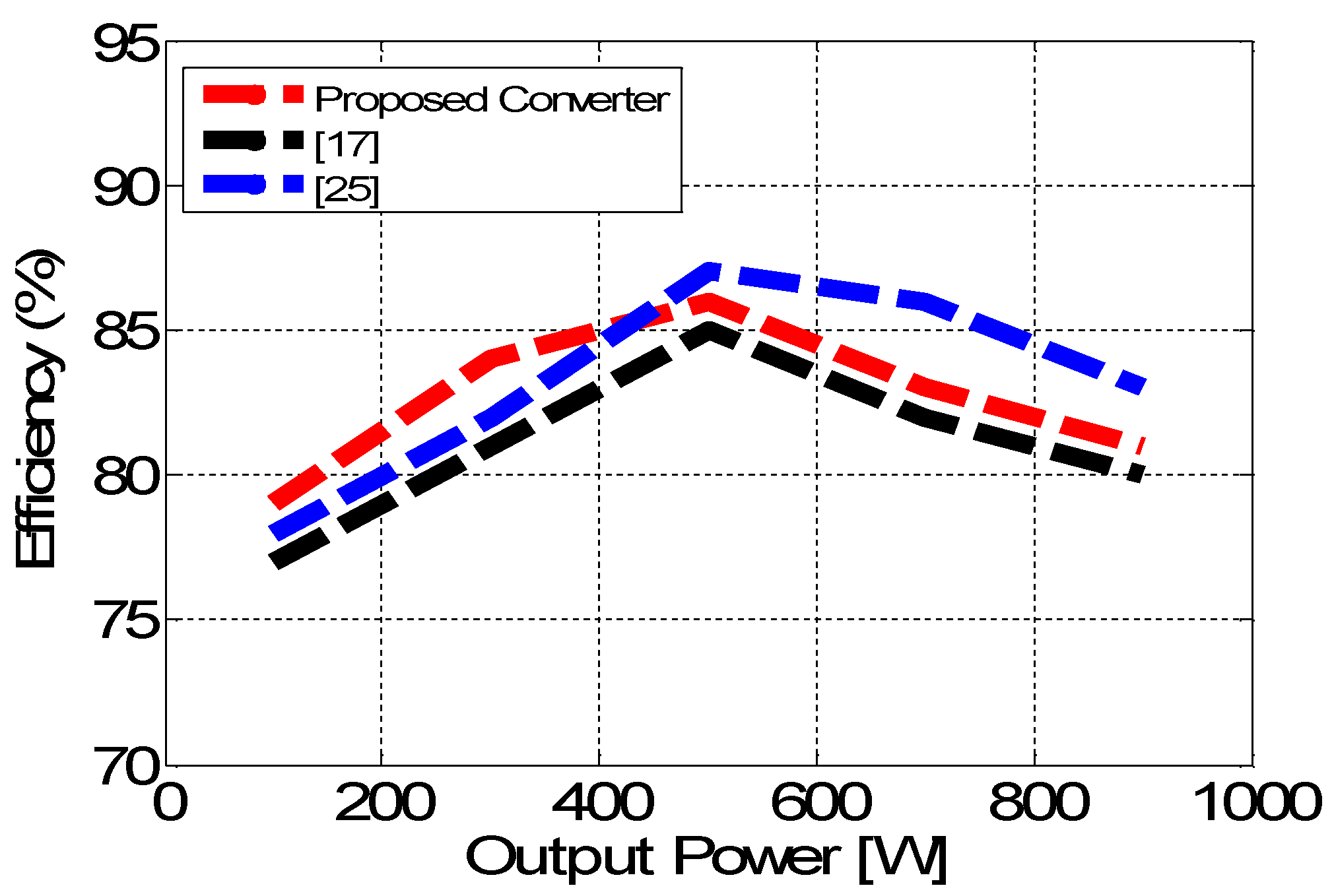
9. Efficiency Analysis
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moghassemi, A.; Padmanaban, S. Dynamic Voltage Restorer (DVR): A Comprehensive Review of Topologies, Power Converters, Control Methods, and Modified Configurations. Energies 2020, 13, 4152. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y.; Su, M.; Li, X.; Ning, S. A Single Phase AC/DC/AC Converter with Unified Ripple Power Decoupling. IEEE Trans. Power Electron. 2017, 33, 3204–3217. [Google Scholar] [CrossRef]
- De Freitas, N.B.; Jacobina, C.B.; Gehrke, B.S.; Cunha, M.F. Transformer-Based Single-Phase AC–DC–AC Topology for Grid Issues Mitigation. IEEE Trans. Ind. Appl. 2019, 55, 4001–4011. [Google Scholar] [CrossRef]
- Felinto, A.S.; Jacobina, C.B.; Fabricio, E.L.L.; de Lacerda, R.P. Six-Leg Three-Phase AC–DC–AC Converter with Shared Legs. IEEE Trans. Ind. Appl. 2021, 57, 5227–5238. [Google Scholar] [CrossRef]
- Ashraf, N.; Abbas, G.; Ullah, N.; Al-Ahmadi, A.A.; Yasin, A.R.; Awan, A.B.; Jamil, M. A Transformerless AC-AC Converter with Improved Power Quality Employed to Step-Down Power Frequency at Output. Energies 2022, 15, 667. [Google Scholar] [CrossRef]
- Vijayagopal, M.; Zanchetta, P.; Empringham, L.; De Lillo, L.; Tarisciotti, L.; Wheeler, P. Control of a Direct Matrix Converter with Modulated Model-Predictive Control. IEEE Trans. Ind. Appl. 2017, 53, 2342–2349. [Google Scholar] [CrossRef]
- Maroti, P.K.; Esmaeili, S.; Iqbal, A.; Meraj, M. High step-up single switch quadratic modified SEPIC converter for DC microgrid applications. IET Power Electron. 2020, 13, 3717–3726. [Google Scholar] [CrossRef]
- Esmaeili, S.; Mahmoudi, A.; Kahourzadeh, S.; Mostaan, A. Dual winding magnetically coupled impedance-source inverters with Dc-rail voltage clamping circuits. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021. [Google Scholar]
- Esmaeili, S.; Karimi, S.; Siadatan, A.; Afjei, E.; Iqbal, A. Tapped switched-coupled-inductors Γ-source inverter. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019. [Google Scholar]
- Esmaeili, S.; Iqbal, A.; Padmanaban, S.; Maroti, P.K.; Samiullah, M.; Lam, J. Asymmetrical switched inductor embedded impedance source inverters with reduced number of components. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020. [Google Scholar]
- Guo, M.; Liu, Y.; Ge, B.; Abu-Rub, H. Optimum Boost Control of Quasi-Z Source Indirect Matrix Converter. IEEE Trans. Ind. Electron. 2018, 65, 8393–8404. [Google Scholar] [CrossRef]
- Bozorgi, A.M.; Hakemi, A.; Farasat, M.; Monfared, M. Modulation techniques for common-mode voltage reduction in the Z-source ultra-sparse matrix converters. IEEE Trans. Power Electron. 2019, 34, 958–970. [Google Scholar] [CrossRef]
- Fang, X.P.; Qian, Z.M.; Peng, F.Z. Single-phase Z-source PWM ACAC converters. IEEE Power Electron. Lett. 2005, 3, 121–124. [Google Scholar] [CrossRef]
- Tang, Y.; Xie, S.J.; Zhang, C.H. Z-source AC-AC converters solving commutation problem. IEEE Trans. Power Electron. 2007, 22, 2146–2154. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Jung, Y.G.; Lim, Y.C. Single-phase AC-AC converter based on quasi-Z-source topology. IEEE Trans. Power Electron. 2010, 25, 2200–2210. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Lim, Y.C.; Kim, Y.-J. A Modified Single-Phase Quasi-Z-Source AC–AC Converter. IEEE Trans. Power Electron. 2011, 27, 201–210. [Google Scholar] [CrossRef]
- Banaei, M.R.; Ahrabi, R.; Elmi, M. Single-phase safe commutation trans-Z-source AC-AC converter. IET Power Electron. 2015, 8, 190–201. [Google Scholar] [CrossRef]
- Banaei, M.R.; Alizadeh, R.; Jahanyari, N.; Najmi, E.S. An ac Z-source converter based on gamma structure with safe-commutation strategy. IEEE Trans. Power Electron. 2016, 31, 1255–1262. [Google Scholar] [CrossRef]
- Aleem, Z.; Yang, H.-K.; Ahmed, H.F.; Winberg, S.L.; Park, J.-W. A Class of Single-Phase Z-Source AC–AC Converters with Magnetic Coupling and Safe-Commutation Strategy. IEEE Trans. Ind. Electron. 2021, 68, 8104–8115. [Google Scholar] [CrossRef]
- Sharifi, S.; Monfared, M. Modified Series and Tapped Switched-Coupled-Inductors Quasi-Z-Source Networks. IEEE Trans. Ind. Electron. 2019, 66, 5970–5978. [Google Scholar] [CrossRef]
- Reddivari, R.; Jena, D. A Negative Embedded Deferential Mode -Source Inverter with Reduced Switching Spikes. IEEE Trans. Circuits Syst. 2020, 7, 2009–2013. [Google Scholar]
- Liu, H.; Zhou, B.; Li, Y. High-Efficiency T-Source Inverter with Low Voltage Spikes across the Switch Bridge. IEEE Trans. Power Electron. 2020, 35, 10554–10566. [Google Scholar] [CrossRef]
- Ahmed, H.F.; Cha, H. A New Class of Single-Phase High-Frequency Isolated Z-Source AC–AC Converters with Reduced Passive Components. IEEE Trans. Power Electron. 2018, 33, 1410–1419. [Google Scholar] [CrossRef]
- Ahmed, H.F.; El Moursi, M.S.; Irshad, T.; El-Saadany, E. Family of single-phase isolated high-frequency transformer integrated improved magnetically coupled Z-source AC–AC converters. IET Power Electron. 2020, 13, 1901–1910. [Google Scholar] [CrossRef]
- He, L.Z.; Nai, J.X.; Zhang, J.H. Single-phase safe-commutation trans-z-source AC-AC converter with continuous input current. IEEE Trans. Ind. Electron. 2018, 65, 5135–5145. [Google Scholar] [CrossRef]
- Esmaeili, S.; Siadatan, A.; Jahromi, A.Z.; Shirazi, P. A filterless single-phase AC-AC converter based on coupled inductors with safe commutation strategy and continuous input current. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 12–17. [Google Scholar]
- Mousavi, S.M.J.; Babaei, E.; Alizadeh, D.; Komurcugil, H. Single-phase AC-AC Z-source converter based on asymmetrical gamma structure with continuous input current and safe commutation strategy. IET Power Electron. 2021, 14, 680–689. [Google Scholar] [CrossRef]
- Esmaeili, S.; Mahmoudi, A.; Kahourzadeh, S. Sinusoidal input current single-phase AC-AC converter based on coupled transformer with reduced turns ratio. In Proceedings of the IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021. [Google Scholar]
- Azimi, E.; Khodaparast, A.; Rostami, M.J.; Adabi, J.; Adabi, M.E.; Rezanejad, M.; Rodrigues, E.M.G.; Pouresmaeil, E. X-Type Step-Up Multi-Level Inverter with Reduced Component Count Based on Switched-Capacitor Concept. Electronics 2020, 9, 1987. [Google Scholar] [CrossRef]
- Khodaparast, A.; Azimi, E.; Azimi, A.; Adabi, M.E.; Adabi, J.; Pouresmaeil, E. A New Modular Multilevel Inverter Based on Step-Up Switched-Capacitor Modules. Energies 2019, 12, 524. [Google Scholar] [CrossRef] [Green Version]









| Parameter | [13] | [15] | [16] | [17] | [18] | [25] | Proposed Converter |
|---|---|---|---|---|---|---|---|
| Ii | |||||||
| - | |||||||
| IL1 | - | ||||||
| IL2 | - | - | - | - | |||
| Num. of capacitors | 3 | 3 | 2 | 3 | 2 | 3 | 3 |
| Num. of inductors + coupled transformer | 3 + 0 | 3 + 0 | 2 + 0 | 2 + 1 | 1 + 1 | 1 + 1 | 2 + 1 |
| Num. of switches | 2 | 4 | 4 | 4 | 4 | 6 | 4 |
| Total num. of components | 8 | 10 | 8 | 10 | 8 | 11 | 10 |
| Parameters | Values |
|---|---|
| Maximum input voltage (Vi) | 100 V |
| input voltage frequency (fin) | 50 Hz |
| switching frequency (fsw) | 20 kHz |
| DSP | TMS320F28335 |
| Load (R) | 30 Ω and 2 Ω |
| Power switch (MOSFET) | IRFP460 |
| C1 | 10 µF |
| C2 | 10 µF |
| L | 1 mH |
| Lf | 1.2 mH |
| Cf | 47 µF |
| LM | 820 µH |
| THD ii | SC in [18] | Proposed Converter |
|---|---|---|
| Boost in-phase mode (D = 0.1) | 50.77% | 5.86% |
| Buck out-of-phase mode (D = 0.78) | 136.72% | 8.94% |
| THD vo | Proposed Converter |
|---|---|
| Boost in-phase mode (D = 0.1) | 2.35% |
| Buck out-of-phase mode (D = 0.78) | 3.83% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeili, S.; Ghobadi, K.; Zare, H.; Jamil, M.; Khan, A.A.; Mahmoudi, A. A Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter. Energies 2022, 15, 4319. https://doi.org/10.3390/en15124319
Esmaeili S, Ghobadi K, Zare H, Jamil M, Khan AA, Mahmoudi A. A Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter. Energies. 2022; 15(12):4319. https://doi.org/10.3390/en15124319
Chicago/Turabian StyleEsmaeili, Soroush, Kasra Ghobadi, Hassan Zare, Mohsin Jamil, Ashraf Ali Khan, and Amin Mahmoudi. 2022. "A Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter" Energies 15, no. 12: 4319. https://doi.org/10.3390/en15124319
APA StyleEsmaeili, S., Ghobadi, K., Zare, H., Jamil, M., Khan, A. A., & Mahmoudi, A. (2022). A Trans-Inverse Magnetic Coupling Single-Phase AC-AC Converter. Energies, 15(12), 4319. https://doi.org/10.3390/en15124319