Data-Based Engine Torque and NOx Raw Emission Prediction
Abstract
:1. Introduction
2. Materials and Methods
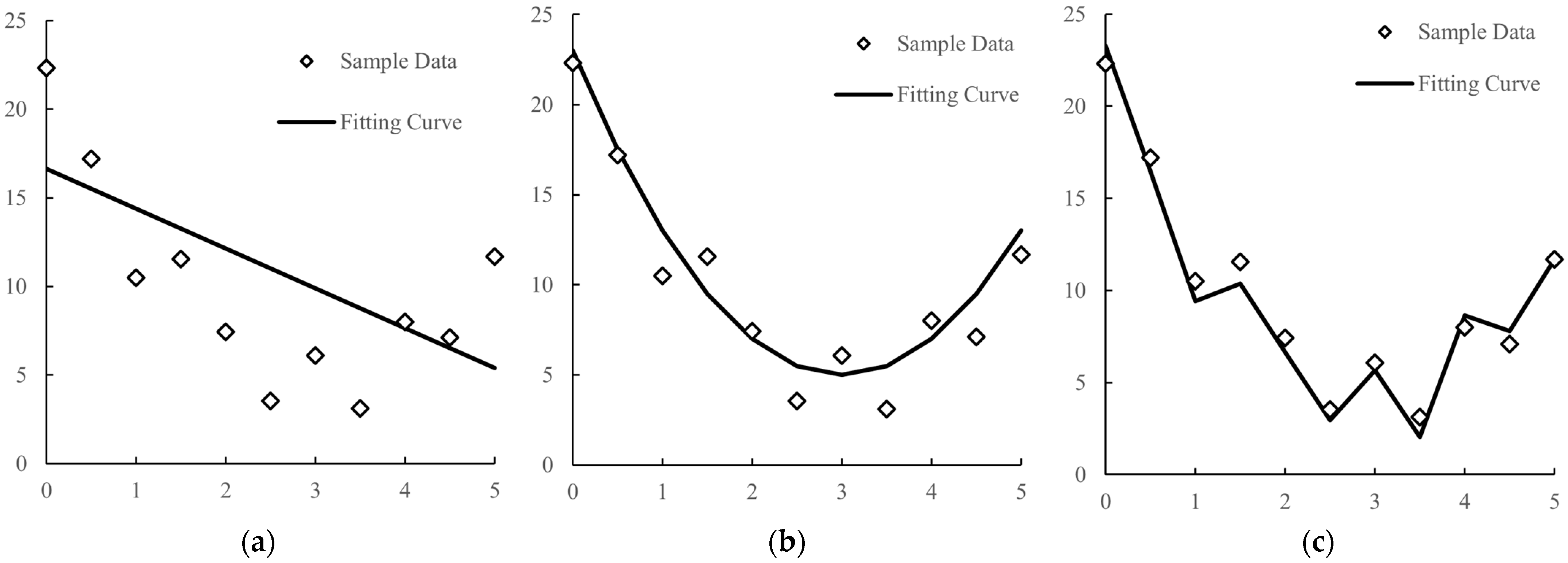
- Bad fitting method;
- The number of features is not well set;
- The data sample is too small, or the data sample is not diverse enough.
- The Gaussian process regression method would be used in this paper to improve the fitting accuracy;
- Correlation analysis is carried out on the main influencing factors of engine torque and NOx raw emission calculation, and the characteristic factors of torque and NOx raw emission calculation are established on this basis;
- By increasing the data sample size, the fitting accuracy could be improved.
2.1. Principle Analysis of Gaussian Process Regression Technology
- The covariance between random variables f(x) can be calculated by the kernel function of the sample points;
- The combination of samples {f(x)} obeys the Gaussian process GP shown in Equation (4).
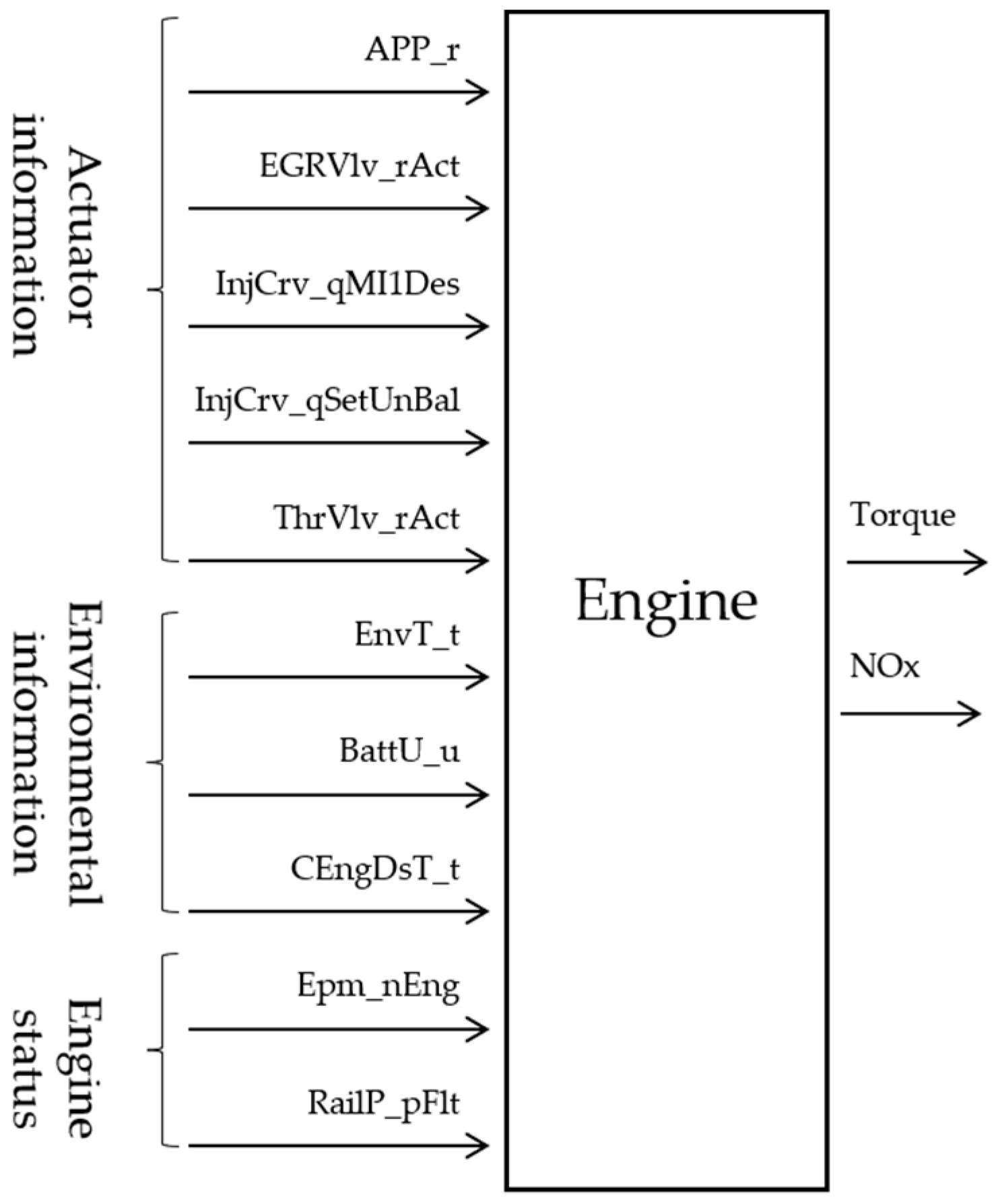
2.2. Analysis of Engine Torque and NOx Raw Emission Main Influencing Factors
- import pandas as pd1
- df1 = pd1.read_excel(‘F:\Dataset_D30.xlsx’)
- result = df1.corr()
- result.to_excel(‘Corr_Result.xlsx’)
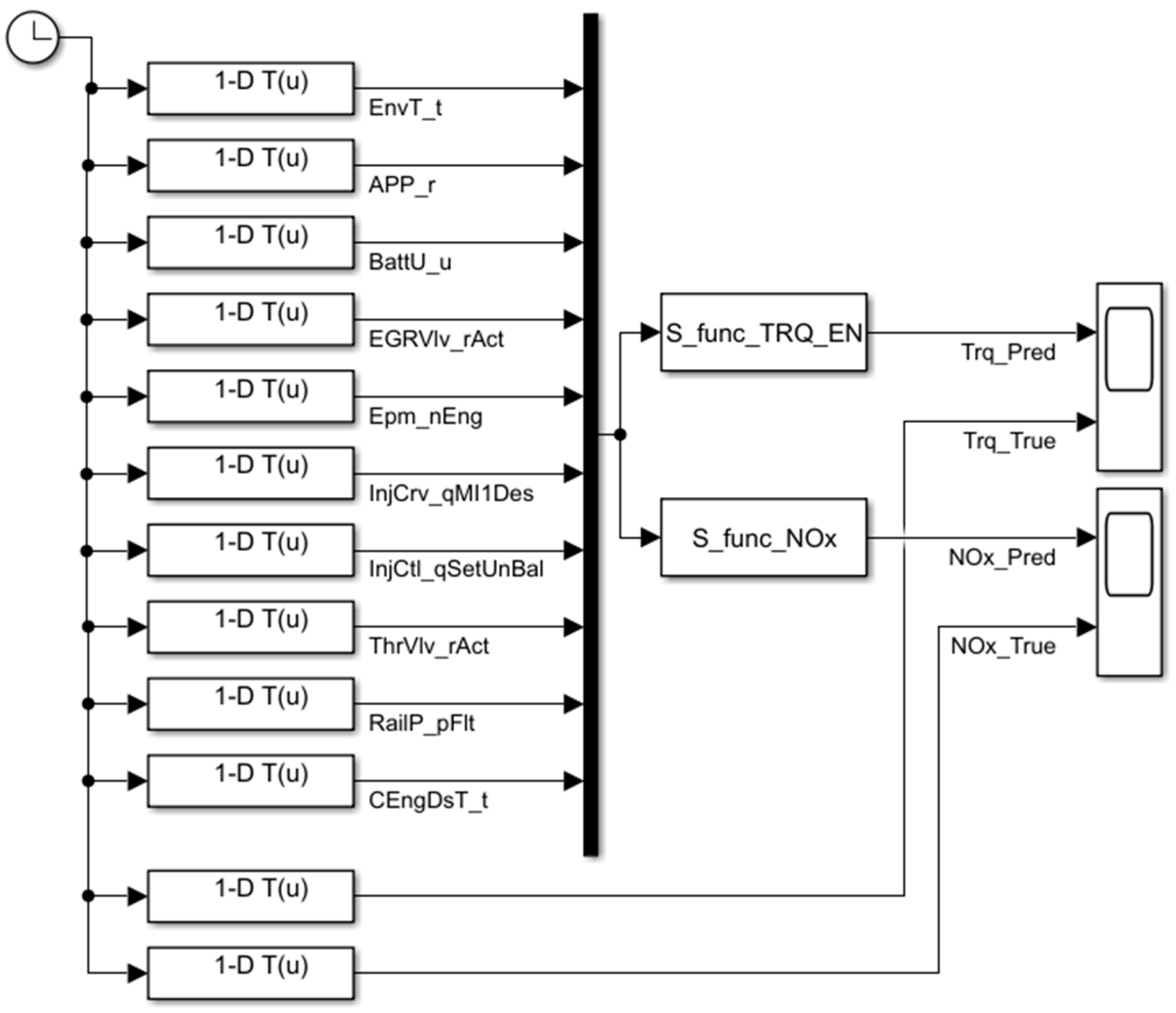
2.3. Construction of Engine Torque and NOx Raw Emission Regression Model
- Actuator information: accelerator pedal percentage (APP_r), EGR valve percentage (EGRVlv_rAct), main injection quantity (InjCrv_qMI1Des), total fuel injection quantity (InjCrv_qSetUnBal), throttle valve percentage (ThrVlv_rAct);
- Environmental status information: ambient temperature (EnvT_t), battery voltage (BattU_u), coolant temperature (CEngDsT_t);
- Engine running status information: engine speed (Epm_nEng), rail pressure (RailP_pFlt).
3. Results
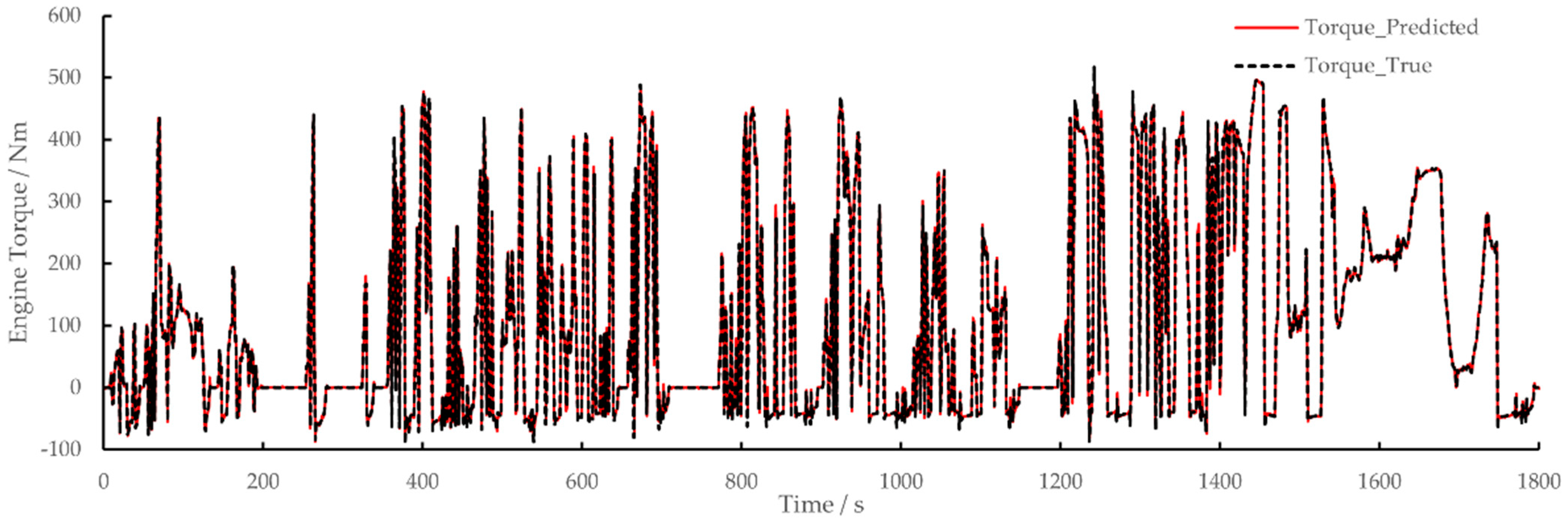
3.1. Model Accuracy Validation
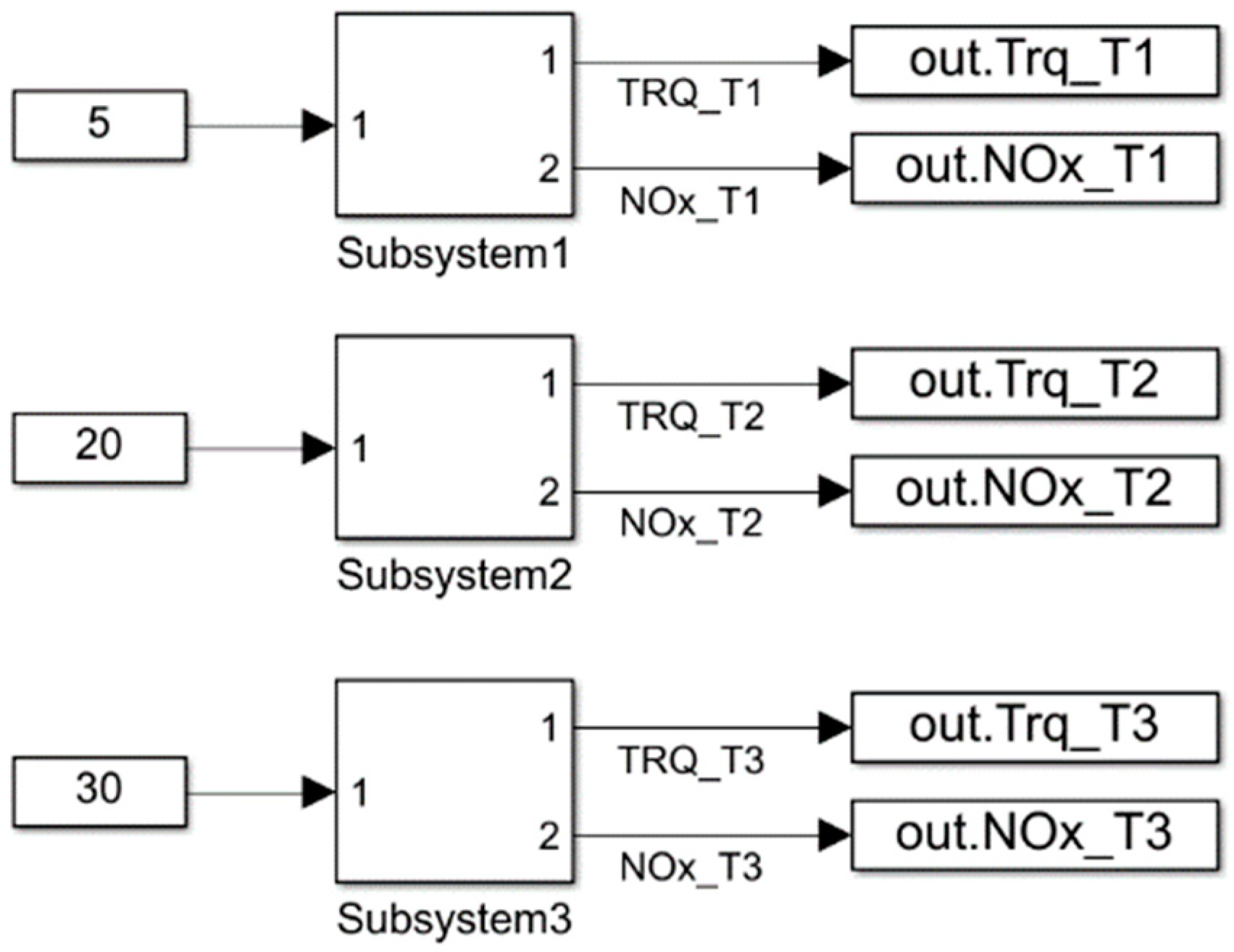
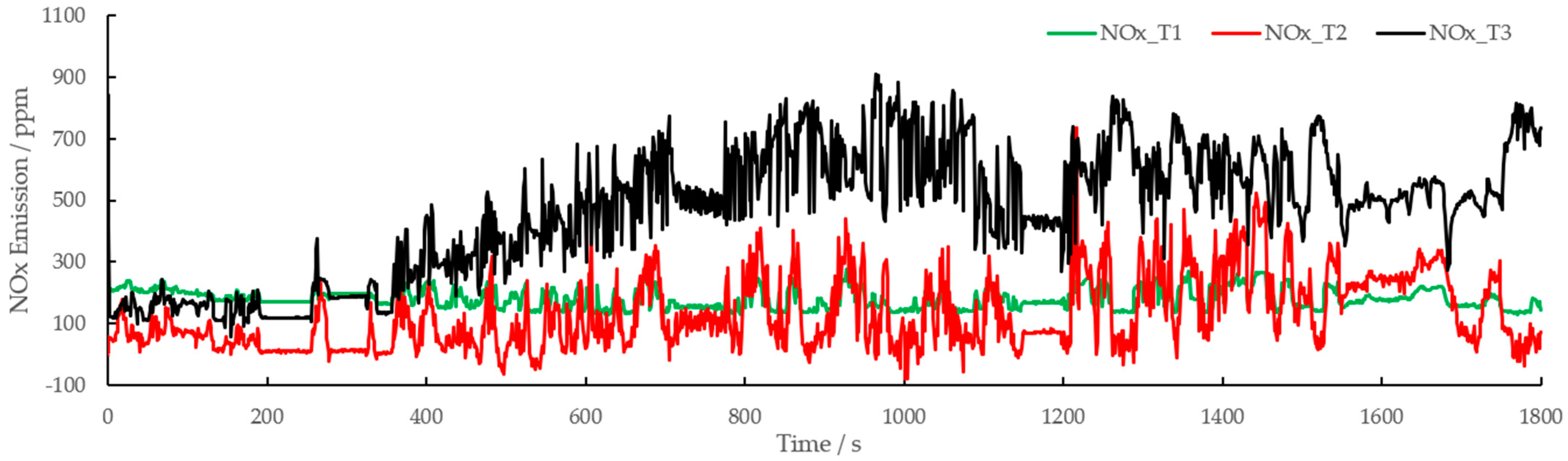
3.2. Influence of Ambient Temperature on Engine Torque and NOx Emission Performance
4. Conclusions
- The Pearson correlation analysis results show that engine torque and NOx raw emission are mainly affected by various factors such as actuator factors, i.e., accelerator pedal percentage and fuel injection timing and quantity, factors such as temperature and exhaust pollutants, and engine operating environmental factors such as ambient temperature and battery voltage. Based on the correlation analysis results, this paper selects a total of 10 input signals from three types of information: actuator information, environmental status information and engine operating status information, to establish an engine torque regression prediction model;
- After training, the RMSE value of the regression model built in this paper reaches 4.6186, and the accuracy is 99.68%;
- The prediction results of the model under a new WHTC cycle condition show that the RMSE value for engine torque prediction is 4.9208, accuracy is 99.6%, RMSE value for NOx raw emission prediction is 72.38, and accuracy is 99.2%. The model prediction is accurate;
- The analysis results of ambient temperature impact on engine torque and NOx emission calculation show that with the increase in ambient temperature, the standard deviation becomes larger, and the value of engine torque and NOx emission becomes more discrete.
- (1)
- Time delay. There is often a time delay between changes in actuator operating conditions and changes in emissions performance, and this time delay is closely related to engine operating conditions;
- (2)
- The performance sometimes has a jumping step characteristic. Taking the prediction of particulate matter emission as an example, when the exhaust gas temperature reaches the light-off temperature of the oxidation catalyst, the particulate matter burns violently, and the particulate matter emission decreases rapidly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bouscayrol, A. Different types of Hardware-In-the-Loop simulation for electric drives. In Proceedings of the IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2146–2151. [Google Scholar]
- Jafari, N.S. Real-time multi-rate HIL simulation platform for evaluation of a jet engine fuel controller. Simul. Model. Pract. Theory 2011, 19, 996–1006. [Google Scholar]
- Gaber, K.; El_Mashade, M.B.; Aziz, G.A.A. Hardware-in-the-loop real-time validation of micro-satellite attitude control—ScienceDirect. Comput. Electr. Eng. 2020, 85, 106679. [Google Scholar] [CrossRef]
- Yu, M.; Tang, X.; Lin, Y.; Wang, X. Diesel engine modeling based on recurrent neural networks for a hardware-in-the-loop simulation system of diesel generator sets. Neurocomputing 2018, 283, 9–19. [Google Scholar] [CrossRef]
- Pogorelov, G.; Kulikov, G.; Abdulnagimov, A.; Badamshin, B. Application of Neural Network Technology and Highperformance Computing for Identification and Real-time Hardware-in-the-loop Simulation of Gas Turbine Engines. Procedia Eng. 2017, 176, 402–408. [Google Scholar] [CrossRef]
- Jun, L.; Shi-hua, Y.; Dong-mei, J.; Rui-ying, L. Research on Test Methods for Special Vehicle Handling and Stability Based on Dynamics Simulation. Acta Armamentarii 2014, 35, 262. [Google Scholar]
- Termous, H.; Shraïm, H.; Talj, R.; Francis, C.; Charara, A. Coordinated control strategies for active steering, differential braking and active suspension for vehicle stability, handling and safety improvement. Veh. Syst. Dyn. 2019, 57, 1494–1529. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Shen, X.; Zhu, J.; Yin, Q.; Xu, L. Analysis of Handling Stability of Hydraulic Hybrid Vehicle based on ADAMS/Car Simulation. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 186, p. 186. [Google Scholar]
- Mutha, M.; Karanjkar, C.; Kadekar, P.; Nikumb, M.; Palanivelu, S. Influence of vehicle parameters on handling characteristics and its control using torque vectoring. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 624, p. 012015. [Google Scholar]
- Hu, J.; Chen, Z.; Yao, Y.; Shi, L.; Deng, K. Study on control-oriented emission predictions of PPCI diesel engine with two-stage fuel injection. Fuel 2022, 320, 123984. [Google Scholar] [CrossRef]
- Xiao, F.; Li, C.; Fan, Y.; Yang, G.; Tang, X. State of charge estimation method for lithium battery based on Gaussian process regression. J. Nav. Univ. Eng. 2021, 33, 55–59. [Google Scholar]
- Li, Y.; Duan, X.; Fu, J.; Liu, J.; Wang, S.; Dong, H.; Xie, Y. Development of a method for on-board measurement of instant engine torque and fuel consumption rate based on direct signal measurement and RGF modelling under vehicle transient operating conditions. Energy 2019, 189, 116218. [Google Scholar] [CrossRef]
- Tsitsilonis, K.M.; Theotokatos, G. A novel method for in-cylinder pressure prediction using the engine instantaneous crankshaft torque. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 131–149. [Google Scholar] [CrossRef]
- Hui, X.; Li, X. Engine Torque Reconstruction Algorithm Based on OBD Data. J. Tianjin Univ. (Sci. Technol.) 2017, 50, 1124–1130. [Google Scholar]
- Varma, P.S.; Bhowmik, S.; Paul, A.; Madane, P.A.; Panua, R. AI-Based ANN Modeling of Performance—Emission Profiles of CRDI Engine under Diesel-Karanja Strategies. In Recent Advances in Mechanical Engineering; Springer: Singapore, 2021. [Google Scholar]
- Mishra, V.K.; Bhowmik, S.; Paul, A.; Yadav, A.; Panua, R. ANFIS Prediction of Performance and Exhaust Emission Characteristics of CRDI Engine Fueled with Diesel–Butanol Strategies. In Recent Advances in Mechanical Engineering; Springer: Singapore, 2021. [Google Scholar]
- Paramasivam, B.; Kumanan, S.; Kavimani, V.; Varatharajulu, M. Fuzzy-based prediction of compression ignition engine distinctiveness powered by novel graphene oxide nanosheet additive diesel–Aegle marmelos pyrolysis oil ternary opus. Int. J. Energy Environ. Eng. 2022, 13, 683–701. [Google Scholar] [CrossRef]
- Deng, T.; Ye, D.; Ma, R.; Fujita, H.; Xiong, L. Low-rank local tangent space embedding for subspace clustering. Inf. Sci. 2020, 508, 1–21. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, X.; Tian, C.; Wang, P.; Zhou, F.; Fujita, H. Inverse projection group sparse representation for tumor classification: A low rank variation dictionary approach. Knowl. Based Syst. 2020, 196, 105768. [Google Scholar] [CrossRef]
- Si, S.; Hsieh, C.-J.; Dhillon, I. Memory efficient kernel approximation. J. Mach. Learn Res. 2017, 18, 682–713. [Google Scholar]
- Rose, S.; Pannek, K.; Bell, C.; Baumann, F.; Hutchinson, N.; Coulthard, A.; McCombe, P.; Henderson, R. Direct evidence of intra- and interhemispheric corticomotor network degeneration in amyotrophic lateral sclerosis: An automated MRI structural connectivity study. Neuroimage 2012, 59, 2661–2669. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Schoffelen, J.-M. A Tutorial Review of Functional Connectivity Analysis Methods and Their Interpretational Pitfalls. Front. Syst. Neurosci. 2016, 9, 175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vinck, M.; Oostenveld, R.; Van Wingerden, M.; Battaglia, F.; Pennartz, C.M. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias—ScienceDirect. NeuroImage 2011, 55, 1548–1565. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, J.; Guo, Z.; Wu, T.; Hou, J.; Cheng, J. Protein model accuracy estimation empowered by deep learning and inter-residue distance prediction in CASP14. Sci. Rep. 2011, 11, 10943. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Zhou, H.; Skolnick, J. DESTINI: A deep-learning approach to contact-driven protein structure prediction. Sci. Rep. 2019, 9, 3514. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Parameter | Value |
|---|---|
| Displacement/L | 2.977 |
| Air intake | Turbo-charged |
| Cylinder arrangement | In-line |
| Rated power/speed (kW/r·min−1) | 125/2800 |
| Compression ratio | 16.0:1 |
| Fuel system | Common rail |
| Fuel injection pressure/MPa | 200 |
| Parameter | Unit | Factor_Trq 1 | Factor_NOx 2 | Minimum | Maximum | Average |
|---|---|---|---|---|---|---|
| Total fuel injection quantity (InjCrv_qSetUnBal) | mg·hub−1 | 0.9922 | 0.6447 | 3.62 | 92.72 | 42.47 |
| Main injection quantity (InjCrv_qMI1Des) | mg·hub−1 | 0.9874 | 0.6557 | 1.62 | 92.72 | 39.42 |
| Main injection activation timing (InjVlv_tiMI1ET) | μs | 0.9543 | 0.7336 | 310.8 | 2127.2 | 776.74 |
| Accelerator (APP_r) | % | 0.9394 | 0.6504 | 0 | 100 | 43.60 |
| Accelerator raw voltage (APP_uRaw1) | mV | 0.9355 | 0.6347 | 752.4 | 4257 | 2127.2 |
| Engine power (PWR_E_EN) | kW | 0.8963 | 04702 | −2.24 | 125.42 | 44.68 |
| Exhaust temperature before turbo (T_EGH_BTUR) | °C | 0.8960 | 0.4872 | 104.5 | 759.2 | 453.75 |
| Exhaust temperature after turbo (T_EGH_BTUR) | °C | 0.8734 | 0.4788 | 63 | 613.9 | 336.89 |
| IMEP 3 | bar | 0.8584 | 0.7163 | −1.43 | 23.32 | 5.78 |
| Oxygen content at exhaust manifold (Y_O2_EGD) | ppm | −0.8549 | −0.3256 | 0 | 832.8 | 170.15 |
| Rail pressure (RailP_pFlt) | hPa | 0.7285 | 0.3017 | 426,600 | 2,020,800 | 1,248,791.99 |
| Air intake pressure | kPa | 0.7698 | 0.3529 | 88.39 | 265.46 | 188.89 |
| Lambda | / | −0.7691 | −0.4509 | 1.09 | 9.55 | 2.54 |
| CO 4 content at exhaust manifold (Y_COL_EGD) | ppm | −0.6685 | −0.3481 | 0 | 4842.06 | 417.97 |
| Air intake temperature | °C | 0.5782 | 0.2308 | 22.8 | 54.4 | 35.11 |
| Exhaust pressure before turbo | kPa | 0.5229 | 0.1999 | 99.92 | 455.04 | 246.46 |
| Main injection timing (InjCrv_phiMI1Des) | ° | 0.4943 | 0.2986 | −6.899 | 20.786 | 5.49 |
| Throttle valve percentage (ThrVlv_rAct) | % | −0.3362 | −0.4300 | 0 | 100 | 38.44 |
| Engine coolant temperature (CEngDsT_t) | °C | 0.2969 | 0.1665 | 66.76 | 92.46 | 88.02 |
| Ambient temperature (EnvT_t) | °C | 0.2158 | 0.0905 | 12 | 32 | 26 |
| EGR valve percentage (EGRVlv_rAct) | % | 0.0698 | −0.2885 | 0 | 100 | 19 |
| Engine speed (Epm_nEng) | r·min−1 | 0.0240 | −0.2180 | 783 | 3007 | 1875.9 |
| Tools | Version Information |
|---|---|
| Matlab | Version 9.10 (R2021a) |
| Simulink | Version 10.3 |
| Deep Learning Toolbox | Version 14.2 |
| Torque | NOx | |
|---|---|---|
| RMSE | 4.6186 | 67.599 |
| R2 | 1.00 | 0.99 |
| MSE | 26.802 | 4569.6 |
| MAE | 1.3671 | 24.522 |
| T1 = 5 °C | T2 = 20 °C | T3 = 30 °C | |
|---|---|---|---|
| Standard Deviation | 72.756 | 158.368 | 185.325 |
| Average Value/Nm | 110.789 | 101.840 | 72.581 |
| Maximum Value/Nm | 285.947 | 533.995 | 440.316 |
| Minimum Value/Nm | 7.979 | −110.268 | −356.967 |
| T1 = 5 °C | T2 = 20 °C | T3 = 30 °C | |
|---|---|---|---|
| Standard Deviation | 31.620 | 114.834 | 203.009 |
| Average Value/Nm | 180.892 | 128.584 | 467.662 |
| Maximum Value/Nm | 278.44 | 736.418 | 908.678 |
| Minimum Value/Nm | 128.252 | −81.206 | 55.030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Shi, X.; Jiang, D.; Liang, Y.; Mi, J.; Fan, H. Data-Based Engine Torque and NOx Raw Emission Prediction. Energies 2022, 15, 4346. https://doi.org/10.3390/en15124346
Yuan Z, Shi X, Jiang D, Liang Y, Mi J, Fan H. Data-Based Engine Torque and NOx Raw Emission Prediction. Energies. 2022; 15(12):4346. https://doi.org/10.3390/en15124346
Chicago/Turabian StyleYuan, Zheng, Xiuyong Shi, Degang Jiang, Yunfang Liang, Jia Mi, and Huijun Fan. 2022. "Data-Based Engine Torque and NOx Raw Emission Prediction" Energies 15, no. 12: 4346. https://doi.org/10.3390/en15124346
APA StyleYuan, Z., Shi, X., Jiang, D., Liang, Y., Mi, J., & Fan, H. (2022). Data-Based Engine Torque and NOx Raw Emission Prediction. Energies, 15(12), 4346. https://doi.org/10.3390/en15124346





