Impact of Solar Inverter Dynamics during Grid Restoration Period on Protection Schemes Based on Negative-Sequence Components
Abstract
:1. Introduction
- Identifying the key differences in negative-sequence quantities between solar inverters and synchronous generators during the restoration period following a grid disturbance;
- Investigating the negative-sequence current characteristics of solar inverters during the grid restoration period; and
- Analyzing the negative impact of the negative-sequence current of solar inverters during the restoration period on the performance of typical protection schemes using a hardware-in-loop simulation based on the RTDS.
2. Methodology
3. Modeling of Solar PV Test Systems
3.1. Solar PV Test System I
3.2. Solar PV Test System II
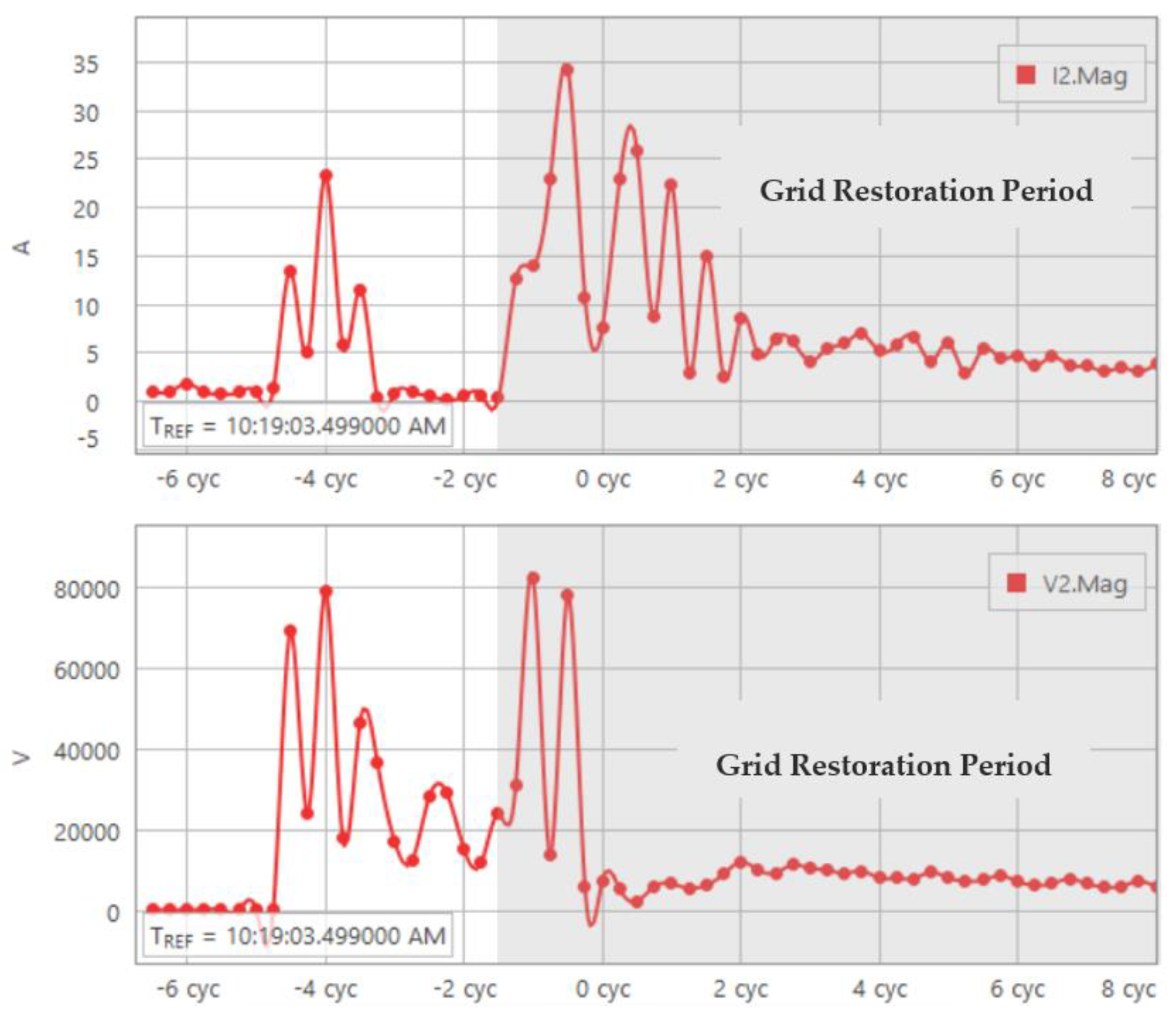
4. Negative-Sequence Current of Solar Inverters versus Synchronous Generators during Grid Restoration Period
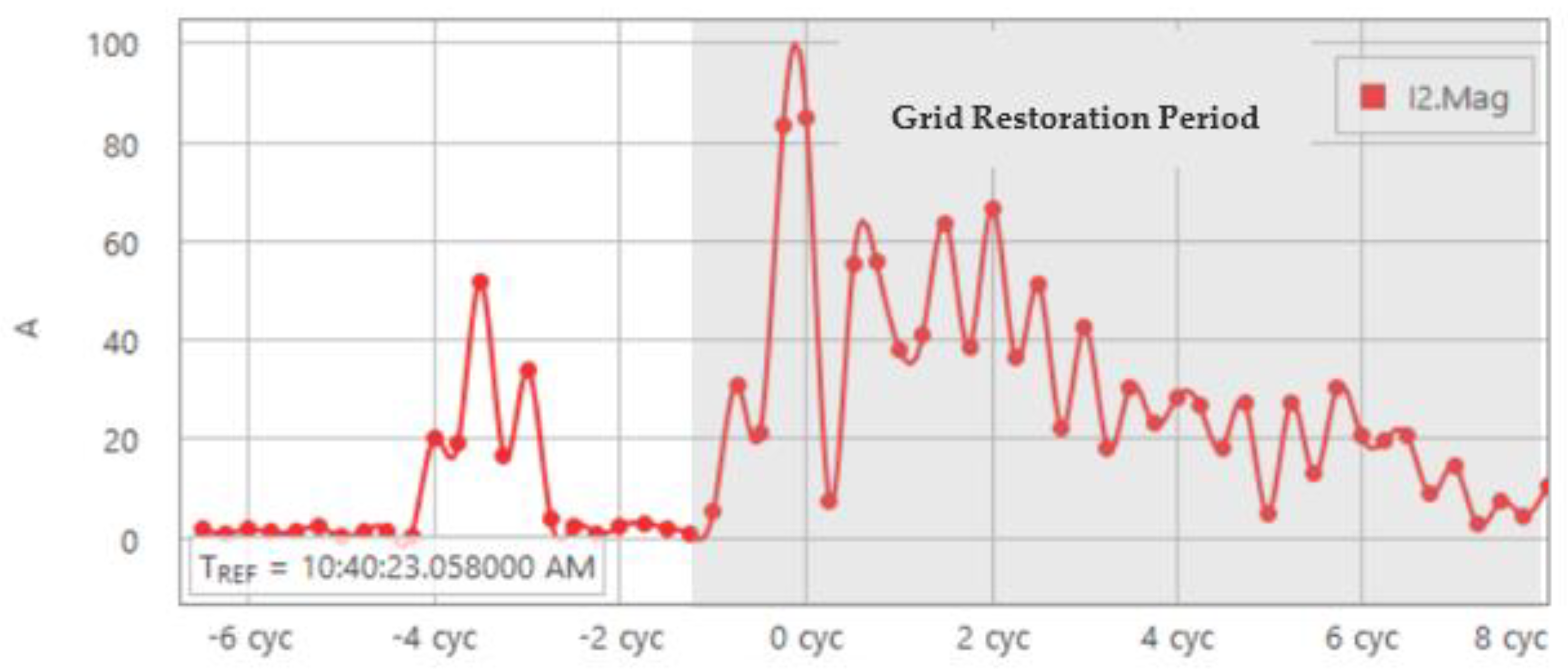
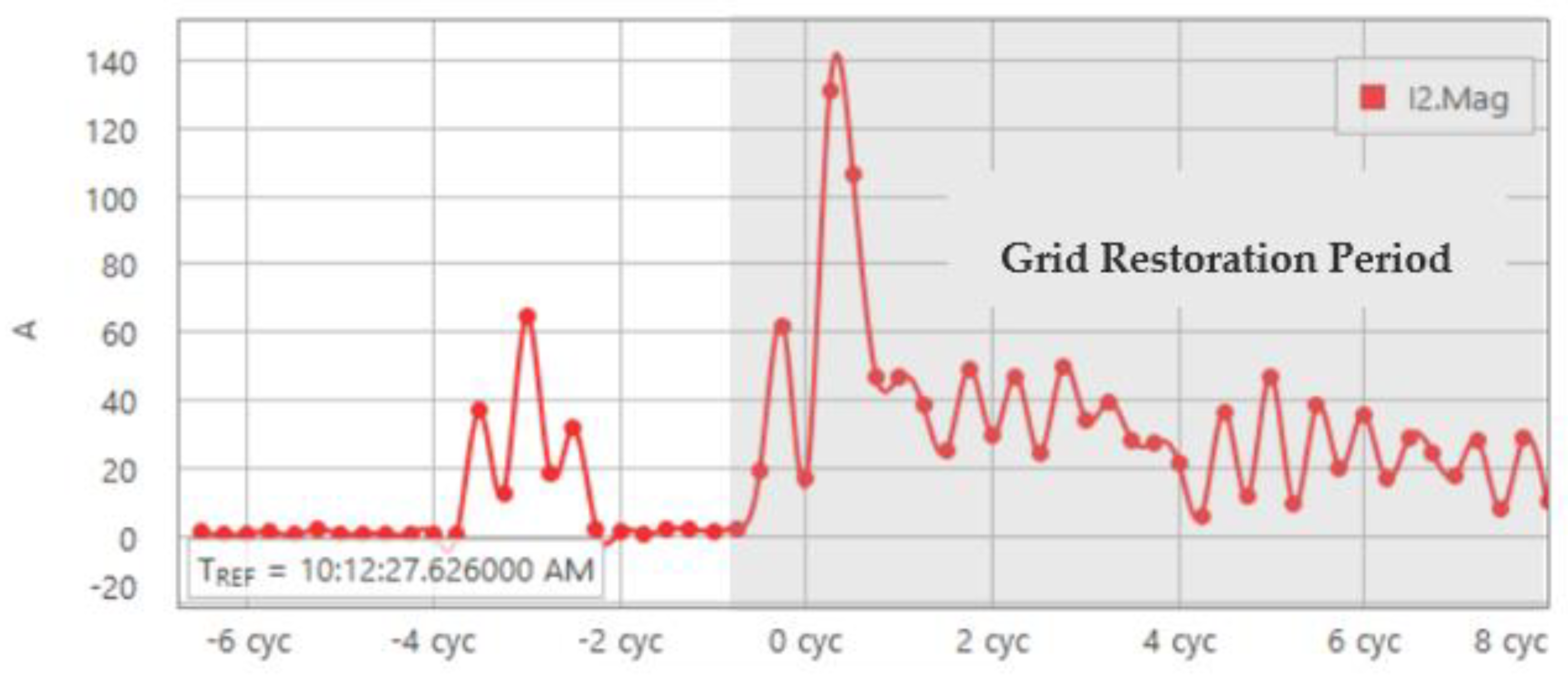
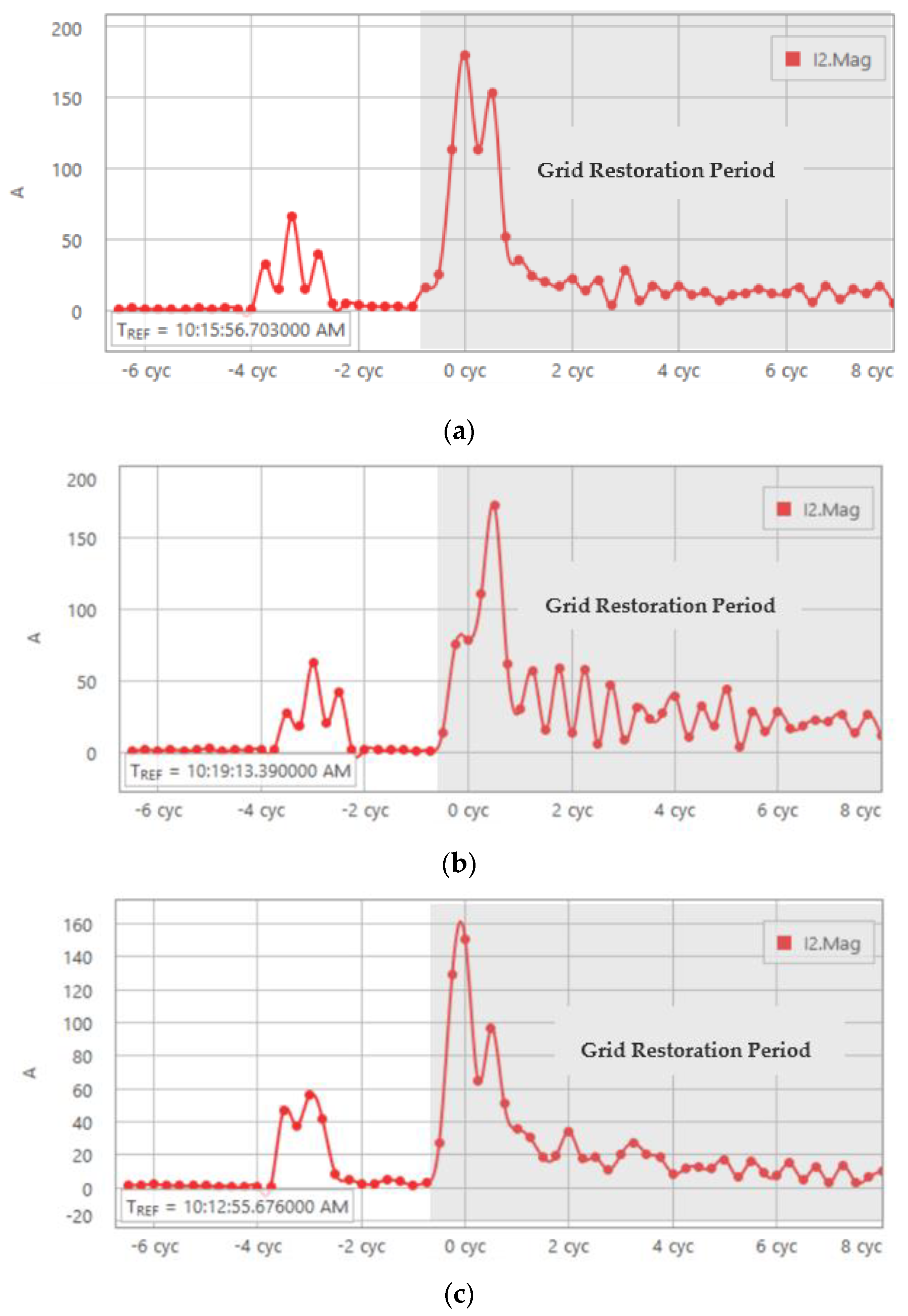
- Unlike the conventional synchronous generator, the solar inverter has a relatively high magnitude of negative-sequence current during the grid restoration period after the fault is cleared. More specifically, during the grid restoration period, the peak value of the negative-sequence current magnitude from the solar inverter was approximately 35 amps and maintained for about 3.5 cycles; on the other hand, the peak value of the negative-sequence current magnitude from the synchronous generator was just close to 3 amps.
- The difference between the phase angle of negative-sequence voltage and current phasors from the solar inverter was −53 degrees with the voltage lagging the current. This means the solar inverter acted as a source during the grid restoration period to inject negative-sequence current into the grid. By contrast, the synchronous generator had a phase angle difference between the negative-sequence voltage and current of 105 degrees with the voltage leading the current, which means the synchronous generator behaves as a load during the grid restoration period to absorb the negative-sequence current from the grid.
5. Characteristic Analysis of Negative-Sequence Current Injected from Solar Inverters during Grid Restoration Period
5.1. Impact of Solar Inverter Number
5.2. Impact of Grid Strength
5.3. Impact of Fault Types
6. Impact of Negative-Sequence Current from Solar Inverters during Grid Restoration Period on Negative-Sequence Quantities-Based Protection Schemes
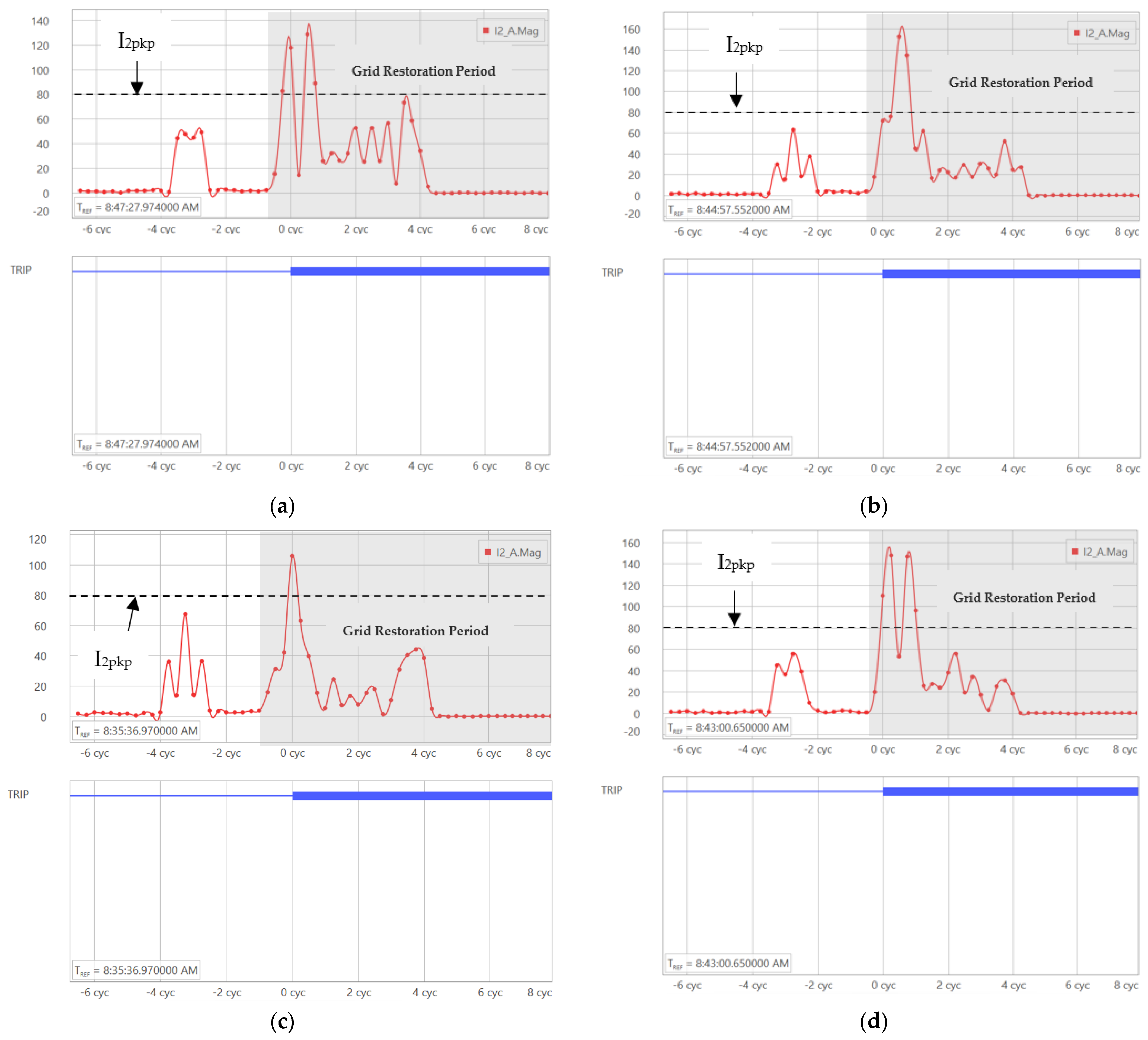
6.1. Maloperation of Instantaneous Negative-Sequence Overcurrent (50Q)
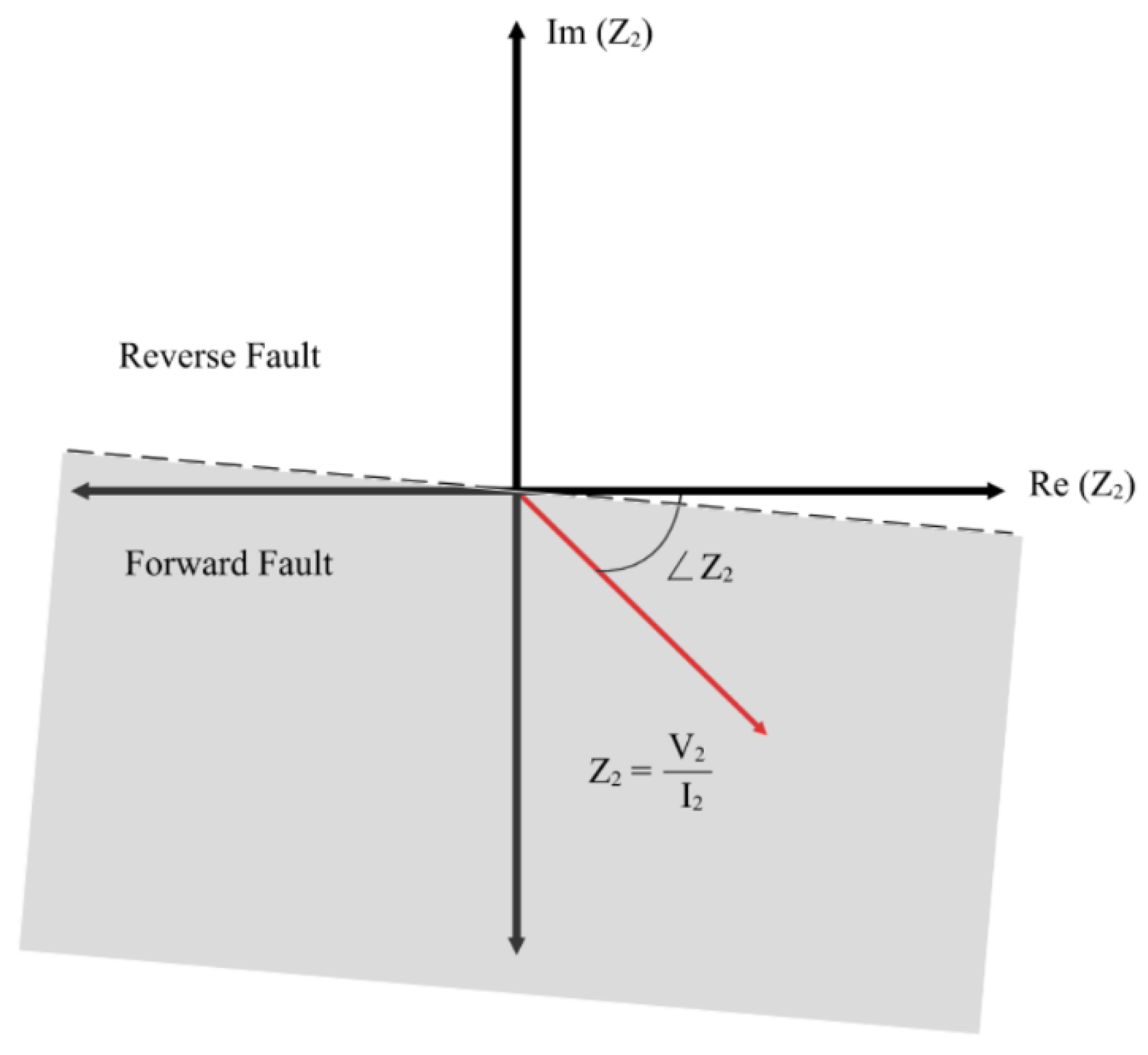
6.2. Maloperation of Directional Negative-Sequence Overcurrent (67Q)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ANSI Element | Setting | Value |
|---|---|---|
| 50Q | 50Q1P—Instantaneous Negative-sequence pickup current I2pkp | 80 A |
| 67Q | Z2F—Forward negative-sequence impedance threshold | 38 Ω |
| Z2R—Reverse negative-sequence impedance threshold | 38.1 Ω | |
| 50QF—Forward negative-sequence current threshold | 0.5 A | |
| 50QR—Reverse negative-sequence current threshold | 0.25 A | |
| a2—Positive-sequence current restraint factor | 0.07 |
References
- IEEE PES Industry Technical Support Task Force. Impact of Inverter Based Generation on Bulk Power System Dynamics and Short-Circuit Performance; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2018. [Google Scholar]
- UL 1741-SA; Standard for Inverters, Converters, Controllers and Interconnection System Equipment for Use with Distributed Energy Resources. UL: Northbrook, IL, USA, 2016.
- Behnke, M.R.; Custer, G.; Farantatos, E.; Fischer, N.; Guttromson, R.; Isaacs, A.; Majumder, R.; Pant, S.; Patel, M.; Reddy-Konala, V.; et al. Impact of Inverter-Based Resource Negative-Sequence Current Injection on Transmission System Protection; Sandia National Laboratories: Albuquerque, NW, USA, 2020.
- Kou, G.; Chen, L.; VanSant, P.; Velez-Cedeno, F.; Liu, Y. Fault characteristics of distributed solar generation. IEEE Trans. Power Deliv. 2020, 35, 1062–1064. [Google Scholar] [CrossRef]
- Erlich, I.; Neumann, T.; Shewarega, F.; Schegner, P.; Meyer, J. Wind turbine negative sequence current control and its effect on power system protection. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Haddadi, A.; Kocar, I.; Karaagac, U.; Mahseredjian, J. Impact of Renewables on System Protection: Wind/PV Short-Circuit Phasor Model Library and Guidelines for System Protection Studies; EPRI: Palo Alto, CA, USA, 2016. [Google Scholar]
- Haddadi, A.; Kocar, I.; Farantatos, E. Impact of Inverter-Based Resources on Protection Schemes Based on Negative Sequence Components; Electric Power Research Institute: Palo Alto, CA, USA, 2019; Available online: https://www.epri.com/research/products/000000003002016197 (accessed on 12 June 2022).
- 1200 MW Fault Induced Solar Photovoltaic Resource Interruption Disturbance Report; North American Electric Reliability Corporation: Atlanta, GA, USA, 2016; p. 2.
- North American Electric Reliability Corporation. 900 MW Fault Induced Solar Photovoltaic Resource Interruption Disturbance Report: Southern California Event: October 9, 2017 Joint NERC and WECC Staff Report; NERC: Atlanta, GA, USA, 2018. [Google Scholar]
- North American Electric Reliability Corporation. April and May 2018 Fault Induced Solar Photovoltaic Resource Interruption Disturbances Report: Southern California Events: 20 April 2018 and 11 May 2018, Joint NERC and WECC Staff Report; NERC: Atlanta, GA, USA, 2019. [Google Scholar]
- San Fernando Disturbance Southern California Event: 7 July 2020 Joint NERC and WECC Staff Report; North American Electric Reliability Corporation: Atlanta, GA, USA, 2020.
- Kang, S.; Shin, H.; Jang, G.; Lee, B. Impact Analysis of Recovery Ramp Rate After Momentary Cessation in Inverter-based Distributed Generators on Power System Transient Stability. IET Gener. Transm. Distrib. 2020, 15, 24–33. [Google Scholar] [CrossRef]
- Pierre, B.J.; Elkhatib, M.E.; Hoke, A. Photovoltaic Inverter Momentary Cessation: Recovery Process is Key. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019. [Google Scholar]
- Choi, N.; Park, B.; Cho, H.; Lee, B. Impact of Momentary Cessation Voltage Level in Inverter-Based Resources on Increasing the Short Circuit Current. Sustainability 2019, 11, 1153. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Piper, D.; Ramasubramanian, D.; Quint, R.; Isaacs, A.; Bauer, R. Modeling Inverter-Based Resources in Stability Studies. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Shin, H.; Jung, J.; Lee, B. Determining the Capacity Limit of Inverter-Based Distributed Generators in High-Generation Areas Considering Transient and Frequency Stability. IEEE Access 2020, 8, 34071–34079. [Google Scholar] [CrossRef]
- Mather, B.; Ding, F. Distribution-connected PV’s response to voltage sags at transmission-scale. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 2030–2035. [Google Scholar]
- Mather, B.; Aworo, O.; Bravo, R.; Piper, P.E.D. Laboratory Testing of a Utility-Scale PV Inverter’s Operational Response to Grid Disturbances. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Kenyon, R.W.; Mather, B.; Hodge, B.-M. Coupled Transmission and Distribution Simulations to Assess Distributed Generation Response to Power System Faults. Electr. Power Syst. Res. 2020, 189, 106746. [Google Scholar] [CrossRef]
- Shin, H.; Jung, J.; Oh, S.; Hur, K.; Iba, K.; Lee, B. Evaluating the Influence of Momentary Cessation Mode in Inverter-Based Distributed Generators on Power System Transient Stability. IEEE Trans. Power Syst. 2020, 35, 1618–1626. [Google Scholar] [CrossRef]
- Li, C.; Reinmuller, R. Fault Responses of Inverter-based Renewable Generation: On Fault Ride-Through and Momentary Ces-sation. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Pierre, B.J.; Elkhatib, M.E.; Hoke, A. PV Inverter Fault Response Including Momentary Cessation, Frequency-Watt, and Virtual Inertia. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018. [Google Scholar]
- RTDS Technologies Inc. Available online: https://www.rtds.com (accessed on 12 June 2022).
- RSCAD—Power System Simulation Software in RTDS; Technologies Inc.: Winnipeg, MB, Canada, 2018.
- Elserougi, A.A.; Massoud, A.M.; Abdel-Khalik, A.S.; Ahmed, S. Bidirectional Buck-Boost Inverter-Based HVDC Transmission System With AC-Side Contribution Blocking Capability During DC-Side Faults. IEEE Trans. Power Deliv. 2014, 29, 1249–1261. [Google Scholar] [CrossRef]
- Calero, F. Rebirth of Negative-Sequence Quantities in Protective Relaying with Microprocessor-Based Relays; Schweitzer Eng. Labs. Inc.: Delhi, India, 2003. [Google Scholar]
- Horak, J. Directional overcurrent relaying (67) concepts. In Proceedings of the 59th Annual Conference Protective Relay Engineers, College Station, TX, USA, 4–6 April 2006; pp. 164–176. [Google Scholar]
- Ohura, Y.; Matsuda, T.; Suzuki, M.; Andow, F.; Kurosawa, Y.; Takeuchi, A. A digital distance relay using negative sequence current. IEEE Trans. Power Deliv. 1990, 5, 79–84. [Google Scholar]

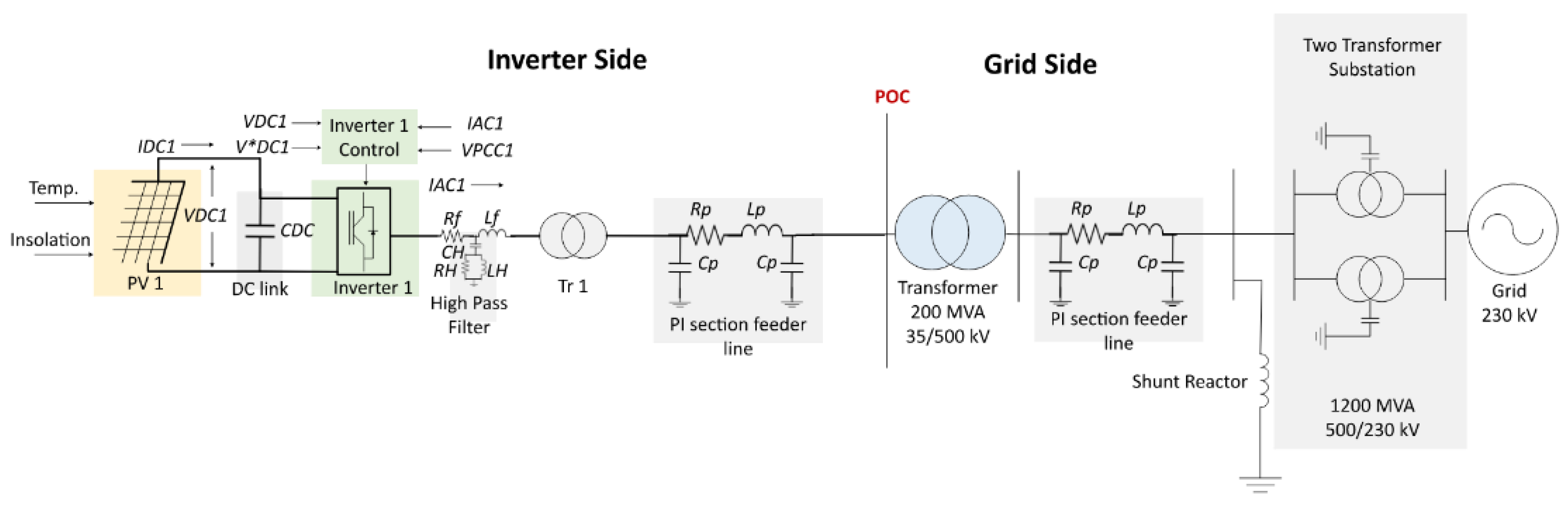
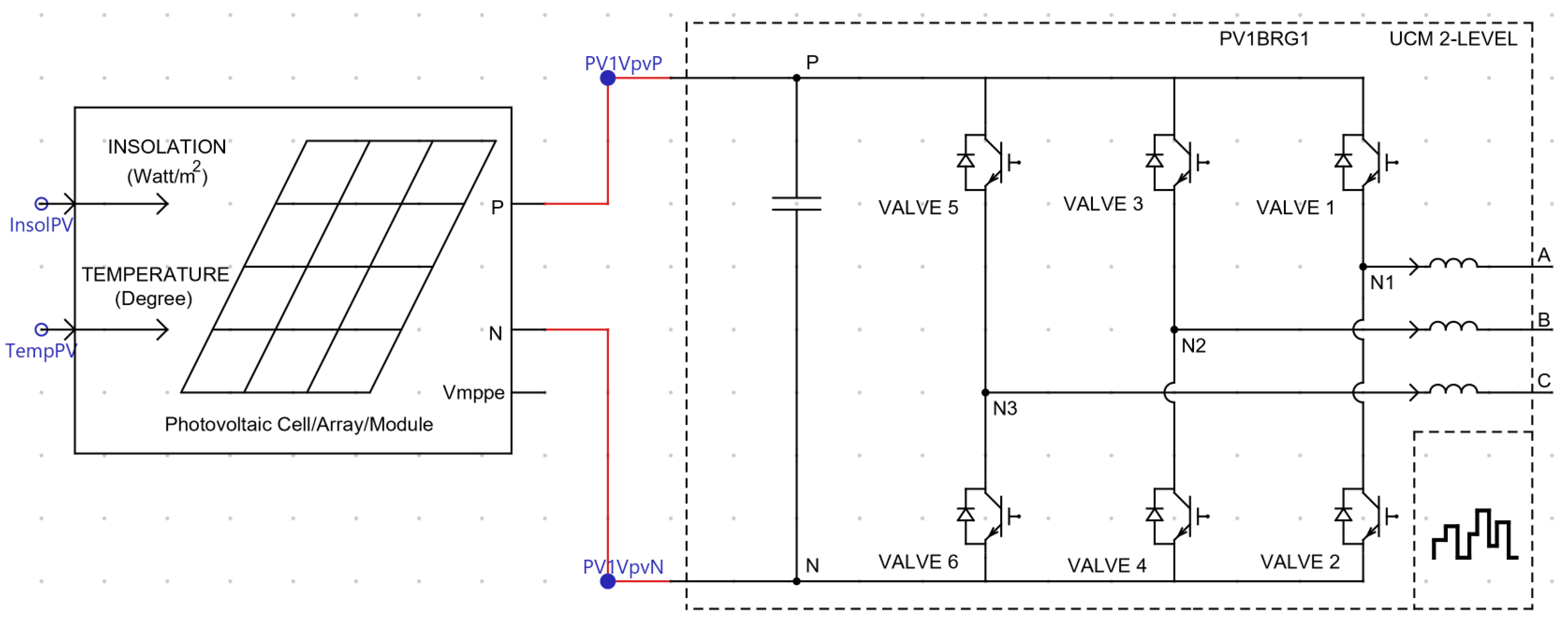
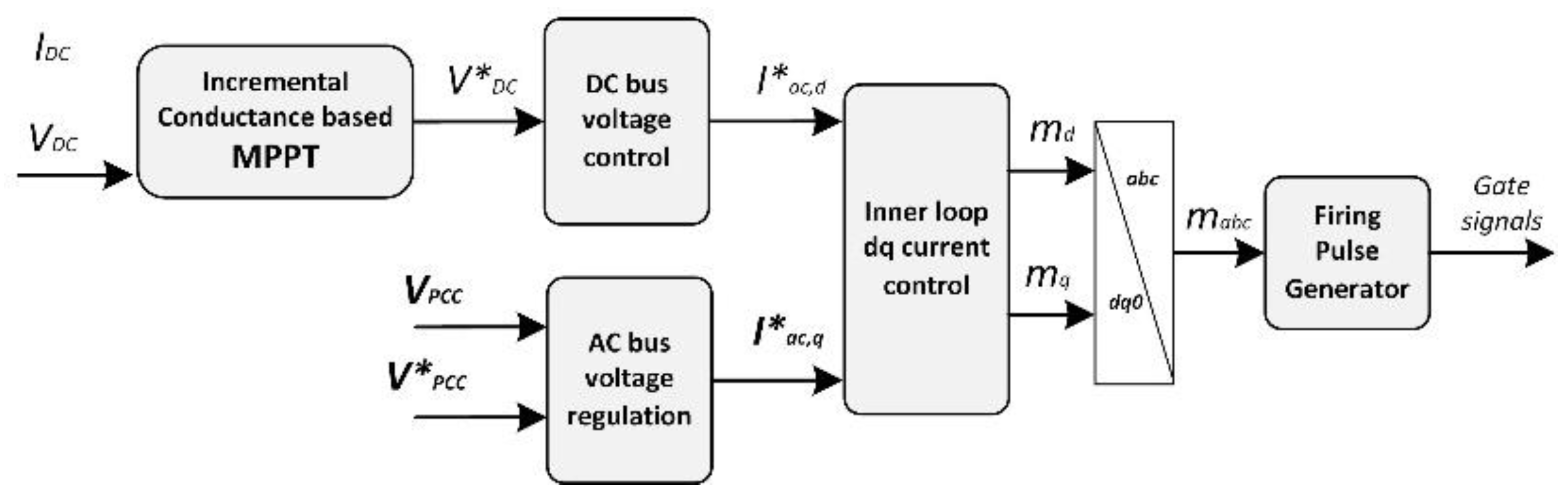




| Components | Parameters | Values |
|---|---|---|
| Step-up Transformer | High Voltage Low Voltage Transformer Rating | 500 kV 35 kV 200 MVA |
| Transmission line | Shunt reactor rating | 498 MVAR |
| Resistance Inductance Capacitance Line Length | 3.80 Ω 0.202 H 2.92 µF 226 km | |
| Step-up Substation | Tertiary Cap Bank Capacitance | 138 μF |
| High Voltage Low Voltage Tertiary Voltage Transformer Rating | 500 kV 230 kV 48 kV 1200 MVA | |
| Grid source | Series Resistance Parallel Resistance Parallel Inductance | 0.84 Ω 120.14 Ω 0.0322 H |
| Voltage (L-L, RMS) Real Power Reactive Power | 230 kV 1600 MW 73 MVAR |
| Components | Parameters | Values |
|---|---|---|
| PV | Number of series cells Number of parallel strings Open circuit voltage Short circuit current Number of modules in series Number of modules in parallel Voltage at Pmax Current at Pmax | 36 1 21.7 V 3.35 A 115 285 17.4 V 3.05 A |
| DC link capacitor | Capacitance | 0.01925 F |
| Inverter | Snubber series capacitance Snubber series resistance | 0.01 μF 800 Ω |
| AC reactor resistance AC reactor inductance | 1 μΩ 80 μH | |
| High pass filter | Resistance Capacitance | 0.039 Ω 7.874 μF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekic, A.; Wu, D.; Jiang, J.N. Impact of Solar Inverter Dynamics during Grid Restoration Period on Protection Schemes Based on Negative-Sequence Components. Energies 2022, 15, 4360. https://doi.org/10.3390/en15124360
Ekic A, Wu D, Jiang JN. Impact of Solar Inverter Dynamics during Grid Restoration Period on Protection Schemes Based on Negative-Sequence Components. Energies. 2022; 15(12):4360. https://doi.org/10.3390/en15124360
Chicago/Turabian StyleEkic, Almir, Di Wu, and John N. Jiang. 2022. "Impact of Solar Inverter Dynamics during Grid Restoration Period on Protection Schemes Based on Negative-Sequence Components" Energies 15, no. 12: 4360. https://doi.org/10.3390/en15124360
APA StyleEkic, A., Wu, D., & Jiang, J. N. (2022). Impact of Solar Inverter Dynamics during Grid Restoration Period on Protection Schemes Based on Negative-Sequence Components. Energies, 15(12), 4360. https://doi.org/10.3390/en15124360






