Improved Body Force Model for Estimating Off-Design Axial Compressor Performance
Abstract
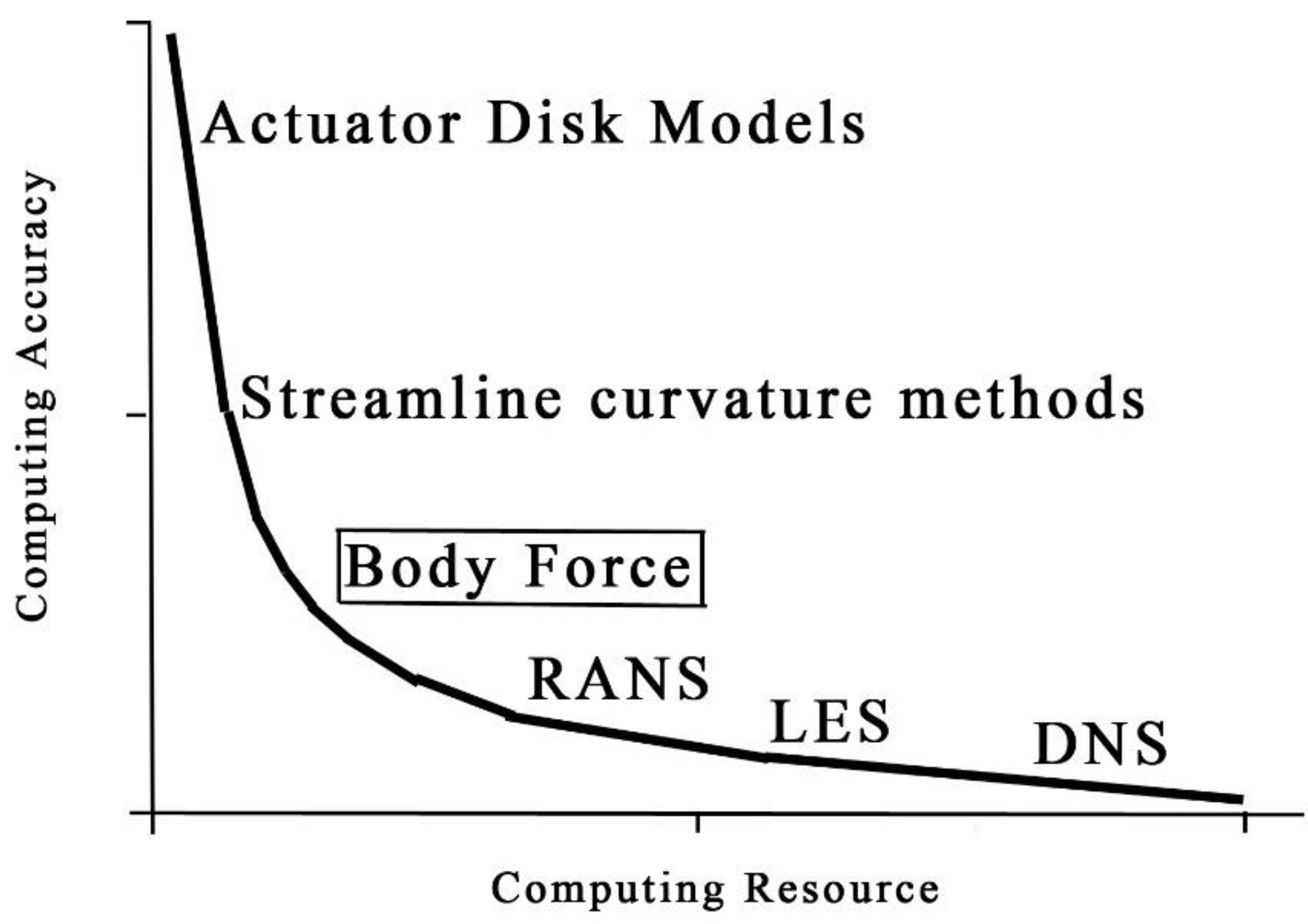
1. Introduction
2. Improved Body Force Model
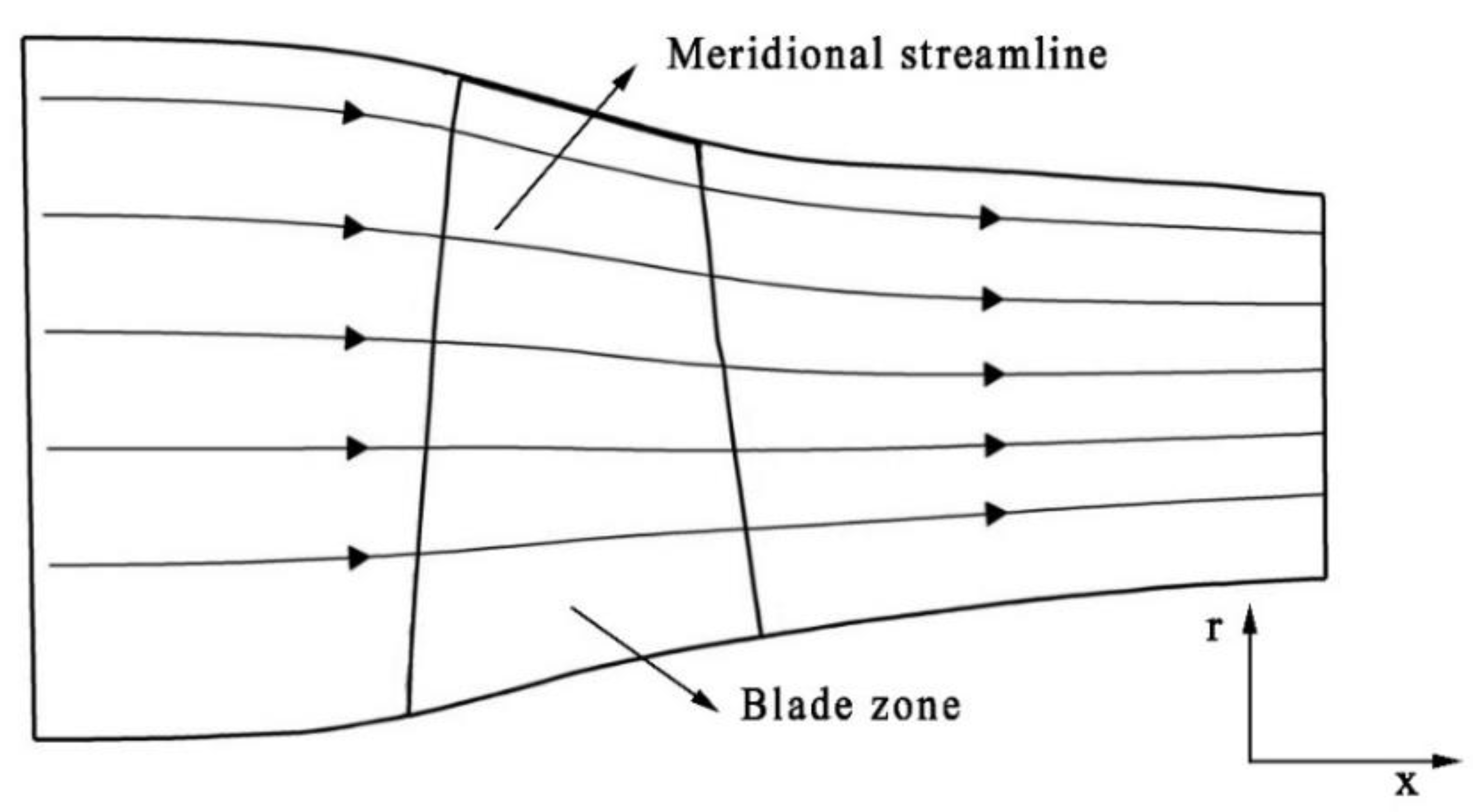
2.1. Governing Equation
2.2. Construction of the Body Force
2.2.1. Normal Body Force
2.2.2. Parallel Body Force
3. Computational Case and Numerical Techniques
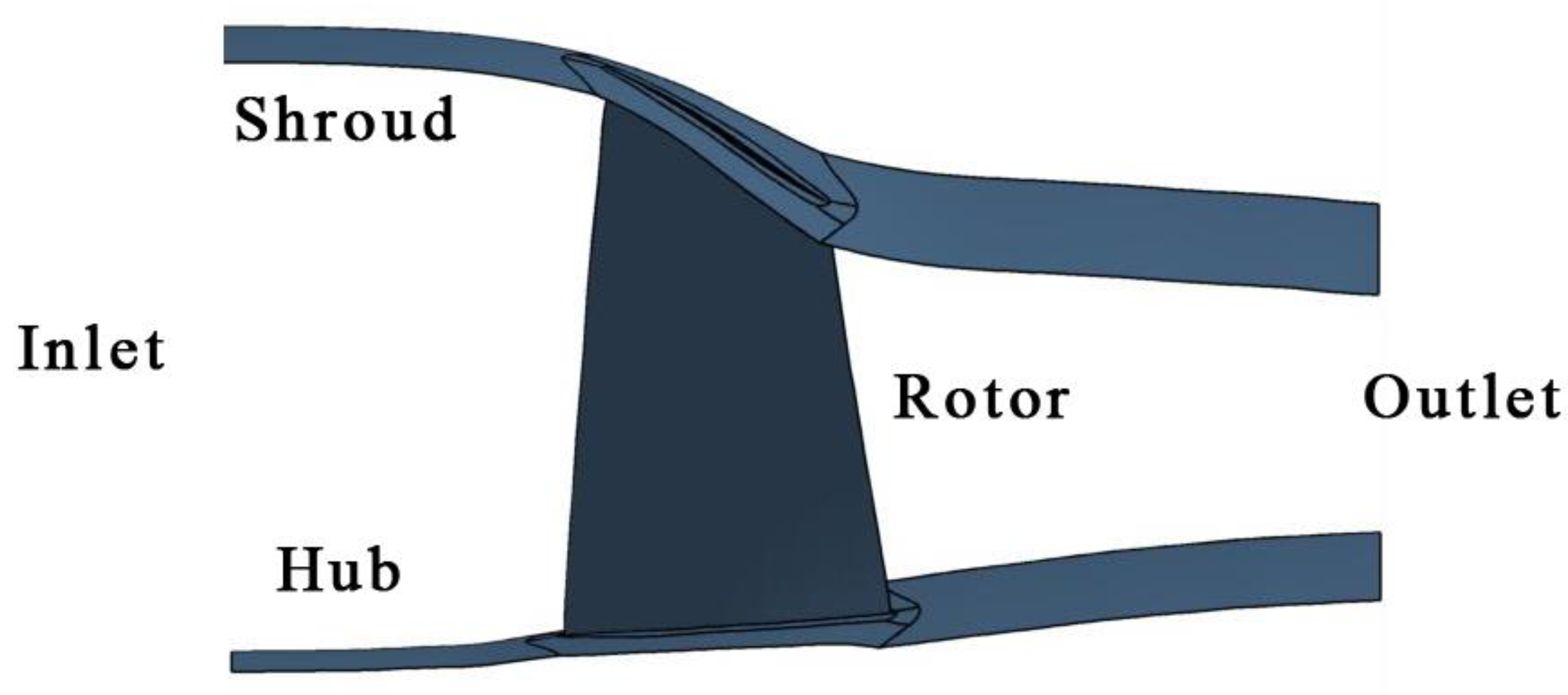
3.1. Compressor Used for Study
3.2. CFD Methods
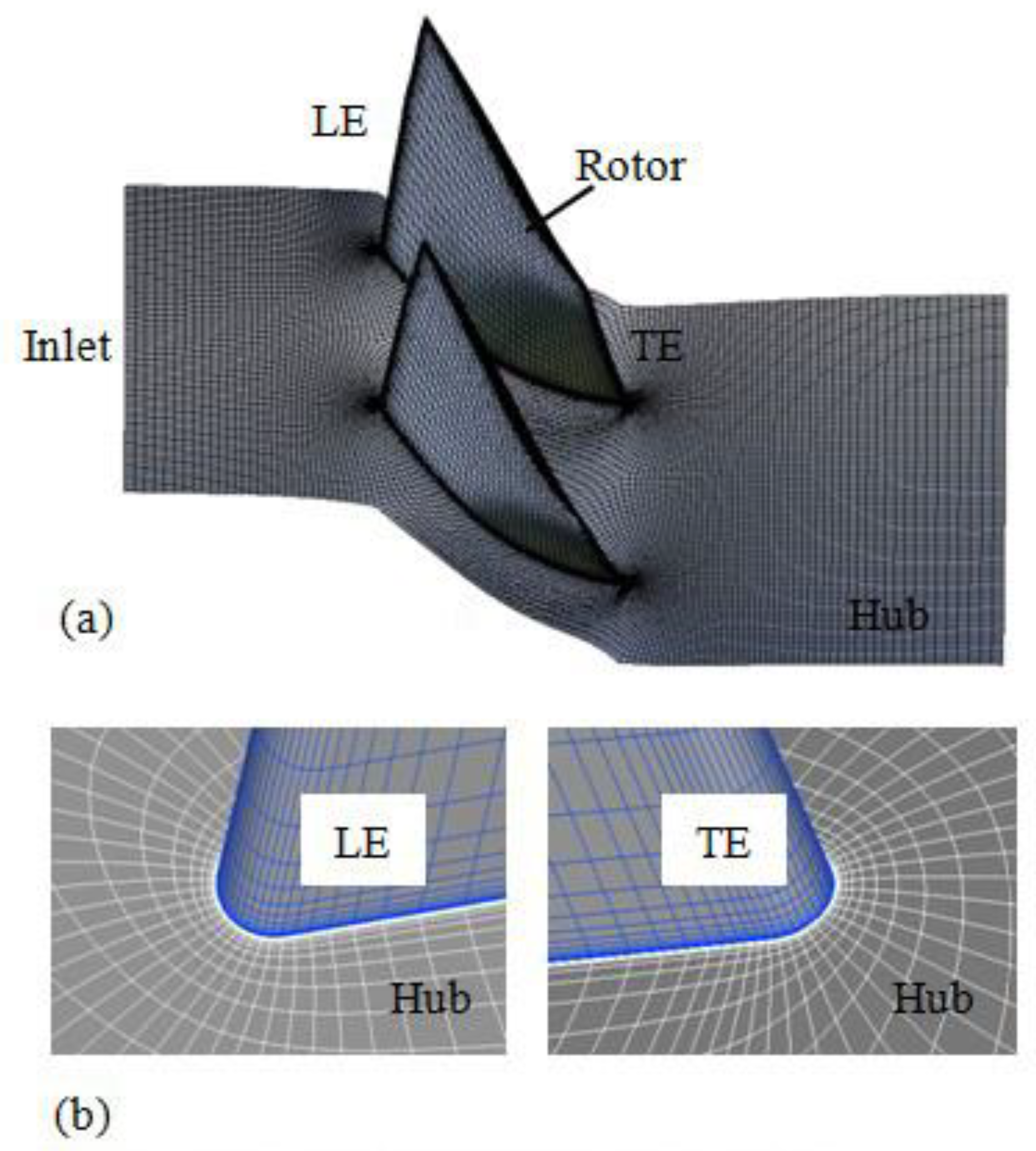
3.2.1. Turbomachinery Flow Simulation
3.2.2. HMNF Flow Simulation
4. Model Validation
5. Conclusions
- Based on the COMSOL software, the improved body force model could directly simulate the viscous flow close to the blade passage walls and the momentum exchange between fluids. The improved parallel force formula is modified using Marble’s results, indicating that the magnitude of the parallel force is proportional to the entropy gradient along the meridional streamline extracted from 3D steady single-passage RANS solutions. Therefore, the modeling process of the body force is easier and more physical.
- The improved normal force formula no longer contains the term g(ṁlocal), which makes the simulation processes more efficient. Compared with those of NUMECA FINE, the total number of grid points for the HMNF module is less at least an order of magnitude, and it takes less time to compute them. The simulation results for the Rotor 37 indicate that the improved body force model could capture the flow field through a turbomachinery blade row well within a proper accuracy range. When 3D, full-annulus, unsteady, multi-row calculations through the compressor or integrated calculations of the aircraft and engine were performed, the improved body forces could be substituted into the RANS equations as the source terms instead of the actual blade rows, and it could greatly reduce the total number of grid points and save significant computer resources, including CPU time and memory.
- Because body forces are added into the governing equations as source terms, the improved body force formula was defined at grid points of the body force domain. The COMSOL software could easily and accurately translate the body force formula inputs extracted from solutions solved by the NUMECA FINE-Turbo EURANUS to grid points of the body force domain. The COMSOL software environment can easily facilitate all steps in the modeling, part definition, meshing, simulation, and data post processing processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ricci, M.; Mosele, S.G.; Benvenuto, M.; Astrua, P.; Pacciani, R.; Marconcini, M. Retrofittable Solutions Capability for Gas Turbine Compressors. Int. J. Turbomach. Propuls. Power 2022, 7, 3. [Google Scholar] [CrossRef]
- Burberi, C.; Michelassi, V.; del Greco, A.S.; Lorusso, S.; Tapinassi, L.; Marconcini, M.; Pacciani, R. Validation of steady and unsteady CFD strategies in the design of axial compressors for gas turbine engines. Aerosp. Sci. Technol. 2020, 107, 106307. [Google Scholar] [CrossRef]
- Li, Y.L.; Sayma, A.I. Computational fluid dynamics simulations of blade damage effect on the performance of a transonic axial compressor near stall. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2242–2260. [Google Scholar] [CrossRef]
- Jian, H.; Hu, W. Numerical Investigation of Inlet Distortion on an Axial Flow Compressor Rotor with Circumferential Groove Casing Treatment. Chin. J. Aeronaut. 2008, 21, 496–505. [Google Scholar] [CrossRef][Green Version]
- Shen, X.B.; Wang, H.F.; Lin, G.P.; Bu, X.Q.; Wen, D.S. Unsteady simulation of aircraft electro-thermal deicing process with temperature-based method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 388–400. [Google Scholar] [CrossRef]
- Sun, H.O.; Wang, M.; Wang, Z.Y.; Magagnato, F. Numerical investigation of surge prediction in a transonic axial compressor with a hybrid BDF/Harmonic Balance Method. Aerosp. Sci. Technol. 2019, 90, 401–409. [Google Scholar] [CrossRef]
- Hu, Y.; Nie, C. Exploration of combined adjustment laws about IGV, stator and rotational speed in off-design conditions in an axial compressor. Sci. China Technol. Sci. 2010, 53, 969–975. [Google Scholar] [CrossRef]
- Chu, F.; Dai, B.; Lu, N.; Ma, X.; Wang, F. Improved fast model migration method for centrifugal compressor based on bayesian algorithm and Gaussian process model. Sci. China Technol. Sci. 2018, 61, 1950–1958. [Google Scholar] [CrossRef]
- Webster, R.; Sreenivas, K.; Hyams, D.; Hilbert, B.; Briley, W.; Whitfield, D. Demonstration of Sub-system Level Simulations: A Coupled Inlet and Turbofan Stage. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar]
- Li, S.; Liu, Y.; Omidi, M.; Zhang, C.; Li, H. Numerical Investigation of Transient Flow Characteristics in a Centrifugal Compressor Stage with Variable Inlet Guide Vanes at Low Mass Flow Rates. Energies 2021, 14, 7906. [Google Scholar] [CrossRef]
- Gong, Y. A Computational Model for Rotating Stall Inception and Inlet Distortions in Multistage Compressors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Hsiao, E.; Naimi, M.; Lewis, J.P.; Dalbey, K.; Gong, Y.; Tan, C. Actuator duct model of turbomachinery components for powered-nacelle Navier-Stokes calculations. J. Propuls. Power 2001, 17, 919–927. [Google Scholar] [CrossRef]
- Hyoungjin, K.; Mengsing, L. Flow simulation of N3X hybrid wing body configuration. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Kim, H.; Liou, M.-S. Optimal Shape Design of Mail-Slot Nacelle on N3-X Hybrid Wing Body Configuration. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2413. [Google Scholar]
- Qiushi, L.; Yongzhao, L.; Tianyu, P.; Da, L.; Ha’nan, L.; Yifang, G. Development of a coupled supersonic inlet-fan Navier–Stokes simulation method. Chin. J. Aeronaut. 2018, 31, 237–246. [Google Scholar]
- Marble, F.E.; Hawthorne, W. Three-dimensional flow in turbomachines. High Speed Aerodyn. Jet Propuls. 1964, 10, 83–166. [Google Scholar]
- Xu, L. Assessing viscous body forces for unsteady calculations. J. Turbomach. 2003, 125, 425–432. [Google Scholar] [CrossRef]
- Ritos, K.; Kokkinakis, I.W.; Drikakis, D. Performance of High-Order Implicit Large Eddy Simulations. Comput. Fluids 2018, 173, 307–312. [Google Scholar] [CrossRef]
- Lange, M.; Vogeler, K.; Mailach, R.; Gomez, S.E. An experimental verification of a new design for cantilevered stators with large hub clearances. J. Turbomach. 2013, 135, 041022. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W.; Wu, C.; Ren, S. Effects of tip clearance size on the performance and tip leakage vortex in dual-rows counter-rotating compressor. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1953–1965. [Google Scholar] [CrossRef]
- Zhu, Y.; Luo, J.; Liu, F. Flow computations of multi-stages by URANS and flux balanced mixing models. Sci. China Technol. Sci. 2018, 61, 1081–1091. [Google Scholar] [CrossRef]


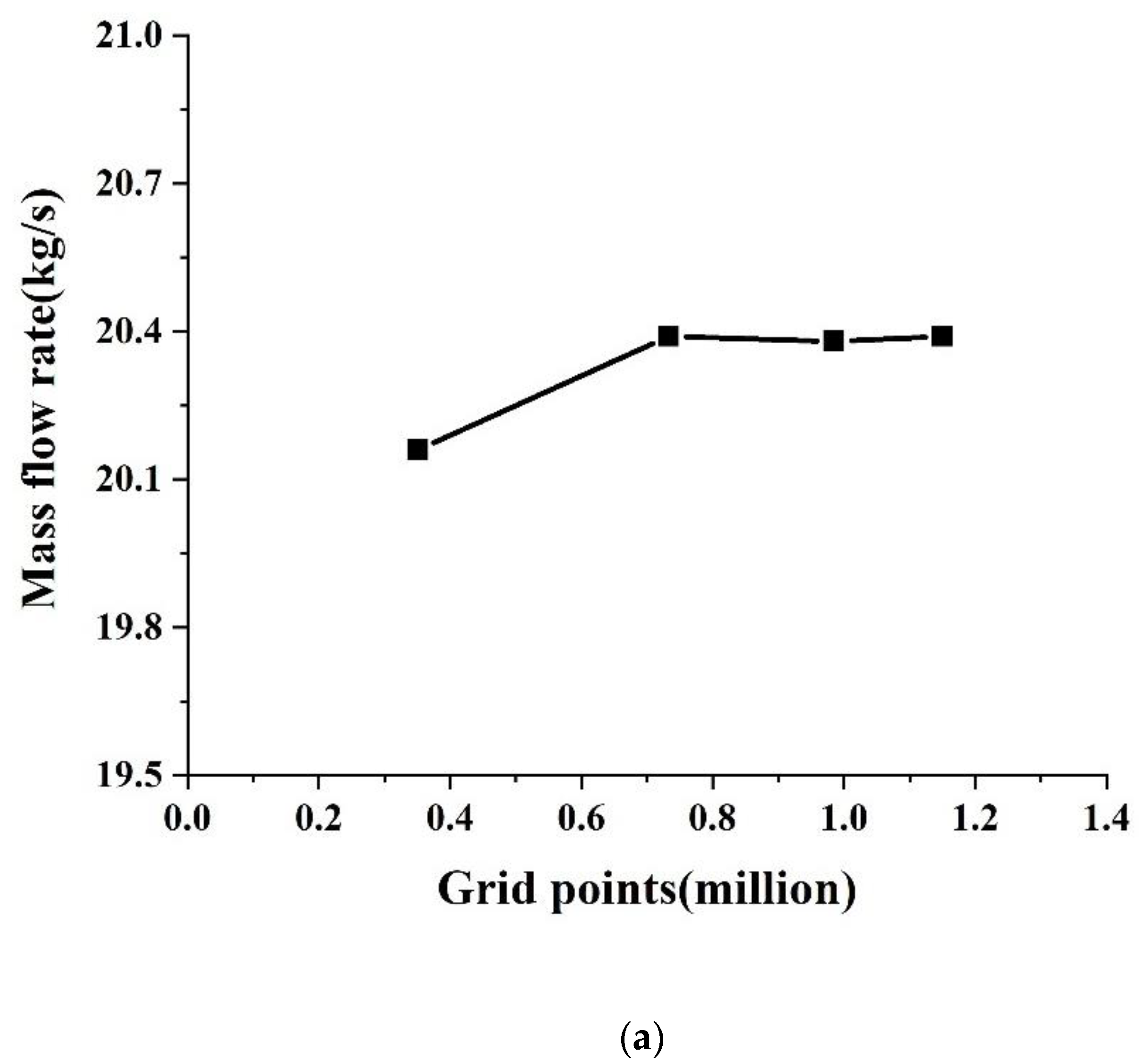
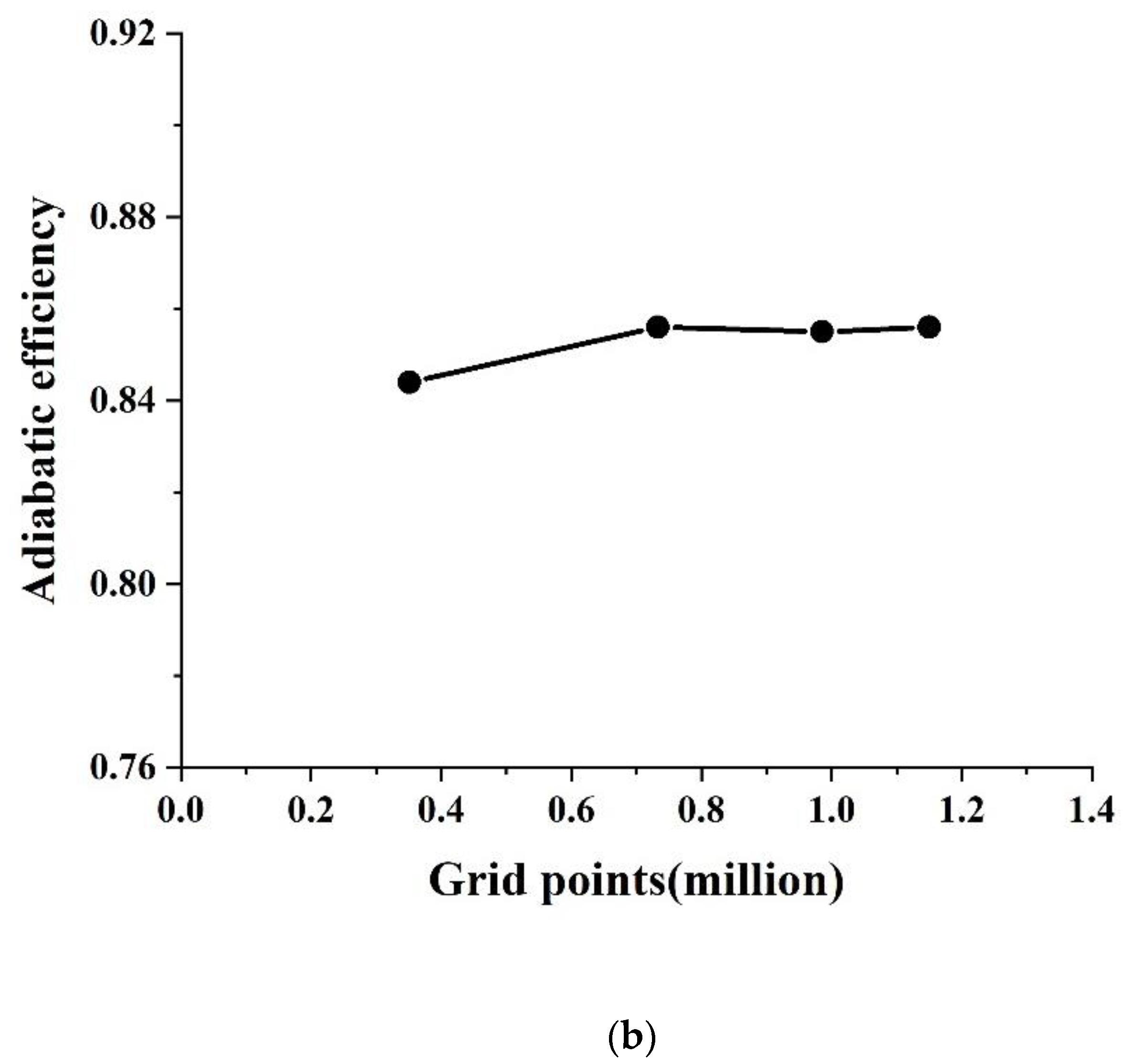

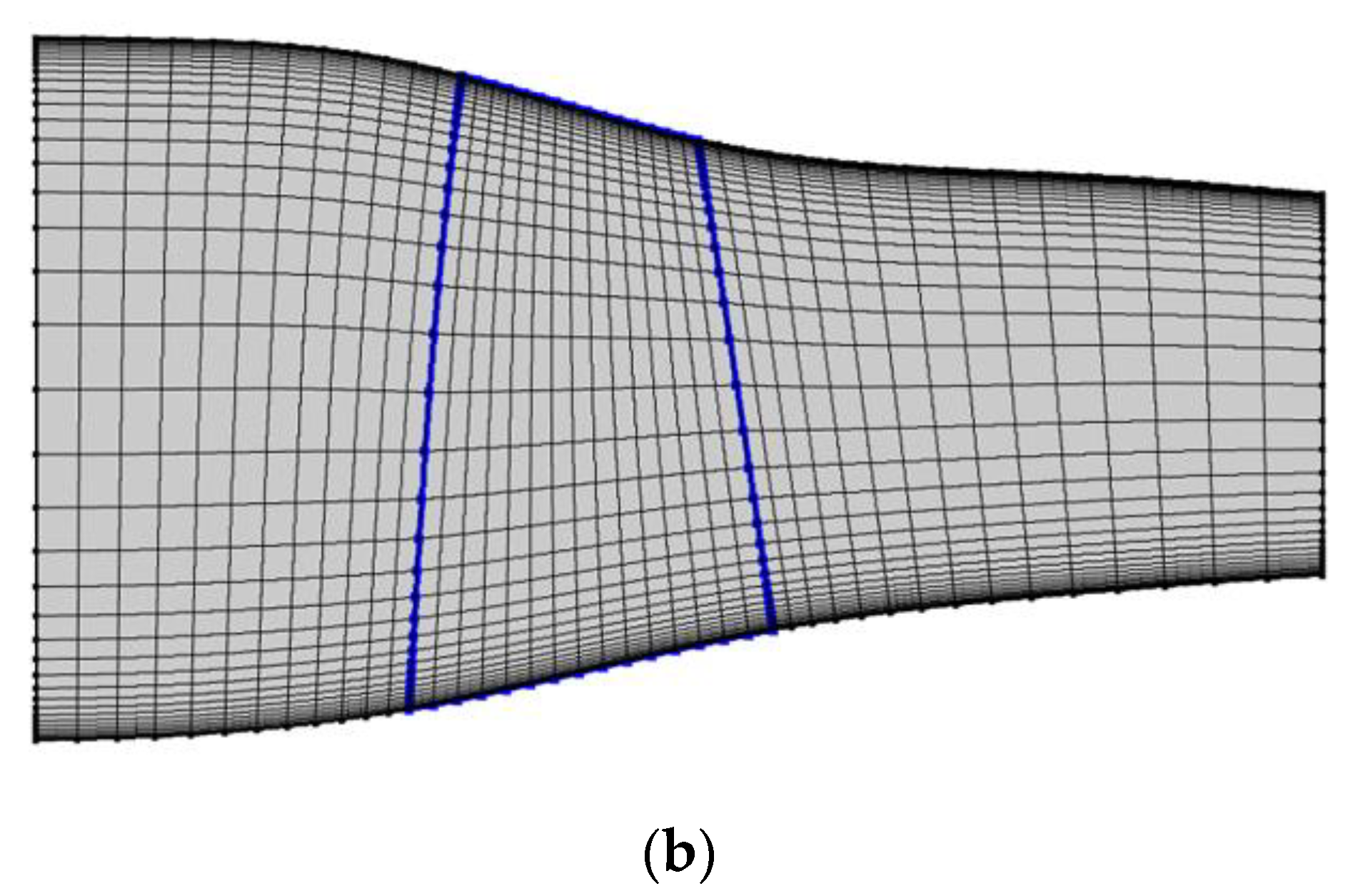

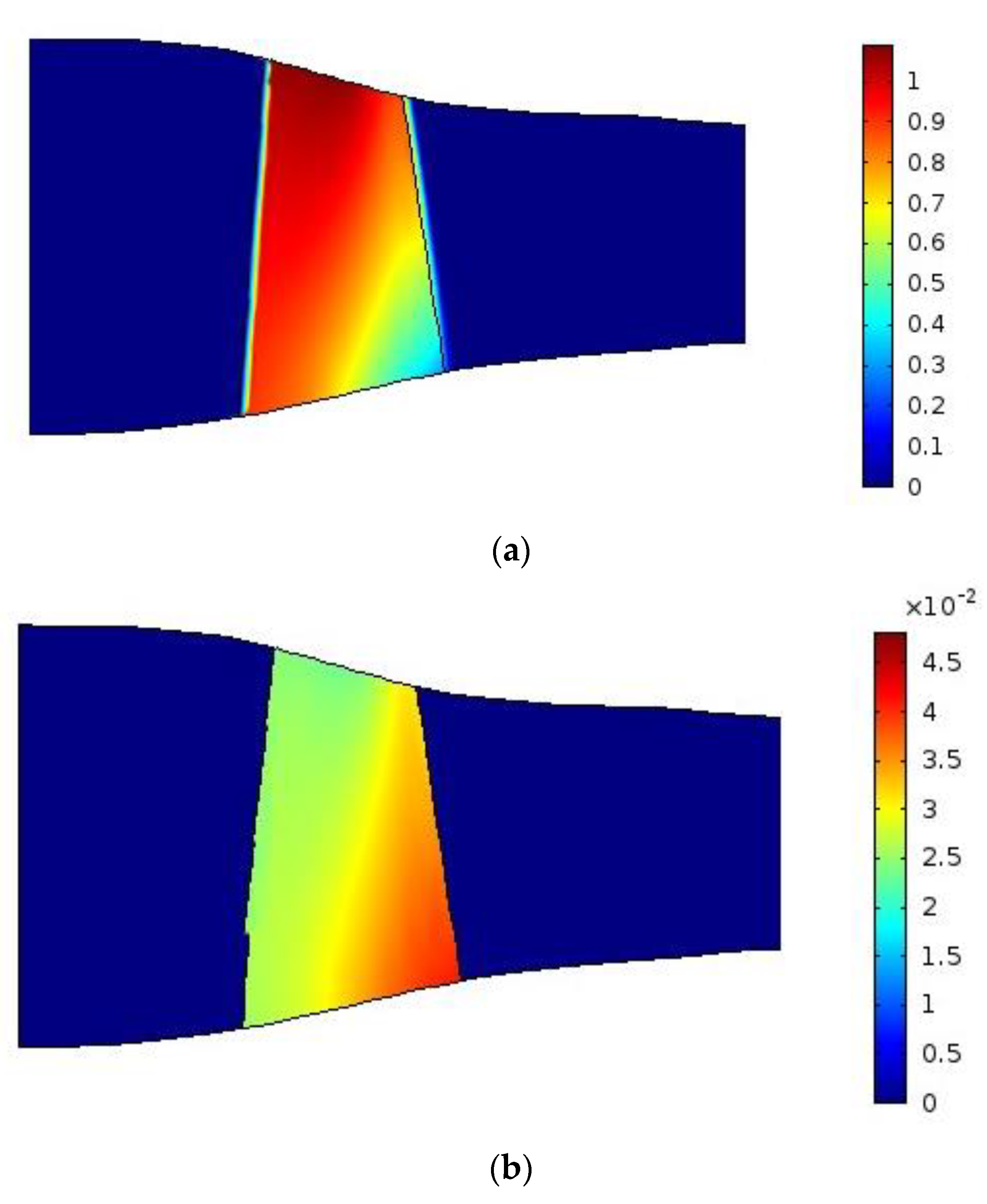

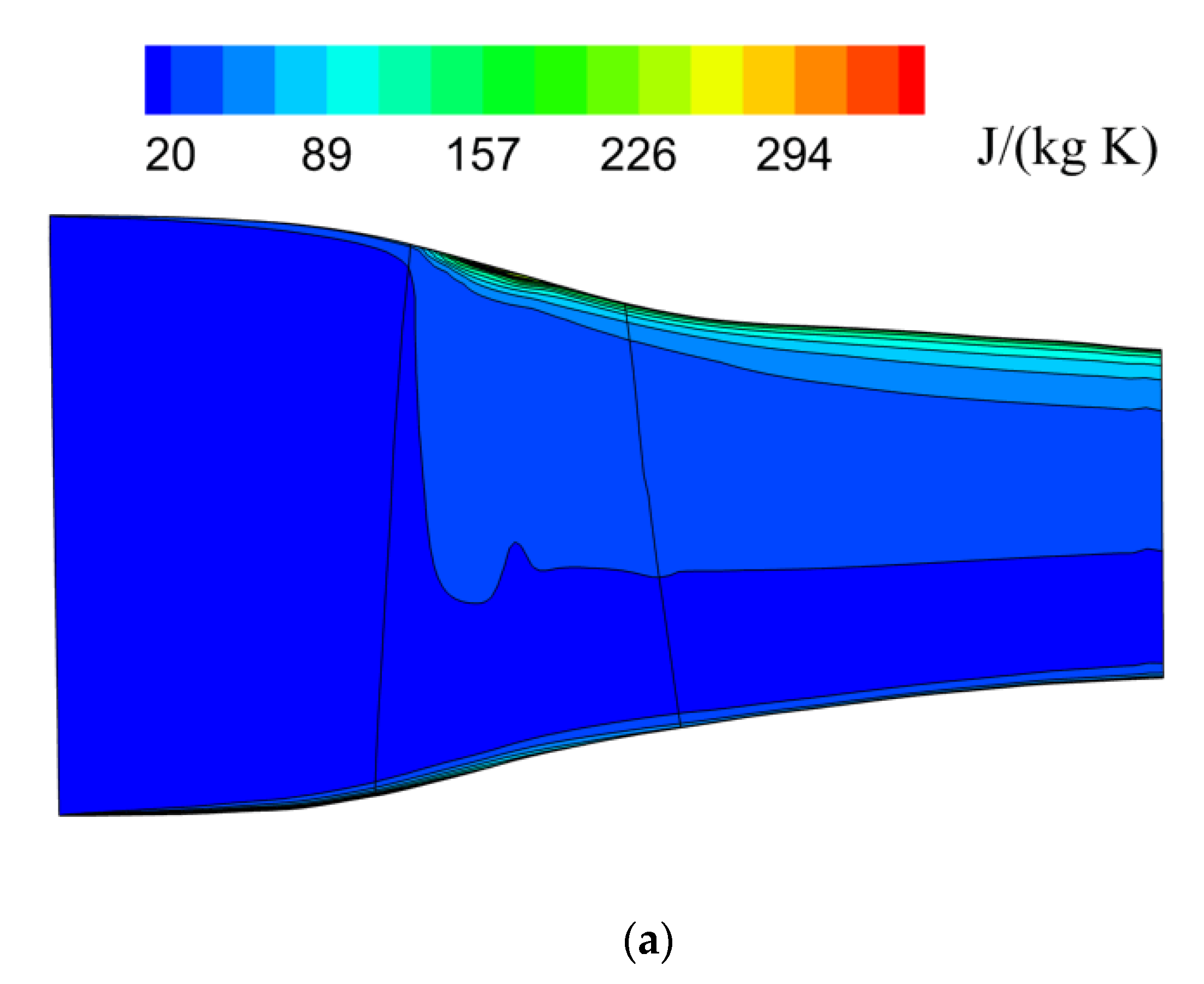

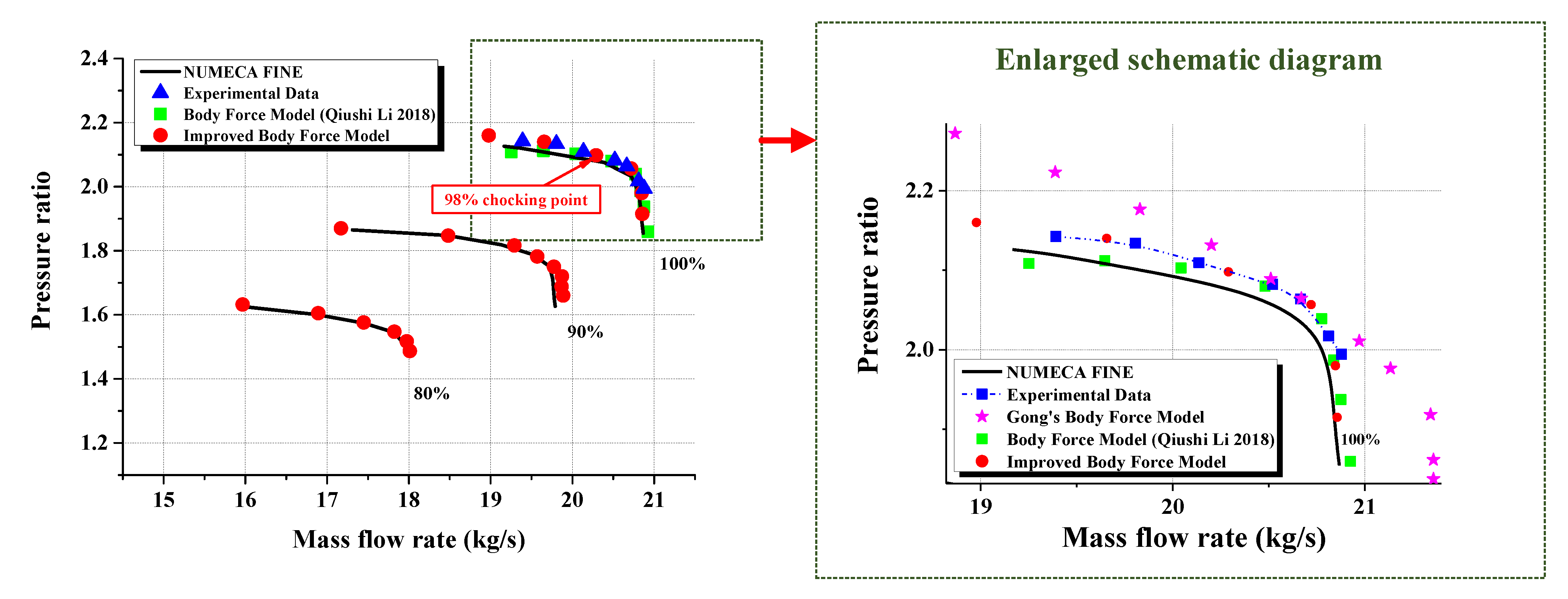
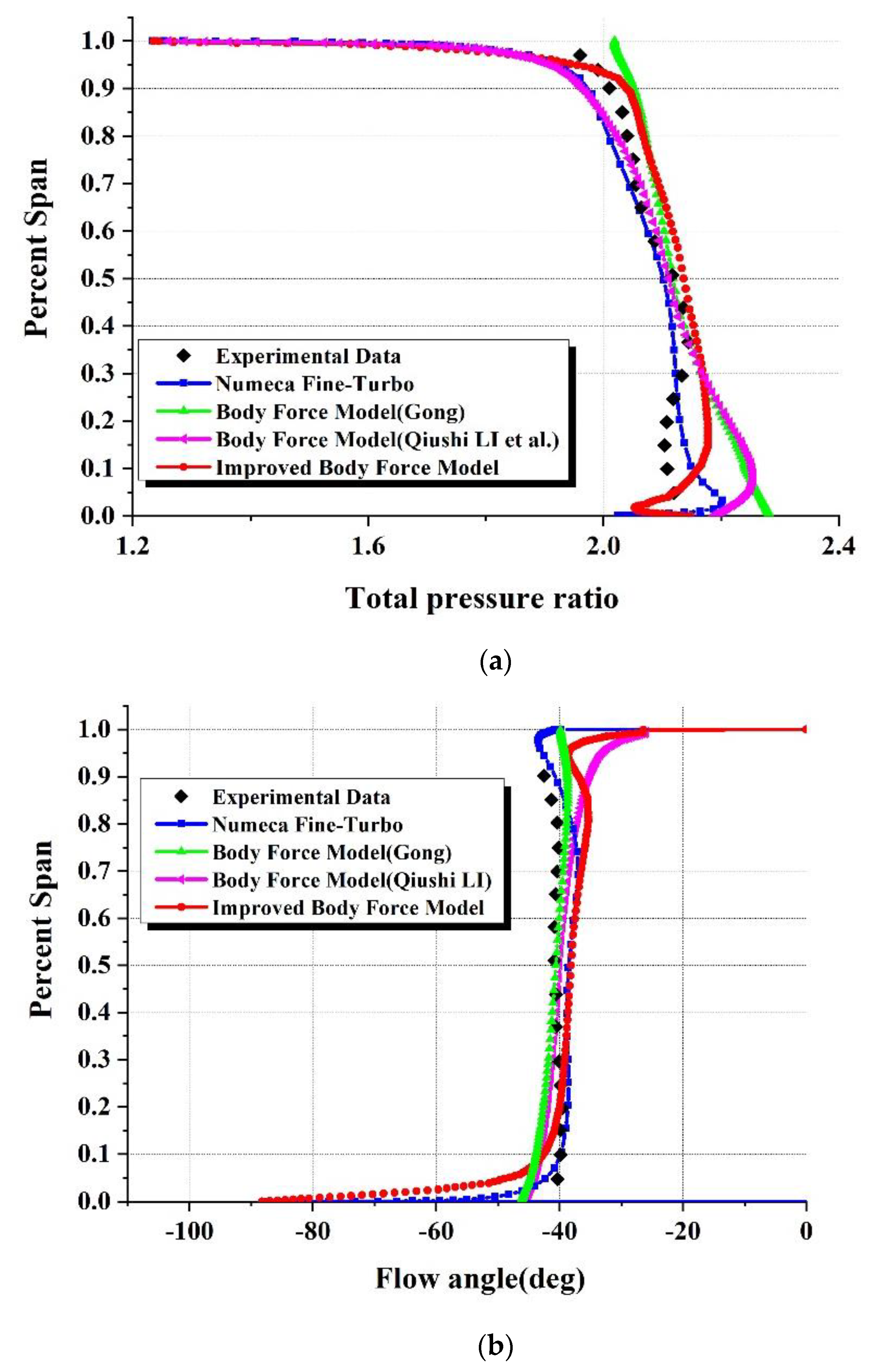

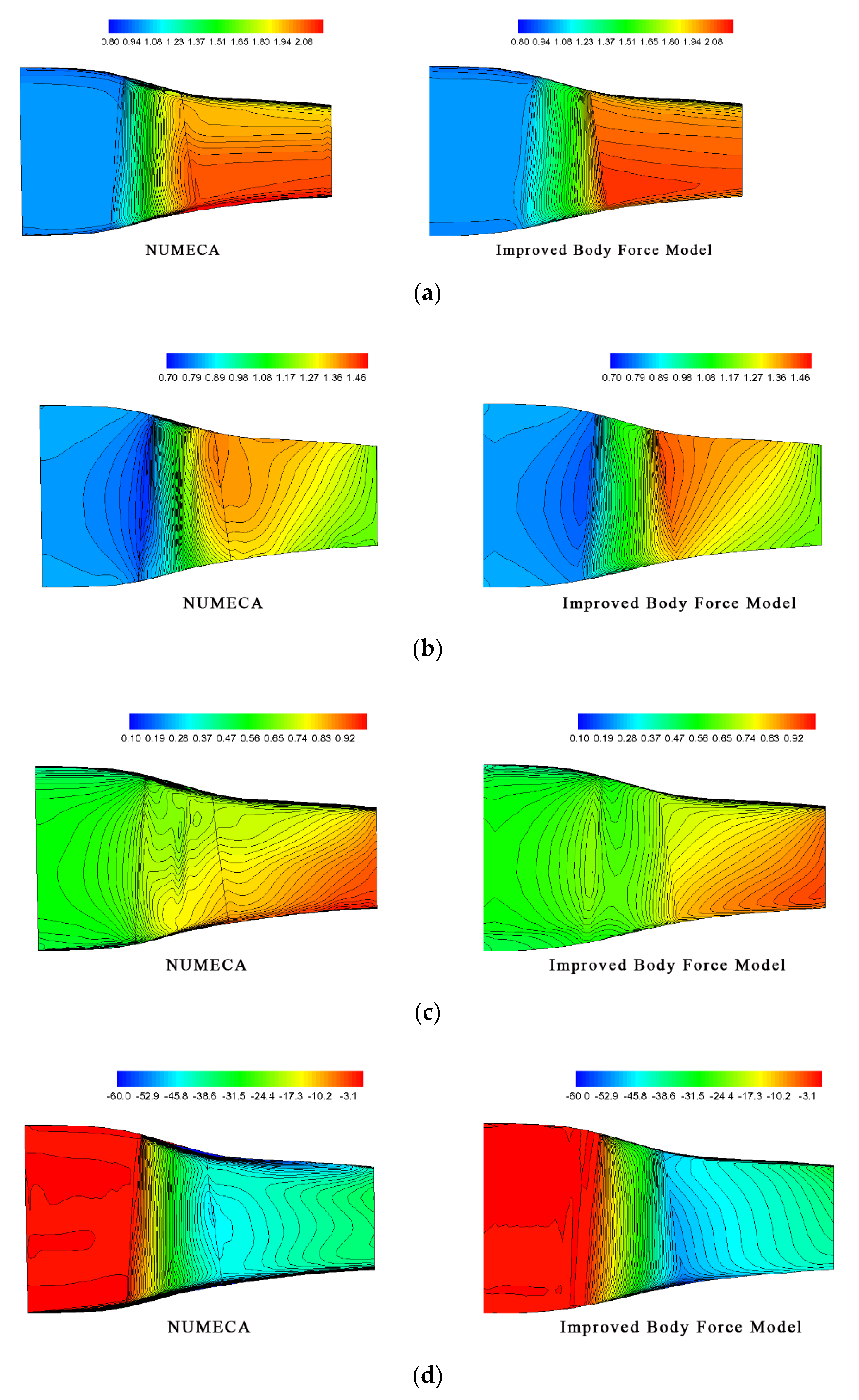
| Parameters | Value |
|---|---|
| Blade number | 36 |
| Inlet hub-to-tip ratio | 0.7 |
| Blade aspect ratio | 1.19 |
| Tip solidity | 1.29 |
| Tip relative inlet Ma | 1.48 |
| Rotating speed (rpm) | 17,188 |
| Mass flow rate (kg/s) | 20.19 |
| Total pressure ratio | 2.106 |
| Adiabatic efficiency (%) | 87.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Lv, Y.; Xia, A.; Zhang, S.; Tuo, W.; Xue, H.; Sun, Y.; He, X. Improved Body Force Model for Estimating Off-Design Axial Compressor Performance. Energies 2022, 15, 4389. https://doi.org/10.3390/en15124389
Huang J, Lv Y, Xia A, Zhang S, Tuo W, Xue H, Sun Y, He X. Improved Body Force Model for Estimating Off-Design Axial Compressor Performance. Energies. 2022; 15(12):4389. https://doi.org/10.3390/en15124389
Chicago/Turabian StyleHuang, Jia, Yongzhao Lv, Aiguo Xia, Shengliang Zhang, Wei Tuo, Hongtao Xue, Yantao Sun, and Xiuran He. 2022. "Improved Body Force Model for Estimating Off-Design Axial Compressor Performance" Energies 15, no. 12: 4389. https://doi.org/10.3390/en15124389
APA StyleHuang, J., Lv, Y., Xia, A., Zhang, S., Tuo, W., Xue, H., Sun, Y., & He, X. (2022). Improved Body Force Model for Estimating Off-Design Axial Compressor Performance. Energies, 15(12), 4389. https://doi.org/10.3390/en15124389






